Quantification and Reduction of Uncertainty in Seismic Resilience Assessment for a Roadway Network
Abstract
:1. Introduction
2. Literature Review
2.1. Transportation Resilience Assessment
2.2. Use of Bayesian Network in Transportation Risk and Resilience Assessment
2.3. Summary
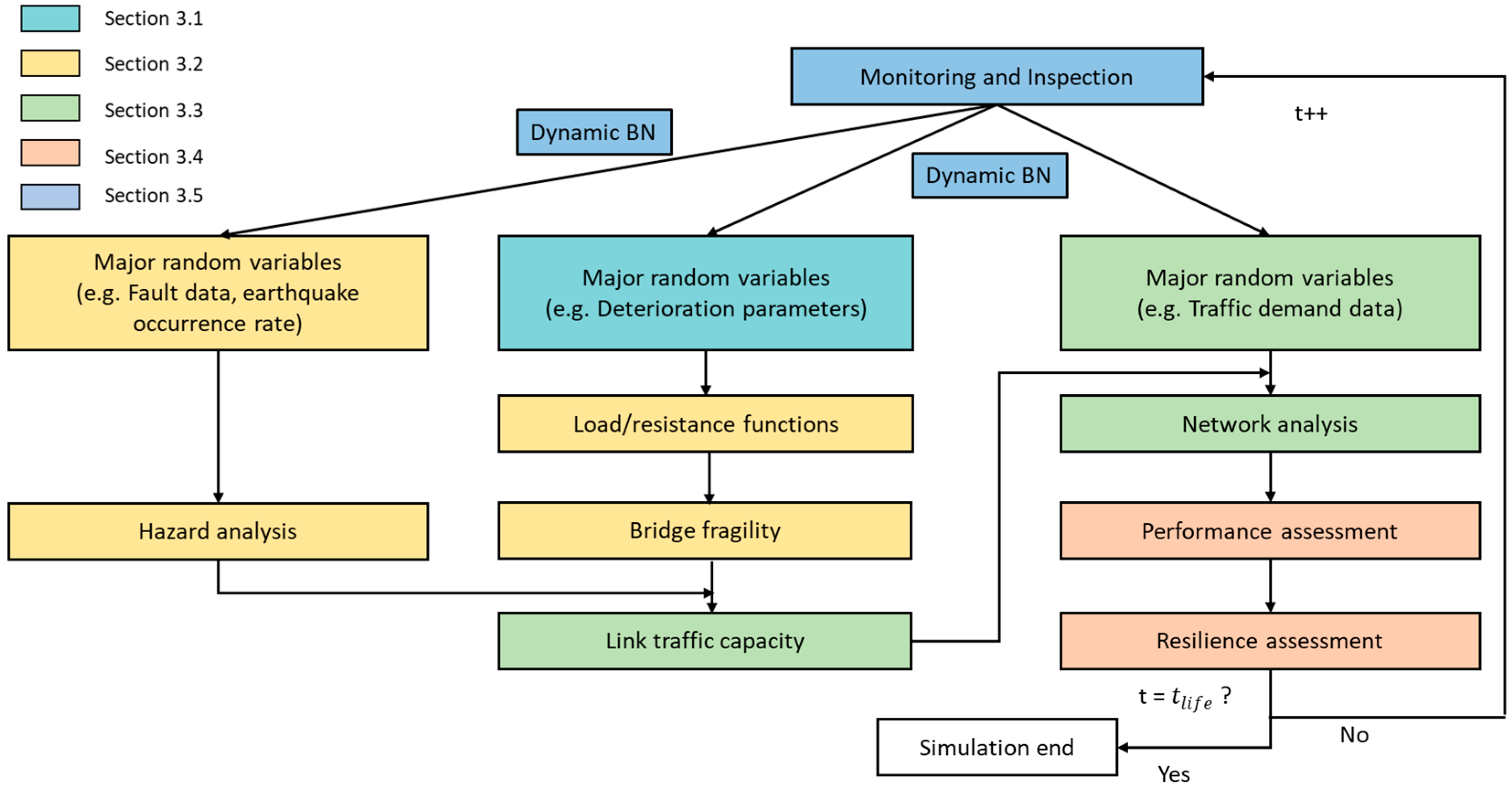
3. Methodology: Dynamic BN-Based Seismic Resilience Assessment Model
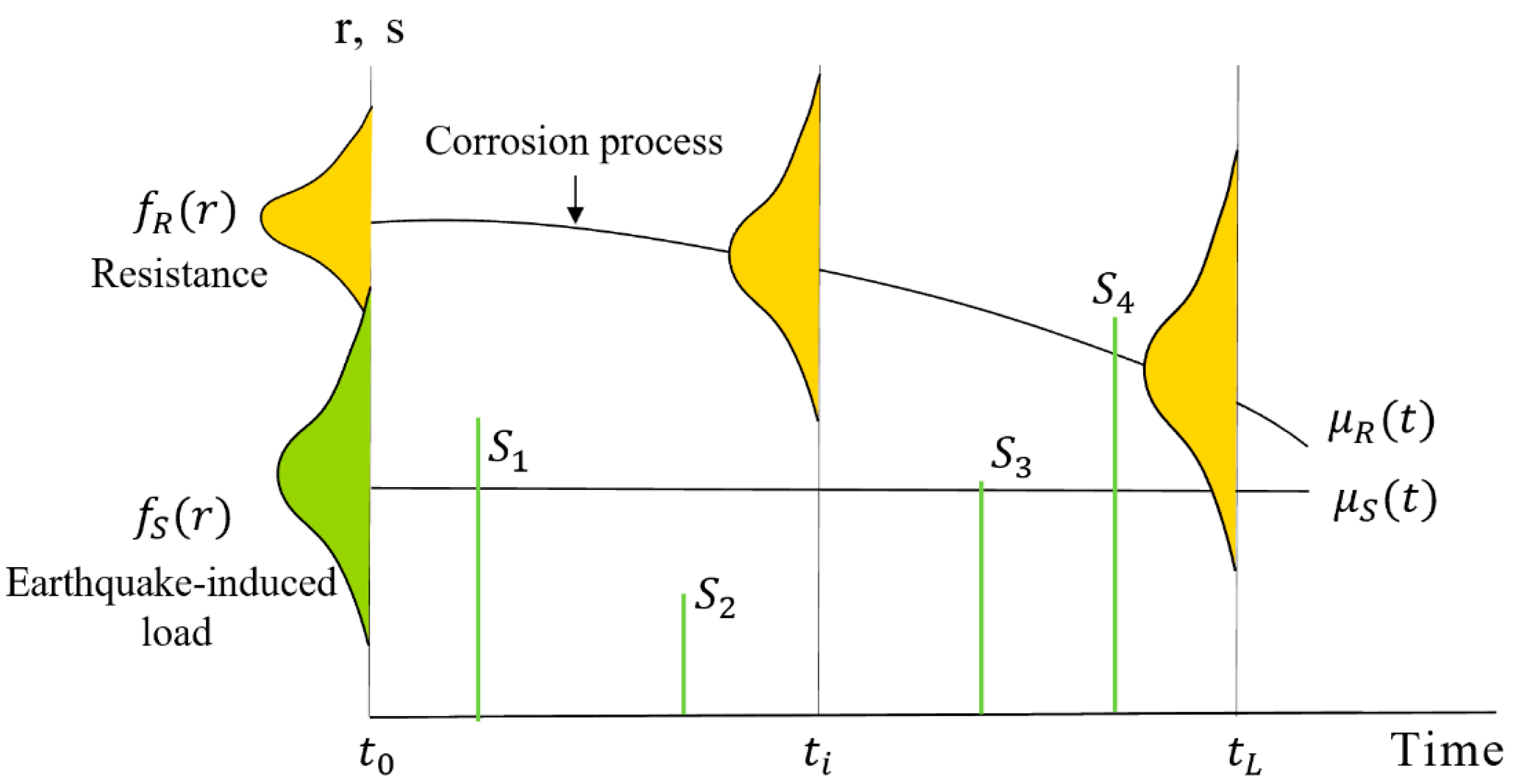
3.1. Time-Dependent Structural Reliability Assessment of Bridges Exposed to Corrosion
3.2. Post-Earthquake Traffic Flow Capacity Assessment of Highway Bridges
3.3. Network Analysis: A Highway Network Involving Multiple Bridges
3.4. Seismic Resilience Assessment of a Highway Network
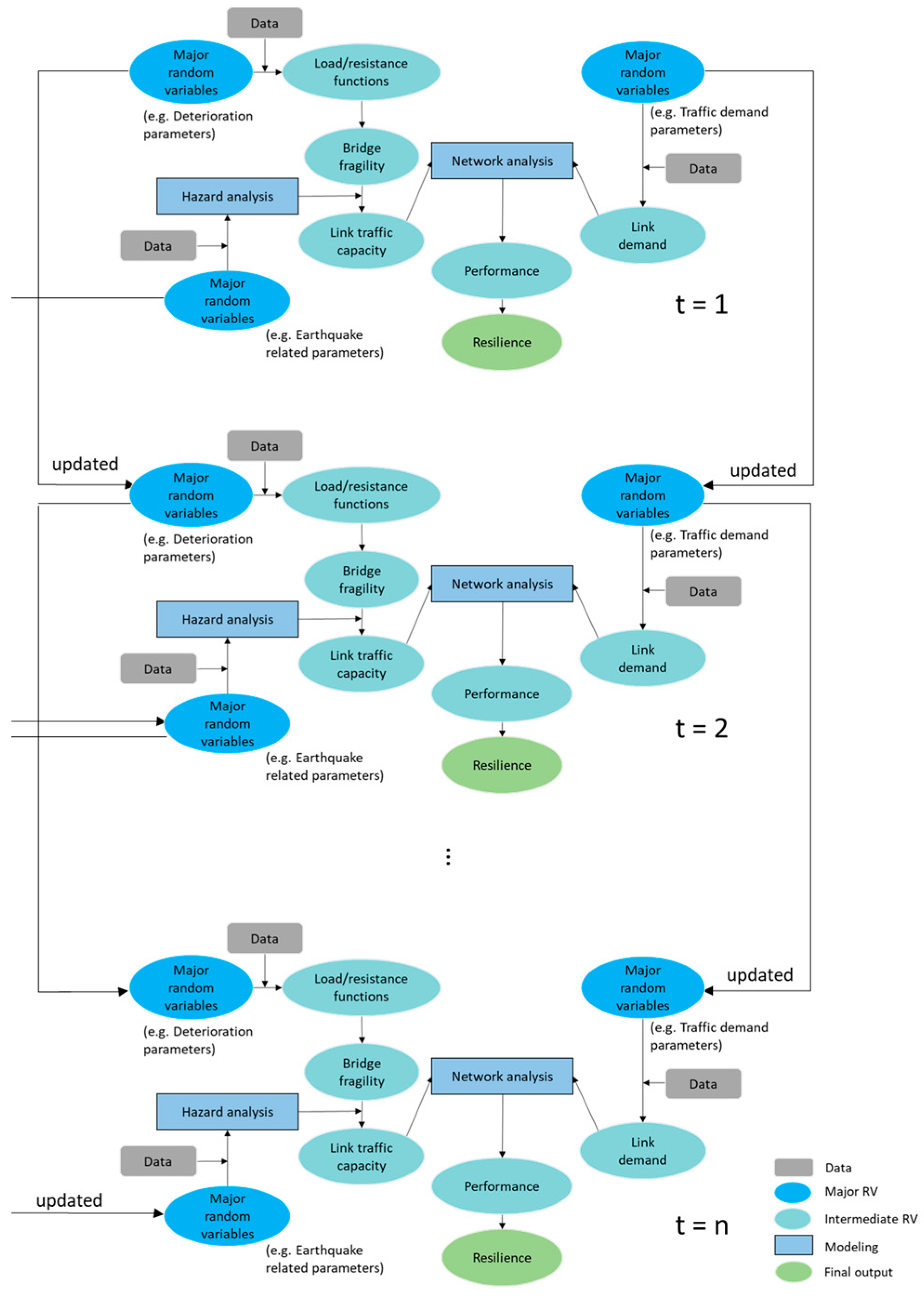
3.5. Uncertainty Quantification and Propagation in Resilience Assessment
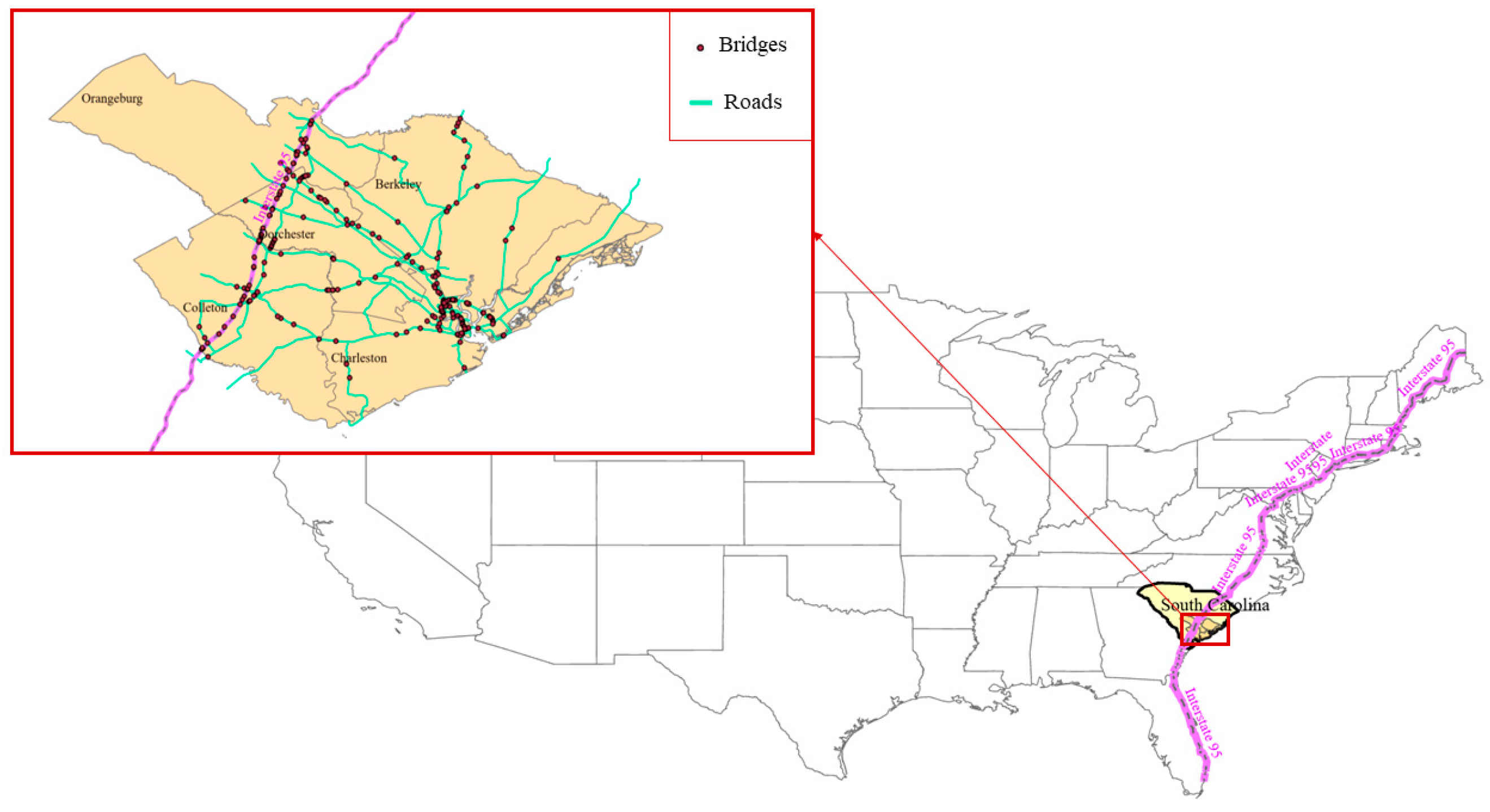
4. Benchmark Problem: A Highway Network in South Carolina, USA
4.1. Overview
4.2. Dynamic Bayesian Updating with Field-Measurement Data
4.3. Network Analysis and Seismic Resilience Assessment
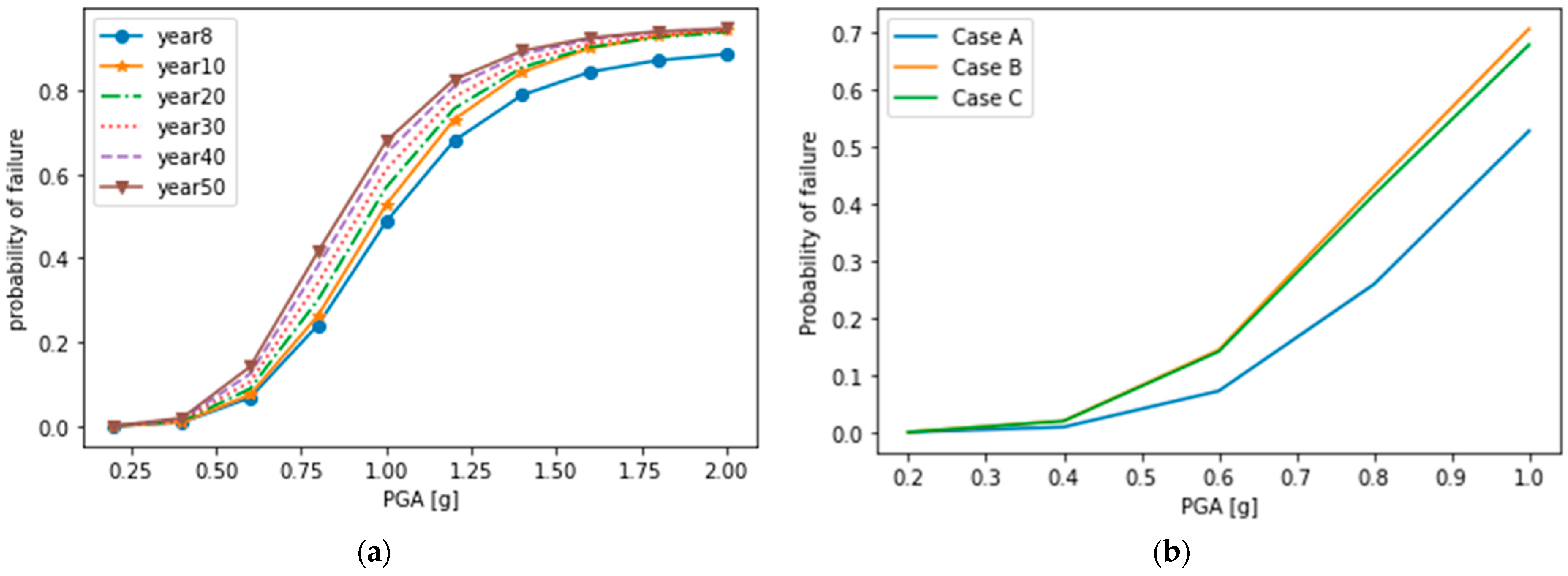
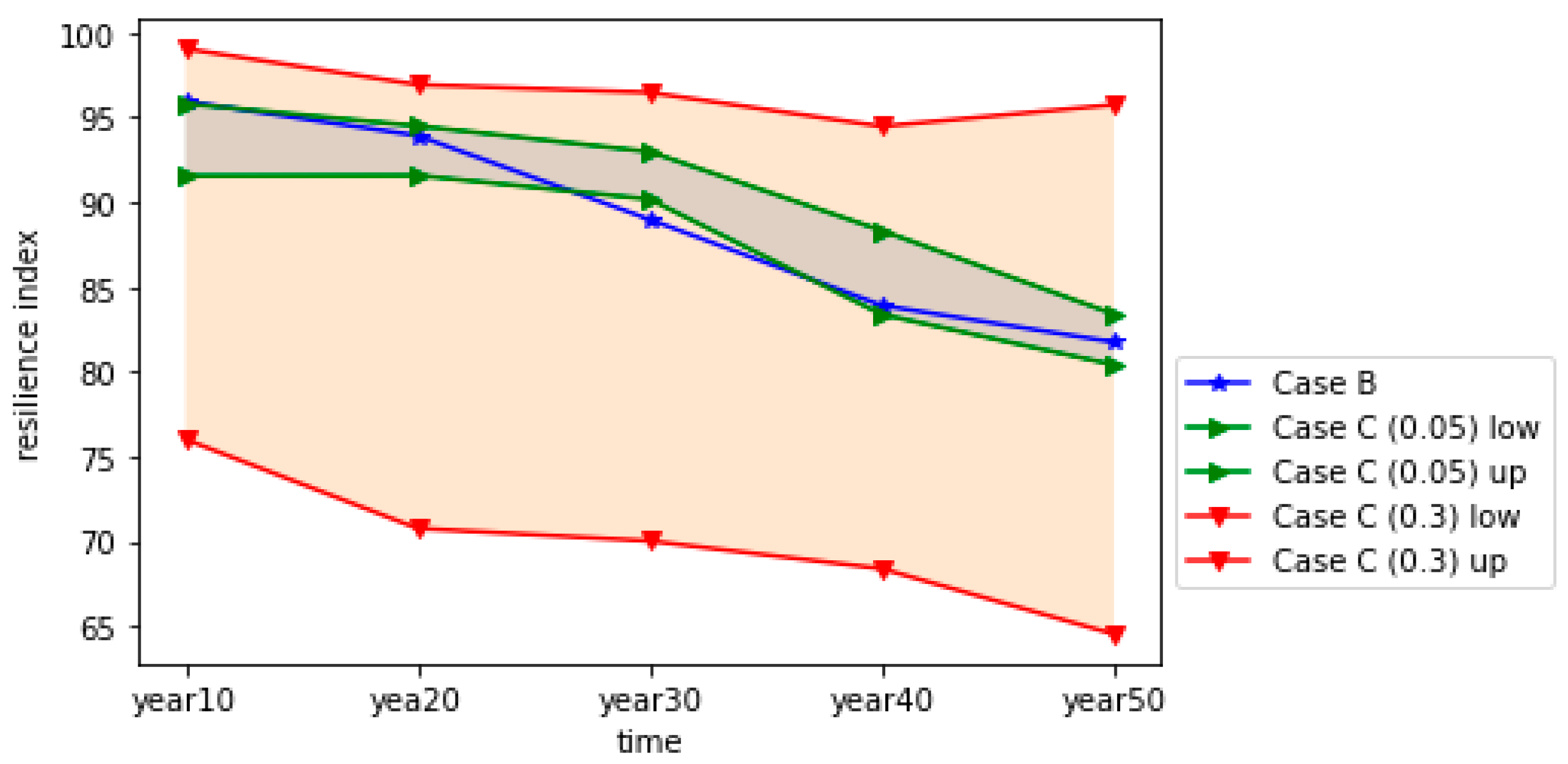
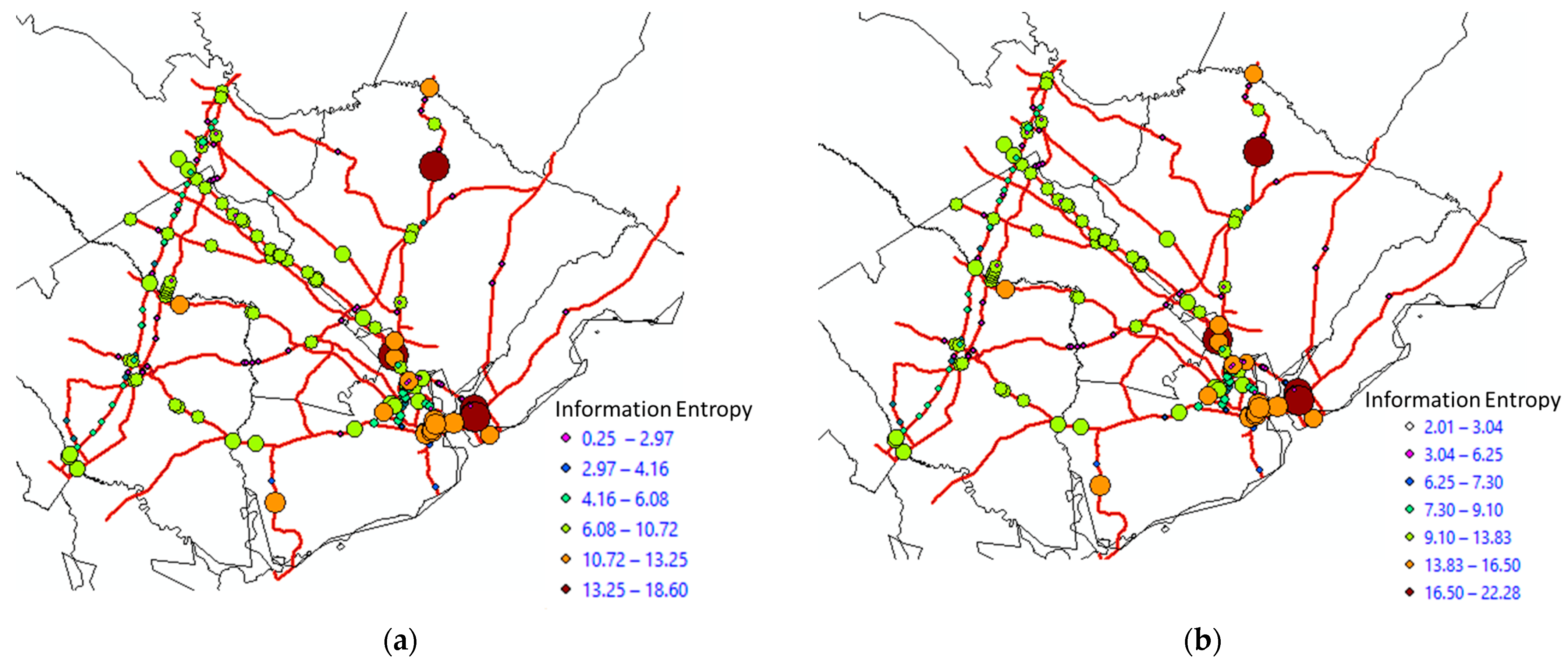
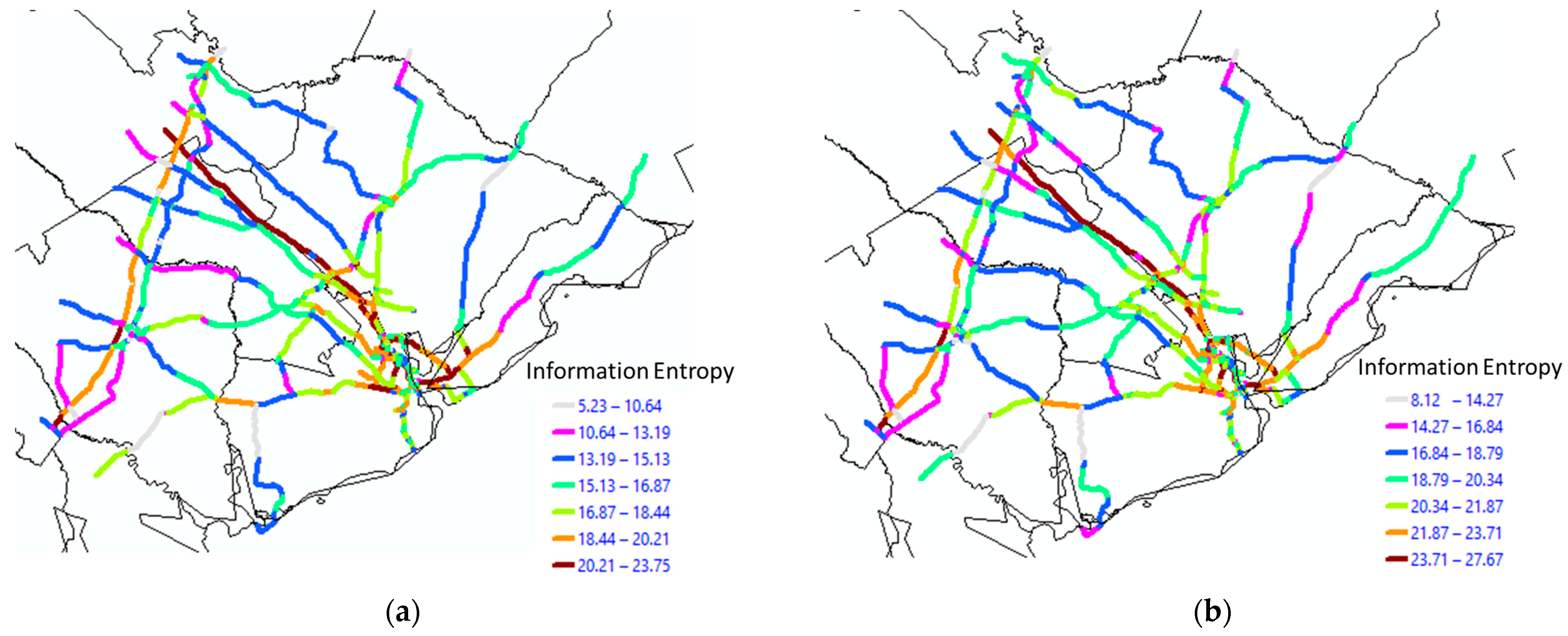
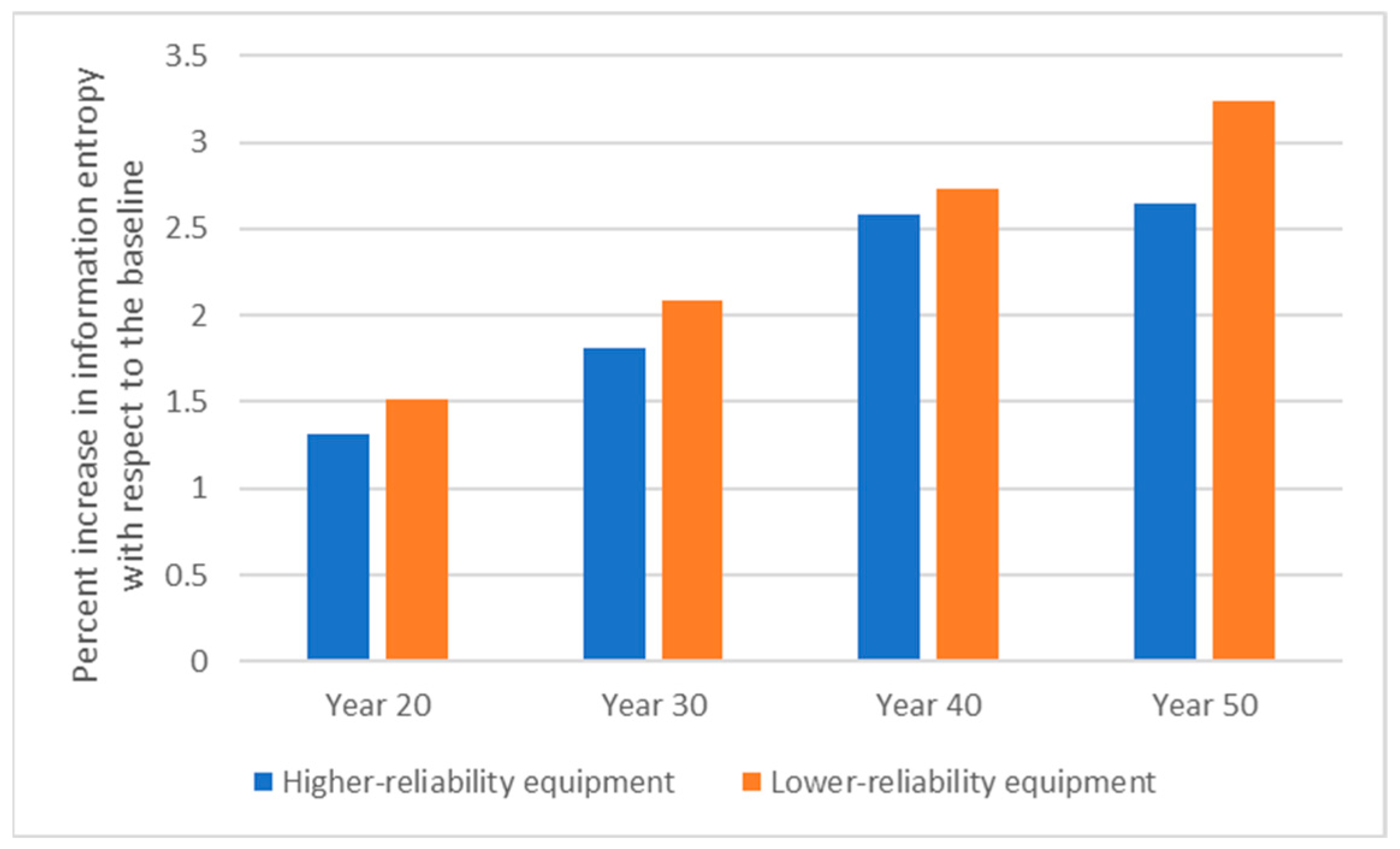
5. Results and Discussion
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Wang, J.; Yang, H. Resilience of transportation systems: Concepts and comprehensive review. IEEE Trans. Intell. Transp. Syst. 2019, 20, 4262–4276. [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; Von Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Chang, S.E.; Shinozuka, M. Measuring improvements in the disaster resilience of communities. Earthq. Spectra 2004, 20, 739–755. [Google Scholar] [CrossRef]
- Bruneau, M.; Reinhorn, A. Overview of the resilience concept. In Proceedings of the 8th U.S. National Conference on Earthquake Engineering, San Francisco, CA, USA, 18–22 April 2006; Volume 2040, pp. 18–22. [Google Scholar]
- Madni, A.M.; Jackson, S. Towards a conceptual framework for resilience engineering. IEEE Syst. J. 2009, 3, 181–191. [Google Scholar] [CrossRef]
- Meerow, S.; Newell, J.P.; Stults, M. Defining urban resilience: A review. Landsc. Urban Plan. 2016, 147, 38–49. [Google Scholar] [CrossRef]
- Bostick, T.P.; Connelly, E.B.; Lambert, J.H.; Linkov, I. Resilience science, policy and investment for civil infrastructure. Reliab. Eng. Syst. Saf. 2018, 175, 19–23. [Google Scholar] [CrossRef]
- Berche, B.; Von Ferber, C.; Holovatch, T.; Holovatch, Y. Resilience of public transport networks against attacks. Eur. Phys. J. B 2009, 71, 125–137. [Google Scholar] [CrossRef]
- Murray-Tuite, P.M. A comparison of transportation network resilience under simulated system optimum and user equilibrium conditions. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; IEEE: New York, NY, USA, 2006; pp. 1398–1405. [Google Scholar]
- Adams, T.M.; Bekkem, K.R.; Toledo-Durán, E.J. Freight resilience measures. J. Transp. Eng. 2012, 138, 1403–1409. [Google Scholar] [CrossRef]
- Ip, W.H.; Wang, D. Resilience evaluation approach of transportation networks. In Proceedings of the 2009 International Joint Conference on Computational Sciences and Optimization, Sanya, China, 24–26 April 2009; IEEE: New York, NY, USA, 2009; Volume 2, pp. 618–622. [Google Scholar]
- Cox, A.; Prager, F.; Rose, A. Transportation security and the role of resilience: A foundation for operational metrics. Transp. Policy 2011, 18, 307–317. [Google Scholar] [CrossRef]
- Liao, T.Y.; Hu, T.Y.; Ko, Y.N. A resilience optimization model for transportation networks under disasters. Nat. Hazards 2018, 93, 469–489. [Google Scholar] [CrossRef]
- Zhang, X.; Miller-Hooks, E.; Denny, K. Assessing the role of network topology in transportation network resilience. J. Transp. Geogr. 2015, 46, 35–45. [Google Scholar] [CrossRef]
- Ganin, A.A.; Kitsak, M.; Marchese, D.; Keisler, J.M.; Seager, T.; Linkov, I. Resilience and efficiency in transportation networks. Sci. Adv. 2017, 3, e1701079. [Google Scholar] [CrossRef]
- Ouyang, M.; Dueñas-Osorio, L.; Min, X. A three-stage resilience analysis framework for urban infrastructure systems. Struct. Saf. 2012, 36, 23–31. [Google Scholar] [CrossRef]
- Zhao, J.; Lee, J.Y.; Wolcott, M.P. Multi-component resilience assessment framework for transportation systems. In Proceedings of the 13th International Conference on Structural Safety and Reliability 2022, Shanghai, China, 20–24 June 2021. [Google Scholar]
- Dui, H.; Liu, K.; Wu, S. Data-driven reliability and resilience measure of transportation systems considering disaster levels. Ann. Oper. Res. 2023. [Google Scholar] [CrossRef]
- Yang, Y.; Pan, S.; Ballot, E. Freight transportation resilience enabled by physical internet. IFAC-Pap. 2017, 50, 2278–2283. [Google Scholar] [CrossRef]
- Otuoze, S.H.; Hunt, D.V.; Jefferson, I. Neural network approach to modelling transport system resilience for major cities: Case studies of lagos and kano (Nigeria). Sustainability 2021, 13, 1371. [Google Scholar] [CrossRef]
- Wang, H.W.; Peng, Z.R.; Wang, D.; Meng, Y.; Wu, T.; Sun, W.; Lu, Q.C. Evaluation and prediction of transportation resilience under extreme weather events: A diffusion graph convolutional approach. Transp. Res. Part C Emerg. Technol. 2020, 115, 102619. [Google Scholar] [CrossRef]
- John, A.; Yang, Z.; Riahi, R.; Wang, J. A risk assessment approach to improve the resilience of a seaport system using Bayesian networks. Ocean. Eng. 2016, 111, 136–147. [Google Scholar] [CrossRef]
- Hosseini, S.; Barker, K. Modeling infrastructure resilience using Bayesian networks: A case study of inland waterway ports. Comput. Ind. Eng. 2016, 93, 252–266. [Google Scholar] [CrossRef]
- Castillo, E.; Grande, Z.; Calviño, A. Bayesian networks-based probabilistic safety analysis for railway lines. Comput.-Aided Civ. Infrastruct. Eng. 2016, 31, 681–700. [Google Scholar] [CrossRef]
- Kammouh, O.; Gardoni, P.; Cimellaro, G.P. Probabilistic framework to evaluate the resilience of engineering systems using Bayesian and dynamic Bayesian networks. Reliab. Eng. Syst. Saf. 2020, 198, 106813. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Nakib, R. Redundancy in highway bridges. Eng. J. 1991, 2003, 28. [Google Scholar]
- Mackie, K.R.; Stojadinović, B. Post-earthquake functionality of highway overpass bridges. Earthq. Eng. Struct. Dyn. 2006, 35, 77–93. [Google Scholar] [CrossRef]
- Padgett, J.E.; DesRoches, R. Bridge functionality relationships for improved seismic risk assessment of transportation networks. Earthq. Spectra 2007, 23, 115–130. [Google Scholar] [CrossRef]
- Shiraki, N.; Shinozuka, M.; Moore, J.E.; Chang, S.E.; Kameda, H.; Tanaka, S. System risk curves: Probabilistic performance scenarios for highway networks subject to earthquake damage. J. Infrastruct. Syst. 2007, 13, 43–54. [Google Scholar] [CrossRef]
- Atadero, R.A.; Jia, G.; Abdallah, A.; Ozbek, M.E. An integrated uncertainty-based bridge inspection decision framework with application to concrete bridge decks. Infrastructures 2019, 4, 50. [Google Scholar] [CrossRef]
- Bu, L.; Qiao, L.; Sun, R.; Lu, W.; Guan, Y.; Gao, N.; Hu, X.; Li, Z.; Wang, L.; Tian, Y.; et al. Time and crack width dependent model of chloride transportation in engineered cementitious composites (ECC). Materials 2022, 15, 5611. [Google Scholar] [CrossRef] [PubMed]
- Gong, C.; Frangopol, D.M. Condition-Based Multiobjective Maintenance Decision Making for Highway Bridges Considering Risk Perceptions. J. Struct. Eng. 2020, 146, 04020051. [Google Scholar] [CrossRef]
- Thoft-Christensen, P.; Jensen, F.M.; Middleton, C.R.; Blackmore, A. Assessment of the Reliability of Concrete Slab Bridges; Structural Reliability Theory; Dept. of Building Technology and Structural Engineering: Aalborg, Denmark, 1996; Volume R9616, No. 157. [Google Scholar]
- Stewart, M.G.; Rosowsky, D.V. Time-dependent reliability of deteriorating reinforced concrete bridge decks. Struct. Saf. 1998, 20, 91–109. [Google Scholar] [CrossRef]
- Ghosh, J. Parameterized Seismic Reliability Assessment and Life-Cycle Analysis of Aging Highway Bridges. Doctoral Dissertation, Rice University, Houston, TX, USA, 2013. [Google Scholar]
- Ghosh, J.; Rokneddin, K.; Padgett, J.E.; Dueñas-Osorio, L. Seismic reliability assessment of aging highway bridge networks with field instrumentation data and correlated failures, I: Methodology. Earthq. Spectra 2014, 30, 795–817. [Google Scholar] [CrossRef]
- Ghasemi, S.H.; Lee, J.Y. Reliability-based indicator for post-earthquake traffic flow capacity of a highway bridge. Struct. Saf. 2021, 89, 102039. [Google Scholar] [CrossRef]
- Chen, A.; Kasikitwiwat, P.; Yang, C. Alternate capacity reliability measures for transportation networks. J. Adv. Transp. 2013, 47, 79–104. [Google Scholar] [CrossRef]
- Kezhiyur, A.J. Analysis of Age-Dependent Resilience for a Highway Network with Aging Bridges. Master’s Thesis, Pennsylvania State University, State College, PA, USA, 2015. [Google Scholar]
- Shannon, C. Claude Shannon. Inf. Theory 1948, 3, 224. [Google Scholar]
- Parhizkar, T.; Balali, S.; Mosleh, A. An entropy based bayesian network framework for system health monitoring. Entropy 2018, 20, 416. [Google Scholar] [CrossRef] [PubMed]
- Rokneddin, K.; Ghosh, J.; Dueñas-Osorio, L.; Padgett, J.E. Seismic reliability assessment of aging highway bridge networks with field instrumentation data and correlated failures, II: Application. Earthq. Spectra 2014, 30, 819–843. [Google Scholar] [CrossRef]
- Faghih-Imani, A.; Eluru, N.; El-Geneidy, A.M.; Rabbat, M.; Haq, U. How land-use and urban form impact bicycle flows: Evidence from the bicycle-sharing system (BIXI) in Montreal. J. Transp. Geogr. 2014, 41, 306–314. [Google Scholar] [CrossRef]
- Kaparias, I.; Eden, N.; Tsakarestos, A.; Gal-Tzur, A.; Gerstenberger, M.; Hoadley, S.; Lefebvre, P.; Ledoux, J.; Bell, M. Development and application of an evaluation framework for urban traffic management and Intelligent Transport Systems. Procedia-Soc. Behav. Sci. 2012, 48, 3102–3112. [Google Scholar] [CrossRef]
- Marchau, V.A.; Walker, W.E.; Van Wee, G.P. Dynamic adaptive transport policies for handling deep uncertainty. Technol. Forecast. Soc. Chang. 2010, 77, 940–950. [Google Scholar] [CrossRef]
- Song, H.W.; Lee, C.H.; Ann, K.Y. Factors influencing chloride transport in concrete structures exposed to marine environments. Cem. Concr. Compos. 2008, 30, 113–121. [Google Scholar] [CrossRef]
- Field, E.H.; Jordan, T.H.; Cornell, C.A. OpenSHA: A Developing community-modeling environment for seismic hazard analysis. Seism. Res. Lett. 2003, 74, 406–419. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jonnalagadda, V.; Lee, J.Y.; Zhao, J.; Ghasemi, S.H. Quantification and Reduction of Uncertainty in Seismic Resilience Assessment for a Roadway Network. Infrastructures 2023, 8, 128. https://doi.org/10.3390/infrastructures8090128
Jonnalagadda V, Lee JY, Zhao J, Ghasemi SH. Quantification and Reduction of Uncertainty in Seismic Resilience Assessment for a Roadway Network. Infrastructures. 2023; 8(9):128. https://doi.org/10.3390/infrastructures8090128
Chicago/Turabian StyleJonnalagadda, Vishnupriya, Ji Yun Lee, Jie Zhao, and Seyed Hooman Ghasemi. 2023. "Quantification and Reduction of Uncertainty in Seismic Resilience Assessment for a Roadway Network" Infrastructures 8, no. 9: 128. https://doi.org/10.3390/infrastructures8090128
APA StyleJonnalagadda, V., Lee, J. Y., Zhao, J., & Ghasemi, S. H. (2023). Quantification and Reduction of Uncertainty in Seismic Resilience Assessment for a Roadway Network. Infrastructures, 8(9), 128. https://doi.org/10.3390/infrastructures8090128





