Dynamic Response Identification of a Triple-Single Bailey Bridge Based on Vehicle Traffic-Induced Vibration Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Analysis Methods
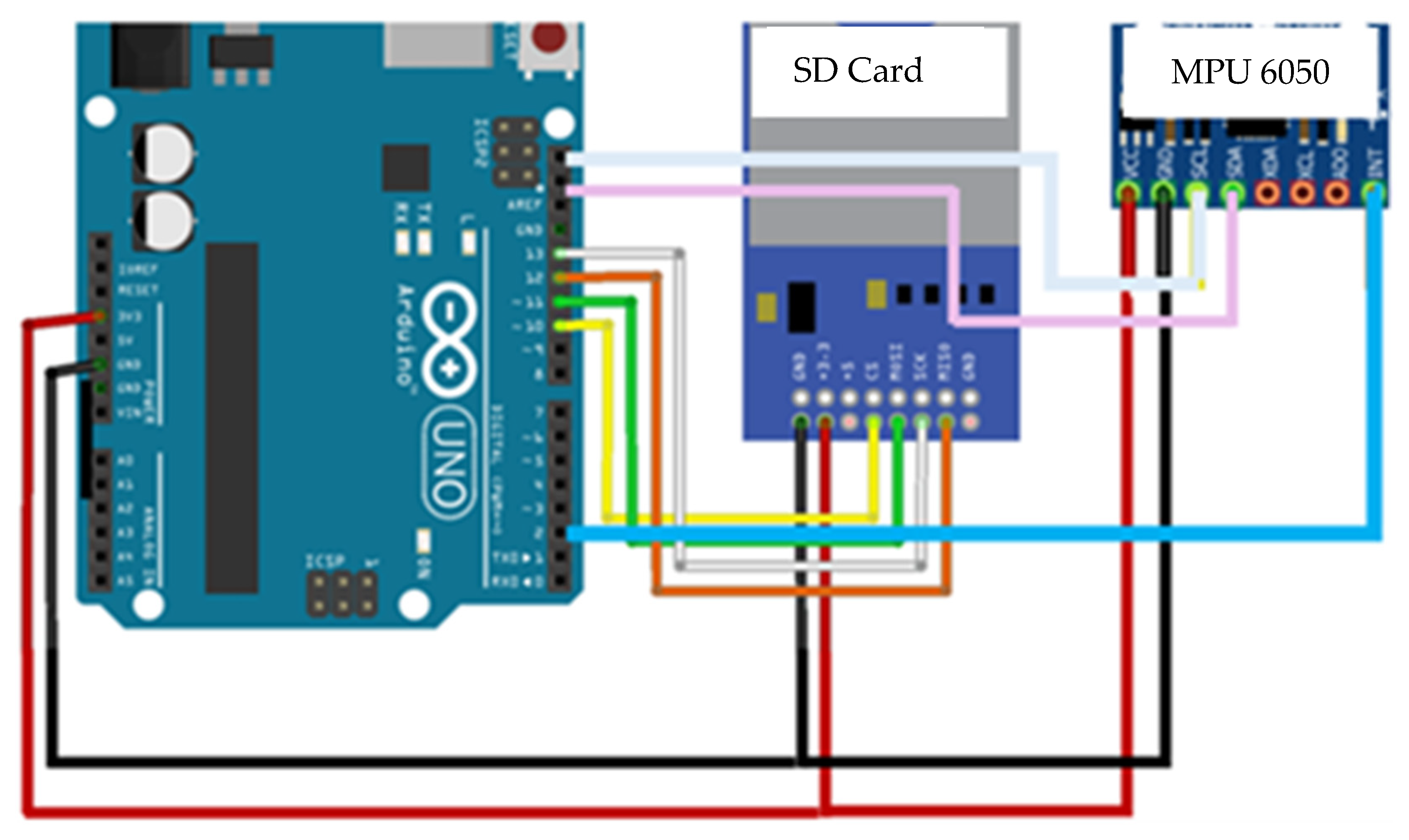
2.2. Measuring Devices
2.3. Bailey Bridge Description
2.4. Bailey Bridge in Feneos (Corinth, Peloponnese, Greece)
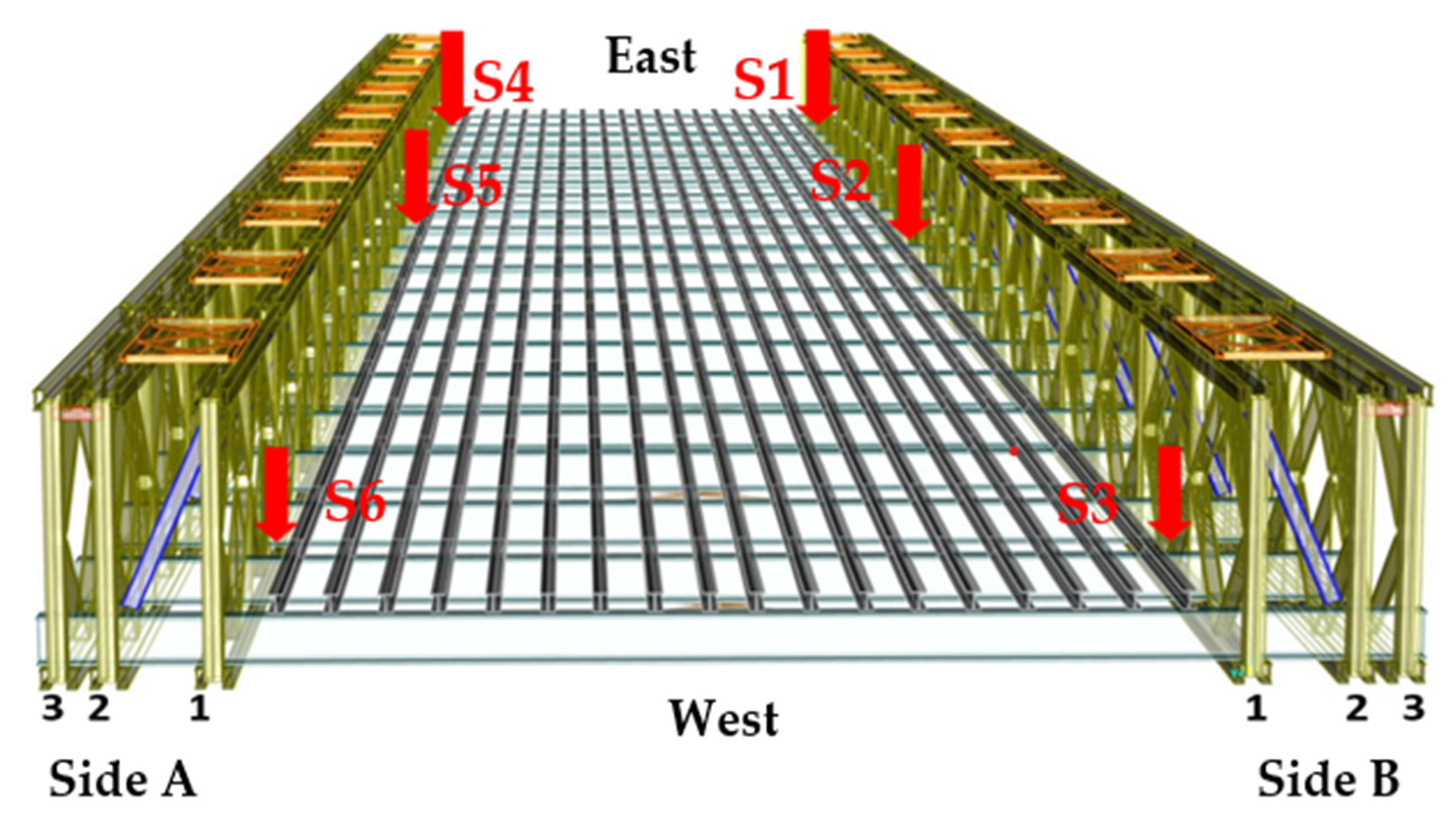
2.5. Bridge Instrumentation
3. Results
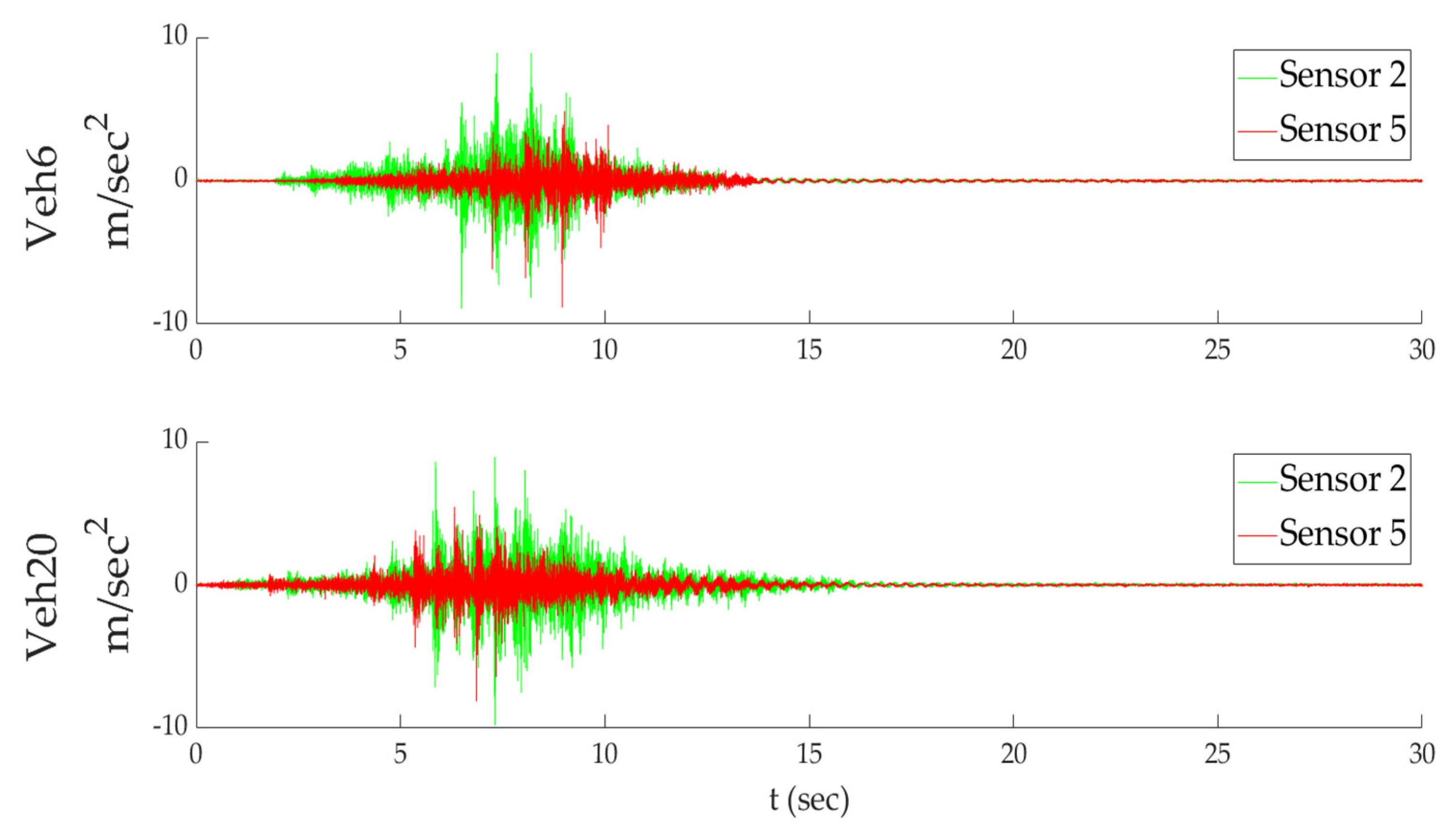
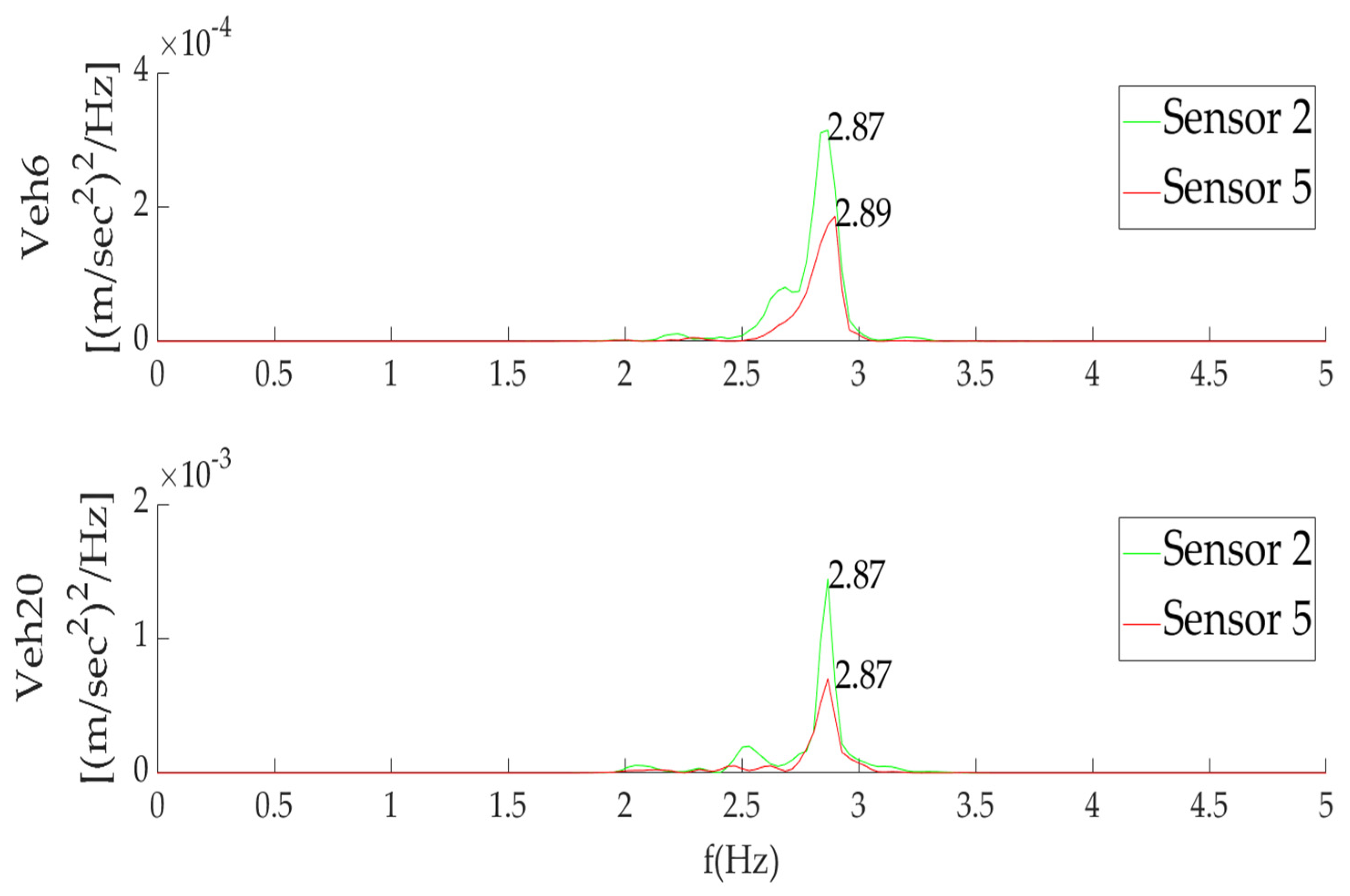
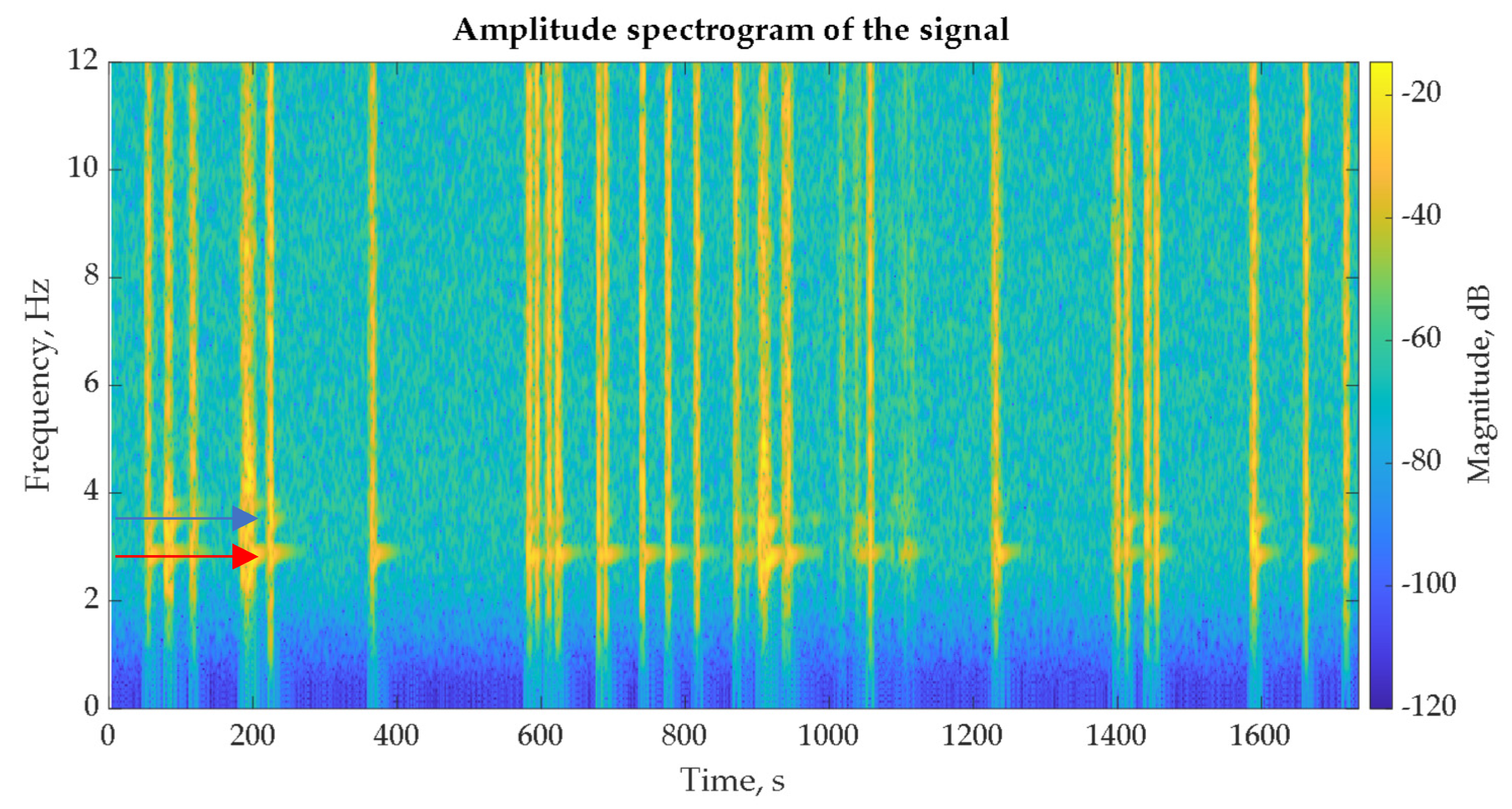
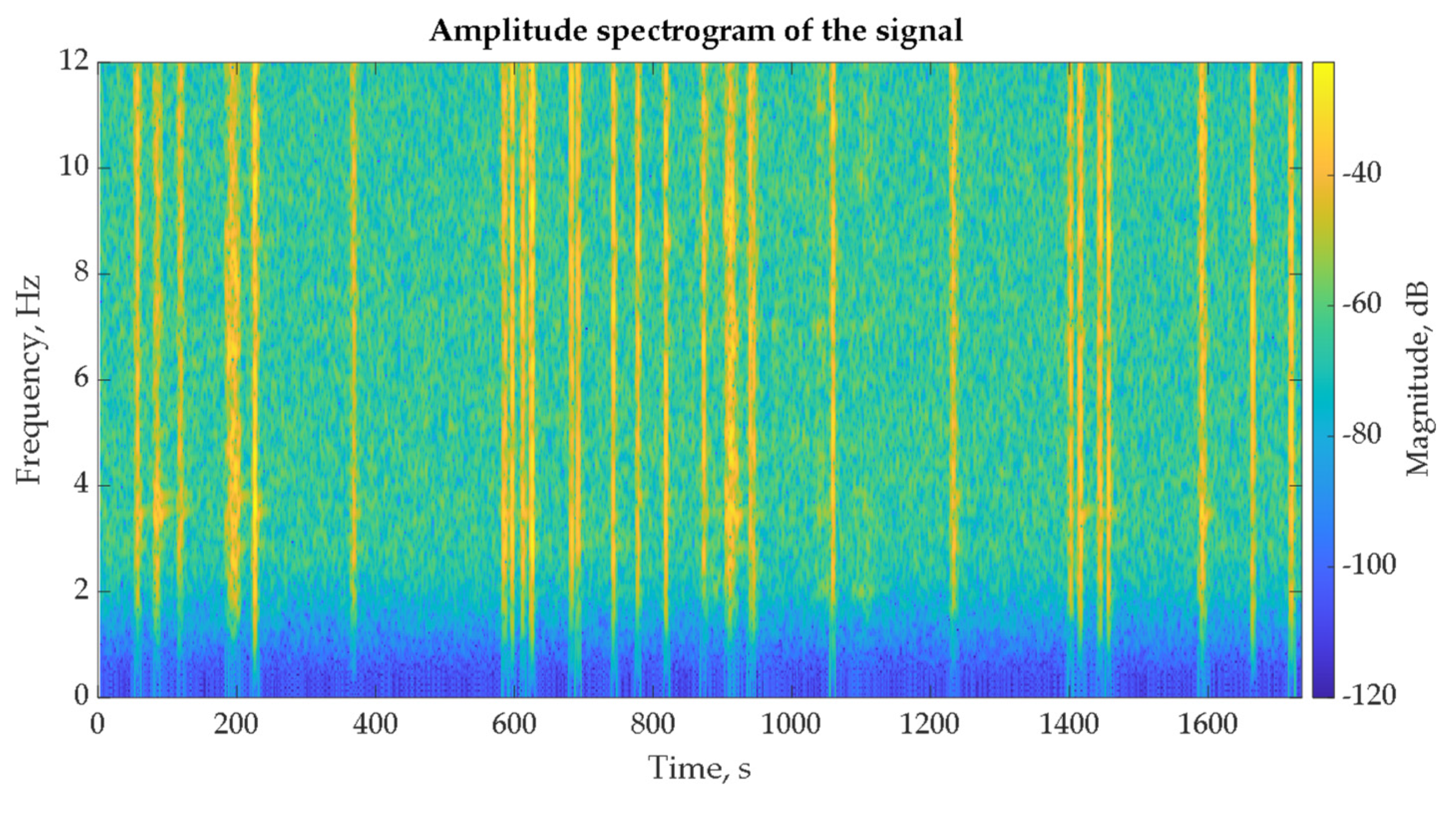
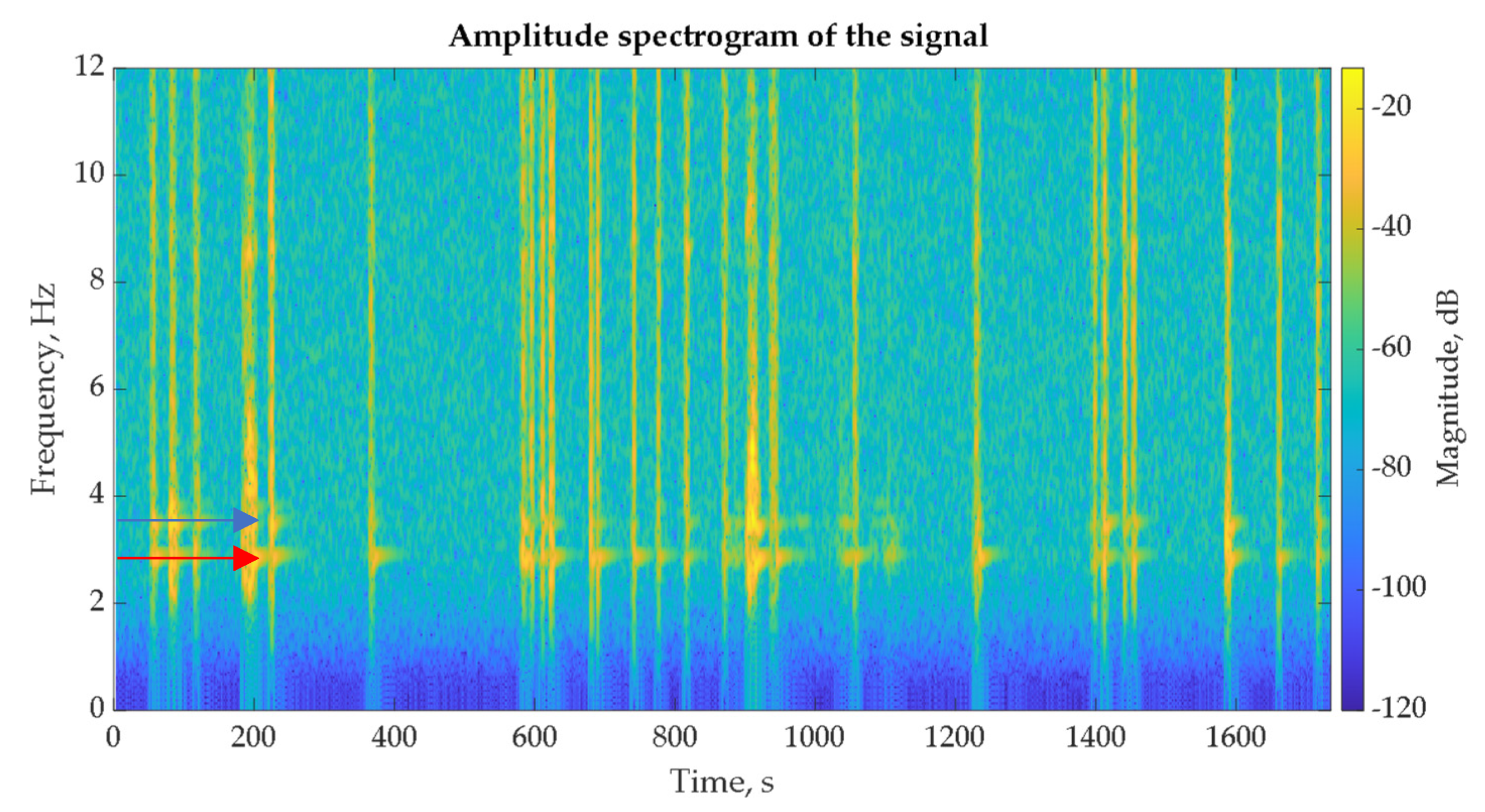
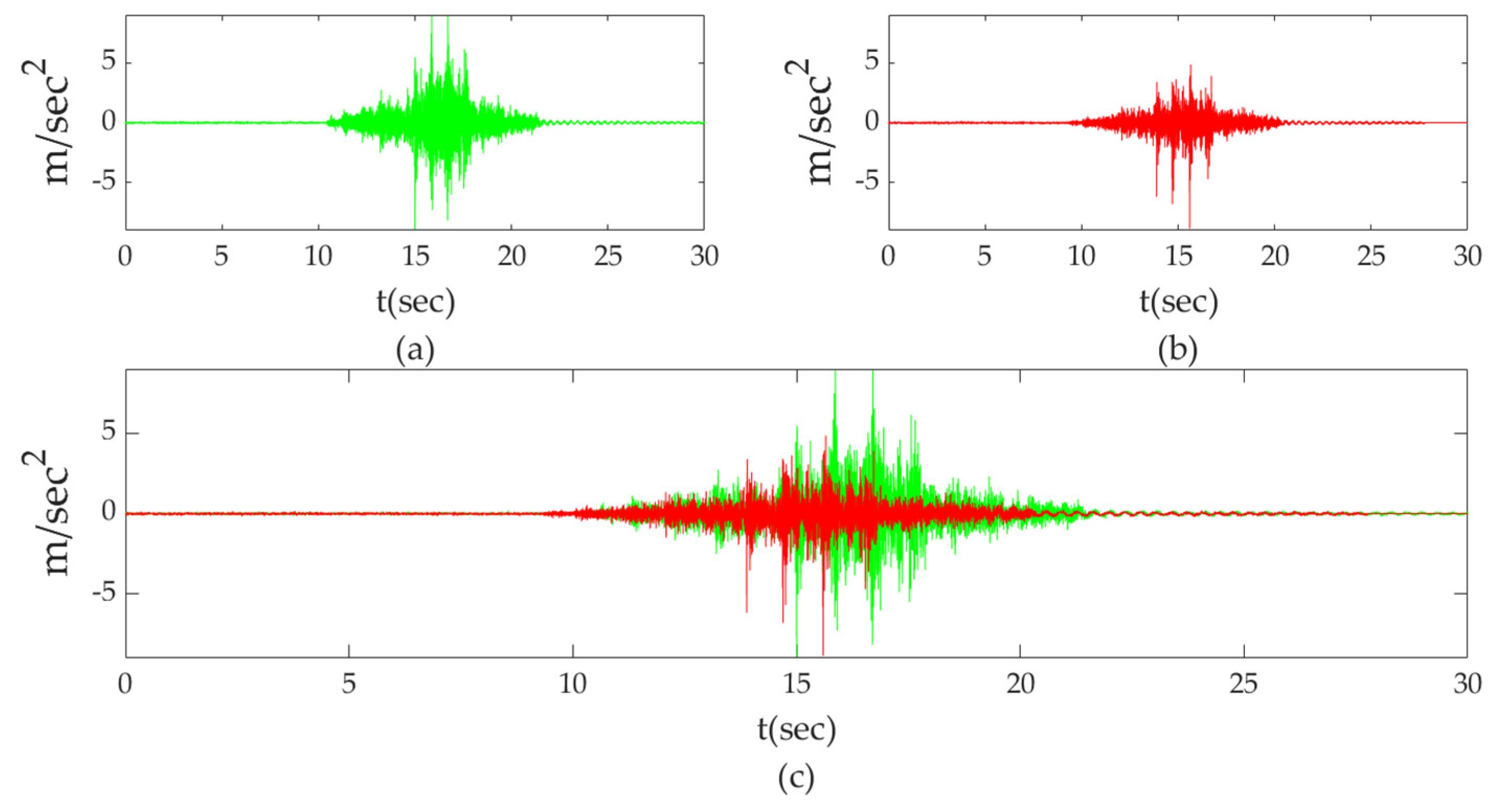
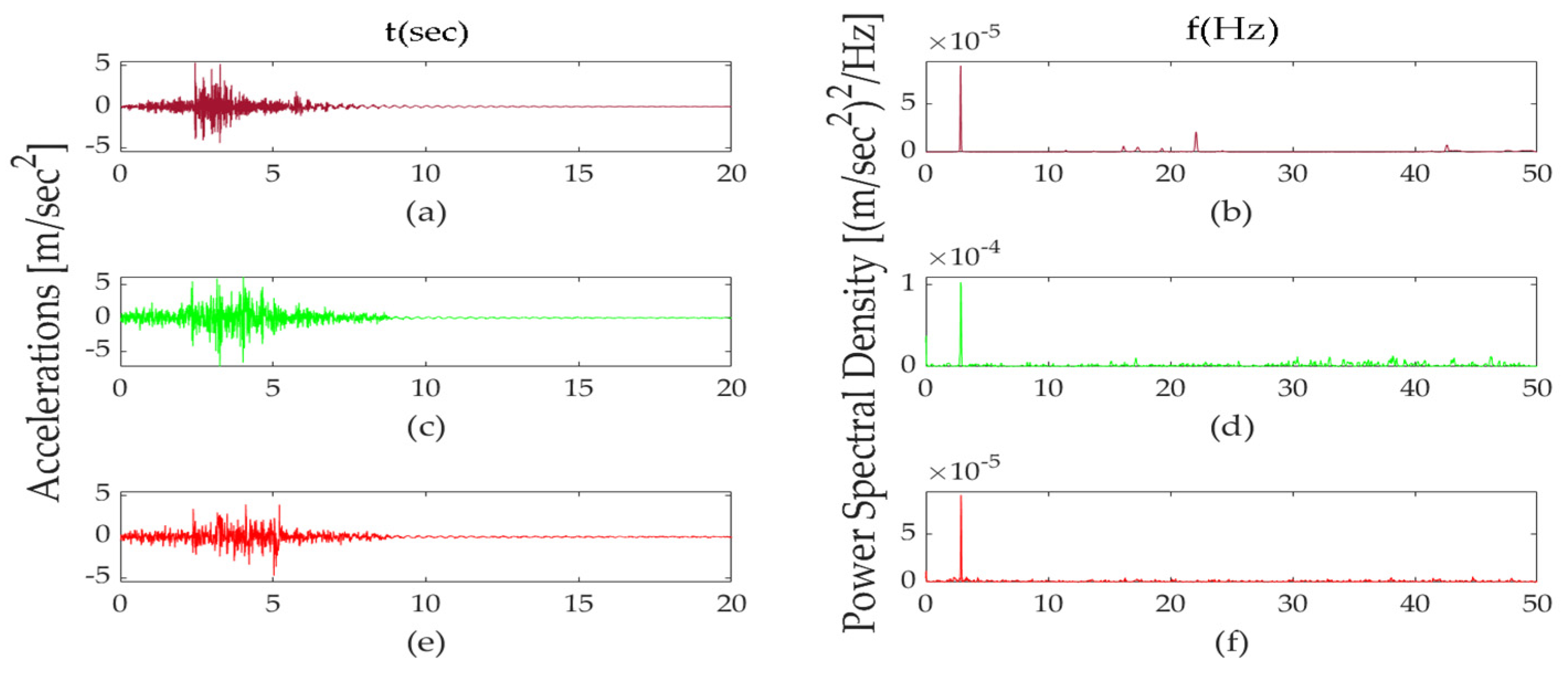
3.1. Results of Time Histories Analysis Due to Traffic-Induced Vibration
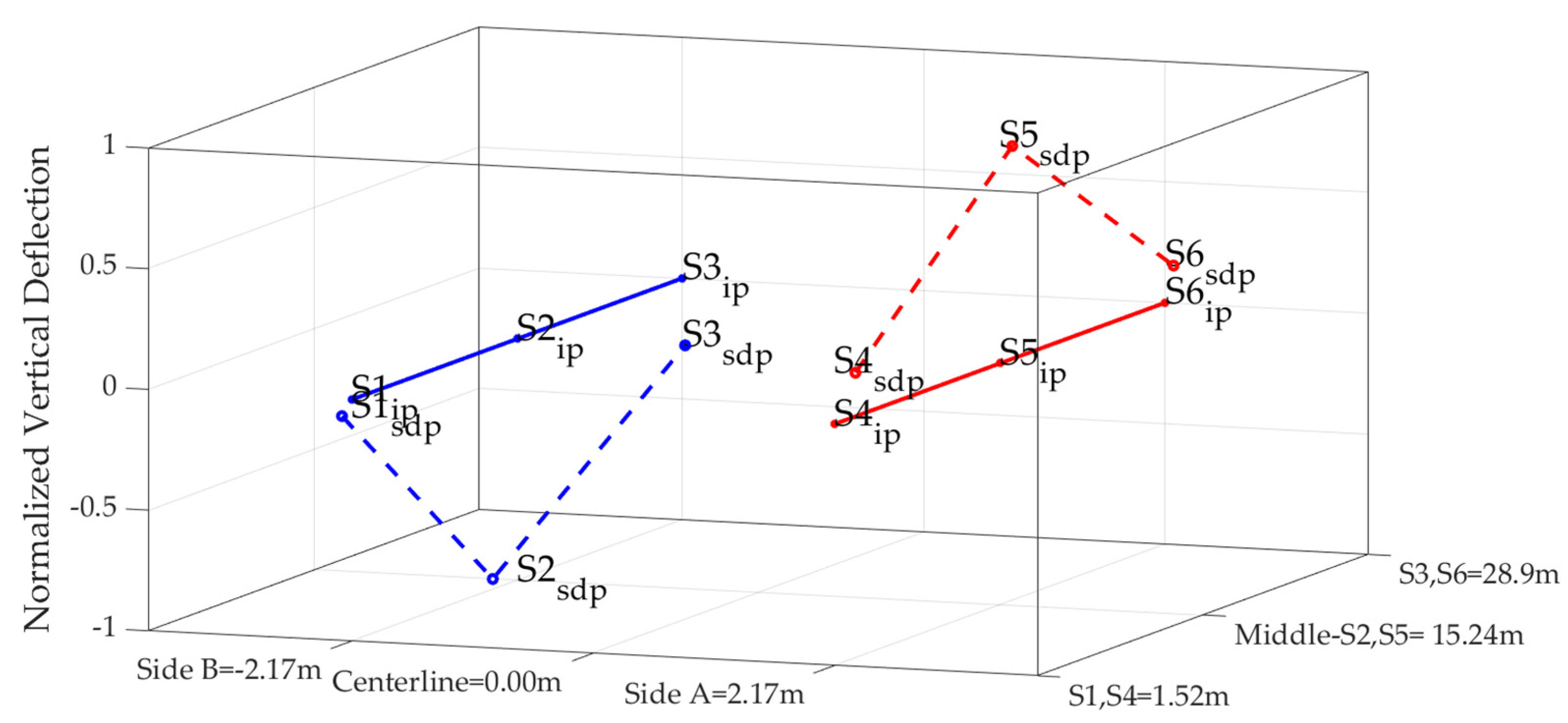
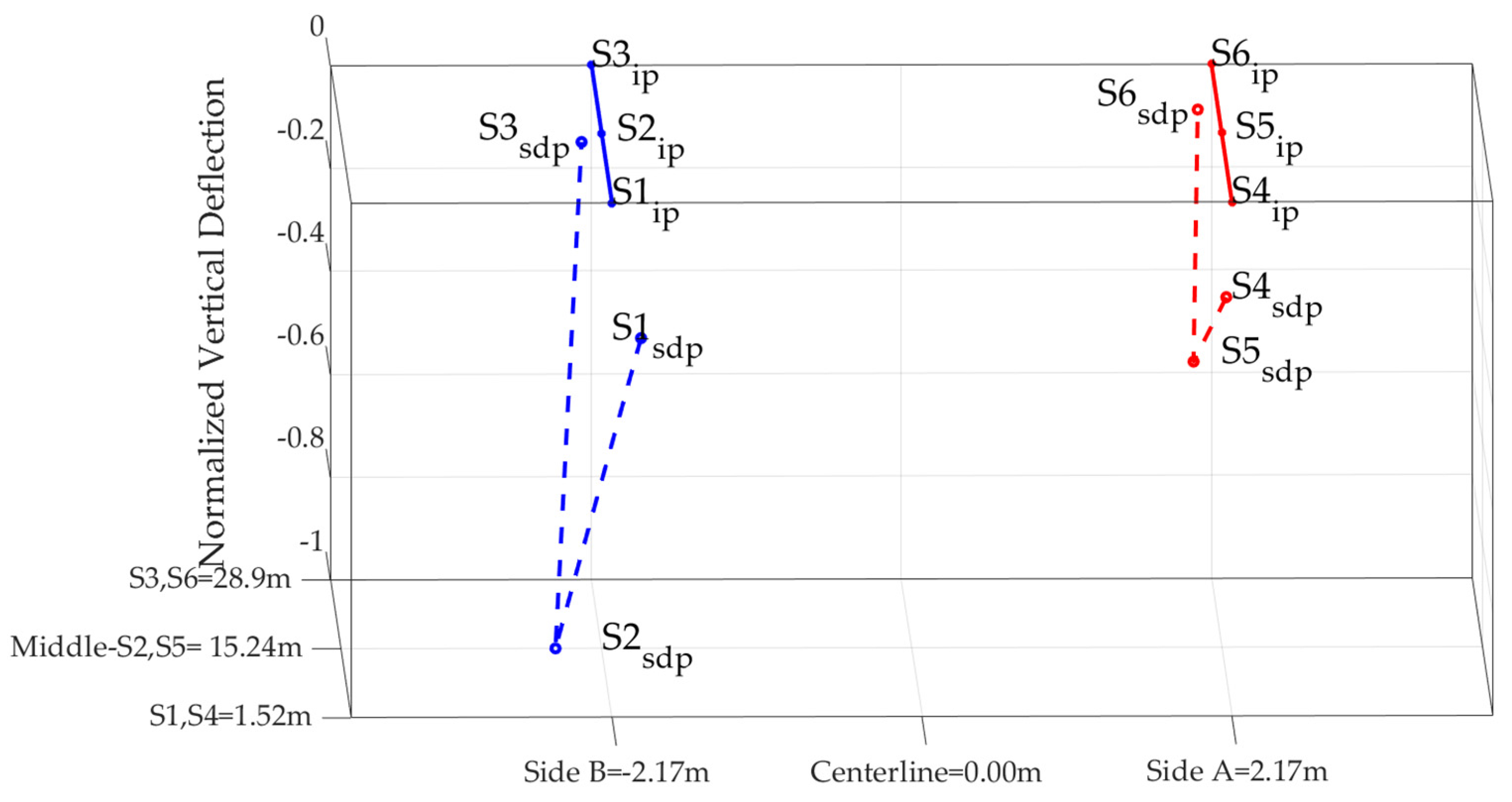
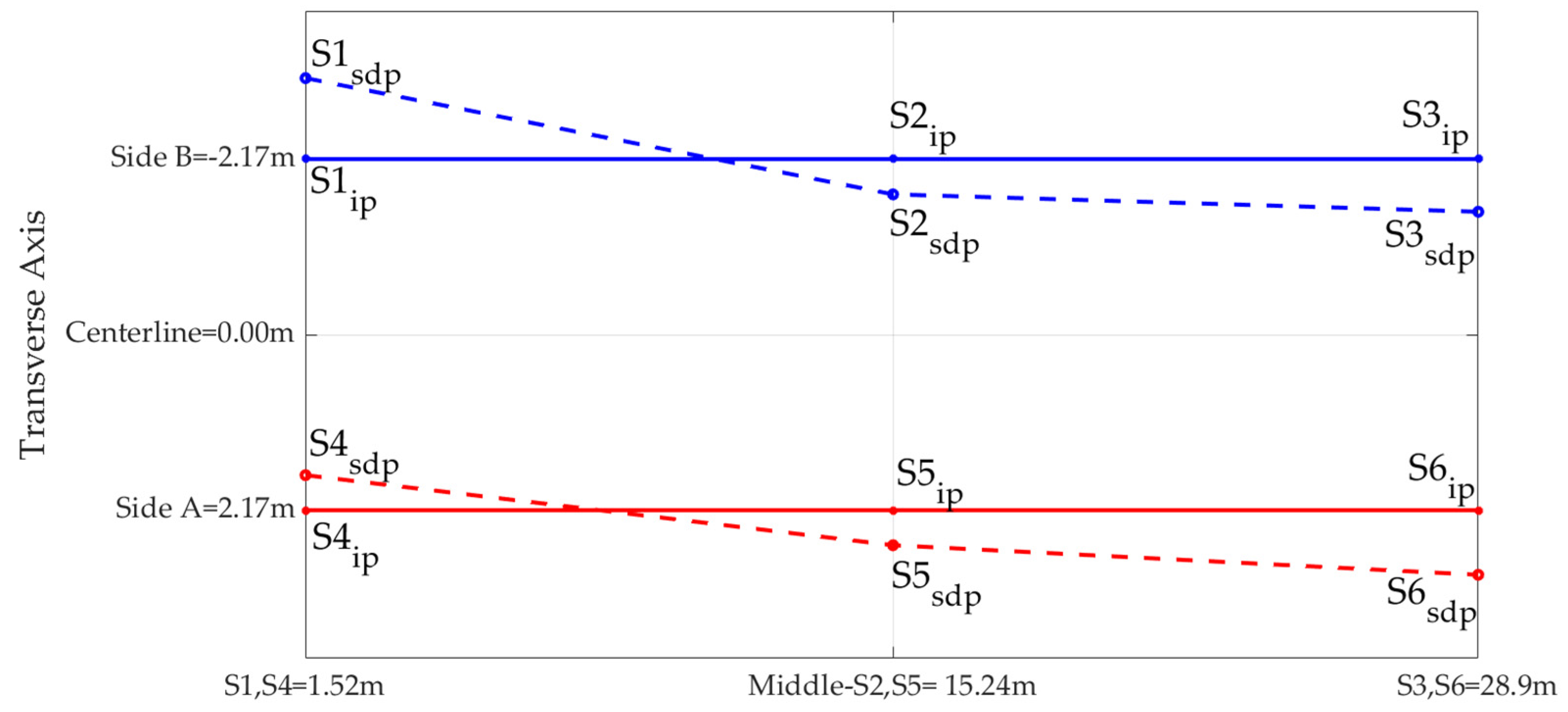
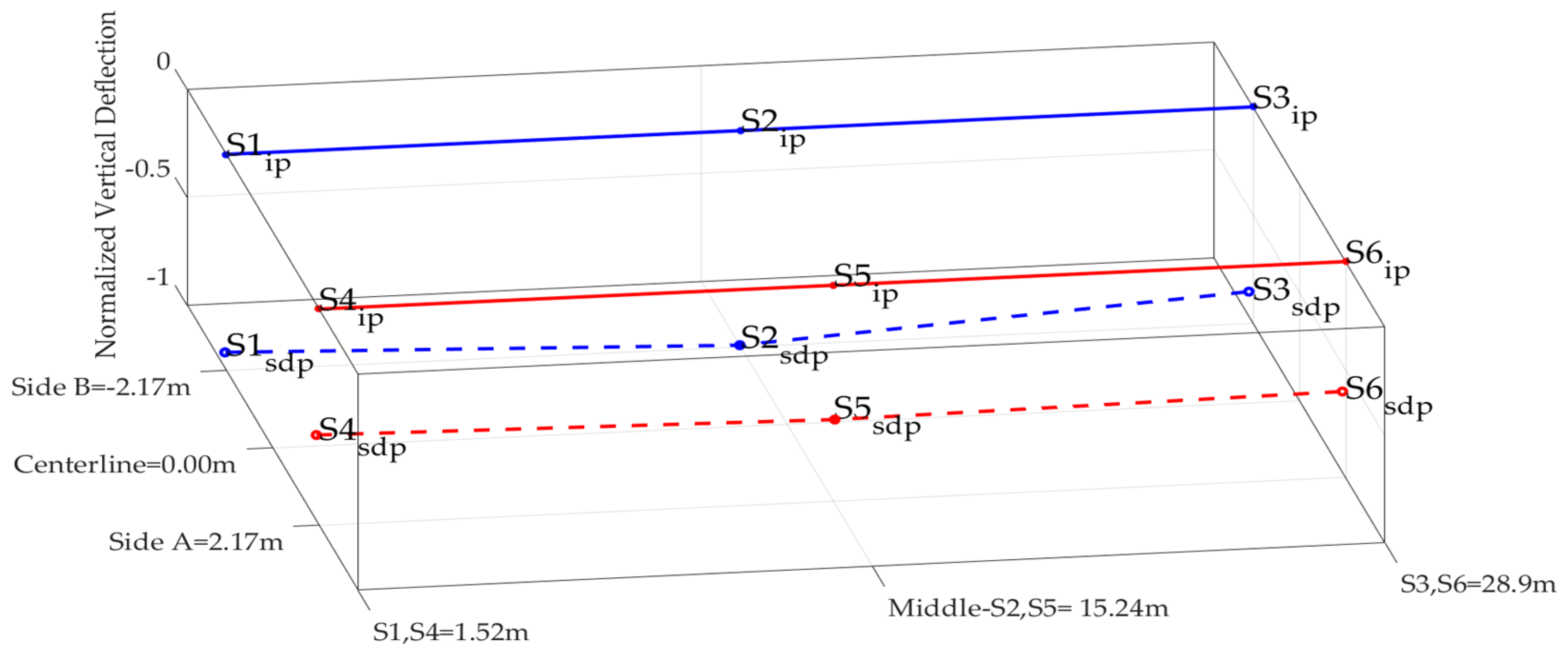
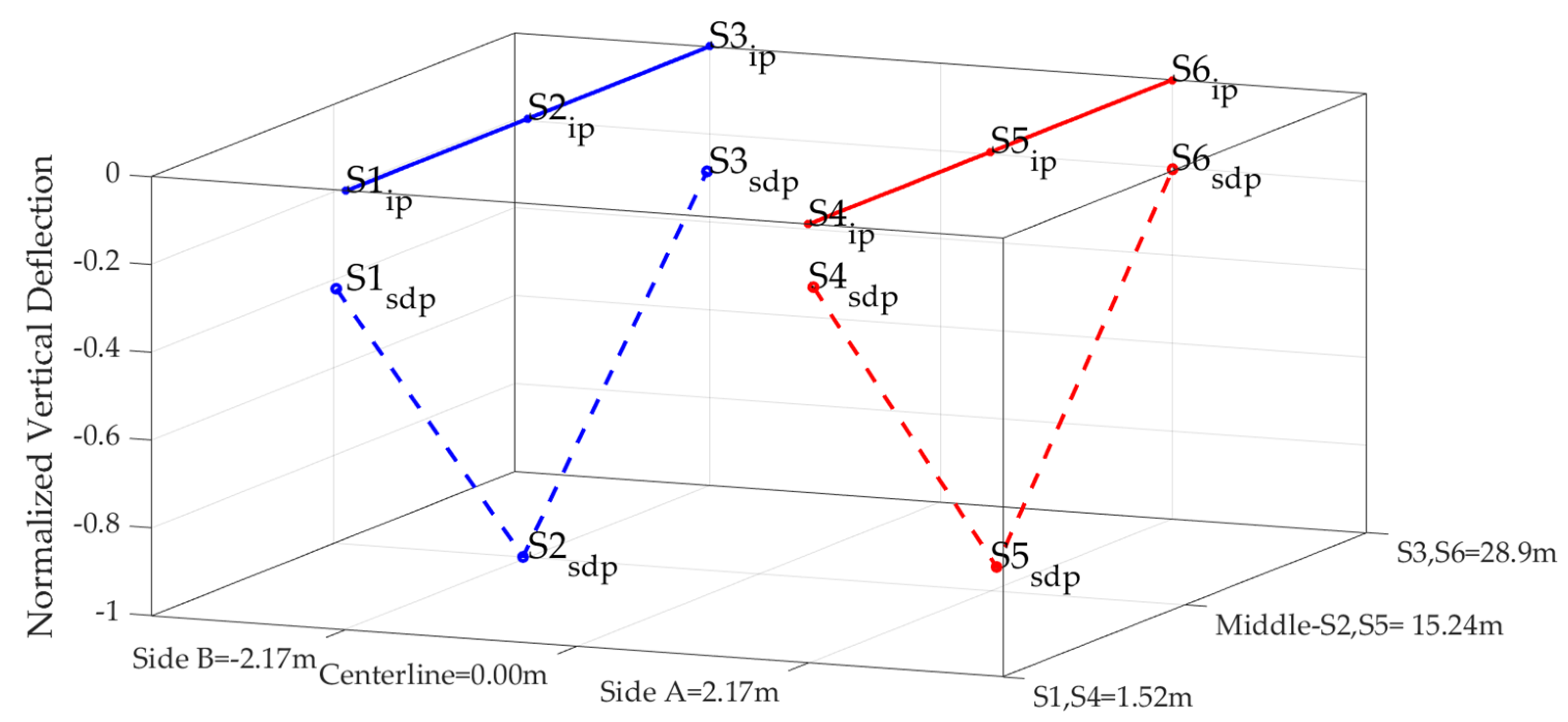
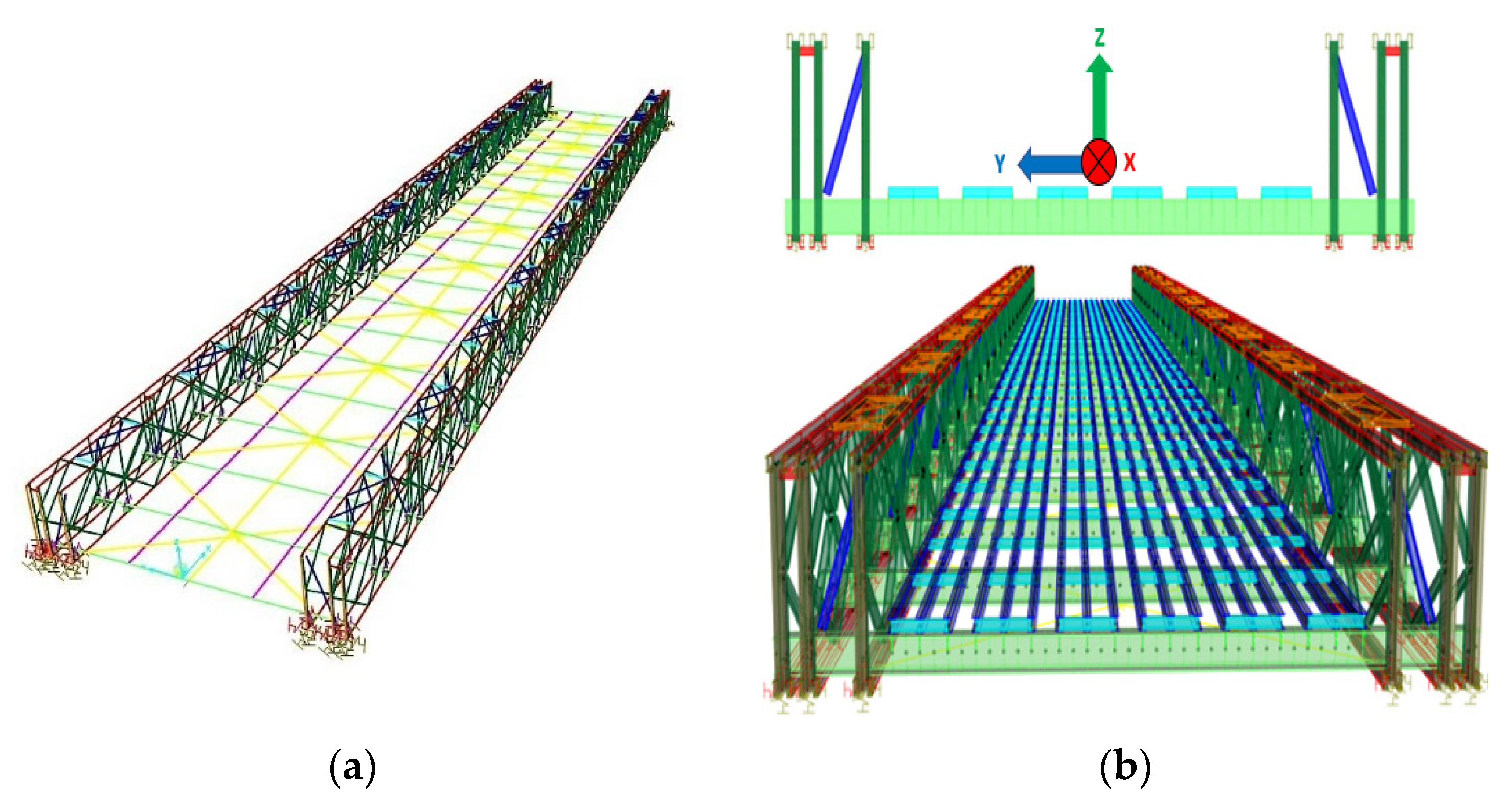
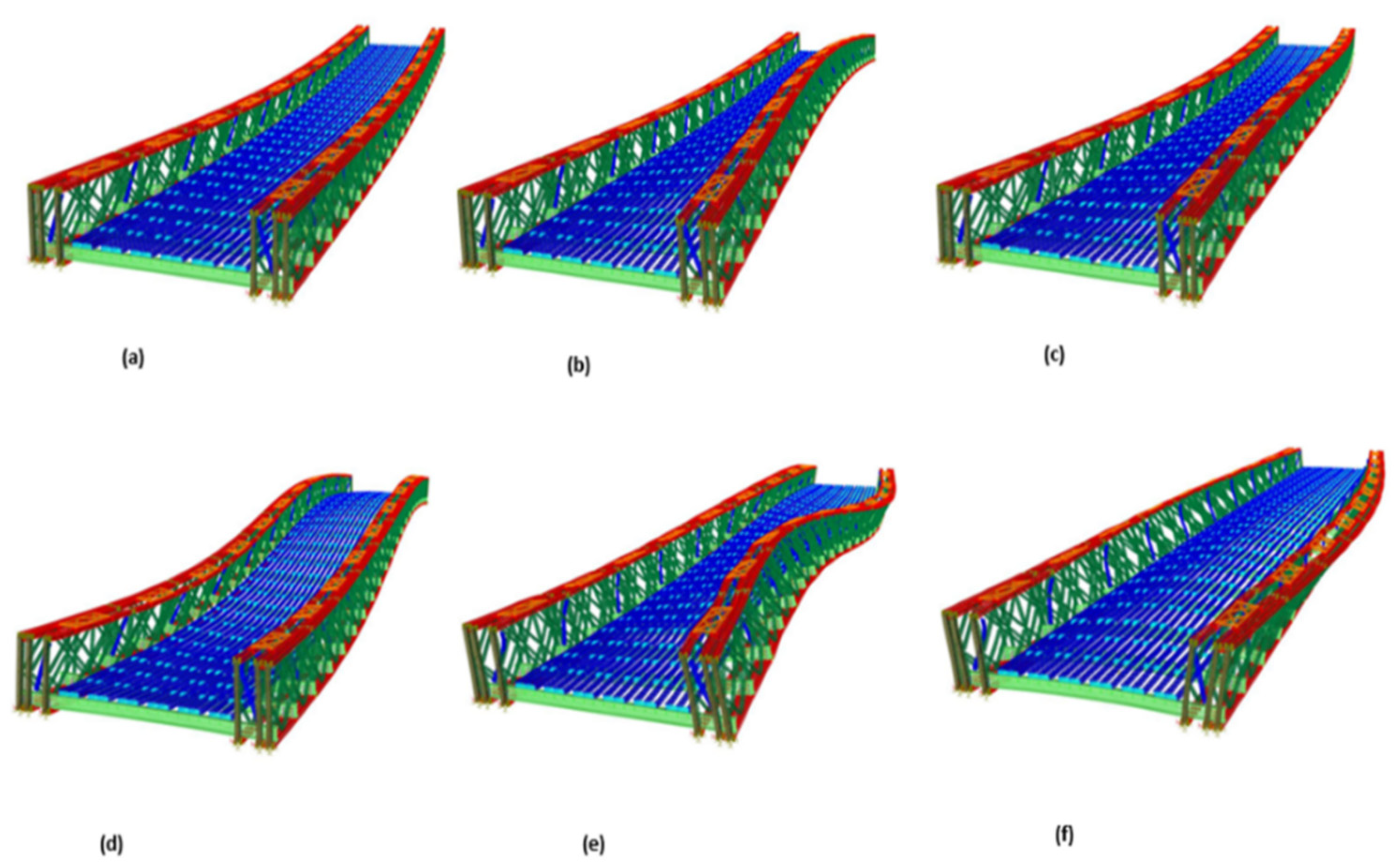
3.2. Finite Element Modeling and Numerical Modal Analysis Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bailey, C.D.; Foulkes, R.A.; Digby-Smith, R. The Bailey Bridge and Its Developments. Symposium of Papers on War-Time Engineering Problems; The Institution of Civil Engineers: London, UK, 1948; pp. 373–410. [Google Scholar]
- Roberts, L.D. The Bailey: The Amazing, All-Purpose Bridge; In Builders and Fighters, 1st ed.; U.S. Army Engineers in World War II: Fort Belvoir, VA, USA, 1992.
- Department of Army (DOA). Field Manual 5-277 Bailey Bridge; Department of Army: Washington, DC, USA, 1986.
- Joiner, J.H. One More River to Cross: The Story of British Military Bridging; Pen & Sword Books Ltd.: Barnsley, UK, 2001. [Google Scholar]
- Final Report. Prefabricated Steel Bridge Systems; FHWA Solicitation NO. DTFH61-03-R-00113; Federal Highway Administration: Washington, DC, USA, 2005.
- Whitman, J.G.; Alder, J.F. Programmed Fatigue Testing of Full-Size Welded Steel Structural Assemblies. Br. Weld. J. 1960, 7, 272–280. [Google Scholar]
- Greenway, L.R. Fatigue Risk in Bailey Bridges. Technical Memorandum; Ministry of Transport: London, UK, 1968.
- Webber, D. Constant Amplitude and Cumulative Damage Fatigue Tests on Bailey Bridges. In Effects of Environment and Complex Load History on Fatigue Life; American Society for Testing and Materials (ASTM STP 462): West Conshohocken, PA, USA, 1970; pp. 15–39. [Google Scholar]
- Marsch, K.J.; Barker, J.V.L. The Fatigue of Military Bridges—Full-Scale Fatigue Testing of Components and Structures; Butterworths: London, UK, 1988. [Google Scholar]
- Associated Consulting Engineers ACE (PVT) Ltd. Evaluation of Bailey Bridge at Ardanu—Final Report (PHASE-I); Associated Consulting Engineers ACE (PVT) Ltd.: Karachi, Pakistan, 1990. [Google Scholar]
- Cullimore, M.S.G.; Webber, D. Analysis of heavy girder bridge fatigue failures. Eng. Fail. Anal. 2000, 7, 145–168. [Google Scholar] [CrossRef]
- King, W.S.; Duan, L. Experimental Investigations of Bailey Bridges. J. Bridge. Eng. 2003, 8, 334–339. [Google Scholar] [CrossRef]
- Parivallal, S.; Narayanan, T.; Ravisankar, K.; Kesavan, K.; Maji, S. Instrumentation and Response Measurement of a Double-Lane Bailey Bridge during Load Test. Strain 2005, 41, 25–30. [Google Scholar] [CrossRef]
- King, W.S.; Wu, S.M.; Duan, L. Laboratory Tests and Analysis of Bailey Bridge Segments. J. Bridge Eng. 2013, 18, 957–968. [Google Scholar] [CrossRef]
- Khounsida, T.; Nishikawa, T.; Nakamura, S.; Okumatsu, T.; Thepvongsa, K. Study on Static and Dynamic Behavior of Bailey Bridge. In Proceedings of the 2019 World Congress on Advances in Structural Engineering and Mechanics (ASEM19), Jeju Island, Korea, 17–21 September 2019. [Google Scholar]
- Prokop, J.; Odrobiňák, J.; Farbák, M.; Novotný, V. Load-Carrying Capacity of Bailey Bridge in Civil Applications. Appl. Sci. 2022, 12, 3788. [Google Scholar] [CrossRef]
- Yang, Y.B.; Li, L.; Wang, Z.L.; Shi, K.; Xu, H.; Qiu, Q.F.; Zhu, F.J. A novel frequency-free movable test vehicle for retrieving modal parameters of bridges: Theory and experiment. Mech. Syst. Signal Process. 2022, 170, 108854. [Google Scholar] [CrossRef]
- Wang, Z.L.; Yang, J.P.; Judy, P.; Shi, K.; Xu, H.; Qu, F.Q.; Yang, Y.B. Recent Advances in Researches on Vehicle Scanning Method for Bridges. Int. J. Struct. Stab. Dyn. 2022, 22. [Google Scholar] [CrossRef]
- Yang, Y.B.; Wang, B.; Wang, Z.; Shi, K.; Xu, H. Scanning of Bridge Surface Roughness from Two-Axle Vehicle Response by EKF-UI and Contact Residual: Theoretical Study. Sensors 2022, 9, 3410. [Google Scholar] [CrossRef]
- Wang, Z.L.; Tan, Z.X.; Yao, H.; Shi, K.; Xu, H.; Yang, Y.B. Effect of soft-end amplification on elastically supported bridges with bearings of unequal stiffnesses scanned by moving test vehicle. J. Sound Vib. 2022, 540, 117308. [Google Scholar] [CrossRef]
- Ge-wie, C.; Omenzetter, P.; Beskhyroun, S. Operational modal analysis of an eleven-span concrete bridge subjected to weak ambient excitations. Eng. Struct. 2017, 151, 839–860. [Google Scholar]
- Rainieri, C.; Fabbrocino, G. Introduction. In Operational Modal Analysis of Civil Engineering Structures; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Qin, S.; Kang, J.; Wang, Q. Operational Modal Analysis Based on Subspace Algorithm with an Improved Stabilization Diagram Method. Shock and Vibration. Hindawi Publ. Corp. 2016, 2016, 7598965. [Google Scholar] [CrossRef]
- Castellanos-Toro, S.; Marmolejo, M.; Marulanda, J.; Cruz, A.; Thomson, P. Frequencies and damping ratios of bridges through Operational Analysis using Smartphones. Constr. Build. Mater. 2018, 188, 490–504. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G. Automated output-only dynamic identification of civil engineering structures. Mech. Syst. Signal Process. 2010, 24, 678–695. [Google Scholar] [CrossRef]
- Magalhaes, F.; Cunha, A. Explaining operational modal analysis with data from an arch bridge. Mech. Syst. Signal Process. 2011, 25, 1431–1450. [Google Scholar] [CrossRef]
- Cheynet, E.; Jakobsen, J.B.; Snæbjörnsson, J. Damping Estimation of Large Wind-Sensitive Structures. Procedia Eng. 2017, 199, 2047–2053. [Google Scholar] [CrossRef]
- Automated Frequency Domain Decomposition (AFDD). Available online: https://www.mathworks.com/matlabcentral/fileexchange/57153-automated-frequency-domain-decomposition-afdd (accessed on 29 July 2022).
- Chowdhuty, R.M.; Ray, C.J. Accelerometers for Bridge Load Testing. NDTE Int. 2003, 36, 237–244. [Google Scholar] [CrossRef]
- Albarbar, A.; Badri, A.; Sinha, J.K.; Starr, A. Performance evaluation of MEMS accelerometers. Measurement 2009, 42, 790–795. [Google Scholar] [CrossRef]
- Neitzel, F.; Weisbrich, S. Vibration Monitoring of Bridges; Technische Universität: Berlin, Germany, 2011. [Google Scholar]
- Elhattab, A.; Uddin, N.; Obrien, E. Extraction of Bridge Fundamental Frequencies Utilizing a Smartphone MEMS Accelerometer. Sensors 2019, 19, 3143. [Google Scholar] [CrossRef]
- Sabato, A. Pedestrian bridge vibration monitoring using a wireless MEMS accelerometer board. In Proceedings of the IEEE 19th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Calabria, Italy, 6–8 May 2015; pp. 437–442. [Google Scholar] [CrossRef]
- InvenSense Inc. MPU-6000 and MPU-6050 Register Map and Descriptions Revision 4.2; InvenSense Inc.: San Jose, CA, USA, 2013. [Google Scholar]
- Aydemir, G.A.; Saranlı, A. Characterization and calibration of MEMS inertial sensors for state and parameter estimation applications. Measurement 2012, 45, 1210–1225. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Z.; Shang, H.; Hu, W.; Qin, G. A time-controllable Allan variance method for MEMS IMU. Ind. Robot. 2013, 40, 111–120. [Google Scholar] [CrossRef]
- Allan, D.W. Statistics of atomic frequency standards. Proc. IEEE 1966, 54, 221–230. [Google Scholar] [CrossRef]
- Groves, D.P. Navigation using inertial sensors. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 42–69. [Google Scholar] [CrossRef]
- Gonzalez, R.; Dabove, P. Performance Assessment of an Ultra Low-Cost Inertial Measurement Unit for Ground Vehicle Navigation. Sensors 2019, 19, 3865. [Google Scholar] [CrossRef]
- Nirmal, K.; Sreejith, A.G.; Mathew, J.; Sarpotdar, M.; Suresh, A.; Prakash, A.; Safonova, M.; Murthy, J. Noise modeling and analysis of an IMU-based attitude sensor: Improvement of performance by filtering and sensor fusion. Proc. Adv. Opt. Mech. Technol. Telesc. Instrum 2016, 9912, 2138–2147. [Google Scholar] [CrossRef]
- IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Laser Gyros. In IEEE Std 647-2006 (Revision of IEEE Std 647-1995); IEEE: Piscataway, NJ, USA, 2006; pp. 1–96. [CrossRef]
- El-Sheimy, N.; Hou, H.; Niu, X. Analysis and modeling of inertial sensors using Allan variance. IEEE Trans. Instrum. Meas. 2008, 57, 140–149. [Google Scholar] [CrossRef]
- Bates, W. Historical Structural Steelwork Handbook; British Constructional Steelwork Association Limited: London, UK, 1991. [Google Scholar]
- Department of Army (DOA). FM 3-34.343-Bailey Bridge; Department of Army: Washington, DC, USA, 2002.
- NATO. STAndardizations AGreement/Edition 8. Military Load Classification of Bridges. Ferries, Rafts and Vehicles; NATO: Brussels, Belgium, 2021. [Google Scholar]
- Department of Army (DOA), Field Manual 5-170-Engineer Reconnaissance; Department of Army: Washington, DC, USA, 1998.
- Van Groningen, C.N.; Paddock, R.A. Smart Bridge: A Tool for Estimating the Military Load Classification of Bridges Using Varying Levels of Information; Argonne National Laboratory: Lemont, IL, USA, 1997.
- Rainieri, C.; Fabbrocino, G. Data Acquisition. In Operational Modal Analysis of Civil Engineering Structures; Springer: New York, NY, USA, 2014; pp. 59–102. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G. Output-only Modal Identification. In Operational Modal Analysis of Civil Engineering Structures; Springer: New York, NY, USA, 2014; pp. 103–210. [Google Scholar] [CrossRef]
- Chopra, K.A. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 4th ed.; Pearson Education Inc.: London, UK, 2012; pp. 54–56. [Google Scholar]
- Rainieri, C.; Fabbrocino, G. Applications. In Operational Modal Analysis of Civil Engineering Structures; Springer: New York, NY, USA, 2014; pp. 211–265. [Google Scholar] [CrossRef]
- Computers & Structures Inc. CSiBridge-CSI Analysis Reference Manual; Computers & Structures Inc.: Berkeley, CA, USA, 2017. [Google Scholar]
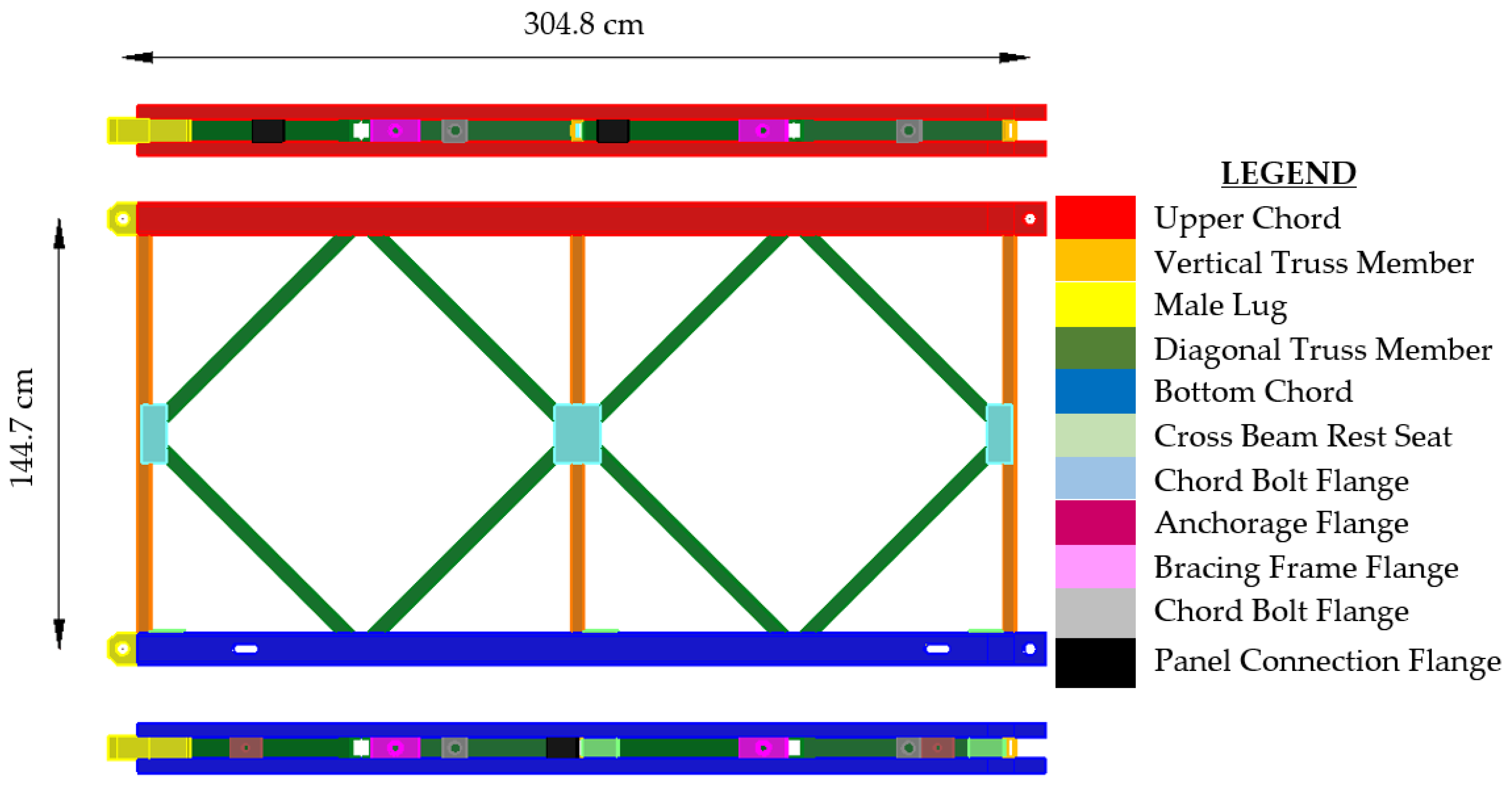
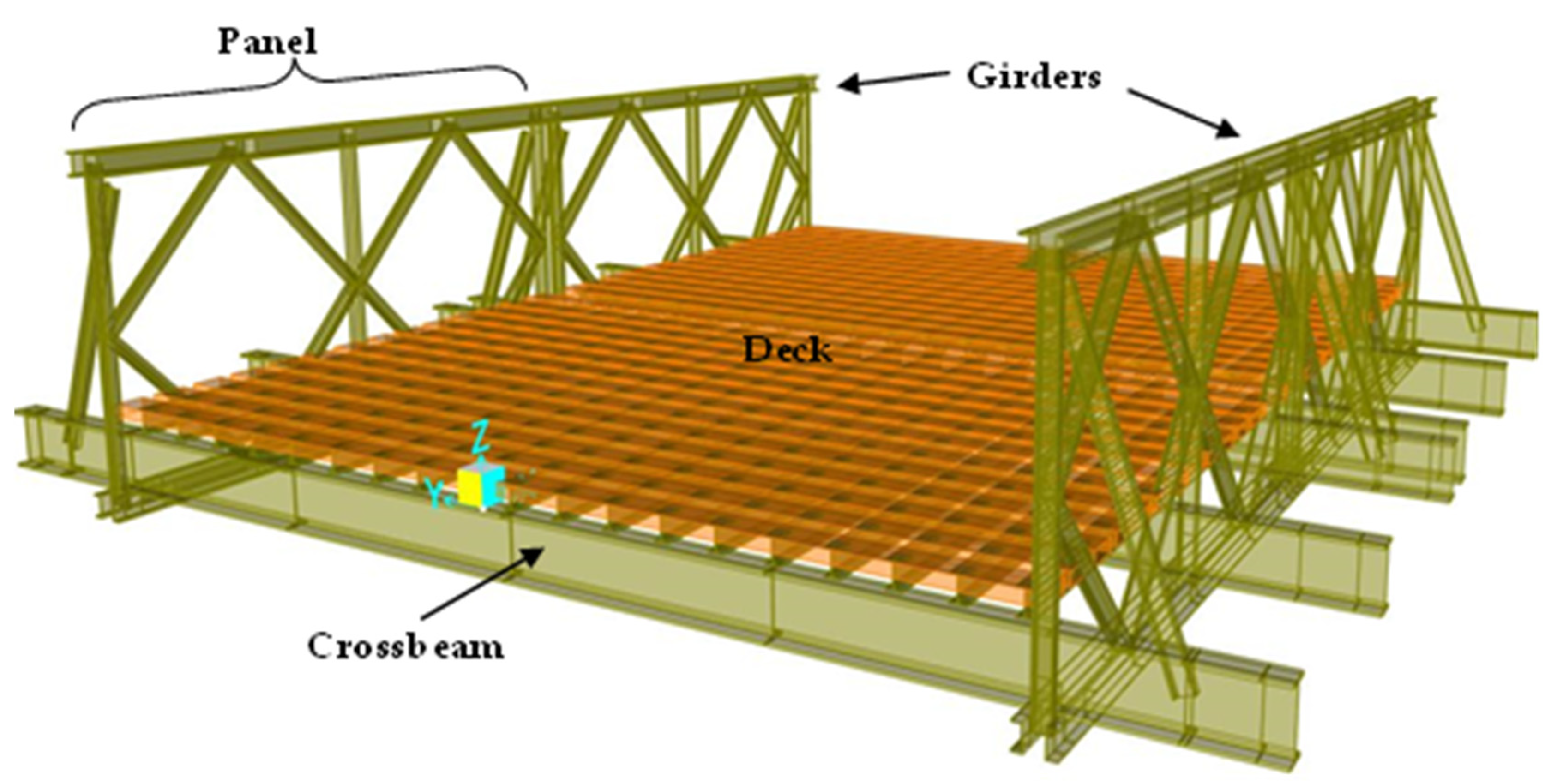



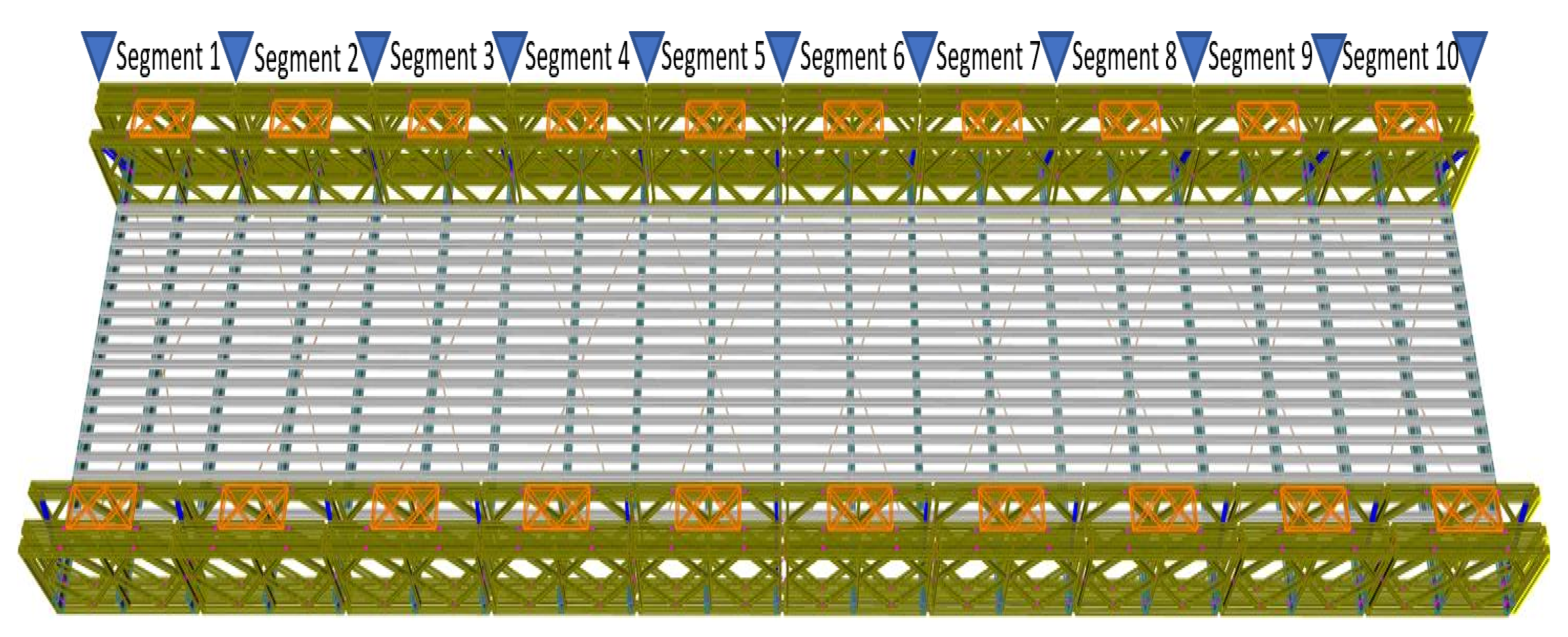




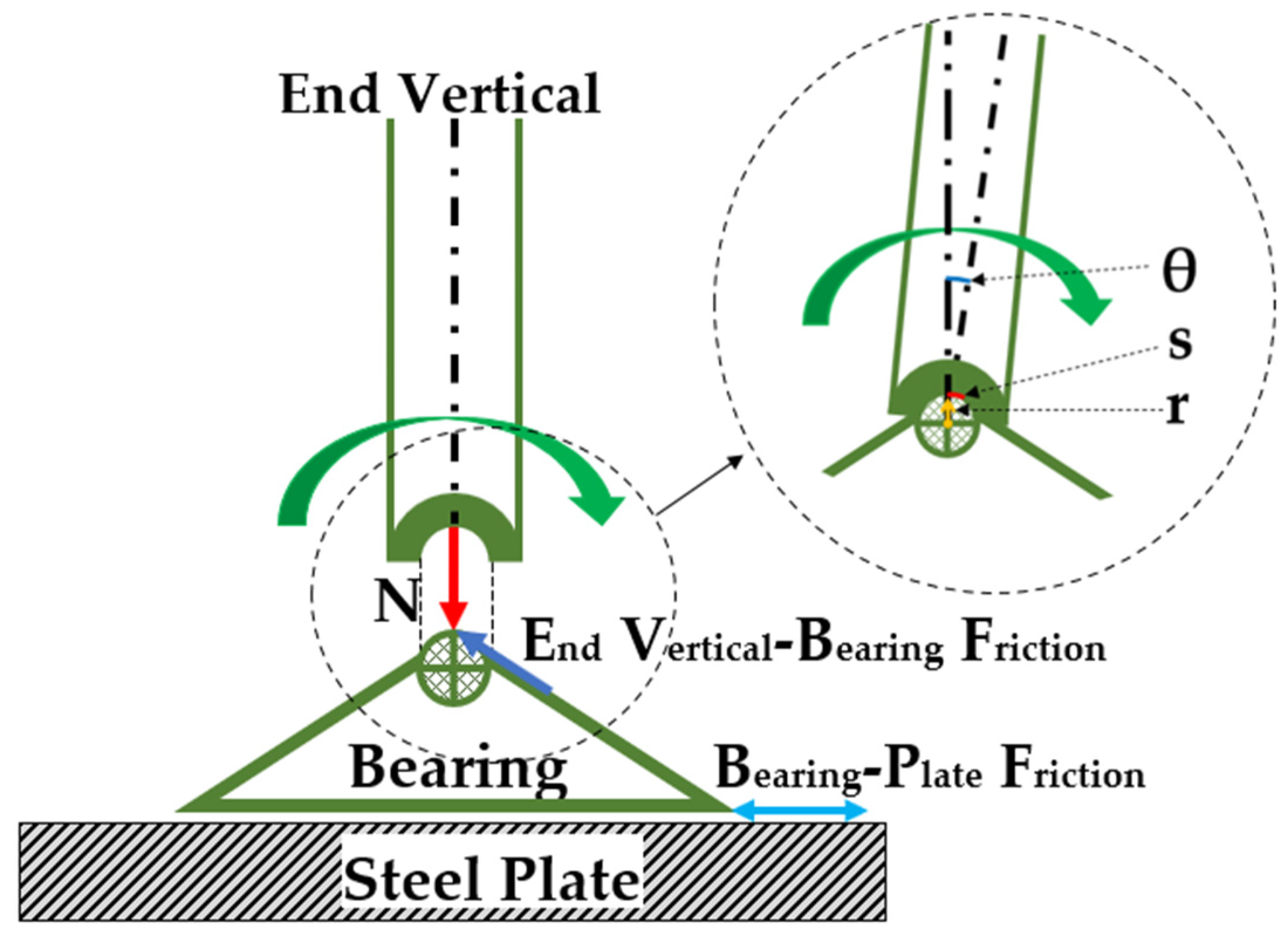

| According to [1] (UK) | According to [3] (USA) | Usual Bridge Engineering Terminology |
|---|---|---|
| Stringers | Stringers | Stringers |
| Chord | Chord | Upper or lower horizontal member of panel |
| Cross girder | Transom | Cross beam |
| Raker | Raker | Vertical bracings |
| Sway brace | Sway brace | Horizontal bracings |
| Pin | Pin | Pin |
| Deck | Deck | Timber deck |
| Chord bolt | Chord bolt | Panel connection bolt 1 |
| Ribband | Ribband | Curb |
| Panel | Panel | Panel of truss girder |
| Gap | Gap | Span |
| Bay | Bay | Segment |
| End Post | End Post | End vertical member |
| Member | Shape | Mass | Depth | Width | Thickness | Area | |
|---|---|---|---|---|---|---|---|
| Web | Flange | ||||||
| kg/m | cm | cm | cm | cm | cm² | ||
| Upper Chord | 10.8 | 10.16 | 4.3 | 0.82 | 0.75 | 13.7 | |
| Bottom Chord | Channel | 10.8 | 10.16 | 4.3 | 0.82 | 0.75 | 13.7 |
| Vertical/Diagonal | Channel | 6.1 | 7.62 | 3.50 | 0.43 | 0.69 | 7.81 |
| Cross Beam | Channel | 37 | 25.4 | 11.4 | 7.62 | 12.96 | 47.42 |
| Stringer 1 | I Section | 7 | 10.2 | 4.4 | 0.43 | 0.69 | 9.48 |
| Vertical Bracing | I Section | 6 | 4.06 | 6.35 | 0.41 | 7.61 | |
| Horizontal Bracing | I Section | 6 | Dia:2.9 cm | 6.61 | |||
| Quality | fy (MPa) | fu (MPa) | Thickness t (mm) | Remarks |
|---|---|---|---|---|
| BS 968 1 | 317.4 | 441.6 ≤ fu ≤ 538.2 | t ≤ 15.88 | Replaced by BS 4360/1968 |
| BS 15 | 220.8 | 386.4 < fu < 455.4 | t ≤ 19.05 | Replaced by BS 4360/1968 |
| Alloy steel | 897 | Manganese-molybdenum |
| Parts Bridge Specified Nomenclature | BS 968 High Tensile Steel | BS 15 Mild Steel | Alloy Steel (Manganese-Molybdenum) |
|---|---|---|---|
| Panel (all members) | + | ||
| Cross Beam | + | ||
| Stringers | + | ||
| Horizontal Bracing | + | ||
| Bracing Frame Panel | + | ||
| Vertical Bracing | + | ||
| End Vertical | + | ||
| Pins | + |
| Traffic Restriction | Vehicle Position on Deck | Max Speed (km/h) | Min Spacing (m) | Authorization to Use |
|---|---|---|---|---|
| Normal | At any place | 40 | 27 | Anyone |
| Caution | On centerline | 13 | 45 | Supervised by the authorities |
| Risk | On centerline | 4 | One vehicle on bridge | Supervised by the authorities |
| Bridge Type | Weight Per Fully Equipped Segment (kN) | Number of Fully Equipped Segments | Total Bridge Weight (kN) | Total Length (m) | Number of Effective lanes | Width of Effective Lane (m) |
|---|---|---|---|---|---|---|
| TS | 40.1 | 10 | 401 | 30.48 | 1 | 3.70 |
| Type of Vehicle | MLC Per Cross Restriction | Max Vehicle’s Weight Based on Expedient Method (kN) | Remarks Expedient Method | ||||
|---|---|---|---|---|---|---|---|
| N 1 | C 2 | R 3 | N | C | R | MLC to kN = MLC × F1 × F2 × F3 | |
| F1:1,15 MLC to short tons | |||||||
| Wheeled | 50 | 57 | 60 | 558 | 635 | 670 | F2: 0.97 Short to metric tons |
| Tracked | 55 | 60 | 66 | 534 | 582 | 640 | F3: 10 metric tons to kN |
| Sensor | Segment | Panel | Position | Distance (m) |
|---|---|---|---|---|
| 1 | 1 | 1st side A (W-E) | Middle vertical member | 1.52 |
| 2 | 5 | 1st side A (W-E) | Third vertical member | 15.2 |
| 3 | 10 | 1st side A (W-E) | Middle vertical member | 28.9 |
| 4 | 1 | 1st side B (W-E) | Middle vertical member | 1.52 |
| 5 | 5 | 1st side B (W-E) | Third vertical member | 15.2 |
| 6 | 10 | 1st side B (W-E) | Middle vertical member | 28.9 |
| Index | Vehicle Type | Direction | Remarks |
|---|---|---|---|
| Veh1 | Farm truck | W-E | |
| Veh2 | Tractor | E-W | |
| Veh3 | Farm truck | E-W | |
| Veh4 | Farm tractor w/trailer | W-E | |
| Veh5 | Tractor 3.5 tn | E-W | |
| Veh6 | Farm truck | E-W | Full load |
| Veh7 | Cargo truck 2.0 tn | E-W | |
| Veh8 | Farm truck | E-W | |
| Veh9 | Van | W-E | |
| Veh10 | Cargo truck 2.0 tn | W-E | |
| Veh11 | Van | W-E | Higher velocity |
| Veh12 | Passenger car | W-E | |
| Veh13 | SUV | W-E | Higher velocity |
| Veh14 | Passenger car | W-E | |
| Veh15 | Farm truck | E-W | |
| Veh16 | Farm truck | W-E | |
| Veh17 | Farm tractor w/trailer | E-W | |
| Veh18 | Passenger cars | W-E | 2 vehicles on the bridge |
| Veh19 | Farm truck | W-E | |
| Veh20 | Farm truck w/trailer | W-E | |
| Veh21 | Passenger car | E-W | |
| Veh22 | Farm truck | E-W | |
| Veh23 | Van | E-W | |
| Veh24 | Farm truck | W-E | |
| Veh25 | Fuel truck | E-W | Full load |
| Veh26 | Passenger car | E-W | Higher velocity |
| Veh27 | Passenger car | W-E |
| Vehicle | Sensor 2 | Sensor 5 |
|---|---|---|
| ζ (%) | ζ (%) | |
| Veh1 | 1.10 | 0.960 |
| Veh4 | 1.05 | 1.05 |
| Veh5 | 1.11 | 1.18 |
| Veh6 | 0.90 | 1.07 |
| Veh17 | 0.98 | 1.17 |
| Veh20 | 0.96 | 0.90 |
| Mean value | 1.02 | 1.05 |
| Case | AFDD at Sensors 1-2-3 | AFDD at Sensors 4-5-6 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Identified Frequencies (Hz) | Identified Frequencies (Hz) | |||||||||||
| 1st | 2nd | 3rd | 4th | 5th | 6th | 1st | 2nd | 3rd | 4th | 5th | 6th | |
| Veh1-2-3 | 2.87 | 3.36 | 5.98 | 6.67 | 9.27 | 13.3 | 2.87 | 3.49 | 5.76 | 6.70 | 8.71 | 11.3 |
| Veh4-5 | 2.82 | 3.40 | 4.39 | 6.93 | 8.51 | 11.8 | 2.76 | 3.49 | 4.36 | 5.11 | 8.51 | 12.1 |
| Veh6 | 2.83 | 6.52 | 7.23 | 8.84 | 9.85 | 11.5 | 2.86 | 7.69 | 9.20 | 9.98 | 11.1 | 12.0 |
| Veh7-8-9-10 | 2.83 | 4.54 | 6.26 | 9.12 | 10.3 | 13.8 | 2.81 | 4.36 | 7.65 | 9.08 | 10.5 | 14.6 |
| Veh11-12 | 2.86 | 3.91 | 5.59 | 9.08 | 12.0 | 14.2 | 2.86 | 6.12 | 8.54 | 10.2 | 11.3 | 16.2 |
| Veh13 | 2.83 | 3.40 | 4.39 | 6.93 | 8.51 | 11.8 | 2.76 | 3.49 | 4.36 | 5.11 | 8.51 | 12.1 |
| Veh14 | 2.87 | 5.50 | 7.59 | 8.53 | 9.32 | 11.1 | 2.87 | 5.35 | 6.39 | 8.51 | 10.4 | 11.9 |
| Veh15 | 2.86 | 4.83 | 6.25 | 8.59 | 9.23 | 11.3 | 2.83 | 3.97 | 6.18 | 8.60 | 10.1 | 11.4 |
| Veh16 | 2.88 | 6.25 | 8.41 | 9.61 | 11.0 | 13.8 | 2.88 | 3.43 | 7.05 | 8.41 | 10.8 | 11.7 |
| Veh17-18 | 2.79 | 3.38 | 4.87 | 6.22 | 9.46 | 11.0 | 2.79 | 3.44 | 4.52 | 4.88 | 8.44 | 11.2 |
| Veh19 | 2.88 | 4.91 | 6.42 | 8.33 | 12.5 | 13.5 | 2.89 | 4.16 | 5.26 | 8.33 | 9.95 | 12.6 |
| Veh20 | 2.86 | 5.46 | 6.61 | 7.59 | 9.45 | 11.1 | 2.86 | 4.99 | 7.01 | 8.79 | 10.5 | 12.8 |
| Veh21-22-23-24 | 3.37 | 5.85 | 8.70 | 10.1 | 11.2 | 14.0 | 2.70 | 3.43 | 4.62 | 7.06 | 8.69 | 12.1 |
| Veh25 | 3.11 | 4.58 | 5.65 | 7.52 | 8.74 | 9.42 | 3.11 | 3.42 | 5.37 | 8.76 | 10.1 | 11.6 |
| Veh26 | 2.81 | 4.21 | 8.40 | 9.10 | 11.5 | 14.5 | 2.83 | 4.49 | 6.55 | 8.70 | 10.6 | 14.6 |
| Veh27 | 2.50 | 4.47 | 7.08 | 9.26 | 10.2 | 13.9 | 2.89 | 5.80 | 7.42 | 8.52 | 11.3 | 12.8 |
| Veh1-27 | 2.83 | 4.52 | 6.22 | 7.57 | 8.52 | 9.41 | 2.78 | 3.46 | 4.53 | 4.89 | 7.05 | 8.52 |
| Case | AFDD at Sensors 1-2-3 | AFDD at Sensors 4-5-6 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Identified ζ (%) | Identified ζ (%) | |||||||||||
| 1st | 2nd | 3rd | 4th | 5th | 6th | 1st | 2nd | 3rd | 4th | 5th | 6th | |
| Veh1-2-3 | 2.79 | 2.6 | 4.6 | 4.2 | 3.9 | 3.9 | 2.98 | 0.82 | 3.21 | 3.45 | 3.28 | 4.78 |
| Veh4-5 | 1.48 | 2.66 | 1.03 | 2.03 | 0.68 | 4.27 | 1.71 | 2.61 | 0.95 | 3.29 | 0.53 | 3.91 |
| Veh6 | 1.87 | 2.97 | 1.86 | 0.89 | 1.13 | 0.76 | 2.47 | 3.06 | 2.69 | 2.63 | 0.72 | 0.73 |
| Veh7-8-9-10 | 1.00 | 4.59 | 4.80 | 4.26 | 4.33 | 3.96 | 1.79 | 4.53 | 4.01 | 3.28 | 4.43 | 1.50 |
| Veh11-12 | 0.61 | 4.92 | 2.71 | 3.04 | 3.71 | 2.57 | 0.59 | 4.51 | 1.45 | 2.27 | 4.17 | 3.03 |
| Veh13 | 1.82 | 2.83 | 1.00 | 1.89 | 0.59 | 4.17 | 1.68 | 2.76 | 0.90 | 3.25 | 0.56 | 3.82 |
| Veh14 | 0.81 | 2.30 | 1.74 | 4.08 | 3.05 | 2.00 | 0.65 | 3.39 | 4.41 | 1.52 | 4.22 | 4.03 |
| Veh15 | 1.31 | 3.75 | 3.89 | 0.86 | 0.79 | 3.42 | 3.14 | 3.56 | 4.85 | 0.68 | 1.13 | 2.65 |
| Veh16 | 0.95 | 2.94 | 4.31 | 2.81 | 0.93 | 1.46 | 2.86 | 2.66 | 3.58 | 1.77 | 1.27 | 1.61 |
| Veh17-18 | 1.97 | 0.64 | 1.36 | 1.41 | 3.16 | 0.44 | 1.90 | 0.73 | 1.22 | 1.29 | 0.98 | 4.13 |
| Veh19 | 0.77 | 2.81 | 2.76 | 3.50 | 1.03 | 0.90 | 0.77 | 2.81 | 2.76 | 3.50 | 1.03 | 0.90 |
| Veh20 | 0.93 | 1.89 | 1.25 | 1.39 | 0.76 | 0.66 | 1.57 | 2.79 | 1.15 | 1.00 | 4.03 | 3.67 |
| Veh21-22-23-24 | 4.07 | 4.30 | 2.85 | 4.33 | 4.56 | 2.36 | 4.57 | 1.87 | 3.60 | 4.55 | 2.48 | 3.59 |
| Veh25 | 1.83 | 1.40 | 2.30 | 2.59 | 0.82 | 0.84 | 0.99 | 0.83 | 2.48 | 0.78 | 4.12 | 0.94 |
| Veh26 | 1.73 | 3.18 | 1.80 | 1.64 | 1.51 | 2.06 | 1.06 | 4.26 | 4.57 | 2.96 | 3.09 | 1.70 |
| Veh27 | 3.50 | 2.84 | 1.75 | 3.37 | 2.42 | 1.02 | 1.87 | 3.53 | 2.96 | 1.34 | 4.27 | 3.76 |
| Veh1-27 | 3.20 | 3.57 | 4.73 | 4.68 | 4.26 | 4.03 | 3.58 | 2.33 | 1.29 | 1.43 | 4.73 | 3.60 |
| Case | AFDD at Sensors 1-2-3 | AFDD at Sensors 4-5-6 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Identified Frequencies (Hz) | Identified Frequencies (Hz) | |||||||||||
| 1st | 2nd | 3rd | 4th | 5th | 6th | 1st | 2nd | 3rd | 4th | 5th | 6th | |
| Veh1…27 | 3.47 | 4.90 | 6.25 | 8.93 | 10.7 | 11.9 | 3.39 | 4.91 | 6.71 | 7.47 | 8.53 | 11.7 |
| Case | AFDD at Sensors 1-2-3 | AFDD at Sensors 4-5-6 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Identified Frequencies (Hz) | Identified Frequencies (Hz) | |||||||||||
| 1st | 2nd | 3rd | 4th | 5th | 6th | 1st | 2nd | 3rd | 4th | 5th | 6th | |
| Veh1-27 | 2.85 | 3.47 | 7.98 | 8.83 | 10.3 | 11.9 | 2.85 | 3.44 | 7.98 | 8.83 | 10.3 | 11.9 |
| Case | AFDD at Sensors 1-2-3 | AFDD at Sensors 4-5-6 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Identified Frequencies (Hz) | Identified Frequencies (Hz) | |||||||||||
| 1st | 2nd | 3rd | 4th | 5th | 6th | 1st | 2nd | 3rd | 4th | 5th | 6th | |
| Veh1-27 | 3.17 | 4.29 | 7.99 | 9.48 | 10.3 | 17.4 | 3.18 | 4.29 | 6.99 | 7.99 | 9.48 | 10.3 |
| Case | AFDD at Sensors 1-2-3 | AFDD at Sensors 4-5-6 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Identified Frequencies (Hz) | Identified Frequencies (Hz) | |||||||||||
| 1st | 2nd | 3rd | 4th | 5th | 6th | 1st | 2nd | 3rd | 4th | 5th | 6th | |
| Veh1-27 | 2.85 | 3.16 | 4.28 | 7.99 | 8.83 | 10.3 | 2.85 | 3.19 | 4.29 | 7.98 | 8.83 | 10.3 |
| Case | AFDD at Sensors 1-2-3 | AFDD at Sensors 4-5-6 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Identified Frequencies (Hz) | Identified Frequencies (Hz) | |||||||||||
| 1st | 2nd | 3rd | 4th | 5th | 6th | 1st | 2nd | 3rd | 4th | 5th | 6th | |
| Veh1-27 | 3.18 | 4.28 | 7.01 | 7.98 | 9.48 | 10.3 | 3.18 | 4.28 | 7.01 | 7.98 | 9.48 | 10.3 |
| Case Analysis | Identified Frequencies (Hz) | Remarks | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | 6th | 1st | 2nd | 3rd | 4th | 5th | 6th | |
| Raw measurements | 2.87 | 3.42 | 4.57 | 7.81 | 8.54 | Non-identified | FDD analysis | |||||
| FE modal analysis | 2.87 | 3.22 | 4.38 | 7.50 | 8.73 | 9.87 | Eigen frequencies | |||||
| Numerical analysis | 2.85 | 3.47 | 4.29 | 7.98 | 8.83 | 9.48 | Vertical and transverse axes | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papavasileiou, V.D.; Gantes, C.J.; Thanopoulos, P.; Lignos, X.A. Dynamic Response Identification of a Triple-Single Bailey Bridge Based on Vehicle Traffic-Induced Vibration Analysis. Infrastructures 2022, 7, 139. https://doi.org/10.3390/infrastructures7100139
Papavasileiou VD, Gantes CJ, Thanopoulos P, Lignos XA. Dynamic Response Identification of a Triple-Single Bailey Bridge Based on Vehicle Traffic-Induced Vibration Analysis. Infrastructures. 2022; 7(10):139. https://doi.org/10.3390/infrastructures7100139
Chicago/Turabian StylePapavasileiou, Vasileios D., Charis J. Gantes, Pavlos Thanopoulos, and Xenofon A. Lignos. 2022. "Dynamic Response Identification of a Triple-Single Bailey Bridge Based on Vehicle Traffic-Induced Vibration Analysis" Infrastructures 7, no. 10: 139. https://doi.org/10.3390/infrastructures7100139
APA StylePapavasileiou, V. D., Gantes, C. J., Thanopoulos, P., & Lignos, X. A. (2022). Dynamic Response Identification of a Triple-Single Bailey Bridge Based on Vehicle Traffic-Induced Vibration Analysis. Infrastructures, 7(10), 139. https://doi.org/10.3390/infrastructures7100139








