Influence of Wall Thickness and Water Content on the Out-of-Plane Stability of Adobe Walls
Abstract
1. Introduction
2. Methodology
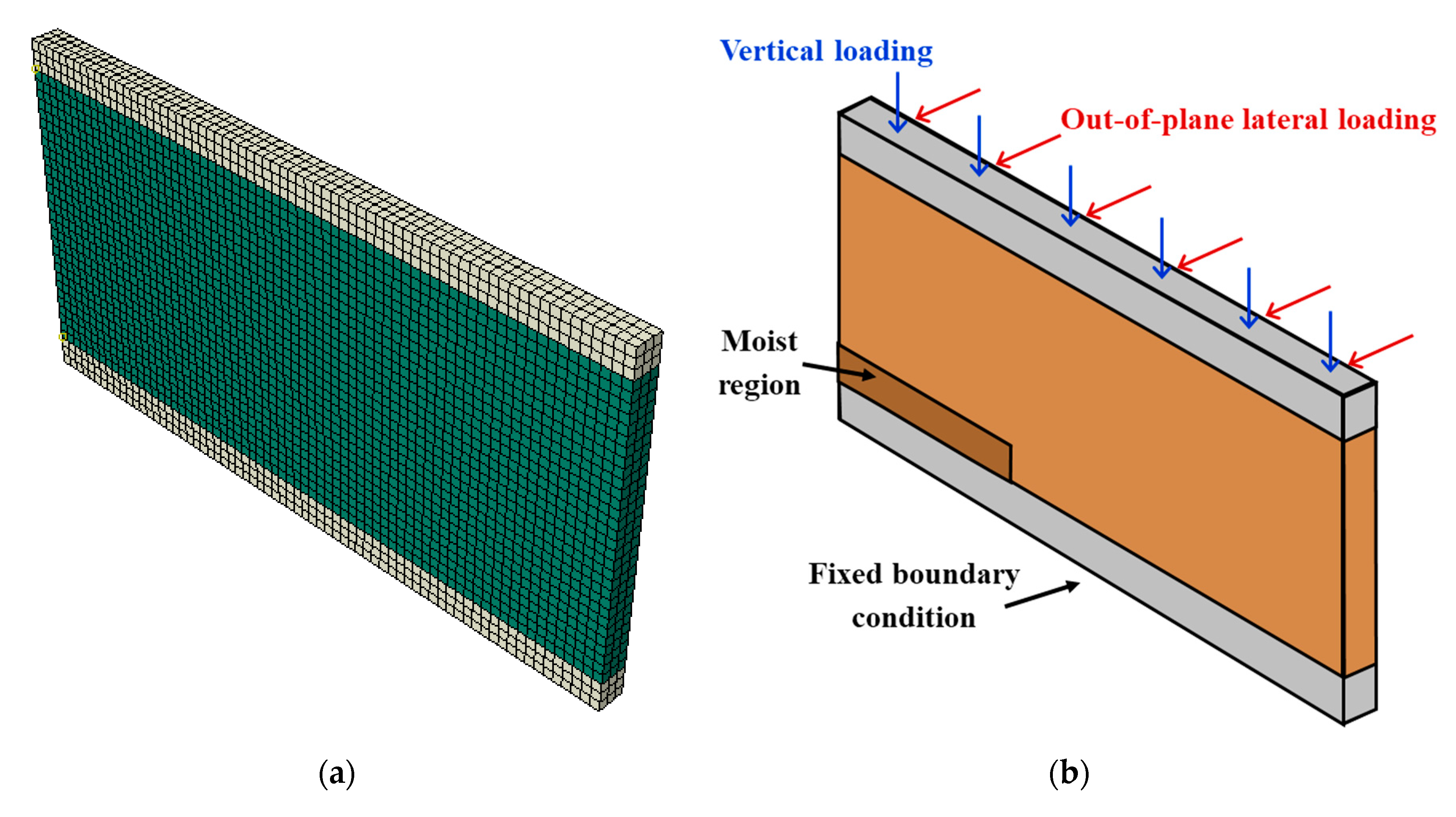
2.1. Model Geometry and Boundary Conditions
2.2. Numerical Approach
2.3. Numerical Analysis
3. Results
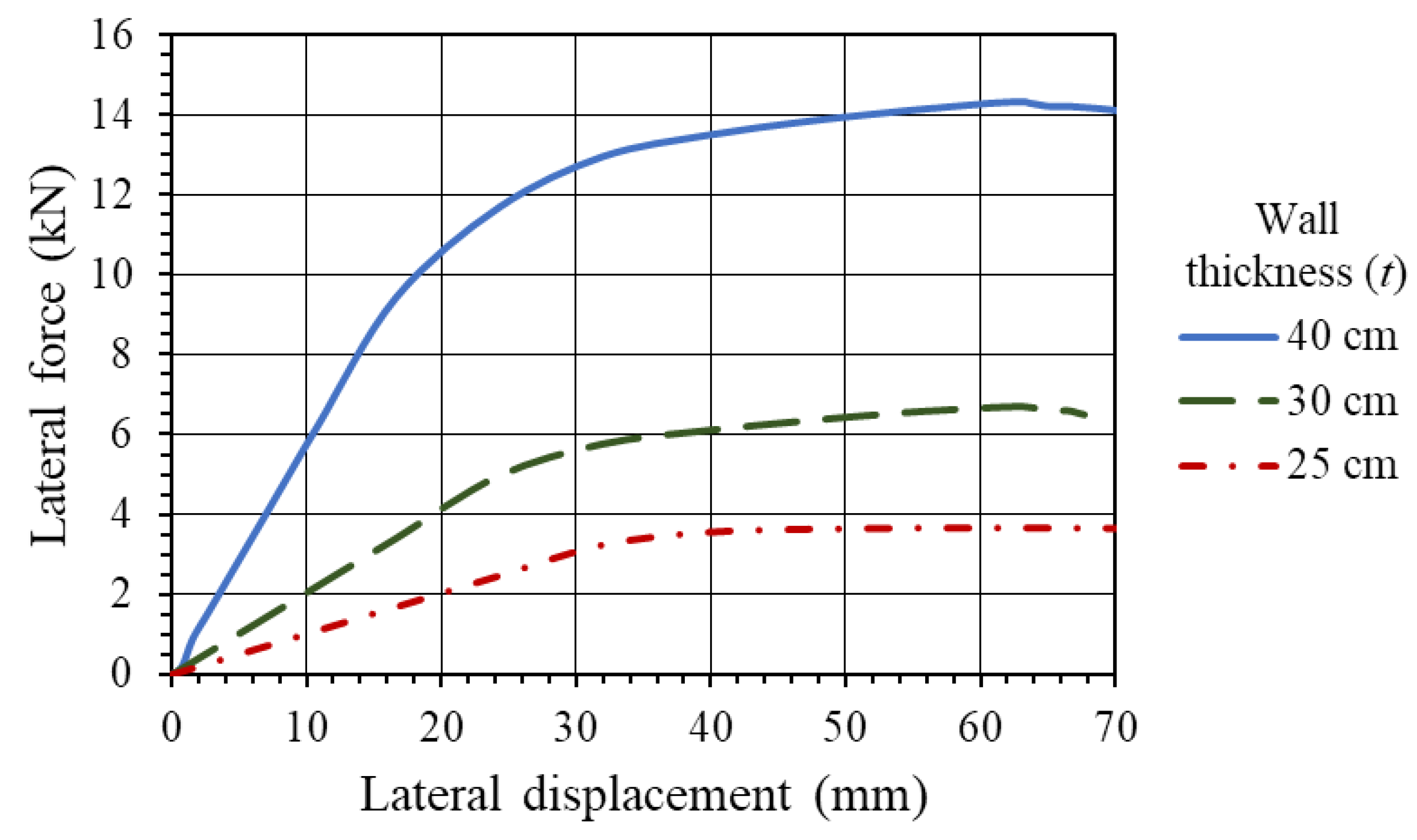
3.1. Dry Walls
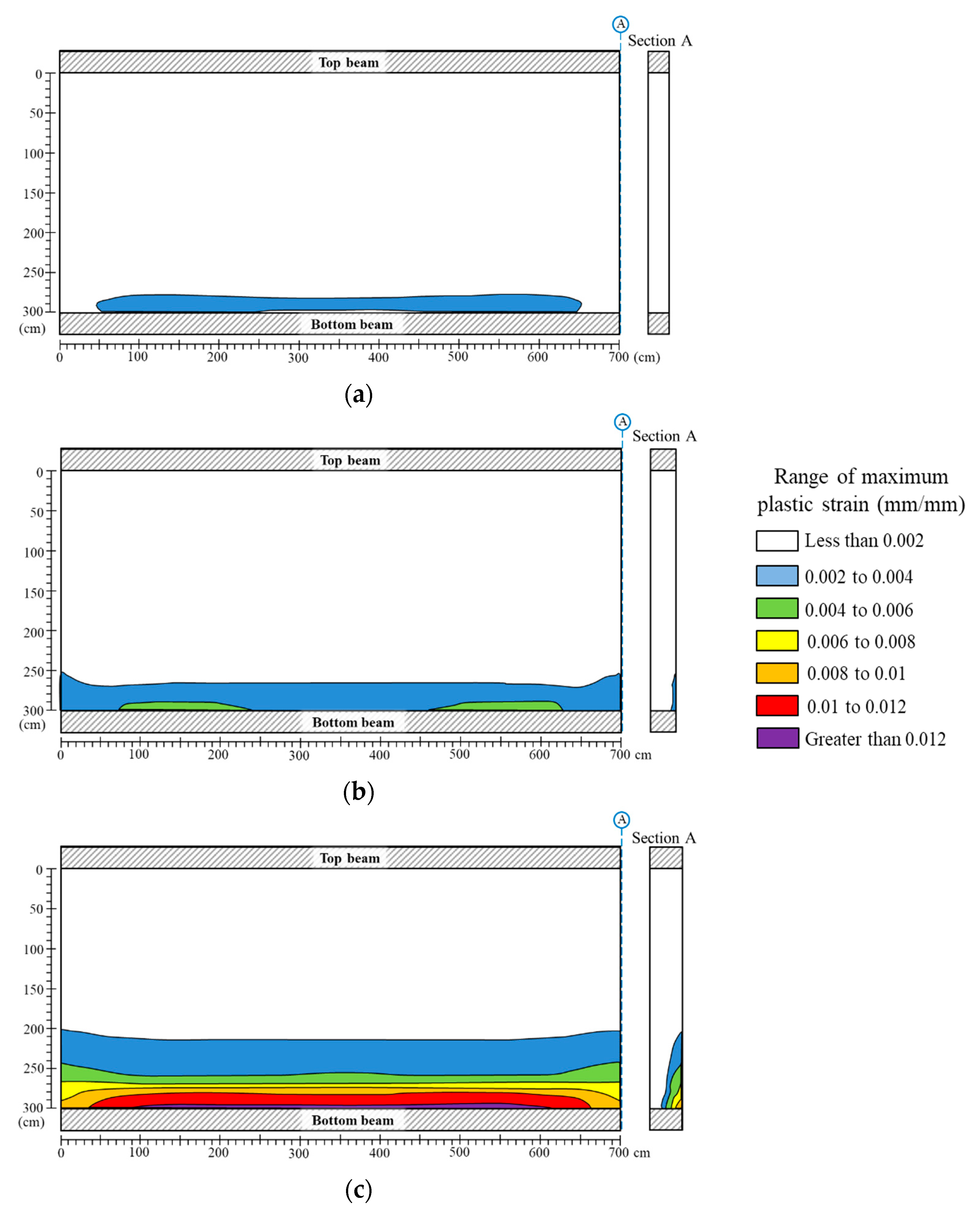
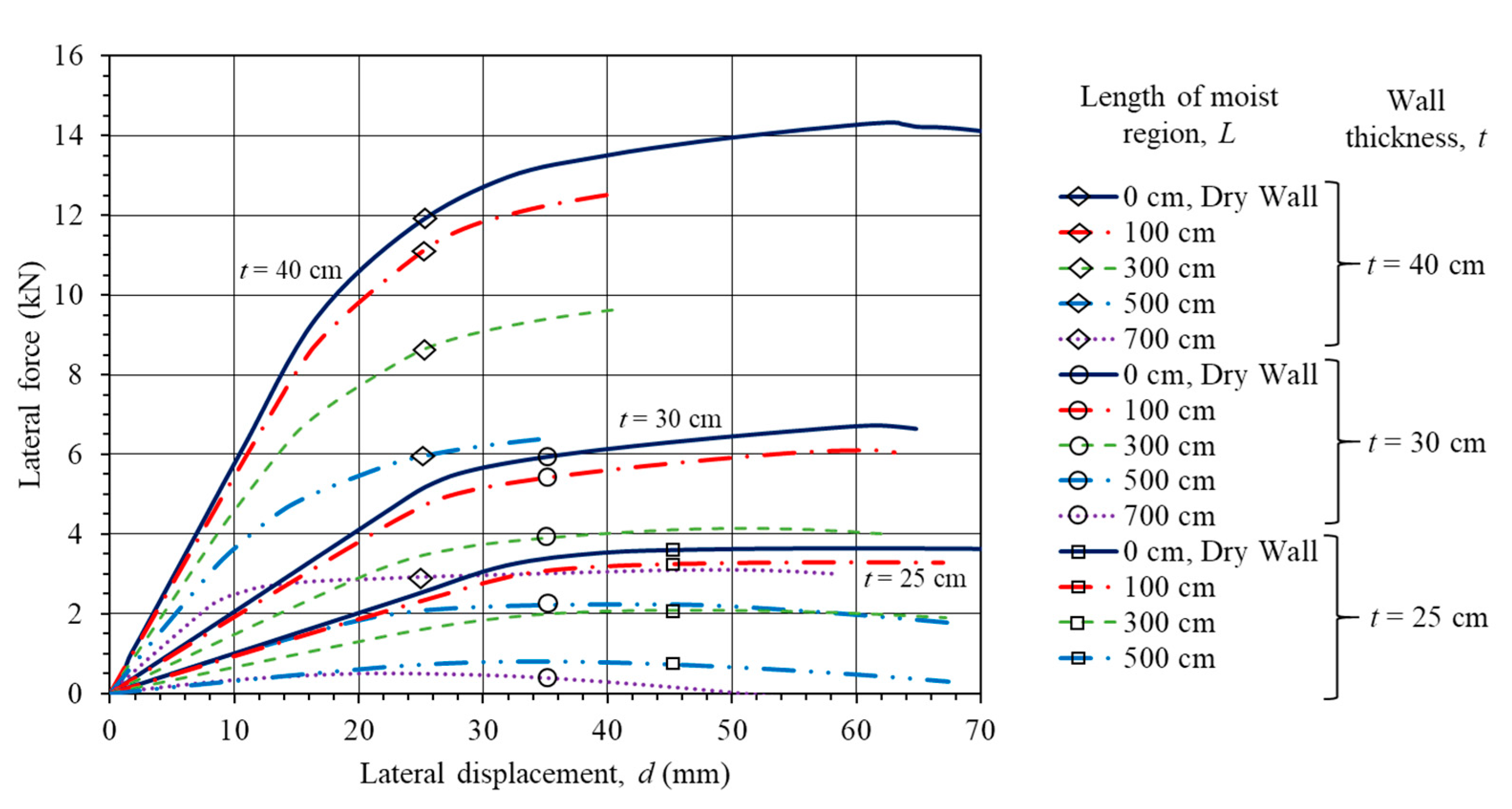
3.2. Walls with a Moist Region along the Base
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Heathcote, K. The thermal performance of earth buildings. Inf. Construcción 2011, 63, 117–126. [Google Scholar] [CrossRef]
- Rainer, L. Deterioration and pathology of earthen architecture. In Terra Literature Review, an Overview of Research in Earthen Architecture Conservation; Avrami, E., Guillaud, H., Hardy, M., Eds.; The Getty Conservation Institute: Los Angeles, CA, USA, 2008; pp. 45–61. [Google Scholar]
- National Park Service, U.S. Department of the Interior. Preservation Brief 5: Preservation of Historic Adobe Buildings. Available online: https://www.nps.gov/tps/how-to-preserve/briefs/5-adobe-buildings.htm (accessed on 25 September 2019).
- Crosby, A. Monitoring moisture at Tumacacori. Apartm. Bull. 1987, 4, 32–44. [Google Scholar] [CrossRef]
- Cornerstones Community Partnerships. Adobe Conservation: A Preservation Handbook; Sunstone Press: Santa Fe, NM, USA, 2006; pp. 51–56. [Google Scholar]
- Zelkowski, P. Sensor Installation for Monitoring of Volumetric Water Content and Temperature in Walls of a Historic Adobe Building. Master’s Thesis, New Mexico State University, Las Cruces, NM, USA, 2020. [Google Scholar]
- 2015 New Mexico Earthen Building Materials Code, Construction Industries Division of the Regulation and Licensing Department, 14.7.4 NMAC (11/15/2016). Available online: http://164.64.110.134/parts/title14/14.007.0004.html (accessed on 25 September 2019).
- Wosick, E.; Gebremariam, T.; Weldon, B.; Bandini, P.; Al-Aqtash, U. Strength characteristics of typical adobe material in the Southwestern United States. In Proceedings of the 9th International Masonry Conference, Guimarães, Portugal, 7–9 July 2014. [Google Scholar]
- Al Aqtash, U.; Bandini, P. Prediction of unsaturated shear strength of an adobe soil from the soil-water characteristic curve. Constr. Build. Mater. 2015, 98, 892–899. [Google Scholar] [CrossRef]
- Martins, T.; Fernandez, J.; Varum, H. Influence of moisture on the mechanical properties of load-bearing adobe masonry walls. Int. J. Arch. Herit. 2019, 13, 841–854. [Google Scholar] [CrossRef]
- Li Piani, T.; Weerheijm, J.; Peroni, M.; Koene, L.; Krabbenborg, D.; Solomos, G.; Sluys, L.J. Dynamic behaviour of adobe bricks in compression: The role of fibres and water content at various loading rates. Constr. Build. Mater. 2020, 230, 117038. [Google Scholar] [CrossRef]
- Zonno, G.; Aguilar, R.; Boroschek, R.; Lourenço, P.B. Experimental analysis of the thermohygrometric effects on the dynamic behavior of adobe systems. Constr. Build. Mater. 2019, 208, 158–174. [Google Scholar] [CrossRef]
- Oliver, A. Fort Selden Adobe Test Wall Project Phase I: Final Report; The Getty Conservation Institute: Los Angeles, CA, USA, 2000. [Google Scholar]
- Memari, A.M.; Grossenbacher, S.V.; Iulo, L.D. Comparative evaluation of structural and water penetration performance of three different masonry wall types for residential construction. J. Civ. Eng. Sci. 2012, 1, 9–21. [Google Scholar]
- San Bartolomé, A.; Quiun, D.; Cabrera, D.; Huaynate, W.; Romero, I.; Pereyra, J. Experimental study on adobe walls with long term water exposure due to floods. In Proceedings of the 12th Canadian Masonry Symposium, Vancouver, BC, Canada, 2–5 June 2013. [Google Scholar]
- Savary, M.; Mehdizadeh Saradj, F.; Shayganmanesh, M.; Tahmasebiboldaji, N.; Sadat Kazemi, A. Improving the adobe material properties by laser material processing. Constr. Build. Mater. 2020, 249, 118591. [Google Scholar] [CrossRef]
- Tarque, N. Numerical Modelling of the Seismic Behavior of Adobe Buildings. Ph.D. Thesis, Università degli Studi “G. d’Annunzio”, Chieti-Pescara, Italy, 2011. [Google Scholar]
- Tarque, N.; Camata, G.; Spacone, E.; Blondet, M.; Varum, H. The use of continuum model for analyzing adobe structures. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. Paper No. 0128. [Google Scholar]
- Illampas, R.; Charmpis, D.C.; Ioannou, I. Laboratory testing and finite element simulation of the structural response of an adobe masonry building under horizontal loading. Eng. Struct. 2014, 80, 362–376. [Google Scholar] [CrossRef]
- Hashemi Rafsanjani, S.; Bakhshi, A.; Ghannad, M.A.; Yekrangnia, M.; Soumi, F. Predictive tri-linear benchmark curve for in-plane behavior of adobe walls. Int. J. Arch. Herit. 2015, 9, 986–1004. [Google Scholar] [CrossRef]
- Al Aqtash, U.; Bandini, P.; Cooper, S.L. Numerical approach to model the effect of moisture in adobe masonry walls subjected to in-plane loading. Int. J. Arch. Herit. 2017, 11, 805–815. [Google Scholar] [CrossRef]
- Sadeghi, N.; Oliveira, D.; Correia, V.M.; Azizi-Bondarabadi, H.; Orduña, A. Seismic performance of historical vaulted adobe constructions: A numerical case study from Yazd, Iran. Int. J. Arch. Herit. 2018, 12, 879–897. [Google Scholar] [CrossRef]
- Parisi, F.; Balestrieri, C.; Varum, H. Nonlinear finite element model for traditional adobe masonry. Constr. Build. Mater. 2019, 223, 450–462. [Google Scholar] [CrossRef]
- Lourenço, P.B. Computational Strategies for Masonry Structures. Ph.D. Thesis, Delft University, Delft, The Netherlands, 1996. [Google Scholar]
- Blondet, M.; Madueño, I.; Torrealva, D.; Villa-García, G.; Ginocchio, F. Using industrial materials for the construction of safe adobe houses in seismic areas. In Proceedings of the Earth Build 2005, Sydney, Australia, 19–21 January 2005. [Google Scholar]
- Varela-Rivera, J.L.; Navarrete-Macias, D.; Fernandez-Baqueiro, L.E.; Moreno, E.I. Out-of-plane behaviour of confined masonry walls. Eng. Struct. 2011, 33, 1734–1741. [Google Scholar] [CrossRef]
- Bean Popehn, J.R.; Schultz, A.E.; Lu, M.; Stolarski, H.K.; Ojard, N.J. Influence of transverse loading on the stability of slender unreinforced masonry walls. Eng. Struct. 2008, 30, 2830–2839. [Google Scholar] [CrossRef]
- Blondet, M.; Vargas, J.; Tarque, N. Observed behavior of earthen structures during the Pisco earthquake (Peru). In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Dowling, D.M. Adobe housing in El Salvador: Earthquake performance and seismic improvement. In Natural Hazards in El Salvador; Rose, W.I., Bommer, J.J., López, D.I., Carr, M.J., Major, J.J., Eds.; Geological Society of America: Boulder, CO, USA, 2004; Volume 375, pp. 281–300. [Google Scholar] [CrossRef]
- Tolles, E.L.; Webster, F.A.; Crosby, A.; Kimbro, E.E. Survey of Damage to Historic Adobe Buildings after the January 1994 Northridge Earthquake; GCI Scientific Program Reports; Getty Conservation Institute: Los Angeles, CA, USA, 1996. [Google Scholar]
- Aqtash, U.A. An Experimental and Numerical Study of Moisture Effects on Soil Strength and Performance of Adobe Walls. Ph.D. Thesis, New Mexico State University, Las Cruces, NM, USA, 2014. [Google Scholar]
- Aqtash, U.A.; Bandini, P. Wall thickness and water content contribution to the out-of-plane instability of adobe walls. In Proceedings of the REHABEND 2020: 8th Euro-American Congress on Construction Pathology, Rehabilitation Technology and Heritage Management, Granada, Spain, 28 September–1 October 2020. in pressing. [Google Scholar]
- Dassault Systèmes Simulia Corp. Abaqus 17.0 Analysis User’s Manual; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2017. [Google Scholar]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids. Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Standards New Zealand. NZS 4297: Engineering Design of Earth Buildings; Standards New Zealand: Wellington, New Zealand, 1998. [Google Scholar]



| Material Input Set | Range of w (%) | Initial Compressive Failure Stress (MPa) | Tensile Failure Stress (MPa) |
|---|---|---|---|
| Nearly dry (Dry wall) | 1 to 3 | 0.514 | 0.051 |
| Partially saturated (Scenario wps) | 7 to 9 | 0.125 | 0.010 |
| Nearly saturated (Scenario wns) | 13 to 15 | 0.028 | 0.002 |
| Length of Moist Region, L (cm) | Partially Saturated (Scenario wps) | Nearly Saturated (Scenario wns) | ||||
|---|---|---|---|---|---|---|
| t = 25 cm | t = 30 cm | t = 40 cm | t = 25 cm | t = 30 cm | t = 40 cm | |
| 0 (Dry wall) | 3.7 | 6.7 | 14.3 | 3.7 | 6.7 | 14.3 |
| 100 | 3.5 | 6.4 | 13.6 | 3.3 | 6.1 | 12.5 |
| 300 | 2.8 | 5.3 | 11.5 | 2.1 | 4.1 | 9.6 |
| 500 | 2.2 | 4.1 | 9.4 | 0.8 | 2.2 | 6.4 |
| 700 | 1.8 | 3.2 | 7.7 | 0.0 | 0.5 | 3.1 |
| Length of Moist Region, L (cm) | Partially Saturated (Scenario wps) | Nearly Saturated (Scenario wns) | ||||
|---|---|---|---|---|---|---|
| t = 25 cm | t = 30 cm | t = 40 cm | t = 25 cm | t = 30 cm | t = 40 cm | |
| 100 | 0.95 | 0.95 | 0.95 | 0.90 | 0.91 | 0.87 |
| 300 | 0.76 | 0.79 | 0.80 | 0.57 | 0.62 | 0.67 |
| 500 | 0.61 | 0.62 | 0.66 | 0.22 | 0.33 | 0.45 |
| 700 | 0.50 | 0.47 | 0.53 | 0.00 | 0.08 | 0.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Aqtash, U.; Bandini, P. Influence of Wall Thickness and Water Content on the Out-of-Plane Stability of Adobe Walls. Infrastructures 2020, 5, 78. https://doi.org/10.3390/infrastructures5090078
Al Aqtash U, Bandini P. Influence of Wall Thickness and Water Content on the Out-of-Plane Stability of Adobe Walls. Infrastructures. 2020; 5(9):78. https://doi.org/10.3390/infrastructures5090078
Chicago/Turabian StyleAl Aqtash, Umaima, and Paola Bandini. 2020. "Influence of Wall Thickness and Water Content on the Out-of-Plane Stability of Adobe Walls" Infrastructures 5, no. 9: 78. https://doi.org/10.3390/infrastructures5090078
APA StyleAl Aqtash, U., & Bandini, P. (2020). Influence of Wall Thickness and Water Content on the Out-of-Plane Stability of Adobe Walls. Infrastructures, 5(9), 78. https://doi.org/10.3390/infrastructures5090078







