Maintenance Modelling of Ceramic Claddings in Pitched Roofs Based on the Evaluation of Their In Situ Degradation Condition
Abstract
1. Introduction
2. Background
3. Methodology
3.1. Maintenance Model
3.2. Deterioration Process
3.3. Life Cycle Cost Analysis
3.4. Efficiency Index and Performance Indicator
4. Case Study: Ceramic Claddings in Pitched Roofs (CCPR)
4.1. Degradation Process
4.1.1. Probabilistic Analysis
4.1.2. Validation
4.1.3. Service Life
4.2. Maintenance Strategies, Assumptions and Costs
4.2.1. Costs of the Interventions
- Minor level: the total area CCPR mainly affected by surface soiling, and accumulation of the debris (anomaly AE-E1) is cleaned. This action includes personal protective equipment (protection fall) installation and low-pressure water jet cleaning.
- Moderate level: the total area CCPR mainly affected by surface dirt, accumulation of debris and biological colonisation (anomaly AE-E1) is cleaned. This action includes personal protective equipment (protection fall) installation, low-pressure water jet cleaning and use of biocides to eliminate biological microorganisms.
- Extensive level: the total area CCPR extensively affected by surface dirt, accumulation of debris, biological colonisation and parasitic vegetation (anomaly AE-E1) is cleaned. This action includes personal protective equipment (protection fall) installation, low-pressure water jet cleaning, the use of biocides to eliminate biological microorganisms and the use of herbicides and manual removal of parasitic vegetation.
- Minor level: cleaning operation of moderate level: repair and/or replacement up to 15% of the cladding affected by peeling/flaking/exfoliation (anomaly AE-F1), replacement up to 5% of the cladding affected by cracking/fracture (anomaly AE-F2), repair up to 5% of the cladding affected by detachment/cladding release (anomaly AE-F3) and repair up to 13% of the cladding affected by misalignment of the cladding (anomaly AE-S2), including replacement of the rafters/framing (tiles supporting system) in a suitable area (when necessary).
- Moderate level: cleaning operation of moderate level: repair and/or replacement up to 23% of the cladding affected by peeling/flaking/exfoliation (anomaly AE-F1), replacement up to 8% of the cladding affected by cracking/fracture (anomaly AE-F2), repair or replacement up to 5% of the cladding affected by detachment/cladding release (anomaly AE-F3) and repair up to 19% of the cladding affected by misalignment of the cladding (anomaly AE-S2), including replacement of the rafters/framing in a suitable area (when necessary).
- Extensive level: cleaning operation of moderate level: repair and/or replacement up to 30% of the cladding affected by peeling/flaking/exfoliation (anomaly AE-F1), replacement up to 10% of the cladding affected by cracking/fracture (anomaly AE-F2), replacement up to 5% of the cladding affected by detachment/cladding release (anomaly AE-F3) and repair up to 25% of the cladding affected by misalignment of the cladding (anomaly AE-S2), including replacement of the rafters/framing in a suitable area (when necessary).
4.2.2. Impacts of the Interventions
4.2.3. Inspection Frequency
4.2.4. Constraints
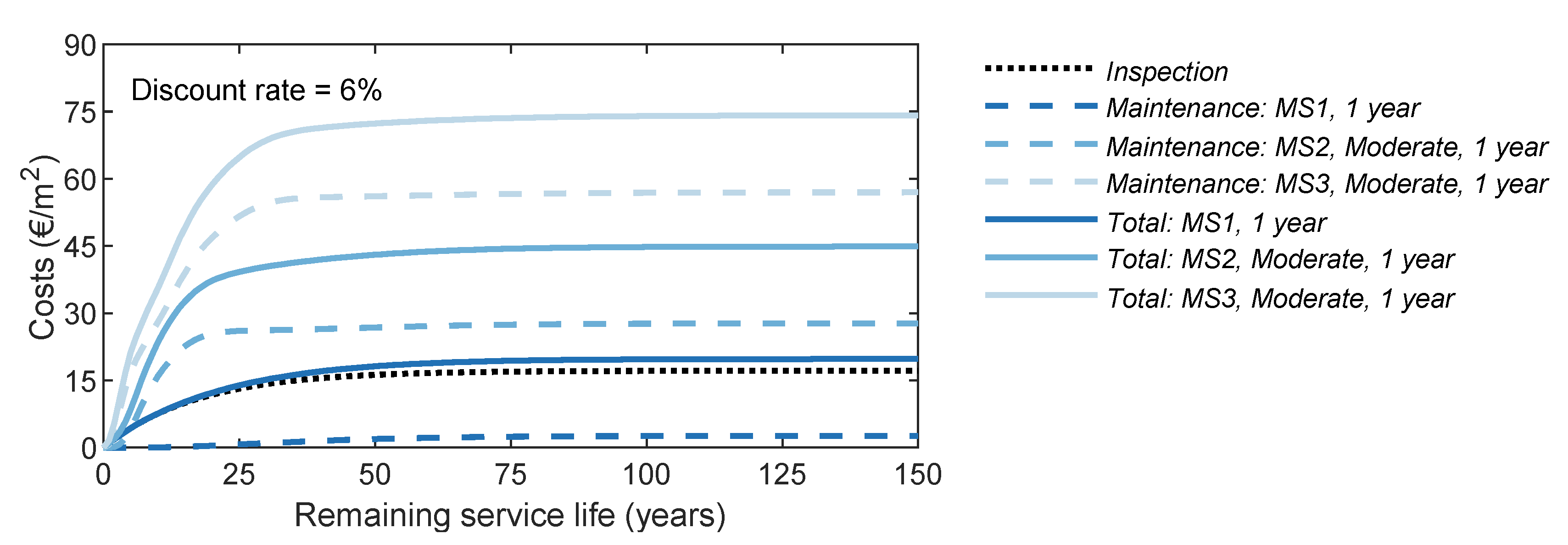
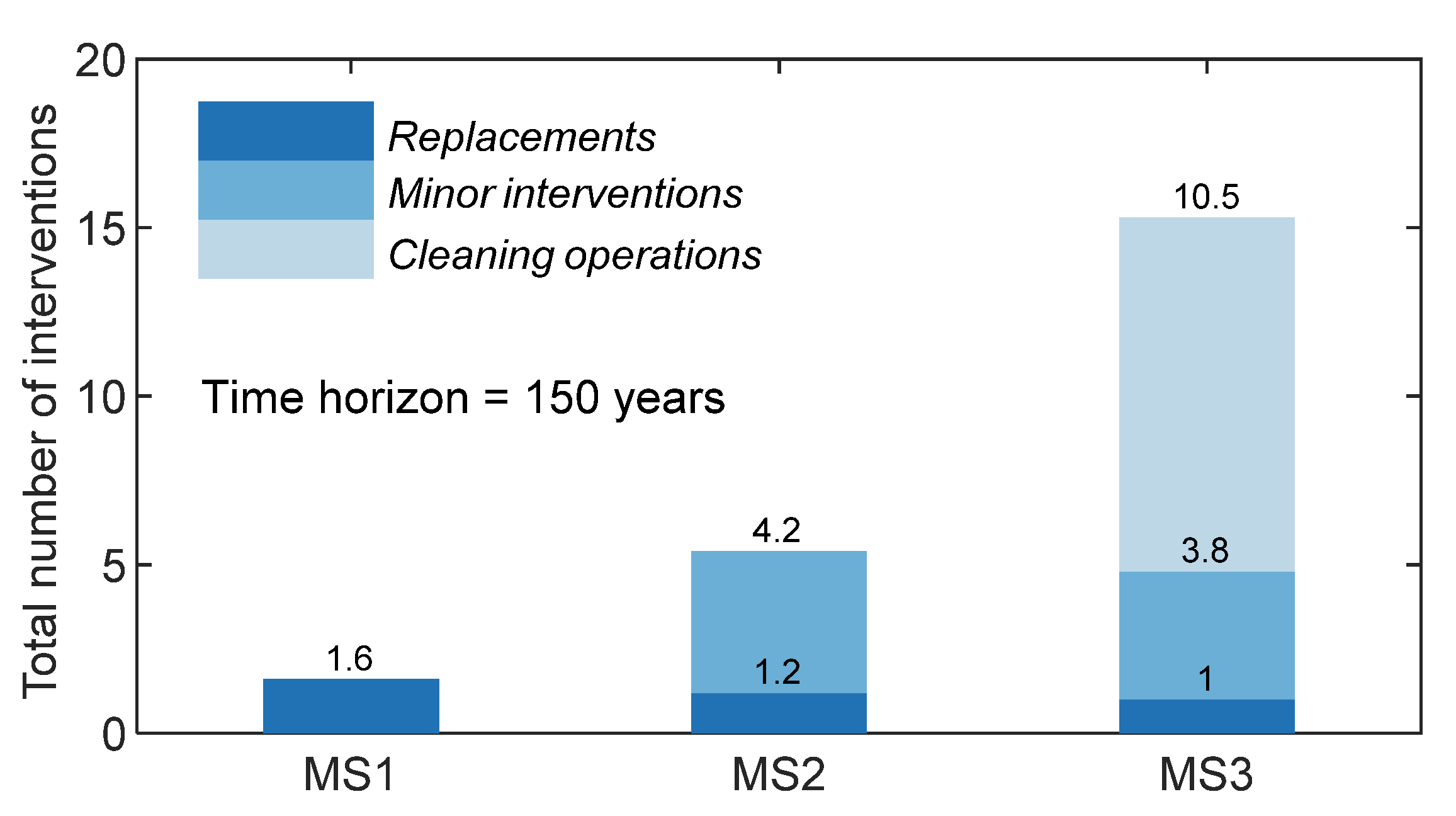
4.3. Maintenance Strategies Comparison
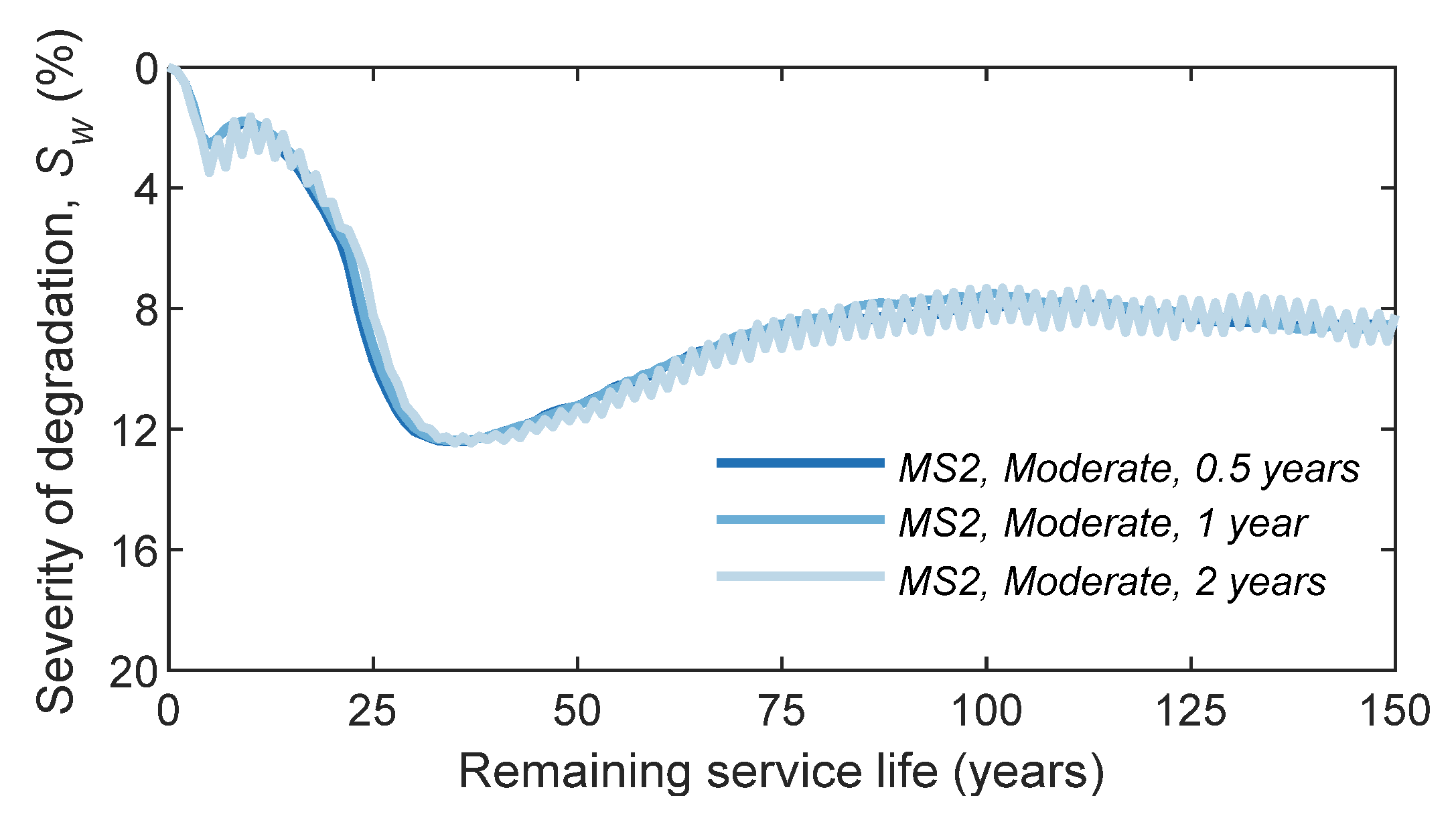
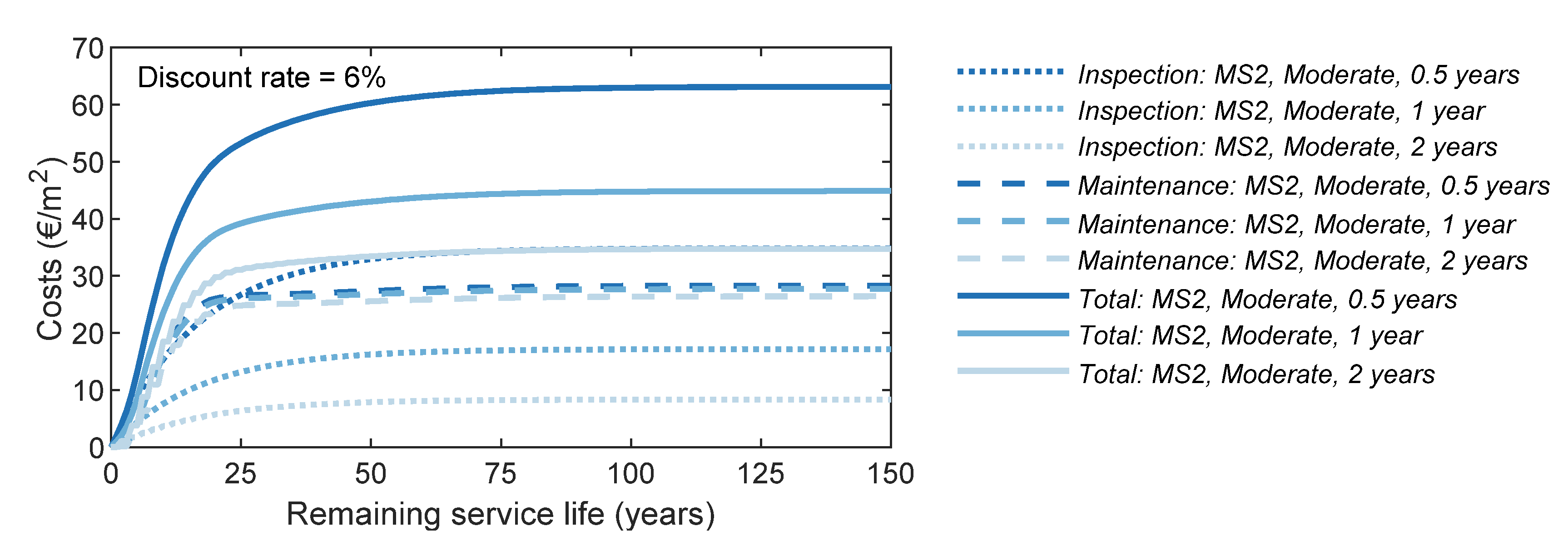
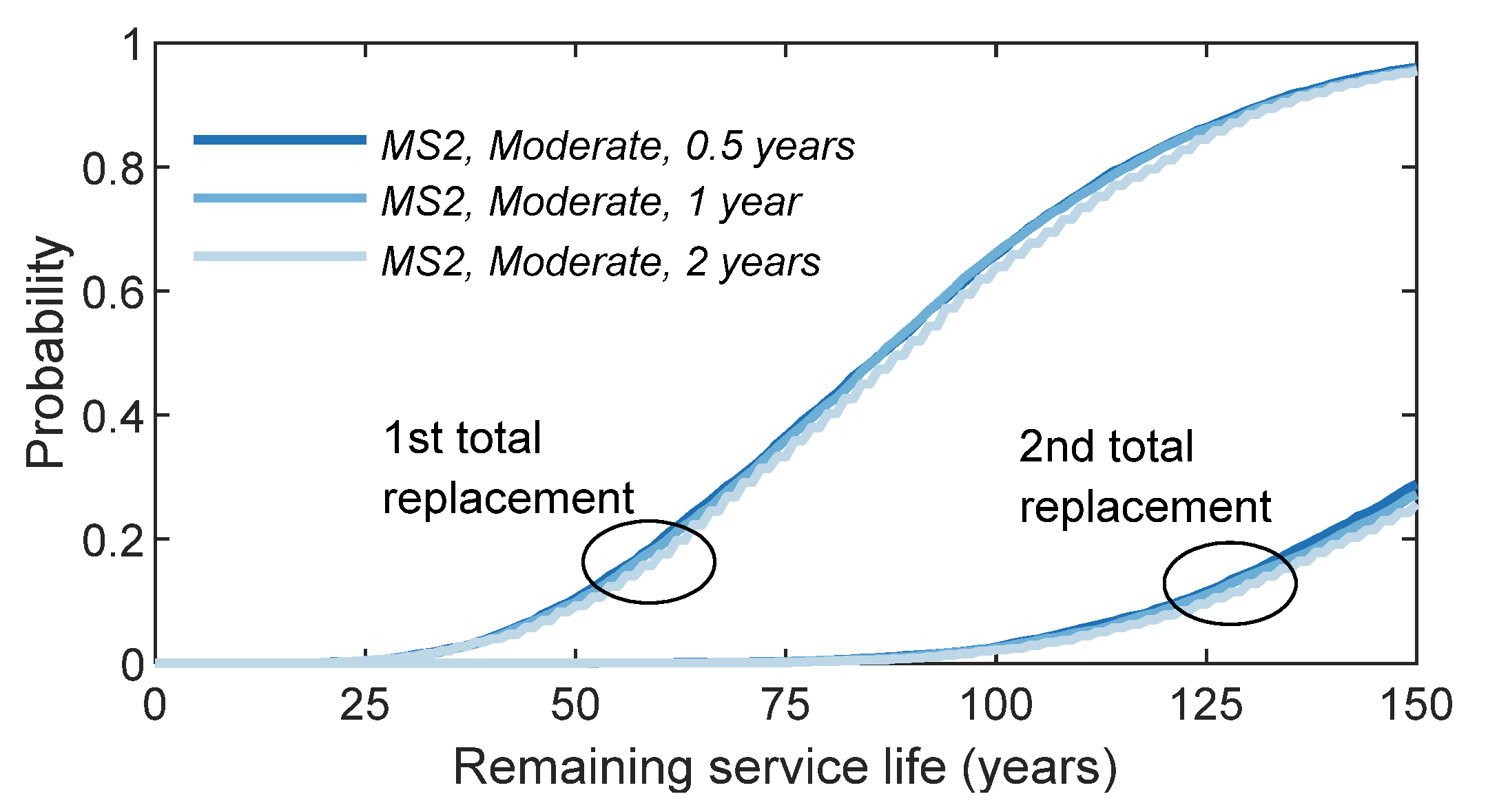
4.4. Inspection Frequency Sensitivity Analysis
5. Multi-Criteria Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shohet, I.M. Key performance indicators for strategic healthcare facilities maintenance. J. Constr. Eng. Manag. 2006, 132, 345–352. [Google Scholar] [CrossRef]
- Lind, H.; Muying, H. Building maintenance strategies: Planning under uncertainty. Prop. Manag. 2012, 30, 14–28. [Google Scholar] [CrossRef]
- Silva, A.; de Brito, J. Do we need a buildings’ inspection, diagnosis and service life prediction software? J. Build. Eng. 2019, 22, 335–348. [Google Scholar] [CrossRef]
- Falorca, J.F. Main functions for building maintenance management: An outline application. Int. J. Build. Pathol. Adapt. 2019, 37, 490–509. [Google Scholar] [CrossRef]
- Eurostat. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Construction_production_(volume)_index_overview (accessed on 15 July 2020).
- Shohet, I.M.; Puterman, M.; Gilboa, E. Deterioration patterns of building cladding components for maintenance management. Constr. Manag. Econ. 2002, 20, 305–314. [Google Scholar] [CrossRef]
- Mobley, R.K. Maintenance Engineering Handbook, 8th ed.; McGraw-Hill Professional: New York, NY, USA, 2014. [Google Scholar]
- Dann, N.; Cantell, T. Maintenance: From philosophy to practice. J. Archit. Conserv. 2005, 11, 42–54. [Google Scholar] [CrossRef]
- Chan, D.W. Sustainable building maintenance for safer and healthier cities: Effective strategies for implementing the Mandatory Building Inspection Scheme (MBIS) in Hong Kong. J. Build. Eng. 2019, 24. [Google Scholar] [CrossRef]
- Ashworth, A. Estimating the life expectancies of building components in life-cycle costing calculations. Struct. Surv. 1996, 14, 4–8. [Google Scholar] [CrossRef]
- Sherwin, D. A review of overall models for maintenance management. J. Qual. Maint. Eng. 2000, 6, 138–164. [Google Scholar] [CrossRef]
- Forster, A.M.; Kayan, B. Maintenance for historic buildings: A current perspective. Struct. Surv. 2009, 27, 210–229. [Google Scholar] [CrossRef]
- Ruparathna, R.; Hewage, K.; Sadiq, R. Multi-period maintenance planning for public buildings: A risk based approach for climate conscious operation. J. Clean. Prod. 2018, 170, 1338–1353. [Google Scholar] [CrossRef]
- BS 8298-1. Code of Practice for the Design and Installation of Natural Stone Cladding and Linin—Part 1: General; British Standards Institution (BSI): London, UK, 2010. [Google Scholar]
- Sandak, A.; Sandak, J.; Brzezicki, M.; Riggio, M. Bio-Based Building Skin; Springer International Publishing: Gateway East, Singapore, 2019. [Google Scholar]
- Garcez, N.; Lopes, N.; de Brito, J.; Silvestre, J. System of inspection, diagnosis and repair of external claddings of pitched roofs. Constr. Build. Mater. 2012, 35, 1034–1044. [Google Scholar] [CrossRef]
- Ilozor, B.D.; Okoroh, M.I.; Egbu, C.E. Understanding residential house defects in Australia from the State of Victoria. Build. Environ. 2004, 39, 327–337. [Google Scholar] [CrossRef]
- Watt, D.S. Building Pathology: Principles and Practice, 2nd ed.; Blackwell Publishing Ltd.: Oxford, UK, 2009. [Google Scholar]
- Yazdani, N.; Dowgul, R.W.; Manzur, T. Deficiency analysis of coastal buildings toward storm damage reduction. J. Perform. Constr. Facil. 2010, 24, 128–137. [Google Scholar] [CrossRef]
- Gullbrekken, L.; Kvande, T.; Jelle, B.P.; Time, B. Norwegian pitched roof defects. Buildings 2016, 6, 24. [Google Scholar] [CrossRef]
- Morgado, J.; Flores-Colen, I.; de Brito, J.; Silva, A. Maintenance planning of pitched roofs in current buildings. J. Constr. Eng. Manag. 2017, 143. [Google Scholar] [CrossRef]
- Kyle, B.R.; Kalinger, P. Service life prediction of roof systems by reliability-based analysis. In Proceedings of the 4th International Symposium on Roofing Technology, Gaithersburg, MD, USA, 17–19 September 1997. [Google Scholar]
- Garcez, N.; Lopes, N.; de Brito, J.; Sá, G. Pathology, diagnosis and repair of pitched roofs with ceramic tiles: Statistical characterisation and lessons learned from inspections. Constr. Build. Mater. 2012, 36, 807–819. [Google Scholar] [CrossRef]
- Ferreira, C.; Neves, L.C.; Silva, A.; de Brito, J. Stochastic maintenance models for ceramic claddings. Struct. Infrastruct. Eng. 2020, 16, 247–265. [Google Scholar] [CrossRef]
- Meijer, F.; Itard, L.; Sunikka-Blank, M. Comparing European residential building stocks: Performance, renovation and policy opportunities. Build. Res. Inf. 2009, 37, 533–551. [Google Scholar] [CrossRef]
- Da Silva, J.M.; Vicente, R. Pathology and defect of building façades and roofs: A state-of-the-art report on building pathology. In Building Pathology; de Freitas, V.P., Ed.; Conseil International du Bâtiment: Rotterdam, The Netherlands, 2013; pp. 123–131. [Google Scholar]
- INE. Censos 2011 Resultados Definitivos—Portugal; Instituto Nacional de Estatística: Lisbon, Portugal, 2012. [Google Scholar]
- Zhang, Y.; Vidakovic, B.; Augenbroe, G. Uncertainty analysis in using Markov chain model to predict roof life cycle performance. In Proceedings of the 10DBMC International Conference on Durability of Building Materials and Components, Lyon, France, 17–19 April 2005. [Google Scholar]
- Alaimo, G.; Accurso, F. The methods for the durability evaluation of pitched roof. In CIB W80 WG3—Test Methods for Service Life Prediction—State of the Art Report on Accelerated Laboratory Test Procedures and Correlation between Laboratory Tests and Service Life Data; Daniotti, B., Re Cecconi, F., Eds.; Conseil International du Bâtiment: Rotterdam, The Netherlands, 2010; pp. 3–13. [Google Scholar]
- ISO 15686-1. Buildings and Constructed Assets—Service Life Planning—Part 2: Service Life Prediction Procedures; International Organization for Standardization (ISO): Geneva, Switzerland, 2012. [Google Scholar]
- Rudbeck, C. Service life of building envelope components: Making it operational in economical assessment. Constr. Build. Mater. 2002, 16, 83–89. [Google Scholar] [CrossRef]
- Ramos, R.; Silva, A.; de Brito, J.; Gaspar, P.L. Methodology for the service life prediction of ceramic claddings in pitched roofs. Constr. Build. Mater. 2018, 166, 386–399. [Google Scholar] [CrossRef]
- Gaspar, P.L.; de Brito, J. Limit states and service life of cement renders on façades. J. Mater. Civ. Eng. 2011, 23, 1396–1404. [Google Scholar] [CrossRef]
- Flores-Colen, I.; de Brito, J.; Freitas, V. Discussion of criteria for prioritization of predictive maintenance of building façades: Survey of 30 experts. J. Perform. Constr. Facil. 2010, 24, 337–344. [Google Scholar] [CrossRef]
- Flores-Colen, I.; de Brito, J. A systematic approach for maintenance budgeting of buildings façades based on predictive and preventive strategies. Constr. Build. Mater. 2010, 24, 1718–1729. [Google Scholar] [CrossRef]
- Flores-Colen, I.; de Brito, J. Discussion of proactive maintenance strategies in façades’ coatings of social housing. J. Build. Apprais. 2010, 5, 223–240. [Google Scholar] [CrossRef]
- Madureira, S.; Flores-Colen, I.; de Brito, J.; Pereira, C. Maintenance planning of façades in current buildings. Constr. Build. Mater. 2017, 147, 790–802. [Google Scholar] [CrossRef]
- Ferreira, C.; Silva, A.; de Brito, J.; Dias, I.S.; Flores-Colen, I. Definition of a condition-based model for natural stone claddings. J. Build. Eng. 2020. [Google Scholar] [CrossRef]
- Molloy, M.K. Performance analysis using stochastic Petri nets. IEEE Trans. Comput. 1982, 913–917. [Google Scholar] [CrossRef]
- Butt, A.A.; Shahin, M.Y.; Feighan, K.J.; Carpenter, S.H. Pavement performance prediction model using the Markov process. Transp. Res. Rec. 1987, 1123, 12–19. [Google Scholar]
- Hawk, H.; Small, E.P. The BRIDGIT bridge management system. Struct. Eng. Int. 1998, 8, 309–314. [Google Scholar] [CrossRef]
- Thompson, P.D.; Small, E.P.; Johnson, M.; Marshall, A.R. The Pontis bridge management system. Struct. Eng. Int. 1998, 8, 303–308. [Google Scholar] [CrossRef]
- Ortiz-García, J.J.; Costello, S.B.; Snaith, M.S. Derivation of transition probability matrices for pavement deterioration modeling. J. Transp. Eng. 2006, 132, 141–161. [Google Scholar] [CrossRef]
- McDuling, J.; Horak, E.; Cloete, C. Service life prediction beyond the ‘factor method’. In Proceedings of the 11DBMC International Conference on Durability of Building Materials and Components, Istanbul, Turkey, 11–14 May 2008. [Google Scholar]
- Caleyo, F.; Velázquez, J.C.; Valor, A.; Hallen, J.M. Markov chain modelling of pitting corrosion in underground pipelines. Corros. Sci. 2009, 51, 2197–2207. [Google Scholar] [CrossRef]
- Silva, A.; de Brito, J.; Gaspar, P.L. Methodologies for Service Life Prediction of Buildings: With a Focus on Façade Claddings; Springer International Publishing: Zurich, Switzerland, 2016. [Google Scholar]
- Sánchez-Silva, M.; Klutke, G.A. Reliability and Life-Cycle Analysis of Deteriorating Systems; Springer International Publishing: Zurich, Switzerland, 2016. [Google Scholar]
- Kalbfleisch, J.D.; Lawless, J.F. The analysis of panel data under a Markov assumption. J. Am. Stat. Assoc. 1985, 80, 863–871. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Kallen, M.J.; van Noortwijk, J.M. Probabilistic models for lifecycle performance of deteriorating structures: Review and future directions. Prog. Struct. Eng. Mater. 2004, 6, 197–212. [Google Scholar] [CrossRef]
- Langdon, D. Life Cycle Costing (LCC) as a Contribution to Sustainable Construction. Guidance on the Use of the LCC Methodology and Its Application in Public Procurement; Davis Langdon Management Consulting: London, UK, 2007. [Google Scholar]
- Housing Association Property Mutual (HAPM). Component Life Manual; E&FN Spon: London, UK, 1999. [Google Scholar]
- RICS. Building Maintenance: Strategy, Planning and Performance; Royal Institution of Chartered Surveyors (RICS): London, UK, 2000. [Google Scholar]
- Bauer, M.; Lair, J.; Wetzel, C. Predictive Model for Future Deterioration; INVESTIMMO Project, Final Technical Report; European Commission: Brussels, Belgium, 2004. [Google Scholar]
- NRCA. The Green roof Systems Manual; National Roofing Contractors Association (NRCA): Rosemont, IL, USA, 2007. [Google Scholar]
- National Association of Home Builders (NAHB). Bank of America Home Equity Study of Life Expectancy of Home Components; Economics Group: Washington, DC, USA, 2007. [Google Scholar]
- Madrigal, L.O.; Lanzarote, B.S.; Bretones, J.M.F. Proposed method of estimating the service life of building envelope. Rev. Constr. 2015, 14, 60–68. [Google Scholar]
- Bechthold, M.; Kane, A.; King, N. Ceramic Material Systems: In Architecture and Interior Design; Birkhäuser: Basel, Switzerland, 2015. [Google Scholar]
- Thai-Ker, L.; Chung-Wan, W. Challenges of external wall tiling in Singapore. In Proceedings of the Qualicer 2006: IX World Congress on Ceramic Tile Quality, Castellón, Spain, 12–15 February 2006. [Google Scholar]
- Raposo, S.; de Brito, J.; Fonseca, M. Planned preventive maintenance activities: Analysis of guidance documents. In Durability of Buildings Materials and Components; de Freitas, V.P., Delgado, J.M.P.Q., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 35–60. [Google Scholar]
- CYPE Price Generator. Available online: http://www.geradordeprecos.info/ (accessed on 24 April 2020).
- Ferreira, C.; Silva, A.; de Brito, J.; Dias, I.S.; Flores-Colen, I. The impact of imperfect maintenance actions on the degradation of buildings’ envelope components. J. Build. Eng. 2020, 33. [Google Scholar] [CrossRef]
- Bana e Costa, C.A. Três convicções fundamentais na prática do apoio à decisão. Soc. Bras. Pesqui. Oper. 1993, 13, 9–20. [Google Scholar]
- Dodgson, J.S.; Spackman, M.; Pearman, A.; Phillips, L.D. Multi-Criteria Analysis: A manual; Department for Communities and Local Government: London, UK, 2009.
- Cochran, J.K.; Chen, H.N. Fuzzy multi-criteria selection of object-oriented simulation software for production system analysis. Comput. Oper. Res. 2005, 32, 153–168. [Google Scholar] [CrossRef]





| Degradation Condition | Anomalies | ka,n | % Area Affected | Severity of Degradation [%] | |
|---|---|---|---|---|---|
| A (kn = 0) | No visible degradation | - | - | Sw ≤ 1 | |
| B (kn = 1) | Aesthetic | Development of parasitic vegetation/biological colonisation | 0.55 | ≤10 | 1 < Sw ≤ 6 |
| Staining, change of colour or of brightness of the tiles | 0.20 | ≤20 | |||
| Functional | Peeling/flaking/exfoliation | 1.00 | ≤10 | ||
| Structural | Misalignment of the cladding | 1.00 | ≤10 | ||
| C (kn = 2) | Aesthetic | Development of parasitic vegetation/biological colonisation | 0.55 | >10 and ≤30 | 6 < Sw ≤ 20 |
| Staining, change of colour or of brightness of the tiles | 0.20 | >20 and ≤50 | |||
| Functional | Peeling/flaking/exfoliation | 1.00 | >10 and ≤30 | ||
| Cracking/fracture | 1.00 | ≤10 | |||
| Detachment/cladding release | 0.20 | ≤5 | |||
| Structural | Pronounced cladding deformation | 1.30 | ≤25 | ||
| Misalignment of the cladding | 1.00 | >10 and ≤25 | |||
| D (kn = 3) | Aesthetic | Development of parasitic vegetation/biological colonisation | 0.55 | >30 and ≤50 | 20 < Sw ≤ 50 |
| Staining, change of colour or of brightness of the tiles | 0.20 | >50 | |||
| Functional | Peeling/flaking/exfoliation | 1.00 | >30 and ≤50 | ||
| Cracking/fracture | 1.00 | >10 and ≤30 | |||
| Detachment/cladding release | 0.20 | >5 and ≤10 | |||
| Structural | Pronounced cladding deformation | 1.30 | >25 and ≤50 | ||
| Misalignment of the cladding | 1.00 | >25 and ≤50 | |||
| E (kn = 4) | Aesthetic | Development of parasitic vegetation/biological colonisation | 0.55 | >50 | Sw > 50 |
| Functional | Peeling/flaking/exfoliation | 1.00 | >50 | ||
| Cracking/fracture | 1.00 | >30 | |||
| Detachment/cladding release | 0.20 | >10 | |||
| Structural | Pronounced cladding deformation | 1.30 | >50 | ||
| Misalignment of the cladding | 1.00 | >50 | |||
| Sojourn Time in Each Degradation Condition | Exponential | Weibull | Lognormal | |
|---|---|---|---|---|
| Mean time–T (years) | TA | 2.7 | 2.8 | 2.7 |
| TB | 5.1 | 4.5 | 4.6 | |
| TC | 148.2 | 67.9 | 91.6 | |
| TD | 7.19 × 104 | 68.1 | 1.87 × 108 | |
| Standard deviation–SD (years) | SDA | 2.7 | 1.2 | 1.5 |
| SDB | 5.1 | 2.6 | 3.4 | |
| SDC | 148.2 | 31.2 | 75.9 | |
| SDD | 7.19 × 104 | 3.1 | 5.33 × 109 | |
| - log L | 76.61 | 68.41 | 70.13 | |
| Degradation Condition | A | B | C | D | E | |
|---|---|---|---|---|---|---|
| Observed | 13 | 13 | 96 | 24 | 0 | |
| Predicted | Exponential | 11.0 | 14.1 | 96.8 | 24.0 | 0.0 |
| Weibull | 12.8 | 13.1 | 97.1 | 23.0 | 0.0 | |
| Lognormal | 12.9 | 12.4 | 97.8 | 22.9 | 0.0 | |
| Relative error (%) | Exponential | 15.1 | 8.4 | 0.9 | 0.1 | - |
| Weibull | 1.5 | 0.5 | 1.2 | 4.2 | - | |
| Lognormal | 0.8 | 4.3 | 1.8 | 4.6 | - | |
| Degradation Condition | Observed | Predicted | Relative Error | |||
|---|---|---|---|---|---|---|
| MC | PN | MC (%) | PN (%) | MC/PN | ||
| A | 13 | 11.4 | 11.0 | 12.0 | 15.1 | 1.0 |
| B | 13 | 14.5 | 14.1 | 11.7 | 8.4 | 1.0 |
| C | 96 | 89.8 | 96.8 | 6.5 | 0.9 | 0.9 |
| D | 24 | 24.7 | 24.0 | 2.8 | 0.1 | 1.0 |
| E | 0 | 5.6 | 0.0 | - | - | - |
| Interventions | Application Zone | Cost (Year 0) [€/m2] | |
|---|---|---|---|
| Inspections | All | 1.03 | |
| Cleaning operations | Minor | B | 12.45 |
| Moderate | 14.00 | ||
| Extensive | 15.77 | ||
| Minor interventions | Minor | C | 20.80 |
| Moderate | 24.14 | ||
| Extensive | 27.10 | ||
| Total replacement | D, E | 59.12 | |
| Interventions | Application Zone | Impact of the Interventions (Probability of Transition to Conditions A (PA), B (PB) or C (PC)) | |||
|---|---|---|---|---|---|
| PA (%) | PB (%) | PC (%) | |||
| Inspections | All | - | - | - | |
| Cleaning operations | Minor | B | 61.5 | 38.5 | - |
| Moderate | |||||
| Extensive | |||||
| Minor interventions | Minor | C | 69.8 | 25.0 | 5.2 |
| Moderate | 70.8 | 24.0 | 5.2 | ||
| Extensive | 70.8 | 24.0 | 5.2 | ||
| Total replacement | D, E | 100 | - | - | |
| Maintenance Strategy | Without Maintenance | MS1, 1-Year | MS2, Moderate, 1-Year | MS3, Moderate, 1-Year | |
|---|---|---|---|---|---|
| Mean time of permanence in each condition | tpA (years) | 2.33 | 7.50 | 16.36 | 35.97 |
| tpB (years) | 4.53 | 11.46 | 28.28 | 26.55 | |
| tpC (years) | 67.63 | 131.04 | 105.35 | 87.48 | |
| tpD (years) | 58.73 | 0.00 | 0.00 | 0.00 | |
| tpE (years) | 16.78 | 0.00 | 0.00 | 0.00 | |
| EI (-) | 0.69 | 0.88 | 0.90 | 0.92 | |
| Cannualised (€/m2) | - | 0.13 | 0.30 | 0.49 | |
| PI (m2/€) | - | 6.70 | 3.02 | 1.86 | |
| Maintenance Strategy | MS2, Moderate, 0.5-Years | MS2, Moderate, 1-Year | MS2, Moderate, 2-Years |
|---|---|---|---|
| tpA (years) | 15.47 | 16.36 | 16.10 |
| tpB (years) | 28.32 | 28.28 | 27.93 |
| tpC (years) | 106.21 | 105.35 | 105.39 |
| tpD (years) | 0.00 | 0.00 | 0.59 |
| tpE (years) | 0.00 | 0.00 | 0.00 |
| EI (-) | 0.90 | 0.90 | 0.90 |
| Cannualised (€/m2) | 0.42 | 0.30 | 0.23 |
| PI (m2/€) | 2.14 | 3.02 | 3.89 |
| Efficiency Index (Criterion 1) | Maintenance Cost (Criterion 2) | Number of Total Replacements (Criterion 3) | Total Rating | Standardised Total Rating | |
|---|---|---|---|---|---|
| MS1, 1-year | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 |
| MS2, Moderate, 1 year | 0.54 | 0.54 | 0.63 | 1.70 | 0.70 |
| MS3, Moderate, 1 year | 1.00 | 0.00 | 1.00 | 2.00 | 1.00 |
| MS2, Moderate, 0.5 years | 0.51 | 0.20 | 0.59 | 1.30 | 0.30 |
| MS2, Moderate, 2 years | 0.50 | 0.72 | 0.66 | 1.89 | 0.89 |
| Weights (%) | 33.3 | 33.3 | 33.3 |
| Efficiency Index (Criterion 1) | Maintenance Cost (Criterion 2) | Number of Total Replacements (Criterion 3) | Total Rating | Standardised Total Rating | |
|---|---|---|---|---|---|
| MS1, 1 year | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 |
| MS2, Moderate, 1 year | 0.54 | 0.54 | 0.63 | 2.24 | 0.62 |
| MS3, Moderate, 1 year | 1.00 | 0.00 | 1.00 | 3.00 | 1.00 |
| MS2, Moderate, 0.5 years | 0.51 | 0.20 | 0.59 | 1.82 | 0.41 |
| MS2, Moderate, 2 years | 0.50 | 0.72 | 0.66 | 2.38 | 0.69 |
| Weights (%) | 50 | 25 | 25 |
| Efficiency Index (Criterion 1) | Maintenance Cost (Criterion 2) | Number of Total Replacements (Criterion 3) | Total Rating | Standardised Total Rating | |
|---|---|---|---|---|---|
| MS1, 1 year | 0.00 | 1.00 | 0.00 | 2.00 | 0.45 |
| MS2, Moderate, 1 year | 0.54 | 0.54 | 0.63 | 2.24 | 0.66 |
| MS3, Moderate, 1 year | 1.00 | 0.00 | 1.00 | 2.00 | 0.45 |
| MS2, Moderate, 0.5 years | 0.51 | 0.20 | 0.59 | 1.50 | 0.00 |
| MS2, Moderate, 2 years | 0.50 | 0.72 | 0.66 | 2.61 | 1.00 |
| Weights (%) | 25 | 50 | 25 |
| Efficiency Index (Criterion 1) | Maintenance Cost (Criterion 2) | Number of Total Replacements (Criterion 3) | Total Rating | Standardised Total Rating | |
|---|---|---|---|---|---|
| MS1, 1 year | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 |
| MS2, Moderate, 1 year | 0.54 | 0.54 | 0.63 | 2.33 | 0.66 |
| MS3, Moderate, 1 year | 1.00 | 0.00 | 1.00 | 3.00 | 1.00 |
| MS2, Moderate, 0.5 years | 0.51 | 0.20 | 0.59 | 1.89 | 0.44 |
| MS2, Moderate, 2 years | 0.50 | 0.72 | 0.66 | 2.55 | 0.77 |
| Weights (%) | 25 | 25 | 50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, C.; Silva, A.; Brito, J.d.; S. Dias, I.; Flores-Colen, I. Maintenance Modelling of Ceramic Claddings in Pitched Roofs Based on the Evaluation of Their In Situ Degradation Condition. Infrastructures 2020, 5, 77. https://doi.org/10.3390/infrastructures5090077
Ferreira C, Silva A, Brito Jd, S. Dias I, Flores-Colen I. Maintenance Modelling of Ceramic Claddings in Pitched Roofs Based on the Evaluation of Their In Situ Degradation Condition. Infrastructures. 2020; 5(9):77. https://doi.org/10.3390/infrastructures5090077
Chicago/Turabian StyleFerreira, Cláudia, Ana Silva, Jorge de Brito, Ilídio S. Dias, and Inês Flores-Colen. 2020. "Maintenance Modelling of Ceramic Claddings in Pitched Roofs Based on the Evaluation of Their In Situ Degradation Condition" Infrastructures 5, no. 9: 77. https://doi.org/10.3390/infrastructures5090077
APA StyleFerreira, C., Silva, A., Brito, J. d., S. Dias, I., & Flores-Colen, I. (2020). Maintenance Modelling of Ceramic Claddings in Pitched Roofs Based on the Evaluation of Their In Situ Degradation Condition. Infrastructures, 5(9), 77. https://doi.org/10.3390/infrastructures5090077








