From Theory to Field Evidence: Observations on the Evolution of the Settlements of an Earthfill Dam, over Long Time Scales
Abstract
1. Introduction
- Increasing population of ageing dams: According to the International Commission on Large Dams (ICOLD), worldwide, there are more than 58,000 registered large (with heights greater than 15 m) dams. However, there also exist thousands of smaller dams that are currently unregistered, which are usually not subject to proper maintenance and monitoring regimes. The European Environmental Agency (EEA) currently estimates that there exist over 7000 large dams in Europe, with thousands more planned to be constructed during the next decade. According to the National Inventory of Dams (NID) in the US, there are also in total 90,580 dams. The 2017 infrastructure report card published by the American Society of Civil Engineers (ASCE) estimates that the average age of existing dams in the US is 56 years old, and that by 2025, 70% of the existing dam infrastructure will exceed their ‘useful’ design lifespan. The number of high hazard dams is also on the rise, and currently accounts for almost 17%, while more than 2000 dams are listed as structurally deficient, requiring a repair investment of nearly $45 billion [2]. The vast majority of dam infrastructure worldwide was constructed during the period 1950–1970; therefore, higher failure rates are anticipated in these dams due to the lower quality design and construction methods. Investigating the time evolution of the response of ageing dams informs the early evaluation of risk and can help direct any necessary interventions.
- Extreme climatic conditions: Recent climate change projections [3,4] indicate that the frequency of shifting weather events will substantially increase, and severe flooding incidents are anticipated to double in Europe by 2050 [5]. Extreme variations in seasonal rainfall patterns are expected to affect dam infrastructure [6], with an increasing magnitude of degradation processes related to the depth of rainfall infiltration inside the dam body, the increase in the fill’s saturation level, and changes in the shear strength and pore water pressure within saturated fill layers. For embankment dams, the hydrostatic pressure induced by flooding and the high permeability of the soil caused by desiccation can result in uncontrolled internal seepage [7]. Modern climatic conditions are expected to significantly affect the structural integrity of hydro-infrastructure due to the high potential of extreme drought and flood events, as evidenced by the incidents of Oroville dam (US) during February 2017 and the Whaley bridge dam (UK) in July 2019. Another main issue arises from the fact that past and existing methods that incorporate the risk of climatic hazards into dam design and assessment methods are based on historical records. This indicates that they do not capture both the current and projected significant climatic variability; therefore, ageing dam infrastructure is expected to be put under stress. Studying the effect that any deviations from historical precipitation records have on existing dams is crucial for the transition towards resilient infrastructure.
- Gap in the knowledge about the long-term behaviour of dams: Relationships and models describing the short and long-term behaviour of dams are based on empirical equations. Such models are limited at times, as dams of similar size and type can behave differently, albeit still within safety limits. These empirical models, developed as far back as 30 years ago, are not incorporating the changing environmental conditions. As a result, investigating the behaviour of dams over long time scales can assist mitigate potential failures due to ageing and their (in) direct impact.
2. Materials and Methods
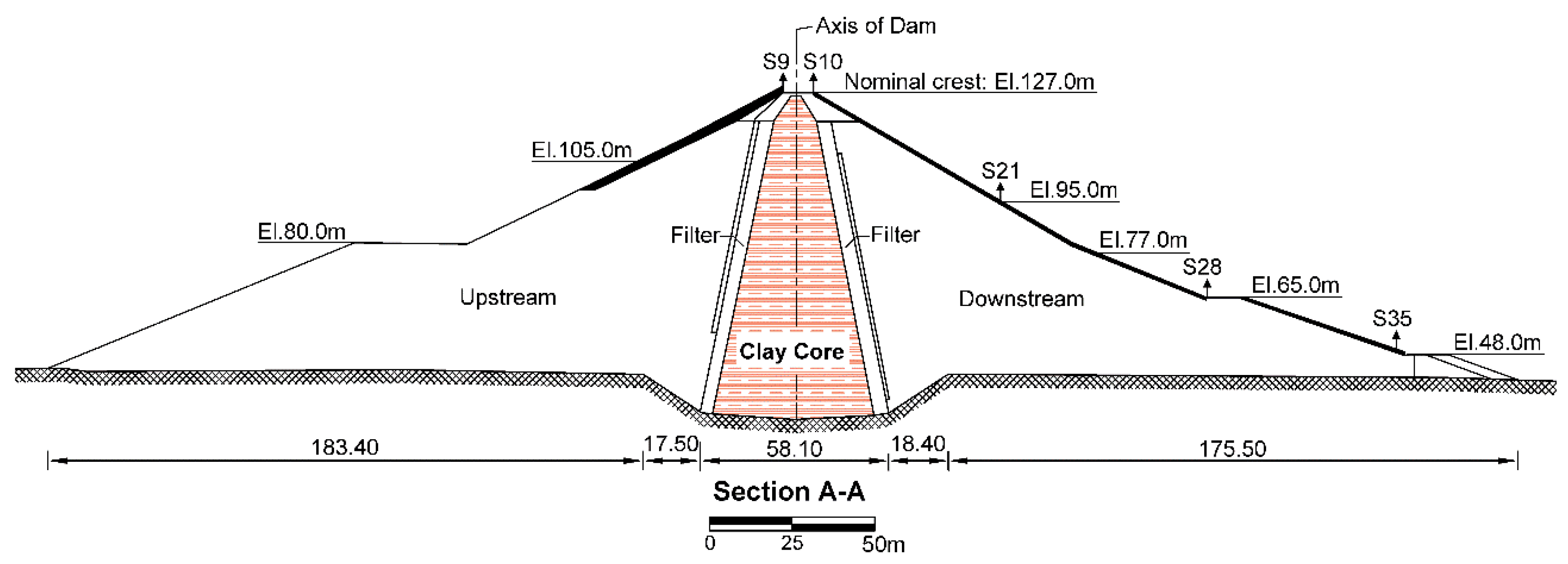
2.1. The Pournari I Dam
2.1.1. Geology and Seismicity at the Dam Site
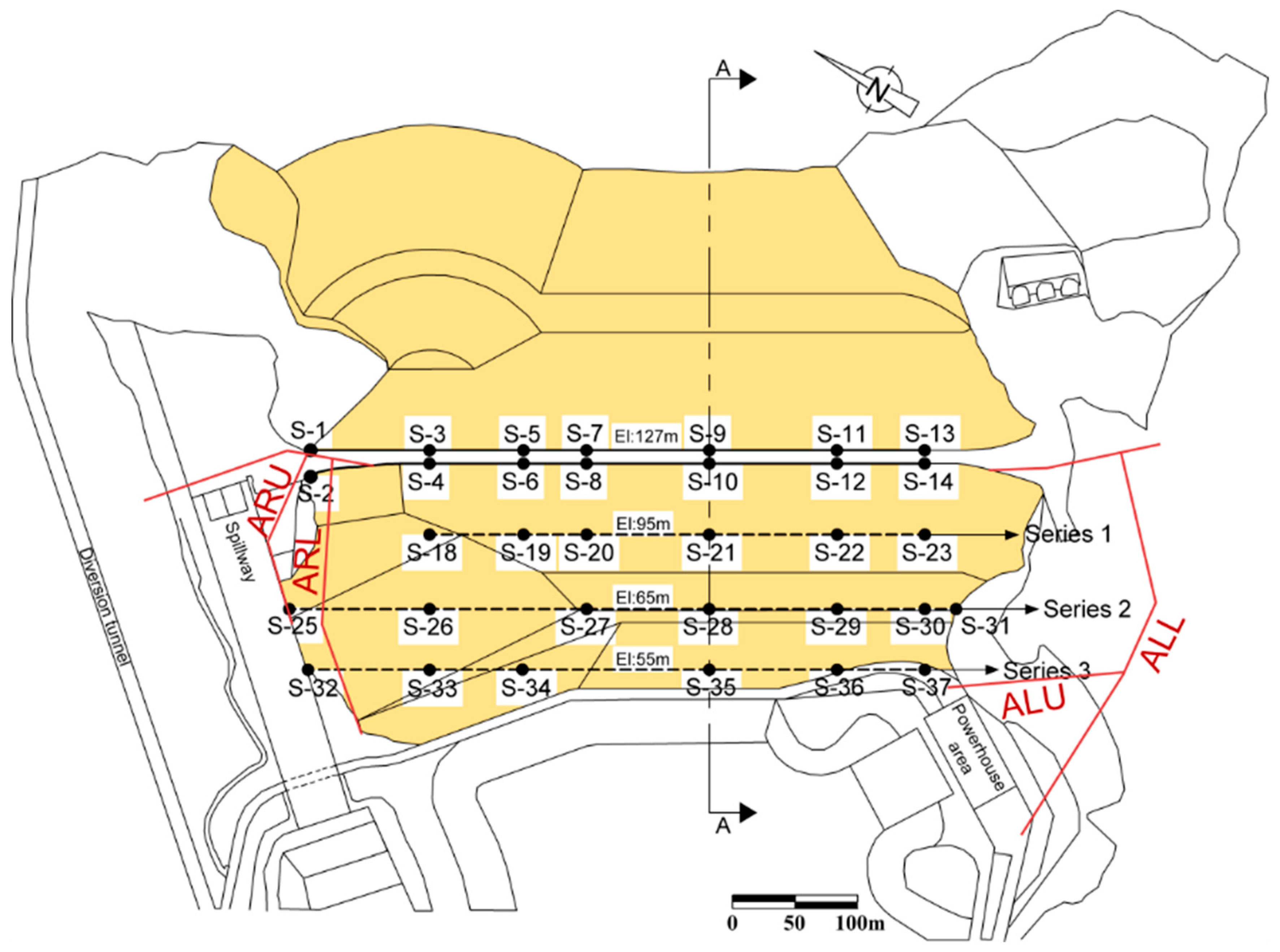
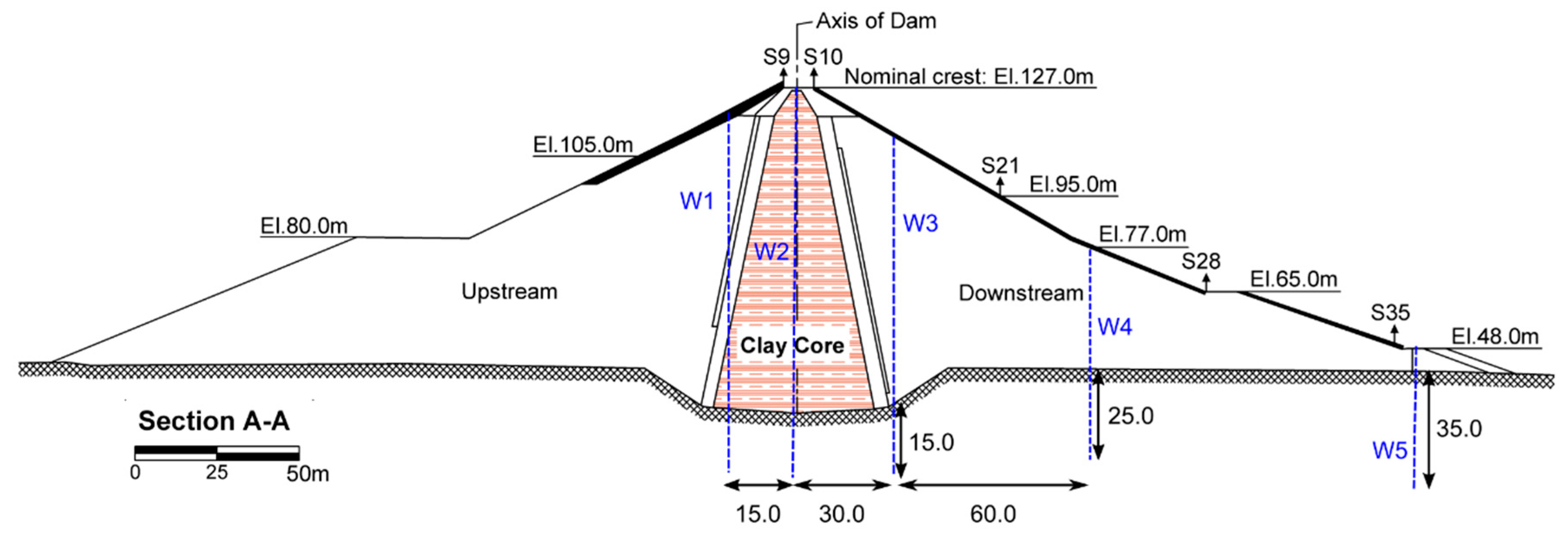
2.1.2. Monitoring at Pournari I dam
2.1.3. Available Monitoring Record
2.2. Methodology
3. Results
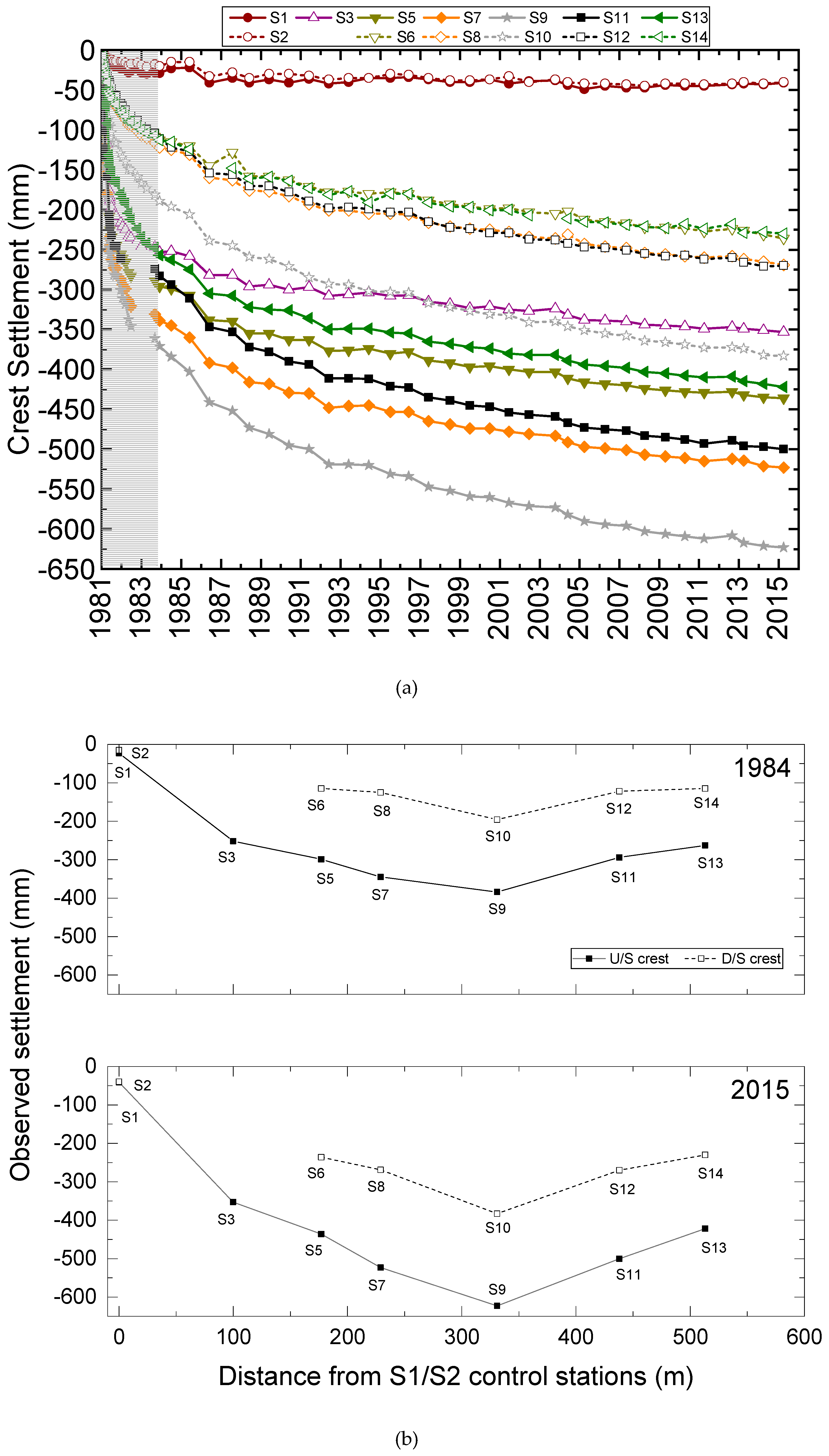
3.1. Step 1: Time Evolution of Vertical Movements for the Control Stations on the Crest and Downstream Shoulder of the Dam
3.1.1. Crest Settlements
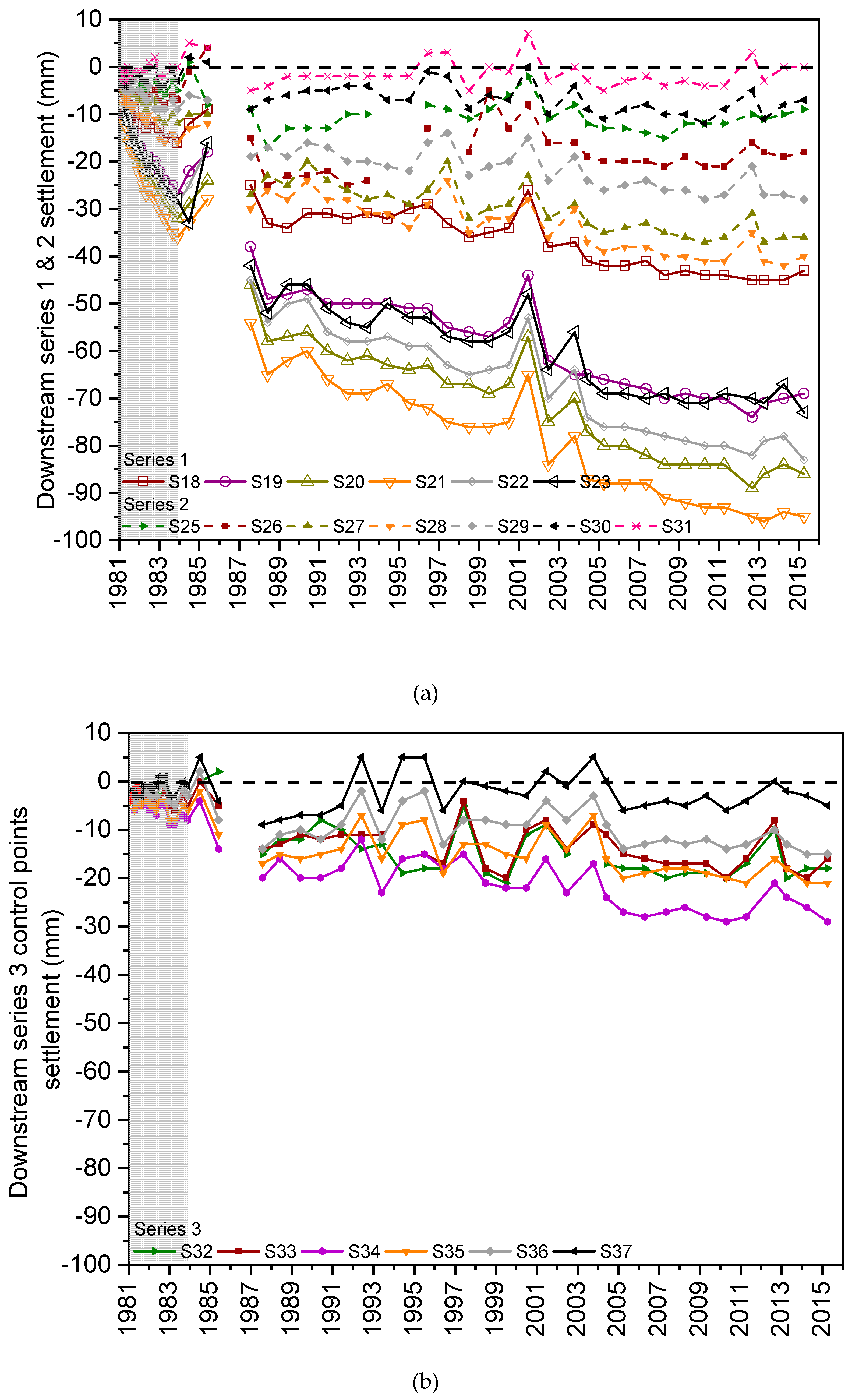
3.1.2. Settlements of the Downstream Shoulder
3.2. Step 2: Effect of Environmental Factors on the Observed Settlements
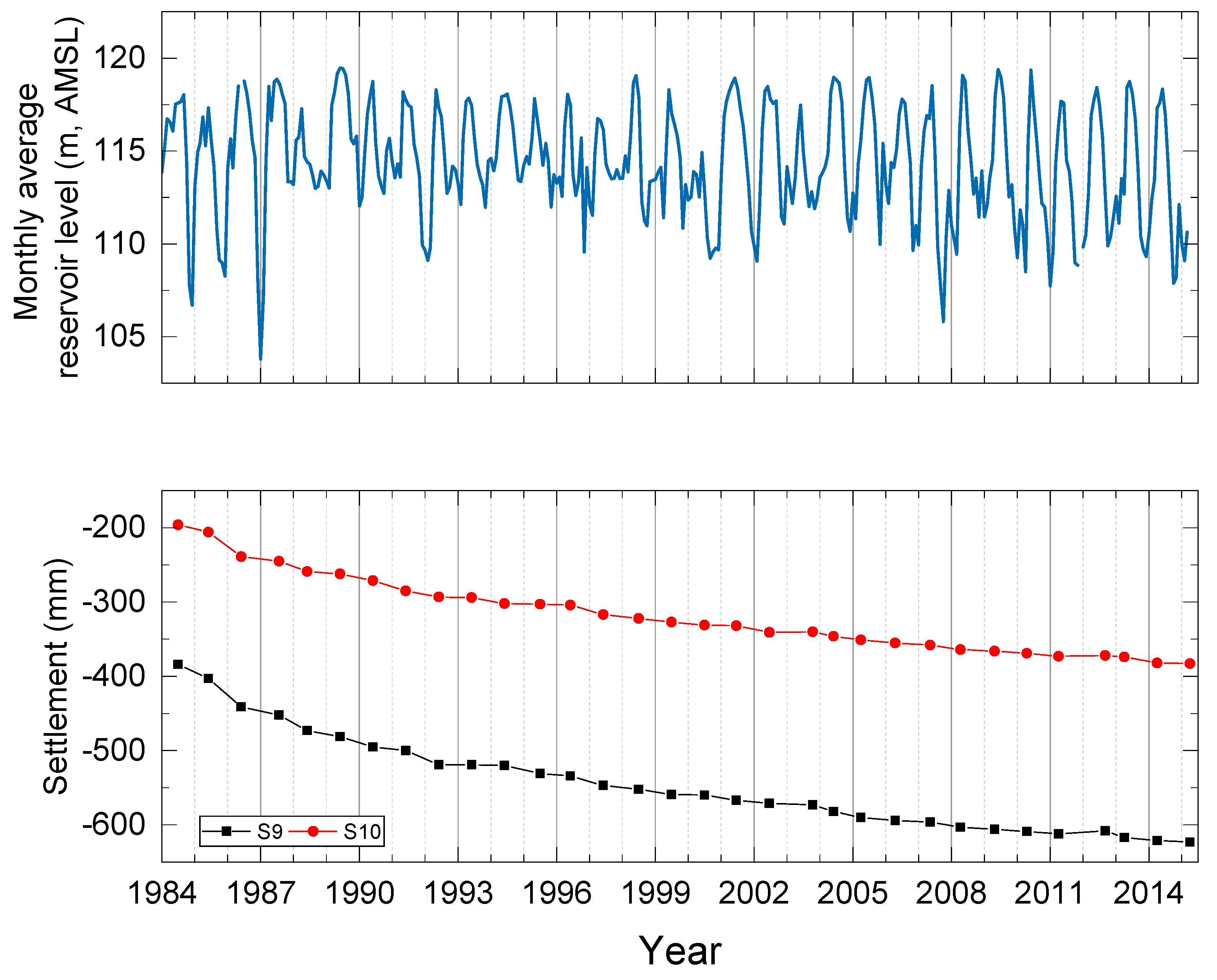
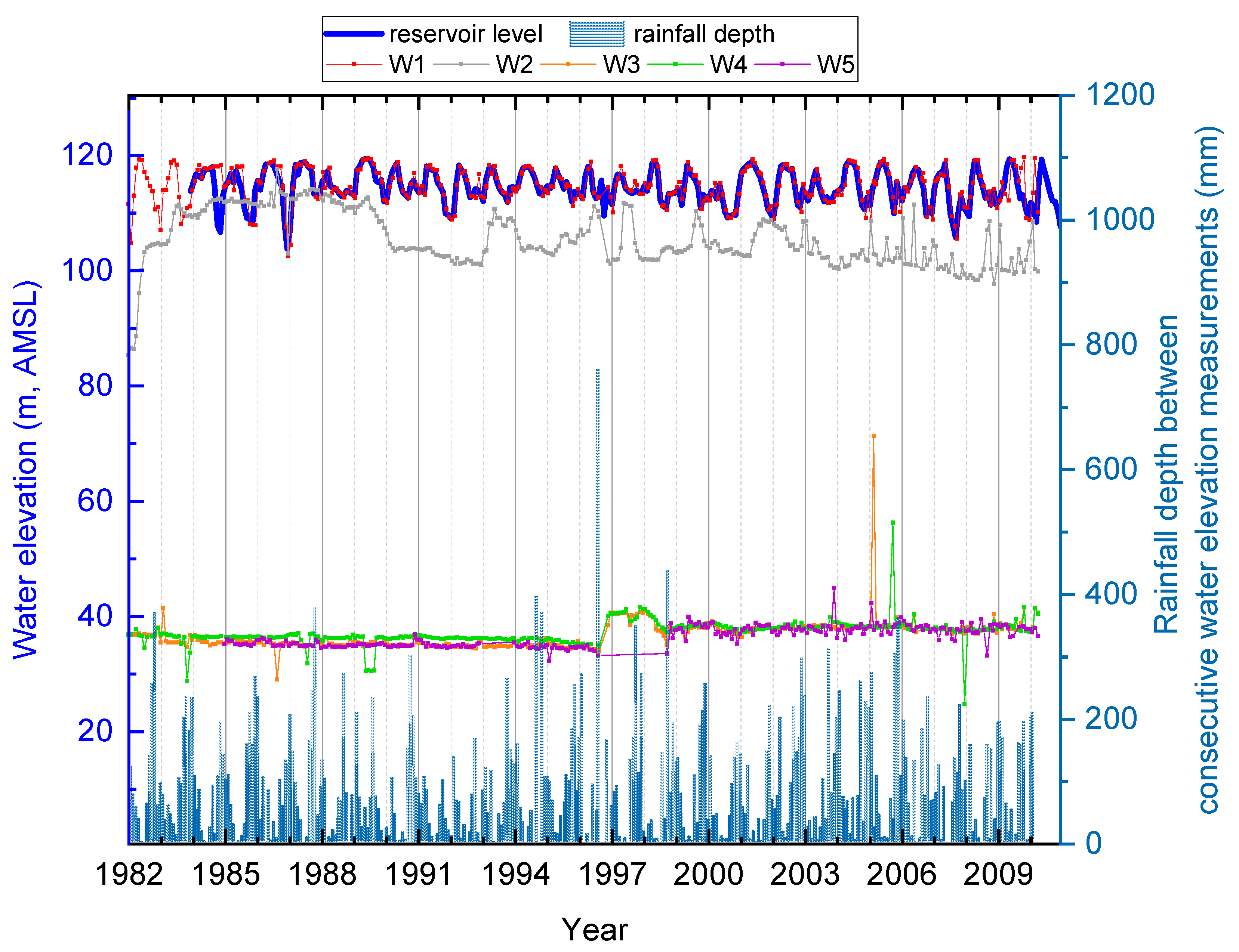
3.2.1. Settlements and Reservoir Level
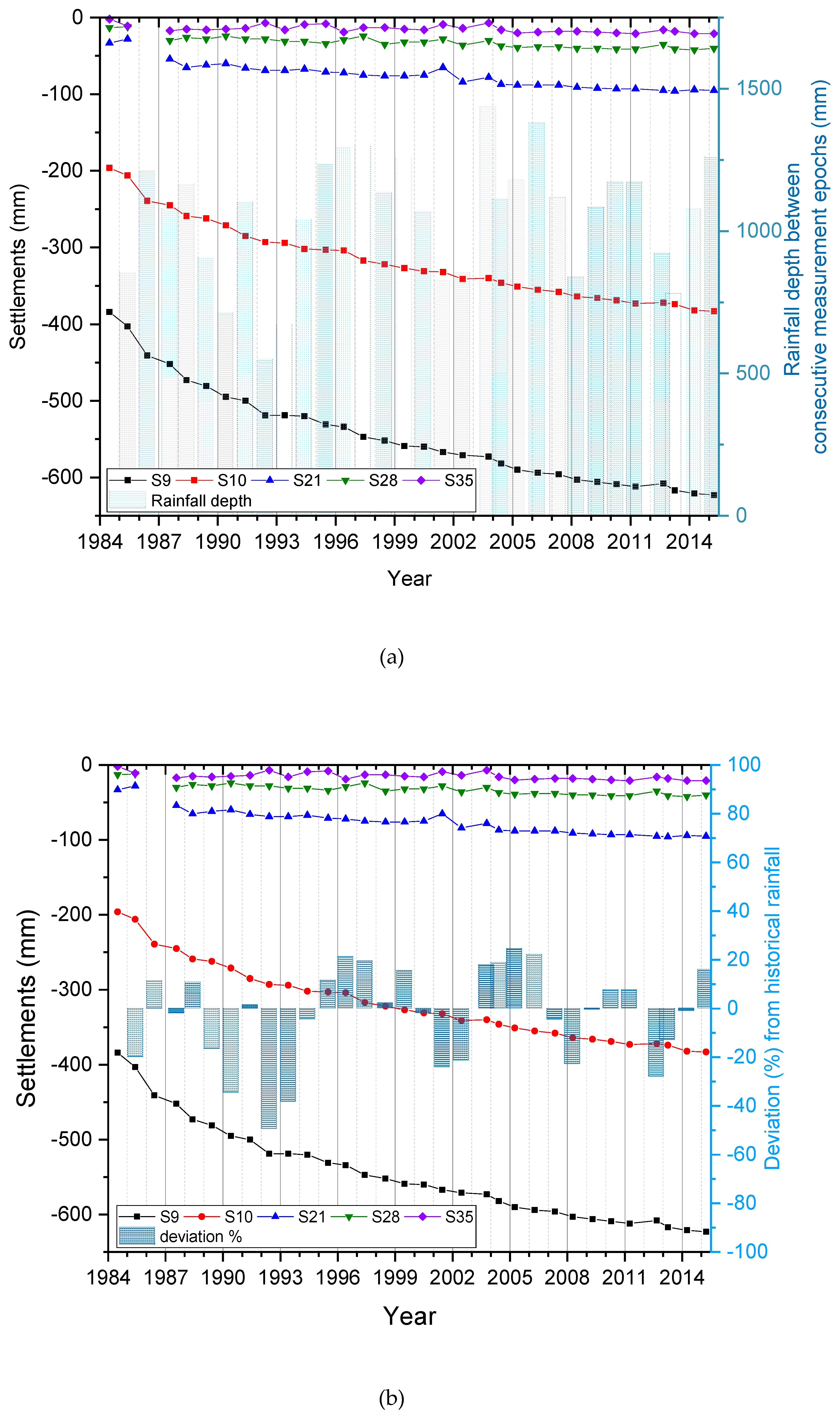
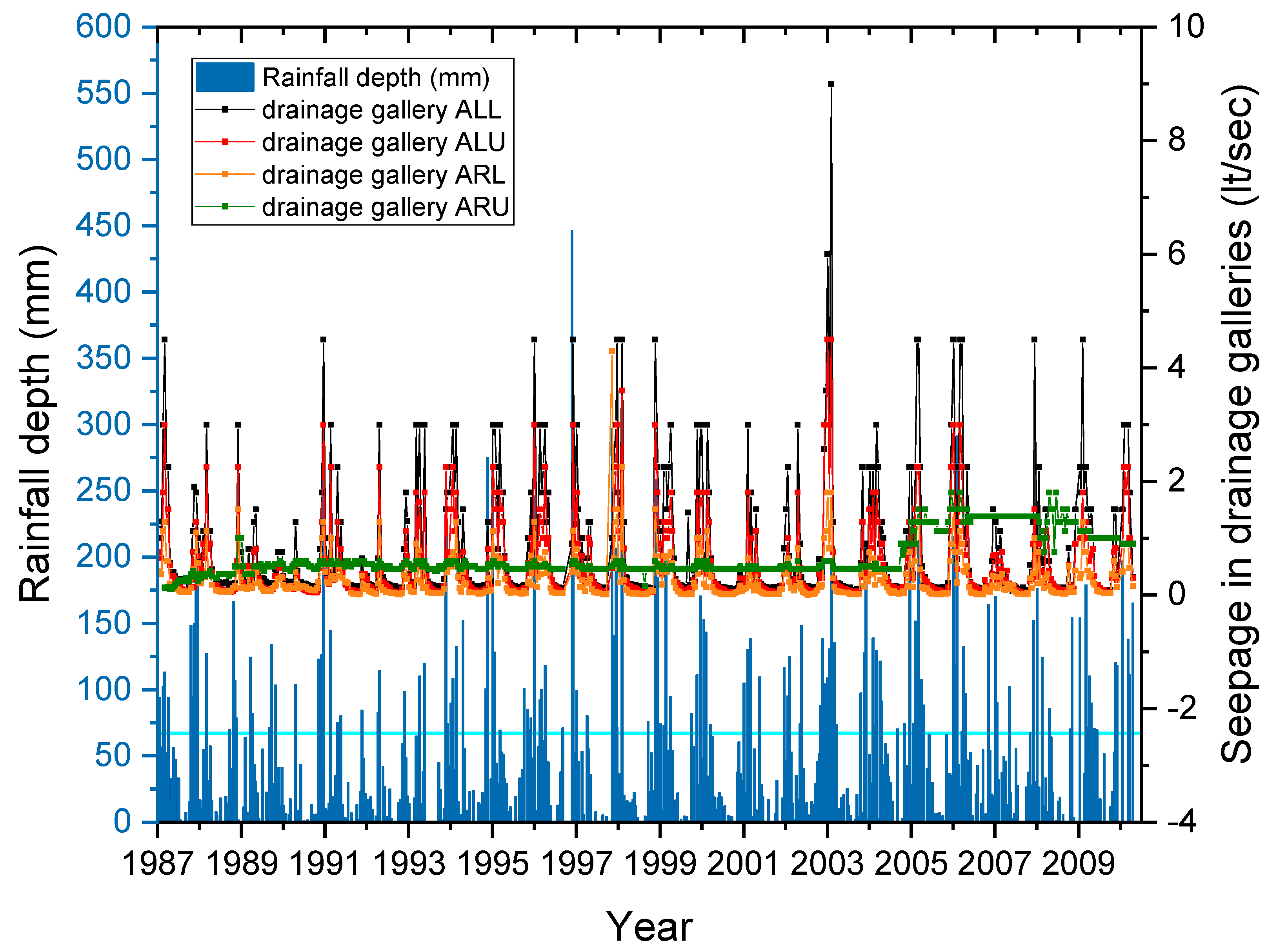
3.2.2. Settlements and Rainfall
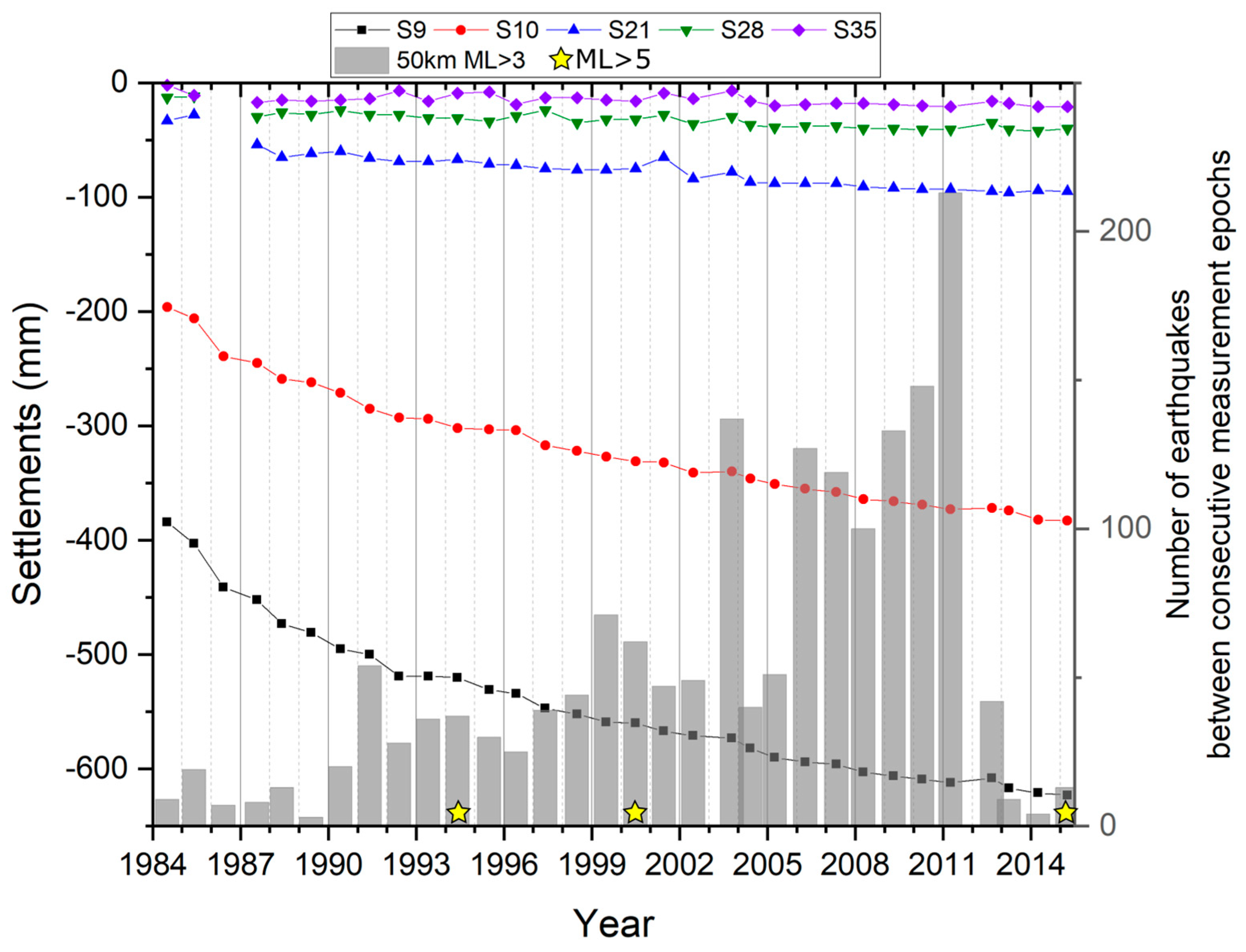
3.2.3. Settlements and Seismicity
4. Discussion
4.1. Observed Settlements and Reservoir Level Fluctuations
4.2. Observed Settlements and Rainfall
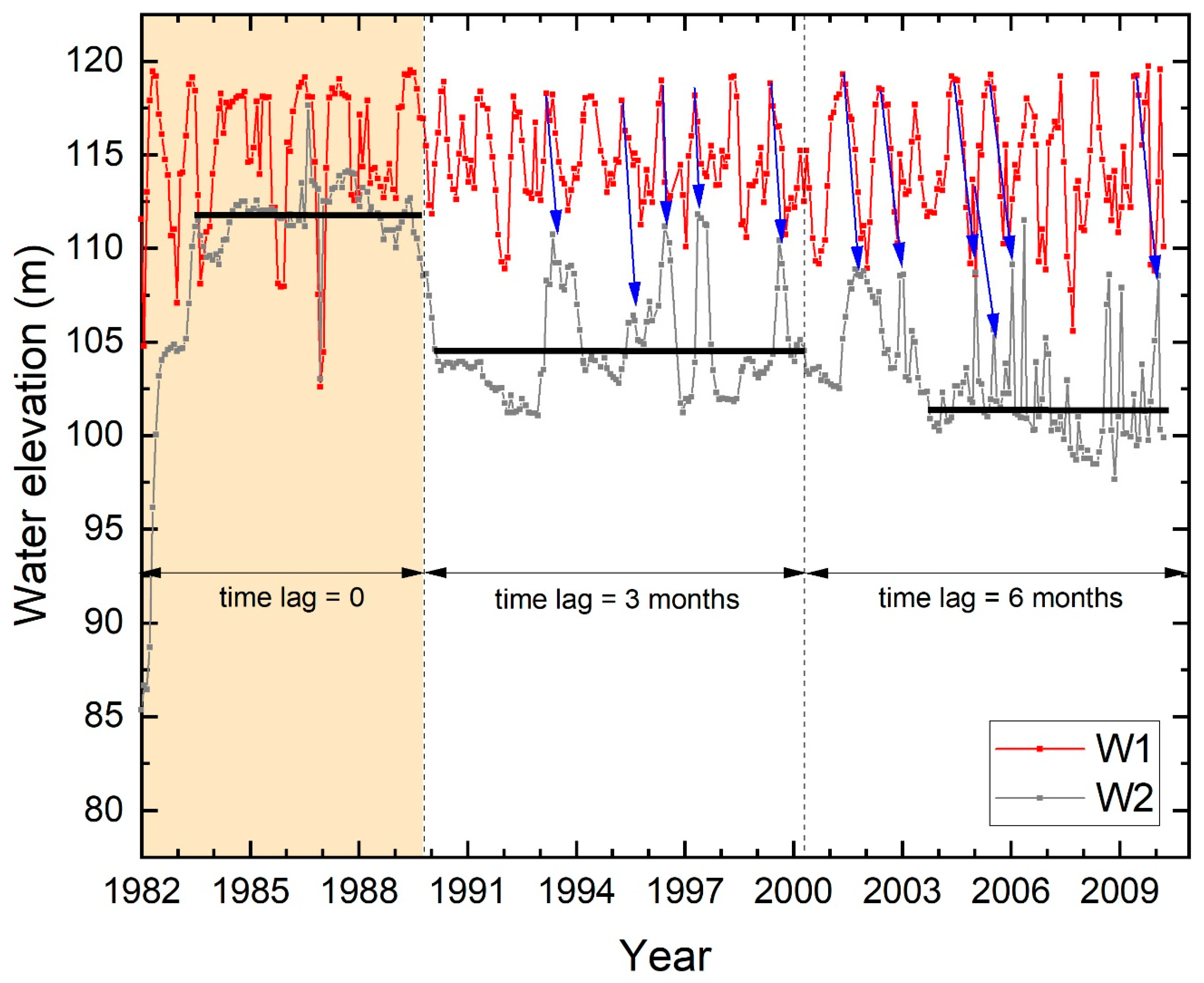
4.3. Time Lag between Recorded Settlements and Reservoir Level Fluctuations
- 1982 to December 1989: During this time period, the hydraulic head in the core (W2 location in Figure 12) does not appear to have a time lag with the reservoir-level fluctuations despite the fact that it does not exactly follow the fluctuation pattern. More specifically, both W1 and W2 appear to have a drop in the hydraulic head in January 1987, with the last simultaneous drop in July 1989 (first dashed line from the left in Figure 14). The shape of the W2 curve between 1982 and late 1989 (highlighted area in Figure 14) is characteristic for the period during which the clay core gets saturated: the hydraulic head increases, and then reaches a plateau, at which point the core is regarded as saturated. The latter has been observed in early studies on unsaturated clays, e.g., [39].
- Early 1990 to mid 2000: During this period, the mean value (104.46 m) of the hydraulic head (second horizontal black line in Figure 14) is decreased compared to the previous time period (111.83 m). The observed peaks in the W2 values appear to have a time lag with the corresponding peaks in W1 (corresponding peaks shown with blue arrows in Figure 14). This time lag is 3 months.
- Mid 2000 to end of record in 2010: During this time period, the mean of the hydraulic head values has dropped further (now at 101.84 m). The observed time lag has increased to 6 months.
4.4. Observed Uplift at the Toe of the Dam
- Rotational slide of the downstream slope. This is not likely to be true, as uplift is not observed at all times, but rather at specific, not necessarily consecutive, measurement epochs. In addition, to the authors’ knowledge, no cracks have been reported from visual inspection, which is another sign that indicates a potential slide.
- Effect of groundwater. This could be a likely factor; however, the absence of relevant data, e.g., pore pressures at the toe of the dam, do not allow any analysis to be made regarding its effect to the observed vertical movements.
- Swelling rocks beneath the dam. Swelling of rocks resulting in deformations has been reported for tunnels. The main contributing factor is the presence of clays or clayey rocks [49]. Ref. [25] mentions the presence of some clay material at the dam foundation level. This could be a possible cause of the observed uplifts, although the fact that this uplift is reversed by the next measurement epoch makes this scenario unlikely.
- Internal erosion that could result in uplift at the toe of the dam. From the available data used in this study, there is no evidence to support this.
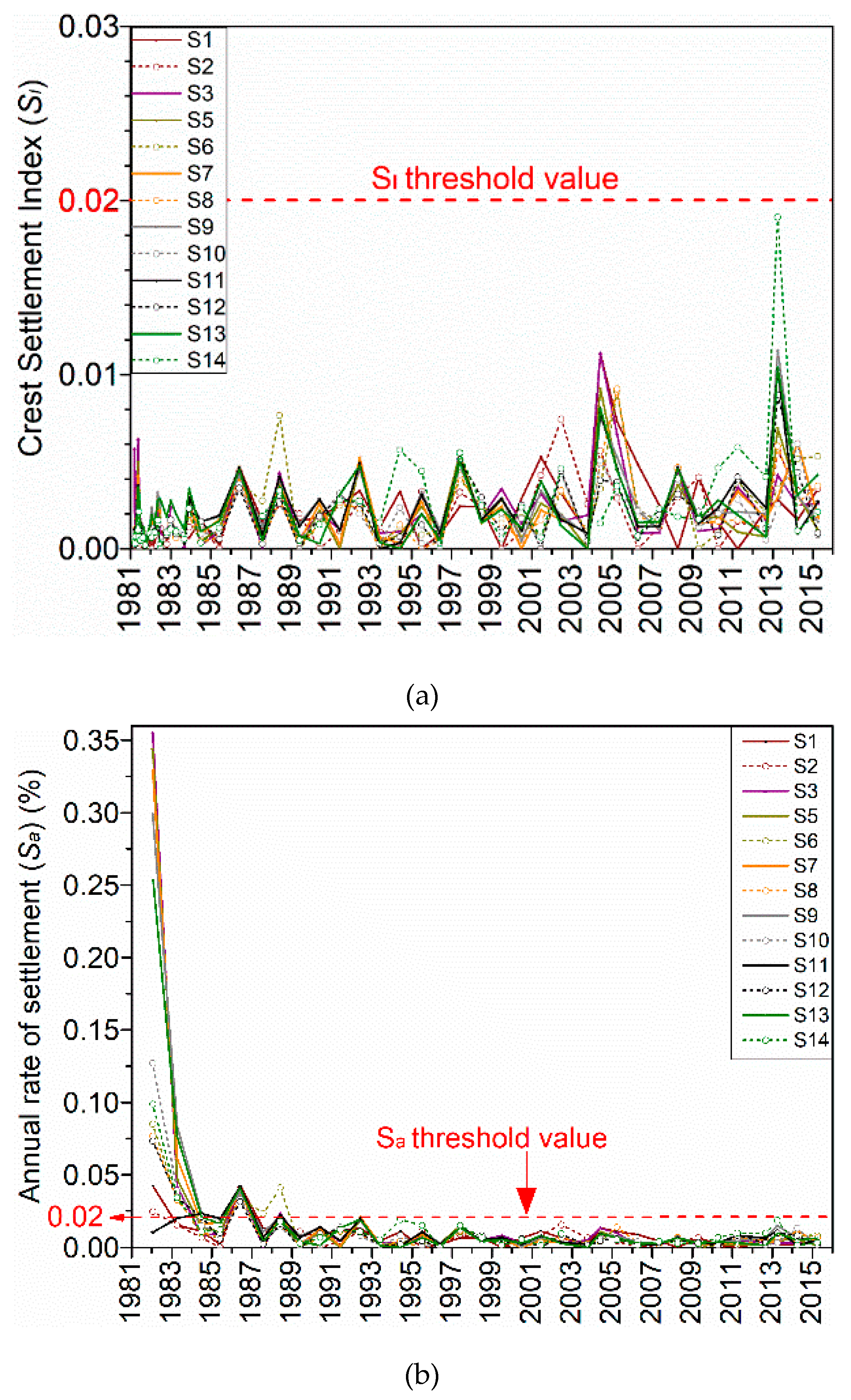
4.5. Time-Dependent Settlements
4.6. Future Research Directions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Michalis, P.; Konstantinidis, F.; Valyrakis, M. The road towards Civil Infrastructure 4.0 for proactive asset management of critical infrastructure systems. In Proceedings of the 2nd International Conference on Natural Hazards & Infrastructure (ICONHIC), Chania, Greece, 23–26 June 2019. [Google Scholar]
- American Society of Civil Engineers 2017 Infrastructure Report Card. Available online: https://www.infrastructurereportcard.org/cat-item/dam (accessed on 31 July 2019).
- Rojas, R.; Feyen, L.; Bianchi, A.; Dosio, A. Assessment of future flood hazard in Europe using a large ensemble of bias-corrected regional climate simulations. J. Geophys. Res. Atmos. 2012, 117, D17109. [Google Scholar]
- Forzieri, G.; Bianchi, A.; e Silva, F.B.; Herrera, M.A.M.; Leblois, A.; Lavalle, C.; Aerts, J.C.J.H.; Feyen, L. Escalating impacts of climate extremes on critical infrastructures in Europe. Glob. Environ. Chang. 2018, 48, 97–107. [Google Scholar] [CrossRef]
- Jongman, B.; Hochrainer-Stigler, S.; Feyen, L.; Aerts, J.C.J.H.; Mechler, R.; Botzen, W.J.W.; Bouwer, L.M.; Pflug, G.; Rojas, R.; Ward, P.J. Increasing stress on disaster risk finance due to large floods. Nat. Clim. Chang. 2014, 4, 264–268. [Google Scholar] [CrossRef]
- Preziosi, M.-C.; Micic, T. An adaptive methodology for risk classification of small homogeneous earthfill embankment dams integrating climate change projections. Civ. Eng. Environ. Syst. 2014, 31, 111–124. [Google Scholar] [CrossRef][Green Version]
- Michalis, P.; Sentenac, P.; Macbrayne, D. Geophysical assessment of dam infrastructure: The mugdock reservoir dam case study. In Proceedings of the 3rd Joint International Symposium on Deformation Monitoring (JISDM), Vienna, Austria, 30 March–1 April 2016. [Google Scholar]
- Michalis, P.; Pytharouli, S.; Raftopoulos, S. Long-term deformation patterns of earth-fill dams based on geodetic monitoring data: The Pournari I Dam case study. In Proceedings of the 3rd Joint International Symposium on Deformation Monitoring (JISDM), Vienna, Austria, 30 March–1 April 2016. [Google Scholar]
- He, X.Y.; Wang, Z.Y.; Huang, J.C. Temporal and spatial distribution of dam failure events in China. Int. J. Sediment Res. 2008, 23, 398–405. [Google Scholar] [CrossRef]
- Yigit, C.O.; Alcay, S.; Ceylan, A. Displacement response of a concrete arch dam to seasonal temperature fluctuations and reservoir level rise during the first filling period: Evidence from geodetic data. Geomat. Nat. Hazards Risk 2016, 7, 1489–1505. [Google Scholar] [CrossRef]
- Boudon, R.; Blin, S.; Pons, E.; Ajzenberg, A. Automatic follow-up of the tri-directional displacements of the Sainte-Croix arch dam (Verdon-France) by motorized total station. In Proceedings of the 4th Joint International Symposium on Deformation Monitoring (JISDM), Athens, Greece, 15–17 May 2019. [Google Scholar]
- Bonelli, S.; Royet, P. Delayed response analysis of dam monitoring data. In Proceedings of the ICOLD European Symposium on Dams in a European Context, Geiranger, Norway, 25–27 June 2001. [Google Scholar]
- Gamse, S.; Oberguggenberger, M. Assessment of long-term coordinate time series using hydrostatic-season-time model for rock-fill embankment dam. Struct. Control Health Monit. 2017, 24, e1859. [Google Scholar] [CrossRef]
- Gamse, S.; Zhou, W.-H. Adaptive parametric identification in dam monitoring by Kalman filtering. In Proceedings of the 4th Joint International Symposium on Deformation Monitoring (JISDM), Athens, Greece, 15–17 May 2019. [Google Scholar]
- Gikas, V.; Sakellariou, M. Settlement analysis of the Mornos earth dam (Greece): Evidence from numerical modeling and geodetic monitoring. Eng. Struct. 2008, 30, 3074–3081. [Google Scholar] [CrossRef]
- Baecher, G.B.; Christian, J.T. The practice of risk analysis and the safety of dams. In Proceedings of the Conference of Geotechnical Engineering, Cairo, Egypt, January 2000. [Google Scholar]
- Tedd, P.; Charles, J.A.; Holton, I.R.; Robertshaw, A.C. The effect of reservoir drawdown and long-term consolidation on the deformation of old embankment dams. Geotechnique 1997, 47, 33–48. [Google Scholar] [CrossRef]
- Guler, G.; Kilic, H.; Hosbas, G.; Ozaydin, K. Evaluation of the movements of the dam embankments by means of geodetic and geotechnical methods. J. Surv. Eng. 2006, 132, 31–39. [Google Scholar] [CrossRef]
- Pytharouli, S.I.; Stiros, S.C. Investigation of the parameters controlling crest settlement of a major earthfill dam based on the threshold correlation analysis. J. Appl. Geod. 2009, 3, 55–62. [Google Scholar] [CrossRef]
- Pytharouli, S. Study of the Long-Term Behaviour of Kremasta Dam Based on the Analysis of Geodetic Data and Reservoir Level Fluctuations. Ph.D. Thesis, University of Patras, Patras, Greek, August 2007. (In Greek). [Google Scholar]
- Charles, J.A. The significance of problems and remedial works at British earth dams. In Proceedings of the BNCOLD-IWES Conference on Reservoirs 1986, Edinburgh, UK, 3–6 September 1986; pp. 123–141. [Google Scholar]
- Dascal, O. Post-construction deformation of rockfill dams. J. Geotech. Eng. 1987, 113, 46–59. [Google Scholar] [CrossRef]
- Pytharouli, S.I.; Stiros, S.C. Estimation of a safety threshold for the crest settlements of embankment dams. In Proceedings of the 2nd National ICOLD Conference on Dams and Reservoirs, Athens, Greece, 7 November 2013. [Google Scholar]
- Public Power Corporation (P.P.C.) S.A. Brochure: Hydroelectric project Pournari. Available online: http://users.itia.ntua.gr/nikos/arx_int/CDfrag/scanarismena/POURNARI/Untitled.pdf (accessed on 1 August 2019).
- Papageorgiou, S.A. Engineering Geology of Dam Foundations in North-Western Greece. Ph.D. Thesis, Durham University, Durham, UK, 1983. [Google Scholar]
- Pavlou, K.; Drakatos, G.; Kouskouna, V.; Makropoulos, K.; Kranis, H. Seismicity study in Pournari reservoir area (W. Greece) 1981–2010. J. Seismol. 2016, 20, 701–710. [Google Scholar] [CrossRef]
- Pytharouli, S.; Stiros, S. Reservoir level fluctuations and deformation of Ladhon Dam. Int. J. Hydropower Dams 2004, 11, 82–84. [Google Scholar]
- Bannister, A.; Raymond, S.; Baker, R. Surveying, 7th ed.; Pearson Education Limited: London, UK, 1998; 512p. [Google Scholar]
- Bommer, J.J.; Crowley, H. The purpose and definition of the minimum magnitude limit in PSHA calculations. Seismol. Res. Lett. 2017, 88, 1097–1106. [Google Scholar] [CrossRef]
- Harder, L.F.; Kelson, K.I.; Kishida, T.; Kayen, R. Preliminary Observations of the Fujinuma Dam Failure Following the March 11, 2011 Tohoku Offshore Earthquake, Japan. Geotechnical Extreme Events Reconnaissance Report No. GEER-25e, 2011. Available online: http://www.geerassociation.org (accessed on 18 September 2019).
- Nespoli, M.; Todesco, M.; Serpelloni, E.; Belardinelli, M.E.; Bonafede, M.; Marcaccio, M.; Rinaldi, A.P.; Anderlini, L.; Gualandi, A. Modeling earthquake effects ongroundwater levels: Evidences from the 2012 Emilia earthquake (Italy). Geofluids 2016, 16, 452–463. [Google Scholar] [CrossRef]
- United States Society on Dams. Observed Performance of Dams During Earthquakes, Volume III. 2014. Available online: http://www.ussdams.org/wp-content/uploads/2016/05/EQPerfo2_v3.pdf (accessed on 18 September 2019).
- Swaisgood, J.R. Embankment Dam Deformations Caused by Earthquakes. In Proceedings of the 7 Pacific Conference on Earthquake Engineering, Christchurch, New Zealand, 13–15 February 2003; Available online: https://www.nzsee.org.nz/db/2003/View/Paper014s.pdf (accessed on 1 October 2019).
- Fiorentino, G.; Furgani, L.; Nuti, C.; Sabetta, F. Probabilistic evaluation of dams base sliding. In Proceedings of the COMPDYN 2015 5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, 25–27 May 2015; Papadrakakis, M., Papadopoulos, V., Plevris, V., Eds.; National Technical University of Athens: Athens, Greece, 2015. [Google Scholar]
- Lawton, F.L.; Lester, M.D. Settlement of rockfill dams. In Proceedings of the 8th International Congress on Large Dams, Edinburgh, UK, 4–8 May 1964; Volume III, pp. 599–613. [Google Scholar]
- Sowers, G.F.; Williams, R.C.; Wallace, T.S. Compressibility of Brocken rock and the settlement of rockfills. In Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering, Toronto, ON, Canada, 8–15 September 1965; Volume 2, pp. 561–565. [Google Scholar]
- Fell, R.; McGregor, P.; Stapledon, D.; Graeme, B. Geotechnical Engineering of Dams; Taylor & Francis: London, UK, 2005; p. 900. [Google Scholar]
- Twort, C.A.; Ratnayaka, D.D.; Malcolm, J.B. 5-Dams, impounding reservoirs and river intakes. In Water Supply, 5th ed.; Twort, A.C., Ratnayaka, D.D., Brandt, M.J., Eds.; Eliane Wigzell: London, UK, 2000; pp. 152–195. [Google Scholar]
- Ventrella, C.; Pelekanos, L.; Skarlatos, D.; Pantazis, G. Finite element analysis of earth dam settlements due to seasonal reservoir level changes. In Proceedings of the XVII ECSMGE-2019 Geotechnical Engineering Foundation of the Future, Reykjavik, Iceland, 1–7 September 2019; ISBN 978-9935-9436-1-3. [Google Scholar]
- Tedd, P.; Charles, J.A.; Holton, J.R.; Robertshaw, A.C. Deformations of embankment dams due to changes in reservoir level. In Proceedings of the 13th International Conference on Soil Mechanics and Foundations Engineering, New Delhi, India, 5–10 January 1994; pp. 951–954. [Google Scholar]
- British Dams, Climate Change Impacts on the Safety of British Reservoirs. Available online: https://britishdams.org/assets/documents/defra-reports/200201Climate%20change%20impacts%20on%20the%20safety%20of%20British%20reservoirs.pdf (accessed on 1 August 2019).
- Alonso, E.E.; Olivella, S.; Pinyol, N.M. A review of Beliche dam. Geotechnique 2005, 55, 267–285. [Google Scholar] [CrossRef]
- Almog, E.; Kelham, P.; King, R. Delivering benefits through evidence: Models of dam failure and monitoring and measuring techniques. In Flood and Coastal Erosion Risk Management Programme; Project: SC080048/R1; Environment Agency: Bristol, UK, 2011. [Google Scholar]
- Chang, C.S.; Duncan, J.M. Analysis of Consolidation of Earth and Rockfill Dams, Volume I, Main Text and Appendices, A. and B.; U.S. Army Engineer Waterways Experiment Station, Contract Report S-77-4, 1977. Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a045332.pdf (accessed on 2 October 2019).
- Davis, J.C. Statistics and Data Analysis in Geology, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2002; p. 656. [Google Scholar]
- Schultz, M.; Stattegger, K. SPECTRUM: Spectral analysis of unevenly spaced paleoclimatic time series. Comput. Geosci. 1997, 23, 929–945. [Google Scholar] [CrossRef]
- Olafsdottir, K.B.; Schulz, M.; Mudelsee, M. REDFIT-X: Cross-spectral analysis of unevenly spaced paleoclimate time series. Comput. Geosci. 2016, 91, 11–18. [Google Scholar] [CrossRef]
- Bonelli, S.; Radzicki, K. Impulse response function analysis of pore pressures in earthdams. Eur. J. Environ. Civ. Eng. 2008, 12, 243–262. [Google Scholar] [CrossRef]
- Kontogianni, V.; Tzortzis, A.; Stiros, S.C. Deformation and failure of the Tymfristos Tunnel, Greece. J. Geotech. Geoenvironmental Eng. 2004, 130, 1004–1013. [Google Scholar] [CrossRef]
- Michalis, P. Pournari I dam (Greece): Analysis of Its Structural Integrity Based on Long-Term Monitoring Data. Master’s Thesis, University of Strathclyde, Glasgow, UK, August 2010. [Google Scholar]



| 1989 | 1992 | 1996 | 1997 | 1999 | 2001 | 2003 | 2012 |
|---|---|---|---|---|---|---|---|
| Series 1 (6) | Series 1 (10) | Series 1 (8) | |||||
| Series 2 (6, S27-31) | Series 2 (13, S26-28) | Series 2 (13) | Series 2 (8) | Series 2 (6) | Series 2 (7) | ||
| Series 3 (10, S34-37) | Series 3 (13) | Series 3 (7) | Series 3 (7) | Series 3 (7) |
| 1989 | 1992 | 1996 | 1997 | 1999 | 2001 | 2003 | 2012 |
|---|---|---|---|---|---|---|---|
| S1-2 (5) | - | - | - | - | S2 (4) | S2-3 (3) | (6) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pytharouli, S.; Michalis, P.; Raftopoulos, S. From Theory to Field Evidence: Observations on the Evolution of the Settlements of an Earthfill Dam, over Long Time Scales. Infrastructures 2019, 4, 65. https://doi.org/10.3390/infrastructures4040065
Pytharouli S, Michalis P, Raftopoulos S. From Theory to Field Evidence: Observations on the Evolution of the Settlements of an Earthfill Dam, over Long Time Scales. Infrastructures. 2019; 4(4):65. https://doi.org/10.3390/infrastructures4040065
Chicago/Turabian StylePytharouli, Stella, Panagiotis Michalis, and Spyridon Raftopoulos. 2019. "From Theory to Field Evidence: Observations on the Evolution of the Settlements of an Earthfill Dam, over Long Time Scales" Infrastructures 4, no. 4: 65. https://doi.org/10.3390/infrastructures4040065
APA StylePytharouli, S., Michalis, P., & Raftopoulos, S. (2019). From Theory to Field Evidence: Observations on the Evolution of the Settlements of an Earthfill Dam, over Long Time Scales. Infrastructures, 4(4), 65. https://doi.org/10.3390/infrastructures4040065