Sewer Pipes Condition Prediction Models: A State-of-the-Art Review
Abstract
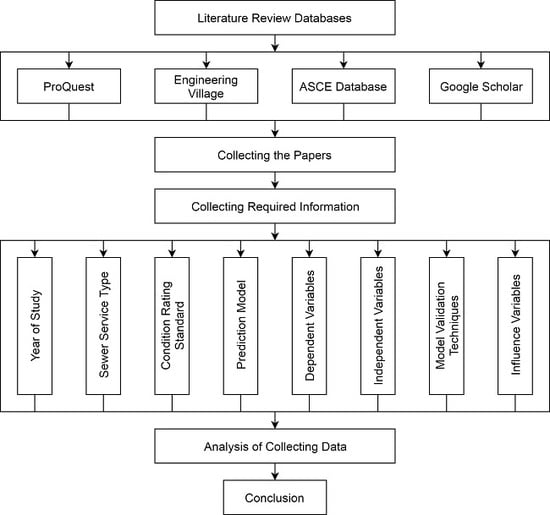
:1. Introduction
2. Sewer Pipe Deterioration
3. Factors Affecting Deterioration of Sewer Pipes
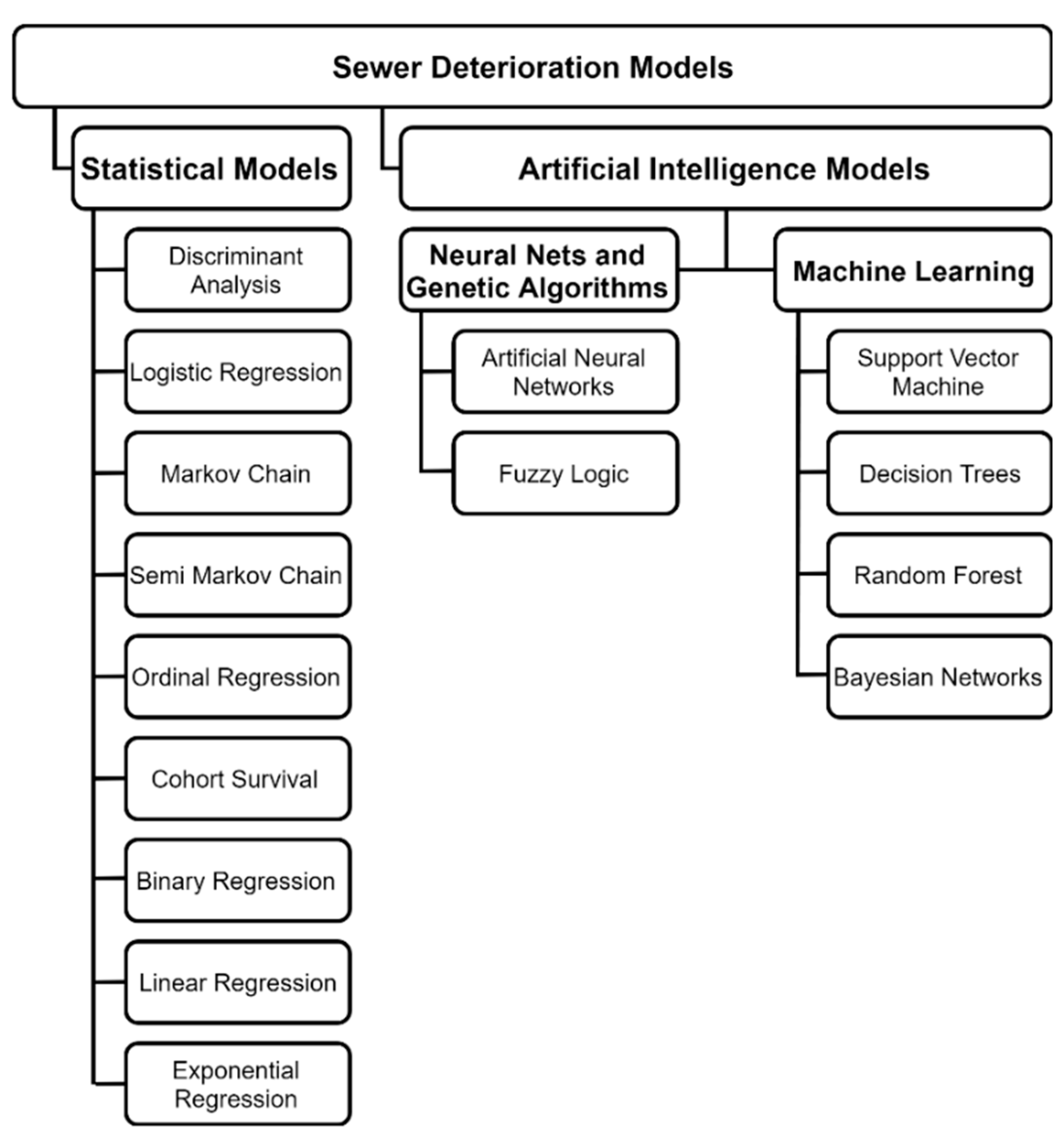
4. Deterioration Models for Sewer Pipes
5. Statistical Models
5.1. Linear Regression Models
5.1.1. Model Description
5.1.2. Previous Studies
5.1.3. Model Discussion
5.2. Markov Chain Models
5.2.1. Model Description
5.2.2. Previous Studies
5.2.3. Model Discussion
5.3. Logistic Regression Model
5.3.1. Model Description
5.3.2. Previous Studies
6. Discussion and Conclusions
7. Future Research Needs
8. Acronyms
| AI | Artificial Intelligence |
| ASCE | American Society of Civil Engineers |
| AWWA | American Water Works Association |
| C | Pipe State Condition |
| CCTV | Closed-circuit Television |
| CIPP | Cured-in-Place Pipe |
| EPA | Environmental Protection Agency |
| Equation | Equation |
| i | Facility Index |
| I/I | Infiltration/Inflow |
| m | Matrix |
| MCMC | Markov Chain Monte Carlo |
| NetCoS | Network Condition Simulator |
| P | Probability |
| Pij | Transition Probability |
| PVC | Polyvinyl Chloride |
| t | Time |
| U.S. | United States |
| Xi | Independent Variable |
| Yi | Dependent Variable for Facility |
| α | Intercept Parameter |
| ϵi | Random Error Term |
| β | Regression Coefficient |
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kaushal, V.; Serajiantehrani, R.; Najafi, M.; Hummel, M. Seismic Hazards Estimation for Buried Infrastructure Systems: Challenges and Solutions. In Proceedings of the 2nd International Conference on Natural Hazards & Infrastructure, Chania, Greece, 23–26 June 2019. [Google Scholar]
- ASCE. Report Card for America’s Infrastructure; American Society of Civil Engineers (ASCE): New York, NY, USA, 2017. [Google Scholar]
- EPA. Report to Congress: Impacts and Control of CSOs and SSOs; EPA: Washington, DC, USA, 2004. [Google Scholar]
- Kaushal, V. Comparison of Environmental and Social Costs of Trenchless Cured-in-Place Pipe Renewal Method with Open-Cut Pipeline Replacement for Sanitary Sewers. Ph.D. Thesis, University of Texas at Arlington, Arlington, TX, USA, 2019. [Google Scholar]
- EPA. Innovation and Research for Water Infrastructure for the 21st Century; EPA: Arlington, VA, USA, 2007. [Google Scholar]
- Ana, E.V.; Bauwens, W. Modeling the structural deterioration of urban drainage pipes: The state-of-the-art in statistical methods. Urban Water J. 2010, 7, 47–59. [Google Scholar] [CrossRef]
- American Water Works Association (AWWA). Buried no Longer: Confronting America’s Water Infrastructure Challenge, Boulder, CO. 2012. Available online: https://www.awwa.org/Portals/0/files/legreg/documents/BuriedNoLonger.pdf (accessed on 1 July 2018).
- Opila, M.C. Structural Condition Scoring of Buried Sewer Pipes for Risk-Based Decision Making. Ph.D. Thesis, University of Delaware, Newark, DE, USA, 2011. [Google Scholar]
- Kaushal, V.; Najafi, M.; Love, J.; Qasim, S.R. Microbiologically Induced Deterioration and Protection of Concrete in Municipal Sewerage System: A Technical Review. J. Pipeline Syst. Eng. Pract. 2019, 11, 03119002. [Google Scholar] [CrossRef]
- Najafi, M.; Gokhale, S.B. Trenchless Technology: Pipeline and Utility Design, Construction, and Renewal; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- EPA. Condition Assessment of Watewater Collection Systems; EPA/600/R-09/049; EPA: Boston, MA, USA, 2009.
- Davies, J.P.; Clarke, B.A.; Whiter, J.T.; Cunningham, R.J. Factors influencing the structural deterioration and collapse of rigid sewer pipes. Urban Water 2001, 3, 73–89. [Google Scholar] [CrossRef]
- Al-Barqawi, H.; Zayed, T. Condition rating model for underground infrastructure sustainable water mains. J. Perform. Constr. Facil. 2006, 20, 126–135. [Google Scholar] [CrossRef]
- Kley, G.; Caradot, N. D1.2. Review of Sewer Deterioration Models; Kompetenzzentrum Wasser Berlin gGmbH: Berlin, Germany, 2013. [Google Scholar]
- Morcuos, G.; Lounis, Z. Maintenance optimization of infrastructure networks using genetic algorithms. J. Autom. Constr. 2004, 14, 129–142. [Google Scholar] [CrossRef]
- Yang, J. Road Crack Condition Performance Modeling Using Recurrent Markov Chains and Artificial Neural Networks. Ph.D. Thesis, Department of Civil and Environmental Engineering, College of Engineering, University of South Florida, Tampa, FL, USA, 2004. [Google Scholar]
- Tran, H.D. Investigation of Deterioration Models for Stormwater Pipe Systems. Ph.D. Thesis, Victoria University, Melbourne, Australia, 2007. [Google Scholar]
- Altarabsheh, A.G. Managing Urban Wastewater System Using Complex Adaptive System Approach. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2016. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2011. [Google Scholar]
- Dasu, T.; Johnson, T. Exploratory Data Mining and Data Cleaning; John Wiley & Son: Hoboken, NJ, USA, 2003. [Google Scholar]
- Rawlings, J.O. Applied Regression Analysis: A Research Tool; Wadsworth & Brooks, Cole Advanced Books & Software: Pacific Grove, CA, USA, 1989. [Google Scholar]
- Chughtai, F.; Zayed, T. Sewer pipeline operational condition prediction using multiple regression. In Proceedings of the Pipelines 2007: Advances and Experiences with Trenchless Pipeline Projects, Boston, MA, USA, 8–11 July 2007. [Google Scholar]
- Chughtai, F.; Zayed, T. Structural condition models for sewer pipeline. In Proceedings of the Pipelines 2007: Advances and Experiences with Trenchless Pipeline Projects, Boston, MA, USA, 8–11 July 2007. [Google Scholar]
- Chughtai, F.; Zayed, T. Infrastructure Condition Prediction Models for Sustainable Sewer Pipelines. J. Constr. Facil. 2008, 22, 333–341. [Google Scholar] [CrossRef]
- Bakry, I.; Alzraiee, H.; Kaddoura, K.; Masry, M.E.; Zayed, T. Condition Prediction for Chemical Grouting Rehabilitation of Sewer Networks. J. Perform. Constr. Facil. 2016, 30, 04016042. [Google Scholar] [CrossRef]
- Bakry, I.; Alzraiee, H.; Masry, M.E.; Kaddoura, K.; Zayed, T. Condition Prediction for Cured-in-Place Pipe Rehabilitation of Sewer Mains. J. Perform. Constr. Facil. 2016, 30, 04016016. [Google Scholar] [CrossRef]
- Madanat, S.; Ibrahim, W.H.W. Poisson Regression Models of Infrastructure Transition Probabilities. J. Transp. Eng. 1995, 121, 267–272. [Google Scholar] [CrossRef]
- Morcous, G.; Rivard, H.; Hanna, A.M. Modeling Bridge Deterioration Using Case-based Reasoning. J. Infrastruct. Syst. 2002, 8, 86–95. [Google Scholar] [CrossRef]
- Moteleb, M. Risk Based Decision Making Tools for Sewer Infrastructure Management. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 2010. [Google Scholar]
- Konstantopoulos, T. Markov Chains and Random Walks; Springer: New York, NY, USA, 2009. [Google Scholar]
- Jeong, H.S.; Baik, H.S.; Abraham, D.M. An ordered probability model approach for developing Markov chain-based deterioration model for wastewater infrastructure systems. In Proceedings of the Pipelines 2005: Optimizing Pipeline Design, Operations, and Maintenance in Today’s Economy, Reston, VA, USA, 21–24 August 2005; pp. 649–661. [Google Scholar]
- Micevski, T.; Kuczera, G.; Coombes, P. Markov Model for Storm Water Pipe Deterioration. J. Infrastruct. Syst. 2002, 8, 49–56. [Google Scholar] [CrossRef]
- Wirahadikusumah, R.; Abraham, D.; Iseley, T. Challenging issues in modeling deterioration of combined sewers. J. Infrastruct. Syst. 2001, 2, 77–84. [Google Scholar] [CrossRef]
- Gat, Y.L. Modelling the deterioration process of drainage pipelines. Urban Water J. 2008, 5, 97–106. [Google Scholar] [CrossRef]
- Scheidegger, A.; Hug, T.; Rieckermann, J.; Maurer, M. Network condition simulator for benchmarking sewer deterioration models. Water Res. 2011, 45, 4983–4994. [Google Scholar] [CrossRef] [PubMed]
- Balekelayi, N.; Tesfamariam, S. Statistical Inference of Sewer Pipe Deterioration Using Bayesian Geoadditive Regression Model. J. Infrastruct. Syst. 2019, 25, 04019021. [Google Scholar] [CrossRef]
- Park, H.A. An Introduction to Logistic Regression: From Basic Concepts to Interpretation with Particular Attention to Nursing Domain. J. Korean Acad. Nurs. 2013, 43, 154. [Google Scholar] [CrossRef]
- Agresti, A. An Introduction to Categorical Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Ariaratnam, S.T.; El-Assaly, A.; Yang, Y. Assessment of Infrastructure Inspection Needs Using Logistic Models. J. Infrastruct. Syst. 2001, 7, 160–165. [Google Scholar] [CrossRef]
- Koo, D.H.; Ariaratnam, S.T. Innovative method for assessment of underground sewer pipe condition. Autom. Constr. 2006, 15, 479–488. [Google Scholar] [CrossRef]
- Ana, E.; Bauwens, W.; Pessemier, M.; Thoeye, C.; Smolders, S.; Boonen, I.; Gueldre, G.D. An investigation of the factors influencing sewer structural deterioration. Urban Water J. 2009, 6, 303–312. [Google Scholar] [CrossRef]
- Lubini, A.T.; Fuamba, M. Modeling of The Deterioration Timeline of Sewer Systems. Can. J. Civ. Eng. 2011, 38, 1381–1390. [Google Scholar] [CrossRef]
- Salman, B.; Salem, O. Modeling Failure of Wastewater Collection Lines Using Various Section-Level Regression Models. J. Infrastruct. Syst. 2012, 18, 146–154. [Google Scholar] [CrossRef]
- Sousa, V.; Matos, J.P.; Matias, N. Evaluation of artificial intelligence tool performance and uncertainty for predicting sewer structural condition. Autom. Constr. 2014, 44, 84–91. [Google Scholar] [CrossRef]
- Kabir, G.; Balek, N.B.C.; Tesfamariam, S. Sewer Structural Condition Prediction Integrating Bayesian Model Averaging with Logistic Regression. J. Perform. Constr. Facil. 2018, 32, 04018019. [Google Scholar] [CrossRef]
- Malek Mohammadi, M.; Najafi, M.; Tabesh, A.; Riley, J.; Gruber, J. Condition Prediction of Sanitary Sewer Pipes. In Proceedings of the ASCE Pipeline Conference, Nashville, TN, USA, 21–24 July 2019. [Google Scholar]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Atique, F. Analysis of Urban Pipe Deterioration Using Copula Method. Ph.D. Thesis, University of Delaware, Newark, DE, USA, 2016. [Google Scholar]
- Salman, B. Infrastructure Management and Deterioration Risk Assessment of Wastewater Collection Systems. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 2010. [Google Scholar]
- Malek Mohammadi, M. Development of Condition Prediction Models for Sanitary Sewer Pipes. Ph.D. Thesis, University of Texas at Arlington, Arlington, TX, USA, 2019. [Google Scholar]
- Malek Mohammadi, M.; Homing, A.; Najafi, M.; Korky, S.J.; Serajiantehrani, R. Development of a Framework for Design and Installation of a New Lining Material for Water Pipeline Renewal. In Proceedings of the ASCE Pipeline Conference, Nashville, TN, USA, 21–24 July 2019. [Google Scholar]
| Physical Factors | Environmental Factors | Operational Factors |
|---|---|---|
| Connections | Backfill type | |
| End invert elevation | Bedding material | |
| Installation method | Ground movement | Blockages |
| Joint type | Groundwater level | Burst history |
| Pipe length | pH | Debris |
| Pipe shape | Road type | Flow velocity |
| Pipe slope | Root interference | Hydraulic condition |
| Sewer age | Soil corrosivity | Infiltration/exfiltration |
| Sewer depth | Soil fracture potential | Previous maintenance |
| Sewer pipe material | Soil moisture | Sediment level |
| Sewer size | Soil type | Sewer function |
| Start invert elevation | Sulfate soil | Surcharge |
| Surface type |
| Authors | Year | Model | Independent Variables |
|---|---|---|---|
| Davies et al. | 2001 | Logistic regression | Age, Material, Diameter, Depth, Length, Sewer Type, Location, Corrosivity, Road Type, Other Factors |
| Ariaratnam et al. | 2001 | Logistic regression | Age, Material, Diameter, Depth, Sewer Type |
| Wirahadikusumah et al. | 2001 | Markov chain | Material, Depth, Soil Type, Groundwater |
| Lubini and Fuamba | 2001 | Logistic regression | Age, Material, Diameter, Length, Slope |
| Micevski et al. | 2002 | Markov chain | Material, Diameter, Soil Type |
| Koo and Ariaratnam | 2006 | Logistic regression | Age, Flow, Other Factors |
| Chughtai and Zayed | 2008 | Linear regression | Age, Material, Diameter, Depth, Length, Slope, Bedding Type, Road Type |
| Gat | 2008 | Markov chain | Age, Diameter, Sewer Type |
| Ana et al. | 2009 | Logistic regression | Age, Material, Diameter, Depth, Length, Slope, Sewer Type, Location |
| Salman and Salem | 2012 | Ordinal regression Logistic regression Binary regression | Age, Material, Diameter, Depth, Length, Slope, Sewer Type |
| Sousa et al. | 2014 | Logistic regression | Age, Material, Diameter, Depth, Length, Slope |
| Bakry et al. | 2016 | Multiple regression | Age, Material, Diameter, Depth, Length, Sewer Type, Soil Type, Groundwater, Surface Type, Traffic |
| Gedam et al. | 2016 | Linear regression | Age, Material, Diameter, Depth |
| Kabir et al. | 2018 | Bayesian logistic regression | Age, Material, Diameter, Depth, Length, Slope, Up Invert, Down Invert, Other Factors |
| Malek Mohammadi et al. | 2019 | Logistic Regression | Age, Material, Diameter, Depth, Length, Slope, Groundwater, Soil Type |
| Balekelayi and Tesfamariam | 2019 | Bayesian Regression | Age, Material, Diameter, Depth, Length, Slope, Groundwater, Residential and Commercial Connections, Repairs, Flushes, Cleaning, Degrease, Backups, and Root Cuts |
| Applicability | Logistic Regression | Markov Chain | Linear Regression |
|---|---|---|---|
| Predicting condition of pipe groups | Moderate | Good | Poor |
| Predicting condition of individual pipes | Good | Moderate | Good |
| Predicting categorical dependent variables | Good | Moderate | Poor |
| Conceptual and computational simplicity | Good | Poor | Good |
| Identifying relationship between dependent and independent factors | Good | Poor | Moderate |
| Calculation of condition probabilities | Good | Good | Poor |
| Flexible to deficiency of data | Moderate | Poor | Good |
| Prediction Models | Advantages | Disadvantages |
|---|---|---|
| Logistic Regression | Does not require too many computational resources, incredibly easy to implement, highly interpretable, not required input features to be scaled, capable of predicting probabilities, does not require normal distribution of independent variables, capable of predicting influence variables | not very useful for non-linear and complex problems, can only predict a categorical outcome |
| Markov Chain | can predict categorical and continuous variables, strong statistical foundation, can be combined with other models, works for complicated distributions in high-dimensional spaces | difficult to implement and validate, requires large number of data, Markov assumptions may not be applicable for all datasets |
| Linear Regression | very easy to implement, capable of predicting influence variables, highly interpretable | can only identify linear relationships between variables, only looks at the mean of the dependent variable, sensitive to outliers |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malek Mohammadi, M.; Najafi, M.; Kaushal, V.; Serajiantehrani, R.; Salehabadi, N.; Ashoori, T. Sewer Pipes Condition Prediction Models: A State-of-the-Art Review. Infrastructures 2019, 4, 64. https://doi.org/10.3390/infrastructures4040064
Malek Mohammadi M, Najafi M, Kaushal V, Serajiantehrani R, Salehabadi N, Ashoori T. Sewer Pipes Condition Prediction Models: A State-of-the-Art Review. Infrastructures. 2019; 4(4):64. https://doi.org/10.3390/infrastructures4040064
Chicago/Turabian StyleMalek Mohammadi, Mohammadreza, Mohammad Najafi, Vinayak Kaushal, Ramtin Serajiantehrani, Nazanin Salehabadi, and Taha Ashoori. 2019. "Sewer Pipes Condition Prediction Models: A State-of-the-Art Review" Infrastructures 4, no. 4: 64. https://doi.org/10.3390/infrastructures4040064
APA StyleMalek Mohammadi, M., Najafi, M., Kaushal, V., Serajiantehrani, R., Salehabadi, N., & Ashoori, T. (2019). Sewer Pipes Condition Prediction Models: A State-of-the-Art Review. Infrastructures, 4(4), 64. https://doi.org/10.3390/infrastructures4040064