Isolated and Single Pedestrians and Pedestrian Groups on Sidewalks

Abstract

Walking freedom can define the quality of an urban area, but this freedom is conditioned by various factors. The research objective is to study pedestrian behavior on sidewalks. Data are collected during on site surveys by means of concealed camcorders. For each pedestrian many factors are observed, such as gender, age, direction, distractions, transport of objects, etc., which could influence pedestrian behavior. Data processing allows the identification of mathematical models describing the average pedestrian’s behavior, subdivided for user type (isolated, single, group). In general, the mean walking pedestrian speed decreases depending on user type (in a linear manner if age class grows for isolated pedestrians, while with the square of age for other user types), of gender, and of facing type. Models obtained for the different pedestrian types were compared to understand the differences in speeds, underlining that pedestrian interferences play a significant role in defining behavior and, therefore, speed. The results support the idea that, to define a smooth pedestrian speed as an indicator of the “walkability” of a path, in addition to considering the path and user’s characteristics, it is also necessary to define the type of user for which the infrastructure is designed.

1. Introduction

Nowadays urban mobility sustainability plays a central role in transport policies worldwide. The central role of this sustainability is walkability, which means the easiness of freely moving within an urban context, a freedom that must be ensured to increasingly wider portions of the population in accordance with the principles of Universal Design and Design for All.

From this point of view pedestrian infrastructure quality is very important, as it must be imagined, designed, and built to ensure the mobility of every individual user. Its task is more important when it is part of more complex modal displacements: in fact, the lack of quality and accessibility of pedestrian pathways from home or work locations to the first available transport means, de facto inhibits the entire moving of a substantial portion of the population, thus leading to the exclusion of these citizens from economic, social, and cultural progress. Therefore, it is necessary to reconsider the pedestrian as the main actor of the urban scenario. To do this, however, it is necessary to know how the pedestrian moves, and how the pedestrian infrastructure characteristics and the flow in which they are moving affect such behavior.

Several groups around the world are currently working on technical and social analyses regarding pedestrian infrastructure design and construction. Consequently, factors affecting pedestrian behavior are investigated in several scientific studies.

Willis et al. [1] consider many factors, such as age, gender, level of mobility, percentage of groups, time of day, etc., finding that walking speed decreases as age increases; in fact, the youngest pedestrians have the highest speeds and adults are significantly faster than elderly pedestrians, who are the slowest category.

Finnis et al. [2] measure the mean pedestrian speed to evaluate the influences on urban planning and pedestrian facilities design in rural and urban municipalities of New Zealand. The data show complex relationships between the environment, personal characteristics of pedestrians, and physical factors. These factors have been taken into account during the model’s construction for the study of pedestrian movements.

Rahman et al. (2012) [3] show that, in Bangladesh, free flow speed is strongly influenced by pedestrians age, gender, and pedestrian facilities characteristics.

In addition, the presence of luggage has greater influences on female pedestrian speed, compared to that of males.

Nazir et al. [4] studied pedestrian free flow speed on sidewalks of Rajshani city, in Bangladesh. Data were collected by camcorder. The study investigates the relationship among flow, speed, density and pedestrian space. The results show that the mean walking speed is influenced by age and gender, and that location characteristics have effects on pedestrian flows.

Other studies recently highlighted the importance of sidewalk managing. Of these, the research published by Corazza et al. [5] is interesting. This study represents an initial attempt to apply sidewalk assessment methodologies belonging to maintenance programs for motorized mode infrastructures. They studied a Sidewalks Condition Index (SCI) to quantify sidewalk conditions and the extent of dangerous distresses that present obstacles for pedestrians.

Most studies consider two different conditions. Some are based on the behavior of the isolated pedestrian, so a pedestrian moving alone on a pedestrian infrastructure without interfering with other pedestrians. Thier behavior is, therefore, exclusively tied to his psycho-physical conditions and personal choices (motive of moving, environmental conditions, etc.). Others consider pedestrians in groups, defining an average behavior that depends on the composition and number of groups and the pedestrian flow. Very few studies consider the behavior of the single pedestrian within a flow.

For this reason, this research has the objective of investigating pedestrian infrastructure characteristics, pedestrians characteristics, and the behavior that pedestrians take along paths, distinguishing between isolated pedestrians, single pedestrians, and groups, to see if and how the presence of other users leads to variations in the individual behavior.

This paper is the development of a previous research carried out by the authors [6,7].

2. Data, Methodology, and Variables

2.1. Area of Study

The study was developed in the city of Cagliari (Sardinia, Italy) in an urban context characterized by activities and services for citizens and the presence of numerous shops.

Table 1. General sidewalk characteristics.

Sidewalks	Width [m]	Average Walking Speed [m/s]	Standard Deviation σ	Pedestrian Volume	Men [%]	Women [%]	Groups [%]
Viale Trieste	2.15	1.20	0.28	715	58.0	42.0	24.6
Via Roma	3.45	1.37	0.27	970	57.5	42.5	33.2
Via B.Rossi	1.45	1.30	0.32	194	53.6	46.4	22.5
Via Sonnino	1.35	1.17	0.28	204	49.0	51	35.2
Via G. Deledda	2.05	1.35	0.31	508	47.0	53.0	46.5
Via Paoli sez.1	2.85	1.21	0.32	795	39.8	60.1	28.1
Via Paoli sez.2	3.95	1.17	0.40	939	38.0	62.0	30.7
Via Leopardi	2.50	1.25	0.30	280	46.0	54.0	39.8
Via M.Santo	1.30	1.30	0.33	267	46.0	54.0	26.1

shows streets; for each one, the average speed values were obtained, starting from video surveys, for a total of about 4800 pedestrians. Table 1 also shows that the average speeds are variable (between 1.17 and 1.37 m/s), values that appear unrelated to pedestrian traffic volume. In fact, the lower flows do not match with lower mean speeds: the maximum mean speed is on the street with the greater pedestrian flow; even sidewalk width seems not to affect the average general behavior. Distribution by gender is always sufficiently balanced and the number of groups is not the majority. The result of the general study has also been verified with the Highway Capacity Manual (HCM) method [8], ensuring that all sidewalks have a Level of Service LOS A.

2.2. Data Collection and Reduction

Surveys are performed during the shops opening hours and on days with good weather conditions with concealed camcorders so as not to influence the spontaneous pedestrians’ behaviors.

In order to determine pedestrians’ speeds, two lines perpendicular to a known distance have been considered for each path. The time taken by each pedestrian to cross the sidewalk section was defined through video processing, based on a grid of lines on the basis of the reference signs and considering that one movie frame corresponds to 1/25 of second. In this way it was possible to define the time taken by each pedestrian to cross the sidewalk section. Speed is calculated as the ratio between the known distance and this time.

For each pedestrian the following data are collected: gender, age, electronic devices use, bulky item carried, disability, pushchairs, direction, etc.

Pedestrians’ age is determined subjectively by an operator and, to reduce the error in age estimation, pedestrians are cataloged in five categories; pedestrians are also distinguished by user type in terms of isolated pedestrian, single pedestrian, and groups. The first is a pedestrian walking alone with no one in the section, the second is a pedestrian walking alone but with others in the section and the third is a group of pedestrians walking together.

Pedestrians characterized by interference influencing their behavior (disabilities, pushchairs, carried loads, etc.) are excluded from the dataset.

Speed analysis shows that pedestrians’ speeds can be approximated by a normal distribution. In fact, the area under the normal distribution graph, for a distance from the mean of ±3σ is, 0.9973. Thus, the probability that data falls within this range is 99.73% and only 0.27% of data [9] are excluded.

This is important because the focus of the study is to determine the average pedestrian behavior: the construction of a normal distribution of pedestrian speeds was made and data outside the range [μ − 3σ; μ + 3σ] were eliminated.

Excluded data refer to pedestrians with abnormal behavior during the journey, for example people who suddenly stop and then resume walking for many reasons, joggers, runners, etc. In fact, these behaviors could have adversely affected the statistical analysis, worsening or, even, inhibiting the determination of sound models

2.3. Methodology and Variables

In order to describe the average behavior of pedestrians, mathematical models are investigated through the described data processing. For each user type, some models are developed using multiple regression in which the dependent variable is related to independent variables by the general equation:

Y = β₀ + β₁X₁ + β₂X₂ + … + β_nX_n + ε

(1)

where:

• Y is the dependent variable;
• X₁, …, X_n are independent variables;
• β₀ is the constant parameter (intercept);
• β₁, …, β_n are model parameters (regression coefficients);
• ε is the error component in the model.

First of all, to define variables belonging to each model, the backward elimination of non-significant variables (p-value > 5%) are used.

The methodology used is cross-validation, in which a single sidewalk dataset for time are excluded; with the remaining data a behavioral model is constructed (named the partial model); later, with the dataset excluded from the construction phase, each model is validated.

Each partial model is verified calculating the R² (coefficient of determination) and the RMSPE (root mean square percent error).

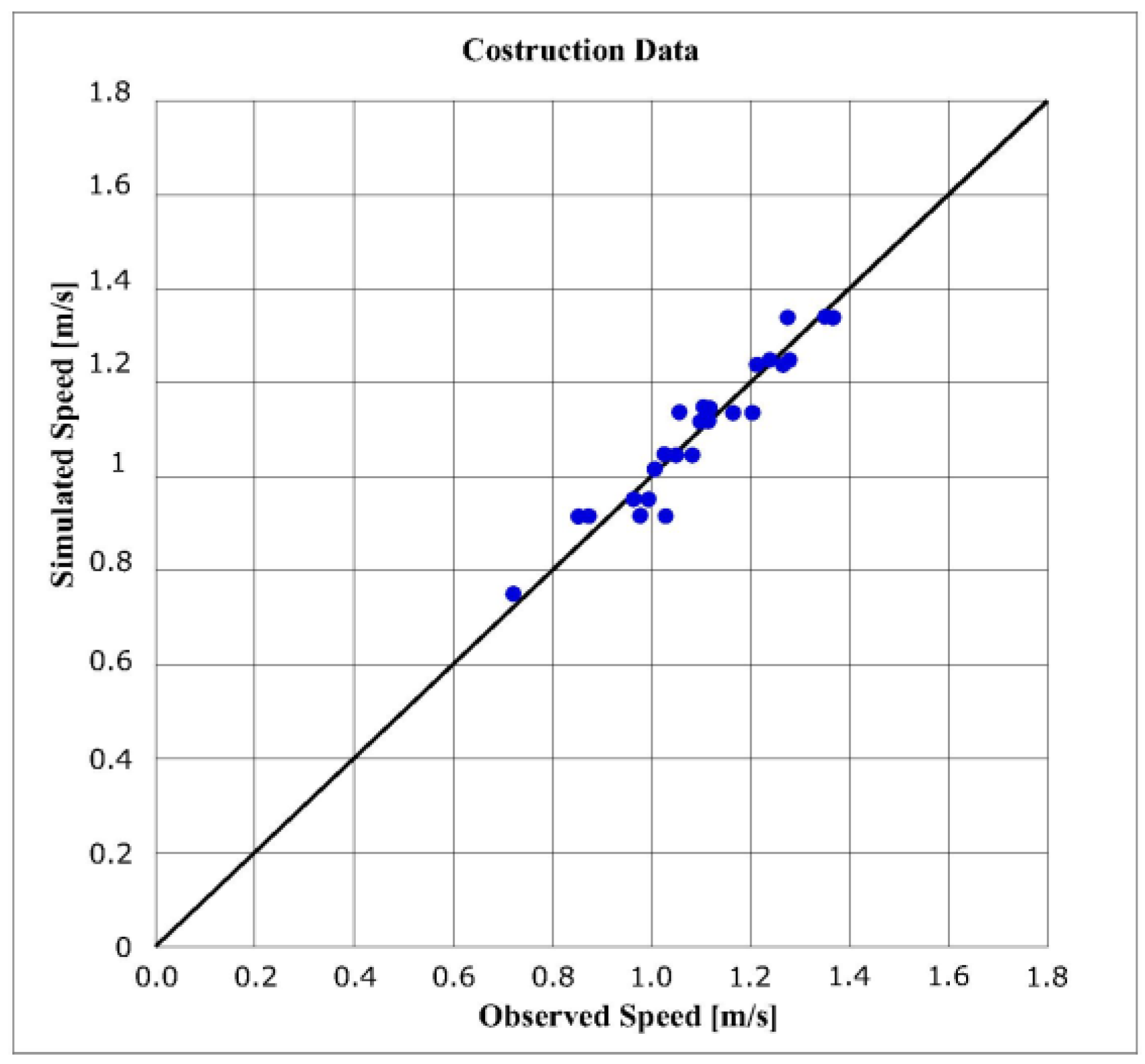
In the model construction phase, it is necessary that observed and simulated speeds have good agreement: this happens if, graphically, data lie roughly on a 45 degree line.

Later, the partial model was validated, using the sidewalk dataset excluded from the construction phase, calculating the coefficient of determination R_v² and RMSPE_v.

Additionally, in the model validation phase, all the considerations mentioned in the model construction phase are valid: observed and predicted speeds have good agreement if, graphically, data lie roughly on a 45 degree line.

Once all the partial models have been determined, if these provide good results, a global model is constructed using all sidewalk datasets and the R² and RMSPE of this global model are calculated; also in this case, observed and predicted speeds have good agreement if, graphically, data lie roughly on a 45 degree line.

If the global model has the same trend as the partial models and the partial models’ parameters always fall within the confidence intervals of the respective global model parameters, then the partial model is considered reliable.

The dependent and independent variables were chosen using the methodology described above. Speed is the variable most used in reference studies and it is the best indicator of pedestrian behavior.

The speed is closely influenced by factors related to pedestrian and path characteristics, which act as the independent variable; in particular, age is the best indicator of psycho-physical pedestrian characteristics and of their skill to walk, while the building face characterizes the path and, therefore, the environment passed through. It has also been tested if gender could be considered a significant variable.

Dependent variables Y are:

• Y₁ = mean walking speed for each age class [m/s];
• Y₂ = mean walking speed for each age class according pedestrians gender [m/s].

Independent variables X_n are:

• X₁ = age classes for each sidewalk. The classes are: 1—from 0 to 18 years old; 2—from 19 to 40 years old; 3—from 41 to 65 years old; 4—from 66 to 75 years old; 5—over 75 years old.
• X₂ = the facing type: 0—blind; 1—accesses; 2—shop windows.
• X₃ = pedestrian gender: 0—female; 1—male.

Those described above are not the only variables that can affect the phenomenon; for this reason other independent variables are also investigated and subsequently excluded by backward elimination, like width section, effective walkway width, obstacles percentage, time of day, pedestrian flow, groups percentage, and pedestrian direction.

Furthermore, as expected, the age class from 0 to 18 years is present in very low percentages and, therefore, the data are excluded.

3. Models for Isolated Pedestrians

Isolated pedestrians are those users moving individually and having no interactions with other pedestrians.

Based on the methodology described above (multiple regression), partial models are constructed and later validated, identifying two models. In the first one the mean walking speed (Y₁) is expressed as a function of age classes (X₁) and facing type (X₂); in the second one the mean walking speed (Y₂) is expressed as a function of age classes (X₁), facing type (X₂), and gender (X₃).

3.1. Model No. 1: Mean Walking Speed, Age Classes, and Facing Type

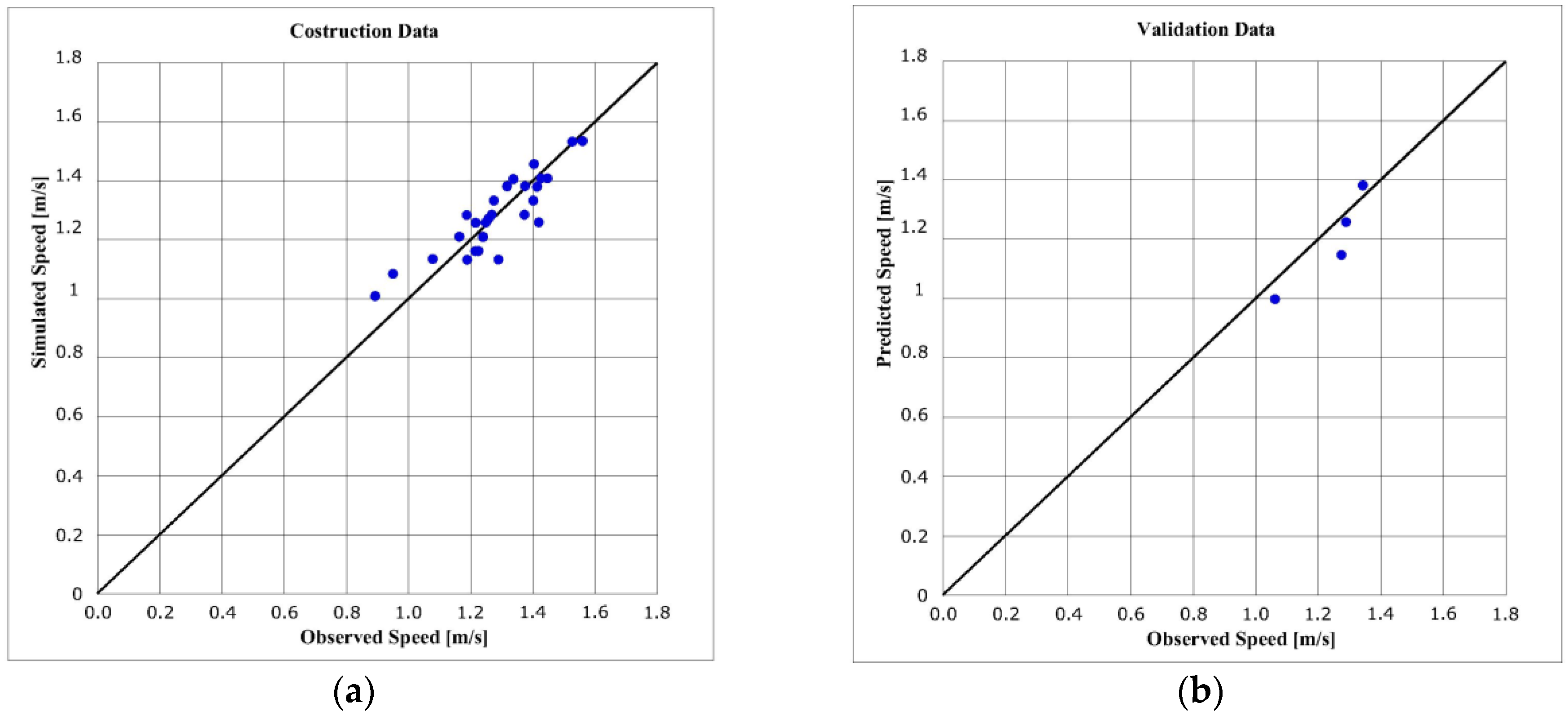
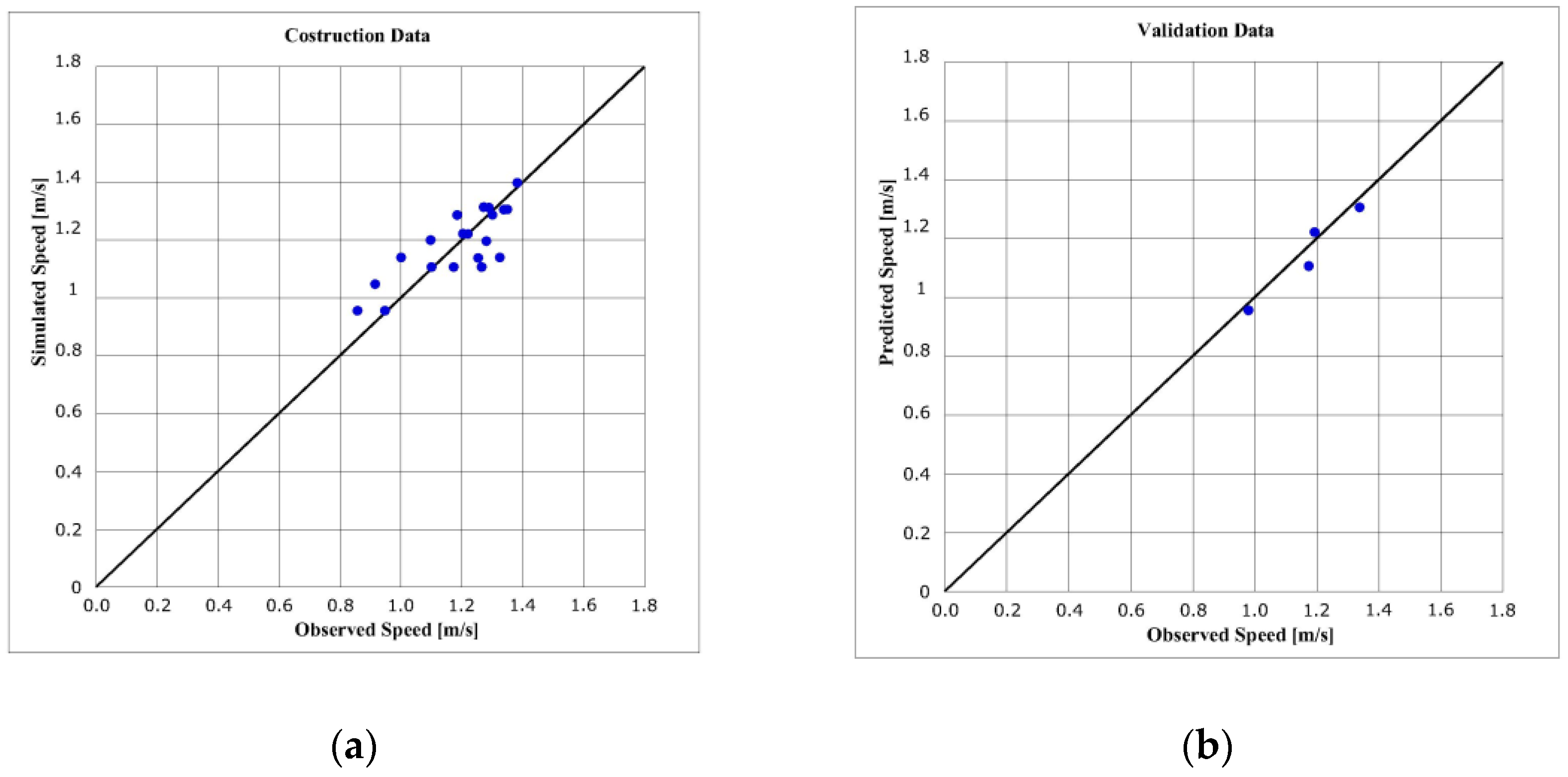
All the partial models were constructed and validated, excluding one sidewalk at a time. To better understand, the case of the partial model, obtained by excluding the sidewalk of Via Paoli sez. 1, is reported as an example. Figure 1 reports the comparison between the observed and estimated datasets:

Y₁ = 1.7769 − 0.1237X₁ − 0.0752X₂

(2)

where R² = 0.79; RMSPE = 0.0607. Validation phase: R_v² = 0.81; RMSPE_v = 0.0652.

As it is possible to see, coefficients of determination and RMSPE indices have good values and the observed and estimated speeds have good agreement.

For all other partial models, similar results are obtained. Thus, using all the sidewalk data at the same time, a global model was constructed:

Y₁ = 1.7522 − 0.1169X₁ − 0.0674X₂

(3)

where R² = 0.77; RMSPE = 0.0624.

Table 2. Global model: regression statistics and ANOVA.

Regression Statistics
Multiple R	0.879398
R Square	0.773341
Adjusted R Square	0.75771
Standard Error	0.076153
Observation	32
Analysis of Variance
Variable	df	SQ	MQ	F	Significance F
Regression	2	0.573811	0.286905	49.47285	<0.0001
Residual	29	0.168178	0.005799
Total	31	0.741989
	Coeff.	Standard Error	t Stat	p-Value	Lower 95%	Upper 95%
Intercept	1.752226	0.048316	36.26633	<0.0001	1.65341	1.851043
(X1) Age Class	−0.11686	0.012902	−9.05795	<0.0001	−0.14325	−0.09048
(X2) Facing Type	−0.0674	0.015325	−4.398	0.000135	−0.09874	−0.03606

reports the regression statistics and Anova of the global model (3).

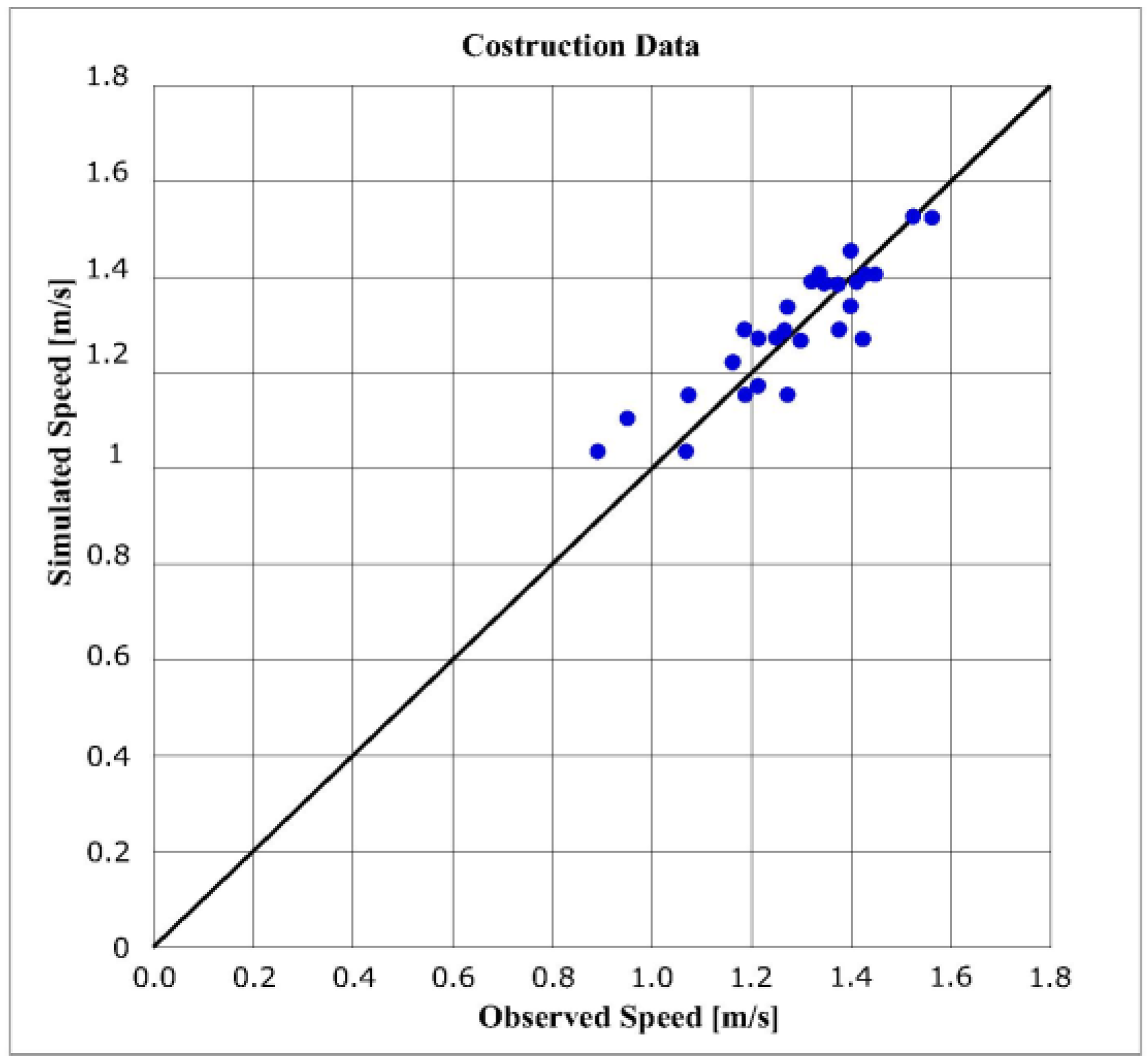
It can therefore be concluded that the global model has the same trend as the partial models. The partial models’ parameters always fall within of confidence intervals of respective global model parameters; the coefficient of determination and RMSPE index have good values. In addition, the observed and estimated speeds have good agreement; in fact, they roughly lie on a 45 degree line (Figure 2).

3.2. Model No. 2: Mean Walking Speed, Age Classes, Facing Type, and Gender

With the same methodology and the steps indicated in Section 3.1 for Model No. 1, the following is achieved.

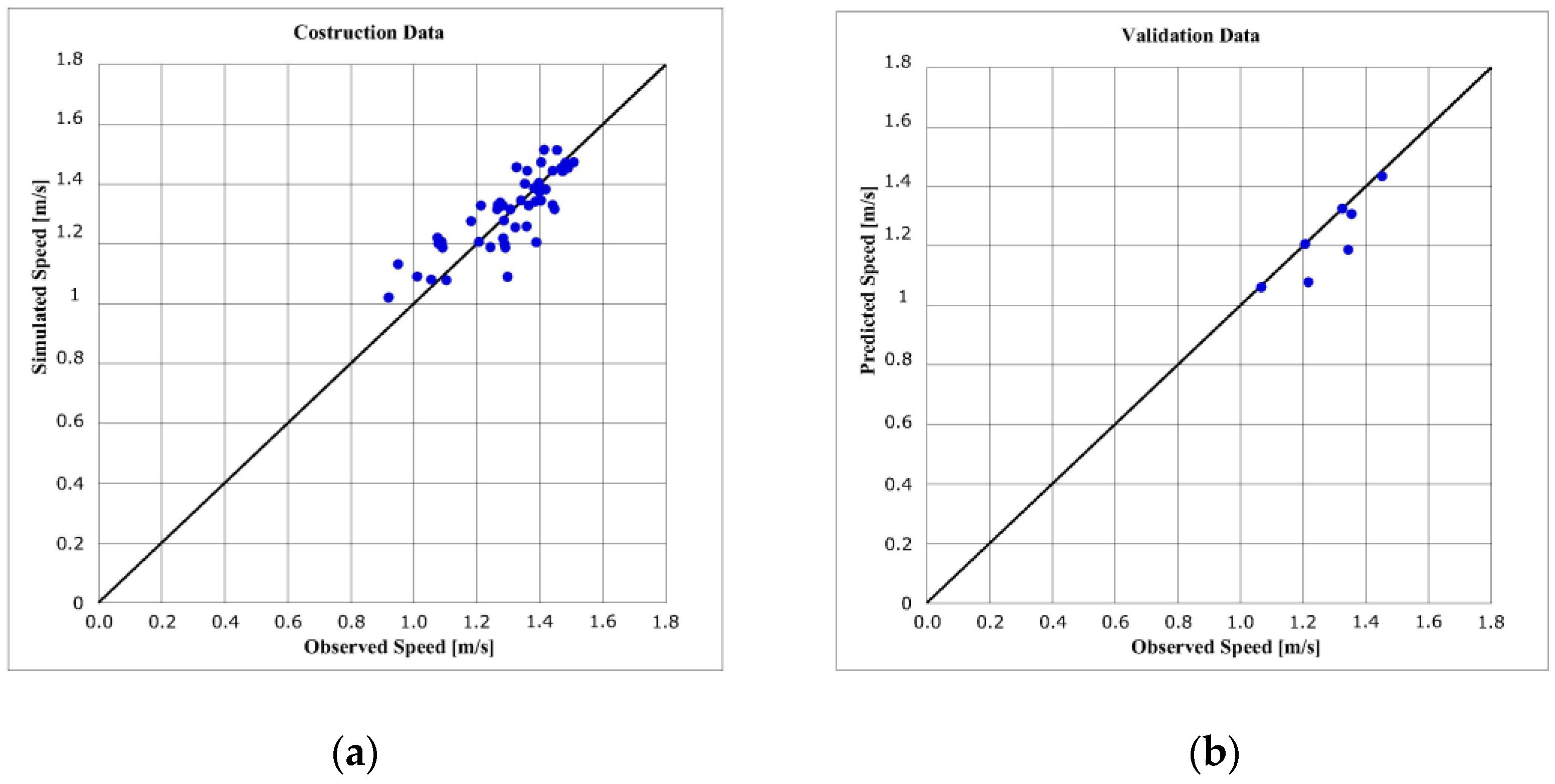
Partial model example excluding Via Paoli sez. 1:

Y₂ = 1.7188 − 0.1264X₁ − 0.0693X₂ + 0.1089X₃

(4)

where R² = 0.74; RMSPE = 0.0683. Validation phase: R_v² = 0.76; RMSPE_v = 0.0647.

Coefficients of determination and RMSPE indices always show good values. In addition, the observed and estimated speeds have good agreement (Figure 3). For all other partial models, similar results are obtained. Thus, using all the sidewalk data at the same time, a global model was constructed:

Y₂ = 1.6999 − 0.1214X₁ − 0.0605X₂ + 0.1099X₃

(5)

where R² = 0.73; RMSPE = 0.0684.

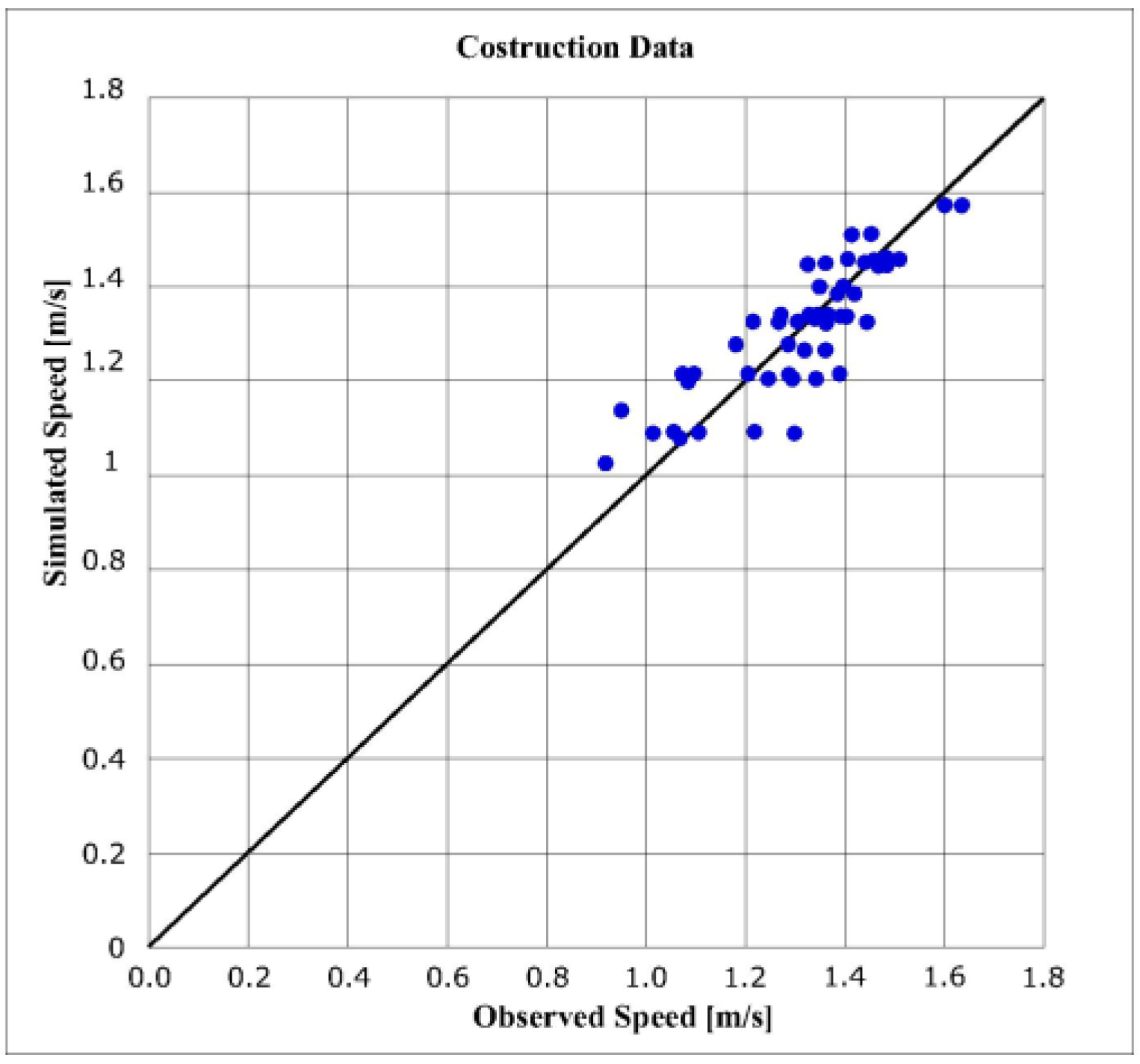
For the global model (5),

Table 3. Global model: regression statistics and ANOVA.

Regression Statistics
Multiple R	0.851898
R2	0.72573
Adjusted R2	0.710205
Standard Error	0.085461
Observation	57
Analysis of Variance
Variable	df	SQ	MQ	F	Significance F
Regression	3	1.02425	0.341417	46.74671	<0.0001
Residual	53	0.387088	0.007304
Total	56	1.411338
	Coeff.	Standard Error	t Stat	p-Value	Lower 95%	Upper 95%
Intercept	1.699911	0.042397	40.09515	<0.0001	1.614874	1.784949
(X1) Age Class	−0.1214	0.011338	−10.7071	<0.0001	−0.14414	−0.09866
(X2) Facing Type	−0.06048	0.012872	−4.69836	<0.0001	−0.0863	−0.03466
(X3) Gender	0.109945	0.022826	4.816716	<0.0001	0.064162	0.155728

reports the regression statistics and Anova and Figure 4 reports the comparison between observed and simulated speeds.

These results show the same conclusions as Model No. 1.

4. Models for Single Pedestrians

The single pedestrians are those users moving alone within the pedestrian flow and having interactions with other pedestrians walking in the same or opposite direction.

With the same methodology and the steps indicated in Section 3 for isolated pedestrians, the following is achieved:

Two partial models were built and validated. In the first, the mean walking speed (Y₁) is expressed as a function of the square of the age classes (X₁) and facing type (X₂); in the second one the mean walking speed (Y₂) is expressed as a function of the square of the age classes (X₁), facing type (X₂), and gender (X₃).

4.1. Model No. 1: Mean Walking Speed, Age Classes, and Facing Type

With the same methodology and the steps indicated in Section 3.1 for Model No. 1, the following is achieved:

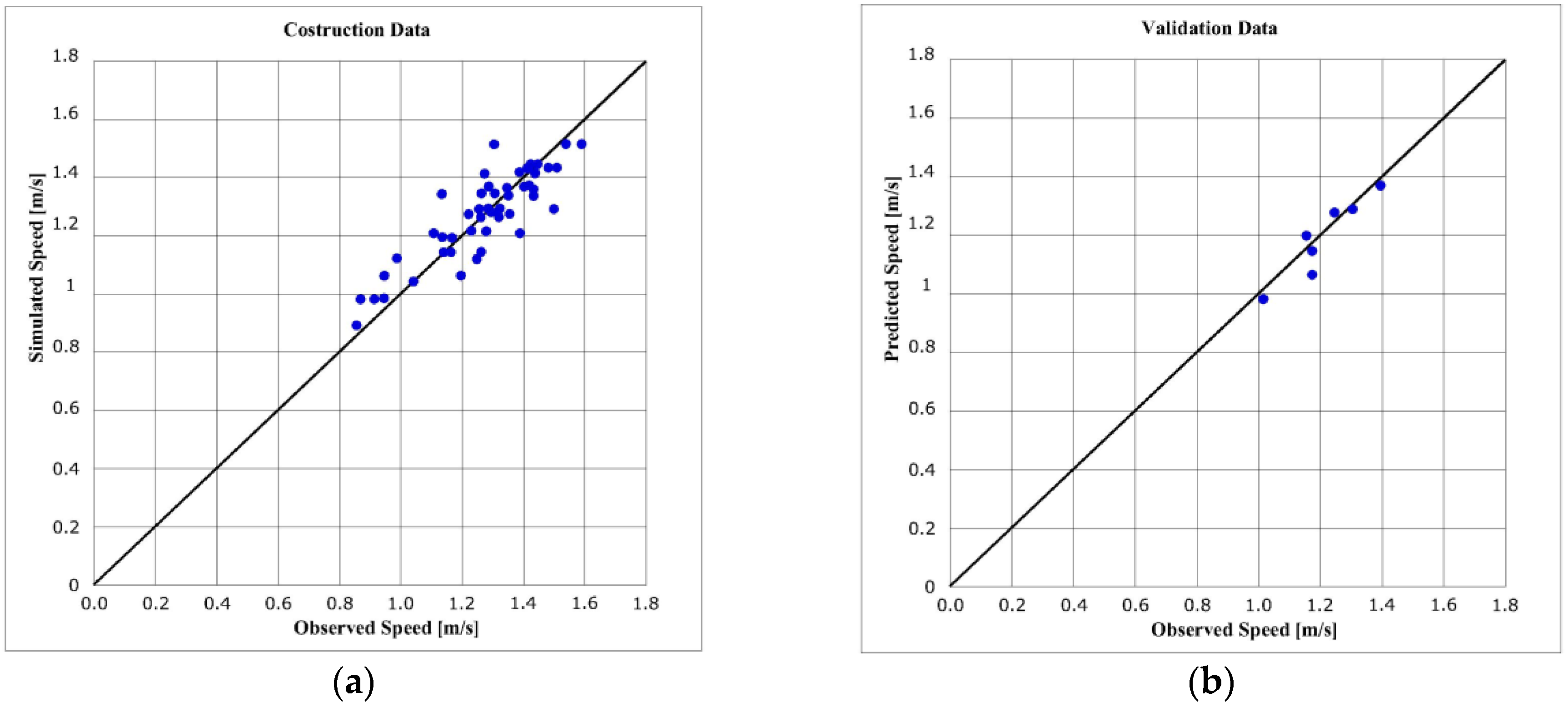
Partial model example excluding Via Paoli sez. 1:

Y₁ = 1.5564 − 0.0167X₁² − 0.0909X₂

(6)

where R² = 0.76; RMSPE = 0.0696. Validation phase: R_v² = 0.93; RMSPE_v = 0.0354.

Coefficients of determination and RMSPE indices always show good values. In addition, observed and estimated speeds have good agreement (Figure 5).

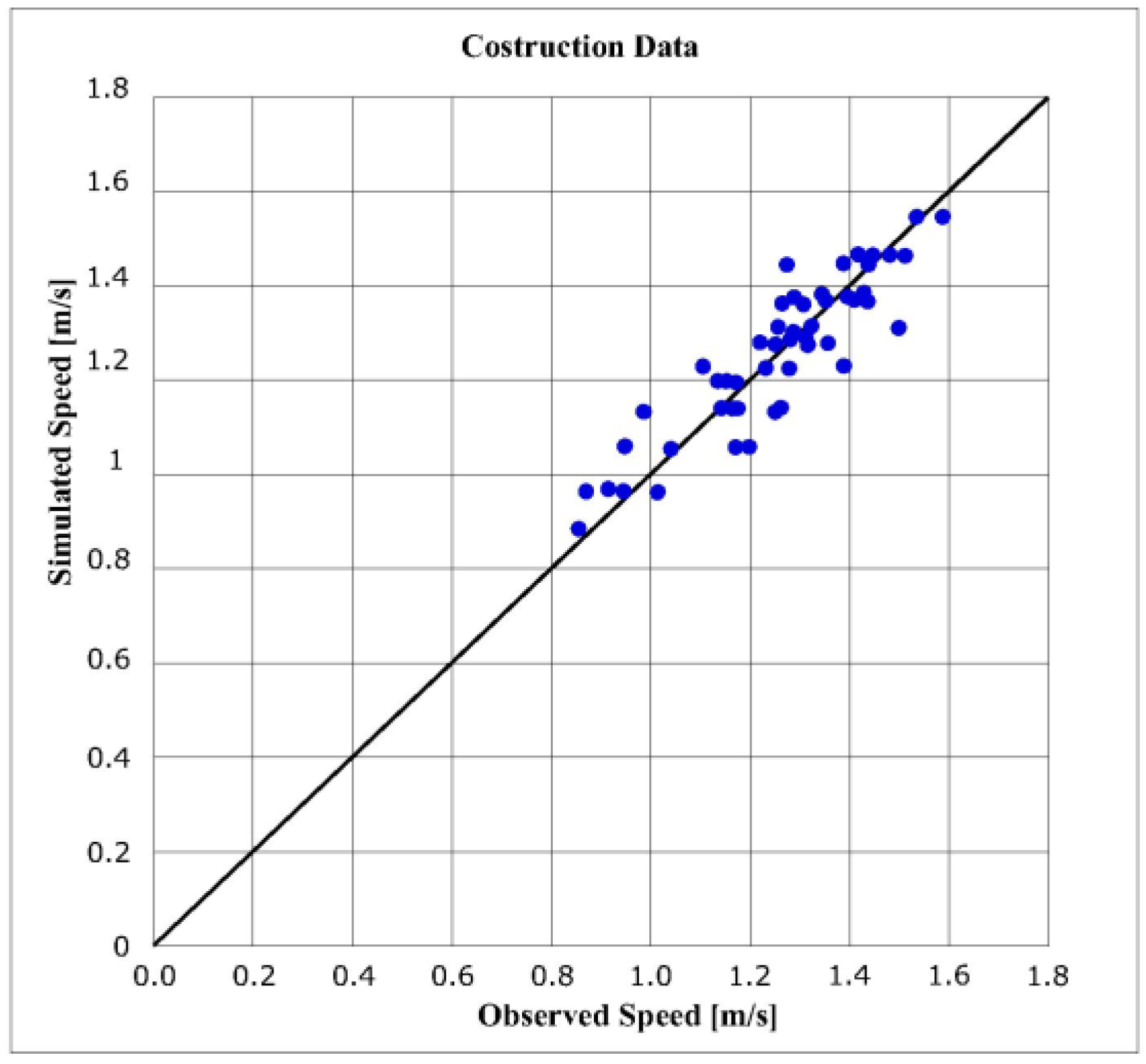
For all other partial models, similar results are obtained. Thus, using all the sidewalk data at the same time, a global model was constructed:

Y₁ = 1.5531 − 0.0165X₁² − 0.0878X₂

(7)

where R² = 0.78; RMSPE = 0.0669.

For the global model (7),

Table 4. Global model: regression statistics and ANOVA.

Regression Statistics
Multiple R	0.881142
R2	0.776411
Adjusted R2	0.761986
Standard Error	0.08138
Observation	34
Analysis of Variance
Variable	df	SQ	MQ	F	Significance F
Regression	2	0.712914	0.356457	53.82367	<0.0001
Residual	31	0.205303	0.006623
Total	33	0.918217
	Coeff.	Standard Error	t Stat	p-Value	Lower 95%	Upper 95%
Intercept	1.553102	0.032839	47.29409	<0.0001	1.486126	1.620078
(X12) Square of Age Class	−0.01651	0.001839	−8.97392	<0.0001	−0.02026	−0.01275
(X2) Facing Type	−0.0878	0.015752	−5.57404	<0.0001	−0.11993	−0.05568

reports the regression statistics and Anova and Figure 6 reports the comparison between observed and simulated speeds.

These results show the same conclusions of Model No. 1 of Section 3.1.

4.2. Model No. 2: Mean Walking Speed, Age Classes, Facing Type, and Gender

With the same methodology and the steps indicated in Section 3.1 for Model No. 1, the following is achieved.

Partial model example excluding via Paoli sez. 1:

Y₂ = 1.5101 − 0.0187X₁² − 0.0755X₂ + 0.0803X₃

(8)

where R² = 0.76; RMSPE = 0.0698. Validation phase: R_v² = 0.88; RMSPE_v = 0.0414.

Coefficients of determination and RMSPE indices always show good values. In addition, the observed and estimated speeds have good agreement (Figure 7).

For all other partial models, similar results are obtained. Thus, using all the sidewalk data at the same time, a global model was constructed:

Y₂ =1.5354 − 0.0191X₁² − 0.0830X₂ + 0.0783X₃

(9)

where R² = 0.82; RMSPE = 0.0596.

For the global model (9),

Table 5. Global model: regression statistics and ANOVA.

Regression Statistics
Multiple R	0.905187
R2	0.819363
Adjusted R2	0.808942
Standard Error	0.074541
Observation	56
Analysis of Variance
Variable	df	SQ	MQ	F	Significance F
Regression	3	1.310593	0.436864	78.62342	<0.0001
Residual	52	0.288934	0.005556
Total	55	1.599526
	Coeff.	Standard Error	t Stat	p-Value	Lower 95%	Upper 95%
Intercept	1.535384	0.025014	61.38175	<0.0001	1.48519	1.585578
(X12) Square of Age Class	−0.01912	0.001419	−13.4676	<0.0001	−0.02197	−0.01627
(X2) Facing Type	−0.08303	0.011298	−7.34962	<0.0001	−0.1057	−0.06036
(X3) Gender	0.078262	0.0202	3.874327	0.000301	0.037727	0.118796

reports the regression statistics and Anova and Figure 8 reports the comparison between observed and simulated speeds.

These results show the same conclusions of Model No. 1 of Section 3.1.

5. Models for Groups

Pedestrians in groups always move together with other pedestrians (one or more).

Their speeds are influenced by group size and interactions with other pedestrians constituting the pedestrian flow.

Only one model is identified; the mean walking speed (Y₁) is expressed as a function of age classes (X₁) and the facing type (X₂).

For this user type, the model expressed as a function of gender was not good because the gender variable lost significance.

Model No. 1: Mean Walking Speed, Age Classes, and Facing Type

With the same methodology and the steps indicated in Section 3.1 for Model No. 1, the following is achieved:

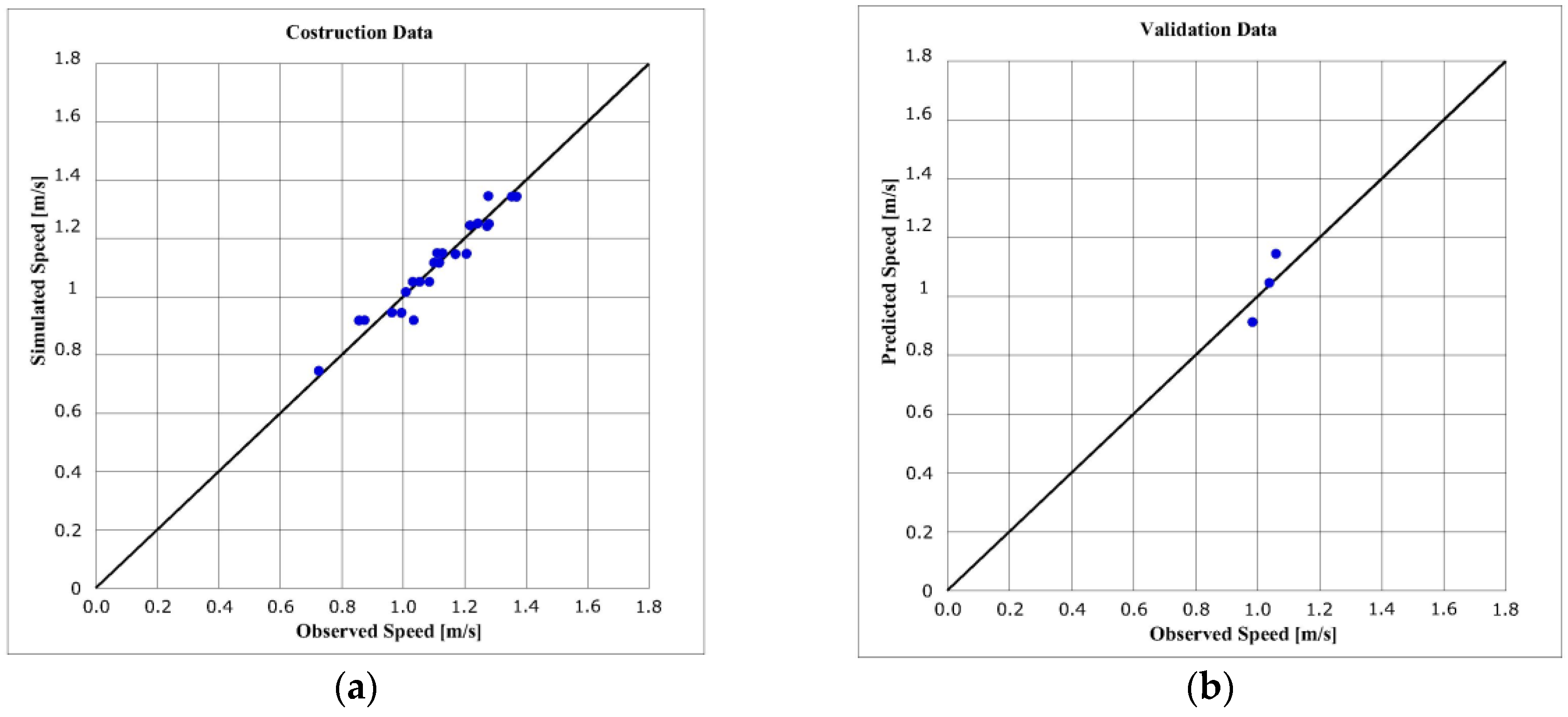
Partial model example excluding via Paoli sez. 1:

Y₁ = 1.4124 − 0.0186X₁² − 0.0969X₂

(10)

where R² = 0.93; RMSPE = 0.0375. Validation phase: R_v² = 0.98; RMSPE_v = 0.0586.

Coefficients of determination and RMSPE indices always show good values. In addition, the observed and estimated speeds have good agreement (Figure 9).

For all other partial models, similar results are obtained. Thus, using all the sidewalk data at the same time, a global model was constructed:

Y₁ = 1.4042 − 0.0179X₁² − 0.0980X₂

(11)

where R² = 0.92; RMSPE = 0.0400.

For the global model (11),

Table 6. Global model: regression statistics and ANOVA.

Regression Statistics
Multiple R	0.959439
R Square	0.920523
Adjusted R Square	0.91441
Standard Error	0.043519
Observation	29
Analysis of Variance
df	SQ	MQ	F	Significance F
2	0.57034	0.28517	150.5698	<0.0001
26	0.049242	0.001894
28	0.619582
	Coeff.	Standard Error	t Stat	p-Value	Lower 95%	Upper 95%
Intercept	1.40423	0.019192	73.16787	<0.0001	1.364781	1.44368
(X12) Square of Age Class	−0.01788	0.00123	−14.5316	<0.0001	−0.02041	−0.01535
(X2) Facing Type	−0.09804	0.008958	−10.9452	<0.0001	−0.11646	−0.07963

reports the regression statistics and Anova and Figure 10 reports the comparison between observed and simulated speeds.

These results show the same conclusions of Model No. 1 of Section 3.1.

6. Comparison between Models

Data analysis has, therefore, led to the definition of models that can represent pedestrian behavior. Below, the obtained models are summarized (

Table 7. Models.

A	Y1 = 1.7522 − 0.1169X1 − 0.0674X2	(3)	Isolated Pedestrians
B	Y1 = 1.5531 − 0.0165X12 − 0.0878 X2	(7)	Single pedestrians
C	Y1 = 1.4042 − 0.0179X12 − 0.0980X2	(11)	Groups
D	Y2 = 1.6999 − 0.1214X1 − 0.0605X2 + 0.1099X3	(5)	Isolated pedestrians
E	Y2 = 1.5354 − 0.0191X12 − 0.0830X2 + 0.0783X3	(9)	Single pedestrians
where:
Y1	Mean walking speed	X2	Facing type
X1	Age classes	X3	Gender

).

Depending on the variable number, they can be divided into two sets.

Models A, B, and C represent the relationship between the mean walking speed, age classes, and facing type, but are deduced from different users types. D and E models have the variable Gender, but represent the same relation between variables.

It is interesting to compare the two model types to understand how user typology can influence their behavior.

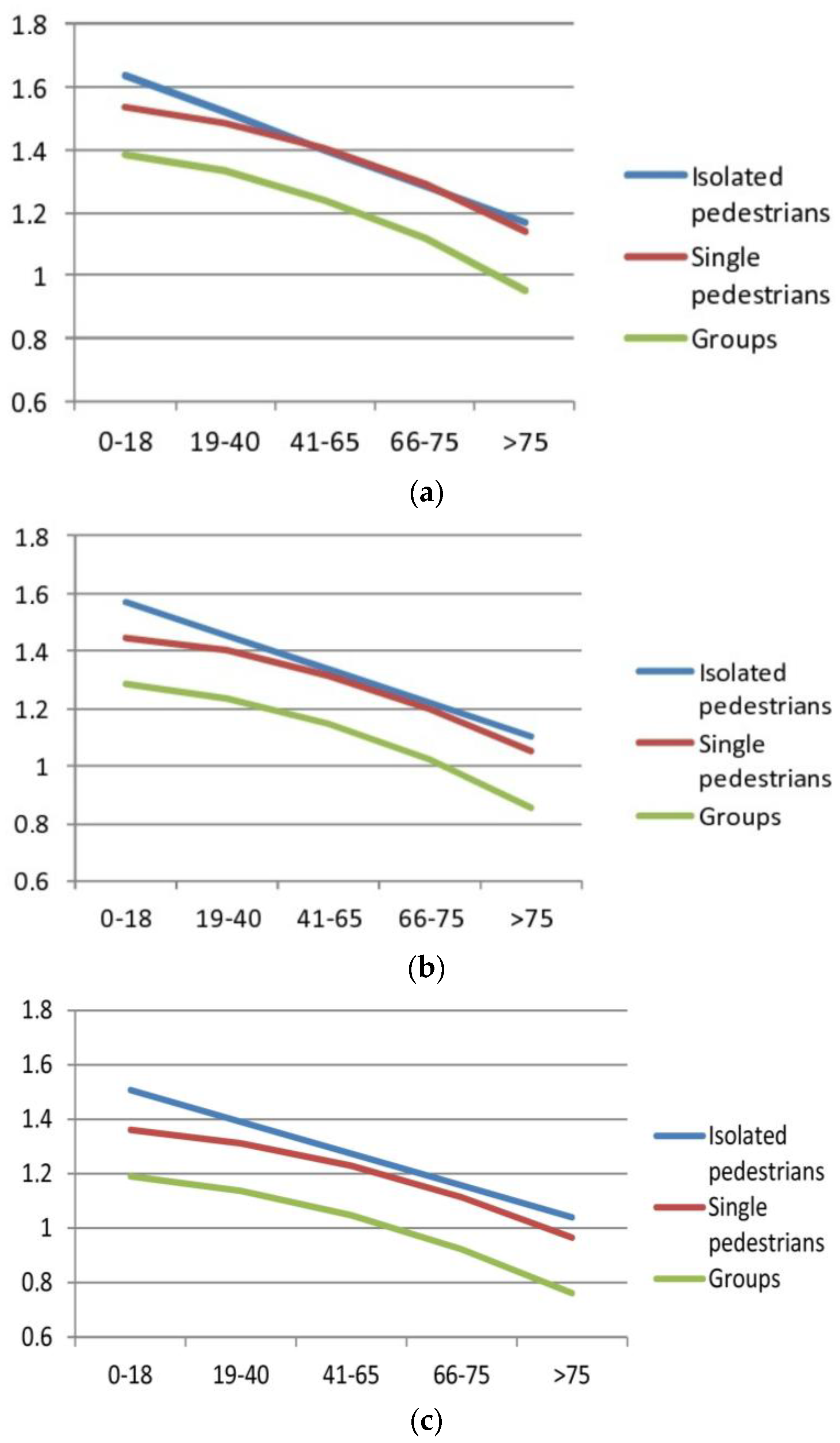
The figures below (Figure 11) represent models A, B, and C, where, for easy readiness, the three facing types being models with two independent variables are considered separately.

From the comparison of the three figures the following considerations can be drawn:

• Whatever the facing type, the three curves keep themselves in the same order, speeds tend to decrease from the isolated pedestrian to the single one and to the groups. This is certainly related to interferences that a user receives from others who, somehow, tend to influence their behavior. Using terminology borrowed from the road, “driving freedom tends to decrease” due to the presence of a pedestrian flow.
• The facing type affects the speed in the sense that the more “interesting” the side is, the slower a pedestrian moves, whatever the movement motive, demonstrating that the attractiveness of the urban context influences the user behavior.
• Differences between the isolated pedestrian and the single pedestrian tend to grow with the variation in the facing. In fact, if in the blind facing they are practically coincident (average difference about 2.15%), in the case of accesses facing there is an average difference of 4% and 6.10% for shop windows facing. They also maintain the same trend: when they grow older they tend to get closer. Even in this case the consideration about the interactions between pedestrians is valid. The single user is affected by those near him and tends to move more slowly. This affirmation is very strong in young people and adults, while it loses meaning for the elderly, demonstrating that when the age-related psycho-physical conditions worsen, speeds not only decrease but are probably related to factors independent of the presence of other road users, such as the general health condition.
• Differences between single pedestrians and groups are, however, clearly marked and the two curves seem to be parallel. The data analysis shows instead that they tend slightly to diverge as the age classes increase. The average differences vary from 11.70% of the first case to 15% of the last, thus being negligible. The strong influence that the presence of a pedestrian flow exerts on user behavior is clear here, while age tends to lose importance.
• Differences between isolated pedestrians and groups, given what was said earlier are, therefore, greater.

It is important to underline that the obtained results concern sidewalk characterized by LOS A according to the HCM methodology. As the pedestrian flow increases, the LOS will worsen, increasing interference between individual users. This will certainly lead to an increase in the highlighted differences. Specifically, isolated pedestrian speeds will remain the same, while single pedestrian and group speeds will further decrease.

In conclusion, it seems clear that in pedestrian speed choice it is impossible to ignore the actual conditions in which the moving takes place and that the reference to the isolated pedestrian can lead to a speed overestimation and, thus, to a reduction in moving times compared to real ones. This can be a safety issue in particular circumstances (pedestrian crosswalks, traffic lights, etc.) or when the local population presents a high number of elderly people.

With regard to the second set of models, analyses have shown how much it was legitimate to expect that male pedestrians move at higher speeds.

7. Conclusions

The study aims to give greater importance to pedestrians, analyzing how they relate with the urban context in which they live and how this context conditions their behavior, to design infrastructures in which they feel an integral part and main actors of the urban scene, giving them the respect they deserve and a new sense of belonging to the city in which they live.

Several groups around the world are currently working on pedestrian movement spaces, a fact that is proven by the interest of infrastructure researchers. In fact, the purpose is to apply the results in the practice of design.

Following this purpose the paper studies the average pedestrian’s behavior, according to pedestrians and path characteristics. For this reason, pedestrians are subdivided into user types: isolated pedestrians, single pedestrians and groups. For each type of user, models emphasize variations in the mean walking speed as a function of independent variables, like age group, gender and facing type.

In general, the mean walking speed decreases with age classes: this confirms that with increasing age comes a decrease in psycho-physical pedestrian characteristics and, therefore, their walking ability. The mean walking speed is also influenced by the facing type, then by the environment passed through: in fact lower speeds are obtained in the presence of shop windows, while higher speeds are obtained with blind overlooking; finally male pedestrians are faster than female.

The mean walking speed of “isolated pedestrians” are, generally, higher than those of “single pedestrians” and “groups”, the latter instead assume the lowest values.

In “isolated pedestrians” the variable age class is in linear form, while in “single pedestrians” and “groups” it is in quadratic form. This is because the “isolated pedestrians” behavior did not suffer influences of other pedestrians, while in “single pedestrians” interactions with other pedestrians, walking in the same direction, or oppositely, have influences on speed and route.

These influences are stronger in the “groups”. The speed of a pedestrian within a group is mainly influenced by the speed of pedestrians walking together (for this reason the gender variable loses statistical significance).

The literature mainly investigates the free-flow speed, i.e., only isolated pedestrians, not taking into account other types of pedestrians who have more interference and influences, both with other pedestrians and with the environment; for this reason, therefore, the other types of users deserve to be more closely investigated.

These results could improve pedestrian behavior research and be useful in planning and design of urban areas, and also in other cities with similar characteristics.