Abstract
Structural health monitoring (SHM) plays a pivotal role in ensuring the integrity and safety of critical infrastructure and mechanical components. While traditional non-destructive testing (NDT) methods offer high-resolution data, they typically require periodic access and disassembly of equipment to conduct inspections. In contrast, SHM employs permanently installed, cost-effective sensors to enable continuous monitoring, though often with reduced detail. This study presents an integrated hybrid SHM-NDT methodology enhanced by deep learning to enable the real-time monitoring and classification of mechanical stresses in structural components. As a case study, a 6-foot-long parallel flange I-beam, representing bridge truss elements, was subjected to variable bending loads to simulate operational conditions. The hybrid system utilized an ultrasonic transducer (NDT) for excitation and piezoelectric sensors (SHM) for signal acquisition. Signal data were analyzed using 1D and 2D convolutional neural networks (CNNs), long short-term memory (LSTM) models, and random forest classifiers to detect and classify load magnitudes. The AI-enhanced approach achieved 100% accuracy in 47 out of 48 tests and 94% in the remaining tests. These results demonstrate that the hybrid SHM-NDT framework, combined with machine learning, offers a powerful and adaptable solution for continuous monitoring and precise damage assessment of structural systems, significantly advancing maintenance practices and safety assurance.
1. Introduction
Structural health monitoring (SHM) and non-destructive testing (NDT) are essential for ensuring the safety and longevity of infrastructure such as bridges, buildings, and aerospace vehicles [1,2]. Critical components such as beams, which serve as key load-bearing elements in many structural systems, require continuous monitoring to maintain their strength, stability, and capacity to safely distribute loads throughout the structure [3,4,5]. The early detection of wear, fatigue, and damage is essential to prevent catastrophic failures and ensure timely maintenance [4,6,7,8].
NDT methods have been utilized for over a century to inspect structural components without causing damage [9]. These techniques include ultrasonic testing, radiographic analysis, magnetic particle inspection, and other approaches that are commonly used to detect cracks, voids, delamination, and other internal flaws across a wide variety of materials [10,11,12]. Among ultrasonic techniques, tools such as ultrasonic contact transducers (UCT) and electromagnetic acoustic transducers (EMATs) are frequently employed to evaluate internal material conditions by transmitting acoustic or electromagnetic waves and analyzing their reflections [13,14]. While highly effective, these methods often require direct access to critical points of interest and can disrupt normal operations by necessitating temporary disassembly or shutdowns [2,10].
In contrast, SHM systems emerged as a solution for continuous, in situ monitoring through the permanent integration of sensors on or within structural components [9]. These systems typically employ piezoelectric or fiber optic sensors to track physical changes such as strain, displacement, or vibrational response over time [14,15]. SHM systems are widely valued for their ability to provide real-time data streams that enable trend analysis and predictive maintenance scheduling [15,16]. However, SHM solutions often face challenges regarding spatial resolution and the precision of damage localization compared to traditional NDT techniques [9,14].
Active SHM techniques are gaining attention due to their ability to detect subtle damage and degradation well before failure occurs [17]. These methods include the use of guided Lamb waves, which propagate along thin structures and are sensitive to damage such as delamination and corrosion [18]. Electromechanical impedance techniques, which analyze changes in electrical impedance due to structural variations, have also been widely adopted for localized damage detection in engineering structures [19]. Another promising technique is time-reversal signal processing, where signals are reconstructed to their original form after propagation through a medium, offering high sensitivity to even minor structural anomalies [20]. These active methods offer significant advantages in precision and reliability, addressing the limitations of passive SHM techniques and bridging the diagnostic gap between SHM and traditional NDT.
While active structural health monitoring (SHM) techniques—such as Lamb wave analysis, electromechanical impedance, and time-reversal methods—significantly enhance the sensitivity and precision of structural diagnostics, they cannot fully replace the comprehensive capabilities of traditional non-destructive testing (NDT) methods. Active SHM improves upon passive approaches by enabling localized damage detection and real-time monitoring, but it may still lack the spatial resolution, depth penetration, and material characterization required for detecting subtle or subsurface defects. Traditional NDT techniques, such as ultrasonic or electromagnetic inspection, remain indispensable for the thorough assessment and confirmation of structural anomalies.
A hybrid SHM-NDT framework leverages the strengths of both approaches: SHM provides continuous condition monitoring and early damage trend identification, while NDT offers detailed validation and higher diagnostic confidence. This layered strategy not only bridges existing performance gaps but also facilitates smarter maintenance planning and improved structural safety in complex, real-world applications. This hybrid approach that combines both NDT and SHM techniques has emerged as a promising solution, integrating the high-resolution diagnostics of NDT with the continuous monitoring capabilities of SHM [4,21]. In such systems, NDT transducers can be used to generate excitation signals from multiple angles, or conversely, SHM sensors can act as the excitation source while NDT equipment performs the inspection [22]. This combination—further enhanced by advanced signal processing techniques and deep learning models—enables more accurate damage classification and real-time monitoring [12,21].
In this study, a hybrid SHM-NDT system was developed and tested on an I-beam subjected to variable loads to demonstrate its broader applicability [17]. Excitation signals were generated using both NDT and SHM equipment and were captured by standard SHM sensors [2,22]. The acquired signals were processed using frequency- and time-frequency domain techniques such as the fast Fourier transform (FFT) and continuous wavelet transform (CWT), and subsequently analyzed using artificial intelligence-based classification models [16,21]. This multifaceted approach highlights the potential of hybrid SHM-NDT systems to deliver robust, accurate, and scalable structural assessment solutions across a range of engineering applications.
2. Theoretical Background
2.1. Signal Processing Techniques
Signal processing methods such as continuous wavelet transform (CWT) and fast Fourier transform (FFT) are essential for extracting meaningful features from sensor data. These techniques enable the analysis of time-frequency characteristics and spectral components of signals, providing critical insights into structural responses under varying load conditions.
The continuous wavelet transform (CWT) transforms a time-dependent signal into a representation incorporating both time and frequency components. This dual-variable representation introduces redundancy, which, while increasing computational demands, enhances the interpretability of the data compared to techniques like the discrete wavelet transform (DWT) [23].
One of CWT’s distinguishing characteristics is its adaptability in window size relative to the frequency of interest. For higher frequencies, shorter windows provide finer temporal resolution, though at the expense of frequency precision. Conversely, longer windows at lower frequencies yield improved frequency resolution while sacrificing time specificity. These properties make the CWT particularly effective for analyzing non-stationary signals, where frequency content varies over time [24,25,26]. This capability positions the CWT as a valuable tool for applications like SHM, where accurate time-frequency analysis is crucial for identifying and assessing surface wave propagation behaviors to identify potential damage mechanisms.
The fast Fourier transform (FFT) is an efficient computational algorithm for determining the discrete Fourier transform (DFT) of a signal, significantly reducing the complexity and time required for calculations. It serves as a cornerstone in engineering and applied mathematics, particularly in signal processing and the analysis of one- and multi-dimensional systems. By converting time-domain data into its frequency-domain representation, the FFT provides critical insights into signal characteristics, such as identifying dominant frequencies [27,28].
2.2. Classification Algorithms
Deep learning and machine learning algorithms play a pivotal role in structural health monitoring (SHM) and non-destructive testing (NDT) systems by enabling advanced data analysis and interpretation. Among these, convolutional neural networks (CNNs), long short-term memory networks (LSTMs), decision trees, and random forests have shown significant potential in processing sensor data, identifying damage patterns, and predicting structural integrity. Each of these algorithms offers unique strengths and limitations, making them suitable for different aspects of hybrid SHM-NDT systems.
2.2.1. Convolutional Neural Networks
Convolutional neural networks (CNNs) are highly effective for extracting features from structured data. For SHM applications, 1D CNNs process sequential data, such as strain or vibration signals, while 2D CNNs are better suited for analyzing time-frequency representations, such as spectrograms. One-dimensional CNNs excel at capturing local patterns in time-series data, offering computational efficiency and simplicity. However, they may struggle with complex spatial relationships and noisy data. Conversely, 2D CNNs are ideal for detecting spatial patterns and analyzing transformed signal data but require higher computational resources and larger datasets to perform effectively. The selection of CNN type depends on the nature of the input data and the desired analysis outcomes [29,30,31,32,33]. Figure 1 below shows the typical architecture of a CNN. This particular example is a 2D CNN as evident from the image input on the left. The input image is a scalogram generated using the CWT, where the color scale ranges from blue to red, with red representing areas of highest signal intensity.
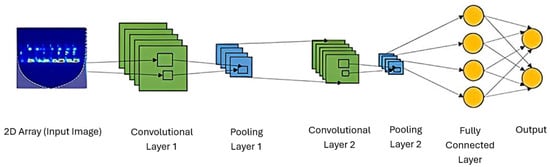
Figure 1.
Example of a CNN architecture showing the various layers.
2.2.2. Long Short-Term Memory
Long short-term memory (LSTM) networks, a type of recurrent neural network (RNN), effectively handle sequential data by addressing the vanishing gradient problem through their unique architecture of cell states and gates (input, output, and forget). This design allows LSTMs to retain or discard information based on its relevance, making them highly effective for capturing long-term dependencies. In structural health monitoring (SHM), LSTMs model the temporal evolution of structural responses, offering insights into load histories and damage progression [34,35]. While computationally intensive and sensitive to tuning, their strengths in predicting complex temporal trends make them a valuable tool for SHM applications. Figure 2 shows the architecture of a LSTM. The diagram illustrates the internal structure of an LSTM cell, including the forget gate, input gate, and output gate.
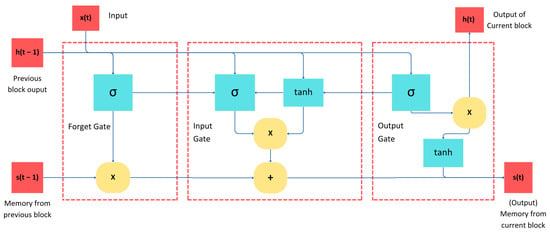
Figure 2.
Example of LSTM architecture, showing the gates which regulate the flow of information.
2.2.3. Decision Trees and Random Forest
Decision trees offer a simple and intuitive approach to data classification and regression. Their hierarchical structure enables clear decision-making, making them easy to interpret and implement. In SHM applications, decision trees can quickly classify damage types or load levels based on sensor data with minimal preprocessing [36]. However, they are prone to overfitting, especially when dealing with small or noisy datasets, and may fail to capture the complex relationships among features. Figure 3 shows the architecture of a Random Forest classifier. It operates by constructing multiple decision trees during training. Each tree is built using a random subset of the training data and features, which helps to reduce overfitting and improve generalization. The final classification is determined through a majority voting scheme across all individual trees.
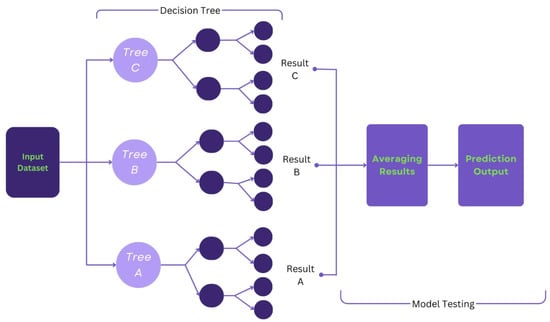
Figure 3.
Example of random forest architecture.
Random forests, an ensemble learning method based on decision trees, mitigate the limitations of individual trees by aggregating predictions from multiple trees trained on random subsets of data and features. This approach enhances accuracy and reduces overfitting, making random forests robust and reliable for SHM tasks. Additionally, they provide feature importance rankings, offering insights into critical parameters influencing structural behavior. However, random forests are computationally expensive and less interpretable than individual decision trees, requiring the careful tuning of hyperparameters to achieve optimal performance [37,38].
The choice of algorithm for SHM depends on the specific application and data characteristics. A comparison of these algorithms is summarized in Table 1, highlighting their strengths, weaknesses, and best use cases.

Table 1.
Comparison of classification algorithms for SHM.
This study investigates the efficacy of integrating SHM and NDT systems with deep learning techniques to enhance the accuracy and efficiency of structural health monitoring. By combining the strengths of both approaches, the hybrid system can achieve real-time damage detection and classification in beams subjected to variable operational stresses. Additionally, the inclusion of load detection as a monitored parameter will provide a more holistic understanding of structural behavior, offering new insights into the interplay between loading conditions and structural health.
3. Materials and Methods
As shown in Figure 4, the experiments were conducted on a 6-foot-long parallel flange I-beam with the following specifications: a depth of 4 inches, a flange width of 3 inches, and thicknesses of 0.3 inches for the web, top, and bottom flanges. Static loading was applied to the I-beam in a four-point bending test configuration to simulate realistic structural stresses. Surface waves were created from the left end of the beam using a PZT, and PZTs, UCTs, and EMATs were each used in separate tests to collect the resulting signal at the right end of the beam. In the four-point bending test, a rectangular or beam-shaped specimen was supported at two outer points, creating a fixed span. Downward force was applied symmetrically at the loading pins located on top of the beam. Test loads were applied by using the Mark-10 Model M5-1000 load gauge and test stand. This setup ensured that the load was distributed evenly across the inner span.
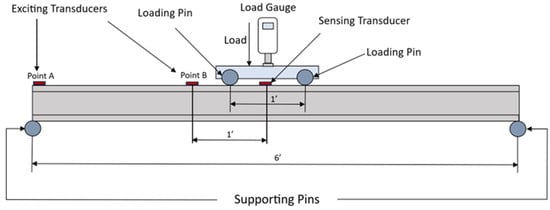
Figure 4.
Diagram showing the experimental setup, highlighting the position of the transducers.
To excite the beam surface, three transducers were used in separate tests. Figure 5, Figure 6 and Figure 7 shows the workflow for each setup.
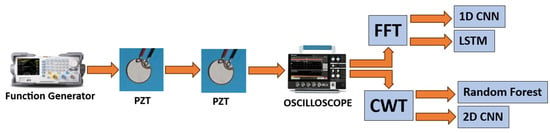
Figure 5.
Workflow for the PZT-PZT setup.
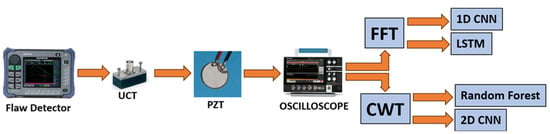
Figure 6.
Workflow for the UCT-PZT setup.
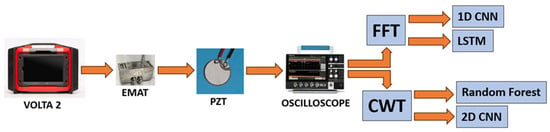
Figure 7.
Workflow for the EMAT-PCT setup.
- PZT excitation–PZT monitoring: PZT attached to the left side of the beam. A Rigol DG 1022 function generator excited the PZT with a swept sine wave in the 100 kHz to 400 kHz range. The data were collected at a 1.25 GS/s frequency sampling rate.
- UCT probe excitation–PZT monitoring: The same method as above was implemented using an Olympus EPOCH 650 portable ultrasonic flaw detector with the UCT probe at a frequency of 250 kHz and sampling frequency of 0.625 GS/s Hz.
- EMAT probe excitation–PZT monitoring: Volta 2, a high-powered portable ultrasonic instrument, was used in conjunction with an EMAT probe to excite Point A and Point B on the beam at a frequency of 1150 kHz. The data were collected at a sampling frequency of 2.5 GS/s.
The response signals were captured using a piezoelectric transducer (PZT) positioned on the beam’s surface. Data acquisition was performed with a Tektronix 2 Series oscilloscope, ensuring the high-resolution capture of the received signals. Figure 6 provides an illustration of the testing configurations employed.
Static loads of 500 N and 1000 N were applied to the beam using a Mark-10 Model M5-1000 load gauge in the four-point bending test setup shown in Figure 8 and Figure 9. The PZT sensor was placed on both the top (same side as the load application where the beam is under compression) and bottom surfaces of the beam (where it is under tension), along with measurements at two points—Point A at the end of the beam and Point B is 1.5” from the midpoint—to measure variations in signal responses under different loading scenarios. Baseline readings were recorded without any applied load to establish reference data for comparative analysis.

Figure 8.
Actual experimental setup for the EMAT-PZT configuration.

Figure 9.
The 500 N being applied using load gauge and stand.
The experiment was repeated 10 times for each load (0 N for the baseline reading, 500 N and 1000 N). The collected data underwent signal processing to extract relevant features for analysis. This involved advanced methods like the fast Fourier transform (FFT) and continuous wavelet transform (CWT). Machine learning and deep learning algorithms, including random forest, vision transformer, LSTM, and CNN, were used to classify the data and identify patterns in the structural responses under varying loads and excitations.
4. Results
The experiments on the I-beam subjected to bending loads (0 N, 500 N, and 1000 N) yielded important insights into the classification capabilities of the machine and deep learning models used. Representative plots of the raw time-domain signal (voltage vs. time), the FFT, and CWT, are presented in Figure 10, Figure 11, and Figure 12, respectively.
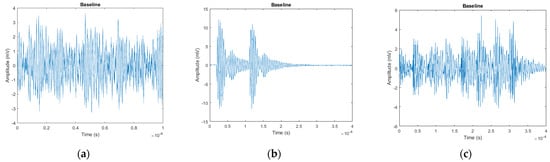
Figure 10.
Time series (V vs. time) plots from signal data received by oscilloscope. (a) PZT-PZT time series signal; (b) UCT-PZT time series signal; (c) EMAT-PZT time series signal.
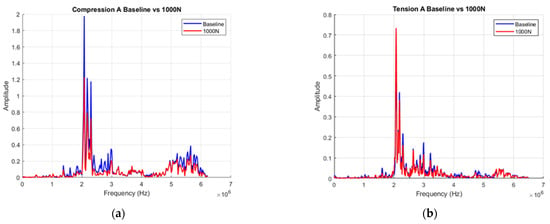
Figure 11.
The FFT plots for the baseline and when 1000 N was applied when (a) the probes were placed on the side of the beam experiencing compression (top side); (b) the probes were placed on the side of the beam experiencing tension (bottom side).
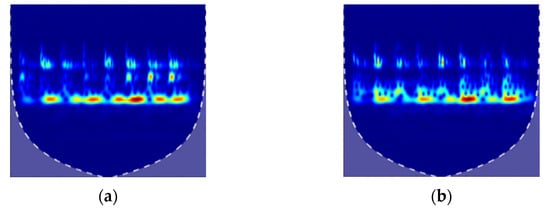
Figure 12.
Showing the CWT of baseline readings from the PZT-EMAT setup. The colors represent the intensity of the signal; (a) transducer at point A for 0 N; (b) transducer at side under compression at point A for 1000 N; (c) transducer at side under tension at point A for 1000 N; (d) transducer at side under tension at point B for 1000 N.
Each configuration (PZT to PZT, UCT to PZT, and EMAT to PZT) yielded promising classification results across all load conditions.
4.1. PZT Excitation–PZT Monitoring (PZT-PZT)
For the PZT-to-PZT setup, all tested algorithms achieved perfect classification accuracy, as shown in Figure 13 and Figure 14.

Figure 13.
Confusion matrices of test cases using 1D and 2D CNN.
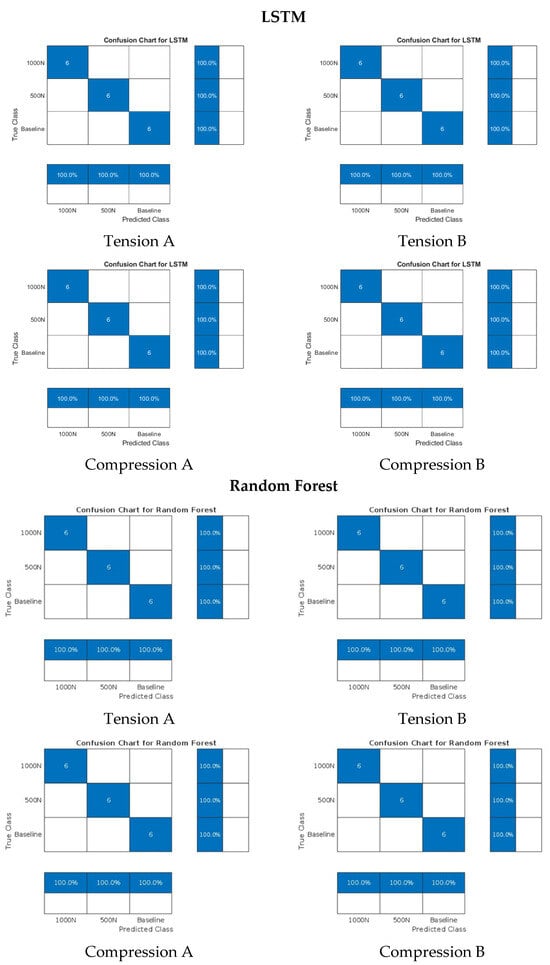
Figure 14.
Confusion matrices for tests using LSTM and random forest.
All the models were trained (FFT for 1D CNN; CWT for 2D CNN) with 4 cases per category (12 in total). After the training, a total of 18 test cases (which were not used in training) were classified with the models. The confusion matrices of the test cases are presented in Figure 13. The similar training and test routine was used for FFT-LSTM and CWT–random forest combination. Confusion matrices are presented in Figure 14, where correct classifications, shown in blue, appear along the diagonal of each chart. The information presented by the confusion matrices is outlined in Table 2.

Table 2.
Performance of signal processing and classification methods for data collected with PZT excitation and PZT monitoring.
4.2. UCT Probe Excitation–PZT Monitoring (UCT-PZT)
The training and test procedure of the PZT-PZT case outlined in Section 4.1 was used. In the case of the UCT-to-PZT setup, the results displayed in Figure 15 and Figure 16, were similarly impressive, with most tests achieving 100% classification accuracy. However, a single misclassification was observed in the random forest model for data collected at Point A on the tension side, as shown in Table 3. This anomaly, involving one misclassified dataset out of 18, is likely attributable to an outlier in the data. While this result demonstrates the robustness of the UCT-to-PZT setup, it also highlights the importance of addressing data anomalies through preprocessing or algorithm refinement to maintain high accuracy.
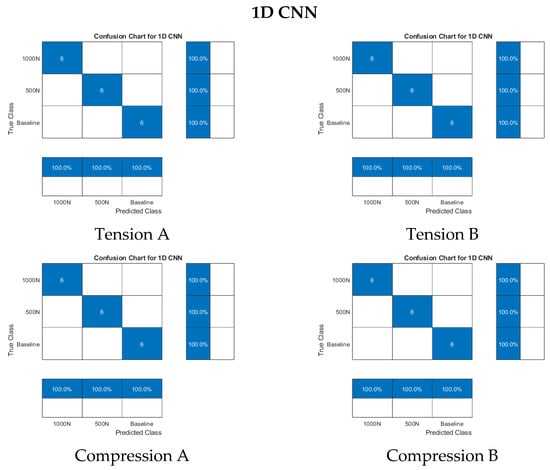
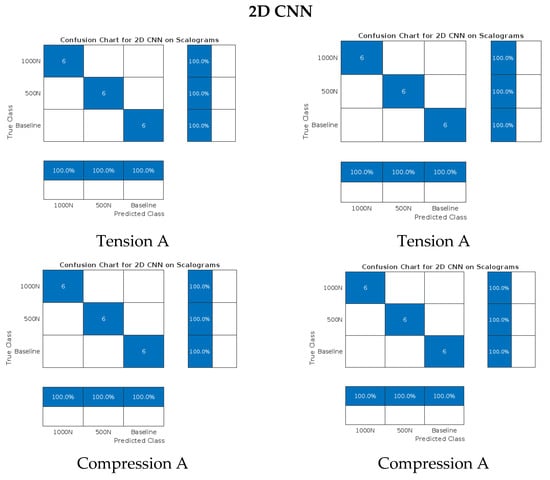
Figure 15.
Confusion matrices for tests using 1D and 2D CNN.
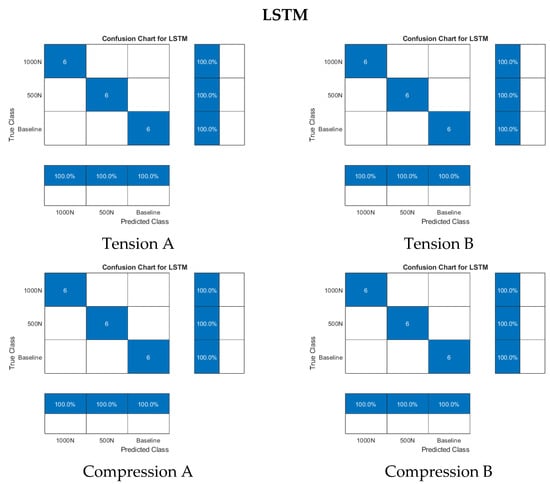
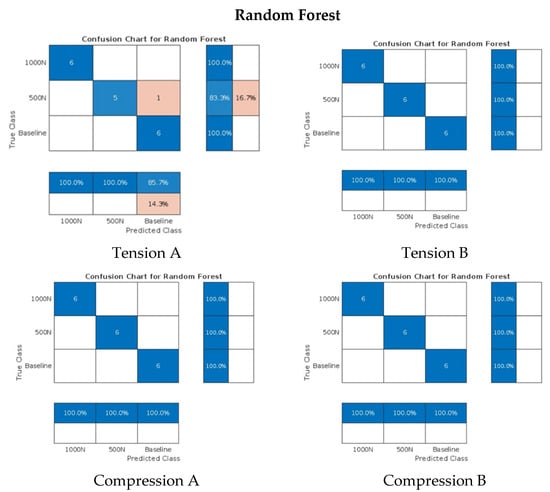
Figure 16.
Confusion matrices for tests using LSTM and random forest.

Table 3.
Performance of signal processing and classification methods for data collected with UCT excitation and PZT monitoring.
4.3. EMAT Probe Excitation–PZT Monitoring (EMAT-PZT)
The training and test procedure of the PZT-PZT case outlined in Section 4.1 was used. The EMAT-to-PZT setup matched the performance of the PZT-to-PZT configuration, achieving 100% classification accuracy across all models Table 4. The successful integration of the EMAT as an excitation source further supports its applicability in structural health monitoring. Notably, the EMAT achieved high accuracy despite the I-beam being constructed from aluminum, a material less ideal for electromagnetic acoustic transduction than steel. This can be attributed to several factors. Aluminum, being a non-ferromagnetic material, has lower electrical conductivity and magnetic permeability compared to steel, which can reduce the efficiency of eddy current generation and acoustic wave excitation. However, the specific setup and optimization of the EMAT in this experiment likely compensated for these limitations. The precise alignment of the EMAT with the beam’s surface, along with the frequency and intensity of the excitation signals, may have enhanced the coupling efficiency, enabling sufficient wave generation and detection. Additionally, the advanced machine learning algorithms used to classify the data likely played a role in extracting meaningful features from the signals, even under suboptimal excitation conditions.

Table 4.
Performance of signal processing and classification methods for data collected with EMAT excitation and PZT monitoring.
5. Discussion
The comparative analysis of the algorithms revealed that while CNNs and LSTM consistently delivered high accuracy by effectively modeling temporal and spatial dependencies in the data, the random forest algorithm showed possible sensitivity to data variability, as evidenced by the single misclassification in the UCT-to-PZT setup. This difference emphasizes the importance of algorithm selection based on the specific characteristics of the data and the application requirements.
The results collectively demonstrate the hybrid system’s ability to provide robust and reliable load classification across different sensing configurations and machine learning methods. The versatility of combining various excitation sources—PZT, EMAT, and UCT—with advanced algorithms illustrates the system’s potential for structural health monitoring applications. This approach not only enhances diagnostic accuracy but also accommodates diverse operational scenarios.
Other studies have explored a hybrid approach involving SHM [39]. However, the hybrid SHM-NDT method offers broader damage detection capabilities, real-world validation, and advanced AI integration. The hybrid sensor network [39] approach is efficient for local damage detection (e.g., bolts and cracks) but lacks the ability to detect loads and internal or material-level defects.
Altabey et al. [40] explores the integration of kernel principal component analysis (KPCA) for feature selection is a strong approach. KPCA helps remove redundant or irrelevant data, improving classification efficiency. Using a genetic optimization algorithm (GOA) to fine-tune k-NN parameters enhances model performance by selecting optimal hyperparameters, leading to improved classification accuracy. The study compares k-NN performance against established machine learning models like convolutional neural networks (CNNs) and support vector machines (SVMs). This provides a clear benchmark to assess the proposed method’s effectiveness. However, while k-NN is a simple and effective algorithm, it may not scale well with large datasets due to its computational inefficiency in high-dimensional spaces. Also, CNNs and SVMs are generally more effective for complex feature extraction and classification in SHM applications. Furthermore, structural health monitoring data often has strong temporal dependencies. The methodology does not mention long short-term memory (LSTM) networks or other time-series models, which could capture evolving damage patterns better than k-NN. Finally, the type, placement, and configuration of sensors can significantly impact SHM accuracy and should be elaborated on. F. Achouri et al. [41] presents a promising approach to damage detection in SHM by integrating a hybrid swarm optimization technique with ANNs. The combination of PSO and BOA potentially improves search efficiency, while ANNs enhance predictive modeling capabilities. CNNs may require large datasets but can outperform ANNs when spatial or localized features are crucial. However, CNNs may require large datasets but can outperform ANNs when spatial or localized features are crucial.
6. Conclusions
In this paper, a hybrid SHM-NDT system was developed to monitor a 6-foot-long parallel flange I-beam subjected to variable loads in a four-point bending test configuration. Dynamic excitation was applied using an EMAT probe, a UCT probe, and a PZT. Response signals were captured using a pi PZT. The collected data were processed using FFT and CWT. Machine learning and deep learning algorithms, including random forest, LSTM, and CNN, were used to classify the data and identify patterns in the structural responses under varying loads and excitations.
The experimental results showed that all tested algorithms achieved perfect classification accuracy in the PZT-to-PZT setup. The UCT-to-PZT setup also demonstrated impressive results, with most tests achieving 100% classification accuracy, though a single misclassification was observed in the random forest model for data collected at one point. Similarly, the EMAT-to-PZT setup achieved 100% classification accuracy across all models. The high accuracy of the EMAT was achieved despite the I-beam being constructed from aluminum, which is less ideal for electromagnetic acoustic transduction than steel.
The primary innovation of this work lies in its integration of diverse excitation and sensing techniques with modern data-driven algorithms with the aim of building a robust, flexible, and highly accurate framework for structural condition assessment. Unlike conventional methods that rely on a single sensing modality, this hybrid approach proved effective in detecting subtle variations under dynamic loading conditions. The study demonstrated that CNNs and LSTM consistently delivered high accuracy by effectively modeling temporal and spatial dependencies in the data. While the random forest algorithm showed a single misclassification, the difference in performance emphasized the importance of algorithm selection. The results suggest that the hybrid system’s ability to provide robust and reliable load classification across different sensing configurations and machine learning methods is very promising. The combination of various excitation sources, namely PZTs, EMATs, and UCTs, with advanced algorithms illustrates the system’s potential for structural health monitoring applications.
Importantly, this study served as a controlled case study to validate the hybrid SHM-NDT concept. While the study was conducted under controlled experimental conditions, the results clearly demonstrate the feasibility and effectiveness of the proposed hybrid SHM-NDT approach. However, the laboratory setting does not fully capture the complexity of real-world environments. Future work will focus on extending this framework to more realistic scenarios, including more complex structural systems, incorporating damage scenarios beyond load variation, and exploring and modifying adaptive learning techniques capable of improving classification performance for evolving structural conditions.
While inverse analysis techniques that combine experimental testing with numerical modeling, such as those advanced by G. Maier using quasi-non-destructive methods have proven effective for material property estimation [42], our study emphasizes a data-driven strategy that leverages real-time sensor feedback and machine learning for load and condition classification. This approach complements model-based techniques by focusing on rapid deployment and pattern recognition in dynamic environments, particularly where direct modeling may be challenging or impractical.
Author Contributions
Conceptualization, R.B. and I.T.; methodology, R.B.; software, R.B. and M.M.V.; data curation, R.B. and A.S.; writing—original draft preparation, R.B.; writing—review and editing, R.B. and I.T.; supervision, I.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data supporting the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SHM | Structural Health Monitoring |
| NDT | Non-Destructive Testing |
| PZT | Piezoelectric Transducer |
| CNN | Convolutional Neural Network |
| 1D CNN | One-Dimensional Convolutional Neural Network |
| 2D CNN | Two-Dimensional Convolutional Neural Network |
| FFT | Fast Fourier Transform |
| CWT | Continuous Wavelet Transform |
| UCT | Ultrasonic Contact Transducer |
| EMAT | Electromagnetic Acoustic Transducer |
| AI | Artificial Intelligence |
References
- Xanthakos, P.P. Theory and Design of Bridges; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Pallarés, F.J.; Betti, M.; Bartoli, G.; Pallarés, L. Structural health monitoring (SHM) and Nondestructive testing (NDT) of slender masonry structures: A practical review. Constr. Build. Mater. 2021, 297, 123768. [Google Scholar] [CrossRef]
- Di Lorenzo, G.; Formisano, A.; Landolfo, R. On the Origin of I Beams and Quick Analysis on the Structural Efficiency of Hot-rolled Steel Members. Open Civ. Eng. J. 2017, 11, 332–344. [Google Scholar] [CrossRef]
- Hussain, B. Integration of Non-Destructive Testing Techniques and Machine Learning Algorithms for Enhanced Structural Health Monitoring of Bridges. Curr. J. Appl. Sci. Technol. 2024, 43, 20–31. [Google Scholar] [CrossRef]
- Mehrabi, A.; Dolati, S.; Malla, P.; Farhangdoust, S.; Azzi, Z. Non-Destructive Testing for Inspection of Bridges and Buildings; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, 2025. [Google Scholar]
- Li, X.; Shi, D.; Yu, Z. Nondestructive Damage Testing of Beam Structure Based on Vibration Response Signal Analysis. Materials 2020, 13, 3301. [Google Scholar] [CrossRef] [PubMed]
- Baba, S.; Kondoh, J. Damage evaluation of fixed beams at both ends for bridge health monitoring using a combination of a vibration sensor and a surface acoustic wave device. Eng. Struct. 2022, 262, 114323. [Google Scholar] [CrossRef]
- Mehrabi, A.; Dolati, S.S.K. Structural Health Monitoring and Performance Evaluation of Bridges and Structural Elements. Infrastructures 2024, 9, 178. [Google Scholar] [CrossRef]
- Fahr, A. Aeronautical Applications of Non-Destructive Testing; DEStech Publications, Inc.: Lancaster, PA, USA, 2013. [Google Scholar]
- Büyüköztürk, O.; Taşdemir, M.A. Nondestructive Testing of Materials and Structures; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Blitz, J.; Simpson, G. Ultrasonic Methods of Non-Destructive Testing; Springer Science & Business Media: Berlin, Germany, 1995. [Google Scholar]
- Bolborea, B.; Baeră, C.; Gruin, A.; Vasile, A.-C.; Barbu, A.-M. A review of non-destructive testing methods for structural health monitoring of earthen constructions. Alex. Eng. J. 2025, 114, 55–81. [Google Scholar] [CrossRef]
- Nguyen, Q.-B.; Nguyen, H.-H. An Efficient Approach for Damage Identification of Beams Using Mid-Span Static Deflection Changes. Eng 2024, 5, 895–917. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U. A Systematic Review of Advanced Sensor Technologies for Non-Destructive Testing and Structural Health Monitoring. Sensors 2023, 23, 2204. [Google Scholar] [CrossRef]
- Goggin, P.; Huang, J.; White, E.; Haugse, E. Challenges for SHM transition to future aerospace systems. In Proceedings of the 4th International Workshop on Structural Health Monitoring: From Diagnostics and Prognostics to Structural Health Management, Standford, CA, USA, 15–17 September 2003; DEStech Publications: Lancaster, PA, USA, 2003; pp. 30–41. [Google Scholar]
- Liu, Z. Smart Sensors for Structural Health Monitoring and Nondestructive Evaluation. Sensors 2024, 24, 603. [Google Scholar] [CrossRef]
- Mei, H.; Haider, M.F.; Joseph, R.; Migot, A.; Giurgiutiu, V. Recent Advances in Piezoelectric Wafer Active Sensors for Structural Health Monitoring Applications. Sensors 2019, 19, 383. [Google Scholar] [CrossRef] [PubMed]
- Gibson, A.; Popovics, J.S. Lamb Wave Basis for Impact-Echo Method Analysis. J. Eng. Mech. 2005, 131, 438–443. [Google Scholar] [CrossRef]
- Na, W.S.; Baek, J. A Review of the Piezoelectric Electromechanical Impedance Based Structural Health Monitoring Technique for Engineering Structures. Sensors 2018, 18, 1307. [Google Scholar] [CrossRef]
- Falcetelli, F.; Venturini, N.; Romero, M.B.; Martinez, M.J.; Pant, S.; Troiani, E. Broadband signal reconstruction for SHM: An experimental and numerical time reversal methodology. J. Intell. Mater. Syst. Struct. 2021, 32, 1043–1058. [Google Scholar] [CrossRef]
- Khodaei, Z.S.; Grigg, S. Aerospace Requirements. In Structural Health Monitoring Damage Detection Systems for Aerospace; Springer: Cham, Switzerland, 2021; p. 73. [Google Scholar]
- Bradfield, G. Improvements in ultrasonic flaw detection. J. Br. Inst. Radio Eng. 1954, 14, 303–308. [Google Scholar] [CrossRef]
- Robertson, D.; Camps, O.; Mayer, J.; Gish, W. Wavelets and electromagnetic power system transients. IEEE Trans. Power Deliv. 1996, 11, 1050–1058. [Google Scholar] [CrossRef]
- Ghazali, K.H.; Mansor, M.F.; Mustafa, M.M.; Hussain, A. Feature extraction technique using discrete wavelet transform for image classification. In Proceedings of the 5th Student Conference on Research and Development, Selangor, Malaysia, 11–12 December 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–4. [Google Scholar]
- Aguiar-Conraria, L.; Soares, M.J. The Continuous Wavelet Transform: A Primer; NIPE-Universidade do Minho: Braga, Portugal, 2011. [Google Scholar]
- Thakral, S.; Manhas, P. Image processing by using different types of discrete wavelet transform. In Proceedings of the Advanced Informatics for Computing Research: Second International Conference, ICAICR 2018, Shimla, India, 14–15 July 2018; Revised Selected Papers, Part I 2. Springer: Cham, Switzerland, 2019; pp. 499–507. [Google Scholar]
- Kammler, D.W. A First Course in Fourier Analysis; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Zhang, Q.; Barri, K.; Babanajad, S.K.; Alavi, A.H. Real-Time Detection of Cracks on Concrete Bridge Decks Using Deep Learning in the Frequency Domain. Engineering 2021, 7, 1786–1796. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Azizjon, M.; Jumabek, A.; Kim, W. 1D CNN based network intrusion detection with normalization on imbalanced data. In Proceedings of the 2020 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Fukuoka, Japan, 19–21 February 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 218–224. [Google Scholar]
- Zhao, J.; Mao, X.; Chen, L. Speech emotion recognition using deep 1D & 2D CNN LSTM networks. Biomed. Signal Process. Control. 2019, 47, 312–323. [Google Scholar]
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C.-I. A Simplified 2D-3D CNN Architecture for Hyperspectral Image Classification Based on Spatial–Spectral Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2485–2501. [Google Scholar] [CrossRef]
- Chang, J.; Sha, J. An efficient implementation of 2D convolution in CNN. IEICE Electron. Express 2017, 14, 20161134. [Google Scholar] [CrossRef]
- Kumar, J.; Goomer, R.; Singh, A.K. Long Short Term Memory Recurrent Neural Network (LSTM-RNN) Based Workload Forecasting Model for Cloud Datacenters. Procedia Comput. Sci. 2018, 125, 676–682. [Google Scholar] [CrossRef]
- Ji, H.; Lou, Y.; Cheng, S.; Xie, Z.; Zhu, L. An Advanced Long Short-Term Memory (LSTM) Neural Network Method for Predicting Rate of Penetration (ROP). ACS Omega 2022, 8, 934–945. [Google Scholar] [CrossRef] [PubMed]
- Rokach, L.; Maimon, O. Decision trees. In Data Mining and Knowledge Discovery Handbook; Springer: New York, NY, USA, 2005; pp. 165–192. [Google Scholar]
- Ali, J.; Khan, R.; Ahmad, N.; Maqsood, I. Random forests and decision trees. Int. J. Comput. Sci. Issues IJCSI 2012, 9, 272. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hasni, H.; Jiao, P.; Alavi, A.H.; Lajnef, N.; Masri, S.F. Structural health monitoring of steel frames using a network of self-powered strain and acceleration sensors: A numerical study. Autom. Constr. 2018, 85, 344–357. [Google Scholar] [CrossRef]
- Altabey, W.A.; Noori, M.; Wu, Z.; Silik, A.; Sarhosis, V. Enhancement of structural health monitoring framework on beams based on k-nearest neighbor algorithm. In Proceedings of the 14th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 12–14 September 2023. [Google Scholar]
- Achouri, F.; Khatir, A.; Smahi, Z.; Capozucca, R.; Brahim, A.O. Structural health monitoring of beam model based on swarm intelligence-based algorithms and neural networks employing FRF. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 621. [Google Scholar] [CrossRef]
- Buljak, V.; Cocchetti, G.; Cornaggia, A.; Maier, G. Assessment of residual stresses and mechanical characterization of materials by “hole drilling” and indentation tests combined and by inverse analysis. Mech. Res. Commun. 2015, 68, 18–24. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).