Impact of Pavement Surface Roughness on TSD Backcalculation Outputs and Potential Mitigation Strategies
Abstract
1. Introduction
2. Processing of TSD Raw Data Measurements
3. International Roughness Index (IRI)
4. Greenwood Engineering TSD Backcalculation Tool
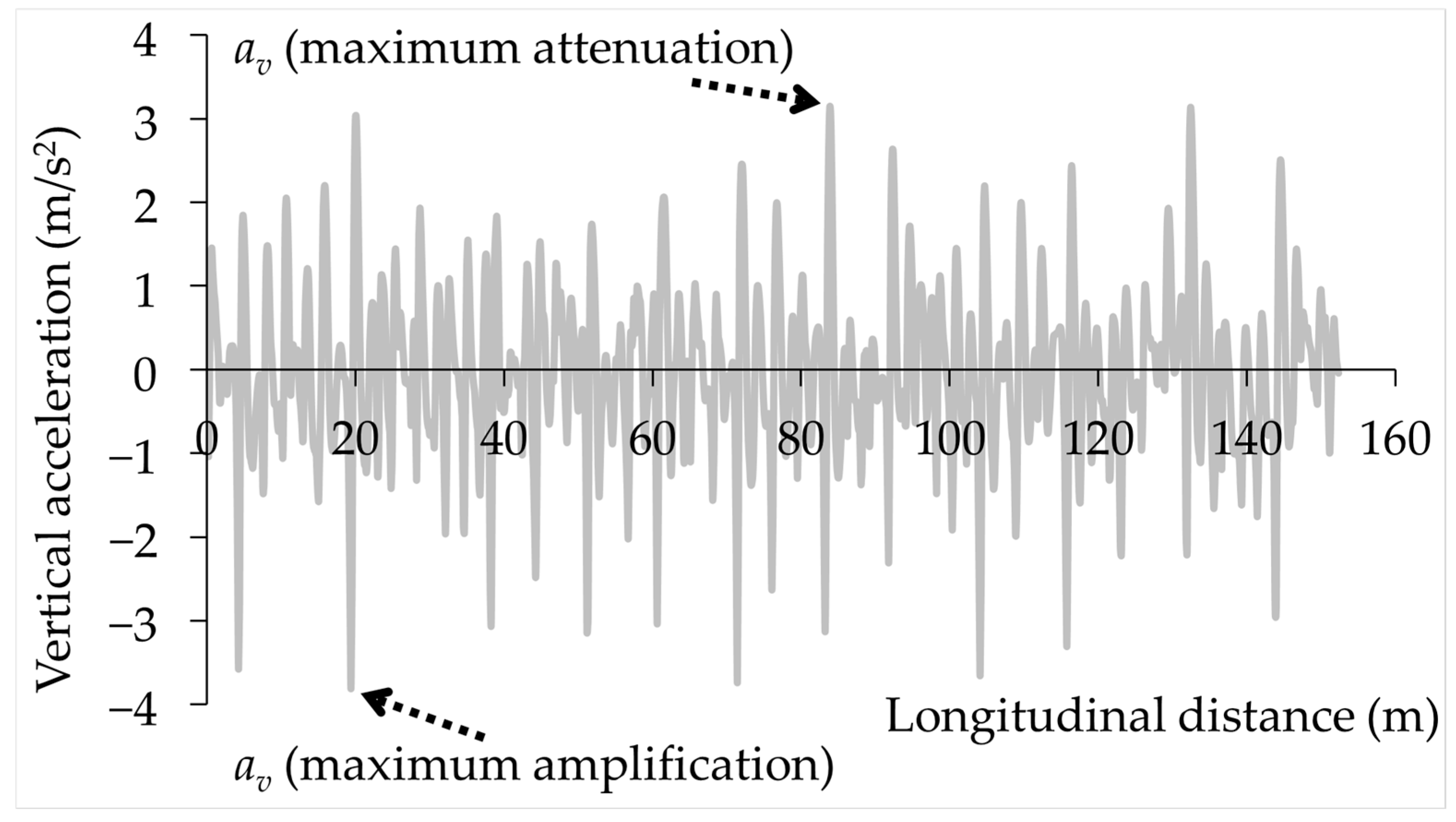
5. Effect of Vertical Acceleration on Tyre Load Magnitude
6. Materials and Methods
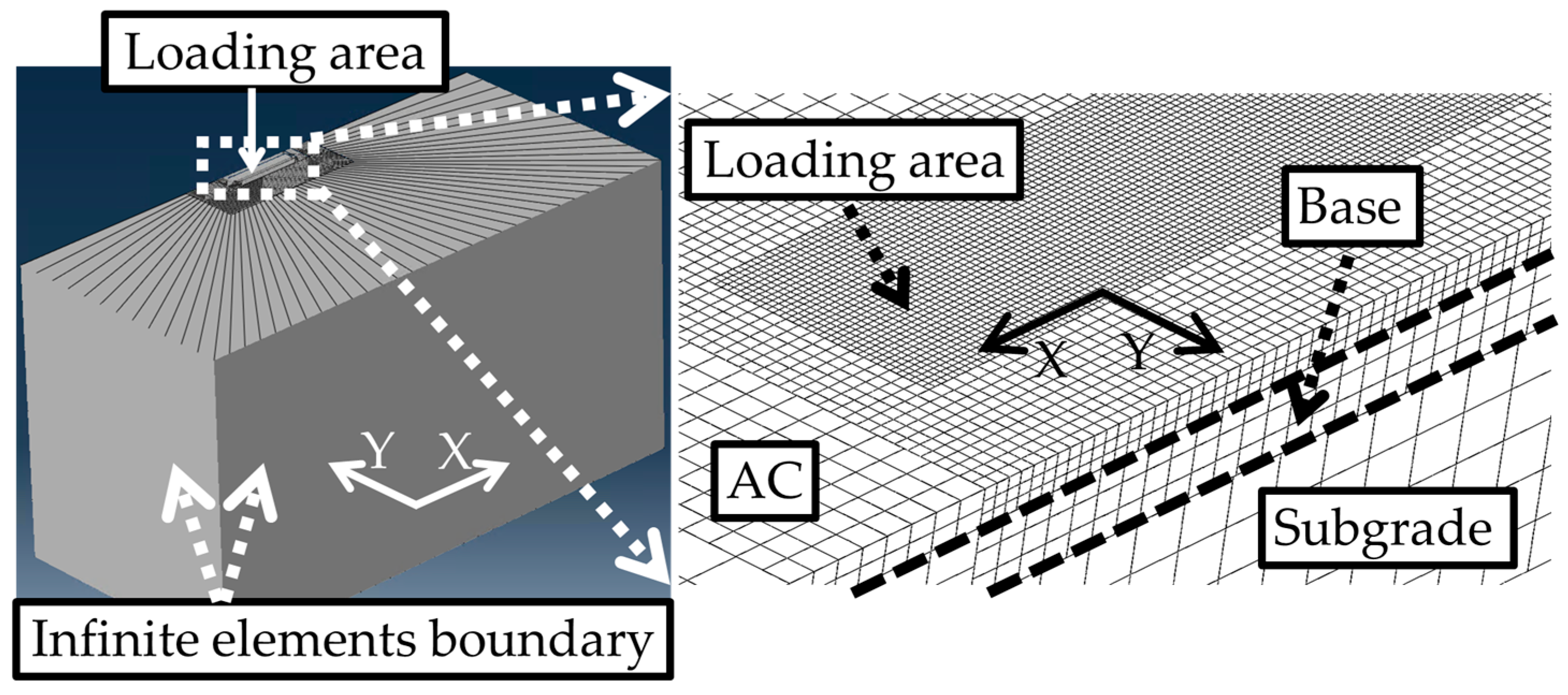
6.1. Pavement Structure in FEM
6.2. Loading Configuration in FEM
6.3. Model Geometry in FEM
7. Results and Discussion
7.1. Validation of the Correct Implementation of the ODE45 Numerical Solver
7.2. Validation of FEM Simulations
7.3. Comparison of FEM and Greenwood Engineering TSD Backcalculation Tool
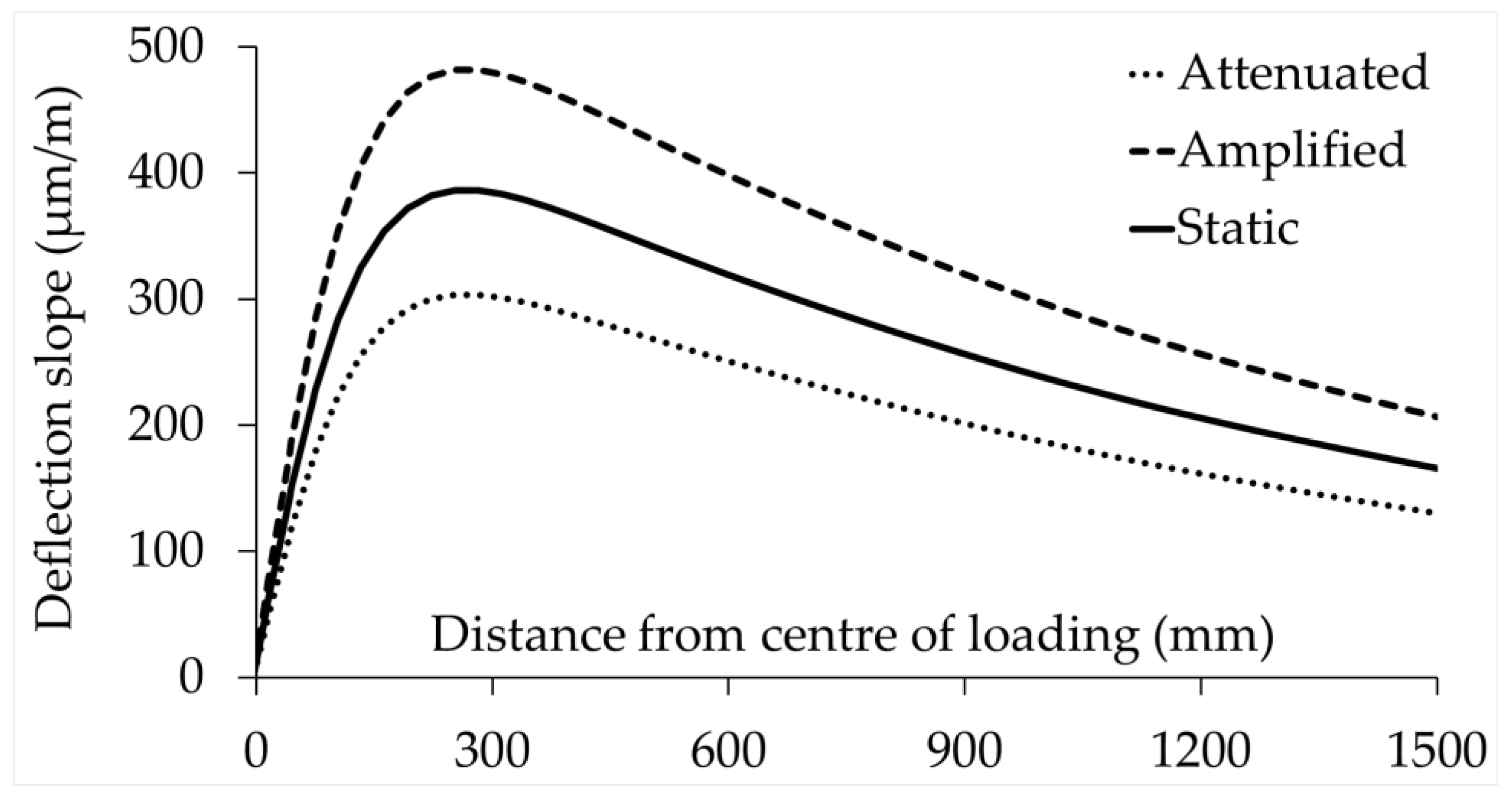
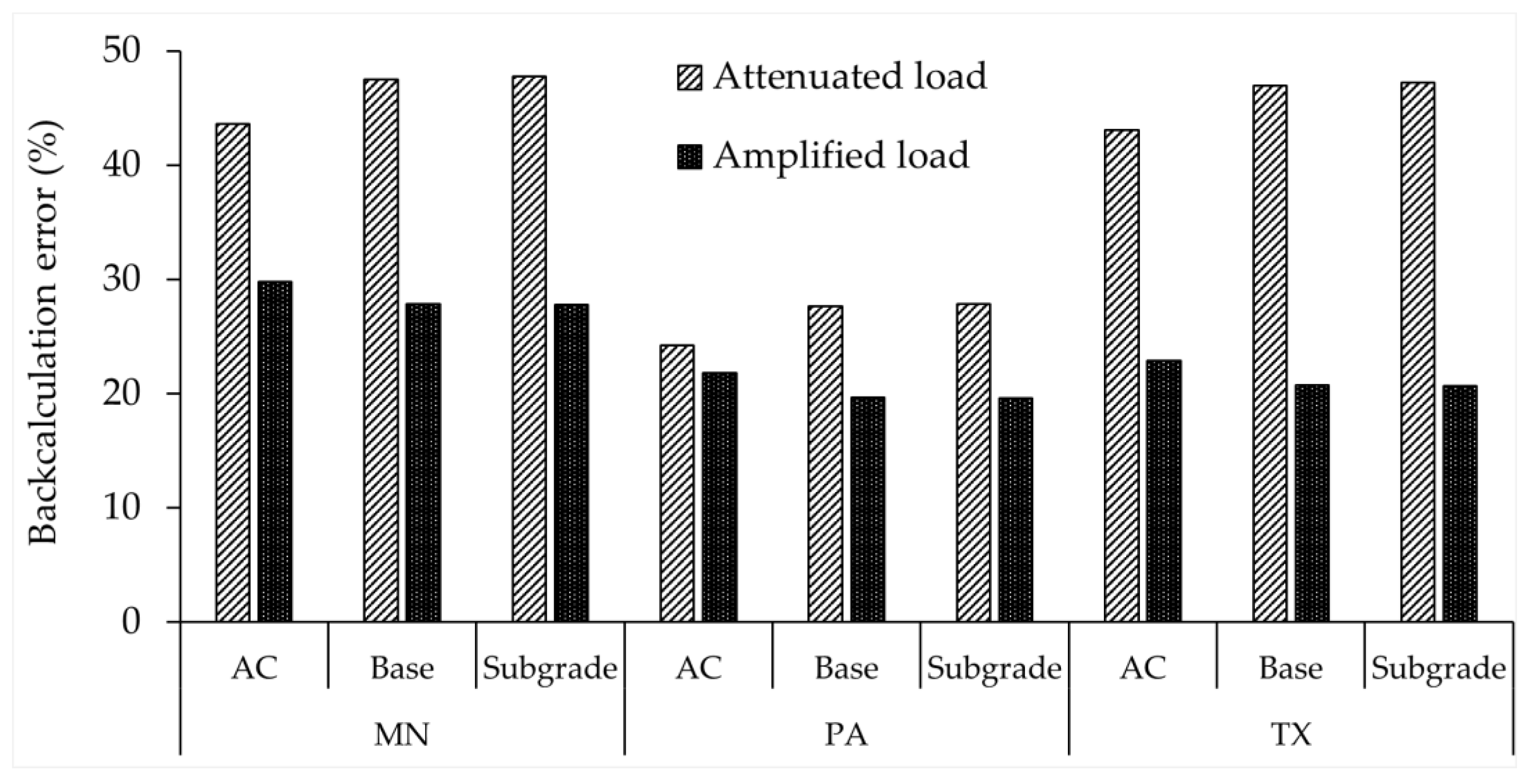
7.4. Effect of Tyre Load Attenuation and Amplification on Backcalculated Moduli
7.5. Effect of Averaging Deflection Slopes on Backcalculated Moduli
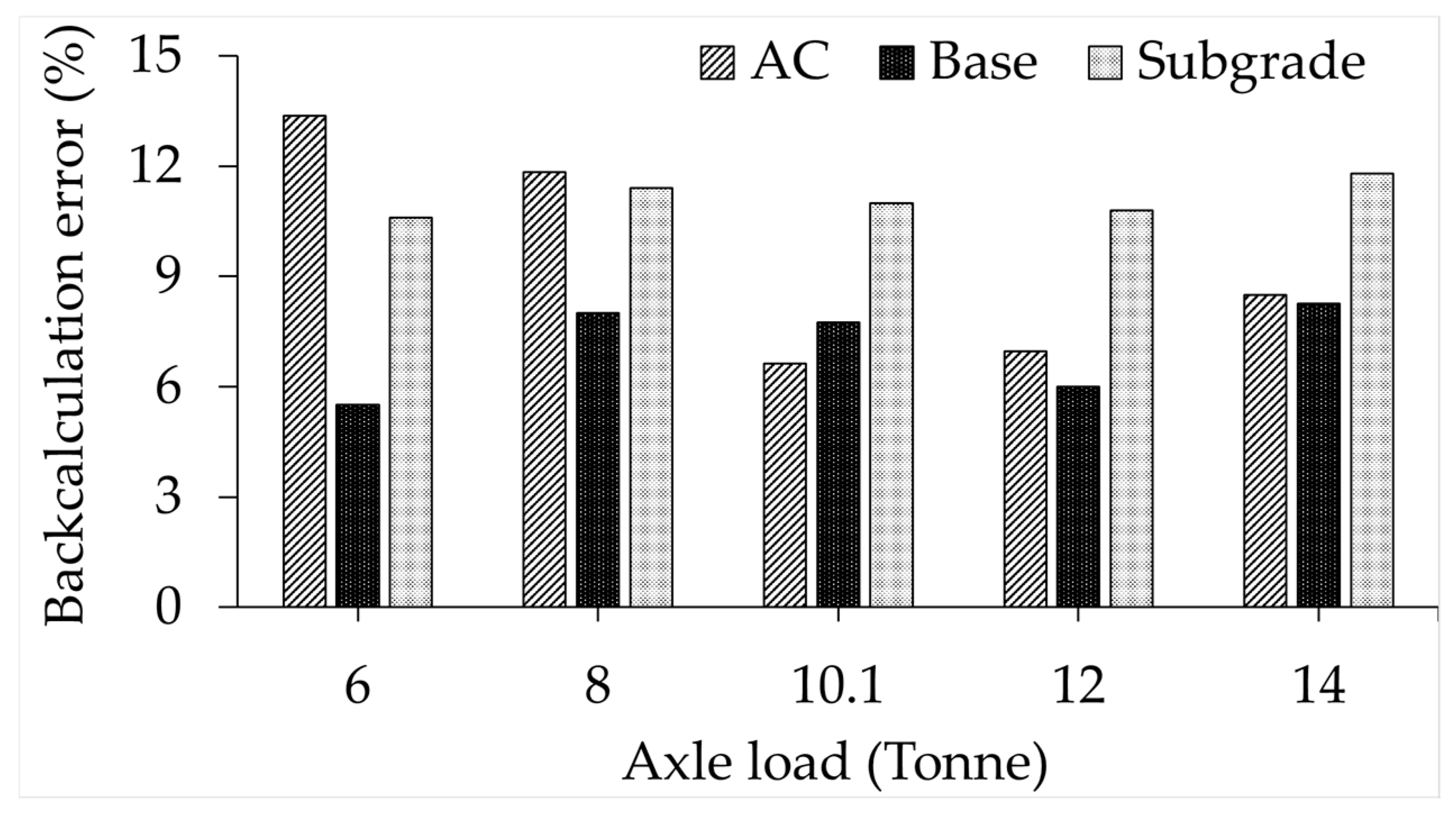
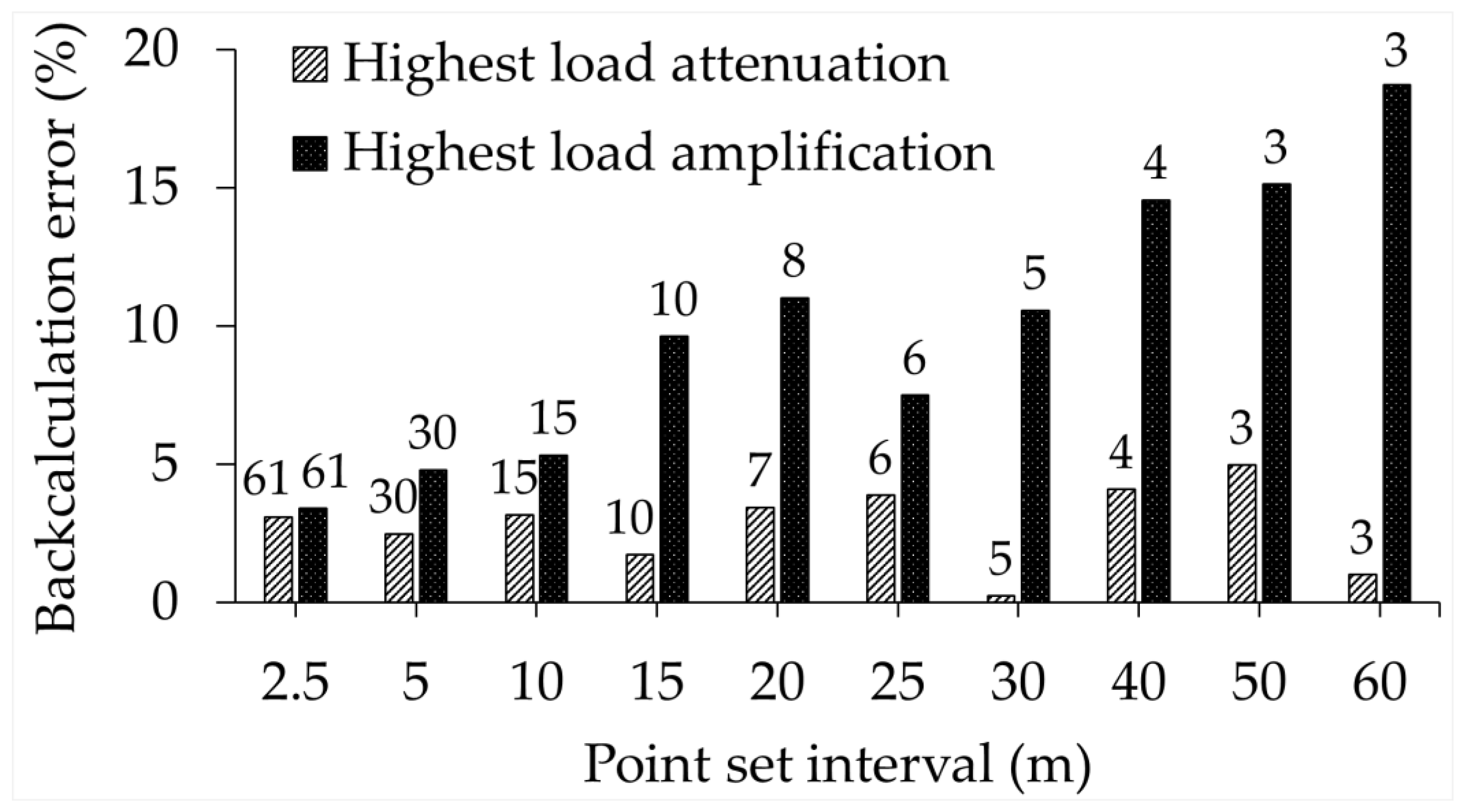
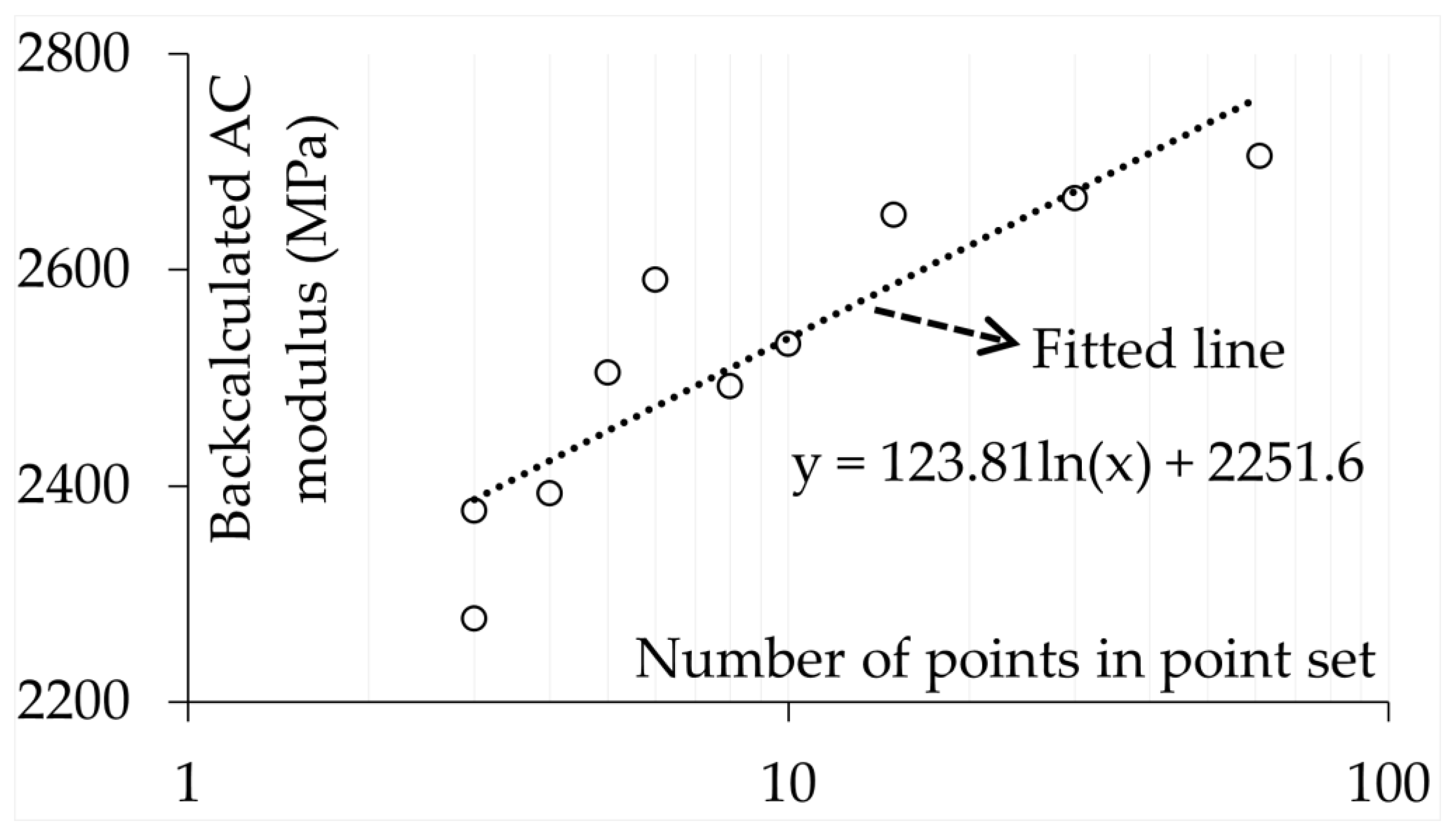
7.6. Effect of Point Set Size on Backcalculation Error
8. Conclusions
9. Limitations of the Study and Path Towards Future Works
- -
- The range of IRI values assigned to the pavement surface roughness conditions lay within a narrow range of 2.77 m/km to 3.18 m/km. For this study, rough pavement surface conditions were selected because they have a stronger influence on backcalculation errors. Under these conditions, the negative effects of pavement surface roughness on backcalculated moduli are more pronounced, emphasising the crucial need for the mitigation strategy for backcalculation errors presented in this study. However, assessing a wider range of IRI values would help examine how general the findings are and allow comparisons between different surface roughness conditions when interpreting the results.
- -
- Sources of epistemic or model uncertainty exist in the FEM simulations, and they can be improved in future studies. These include simplifying the viscoelastic behaviour of the AC layer to linear elastic behaviour, ignoring the nonlinear stress-dependent and cross-anisotropic behaviour of the base and subgrade layers, neglecting the effects of moisture change on subgrade stiffness, and using the golden car’s suspension system characteristics to represent the suspension system of the TSD vehicle.
- -
- Given the sources of uncertainty present in the FEM simulations, the deterministic framework used for backcalculation in this study, which produces a unique solution for the backcalculated moduli without considering confidence intervals, appears to be inadequate. In addition to the epistemic uncertainties already discussed, sources of aleatoric or data uncertainty also exist in the TSD backcalculation process. These may include spatial variability in material properties and pavement layers’ thicknesses, TSD measurement noise, and the way IRI averages the surface over distance, which can hide local defects that affect tyre vertical accelerations. Considering all sources of uncertainties, a probabilistic framework for backcalculation that includes uncertainty quantification and provides posterior distributions of the backcalculation outputs, rather than single deterministic values, would be highly valuable. The probabilistic backcalculation approach is a powerful tool for inverse problem solving, as, for example, the Bayesian inference framework has been successfully applied in previous studies [60,61].
- -
- Although only one pavement structure was analysed in this study, the methodology developed to mitigate the negative effect of pavement surface roughness on the backcalculated moduli of pavement layers remains valid and can be applied to different pavement system configurations. However, it is recommended that future studies evaluate a wider range of pavement structures to establish a comprehensive framework for determining the required number of points in a point set to mitigate backcalculation errors to any target error tolerance level.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2.5D | Two-and-a-half-dimensional |
| 3D | Three-dimensional |
| AC | Asphalt concrete |
| ANN | Artificial neural network |
| CEKF | Constrained extended Kalman filter |
| DLC | Dynamic load coefficient |
| FEM | Finite element method |
| FWD | Falling weight deflectometer |
| GPR | Ground-penetrating radar |
| IRI | International Roughness Index |
| LTPP | Long-Term Pavement Performance |
| MAPE | Mean absolute percentage error |
| MN | Minnesota |
| ODE | Ordinary differential equation |
| PA | Pennsylvania |
| SAFEM | Semi-analytical finite element method |
| SDR | Standard Data Release |
| SHRP | Strategic Highway Research Program |
| TSD | Traffic speed deflectometer |
| TX | Texas |
References
- Douglas, A.S.; Lee, H.; Beckemeyer, C.A. Development of the Rolling Wheel Deflectometer (RWD); Report No. FHWA-DTFH-61-14-H00019; Federal Highway Administration, U.S. Department of Transportation: Washington, DC, USA, 2020. [Google Scholar]
- Rada, G.R.; Nazarian, S.; Visintine, B.A.; Siddharthan, R.; Thyagarajan, S. Pavement Structural Evaluation at the Network Level: Final Report; Report No. FHWA-HRT-15–074; Federal Highway Administration, U.S. Department of Transportation: Washington, DC, USA, 2016. [Google Scholar]
- Krarup, J.; Rasmussen, S.; Aagaard, L.; Hjorth, P.G. Output from the Greenwood Traffic Speed Deflectometer. In Proceedings of the 22nd ARRB Conference—Research into Practice, Canberra, Australia, 29 October–2 November 2006. [Google Scholar]
- Canestrari, F.; Ingrassia, L.P.; Spinelli, P.; Graziani, A. A New Methodology to Assess the Remaining Service Life of Motorway Pavements at the Network Level from Traffic Speed Deflectometer Measurements. Int. J. Pavement Eng. 2023, 24, 2128349. [Google Scholar] [CrossRef]
- Shen, K.; Wang, H. Prediction of Critical Strains of Flexible Pavement from Traffic Speed Deflectometer Measurements. Constr. Build. Mater. 2024, 411, 134770. [Google Scholar] [CrossRef]
- Zhang, M.; Gong, H.; Jia, X.; Jiang, X.; Feng, N.; Huang, B. Determining Pavement Structural Number with Traffic Speed Deflectometer Measurements. Transp. Geotech. 2022, 35, 100774. [Google Scholar] [CrossRef]
- Nielsen, C.P.; Nahoujy, M.R.; Jansen, D. Measuring Joint Movement on Rigid Pavements using the Traffic Speed Deflectometer. J. Transp. Eng. Part B Pavements 2023, 149, 04023002. [Google Scholar] [CrossRef]
- Nasimifar, M.; Thyagarajan, S.; Sivaneswaran, N. Backcalculation of Flexible Pavement Layer Moduli from Traffic Speed Deflectometer Data. Transp. Res. Rec. 2017, 2641, 66–74. [Google Scholar] [CrossRef]
- Nielsen, C.P. Visco-elastic Back-calculation of Traffic Speed Deflectometer Measurements. Transp. Res. Rec. 2019, 2673, 439–448. [Google Scholar] [CrossRef]
- Marcondes, J.A.; Snyder, M.B.; Singh, S.P. Predicting Vertical Acceleration in Vehicles through Road Roughness. J. Transp. Eng. 1992, 118, 33–49. [Google Scholar] [CrossRef]
- Misaghi, S.; Tirado, C.; Nazarian, S.; Carrasco, C. Impact of Pavement Roughness and Suspension Systems on Vehicle Dynamic Loads on Flexible Pavements. Transp. Eng. 2021, 3, 100045. [Google Scholar] [CrossRef]
- Siddharthan, R.V.; Yao, J.; Sebaaly, P.E. Pavement Strain from Moving Dynamic 3D Load Distribution. J. Transp. Eng. 1998, 124, 557–566. [Google Scholar] [CrossRef]
- Zihan, Z.U.; Elseifi, M.A.; Icenogle, P.; Gaspard, K.; Zhang, Z. Mechanistic-based Approach to Utilize Traffic Speed Deflectometer Measurements in Backcalculation Analysis. Transp. Res. Rec. 2020, 2674, 208–222. [Google Scholar] [CrossRef]
- Wu, C.; Wang, H.; Zhao, J.; Jiang, X.; Qiu, Y. Asphalt Pavement Modulus Backcalculation using Surface Deflections under Moving Loads. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 1246–1260. [Google Scholar] [CrossRef]
- McCormack, R. TRUCKSIM—A Log Truck Performance Simulator. J. For. Eng. 1990, 2, 31–37. [Google Scholar] [CrossRef]
- Shen, K.; Wang, H. Impact of Dynamic Loading on Pavement Deflection Measurements from Traffic Speed Deflectometer. Measurement 2023, 217, 113086. [Google Scholar] [CrossRef]
- Dai, J.; Adhikari, S.; Wen, M. Uncertainty Quantification and Propagation in Atomistic Machine Learning. Rev. Chem. Eng. 2025, 41, 333–357. [Google Scholar] [CrossRef]
- Flintsch, G.W.; Ferne, B.; Diefenderfer, B.; Katicha, S.; Bryce, J.; Nell, S. Evaluation of Traffic-Speed Deflectometers. Transp. Res. Rec. 2012, 2304, 37–46. [Google Scholar] [CrossRef]
- Katicha, S.W.; Flintsch, G.W.; Ferne, B. Optimal Averaging and Localized Weak Spot Identification of Traffic Speed Deflectometer Measurements. Transp. Res. Rec. 2013, 2367, 43–52. [Google Scholar] [CrossRef]
- Katicha, S.W.; Flintsch, G.; Bryce, J.; Ferne, B. Wavelet Denoising of TSD Deflection Slope Measurements for Improved Pavement Structural Evaluation. Comput.-Aided Civ. Infrastruct. Eng. 2014, 29, 399–415. [Google Scholar] [CrossRef]
- Katicha, S.W.; Bryce, J.; Flintsch, G.; Ferne, B. Estimating “True” Variability of Traffic Speed Deflectometer Deflection Slope Measurements. J. Transp. Eng. 2015, 141, 04014071. [Google Scholar] [CrossRef]
- Wu, C.; Duan, Y.; Wang, H. Signal Denoising of Traffic Speed Deflectometer Measurement Based on Partial Swarm Optimization–Variational Mode Decomposition Method. Sensors 2024, 24, 3708. [Google Scholar] [CrossRef]
- Rada, G.; Nazarian, S.; Tirado, C.; Beizaei, M.; Flintsch, G.; Katicha, S. Verification of Traffic Speed Deflection Devices’ (TSDDs) Measurements: Final Report; Project No. 10-105; NCHRP Transportation Research Board of the National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 2023. [Google Scholar]
- Zhang, M.; Fu, G.; Ma, Y.; Xiao, R.; Huang, B. Speed and Temperature Superposition on Traffic Speed Deflectometer Measurements. Transp. Geotech. 2023, 40, 100990. [Google Scholar] [CrossRef]
- Hoffmann, K. An Introduction to Measurements Using Strain Gages; Hottinger Baldwin Messtechnik GmbH: Darmstadt, Germany, 1989. [Google Scholar]
- Florin, A.; Ioan-Cozmin, M.-R.; Liliana, P. Passive Suspension Modeling Using MATLAB, Quarter Car Model, Input Signal Step Type. In Proceedings of the 17th International TEHNOMUS Conference (New Technologies and Products in Machine Manufacturing Technologies), Suceava, Romania, 17–18 May 2013; pp. 258–263. [Google Scholar]
- Sandage, R.N.; Patil, P.M.; Patil, S. Simulation Analysis of 2DOF Quarter Car Semi-Active Suspension System to Improve Ride comfort—A review. Int. J. Appl. Innov. Eng. Manag. (IJAIEM) 2013, 2, 339–345. [Google Scholar]
- Cruz, O.G.D.; Mendoza, C.A.; Lopez, K.D. International Roughness Index as Road Performance Indicator: A Literature Review. In Proceedings of the International Conference on Contemporary and Sustainable Infrastructure (ICCSI), Bangalore, India, 21–22 May 2021. [Google Scholar] [CrossRef]
- Pawar, P.R.; Mathew, A.T.; Saraf, M. IRI (International Roughness Index): An Indicator of Vehicle Response. In Materials Today, Proceedings of the International Conference on Materials, Manufacturing and Modelling (ICMMM), Vellore, India, 9–12 March 2017; Elsevier Ltd.: Amsterdam, The Netherlands, 2018; Volume 5, pp. 11738–11750. [Google Scholar] [CrossRef]
- Arhin, S.A.; Noel, E.C. Predicting Pavement Condition Index Using International Roughness Index in Washington DC: Final Report; Report No. DDOT-RDT-14-03; Department of Transportation: Washington, DC, USA, 2014. [Google Scholar]
- Múčka, P. International Roughness Index Specifications Around the World. Road Mater. Pavement Des. 2017, 18, 929–965. [Google Scholar] [CrossRef]
- Di Mascio, P.; Loprencipe, G.; Moretti, L.; Puzzo, L.; Zoccali, P. Bridge Expansion Joint in Road Transition Curve: Effects Assessment on Heavy Vehicles. Appl. Sci. 2017, 7, 599. [Google Scholar] [CrossRef]
- Sayers, M.W.; Karamihas, S.M. The Little Book of Profiling: Basic Information About Measuring and Interpreting Road Profile; Transportation Research Institute, University of Michigan: Ann Arbor, MI, USA, 1998. [Google Scholar]
- Greenwood Engineering. TSD Viscoelastic back Calculation. Available online: https://vbc.greenwood.dk/ (accessed on 6 October 2023).
- Maser, K.; Schmalzer, P.; Shaw, W.; Carmichael, A. Integration of Traffic Speed Deflectometer and Ground-Penetrating Radar for Network-Level Roadway Structure Evaluation. Transp. Res. Rec. 2017, 2639, 55–63. [Google Scholar] [CrossRef]
- Federal Highway Administration. LTPP Standard Data Release, Long-Term Pavement Performance Program, SDR 37. Available online: https://infopave.fhwa.dot.gov/Data/StandardDataRelease (accessed on 11 December 2023).
- Bilodeau, J.-P.; Gagnon, L.; Doré, G. Assessment of the Relationship Between the International Roughness Index and Dynamic Loading of Heavy Vehicles. Int. J. Pavement Eng. 2017, 18, 693–701. [Google Scholar] [CrossRef]
- MATLAB, version 9.13.0; The MathWorks Inc.: Natick, MA, USA, 2022.
- ABAQUS; Dassault Systèmes Simulia Corp.: Johnston, RI, USA, 2022.
- Liu, X.; Al-qadi, I. Integrated Vehicle–Tire–Pavement Approach for Determining Pavement Structure–Induced Rolling Resistance under Dynamic Loading. Transp. Res. Rec. 2022, 2676, 398–409. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Sun, Z.; Hakim, B.; Indraratna, B.; Al-Tabbaa, A. Probabilistic Simulation of TSD-based Pavement Deflections for Bayesian Updating of Material Parameters. Transp. Geotech. 2025, 55, 101715. [Google Scholar] [CrossRef]
- Nasimifar, M.; Kamalizadeh, R.; Heidary, B. The Available Approaches for using Traffic Speed Deflectometer Data at Network Level Pavement Management System. Measurement 2022, 202, 111901. [Google Scholar] [CrossRef]
- Mejłun, Ł.; Judycki, J.; Dołżycki, B. Comparison of Elastic and Viscoelastic Analysis of Asphalt Pavement at High Temperature. Procedia Eng. 2017, 172, 746–753. [Google Scholar] [CrossRef]
- Moffatt, M. Guide to Pavement Technology Part 2: Pavement Structural Design; Austroads Ltd.: Sydney, Australia, 2017. [Google Scholar]
- NOAA National Centers for Environmental Information. Climate at a Glance: Statewide Time Series. Available online: https://www.ncei.noaa.gov/access/monitoring/climate-at-a-glance/statewide/time-series (accessed on 2 December 2025).
- Brown, S.F.; Pappin, J. Analysis of Pavements with Granular Bases. Transp. Res. Rec. 1981, 810, 17–23. [Google Scholar]
- Uzan, J. Characterization of Granular Material. Transp. Res. Rec. 1985, 1022, 52–59. [Google Scholar]
- Al-Qadi, I.L.; Wang, H.; Tutumluer, E. Dynamic Analysis of Thin Asphalt Pavements by using Cross-Anisotropic Stress-Dependent Properties for Granular Layer. Transp. Res. Rec. 2010, 2154, 156–163. [Google Scholar] [CrossRef]
- Tarefder, R.A.; Ahmed, M.U.; Rahman, A. Effects of Cross-Anisotropy and Stress-Dependency of Pavement Layers on Pavement Responses under Dynamic Truck Loading. J. Rock Mech. Geotech. Eng. 2016, 8, 366–377. [Google Scholar] [CrossRef]
- Kazemi, N.; Saleh, M.; Lee, C.-L. Effect of the Stress Dependency and Anisotropy of Unbound Granular Base and Subgrade Materials on TSD Deflection Slopes. In Proceedings of the International Conference on Transportation and Development (ICTD), Atlanta, GA, USA, 15–18 June 2024; pp. 327–337. [Google Scholar] [CrossRef]
- Kazemi, N.; Saleh, M.; Lee, C.-L. Effect of Nonlinear Stress-Dependency and Cross-Anisotropy on the Backcalculation Outputs from the TSD Deflection Slopes and the Effect on Estimated Pavement Performance. Int. J. Pavement Eng. 2024, 25, 2417967. [Google Scholar] [CrossRef]
- Hamidi, A.; Hoff, I.; Mork, H. A Sensitivity Analysis on the Simulated Measurements of Traffic Speed Deflection Devices. Int. J. Pavement Eng. 2024, 25, 2447461. [Google Scholar] [CrossRef]
- ABAQUS 2016 User Subroutines Reference Guide; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2015.
- Fortran Compiler, Intel Corporation: Santa Clara, CA, USA, 2023.
- ABAQUS Theory Manual: Version 6.11; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2011.
- Wardle, L. CIRCLY and Mechanistic Pavement Design: The Past, Present and Towards the Future; Mincad Systems: Richmond, Australia, 2010. [Google Scholar]
- Uzan, J. JULEA (Jacob Uzan Layered Elastic Analysis); Technion University: Haifa, Israel, 1976. [Google Scholar]
- Kim, S.; Kim, H. A New Metric of Absolute Percentage Error for Intermittent Demand Forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Lewis, C.D. Industrial and Business Forecasting Methods: A Practical Guide to Exponential Smoothing and Curve Fitting; Butterworth Scientific: London, UK, 1982; ISBN 978-0408005593. [Google Scholar]
- Wang, H.; Zhou, W.; Wang, H.; Li, G. A DeepONets-based Resolution Independent ABC Inverse Method for Determining Material Parameters of HAZ. Eng. Fract. Mech. 2025, 315, 110843. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, X.; Wen, Z.; Wang, H. Resolution-Independent Generative Models based on Operator Learning for Physics-Constrained Bayesian Inverse Problems. Comput. Methods Appl. Mech. Eng. 2024, 420, 116690. [Google Scholar] [CrossRef]



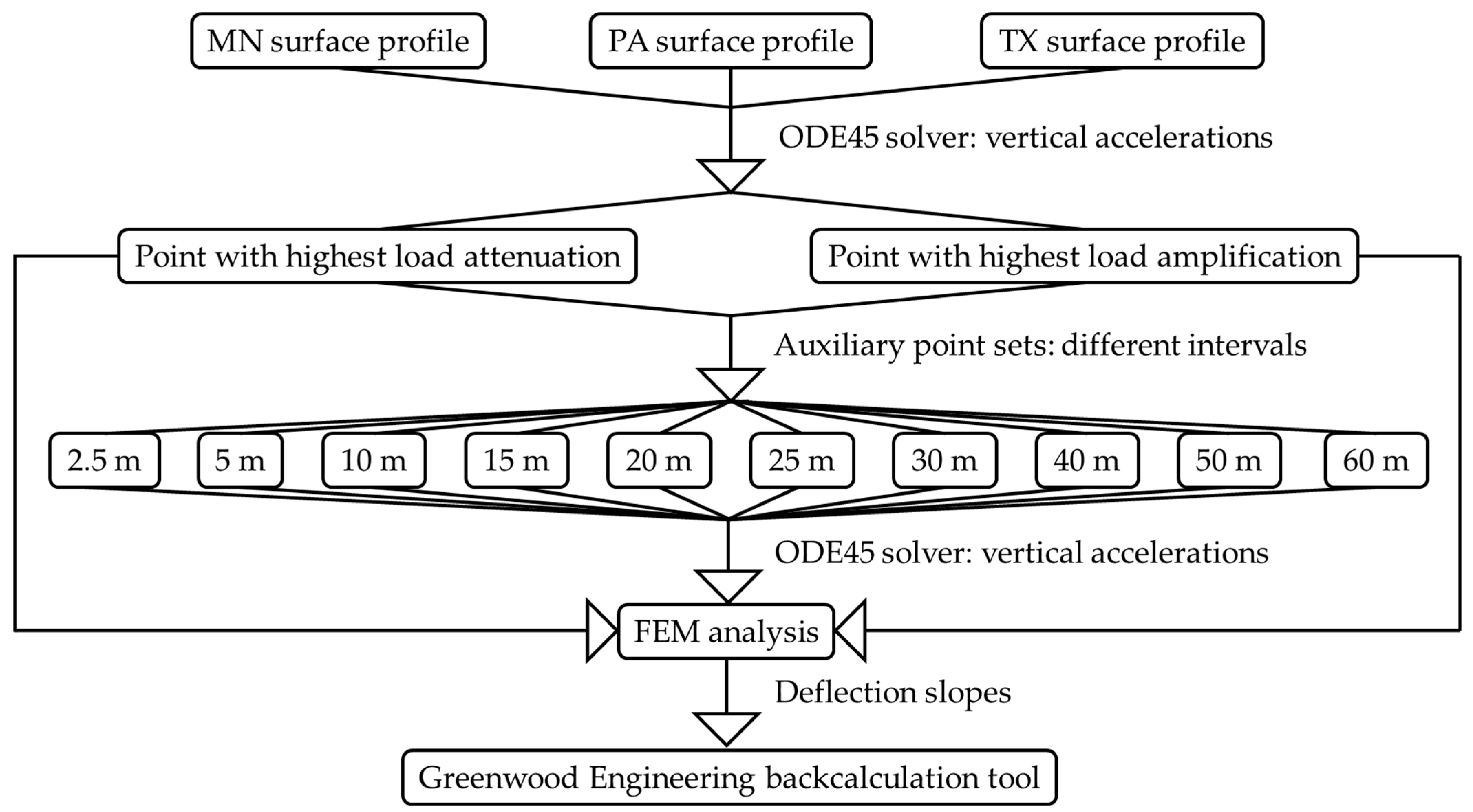
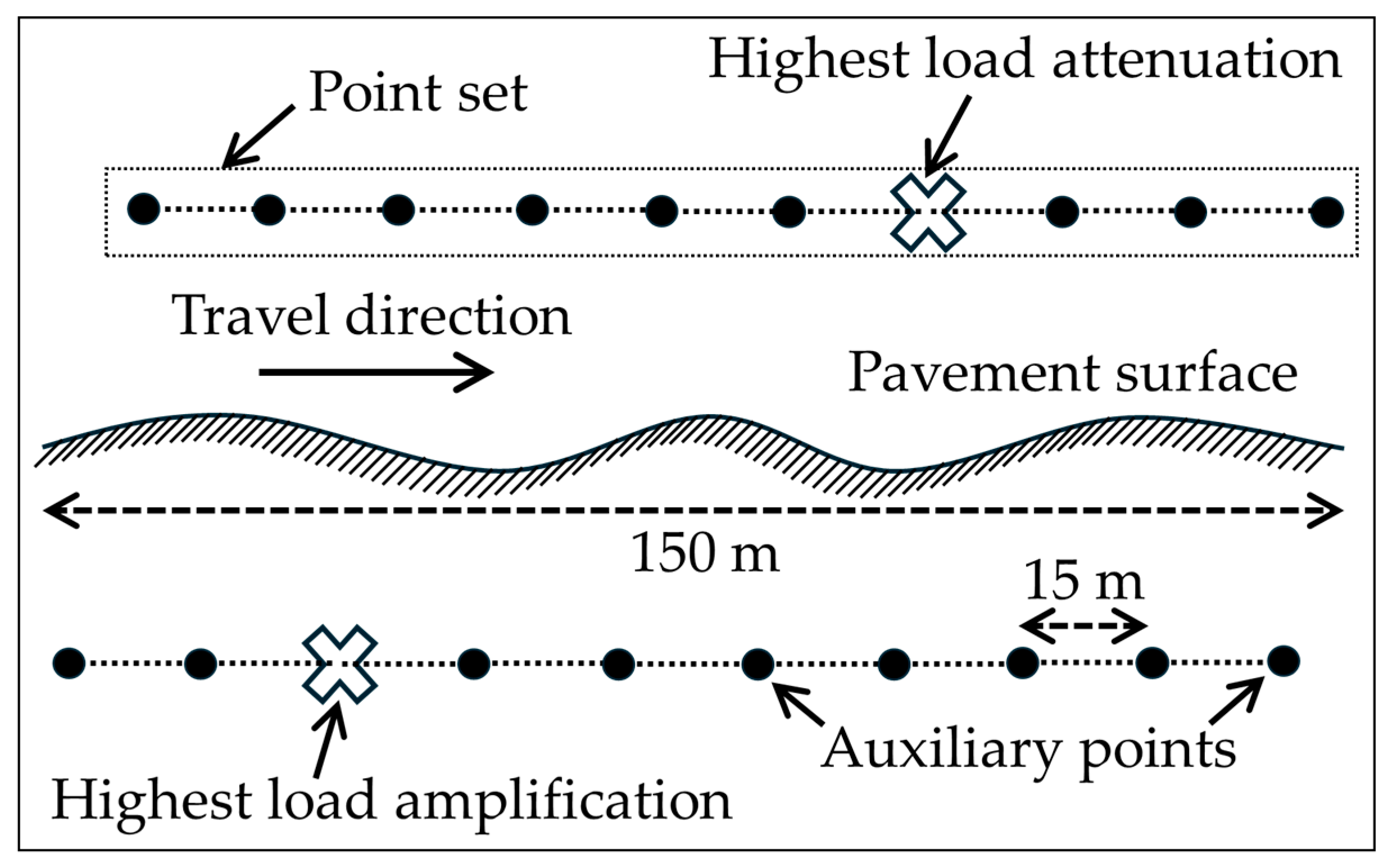
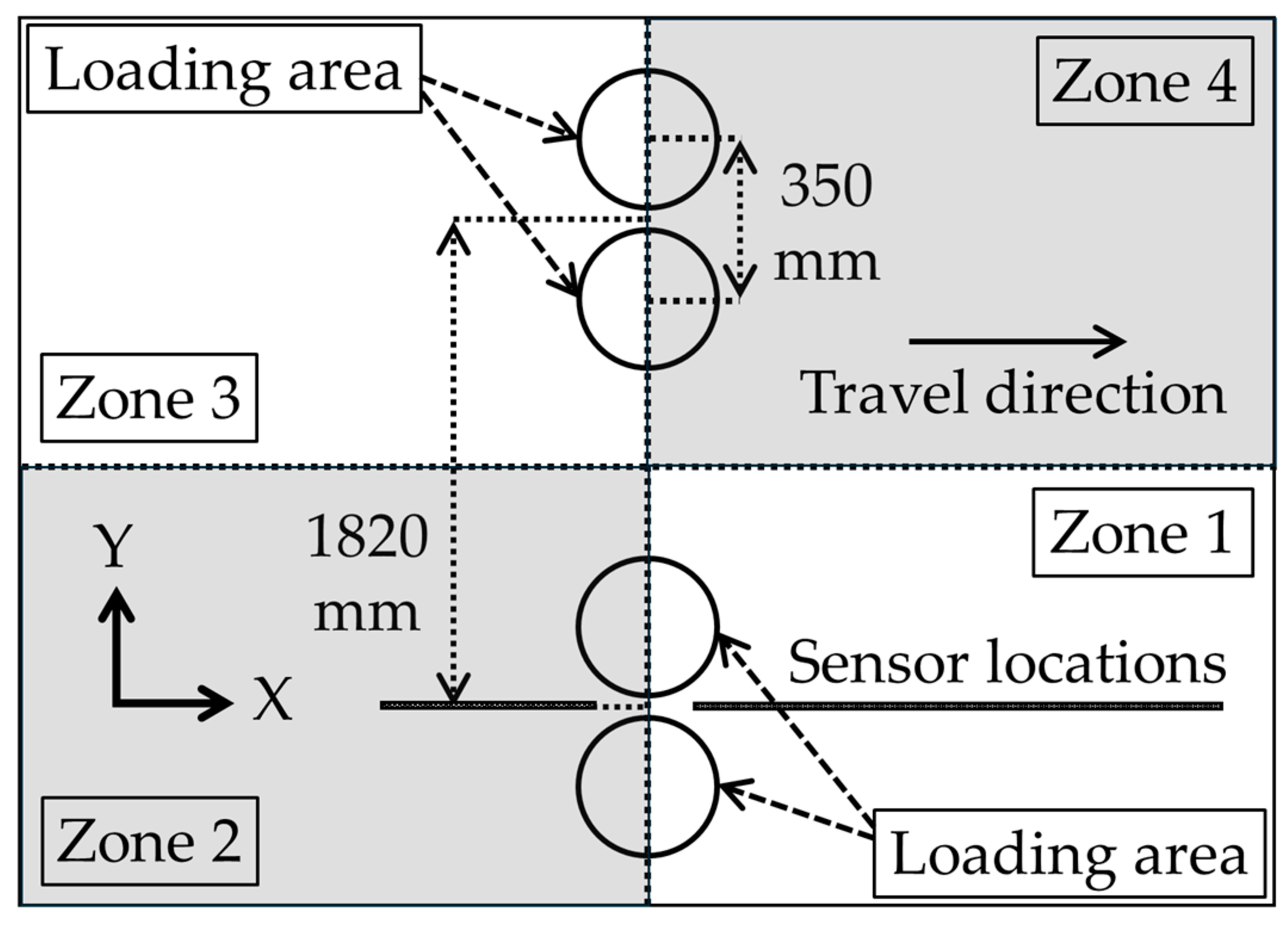
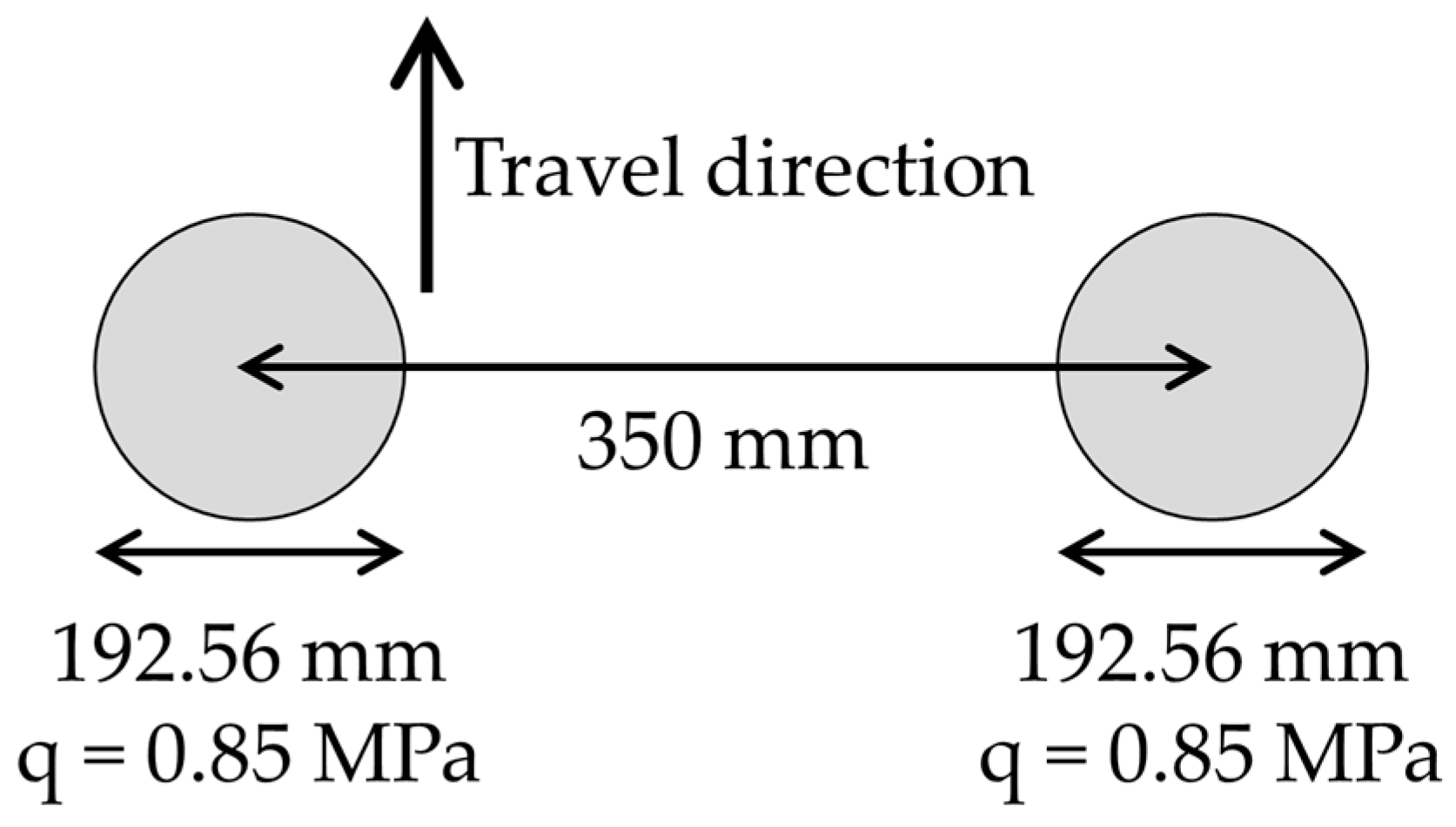



| IRI Scale (m/km) | Roughness Level |
|---|---|
| ≤0.95 | Very smooth |
| 0.96–1.89 | Smooth |
| 1.9–2.68 | Fair |
| 2.69–3.47 | Rough |
| ≥3.48 | Very rough |
| Ratio | Unit | Value |
|---|---|---|
| mu/ms | Dimensionless | 0.15 |
| ks/ms | 1/s2 | 63.3 |
| kt/ms | 1/s2 | 653 |
| cs/ms | 1/s | 6 |
| State | Survey Date | SHRP * ID | Run Number | Visit Number | IRI (m/km) |
|---|---|---|---|---|---|
| Texas (TX) | 25 April 1991 | 5024 | 3 | 48502402 | 2.77 |
| Pennsylvania (PA) | 8 October 1991 | 9027 | 1 | 2902703 | 3.04 |
| Minnesota (MN) | 16 July 1997 | A330 | 4 | 27A33007 | 3.18 |
| Layer | Modulus (MPa) | Thickness (mm) | Poisson’s Ratio |
|---|---|---|---|
| AC | 3000 | 150 | 0.4 |
| Base | 400 | 300 | 0.35 |
| Subgrade | 50 | Semi-infinite | 0.45 |
| State of Surface Profile | IRI by ODE45 Solver (m/km) | IRI from LTPP (m/km) |
|---|---|---|
| MN | 3.25 | 3.18 |
| PA | 3.12 | 3.04 |
| TX | 2.84 | 2.77 |
| Axle Load (Tonne) | AC Modulus (MPa) | Base Modulus (MPa) | Subgrade Modulus (MPa) |
|---|---|---|---|
| 6 | 2599 | 422 | 44.7 |
| 8 | 2645 | 432 | 44.3 |
| 10.1 | 2801 | 431 | 44.5 |
| 12 | 2791 | 424 | 44.6 |
| 14 | 2745 | 433 | 44.1 |
| Backcalculated Modulus (MPa) | ||||
|---|---|---|---|---|
| State Profile | Layer | Static Load | Attenuated Load | Amplified Load |
| MN | AC | 2801 | 4022 | 1967 |
| Base | 431 | 635 | 311 | |
| Subgrade | 44.5 | 65.8 | 32.2 | |
| PA | AC | 2801 | 3480 | 2190 |
| Base | 431 | 550 | 346 | |
| Subgrade | 44.5 | 56.9 | 35.8 | |
| TX | AC | 2801 | 4007 | 2160 |
| Base | 431 | 633 | 341 | |
| Subgrade | 44.5 | 65.6 | 35.3 | |
| State Profile | Loading | Layer | MAPE (%) of Predictive Equation |
|---|---|---|---|
| MN | Attenuated | AC | 2.1 |
| Base | 2.1 | ||
| Subgrade | 2.1 | ||
| Amplified | AC | 1.9 | |
| Base | 1.9 | ||
| Subgrade | 1.9 | ||
| PA | Attenuated | AC | 3.2 |
| Base | 3.2 | ||
| Subgrade | 3.2 | ||
| Amplified | AC | 2 | |
| Base | 2 | ||
| Subgrade | 2 | ||
| TX | Attenuated | AC | 3 |
| Base | 3 | ||
| Subgrade | 3 | ||
| Amplified | AC | 1.7 | |
| Base | 1.7 | ||
| Subgrade | 1.7 |
| MAPE | Prediction Accuracy |
|---|---|
| <10% | High |
| 10–20% | Good |
| 20–50% | Reasonable |
| >50% | Inaccurate |
| State Profile | Loading | Layer | Pmin for 5% Error | Pmin for 10% Error |
|---|---|---|---|---|
| MN | Attenuated | AC | 1 | 1 |
| Base | 3 | 1 | ||
| Subgrade | 3 | 1 | ||
| Amplified | AC | 28 | 9 | |
| Base | 16 | 6 | ||
| Subgrade | 15 | 5 | ||
| PA | Attenuated | AC | 5 | 2 |
| Base | 9 | 4 | ||
| Subgrade | 10 | 4 | ||
| Amplified | AC | 8 | 2 | |
| Base | 4 | 1 | ||
| Subgrade | 4 | 1 | ||
| TX | Attenuated | AC | 5 | 2 |
| Base | 8 | 3 | ||
| Subgrade | 9 | 3 | ||
| Amplified | AC | 14 | 2 | |
| Base | 5 | 1 | ||
| Subgrade | 5 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazemi, N.; Saleh, M.; Lee, C.-L. Impact of Pavement Surface Roughness on TSD Backcalculation Outputs and Potential Mitigation Strategies. Infrastructures 2025, 10, 350. https://doi.org/10.3390/infrastructures10120350
Kazemi N, Saleh M, Lee C-L. Impact of Pavement Surface Roughness on TSD Backcalculation Outputs and Potential Mitigation Strategies. Infrastructures. 2025; 10(12):350. https://doi.org/10.3390/infrastructures10120350
Chicago/Turabian StyleKazemi, Nariman, Mofreh Saleh, and Chin-Long Lee. 2025. "Impact of Pavement Surface Roughness on TSD Backcalculation Outputs and Potential Mitigation Strategies" Infrastructures 10, no. 12: 350. https://doi.org/10.3390/infrastructures10120350
APA StyleKazemi, N., Saleh, M., & Lee, C.-L. (2025). Impact of Pavement Surface Roughness on TSD Backcalculation Outputs and Potential Mitigation Strategies. Infrastructures, 10(12), 350. https://doi.org/10.3390/infrastructures10120350







