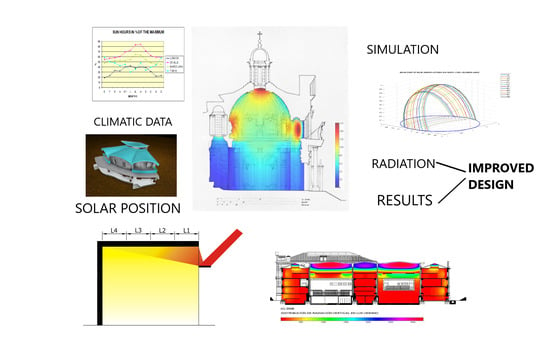
New Simulation Tool for Architectural Design in the Realm of Solar Radiative Transfer

Abstract

In this paper, we devise a system for architectural simulations that considers the volumetric and three-dimensional properties or the energy sources involved in the energy exchanges within or around edifices and built or urban spaces. The advances are based in optics theory evolving from the assumptions presented in the book The Photic Field by P. H. Moon and D. E. Spencer, with added improvements suggested by D. DiLaura. Such procedure is deftly performed by means of solving complex integral equations, which were unavailable until recently and originate in the research developed by the authors. This experimental software is called DianaX. The advantages of this new system allow for a clearer visualization of the performance of buildings in terms of radiated energy. Reductions in the amounts of used energy can be achieved precisely by means of the design process of the software, which can be considered in some respects as a Design Tool. With this tool, the analysis of heritage building paradigms is feasible as it assesses the potential of new foreseen projects taking into account new artificial lighting devices that deviate from the conventional linear or point approach in the domain. The main finding demonstrated is the feasibility and appropriateness of this method to address the problems posed. As future prospects, we would like to increase the catalogue of designs that can benefit from the conscious use of our tool for scientific design.

1. Introduction

Traditionally, the energy simulation of architectural spaces is not intended for design as it does not take into account the spatial complexity of shapes [1]. As in other types of simulation, such as those for structural engineering, the acting magnitudes are customarily conducted through linear or at best bi-dimensional fields. This is due to several reasons: on the one hand, thermal fields are generally considered as scalar and, on the other, the idea cherished by engineering of a minimum inhabitable space with fixed planar floor and ceiling discourages the exploration of richer spatial configurations that can offer more visual attraction.

The traditional tools used to tackle this problem contemplate only the modelling of the sky conceived as a discretized hemisphere and mainly take into account the sky conditions which have shown too much variability and generally tend to disregard over-abundant solar radiation [2]. The design of reflective and protective means over-imposed to glazed apertures has not advanced very much due to this kind of approach Instead, we focus on the manifold geometric subtleties that may appear in the design of the interior of buildings, identifying which types of design strategies enhance the diffusion and distribution of radiation that is finally enjoyed by the users and not in achieving theoretical energy balances at the expense of creating discomfort.

In this way, we can analyse very different designs corresponding to sundry tectonic cultures and asses their applicability and adequacy from the perspective of perception and phenomenology and not only of building codes and regulations. Then, new software capable of overcoming the former constraints has been experimentally developed by Cabeza-Lainez and is called DianaX; it is available in reference [1] and also by special appointment with the department.

Technically speaking, to perform the aforementioned study, we need to solve a non-negligible mathematical complexity in this issue, which has resulted in the abandonment of the research of heat transfer when the problem is three-dimensional as it happens in architectural design. In the following, we explain briefly the physical fundamentals of our approach.

If the surfaces in Figure 1, named A_i and A_j, radiate in a diffuse mode, the problem is reduced to finding the balance of energy between them. Neglecting the potential losses of the procedure [3,4], we only need to solve the mutual interchange of radiation that is provided by the shapes involved as the two sources present the same intensity.

The magnitudes θ_i and θ_j correspond to the angles enclosed by the normal lines to the unit areas dA_i and dA_j (Figure 1), where r_ij stands for an arbitrary distance that colligates the unit surface sources dA_i and dA_j.

Setting to facilitate calculations, a phase of negligible rebound reflections from the first source to the second one, the radiation is not redirected and the energy exchange amounts to:

$$d{\varphi }_{ij}=\left(E_i-E_j\right)\cos {\theta }_i\cos {\theta }_j\frac{d{A}_{i}d{A}_j}{\pi r_{ij}^2}$$

(1)

where E_i and E_j correspond to the level of energy (in W/m²) expelled by the respective sources i and j.

In the following, we designate a non-dimensional entity called, configuration factor (sometimes form factor), F_ij that provides the ratio of radiation that is expelled from source i caught by source j. Thus, in accordance, the energy that departs from source i and reaches source j can be defined as E_iA_iF_ij and, correspondingly E_jA_jF_ji amounts to the energy that passes from source j to source i.

In this case, Equation (2) can be expressed in the form:

$$d\varphi =E_i{A}_i{F}_{ij}-E_j{A}_j{F}_{ji}.$$

(2)

When we focus on a temporarily constant stage of the problem, where we cannot identify variations in the energy exchange and the estimated fugues of flux that can be attributed to the wayof emission become nominal, we can say that dϕ = 0, which means that E_iA_iF_ij = E_jA_jF_ji, an expression known as Lambert’s reciprocity theorem [3].

In 1764, the Swiss polymath Lambert published his singular treatise Photometria, written in Germanized Latin. In it, he explained his celebrated sixteenth theorem (XVI), also known as the reciprocity principle that states that: “If two surfaces are equally luminous and face each other in some manner, the flux that reaches from each one of them onto the other must be the same” [5].

Such theorem, in turn, allows us to formulate the question in terms of symbolic calculus and, thus, we arrive to the canonical equation that rules over every radiative exchange.

The former generates an asymmetric algebra based in two principles [6]. Cabeza-Lainez obtained without integration the exact solution to numerous shapes applicable in design. This is the basis for the new experimental simulation tool that we present in this paper and that is called DianaX.

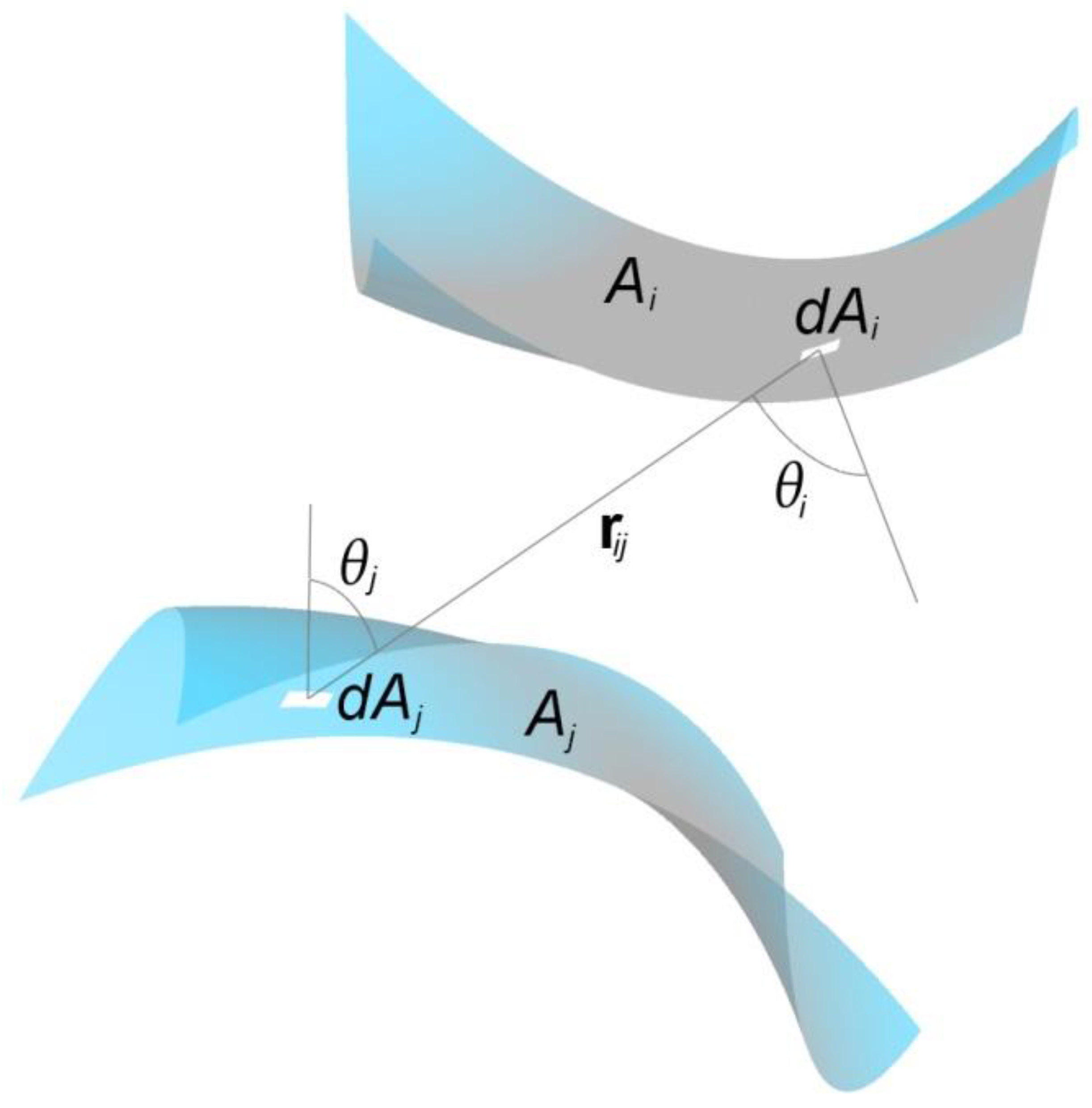
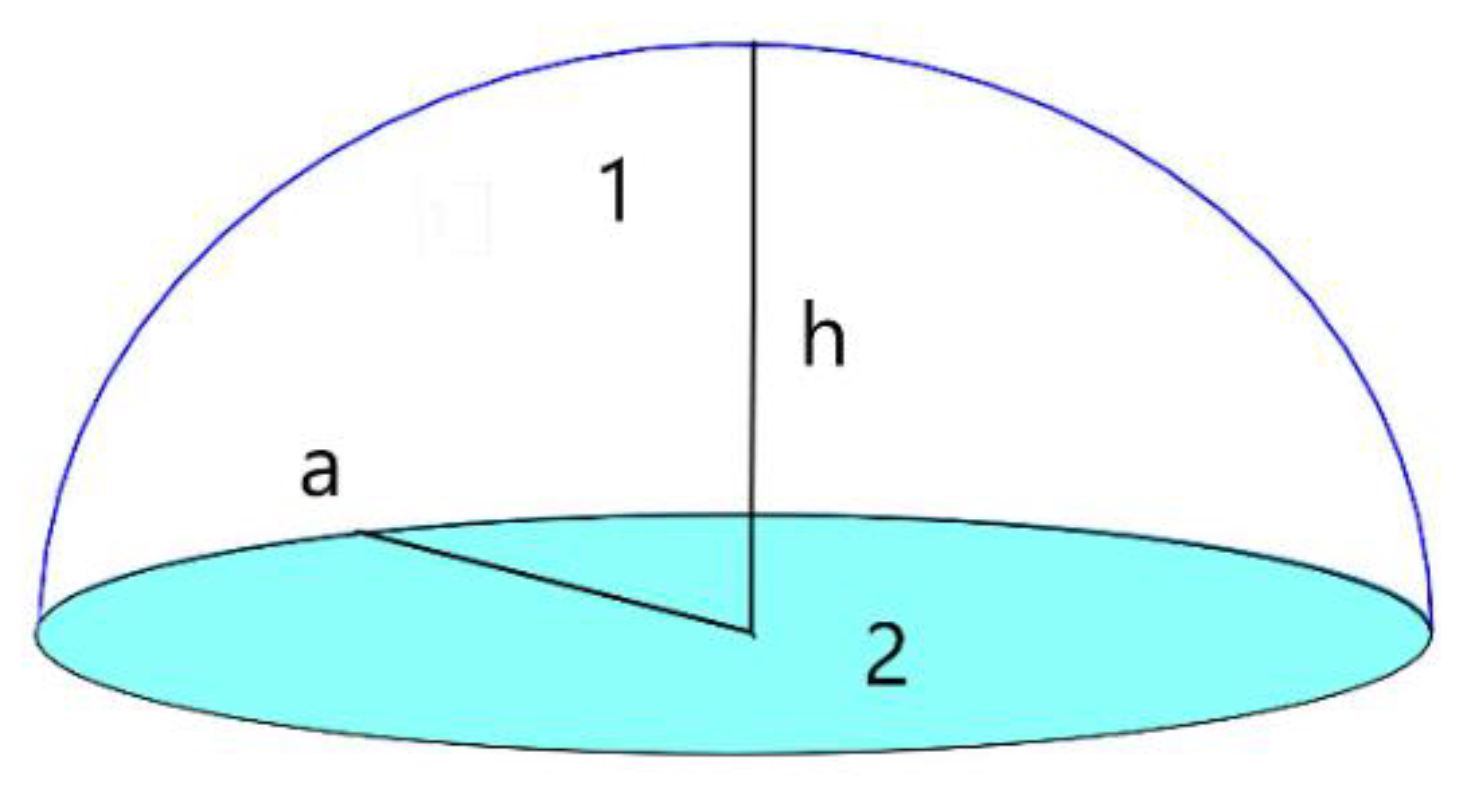
2. Methodology

In order to explain how the proposed method works, we will take one of the simplest possible volumes that is enclosed by two surfaces, namely, the spherical cap. In it, by geometric operations deriving from the algebra mentioned previously and knowing the involved areas, the radiant exchange between the cap and itself, F₁₁, is always h/D [6], where h is the height of the cap perpendicular to the base of diameter D = 2 R, with R being the radius of the whole sphere. This expression, which coincides with the ratio of areas of the cap and the whole sphere (see Figure 2), is a particular case of Cabeza-Lainez’s first principle, simple enough to facilitate all the ensuing calculations and development of the software.

It is known that the relations between the areas of the cap and any limiting circle are:

A₁ = 2πRh

(3)

A₂ = πa²

(4)

Generally speaking, a ≠ R:

A_tot = 4πR²

(5)

F₁₁ =A₁/A_tot = h/(2R) = h/D

(6)

A₁ is obtained from Equation (3) as function of R and h. For the whole sphere, whose total area is A_tot (5), F₁₁ = h/D = 1 and, for the hemisphere, the only case in which R = a, F₁₁ = h/D = 1/2 and so forth.

From here stem the first four principles of Cabeza-Lainez [6], which allow us to solve all algebraic operations, including addition and the scalar product of configuration factors that may appear in three-dimensional energy exchanges. For example, a spherical cap is the simplest section that we can apply to a sphere but there are more possibilities detailed in the references [7].

By means of the procedures detailed in the bibliography [8,9], it is possible to assemble computer tools of high accuracy to know in detail the distribution of radiant energy, be it heat, light or sound, in any kind of space or precinct, taking into account their constructive features.

This tool is called method of form factors and has been developed by Cabeza-Lainez. It is based in finding the exchange ratios by virtue of the factors previously defined, which can be of application in each particular case. The tool implies an important advance to know the distribution radiation in all its forms, but it also entails the accurate design of the elements involved in these exchanges, contributing to the mitigation of climate change, for instance, and adding significant psychologic and physiologic bonuses due to the introduction of direct solar radiation in the spaces [10] and the perceptive advantages that it entails.

In the following section, we analyse several designs to find the behaviour of radiative energy in complex spaces, mainly emitted by fenestration or luminaries. We divide this into three sections, buildings from the past, especially temples or churches, contemporary buildings and projects yet to be realized.

3. Results of Utilizing the Simulation Tools

In this section, we present several architectural paradigms as well as projects yet to be realized in which the authors had some intervention. They have been simulated with the experimental software DianaX, developed by Cabeza-Lainez [1], and the figures and quantities presented correspond to the output of this tool. The main input in all cases is external solar radiation in the location considered as well as the characteristics of the building materials, such as glazing and opaque walls; interior veneers can also be important in some cases.

3.1. Simulations of Radiative Transfer in Buildings of the Past

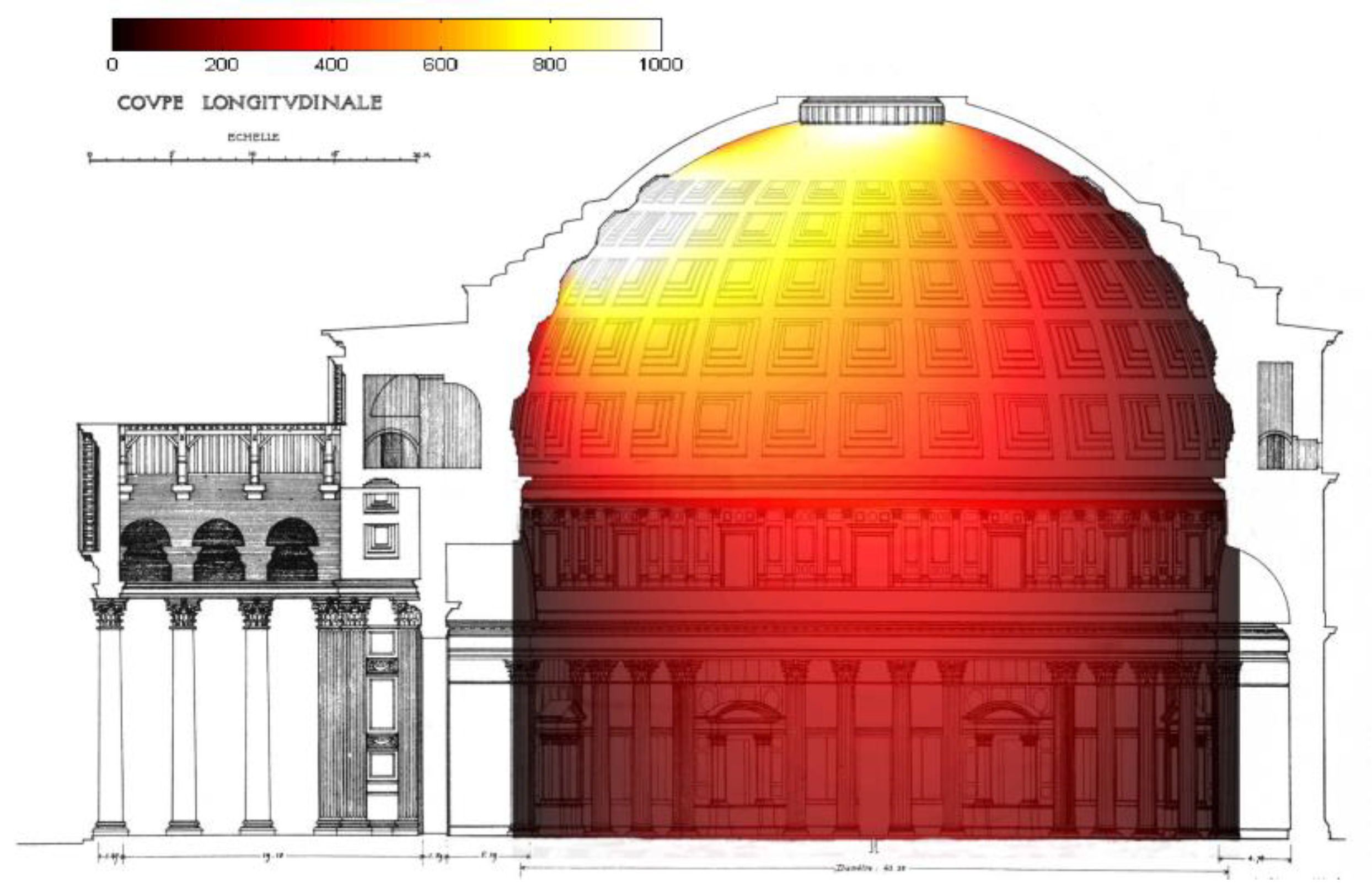
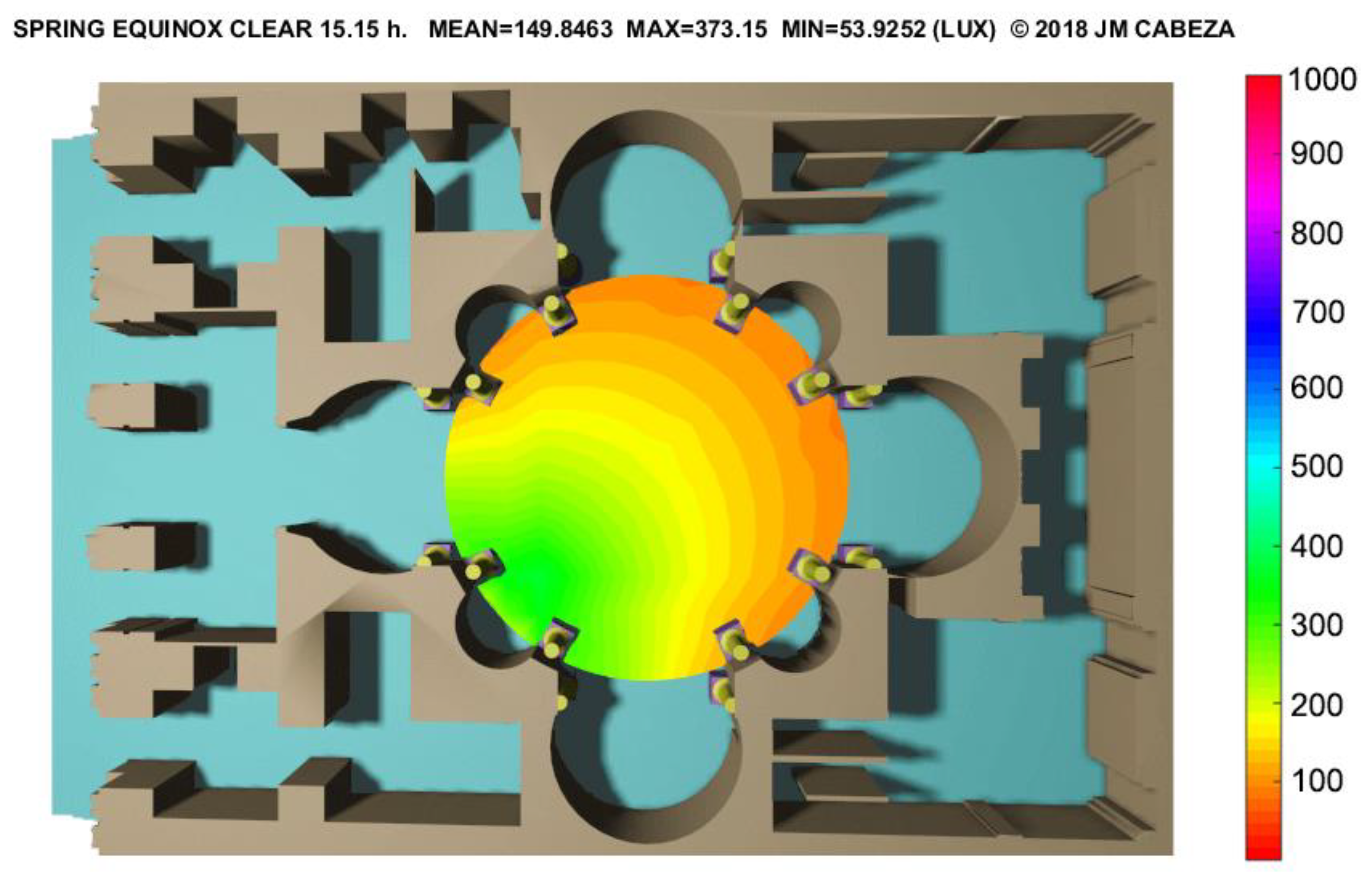
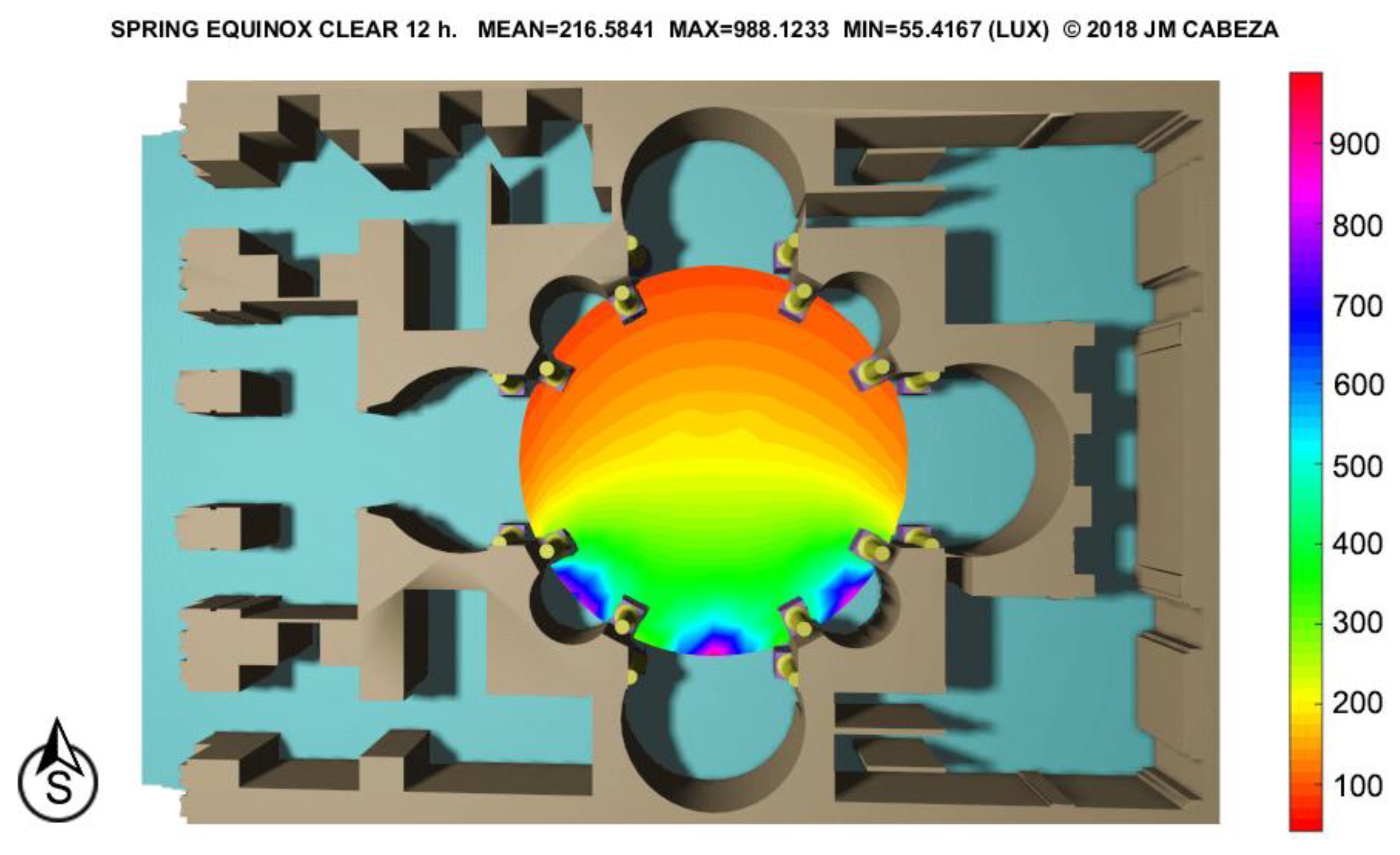
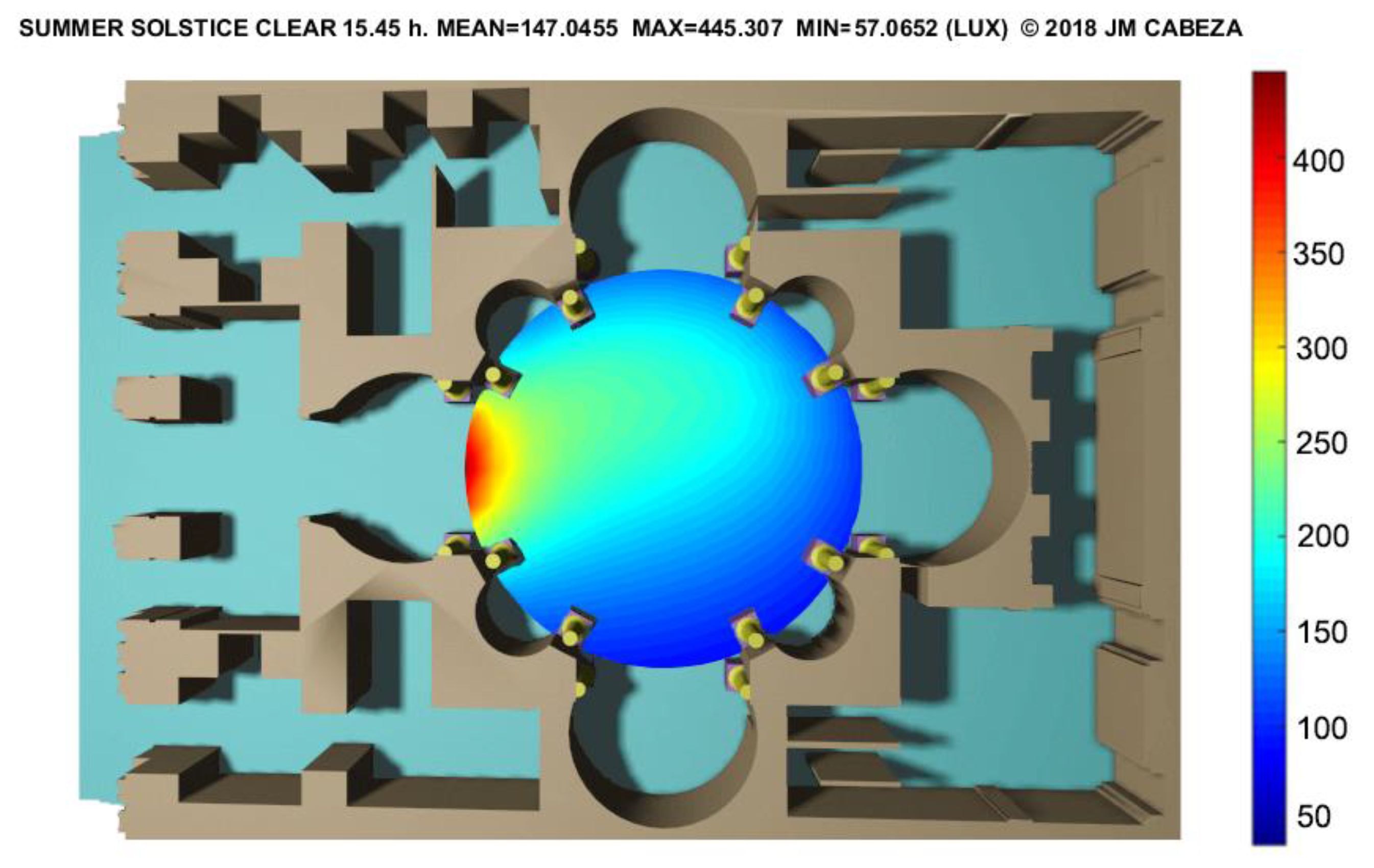
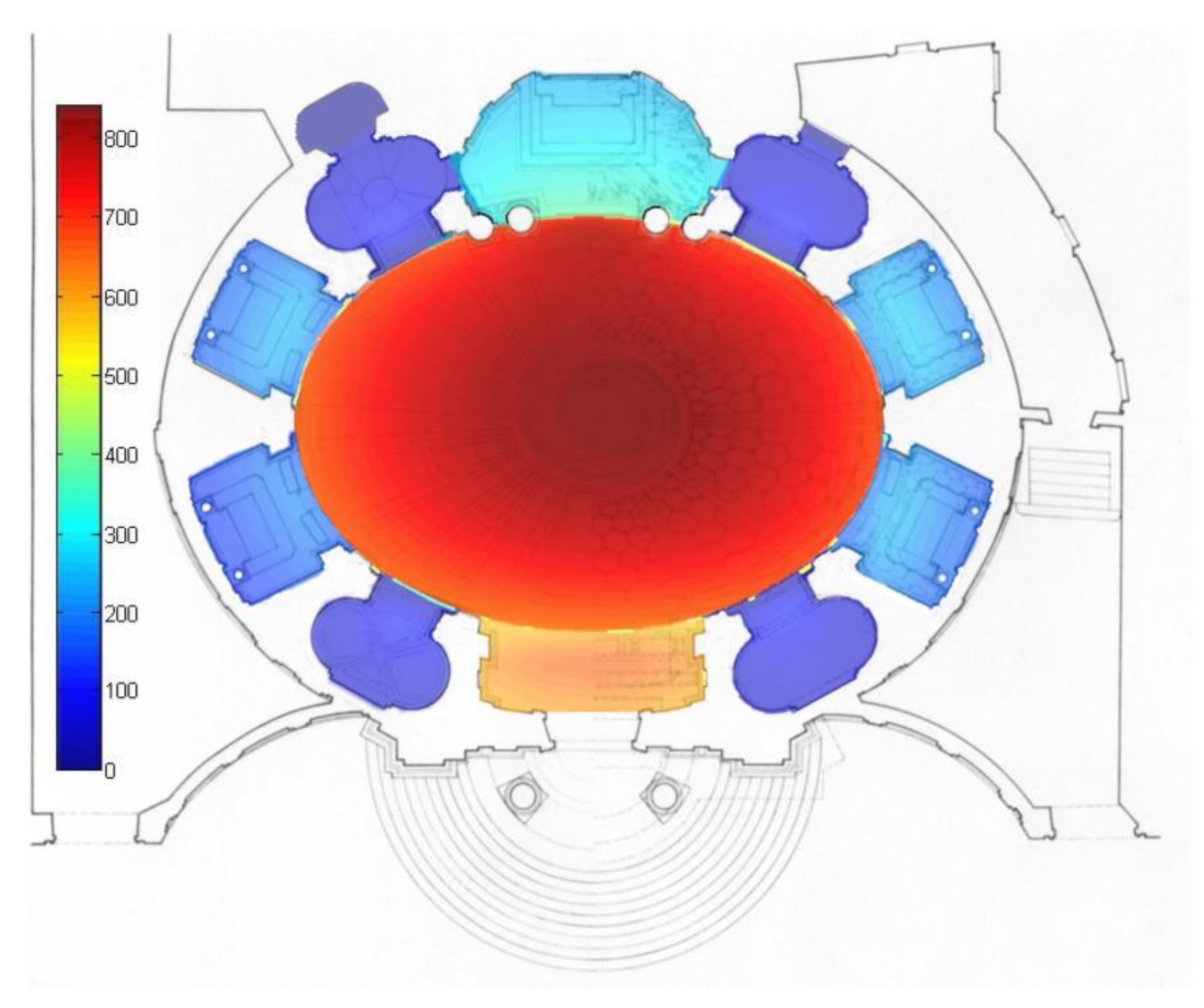
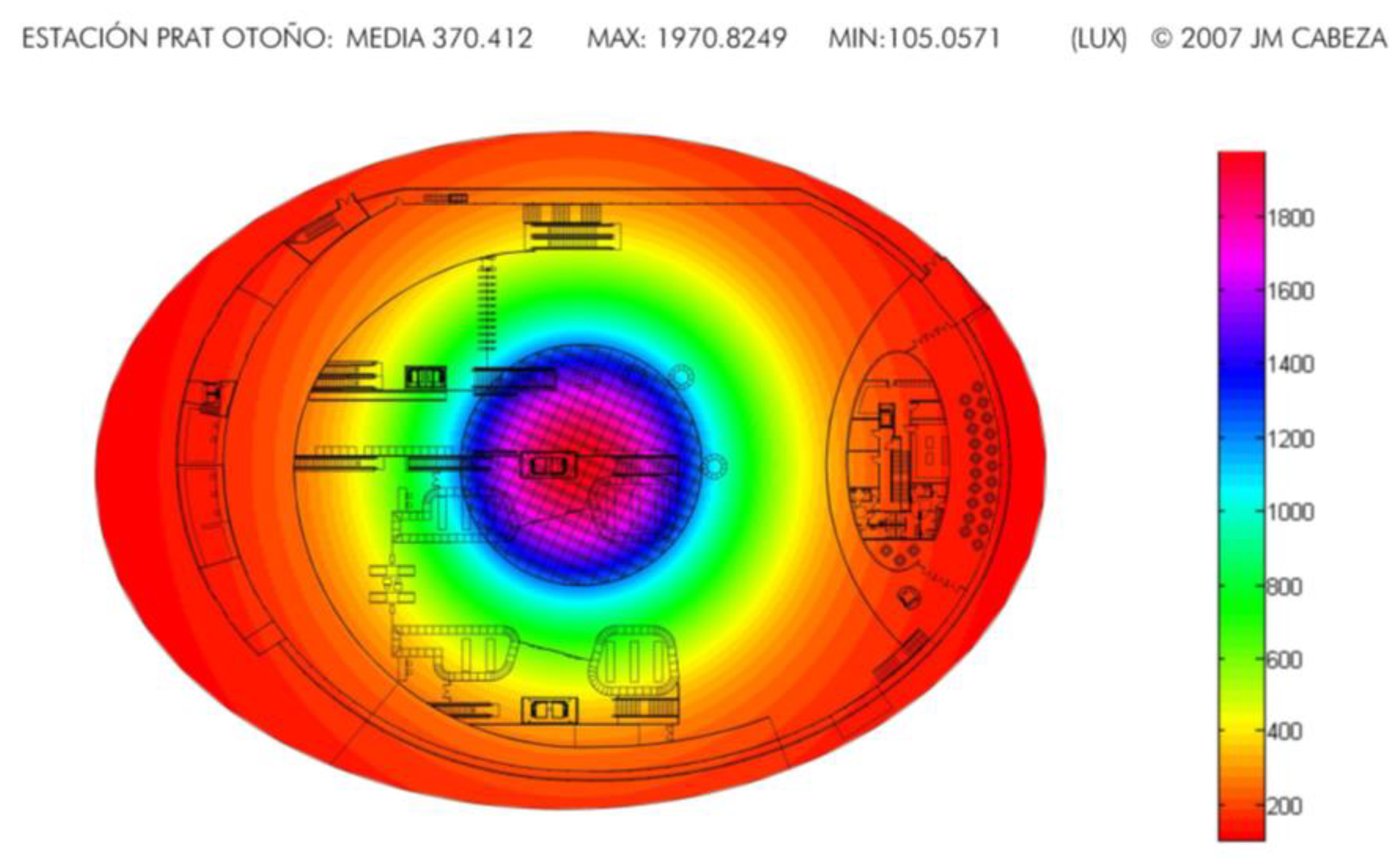
3.1.1. The Roman Pantheon

This is a well-known architectural paradigm in which we identify two sources of radiation, the oculus and a rotating solar patch depicted in the inside of the magnificent dome (Figure 3). Sectional simulation contributes to the understanding of this singular space.

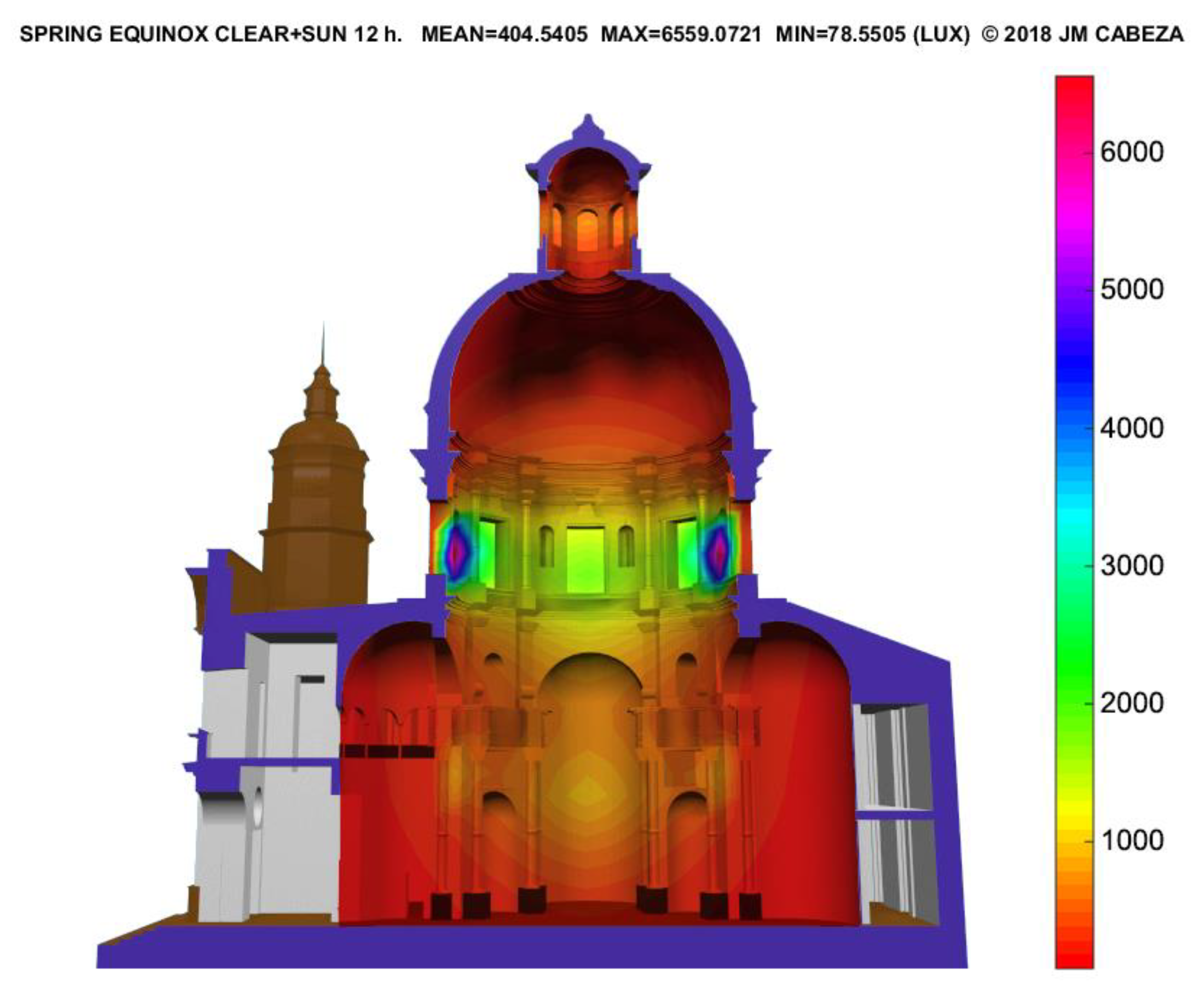
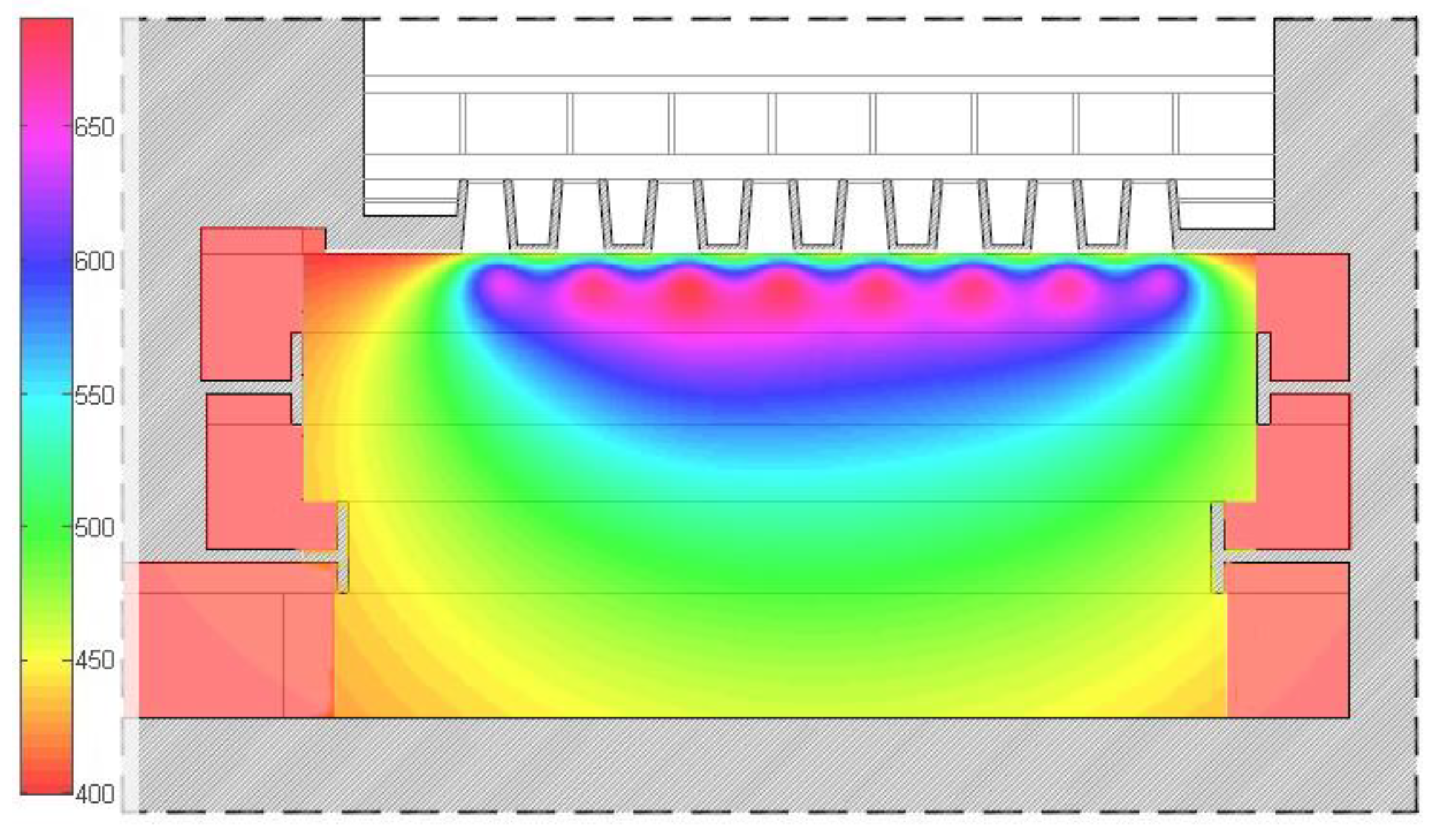
3.1.2. The Church of St. Louis of France (Seville)

It is an 18th-century baroque church in the historic center of Seville, possessing only eight clerestory windows and a lantern over the dome. Radiation here serves to enhance and extensive iconographic program for illustration of the Jesuit novices [8,11].

After the careful calculations performed by virtue of our software, we obtained the graphs presented in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 and the values of illuminance as output, on which we comment briefly in the following paragraphs.

In spring, the situation of luminous radiation is favourable; during the entire daylighting time, the average values are in the vicinity of 150 lux and values ranging from 200 to 300 lux are normally found (Figure 4). At noon (Figure 5), the mean illuminance is about 200 lux and a maximum of some 1000 lux can be obtained at most parts of the usable floor plan. The distribution of radiation is variegated but does not lead to excessive contrast, as it moves in crescendo from the threshold of 200 lux up to 500 in the altarpiece of the northern arm of the church, where sunrays fall around the beginning of spring.

During the warm season around late June, the illuminance values may reach 150 lux throughout the day (Figure 6), but at midday, some figures over 300 lux are registered.

The simulations reveal the adequate performance of light under the typical scenario in Seville, which is characterised by sunny skies ( Figure 6; Figure 7). Following the Spanish Meteorological Agency for the standard values in a year at the selected location, we completed the input parameters with the tool Energy Plus and the registers of the local weather institution. Outside winter, the occurrence of sunny skies is near 90% for the city of Seville.

The illumination’s vertical components are not too flat or steep and maintain an adequate angle that allows for a compatible perception of the displays that cover the surfaces of the church as was the baroque norm, but it is certainly not the case of the Pantheon (Figure 3) and the buildings that were directly derived from it or had to be accommodated in ancient Roman structures. We present the simulations of the section of the church for spring clear sky (Figure 7) and cloudy sky (Figure 8) respectively.

The dynamic characteristics of lighting are less acute for the rare situation of cloudy sky, but can still be noticed and have been validated through sensor measurements. The sensors were placed at regular intervals in the lower levels of the spaced and acquired registers for alternate periods of six months.

To summarize, the results presented in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show that the daylighting field is adequate, starting at a minimum of 100 lux, in plan for an overcast situation (less than 10% of the time). In other conditions, values of over 300 lux can be obtained and averages of 200 lux are safely reached in the core of the church for more than half of the daylighting hours.

3.1.3. The Church of St. Andrew on the Quirinal (Rome)

This church of elliptic plan is an important referent of Baroque architecture, which was constructed by G. L. Bernini also for the Society of Jesus [12]. Due to its singular shape, so different to a cuboid, it is difficult to simulate, but our tool is capable of analyzing such unusual curved geometries with advantage and precision (Figure 9).

In the sectional distribution of radiation, we can appreciate subtleties such as the role played by the lantern and the chapel of the saint with windows embedded in the wall and hidden from view in the outside (Figure 10).

The distribution in the plan is interesting not only because of the high intensities achieved, but also due to the subsidiary role played by the eight chapels that remain mostly in the dark, in contrast with the chapel of the saint in the minor axis of the ellipse and that is illuminated in a clearer way (Figure 11).

In the next subsection, we discuss in brief detail two paradigms of contemporary modern architecture: the Rautatalo building in central Helsinki by Alvar Aalto [13] (Figure 12) and the Glass House by Philip Johnson [14] (Figure 13).

3.2. Simulations of Contemporary Buildings by A. Aalto and P. Johnson

The Rautatalo atrium features 40 conical lightwells, revealed as circles in the ceiling that add a distinct type of illumination to this singular space conceived as a department store (now the venue for Nordea bank). Lighting levels are much reinforced in the plan and sections of the atrium, but the ceiling remains in stark contrast with the brightly illuminated circles and the rest of the surface [15].

Regarding the Glass house [14], a bolder simulation experiment was conducted since we studied different cases as if only one façade was glazed and, then, successively adding the other three façades step by step (Figure 13a–d). Thus, the contribution of each one of the four façades can be better appreciated. The first one is the southern façade (Figure 13a) and then north (Figure 13b), west (Figure 13c) and east (Figure 13d).

The second proposal that we consider interesting is glazing on the four faces but comparison with a window of half the height of the original (upper part) (Figure 14).

The Glass House by P. Johnson has a rectangular plan of 10 × 17 m, and its height is of 3.65 m; external intensities of radiation considered are the average in a clear spring day in New Canaan, Connecticut, USA, that is, 5000 lux to the South, 3000 lux to the East and West and finally 2000 lux in the north. The resulting illuminance is obtained at the floor level.

The reflection coefficients considered were set as: brick floor 0.2, grey ceiling 0.5 and glazed envelope at 0.3 since the transmittance of the glass was considered at 0.7. It is important to stress that, in order to calculate daylighting radiation, we did not consider external obstructions, annexed buildings or vegetation nor externally reflected sunrays. In this example, direct radiation was not taken into account.

The levels found in the case of daylight show that the highest values are in the vicinity of the glass wall but are significantly reduced towards the inner part of the home [16]. If there was one single glass wall, the distribution of light would be rather uneven, but as we add more glazed walls to the equation, luminous uniformity rises and visual comfort is improved.

It is noticeable that the amount of light available is rather high, reaching 1193 lux on average. In this sense, we produced the simulation of Figure 14, in which we reduce the height of the window to a half as if we had an opaque window sill of 1.8 m.

By reducing the size of the openings, we can see how the illuminance is reduced to a half, from 1193 lux with full windows to 606 lux as average, in Figure 14a. Obviously, a totally glazed façade reinforces the connection with the environment and the landscape, but it is still interesting that, with half the size of the glass, there are significant levels that offer optimum visual comfort and save energy as well. The conclusion is that, if not for subjective design considerations, the excess glazing would be redundant from a radiation point of view [17,18,19,20].

In the last subsection of this section, we present three unbuilt projects, namely, a cultural centre in San Sebastian (Donosti) by Arch. Pablo Rico Pérez, the railway hub at Barcelona’s airport that was the first entry at a competition in 2010 by Archs. Cesar Portela and Antonio Barrionuevo with assistance from J. Cabeza-Lainez, and finally a project of artificial lighting at a model school by Arch. Lorenzo Muro.

3.3. Simulations of Architectural Projects

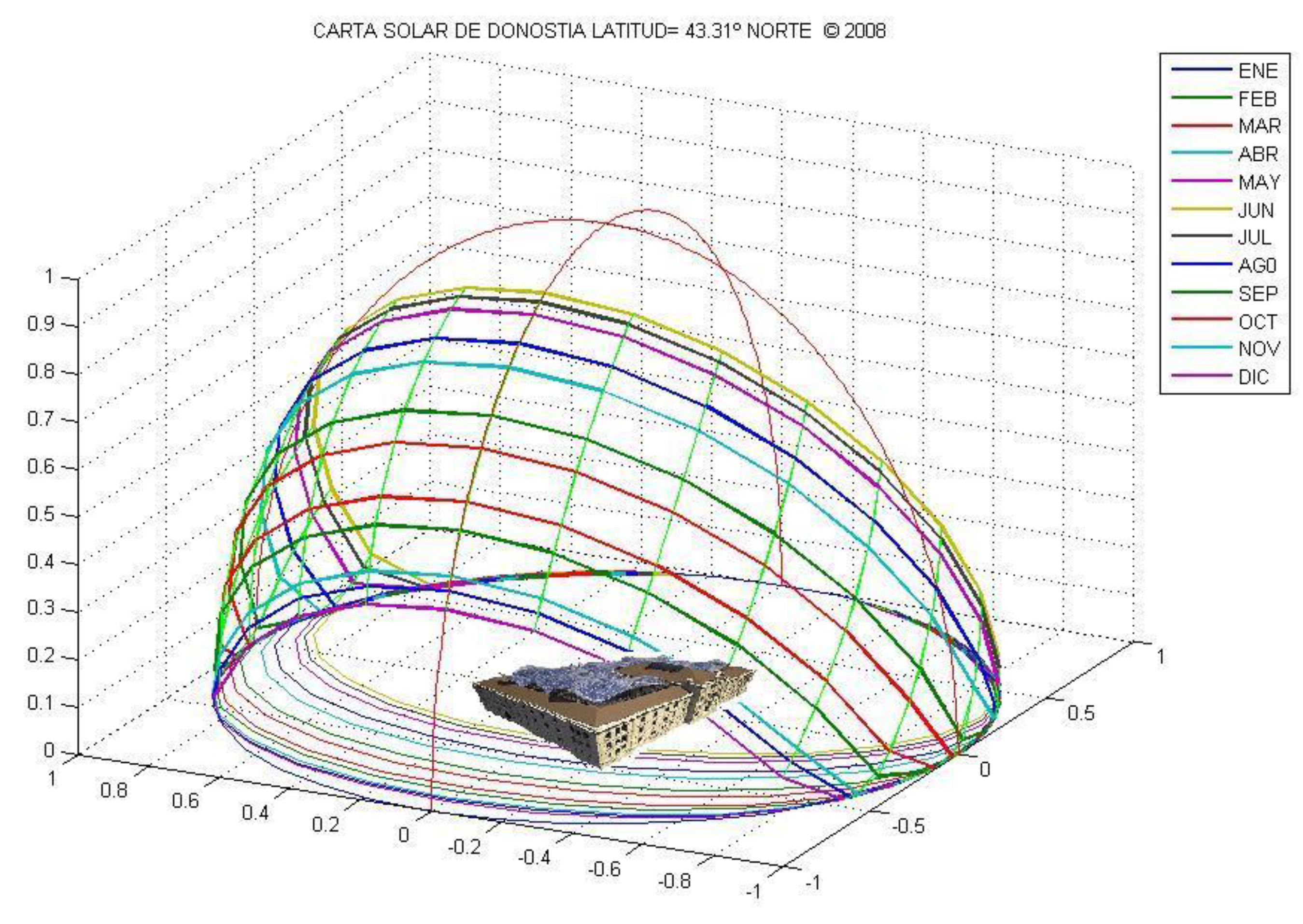
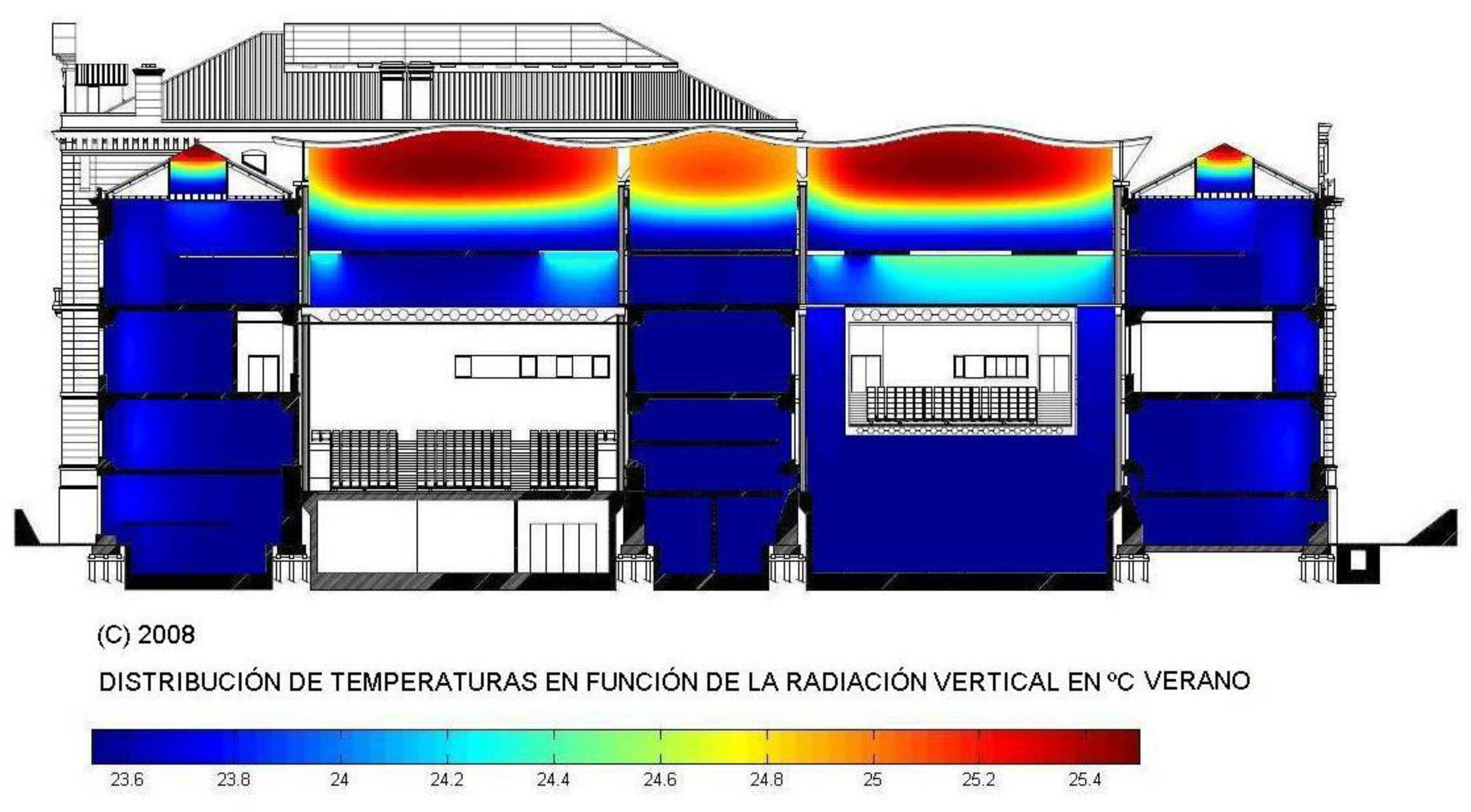
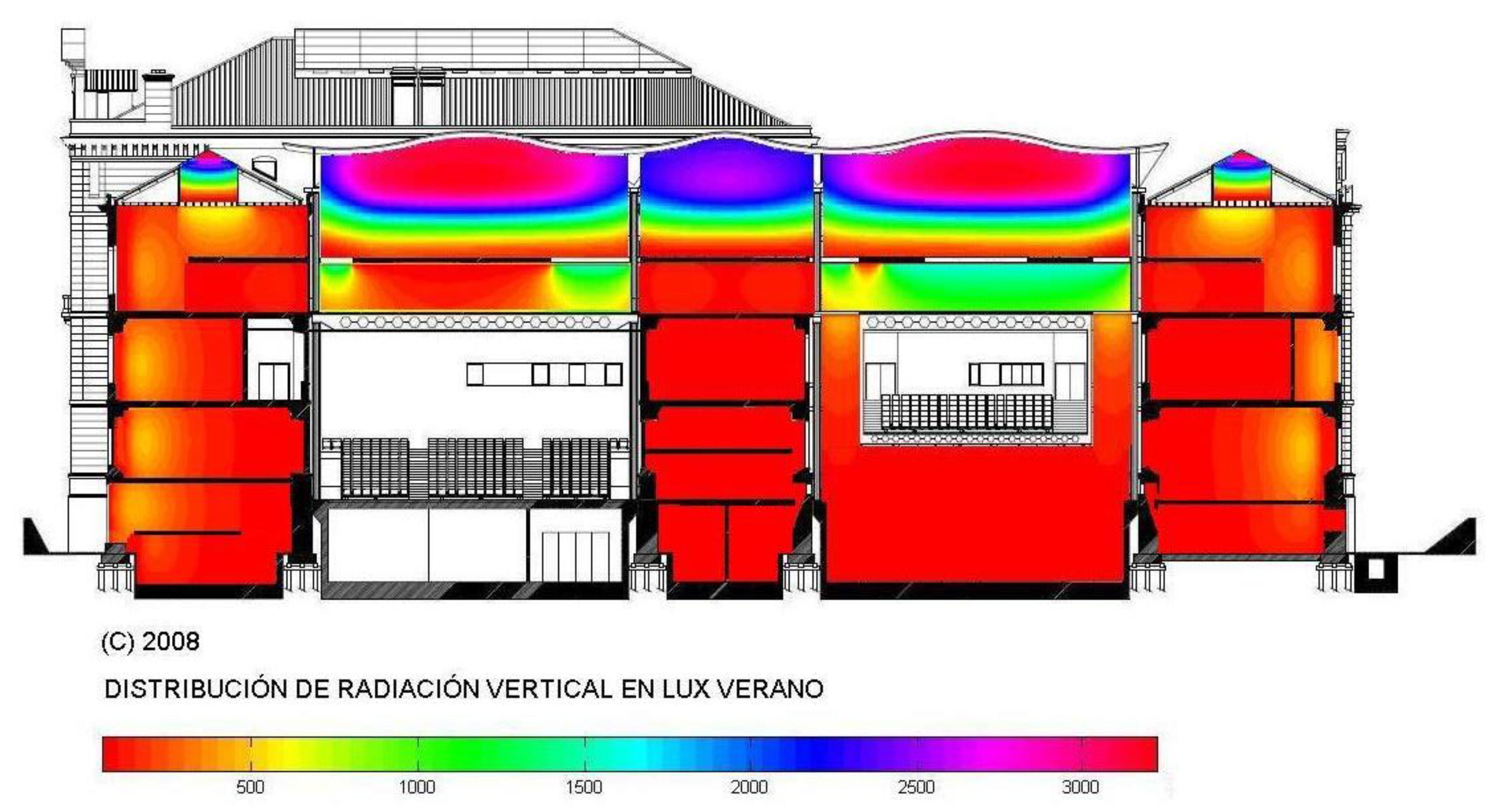
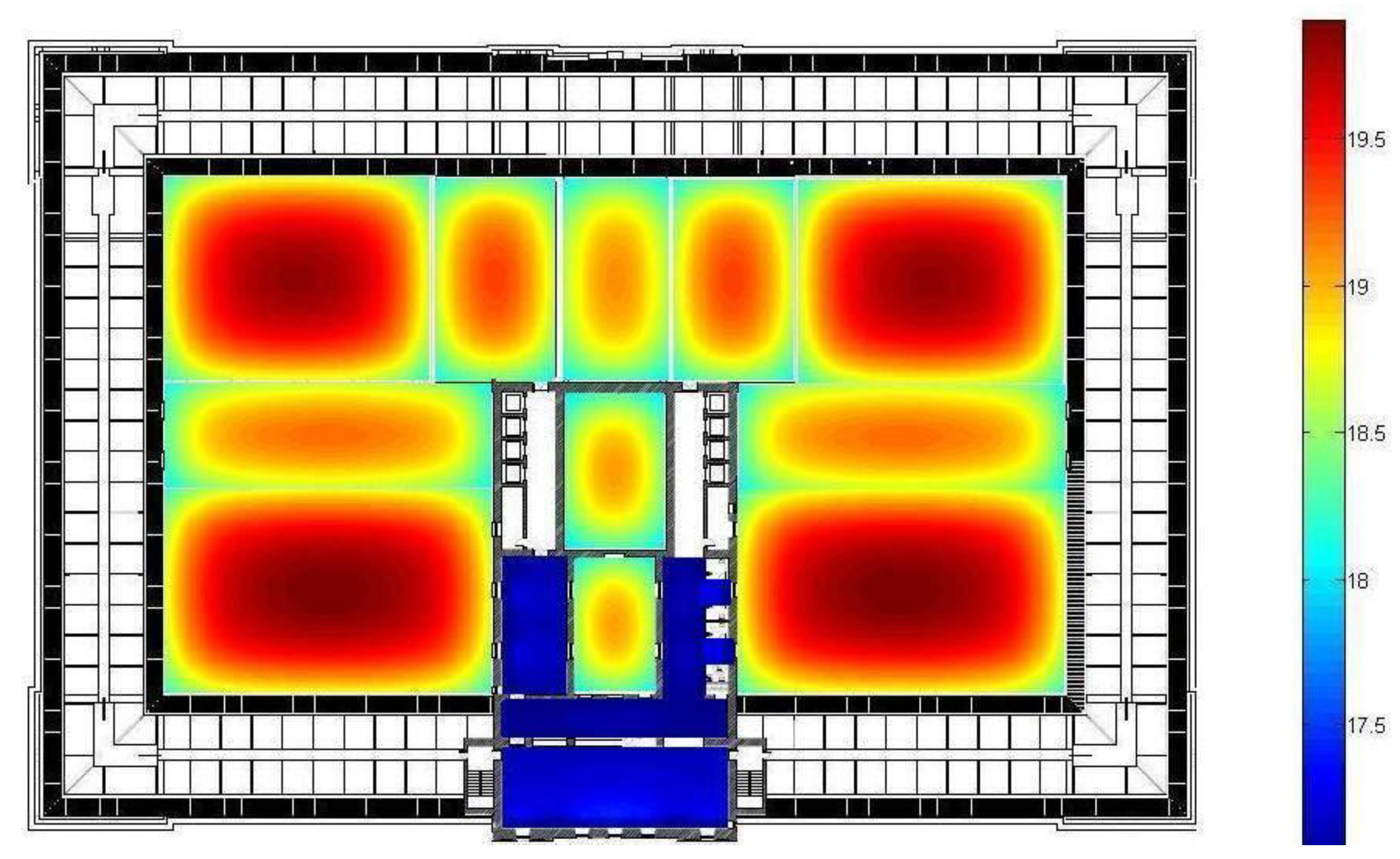
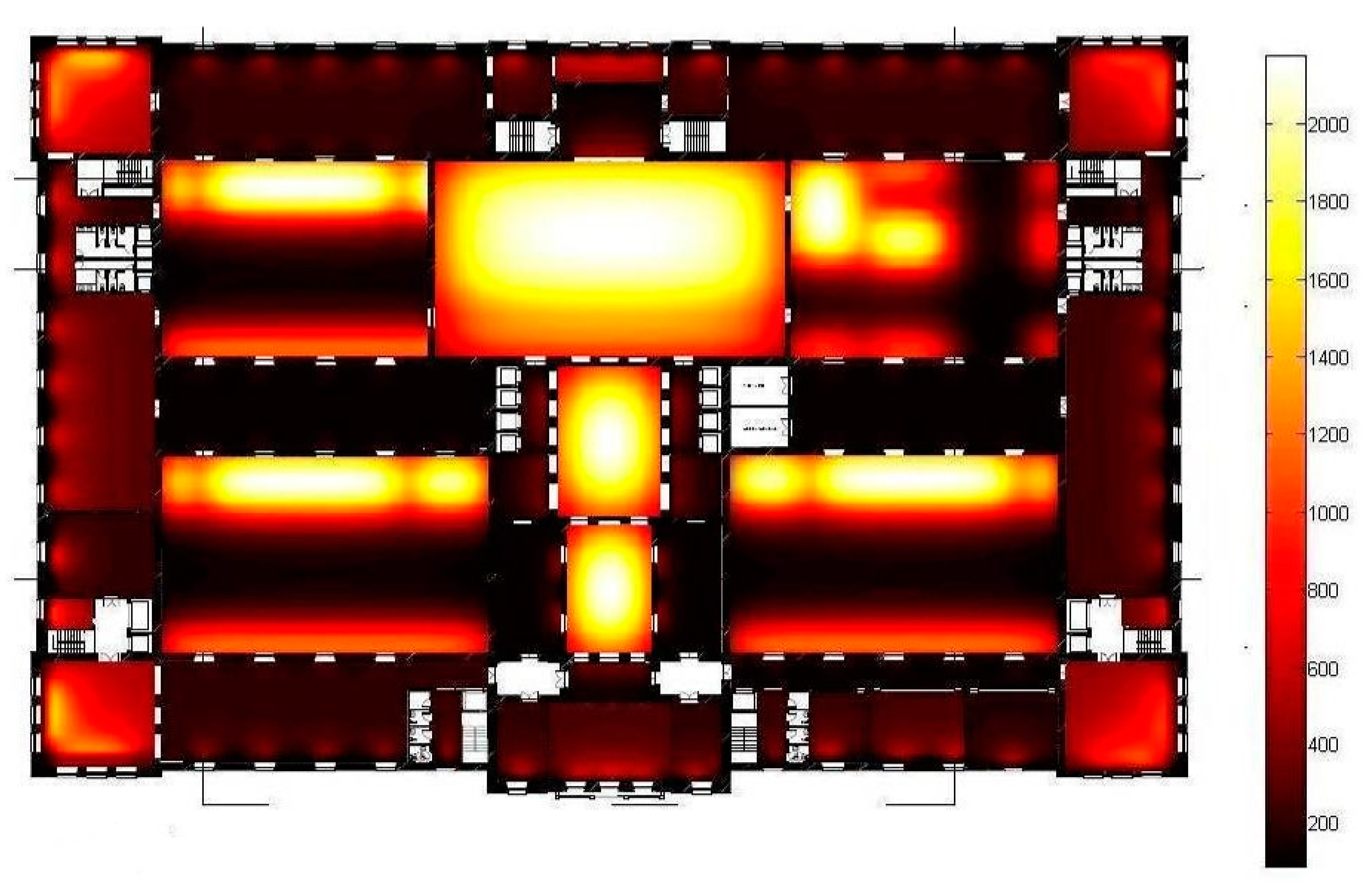
3.3.1. Conversion Project of an Old Tobacco Factory in Donosti (San Sebastian) into a New Cultural Center Called Tabakalera

This project was a competition entry in which all the refurbishments proposed were strictly based on simulations with DianaX. In this case, the simulation included temperature levels to be achieved by the implementation of diverse strategies (Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21).

The project is organized through former courtyards that are now partly covered and reused, and include PV systems on the ceiling and new types of filters for radiation [21,22,23]. It follows the inner distributions of temperature and radiation both in the section and plan Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21.

3.3.2. Project for a Transport Hub at Barcelona Airport

This project included the railway station as well as the subway and buses, and it was meant to be a hub for all transport systems in the airport. It was named Campo dei Miracoli (Italian for field of miracles) [24,25,26,27]. Its main feature was a covered elliptic atrium with special blind systems to control the light in the lobby of the central station [28,29,30] (Figure 22, Figure 23 and Figure 24).

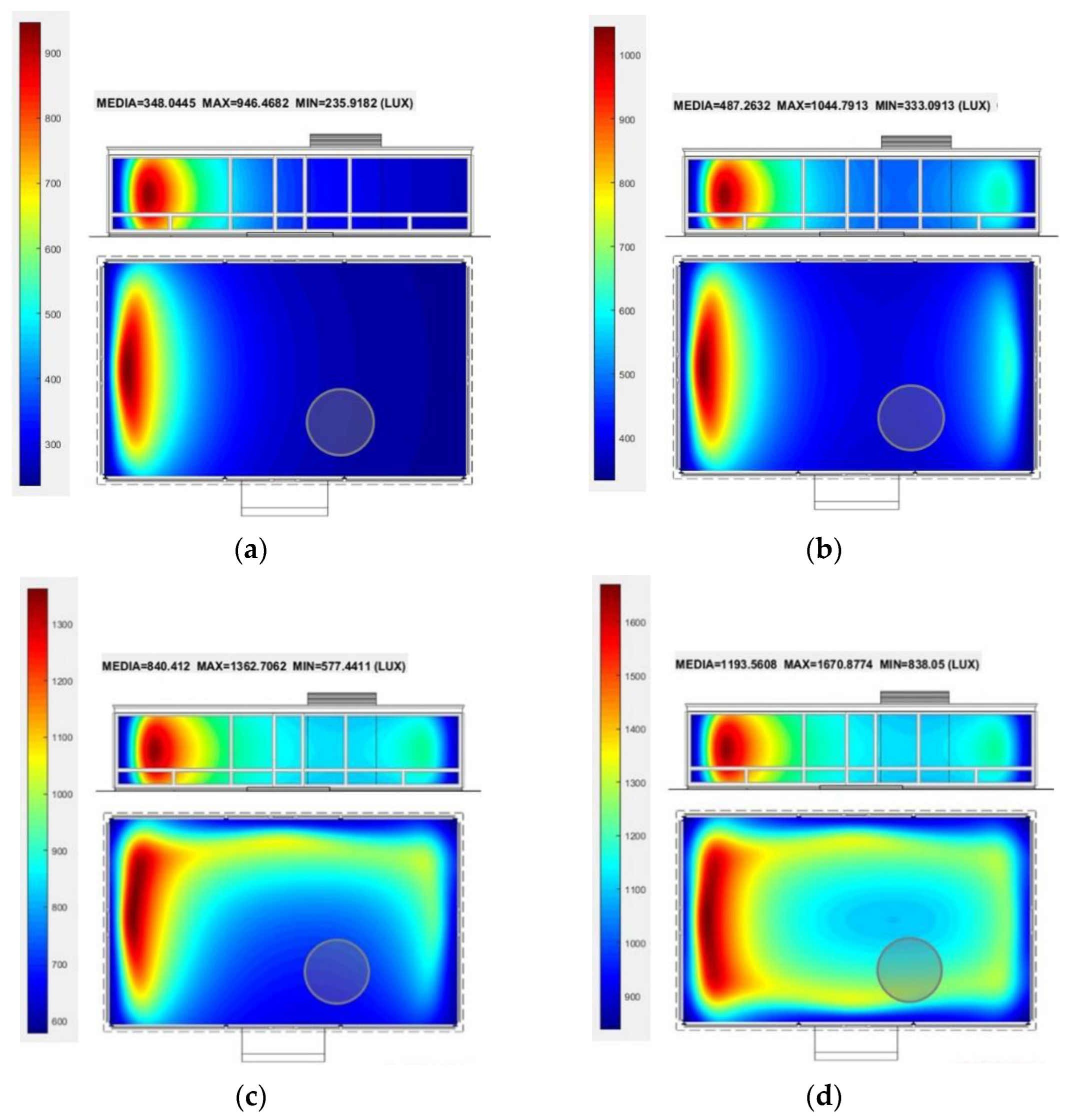
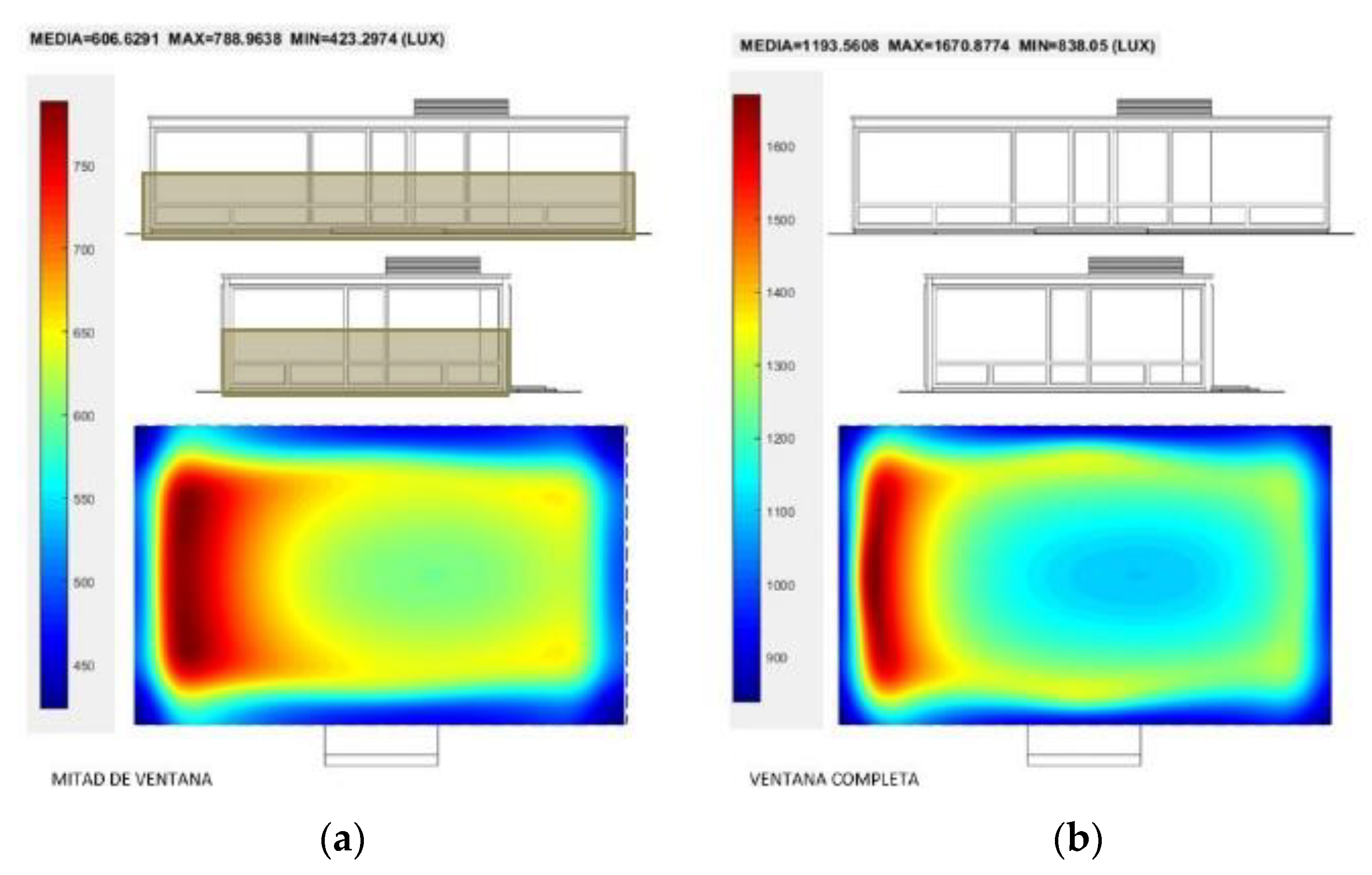
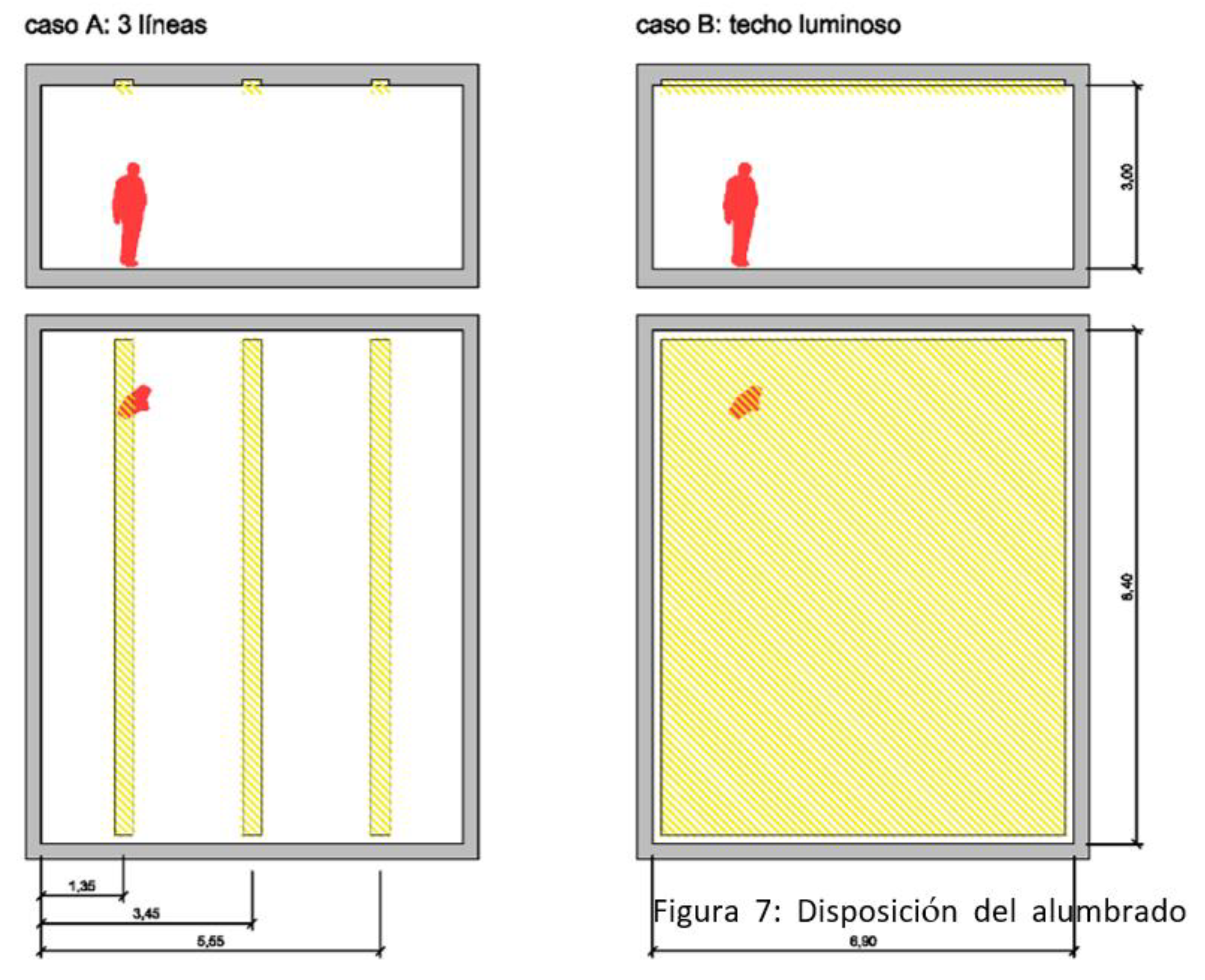
3.3.3. Artificial Lighting of School Comparing Two Types of Luminaires and Our SOFTWARE against Lightscape 3.2

In this example, we can assess how interior lighting is viable with surface source instead of the customary linear sources.

Firstly, we introduce a model classroom, which has specific regulations in Spain, including directions related to its dimensions and to the lighting systems employed. Two different conditions were simulated: a continuous lighting ceiling (floodlight) and three lines of luminaires distributed in the ceiling [31]. Both configurations have in origin the same total luminous flux (total).

The classroom is defined as an open space with a rectangular plan of 6.90 m. by 8.40 m. and a height of 3.0 m. The walls have a smooth finish with the usual reflection coefficients and no daylight was considered in the example. Such coefficients are: ceramic floor 0.2, walls 0.5 and ceiling 0.7. The luminaires are composed of LED panels with a diffuser. The working plan is set on the floor (Figure 25)

The illuminance level to be achieved in the classroom is of 500 lux (School regulations and UNE 12464.1-European norm for interior lighting).

1

Linear lighting. Three line fixtures of luminaires are set on the ceiling and orientated longitudinally and parallel to the wider side of the room. The dimensions of such lines are fixed at 0.30 m. by 8.40 m and 12,600 lumens. In the classroom, there are three lines 2.1 m apart from axis to axis and centred with respect to the Y-axis (Figure 25).

2

Surface source. A luminaire covering the whole breadth of the ceiling is proposed with dimensions 6.9 m by 8.40 m and to a height of 3 m. This luminaire has 37,800 lm.

As can be observed in the results output (Figure 26), the luminous ceiling can be an option with similar levels on the floor as compared with the linear source, but the distribution is much more homogeneous, especially in the upper section of the walls (

Table 1. Surface lighting vs. linear lighting calculation with DianaX. Prepared by the authors.

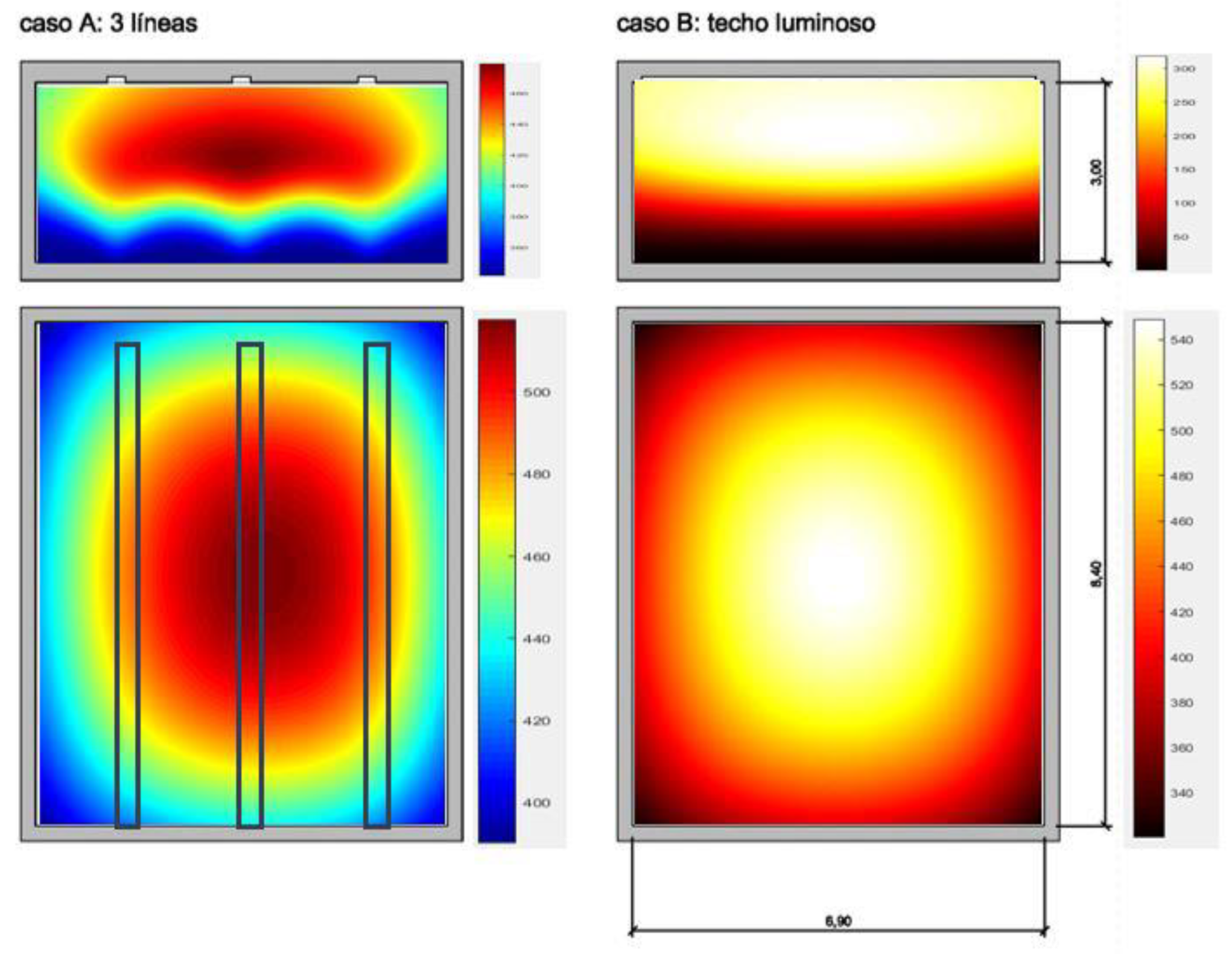
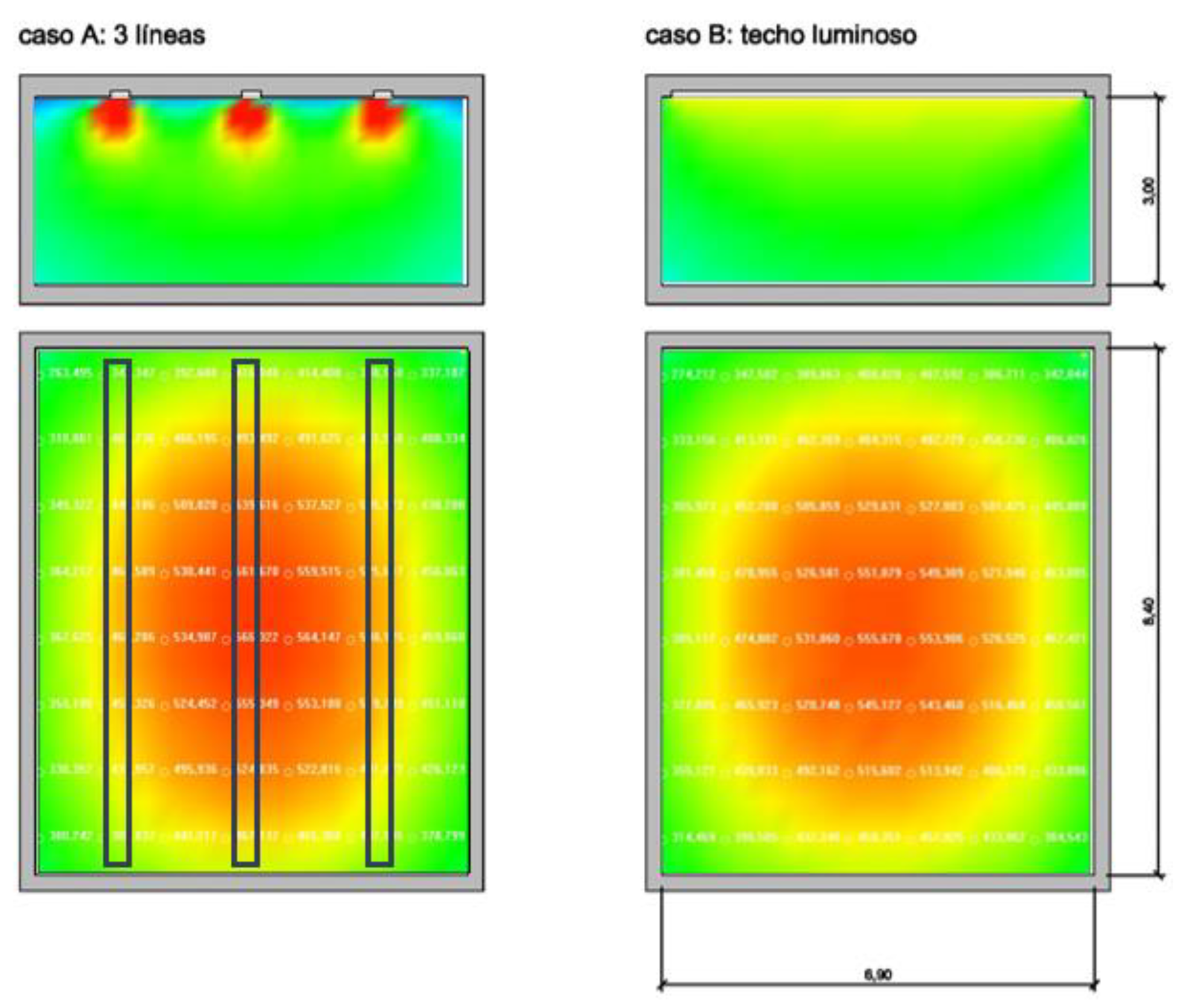
3 lines (0.30 × 8.40 m)	surface (6.90 × 8.40 m)
12600 lm each line	37800 lm surface
5000 lx each line	652.17 lux surface
Reflection 0.70 0.50 0.20	Reflection 0.30 0.50 0.20 (reflection from the ceiling = translucent glazing 30%)

;

Table 2. Superficial lighting vs. linear lighting. Calculations results with DianaX by Lorenzo Muro and Joseph Cabeza-Lainez.

Em [lx] 466	Em [lx] 454
Emin [lx] 390	Emin [lx] 320
Emax [lx] 518	Emax [lx] 550
Emin/Em 0.837	Emin/Em 0.706

and Figure 26). Such quality is particularly important in classrooms because it is in this area where the blackboards are usually located [32].

We do not possess evidence of the classroom provided with luminous ceiling in Spain, but it is a system used in similar environments, such as offices, and the architectural lighting pioneer P. H. Moon often commented on them. A great deal of buildings representative of the modern movement of authors such as Mies van der Rohe, Eero Saarinen or SOM [33] have offices illuminated by continuous luminous ceiling. In most of them, the lighting designer is Richard Kelly (1910–1977), a forerunner of architectural lighting. There are instead thousands of classrooms illuminated by linear sources since the regulations demand it. However, starting from our simulations, the rules can be reformulated in search for a better visual environment (Figure 27 and

Table 3. Surface lighting vs. linear lighting. Calculations with Lightscape 3.2. by Lorenzo Muro.

Em [lx] 452	Em [lx] 452
Emin [lx] 221	Emin [lx] 230
Emax [lx] 571	Emax [lx] 559
Emin/Em 0.489	Emin/Em 0.509

).

To confirm the data obtained with other programs frequently used by designers, the same calculations were analysed with the software Lightscape 3.2, obtaining very similar values in both cases and thus we considered the DianaX tool as a valid tool for radiative simulation.

4. Discussion

In this article, we showed that several approaches of simulation, involving environmental properties, can be employed satisfactorily to improve the design of spatial configurations without disregarding the intangible values of the buildings considered. Such kind of holistic approach is novel in the realm of Architecture, Heritage and especially Project Design [34]. This is the result of a series of experiences that we have launched on a new field that we have called scientific design in the sense that the decision-making process is informed by objective determinations founded on science [1,5].

In this paper, we demonstrated that our simulation tool can be applied in many different situations that appear in the design of architectural spaces, be it from the past, the present or even future projects [35,36]. Several branches of building activities, for example, can be enhanced in the provision of supplementary means for energy or other aspects. Other procedures and tools have failed in this task because they do not possess versatility to include geometries other than the parallelepiped and need to assign any possible form to it. Additionally, they do not deal with direct sunlight referring only to the sky condition, which makes calculations rather clumsy and variable [37].

What is dominant, on the contrary, in our method is the thorough knowledge of the geometries involved in the problem and the careful insight into the mathematical definitions in which these forms are enclosed. Some especially crafted forms could prove more appropriate than others to convey the forces that allow for the habitability and amenity [38,39] of the designs that we are bound to be created when facing any new development within urban or landscape boundaries.