Abstract
During the execution of construction projects, uncertain events, such as delays, prolongations and disruptions of project activities, have the potential to cause a significant deviation between the planned and realized state of a project. As a result, progress on important project objectives can decrease and this leads to critical delays as well as heavy profit loss. For this reason, we propose the implementation of the customized evolutionary algorithm to generate resilient baseline schedules which include a sufficient number of time floats to absorb the negative impact of uncertainty. This way, the baseline solution is searched as a trade-off between project duration, its final profit and the overall baseline stability. The proposed algorithm is applied to real construction project data and the results of the analysis suggest improved stability for resilient baseline schedules. Application of the genetic algorithm to solve the existing multi-objective problem enables practical implementation of new technologies and methods in construction management. Resilient baseline schedules can be used in an uncertain environment to achieve more accurate predictions and support decision making in the areas of construction scheduling and costing.
1. Introduction
Construction projects are performed in complex dynamic surroundings where uncertainty and risk can negatively affect the achievement of time, budget, and quality goals [1]. Therefore, in the construction industry, it is extremely important to effectively manage project objectives such as duration, cost and quality, as well as the associated uncertainty [2]. For this reason, a realization of forecasted project goals depends on calculating reliable baseline schedules, where the goal is not only to minimize project duration or maximize final profit but also to minimize the deviation between the planned and realized state. One way to overcome uncertain disruptions in the baseline schedule is to act proactively and build resilience into the scheduling process [3].
Resilience in a broad context can be determined either as the speed to recover an equilibrium state or as the magnitude of disruption that can be absorbed within the original equilibrium state [4]. Thus far, research in resilient project scheduling has relied more on the second interpretation of resilience, investigating the proactive methods for building reliable baseline schedules with the increased ability to absorb the negative impact of uncertainty throughout the execution state.
In recent years, there have been several research studies that show the importance of proactive resilience in construction scheduling under uncertain conditions. Most of the studies define the project scheduling with the resilience criteria as the complex trade-off between the stability of a schedule and satisfaction of other project objectives, such as makespan minimization [4,5,6,7]. Accordingly, resilience is built into the baseline schedule by inserting sufficient time floats which serve as time buffers for absorbing the negative impact of uncertain disruptions.
Considering the scheduling problem for construction projects, a prevailing method in academic studies is to build upon the basic resource-constrained project scheduling problem (RCPSP). This is a fundamental and challenging problem in project scheduling, applicable to construction management, as well as to other industries, where the principal concern is how to organize a considerable number of activities under limited resources for the highest performance. The application of the underlying RCPSP method to resilient scheduling is inherent in designing reliable baseline schedules for construction projects. For a review of the extensive literature in resource-constrained scheduling problems, we refer to Brucker et al. [8], Pellerin et al. [9], Hartmann and Briskorn [10], Franco-Duran and Garza [11] and Habibi et al. [12], for example.
The first study of resilience in proactive project scheduling with resource constraints and uncertain activity durations considers resilience as the magnitude of disruptions that can be absorbed before the schedule departs from its equilibrium [5]. In their research, authors [5] explore the equilibrium of a baseline schedule as the duration-related concept: an equilibrium state represents a makespan for which the project’s duration is minimized, yet the realized performances are stable. Therefore, the baseline solution is considered to be more resilient when there is less makespan tardiness and the deviation of start times is lower. In another study, the concept of resilience has been applied to a construction project case study [4]. This time, a multi-objective scheduling framework was developed under generalized precedence relationships and the resilience criteria. The stability of a baseline schedule is improved through a combination of time buffers and activity floats, and resilience is again regarded as a magnitude of disturbance absorption before the project baseline changes its structure. Proactive resilience in construction scheduling has also been analyzed by a recent study [7], where the equilibrium of a project is extended to measure not only time deviation but also the difference between the planned and realized profit from the contractor’s perspective. This way, resilient project scheduling has been enriched by the comprehensive optimization model, which puts baseline scheduling under uncertainty into a more practical setting for complex construction projects.
No matter which technical definition is preferred to describe the resilience of a baseline schedule, an important question remains: how to reliably measure the negative impact of disruptions that can be absorbed into the original solution? One approach in proactive scheduling is to employ simulation techniques to approximate the expected performance under uncertain conditions. This way, the deviation between planned and realized states can be calculated [5]. However, this approach is time-consuming, especially when it comes to integrating simulation and optimization practices. Therefore, the practical solution is to employ a surrogate measure (SM) which could estimate the behavior of the baseline schedule under uncertain conditions. The current literature proposes different measures to illustrate the resilience of a project, such as slack-based functions [5], the combination of activities’ floats and risks associated with the completion of a project [4], and weighted resource-constrained free floats [6], among others.
Although progress has been made in investigating project resilience, the application of a comprehensive resilience framework on complex construction projects remains limited. This research, therefore, investigates a solution technique for the latest optimization problem [7] when it comes to resilience scheduling in construction projects. We have developed a customized genetic algorithm (GA) to enable the solving process for the large project networks in the context of proactive resilient scheduling. The purpose of this study is to assess the applicability of the existing optimization tools and techniques on the problem of resilient scheduling, where the systems’ equilibrium is appraised in relation to both makespan tardiness and the final profit deviation. Moreover, one of the central questions examines whether the baseline solutions with higher SM values show a better response to uncertainty. This analysis is based on real data from the construction project, and it will be discussed in more detail in the following chapters.
2. Methods
2.1. Resilient Scheduling Framework
Figure 1 illustrates the application of the framework for project resilience in proactive scheduling in the construction industry. Geambasu [13], who was first to introduce the concept of project resilience, recognizes resilience facilitators at each management level. For instance, the legitimacy and common vision of project objectives are recognized as resilience enablers on the strategic level. Accordingly, the project objectives for construction schedules are set at the highest level of the proactive resilience approach. The long-term vision is to minimize the duration of a construction project while maximizing the final profit.
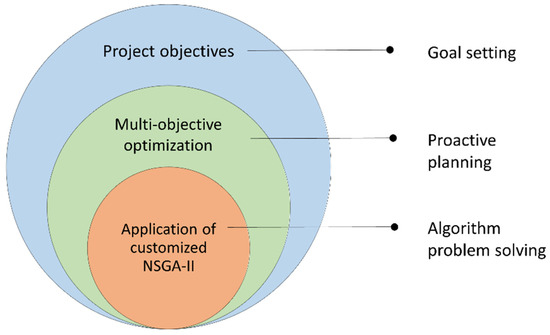
Figure 1.
Underlying levels of proactive resilient scheduling in construction projects.
In the next stage of resilience build-up, the multi-objective optimization problem is adapted to incorporate stability into the proactive scheduling process. Previous studies have proposed the explicit mathematical model which aims to improve the probability of reaching project objectives [7]. The authors have employed the resilience surrogate measure as an additional optimization objective in the underlying problem of simultaneous makespan minimization and final profit maximization. The idea is to provide enough resource-technology float time in the baseline schedule so the impact of uncertainty can be absorbed as much as possible. This is again aligned with the fundamental project resilience framework [13], where proactive planning is recognized as one of the main resilience facilitators at the intermediate management level.
Finally, at the structural level of project resilience, Geambasu [13] suggests the use of advanced technology to reduce the overall complexity. Due to the rapid development of technology for combinatorial optimization, the size and scope of problems that can be solved continuously increase [14]. Therefore, by using state-of-the-art optimization technology, we were able to customize a genetic algorithm and propose a novel solution process for the complex problem of proactive resilience scheduling. We have applied the Non-dominated Sorting Genetic Algorithm-II (NSGA-II) [15] to the construction project scheduling problem since the considerable amount of input information requires the use of metaheuristic techniques in order to obtain a feasible solution in computationally effective time. Due to its versatility and usability, the NSGA-II has become one of the standard approaches to solving various scheduling problems in the construction industry, which has been tested in different studies [16]. Some of the recent models in the construction scheduling which have been solved by NSGA-II focus on optimizing other important aspects along with the project makespan minimization, such as material procurement [17,18], crew planning [19], project prioritization [20], location and workspace congestion [21], as well as project financing [22]. Due to metaheuristics’ efficiency in similar construction scheduling problems, we decided to apply the NSGA-II algorithm from the open-source framework pymoo [23] that allows customization of the algorithm to the user needs.
The main contribution of this paper is an application of the customized genetic algorithm to the existing problem of resilient project scheduling. The concise workflow of the NSGA-II algorithm applied to the problem of resilient scheduling for construction projects follows the general procedure depicted in Figure 2. In a nutshell, an optimization problem is represented as the extended RCPSP framework: the optimal baseline schedule tends to simultaneously minimize project duration and maximize final profit, while being resilient to uncertain disruptions. A resilient scheduling problem, for which we propose the solving algorithm, was introduced in a recent research study [7]. However, due to the clarity and repeatability of solving process, we’ll explain the problem in more detail in Section 2.3. Subsequently, the multi-objective optimization problem is being solved by the proposed genetic algorithm, which is thoroughly explained in Section 2.5.
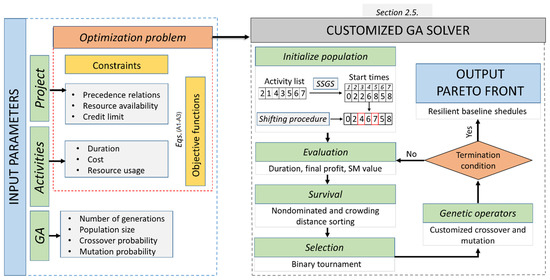
Figure 2.
General workflow considering the application of GA on the resilient scheduling problem for construction projects.
Once the termination condition for the customized NSGA-II algorithm is met, the result is obtained as the Pareto front of multiple baseline schedules. Following the proposed framework, we were able to apply the customized GA to the existing construction project and validate the solving process. Validation on a test case is shown in Section 3.
2.2. Optimization in Resilient Scheduling
Previous research on resilient project scheduling is largely based on adopting the optimization approach to overcome the adverse effects of uncertainty. As can be seen from several studies [4,5,6,7], the prevailing method is to search for a proactive baseline schedule through the optimization process, so the output solution contains enough time slacks or time buffers that would absorb the anticipated disruptions. Thus far, different multi-objective mathematical models have been proposed in which one or more of the objective functions tend to improve the project resilience through the use of different surrogate measures. Some of the recent studies on optimizing project schedules with resilience criteria are briefly summarized in Table 1.

Table 1.
Summary of recent papers on proactive resilient scheduling in project optimization.
The previous solution techniques for resilient scheduling with finance flow calculations included were focused solely on exact procedures [7]. Due to the numerical complexity of the underlying RCPSP problem, which is known to be NP-hard [24], the previous study [7] was restricted to solving only problems of limited size. Therefore, the present research facilitates resilient scheduling in real construction projects, since the application of the customized NSGA-II algorithm enables solving the problems with a considerable amount of input variables.
2.3. Optimization Problem
This research is a follow-up study on the previously introduced multi-objective resilient scheduling problem in the construction industry [7]. The proposed algorithm is applied to the existing optimization problem, for which the full mathematical model is provided in Appendix A. During the optimization process, the Pareto front is searched with the goal of determining resilient baseline schedules. The proposed solving algorithm examines the vast solution space to simultaneously satisfy following objectives:
- Minimize the duration of a project;
- Maximize the final profit (i.e., minimize the overall expenses);
- Maximize the surrogate measure for resilience.
Considering the calculation of surrogate measure for resilience, the idea is to maximize the weighted sum of resource-technology free float , for all activities in the set of project activities , so the floats are distributed properly throughout the baseline schedule. Therefore, in order to obtain SM value, we multiply the float amount of each activity by its weight wi, as shown in Equation (1).
Calculation of the value means that we determine the amount of time for which an activity can be prolonged without postponing the start times of succeeding activities. At the same time, non-violation of both precedence and resource constraints must be ensured. The weights wi are obtained by summing , , and , which are expressed as shown in Equations (2)–(6), respectively.
Finally,
Notice that:
- Equation (2) calculates the relative number of successors per activity, . The number of both direct and indirect successors for the activity is divided by the number of all activities in a project (both dummy start and dummy end are included);
- Equation (3) measures the relative duration of the activity, ;
- Equation (4) states the relative cost of the activity, ;
- Equation (5) determines relative resource usage as required by the activity, .
- Equation (6) calculates the weight of the activity, .
As can be seen in [7], by weighting the resource-technology free float , resilience in the baseline schedule is built properly since it is more important to provide bigger to the activities which are considered as more prone to the negative impact of uncertainty (activities with the high number of successors, longer and more expensive activities, activities with high resource consumption).
Considering the optimization constraints, they refer to the following:
- Each activity, including the dummy start and end, can be started only once;
- Precedence relations between activities must be respected;
- At the end of each month, the cumulative cash gap (before receiving the payment from the investor) must not exceed the permitted credit limit;
- Resource constraints must be respected at all times;
- No pre-emption of activities is allowed.
To determine the final profit from the role of the contractor, we have followed the established finance flow calculations for the construction projects as seen in the existing literature [25,26].
To the best of our knowledge, this is the first study to employ the NSGA-II algorithm to the problem of resilient scheduling, if resilience of the baseline schedule is regarded as an increased probability of reaching two project objectives: expected due date and profit. This way, the budgeting of the baseline schedule is considered along with the scheduling phase, providing an additional level of financial stability in the baseline schedule [7]. According to [22], finance requirements should be regarded as a critical resource that contractors in the construction industry must timely procure. Otherwise, due to lack of finances, contractors may find themselves unable to execute important construction activities, which in turn could cause negative impacts both to reaching project milestones and respecting the financial requirements of the project.
2.4. Research Design
For this research, we used the Python programming language and pymoo open-source framework [23] to develop the customized algorithm for solving the multi-objective problem of resilient project scheduling. The general framework of solving process is shown in Figure 3.
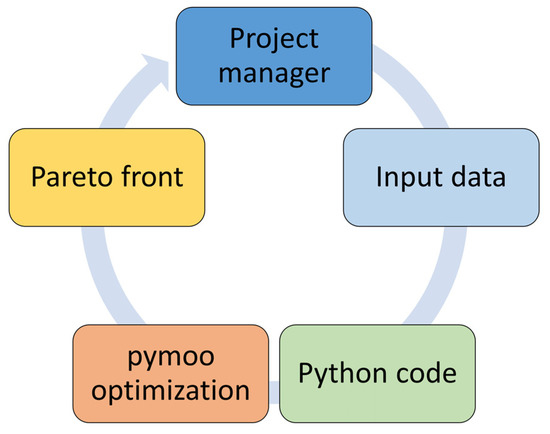
Figure 3.
Conceptual framework for solving the multi-objective resilient scheduling problem.
First, the solving process begins with a project manager who is required to input project data (e.g., project start time, list of activities and their precedence relations, duration time and direct cost for each activity, resource consumption and availability, financial requirements for the project, etc.). Gathered data are loaded into the Python programming code, which is based on the existing mathematical model [7]. After that, the optimization problem is solved by the customized NSGA-II algorithm from the pymoo open-source framework. This algorithm will be explained in more detail in the following section. Finally, the result is obtained as a Pareto front of solutions, which is represented by several baseline schedules with different values of makespan, profit and resilience, i.e., different objective values. At the end, a project manager is responsible for reviewing the obtained solutions and selecting the most suitable baseline schedule according to project requirements.
2.5. Customized Genetic Algorithm
Genetic algorithms, which belong to the larger class of evolutionary algorithms, work with a population of solutions, so the diverse set of Pareto solutions can be found in one single run of the algorithm [15]. In this research, we customized the NSGA-II to solve the problem of resilient scheduling in the construction industry.
2.5.1. Initialization for the Genetic Algorithm
The procedure of solving the multi-objective problem with a genetic algorithm starts with generating an initial population. Visualization of the initialization process is illustrated on a simple example in Figure 4. Considering the common metaheuristic approach in solving RCPSP problems, which is to operate on a representation of the schedule rather than on the schedule itself [27], the initial population is created at random, where individuals are represented through precedence feasible activity lists. Regarding accepted practices in project scheduling, most of the genetic operations in the proposed algorithm are performed on the activity list for each individual in a population. However, due to the sensitivity of the underlying problem, our approach calls for a meticulous examination of slight changes in a baseline schedule. Therefore, every individual in a population is required to consist of two main parts: the first is the precedence feasible activity list, while the second represents a particular baseline schedule built from the activity list itself.
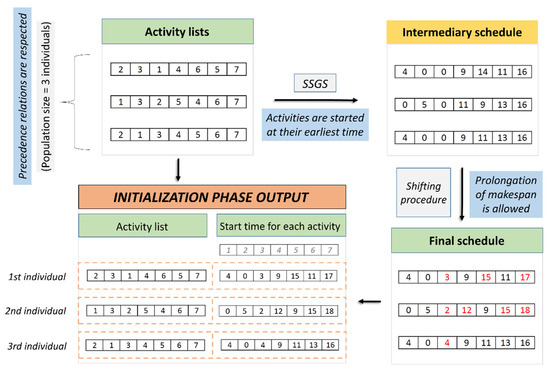
Figure 4.
Another common approach to building a baseline schedule is to utilize the parallel schedule generation scheme (PSGS), which iterates over the decision points in time, represented by completion times of previously scheduled activities [28]. However, in this research, serial schedule generation scheme (SSGS) is selected over PSGS because the latter method searches in a smaller solution space than the former, so the optimal schedule may not be found when considering a regular performance measure, such as project minimization [29].
Another commonplace procedure is to use SSGS to schedule the start of each activity for the earliest feasible moment. This procedure would make sense if we were searching only for a minimal makespan. However, the underlying resilient scheduling problem may guide the search for optimal solutions beyond the minimal duration of a project: it is highly possible that a somewhat prolonged schedule will have a better resilience measure due to the presence of enough time floats in the baseline solution. Other than that, numerous technological constraints in construction projects bind the solution space in which activity lists are searched for, resulting in a relatively small number of precedence feasible combinations of activity lists.
For these reasons, in our research, we allow the prolongation of the schedule originally built by the SSGS procedure. We propose the shifting procedure to search for a high number of diverse individual solutions through the number of generations. In the shifting procedure, a baseline schedule is at first randomly prolonged up to the maximal percentage of the original SSGS schedule, and then each activity is randomly shifted within the available time frame.
2.5.2. Evaluation
After generating the initial population of solutions, the fitness of each individual is evaluated regarding the project’s duration, baseline profit, and value of a weighted resource-technology free float, i.e., an SM value. The calculations are conducted based on the existing mathematical model presented in Appendix A. To evaluate all objective functions, only the information from the second part of the candidate solution is needed. The fitness of an individual is evaluated based on the particular baseline schedule and accompanying resource usage data, so the surrogate measure value can be accurately calculated.
2.5.3. Survival and Selection
The survival phase is often regarded as the core of a genetic algorithm [23]. For multi-objective problems, sorting the individuals by their fitness functions is not as straightforward as in single-objective optimization problems. To overcome the slow process of sorting the individuals in a population by comparing each solution with every other solution in a population, the NSGA-II algorithm brings an effective and fast non-dominant sorting approach paired with crowding-distance calculation [15]. This part of the algorithm is applied directly from the open-source framework [23] to solve the multi-objective resilient project scheduling problem.
Before applying the genetic operators, individuals need to be selected to participate in the crossover procedure. Selection of the parents is accomplished through the binary tournament procedure, which has been helpful for faster convergence. Here, random pairs of individuals enter the competition tournament and only the winner can proceed to further steps.
2.5.4. Genetic Operators
After the selection phase, the current population consecutively confronts crossover and mutation steps, where the genetic material of two-parent individuals is exchanged. The aim of this process is to improve the fitness of two offspring that will derive from their parents. In this research, we customized genetic operators in the following manner.
For the crossover part, we allow for a certain percentage of individuals to skip the crossover procedure completely. In this case, all data which are carried with an individual are simply transferred to the next stage, i.e., to the mutation process. The intention behind this decision is that we try to enhance the preservation of the favorable genetic material in our solutions. Often, the offspring produced from the exceptionally fit parent solutions results in lower fitness values. On the other hand, for those individuals where the crossover is performed, we use the simple one-point crossover operator [30] on the activity lists of two parents, since the offspring individual encoded in this manner will preserve precedence feasibility, which is extremely important in construction scheduling. From newly produced activity lists, we create an initial baseline schedule by use of SSGS and again apply the shifting procedure to search for resilient solutions, as shown in Figure 5.
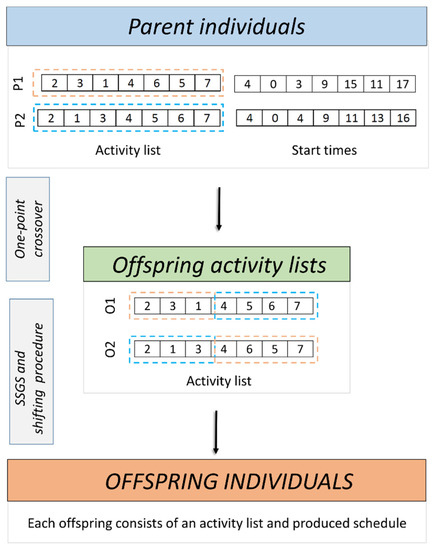
Figure 5.
Visualization example for the crossover procedure.
After the crossover has taken its place, a mutation operator performs on the current population. For the same reasons as previously described, in this stage, we also perform actual mutation only on a certain percentage of individuals. If a mutation is conducted, the algorithm randomly selects which type of mutation will be performed. The first mutation type is performed on the activity list part of the candidate solution: two activities will exchange their positions if this move results in a precedence feasible activity list. The exchange procedure continues until mutation has been achieved. The second mutation type refers to fine-tuning of the current schedule. Therefore, the mutation is executed only on the second part of the candidate solution. This action causes only slight changes in the current baseline: if there is enough resource-technology free float for an activity, its start is randomly shifted to a new position in the given time frame. This way, we again try to enhance the diversity of the elitist population while searching for Pareto solutions through the number of generations. The described loop continues until the stopping criterion is met. In this case, we opt for a certain number of generations.
3. Application of Customized Algorithm on a Test Case
The customized NSGA-II algorithm was applied to the case study to validate the proposed framework for proactive resilient scheduling in a construction project. For this study, real-life project data are used from a publicly available database [31,32]. We opted for a construction project named “Claeys-Verhelst Premises” since existing data include comprehensive information needed for a detailed resilience analysis. Due to the complexity of the underlying case study, the customized NSGA-II ran for 100 generations, where the population size was bound to 20 individuals. Mutation probability was set to 0.4, while the crossover percentage was chosen as 0.7. To ensure the computational feasibility, the optimization process was terminated when the maximal number of generations was reached.
3.1. Project Description
The selected project considers an expansion of the company premises through the construction of a new three-floor building harboring a warehouse, office space, a small showroom, and recreational facilities for the employees. The construction of the commercial building has taken place in Oudenburg, Belgium. The planned duration of a construction project was 442 days, considering standard eight-hour working days. The precedence network of the project consists of 49 non-dummy activities. Additional project data include information about resources, costs and durations of activities in the project, both in the planned and realized state. Required input on contract terms and financial data was not available from the database, so the cash flow calculation is performed based on hypothetical information, as can be seen in Table 2. All financial costs in Table 2 (TDC, Overheads, Mobilization, Tax, Markup, Bond and other monthly payments) are expressed in EUR.

Table 2.
Financial data and contract terms for the test case.
3.2. Steps for Resilience Analysis
As the result of the optimization process, a diverse set of baseline solutions is obtained. In this set, each baseline solution will produce a unique combination considering the project’s duration, final profit, and surrogate measure value. It is now up to a project manager to assess the project’s requirements and decide which baseline solution will be chosen among others.
In this analysis, the goal is to assess the resilience performance of different baseline solutions under real-life settings. Here, we are comparing the deviation between the planned and realized states of the construction project by use of real project data. When comparing two solutions, a baseline schedule with a lower deviation between the planned and realized state is considered to be more resilient to uncertainties. In resilience analysis, we focus on the deviation in the two most important estimates for every project manager: deviations considering the project’s duration and final profit.
As shown in Figure 6, the first step of the resilience analysis is to select a baseline schedule with the highest surrogate measure value from the obtained Pareto set of solutions. This way, we model the behavior of the project manager who is interested in obtaining the most resilient baseline solution. Objective functions of minimized project duration and maximized profit can be used as additional criteria if there are several baseline solutions with equal surrogate measure values. After that, we use the real project data to calculate deviations between baseline predictions and realized states.

Figure 6.
Resilience analysis steps.
In real life, on account of uncertain disruptions, there will be inevitable changes considering activities’ durations and costs. During execution, a project manager is responsible for timely updating of the schedule of a project by using reactive procedures, considering the data available in specific decision moments [33]. However, it is a challenging task to reconstruct project managers’ decisions with absolute certainty, so the current resilience analysis relies on the use of an algorithmic approach to reliably generate realized schedules when actual performances are known. By applying the same serial generation scheme (SSGS) algorithm to different baseline solutions, we can objectively estimate their resilience behavior.
3.3. Realized State Simulation
To generate the realized schedule and to calculate deviations between planned and realized states, we applied robust serial schedule generation scheme (SGS) [34] on the precedence feasible activity list, where actual durations and costs for all activities are known from the project database. In this analysis, we go for the robust serial SGS procedure over the parallel one since the general method was already embedded in the body of the existing algorithm code and needed only small coding interventions. Presumptions on the completeness of schedules built by robust serial SGS are the same as for their non-robust variants, meaning that the serial procedure generates a larger class of schedules than the parallel one [34].
An activity list is obtained as a first part of the selected Pareto solution, which always consists of two elements: a precedence feasible activity list and a complete baseline schedule. Therefore, we are generating a realized schedule by iterating through an activity list, but instead of starting these activities in the earliest possible moment, we schedule them at their feasible positions that are as close as possible to their planned starting time in a baseline schedule [34]. Naturally, during the robust serial SGS, we employ durations and total costs of activities from the actual project data, rather than the baseline predictions which were used only to obtain a Pareto set of solutions in the first place.
Finally, the analysis is performed by comparing realized performances of the most resilient Pareto solution and the behavior of the baseline solution provided in the project’s database. However, when it comes to analyzing the realized performances, note that the robust serial SGS approach is just one way to approximate reality. Rather than using a solely algorithmic approach, the state actually realized relies also on decisions taken by a person, considering the information available in the certain decision moment. Therefore, a realized state can differ from the overall output solution produced by robust serial SGS. Altogether, in this research, a robust serial SGS is needed as an approach to make an objective evaluation on the performances of different baseline schedules, when both planned and actual realizations of activities’ durations and costs are known.
3.4. Resilience Analysis on Project Data
The results for the resilience analysis are obtained by comparing the most resilient solution from the Pareto front with the original baseline, as provided in the project’s database. Except for the original scenario based on real data (Scenario 1), we included three additional hypothetical scenarios. Scenario analysis was used for a more comprehensive examination of the behavior alternatives in the realization of a construction project. As follows, a more detailed evaluation of the project data can show the impact of possible alternative outcomes in the comprehensive resilience analysis. Table 3 lists the sample data which was modified in relation to the real input data, with the purpose of modelling different scenarios. This way, we estimate the behavior of the resilient baseline schedule in response to uncertain impacts (prolongation of certain activities and their increase in total cost). In each additional scenario, we chose three different uncertain activities, based on the data for risk analysis in the case study, and we change their durations and their direct costs. In the scenario analysis, we explored different combinations of realized states for the activities with the broad duration distribution profiles, according to real project data.

Table 3.
Scenario sample data.
In the first modified scenario (Scenario 2), we changed the hypothetical duration and cost for the following activities: “demolition”, “facades” and “outside windows”. Afterwards, in Scenario 3 we altered the duration and cost for “building permit”, “polished concrete” and “floors”. Finally, the modified activities in Scenario 4 are: “hire contractor”, “foundation beam” and “drywall”. These activities were selected based on risk analysis, which is available in the database for the project [31,32]. For all modified activities, uncertainty levels are considered to be high and they have a wide distribution of their duration profiles.
As can be seen from the results of the resilience analysis in Figure 7, both makespan deviation and profit deviation are significantly lower for the most resilient baseline schedule than for the original baseline schedule provided by the case study, when the robust serial SGS procedure was followed to simulate the realized state of the project. Considering the units in the conducted analysis, makespan deviation is shown as days of project prolongation from the planned duration, while the profit deviation is displayed in thousands of financing units (in EUR). In the original scenario, the makespan deviation between planned and realized state for the most resilient baseline solution is 5 days, while the realized profit is smaller for 19.68 thousand financing units. To compare, the real baseline solution performs significantly worse: makespan deviation results in 88 days of delay, while the profit is decreased by 123.7 thousand financing units. In Scenario 2, the most resilient baseline shows no project tardiness at all, and profit deviation is also drastically low: only 4.45 thousand financing units. Scenario 3 produces similar results: 15 days of project tardiness for the most resilient case and profit deviation of 29.66 thousand financing units. The original baseline in Scenario 3 gives 98 days of time delay and EUR 133,510 profit delay. To conclude, Scenario 4 exhibits a time delay of 33 days and a profit deviation of EUR 62,710 for the most resilient case, compared to a time delay of 116 days and a profit deviation of EUR 164,710 for the original solution.
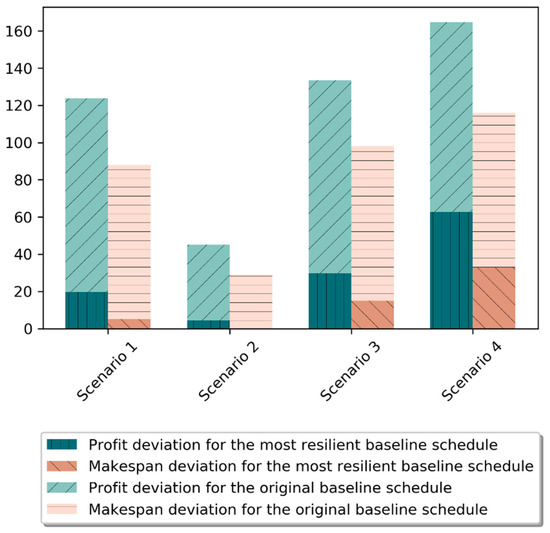
Figure 7.
Results of the resilience analysis: comparing the most resilient solution with an original baseline.
However, in this case, the price for making the baseline solution resilient to uncertainties is not negligible: the most resilient makespan is 18.78% longer than the original one. Therefore, the additional set of resilience analysis examines behavior for the entire Pareto front, cumulatively across all scenarios. To distinguish between different baseline solutions, two groups of baseline schedules are set up: on the one hand, there are makespans with moderate SM values and lower baseline durations and, on the other hand, there are longer baselines with higher SM values. When compared to the original baseline, the former group had on average 7.15% lower duration, while the latter makespans were on average 8.82% longer than the original one. It can be seen from data in Figure 8 that the obtained Pareto set of solutions consists of only 15% schedules with high SM values (higher than 80 SM units), while the remained baselines have moderate SM values (between 35 and 80 SM units).
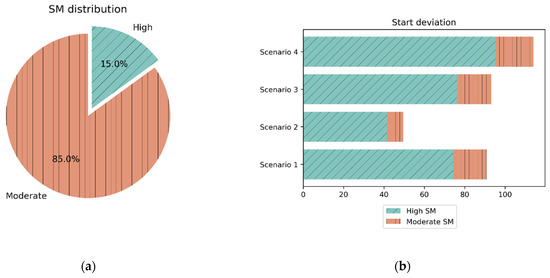
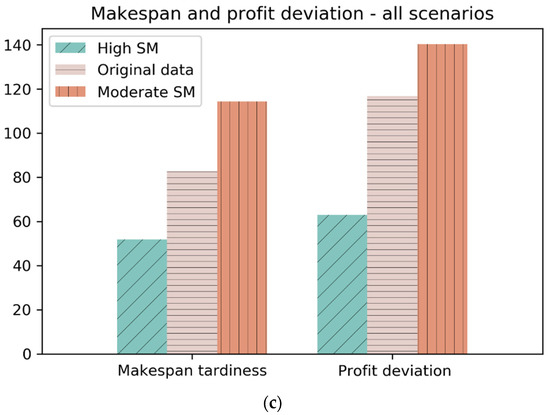
Figure 8.
Cumulative resilience analysis results: (a) SM value distribution in the obtained Pareto front; (b) absolute start time deviations for all Pareto solutions; (c) makespan and profit deviation distributed by SM value when all scenarios are included.
This time, not only were makespan and profit deviation examined across all scenarios but also the start time deviations calculated for a comprehensive resilience analysis. As shown in Figure 8, Scenario 1 and Scenario 3 produce very similar results: average start deviations are 74.34 and 76.11 days for schedules with high SM values, together with 90.86 and 93.1 days for schedules with moderate SM values. Scenario 2 shows the following results: average start deviation is 41.59 days for schedules with high SM values, and 49.55 days for schedules with moderate SM values. Along with that, Scenario 4 reveals 95.14 days of average start deviation for high SM and 114.0 days for moderate SM.
From the graph above, it can be seen that baseline schedules with high SM values have on average 37% lower makespan tardiness and roughly 46% lower profit deviation than the baseline solution. On the other hand, baseline schedules with moderate SM values show 28% higher makespan tardiness and circa 20% higher profit deviation than the original solution.
4. Discussion and Conclusions
This research analyzes resilience behavior of the baseline solution for a real construction project. First, the NSGA-II algorithm was customized and applied to the existing multi-objective optimization problem for improving the resilience of the baseline schedule. This enabled finding the resilient baseline schedules for a complex precedence network in a construction project. It was hypothesized that the baseline solution with a higher SM value should demonstrate increased stability when comparing planned and realized states. The results of the resilience analysis indicate a positive correlation between the improvement of SM value in the baseline solution and lower deviation of other project objectives in the realized state. Both the project tardiness and the profit deviation decreases as the SM value improves. Moreover, deviation in activities’ start times is also reduced for the baseline solutions with higher SM values. This way, the stability of baseline schedules is improved and the effectiveness of the scheduling process in construction projects is enhanced.
These results may be explained by the fact that baseline solutions with a higher SM value tend to have longer durations of their makespans. Accordingly, prolonged baselines include more time floats which can absorb the negative impact of uncertain events during the execution of a construction project. Hence, in further research, we suggest more focus on the analysis of the cases which have diverse SM values and approximately equal results of their other two objective functions: project duration and final profit. Further studies on the interaction between makespan prolongation and resilience improvement are therefore recommended.
Another important research question that could be asked considers reliable simulation of the project execution state. In this research, we relied on the robust serial SGS to model the realized state when durations and costs for all activities were known based on the real data information. However, not only are other algorithmic approaches available to simulate the behavior of the construction project (e.g., robust parallel SGS), but also different reactive procedures are being investigated which could assist project managers when deciding on optimal execution of activities in complex construction projects. Future studies on both proactive and reactive scheduling are suggested for further progress and a better understanding of construction project resilience.
Since this is the first time that the existing resilience scheduling problem [7] has been solved for a larger construction project by the use of the metaheuristic algorithm, a comparison of presented outputs with results obtained by different methods would require further investigation. Therefore, we suggest future research regarding the application of different computational intelligence paradigms, such as Particle Swarm Optimization (PSO), Simulated Annealing (SA), Tabu Search (TS), for example. This way, the solving process for resilient scheduling in complex construction projects could be analyzed in more depth by comparing distinguishing features and performances of different metaheuristic methods.
This research contributes to existing knowledge considering proactive resilience in construction scheduling by proposing the novel solving process. A customized NSGA-II algorithm has been applied to the optimization problem, where resilience of a baseline schedule is evaluated in relation to two project objectives. Based on the findings of the test case analysis, it can be suggested that the application of evolutionary optimization tools can help project managers to seek resilient baseline schedules by acknowledging the uncertain disruptions as early as in the planning phase of a construction project.
The proposed approach has introduced a practical solution for improved construction planning in terms of reliability of baseline scheduling and costing practices. The advantage of the presented framework is that it does not require any additional input information, as is the case in the standard planning procedure. Once the project information is gathered (list of activities, their planned durations and direct cost, precedence relations, resource constraints, financial requirements, etc.), the rest of the proposed solving process is straightforward. However, since the presented research was conducted mainly by using the Python programming language, we recommend a synthesis of the proposed solving procedure with the existing planning applications as a future research direction. This way, a more user-friendly solution could be developed for simultaneous optimization and planning practice in the software environment which is familiar to project managers. In conclusion, integrated use of optimization methods and latest programming tools throughout the scheduling and costing process can lead to better preparedness and to minimization of the overall deviation between the planned and realized state, which in turn can have a positive effect on reaching the project goals, such as overall duration and final profit.
Author Contributions
Conceptualization, M.M., S.K. and J.S.; methodology, M.M., S.K. and J.S.; software, M.M.; validation, M.M.; formal analysis, M.M.; investigation, M.M.; resources, M.M.; data curation, M.M.; writing—original draft preparation, M.M.; writing—review and editing, M.M., S.K. and J.S.; visualization, M.M.; supervision, S.K. and J.S.; project administration, S.K.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Project real case data publicly available at https://www.projectmanagement.ugent.be/research/data/realdata (accessed on 14 October 2021). Other analysis data available on request from the corresponding author.
Acknowledgments
This research is partially supported through project KK.01.1.1.02.0027, a project co-financed by the Croatian Government and the European Union through the European Regional Development Fund—the Competitiveness and Cohesion Operational Programme.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The Appendix A contains details supplemental to the existing optimization problem [7], for which the customized NSGA-II solving process was developed and explained throughout of this research article. Table A1 summarizes the notation used in the optimisation model. The multi-objective optimisation model (MOO) for resilient baseline scheduling in construction projects is expressed as follows:

Table A1.
Parameters and sets used in the optimization problem.
Table A1.
Parameters and sets used in the optimization problem.
| Symbol | Description |
|---|---|
| T | Length of the planning horizon (t = 1, 2, …, m) |
| Binary decision variable which equals 1 if activity i starts at the time t, 0 otherwise | |
| A | Set of project activities (i = 1, 2, …, n), including dummy start 0 and dummy end n + 1 |
| E | Set of precedence relations |
| R | Set of project resources (r = 1, 2, …, k) |
| Weight of activity i | |
| Expected duration for activity i | |
| Deterministic cost of activity i | |
| Consumption of resource r as required by activity i | |
| Availability of resource r during project time T | |
| q | Start of the time period for which the resource constraint is checked |
| Resource-technology free float for activity i | |
| Final profit at the end of a project | |
| End of the month considering project timeline (time step used when calculating Cash Flow), (eom = 1, 2, …, l) | |
| Cumulative cash flow value at the end of the month eom | |
| Payment at the end of the project timeline | |
| Total interest charges at the end of the month eom | |
| ir | Interest rate per period |
| Credit limit for the project |
References
- Schatteman, D.; Herroelen, W.; Van de Vonder, S.; Boone, A. Methodology for Integrated Risk Management and Proactive Scheduling of Construction Projects. J. Constr. Eng. Manag. 2008, 134, 885–893. [Google Scholar] [CrossRef]
- Isah, M.A.; Kim, B.-S. Integrating Schedule Risk Analysis with Multi-Skilled Resource Scheduling to Improve Resource-Constrained Project Scheduling Problems. Appl. Sci. 2021, 11, 650. [Google Scholar] [CrossRef]
- Han, F.; Bogus, S.M. Evaluating Construction Work Disruptions Using Resilient Short-Interval Scheduling: A Case Study. In Proceedings of the Construction Research Congress 2018, American Society of Civil Engineers, New Orleans, LA, USA, 2–4 April 2018; pp. 533–543. [Google Scholar]
- Torabi Yeganeh, F.; Zegordi, S.H. A Multi-Objective Optimization Approach to Project Scheduling with Resiliency Criteria under Uncertain Activity Duration. Ann. Oper. Res. 2020, 285, 161–196. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, Y.; Xiong, J. Resilience Analysis for Project Scheduling with Renewable Resource Constraint and Uncertain Activity Durations. J. Ind. Manag. Optim. 2015, 12, 719–737. [Google Scholar] [CrossRef][Green Version]
- Milat, M.; Knezic, S.; Sedlar, J. A New Surrogate Measure for Resilient Approach to Construction Scheduling. Procedia Comput. Sci. 2021, 181, 468–476. [Google Scholar] [CrossRef]
- Milat, M.; Knezić, S.; Sedlar, J. Resilient Scheduling as a Response to Uncertainty in Construction Projects. Appl. Sci. 2021, 11, 6493. [Google Scholar] [CrossRef]
- Brucker, P.; Drexl, A.; Mo, R.; Pesch, E. Resource-Constrained Project Scheduling: Notation, Classification, Models, and Methods. Eur. J. Oper. Res. 1999, 112, 3–41. [Google Scholar] [CrossRef]
- Pellerin, R.; Perrier, N.; Berthaut, F. A Survey of Hybrid Metaheuristics for the Resource-Constrained Project Scheduling Problem. Eur. J. Oper. Res. 2020, 280, 395–416. [Google Scholar] [CrossRef]
- Hartmann, S.; Briskorn, D. An Updated Survey of Variants and Extensions of the Resource-Constrained Project Scheduling Problem. Eur. J. Oper. Res. 2022, 297, 1–14. [Google Scholar] [CrossRef]
- Franco-Duran, D.M.; de la Garza, J.M. Review of Resource-Constrained Scheduling Algorithms. J. Constr. Eng. Manag. 2019, 145, 03119006. [Google Scholar] [CrossRef]
- Habibi, F.; Barzinpour, F.; Sadjadi, S.J. Resource-Constrained Project Scheduling Problem: Review of Past and Recent Developments. J. Proj. Manag. 2018, 3, 55–88. [Google Scholar] [CrossRef]
- Geambasu, G. Expect the Unexpected: An Exploratory Study on the Conditions and Factors Driving the Resilience of Infrastructure Projects. Ph. D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2011. [Google Scholar]
- de la Banda, M.G.; Stuckey, P.J.; Van Hentenryck, P.; Wallace, M. The Future of Optimization Technology. Constraints 2014, 19, 126–138. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- ElMenshawy, M.; Marzouk, M. Automated BIM Schedule Generation Approach for Solving Time-Cost Trade-off Problems. Eng. Constr. Archit. Manag. 2021, 28, 3346–3367. [Google Scholar] [CrossRef]
- Kar, S.; Kothari, C.; Jha, K.N. Developing an Optimum Material Procurement Schedule by Integrating Construction Program and Budget Using NSGA-II. J. Constr. Eng. Manag. 2021, 147, 04021017. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, N. Project Scheduling and Material Ordering Problem with Storage Space Constraints. Autom. Constr. 2021, 129, 103796. [Google Scholar] [CrossRef]
- Elkabalawy, M.; Moselhi, O. Optimized Resource-Constrained Method for Project Schedule Compression. Eng. Constr. Archit. Manag. 2021. [Google Scholar] [CrossRef]
- El-Abbasy, M.S.; Elazouni, A.; Zayed, T. Generic Scheduling Optimization Model for Multiple Construction Projects. J. Comput. Civ. Eng. 2017, 31, 04017003. [Google Scholar] [CrossRef]
- Tao, S.; Wu, C.; Sheng, Z.; Wang, X. Space-Time Repetitive Project Scheduling Considering Location and Congestion. J. Comput. Civ. Eng. 2018, 32, 04018017. [Google Scholar] [CrossRef]
- El-Abbasy, M.S.; Elazouni, A.; Zayed, T. Finance-Based Scheduling Multi-Objective Optimization: Benchmarking of Evolutionary Algorithms. Autom. Constr. 2020, 120, 103392. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Blazewicz, J.; Lenstra, J.K.; Kan, A.H.G.R. Scheduling Subject to Resource Constraints: Classification and Complexity. Discret. Appl. Math. 1983, 5, 11–24. [Google Scholar] [CrossRef]
- Au, T.; Hendrickson, C. Profit Measures for Construction Projects. J. Constr. Eng. Manag. 1986, 112, 273–286. [Google Scholar] [CrossRef]
- Elazouni, A.M.; Metwally, F.G. Finance-Based Scheduling: Tool to Maximize Project Profit Using Improved Genetic Algorithms. J. Constr. Eng. Manag. 2005, 131, 400–412. [Google Scholar] [CrossRef]
- Kolisch, R.; Hartmann, S. Heuristic Algorithms for the Resource-Constrained Project Scheduling Problem: Classification and Computational Analysis. In Project Scheduling; International Series in Operations Research & Management Science; Springer: Boston, MA, USA, 1999. [Google Scholar]
- Demeulemeester, E.; Herroelen, W. Project Scheduling; International Series in Operations Research & Management Science; Kluwer Academic Publishers: Boston, MA, USA, 2002; Volume 14. [Google Scholar]
- Kolisch, R. Serial and Parallel Resource-Constrained Project Scheduling Methods Revisited: Theory and Computation. Eur. J. Oper. Res. 1996, 90, 320–333. [Google Scholar] [CrossRef]
- Hartmann, S. A Competitive Genetic Algorithm for Resource-Constrained Project Scheduling. Nav. Res. Logist. 1998, 45, 733–750. [Google Scholar] [CrossRef]
- Vanhoucke, M.; Coelho, J.; Batselier, J. An Overview of Project Data for Integrated Project Management and Control. J. Mod. Proj. Manag. 2016, 3, 6–21. [Google Scholar]
- Batselier, J.; Vanhoucke, M. Construction and Evaluation Framework for a Real-Life Project Database. Int. J. Proj. Manag. 2015, 33, 697–710. [Google Scholar] [CrossRef]
- Dahmani, S.; Ben-Ammar, O.; Jebali, A. Resilient Project Scheduling Using Artificial Intelligence: A Conceptual Framework. In Advances in Production Management Systems. Artificial Intelligence for Sustainable and Resilient Production Systems; Dolgui, A., Bernard, A., Lemoine, D., von Cieminski, G., Romero, D., Eds.; IFIP Advances in Information and Communication Technology; Springer International Publishing: Cham, Switzerland, 2021; Volume 630, pp. 311–320. ISBN 978-3-030-85873-5. [Google Scholar]
- Van de Vonder, S.; Ballestín, F.; Demeulemeester, E.; Herroelen, W. Heuristic Procedures for Reactive Project Scheduling. Comput. Ind. Eng. 2007, 52, 11–28. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).