Abstract
Fostering the development of additive manufacturing (AM) in the context of mass production is a key factor to ensure its adoption in the industry. It should be remembered that this technology intrinsically makes it possible to produce parts with unexpected complexities in terms of shape and structure, but this comes at a price: time. To overcome this productivity barrier, AM technology providers are developing 3D printing machines with high-speed performance and mass reproduction means in a single run. Although such trends can be seen as a natural evolution of this technology with respect to current consumption patterns, it still remains a scientific issue on production planning to be tackled. The objective is to address the on-demand production planning of different AM parts in FabLabs composed of unrelated parallel 3D printers. A novel framework is introduced to consider part orientation, path planning, and part-to-printer assignment, with a specific focus on fused filament fabrication technique. By targeting a minimum production time, it exhibits reasoning algorithms implemented in a Python application. A case study with a batch of six non-identical parts and two fused filament fabrication 3D printers is introduced to illustrate the added value of the framework and its operational side.
1. Introduction
Additive manufacturing (AM) is currently considered as a key technology that brings together processes and techniques to produce—in a layer-by-layer deposition mode—objects or assemblies [1]. Therefore, it provides more design freedom than the formative and subtractive manufacturing techniques widely accepted and mastered in industry and academia [2]. With AM, the complexity in terms of shape and structure is free, but the printing time can be significant, which breaks with current mass production rates in the industry [3]. This is the reason why AM has been mainly used for rapid prototyping purposes and complex parts (with added value) manufacturing. Today, a part of the concerns is devoted to increasing productivity to meet the industrial needs for mass customization/personalization. In such a context, efforts are currently being made to produce a batch of parts, while maintaining the same AM technique and machine, therefore leading to the development of 3D printers with better performances and higher printing volumes [4].
In addition, the development of AM has also led to the emergence of FabLabs and 3D printing hubs/platforms [5,6,7] by providing flexible/efficient means and tools to foster ideation, learning, concept validation, and even the realization of parts/products on demand. In short, these manufacturing platforms—dedicated to heterogeneous demands—make it possible to stimulate creativity and innovation while removing barriers over departments/services of the company. In this case, new methods and tools—similar to the existing ones for structuring production systems—must be investigated now to increase their productivity.
Among the available processes and techniques from ISO/ASTM 52900 standard [8] that could potentially be available in FabLabs or hubs, material extrusion and its leading technique—fused filament fabrication (FFF)—has the advantage of being supported by a strong open source community while being subject to continuous improvement since the disruptive RepRap project in 2005 [9]. Such advances have enabled a gradual shift from rapid prototyping towards mass customization with production capabilities of small batches of plastic parts [10]. However, to reach an industrial threshold, this technique—which is mainly used for plastic parts—must face its current limitations in terms of weak mechanical performances and low production rate [11]. Compared to other subtractive or formative manufacturing processes, the FFF technique does not require any fixture or tooling, which significantly reduces the production cost. However, a post-treatment step is often necessary to both support material removal and surface finishing of the parts. Augmenting the FFF technique via an industry-like production logic calls into question or requires the evolution of pre-established models and methods, especially at the production-planning and supply-chain stages [12,13]. In its actual shape, the FFF technique demands the prior analysis of a part geometric definition for process-parameter selection, and path-planning specifications consistent with machine capabilities [14,15]. The part can be scaled, positioned, and oriented on the 3D printer bed. The last parameter is critical as it influences the manufacturing time with potentially support structures, and the mechanical performances of the part due to the intrinsic anisotropy induced by the process [16,17,18,19]. Once all parameters have been set up, instructions— in G-code format—are sent to the 3D printer.
Production planning and scheduling combined with AM technology have already received attention from researchers in recent years. Research work has been mainly focused on nesting, 2D packing, and 3D packing problems with powder-based processes [20]. For this specific AM process, research efforts have attempted to gather multiple parts and to optimize their position for a given batch [21,22,23]. Li et al. [12] have introduced two heuristics, namely, best fit and adaptive fit, for part-to-printer assignment to reduce the cost per volume by maximizing the number of parts in a single batch. Although such initiatives seem to be promising, the developed reasoning procedures are not suitable enough for the FFF technique. In the context of on-demand production, the FFF 3D printers do not need to be overloaded with multiple parts for a single run. To prevent manufacturing defects, it is better to organize production according to a one-part-to-one-machine strategy. As a consequence, nesting algorithms will not be addressed in the present paper. Arroyo et al. [24] have presented a heuristic in the context of production planning with a set of unrelated parallel FFF 3D printers that enables the realization of different sized jobs. Based on a greedy algorithm, their heuristic exhibits better performances than other works related to discrete differential evolution, ant colony optimization, and simulated annealing. Similarly, Ransikanbum et al. [25] have optimized the workload balance between FFF 3D printers in a way to reduce the total cost of the parts and the total completion time. Recently, Li et al. [26] have analyzed different approaches to the production of multiple parts in an industrial context. They have compared centralized and decentralized production systems in terms of cost and response time. More recently, Zhang et al. [27] have solved the part-to-printer assignment and part placement for stereolithography (SLA) technique. To do so, they have introduced a combination of heuristic and genetic algorithm that can be applied and adapted to the FFF technique. Despite the current research efforts—which are mainly focused on the nesting of multiple parts in a single printing run—there is still a lack of methods and tools to bring multiple unoriented geometric models to single-run production. This is typically an issue with the FFF technique where multi-part production does not provide any efficiency and productivity gain. In such a context, it is important to consider, as a whole, part orientation, path planning, and part-to-printer assignment. As a consequence, the objective of the paper is to address on-demand production planning of different (non-identical) and unoriented AM parts in FabLabs/hubs composed of unrelated parallel 3D printers with a specific focus on the FFF technique.
The paper is organized as follows. Section 2 presents the multi-part production planning framework for AM, in which part orientation, path planning and part-to-printer assignment are jointly processed with a greedy algorithm. Next, in Section 3, a tool implementation of the framework is proposed to demonstrate its applicability, and a case study is introduced and discussed. Last, the conclusion is given in Section 4.
2. Materials and Methods
On-demand production of multiple non-identical parts with AM technology requires addressing three important steps, namely, part orientation, path planning, and part-to-printer assignment. Figure 1 shows a flowchart describing the aforementioned steps and input/output information starting from a heterogeneous demand in terms of geometric models to appropriate machine instructions for the AM hubs. The part orientation step consists in finding the best orientation by minimizing either the support volume or the build time, or maximizing the mechanical properties of the part. This step is processed as many times as there are parts. In a more detailed way, the reasoning algorithm evaluates the printability of the geometric models of the parts for a given orientation according to relevant parameters, such as the overhang area and the bed adhesion surface. Here, the latter is essential to hold the part during the FFF 3D printing process.

Figure 1.
Proposed multi-part production planning framework for AM.
Once the best orientations have been determined for all input parts, a path planning step is then processed. The FFF technique uses a layered material deposition model, to which extrusion paths can be specified at each layer. This step aims at slicing the part geometric model with a fixed layer height along the normal axis of the printer bed. The parameters’ values will depend on the optimum settings for each machine. At each layer, the contour of the part is extracted to determine both the surface to print and the infill strategy (i.e., geometric pattern and density). This step also considers additional features (temporary) to ensure the part adhesion on the printer bed and supports when there are overhang surfaces. The latter is determined according to the angle after which a surface cannot be printed smoothly. This angle value is defined based on the machine parameters (nozzle diameter, fan speed, layer height, etc.). Once all parameters have been determined, build time—which includes the printer’s head travel, its acceleration, and maximum velocity—can be estimated, and machine instructions are then expressed in G-code format. The remaining step—to which a mathematical model is developed hereafter—aims at assigning parts to the FFF 3D printers of the FabLab/hub.
Addressing production planning issues with AM requires a prior formal description of the problem to be solved. The aforementioned on-demand manufacturing of heterogeneous parts with unrelated FFF 3D printers (i.e., machines) imposes assumptions to be considered in order to define the mathematical model, which can be listed as follows:
- A job refers to a single part being built on a machine. It cannot be decomposed into sub-jobs;
- There is no preemptive job;
- All the parts have the same material;
- All machines have an optimal set of parameters and are able to build any geometry with an 100 % success rate;
- All the parts can be manufactured on any machine with any orientation;
- The jobs are independent;
- All machines are parallel and unrelated—they can process the same part but with a different processing time;
- Part removal and manufacturing setup times are neglected.
Built on this, a mathematical model for part-to-printer assignment is proposed and described by using the following notations highlighting indices, sets, and parameters:
- Indicesmachinesparts to be manufacturedjobs
- Setsset of machinesset of jobs of the machines mset of partsset of parts to be manufactured by the machine m
- Parametersprocessing time of the part p on the machine mrealisation of the part p on the machine mcompletion time of the machine mmaximum completion time among the machines
Before producing a set of parts P with a set of machines M, the orientation of the parts in a proper build direction has to be addressed in order to reduce their manufacturing time. The point is critical to avoid overhang surfaces and then to minimize additional support required to print them. Although multiple parts can be printed on the same job, there is no advantage with the FFF technique in realizing multiple parts at once, unlike the powder-based processes. With the latter, gathering multiple parts allows one to reduce the production time. As for the FFF technique, the approach is totally different; if multiple parts are printed in a single run and one fails due to warping effect or other issues, it will lead to a failure of the entire job. In the present case, a print job will consist of a single-part printing operation p on a machine m. Once the part is oriented, the path planning can be generated for a given machine, and then the processing time of the job for a machine can be determined from the set of instructions. With the build time of each part for each available 3D printer, a part-to-printer assignment needs to be made. The completion time of a machine is the sum of the production time of all the jobs, as expressed in Equation (1). This step is called the part-to-printer assignment and consists of minimizing the maximum processing time , such as described in Equation (2), of the longest time-consuming machine (Equation (3)), shown in Figure 2.
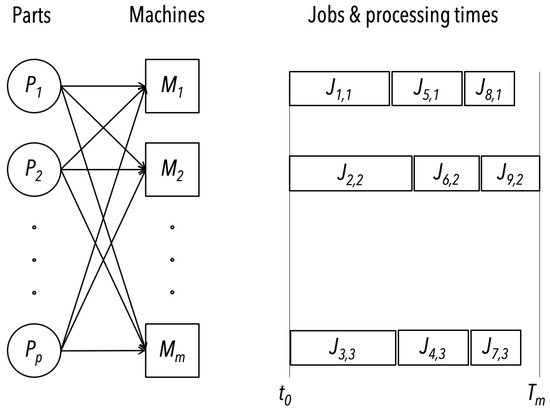
Figure 2.
Illustration of the part-to-printer assignment (the width of the jobs are proportional to their processing times).
In the context of FabLabs/hubs, the machines (FFF 3D printers) ensure continuous production by using ejection solutions to remove automatically printed parts without human intervention. As an example, with the black belt 3D printers or the Quinly accessories [28,29], it is then possible to remove 3D printed parts from FFF 3D printers. Without such a solution, delays could occur between two consecutive jobs, which would significantly increase production times. Here, the FabLab/hub is composed of unrelated parallel machines that are able to perform the same function but have different capabilities or capacities [30]. In addition, they exhibit the same printing volume but offer different production times. This is due to the performances of the machines’ hardware (e.g. nozzle’s diameter, stepper motors drivers, etc.) and the adapted process planning software’s parameters such as printing speed, layer height, etc. It is worth noting that a job in AM-oriented production cannot be decomposed into sub-jobs in order to balance the production. Indeed, splitting a job consists of partitioning the part into several bodies, which will later require assembly operations. Such considerations are not addressed in this paper but are potentially an interesting avenue to balance the production. Lastly, in this proposed model, it is assumed that parts to be produced have the same material and all FFF 3D printers will always have sufficient material to perform jobs.
3. Results
The proposed framework and its underlying components can be implemented through a set of tools and applications in order to process heterogeneous 3D STL files in a way to be rightly assigned to FFF 3D printers of the FabLab/hub.
Figure 3 shows, for each step of the framework, a dedicated application that has either been used or specifically developed. This is the case for the part orientation step, to which an open-source Python application called Tweaker—which is able to find an optimal orientation of an object on a FFF 3D printer— has been adopted [31]. Its reasoning capacities are aligned with the defined parameters (in the previous section) to be optimized for ensuring the good printability of the parts. As for the path planning step, another open-source tool has been considered and integrated, CuraEngine 4.6.3. Developed as a Cura backend from Ultimaker, it is widely used in the FFF community since it works with any kind of FFF 3D printer and is suitable enough to analyze parts’ geometries, define trajectory paths, estimate build times, and generate machines’ instructions. Build time estimations for all parts are important as they will be used to the part-to-printer reasoning step. This last step is built upon the aforementioned mathematical model, to which a heuristic—using the longest processing time (LPT) rule [32]—has been implemented in a dedicated Python application. The Algorithm 1 has been developed to control information flows between the components of the framework. More particularly, it consists in attributing the jobs—which are sorted by decreasing order of processing times—to the FFF 3D printers of the FabLab/hub so as to minimize the maximum processing times of the machines.
| Algorithm 1: Independent parts production planning with unrelated parallel FFF 3D printers. |
 |

Figure 3.
Implementation of the framework through Tweaker, CuraEngine, and a greedy algorithm-based application.
To demonstrate how the implemented framework works, a batch of six different parts (names A to F as illustrated in Figure 4) is introduced. The objective is to first analyze the related STL files in terms of part orientation, then to construct their path plans and build times so as to allocate jobs to two RepRap machines (named Machine 1 and Machine 2) with a maximum build volume of 20 × 20 × 20 cm. By using Tweaker application and CuraEngine software, the oriented parts are subject to build time estimation (see Figure 5). Table 1 sums up the resulting build time per part per machine.
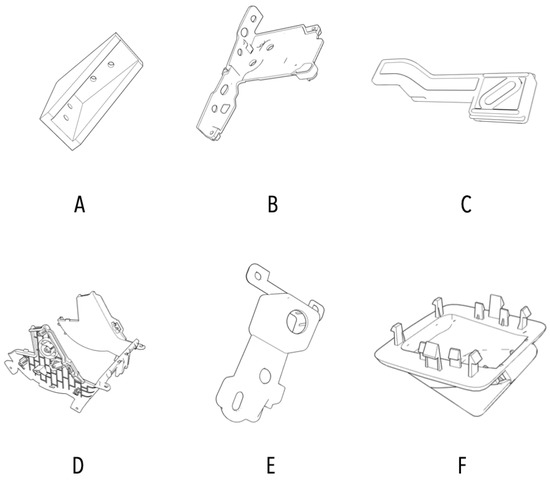
Figure 4.
Set of parts to be considered for production planning.
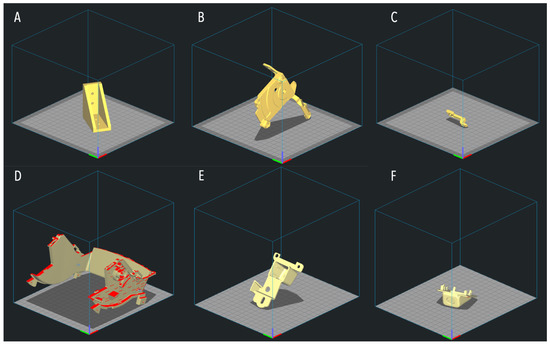
Figure 5.
Parts with their optimized orientations in Cura software using Tweaker application.

Table 1.
Estimation of build times per part per machine and average processing times.
With the build time per part determined from the previous step, the average build time can be calculated. Once the average processing time is determined for each part, it is then possible to sort them by applying the LPT rule. It consists in sorting the parts from the longest to process to the fastest to process, as shown in Table 2. The part with the longest build time is at the left of the table (i.e., part D), and the fastest part to be processed is at the right side of the table (i.e., part C). The original set of parts, ranging from A to F, is now ordered as follows: D, B, E, A, F, and C. At this step, each part needs to be assigned to an FFF 3D printer in order to be produced. To assign a part, an iteration is made involving three parameters. First, it is needed to determine the total processing time for each FFF 3D printer. This can be calculated by computing the sum of the build times of the parts that have been allocated to the FFF 3D printers. These parameters are shown in column (i) in Table 2. Secondly, it is required to know the build time of a part to a given FFF 3D printer. This has been previously determined by the CuraEngine software and is shown in column (ii) in Table 2. Then, the sum of the current building times in column (i) is added to the building time of the part for every FFF 3D printer in column (ii) to determine what the total processing time of an FFF 3D printer will be if the part is assigned to it. This value is written in column (iii). At the end of each iteration, the part assigned to the FFF 3D printer will have the lowest building time. By following such steps, the maximum build time can be minimized.

Table 2.
(i) Printer’s built time before assigning the current part; (ii) build time of the current part; and (iii) total build time.
The case study can be followed by using Table 2 and Figure 6. It starts with the longest part to be processed, which is part D. At the first iteration, the total build time of each FFF 3D printer is zero because no part has been assigned to any printer, as shown in Table 2 column (i). Then, the processing time of part D for each printer is added in column (ii), and the sum of the columns (i) and (ii) provides column (iii). The latter represents the processing time of each machine if the part is assigned to them. At this point, the lowest value is the case where the part D is allocated to the Machine 2 because it has the lowest total build time (see Figure 6b). For this first iteration, the part is attributed to the Machine 2. In Figure 6, a part assigned to Machine 1 is represented by a blue circle, whereas the part with a red circle stands for assignment to Machine 2.
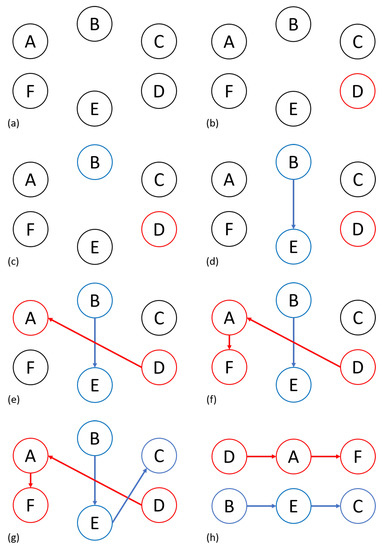
Figure 6.
Part-to-printer assignment iterations. Black circles represent the remaining parts to be assigned; blue circles represent the parts allocated to Machine 1 and red circles to Machine 2. (a) Initial state (b), iteration 1 (c), iteration 2 (d), iteration 3 (e), iteration 4 (f), iteration 5 (g), and iteration 6 (h) results.
The second iteration occurs with part B. As part D has been assigned to Machine 2, the current total build time for Machine 1 is still zero. As for Machine 2, part D has been assigned to it, so the current total build time of Machine 2 becomes the build time of part D. The total build time column (iii) for each machine is calculated by adding column (i) and column (ii). This time, we observe that the lowest total build time shown for part B in column (iii) is the lowest if the part is assigned to Machine 1. Part B is assigned to Machine 1, as shown Figure 6c. The same iteration is done for all the parts until all they are assigned to the FFF 3D printers. The results of the greedy algorithm are shown in Figure 6h. At the end of this reasoning step, parts D, A, and F are assigned to Machine 2, and parts B, E, and C are assigned to the Machine 1.
4. Discussion
The proposed work can be applied in FabLabs/hubs with 3D printing machines equipped with automatic ejection systems or just on a simple offline hub of machines. In the first case, the G-code files listed per machine can be added straight away on the printing list of each machine. In the second case, parts to be printed can require a manual intervention whether at the beginning of the job or at its end. If additional parts are introduced into the initial batch or if a machine is stopped for technical reasons during the production process, the proposed framework will be able to consider these new parameters. To do so, a new calculation for the remaining parts to be printed with the working FFF 3D printers can be done.
Furthermore, some of the assumptions made in the paper need to be discussed in order to present new perspectives. As for FabLab/hub of FFF 3D printers, the opportunity of splitting a job by partitioning a part into sub-parts has not been considered. However, such an approach will let the authors address two different important scientific issues at a later point. Indeed, considering part partitioning can be seen as a strategic action to balance production through a set of FFF 3D printers. This may also result in a decrease of the maximum processing time by removing some of the workloads on the machine with the longest processing time on another machine. Another key issue related to part partitioning concerns large-scale parts to which the question of splitting is of interest and will be addressed later.
5. Conclusions
In this paper, a multi-part production planning framework for AM in the context of unrelated parallel FFF 3D printers in FabLabs/hubs has been proposed and implemented through a set of applications and illustrated via a case study. It includes, as main pillars, part orientation, path planning with build-time estimation, and part-to-printer components in a way to analyze heterogeneous part geometric models (STL files) towards the assignment of machine instructions (G-code files) to the available FFF 3D printers. The implementation strategy has been to consider and gather existing independent functional applications (such as Tweaker and CuraEngine) and to develop a new one (greedy algorithm-based application) to fully cover the main components of the framework in a seamless manner. As a result, the framework implementation is suitable to be reused in any FabLabs or AM hubs, to which demands and 3D printing machines are heterogeneous. By following such a tool’s architecture, each step of the AM production planning can be addressed independently and then can be tuned or even replaced in order to improve the final output.
Author Contributions
T.C.: Conceptualization; Methodology; Software; Writing original draft. F.D.: Conceptualization; Methodology; Writing—review and editing; Supervision. S.G.: Funding acquisition; Supervision. All authors have read and agreed to the published version of the manuscript.
Funding
The research work was funded by the French National Agency for Research Agency for Research and Technology (ANRT) in conjunction with the French “Investissements d’Avenir” program, project ISITE-BFC (contract ANR-15-IDEX-0003).
Informed Consent Statement
The authors are consent for publication.
Data Availability Statement
Not available.
Acknowledgments
The research activity has been made in collaboration with Segula company as part of a CIFRE contract (Industrial Standards of Research Training) by the French National Agency for Research Agency for Research and Technology (ANRT) in conjunction with the French “Investissements d’Avenir” program, project ISITE-BFC (contract ANR-15-IDEX-0003).
Conflicts of Interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
References
- Dzemko, M.; Engelmann, B.; Hartmann, J.; Schmitt, J. Toward Shifted Production Strategies Through Additive Manufacturing: A Technology and Market Review for Changing Value Chains. Procedia CIRP 2019, 86, 228–233. [Google Scholar] [CrossRef]
- Sossou, G.; Demoly, F.; Montavon, G.; Gomes, S. An additive manufacturing oriented design approach to mechanical assemblies. J. Comput. Des. Eng. 2018, 5, 3–18. [Google Scholar] [CrossRef]
- André, J.C. From Additive Manufacturing to 3D/4D Printing 1: From Concepts to Achievements; ISTE J. Wiley & Sons: London, UK; Hoboken, NJ, USA, 2017. [Google Scholar]
- Eyers, D.R.; Potter, A.T. Industrial Additive Manufacturing: A manufacturing systems perspective. Comput. Ind. 2017, 92–93, 208–218. [Google Scholar] [CrossRef]
- Mikhak, B.; Lyon, C.; Gorton, T.; Gershenfeld, N.; McEnnis, C.; Taylor, J. Fab Lab: An Alternate Model of Ict for Development. 2002. Available online: http://cba.mit.edu/events/03.05.fablab/fablab-dyd02.pdf (accessed on 20 January 2022).
- Gershenfeld, N. FAB: The Coming Revolution on Your Desktop–From Personal Computers to Personal Fabrication. 2005. Available online: https://www.semanticscholar.org/paper/FAB%3A-The-Coming-Revolution-on-Your-Desktop–from-to-Gershenfeld/f49ea96b1394e5011204ddc5e18163f58e018381 (accessed on 20 January 2022).
- Gershenfeld, N. How to Make Almost Anything: The Digital Fabrication Revolution. Foreign Aff. 2012, 91, 43–57. [Google Scholar]
- ISO/ASTM 52900:2015; Additive Manufacturing—General Principles—Terminology. 2015. Available online: https://tajhizkala.ir/doc/ASTM/ISO%20ASTM%2052900-15.pdf (accessed on 20 January 2022).
- Jones, R.; Haufe, P.; Sells, E.; Iravani, P.; Olliver, V.; Palmer, C.; Bowyer, A. RepRap—The replicating rapid prototyper. Robotica 2011, 29, 177–191. [Google Scholar] [CrossRef] [Green Version]
- Oh, Y.; Zhou, C.; Behdad, S. Production Planning for Mass Customization in Additive Manufacturing: Build Orientation Determination, 2D Packing and Scheduling. In Proceedings of the ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 2A: 44th Design Automation Conference, Quebec City, QC, Canada, 26–29 August 2018; V02AT03A033. ASME: Quebec City, QC, Canada, 2018. [Google Scholar] [CrossRef]
- Thibaut, C.; Frédéric, D.; Gomes, S. A hybrid additive manufacturing platform based on fused filament fabrication and direct ink writing techniques for multi-material 3D printed. Int. J. Adv. Manuf. Technol. 2021. Under Review. [Google Scholar]
- Li, Q.; Kucukkoc, I.; Zhang, D.Z. Production planning in additive manufacturing and 3D printing. Comput. Oper. Res. 2017, 83, 157–172. [Google Scholar] [CrossRef]
- Rossit, D.A.; Tohmé, F.; Frutos, M. Industry 4.0: Smart Scheduling. Int. J. Prod. Res. 2019, 57, 3802–3813. [Google Scholar] [CrossRef]
- Bikas, H.; Stavropoulos, P.; Chryssolouris, G. Additive manufacturing methods and modelling approaches: A critical review. Int. J. Adv. Manuf. Technol. 2016, 83, 389–405. [Google Scholar] [CrossRef] [Green Version]
- Livesu, M.; Ellero, S.; Martínez, J.; Lefebvre, S.; Attene, M. From 3D models to 3D prints: An overview of the processing pipeline. Comput. Graph. Forum 2017, 36, 537–564. [Google Scholar] [CrossRef] [Green Version]
- Alexander, P.; Allen, S.; Dutta, D. Part orientation and build cost determination in layered manufacturing. Comput.-Aided Des. 1998, 30, 343–356. [Google Scholar] [CrossRef]
- Ahn, S.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic material properties of fused deposition modeling ABS. Rapid Prototyp. J. 2002, 8, 248–257. [Google Scholar] [CrossRef] [Green Version]
- Casavola, C.; Cazzato, A.; Moramarco, V.; Pappalettere, C. Orthotropic mechanical properties of fused deposition modelling parts described by classical laminate theory. Mater. Des. 2016, 90, 453–458. [Google Scholar] [CrossRef]
- Song, Y.; Li, Y.; Song, W.; Yee, K.; Lee, K.Y.; Tagarielli, V. Measurements of the mechanical response of unidirectional 3D-printed PLA. Mater. Des. 2017, 123, 154–164. [Google Scholar] [CrossRef]
- Oh, Y.; Witherell, P.W.; Lu, Y.; Sprock, T.A. Nesting and Scheduling Problems for Additive Manufacturing: A Taxonomy and Review; Elsevier: Amsterdam, The Netherland, 2020; Volume 36. [Google Scholar]
- Freens, J.P.; Adan, I.J.; Pogromsky, A.Y.; Ploegmakers, H. Automating the production planning of a 3D printing factory. In Proceedings of the 2015 Winter Simulation Conference (WSC), Huntington Beach, CA, USA, 6–9 December 2015; pp. 2136–2147. [Google Scholar] [CrossRef]
- Chergui, A.; Hadj-Hamou, K.; Vignat, F. Production scheduling and nesting in additive manufacturing. Comput. Ind. Eng. 2018, 126, 292–301. [Google Scholar] [CrossRef]
- De Antón, J.; Senovilla, J.; González, J.; Acebes, F. Production planning in 3D printing factories. Int. J. Prod. Manag. Eng. 2020, 8, 75. [Google Scholar] [CrossRef]
- Arroyo, J.E.C.; Leung, J.Y.T. Scheduling unrelated parallel batch processing machines with non-identical job sizes and unequal ready times. Comput. Oper. Res. 2017, 78, 117–128. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Ha, S.; Ma, J.; Kim, N. Multi-objective optimization analysis for part-to-Printer assignment in a network of 3D fused deposition modeling. J. Manuf. Syst. 2017, 43, 35–46. [Google Scholar] [CrossRef]
- Li, Y.; Yang, C.; Hu, Q.; Zhou, S.; Ma, L.; Lim, M.K. The influence of additive manufacturing on the configuration of make-to-order spare parts supply chain under heterogeneous demand. Int. J. Prod. Res. 2019, 57, 3622–3641. [Google Scholar] [CrossRef]
- Zhang, J.; Yao, X.; Li, Y. Improved evolutionary algorithm for parallel batch processing machine scheduling in additive manufacturing. Int. J. Prod. Res. 2020, 58, 2263–2282. [Google Scholar] [CrossRef]
- The Printer—BlackBelt 3D: The Benchmark in Belt Printing. Available online: https://blackbelt-3d.com/the-blackbelt-3d-printer/ (accessed on 2 February 2021).
- Saunders, S. 3DQue Enables Automated, Wireless 3D Printing with New Pi Kit for Quinly. Available online: https://3dprint.com/276288/3dque-further-enables-automated-wireless-3d-printing-with-new-pi-kit-for-quinly/ (accessed on 2 February 2021).
- Logendran, R.; Subur, F. Unrelated parallel machine scheduling with job splitting. IIE Trans. 2004, 36, 359–372. [Google Scholar] [CrossRef]
- Schranz, C. Tweaker-Auto Rotation Module for FDM 3D Printing. Ph.D. Thesis, Salzburg Research, Salzburg, Austria, 2016. [Google Scholar] [CrossRef]
- Frenk, J.B.G.; Rinnooy Kan, A.H.G. The Asymptotic Optimality of the LPT Rule. Math. Oper. Res. 1987, 12, 241–254. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).