Abstract
The impact of projectiles in reinforced or unreinforced concrete is of prime importance in applied mechanics and engineering. Parameters such as penetration depth, velocity or energy of the projectile, and the geometry and the angle of attack of the projectile are the most critical factors, among several others, that determine whether the concrete body will tolerate damage due to the impact or not. For numerical simulations of damage, the Riedel-Hiermaier-Thoma (RHT) concrete failure is an established approach, which is also used in this research. In this work, numerical simulations have been performed on shooting a rigid large-scale projectile with different tip contours at a concrete target that is reinforced with steel. For each tip contour, the angle of attack varied. The penetration depth of the projectile tip and the damage of the target were reported for the different tip contours as a function of the angle of attack. The results show that the maximal damage occurred at ~45° of the angle of attack, while penetration of the projectile into the target increased with increasing the angle of attack.
1. Introduction
Concrete is a composite material with a plethora of applications in engineering, such as construction and protection against projectile impact [1]. The evolution of damage in composite materials and the impact effects of projectiles have been investigated through multiple simulative or experimental studies [1,2,3,4,5,6,7,8]. In the open literature, there are reports of different approaches used and developed to simulate projectile impact on concrete. One example is the Kong−Fang material model combined with smooth particle hydrodynamics (SPH) to define the parameters of concrete under impact [1]. In this approach, the damage of the concrete is compared to the simulation through the finite element method (FEM). The results show that the SPH method has computational advantages. Another research work looked at the impact of long projectiles in concrete with and without reinforcement [3]. It has been found that with a lower velocity of the projectile, scabbing (the ejection of fragments of the target on the other side of the impact) decreases for reinforced concrete compared with the unreinforced counterpart. A different approach for the simulation of a projectile in concrete was to use a smoothed particle Galerkin method, which showed computational advantages that make this method very appealing [9]. Here, the projectile velocity over time and penetration depth were used for comparison. Another paper investigated the influence of low- and high-velocity projectiles, one was a sphere and the other was an ogive-nosed projectile, on reinforced concrete using the concrete damage plasticity (CDP) model and the Johnson−Holmquist damage model (JH-2) [10]. The results show that for the spherical projectile, a slight increase in Von Mises stresses was observed as the velocity increased. For the ogive-nosed projectile, the damage propagated quickly through the target using the CDP model. Compared with the JH-2 model, the CDP model showed severe fractures throughout the length of the target.
Another work looked at the projectile impact on ultra-high-performance fiber-reinforced concrete (UHPFRC) through physical tests and numerical simulation, using the DFHcoh-KST (Denoual-Forquin-Hild cohesion with Krieg-Swenson-Taylor) model [11]. Here, the penetration depth and deceleration were investigated. The results show that the friction between the projectile and target influenced the deceleration significantly, while when the ratio of tunneling radius to projectile radius was below ¼, a significant influence on the deceleration was not given. Another study investigated the impact of a projectile on a concrete slab using a 3D Eulerian-Lagrangian method to overcome the problem of the simulation of a multi-material interface [12]. Impact velocities over time were reported for different concrete slabs as the results of the numerical simulations. The results for projectile penetration showed a good similarity with the physical tests, but also with previous numerical simulations.
Another work utilized experiments to validate material properties for the RHT (Riedel-Hiermaier-Thoma) concrete model [13]. The results from numerical simulations using the RHT model showed that the default parameters of the model may slightly underestimate the impact for some cases. Additionally, the model showed a significant effect of the compressive strength on the results. Another study used the Concrete Damage Rel3 model for the simulation of UHPC (ultra-high-performance concrete) targets, with and without fibers, while comparing the results with the experimental data [14]. The results show that the concrete reinforced with steel fibers had advantages in impact resistance and the impact crater diameter compared with the concrete reinforced with other fibers. Furthermore, the results show comparability of the variation of the crated diameter between the simulation and experiments.
The impact resistance of pre-damaged concrete targets was also investigated [15]. The penetration depth was compared between individual projectiles and two-stage munitions, which showed that two-stage munitions caused a higher depth of penetration. Another work compared the experimental data with simulations of a projectile impacting a concrete target under a specific angle, and compared the penetration depth [16]. The simulation utilized the PENE3D code using the finite difference method. The results of the penetration were that the error in penetration between the test and simulation tended to reduce with an increase in the penetration depth. The difference in the residual velocity and residual proportion of kinetic energy were investigated in another work to see the difference between a spiral projectile and an oval projectile for the interaction with concrete [17]. It showed an increase for both values, and also that the interaction between the target and the spiral induced the rotation of the projectile.
To find a reliable methodology for simulating projectile impact on structures located in the zones where projectile impact can occur was the goal of an independent study [18]. The effort utilized an RHT concrete failure model, while the projectile material allowed for deformation. Many different FEM software packages were used for this investigation. The findings led to the conclusion that LS-Dyna combined with an RHT concrete failure model led to the most suitable results for the projectile impact.
Experiments and simulations were performed on prestressed reinforced concrete targets, investigating the eroded material at the rear of the target [19]. A JC (Johnson-Cook) material model was used for the reinforcement, while an HJC (Holmquist-Johnson-Cook) model was used for the concrete. The results show that the prestressed concrete target showed a reduction in eroded material at the back.
Theoretical and experimental studies were conducted to investigate the penetration mechanisms of high-velocity projectiles (500 m/s to 1700 m/s) in concrete targets [20]. The results from these investigations show that there was a linear correlation between the impact velocity and the diameter and depth of the craters in the concrete targets. The performance of UHPFRC under projectile impact was examined using 7.62 mm diameter bullets, while steel fibers of different lengths were used for reinforcement [21]. The study showed that by varying the ratio of short to long fibers, and also by changing the number of fibers, the material volume loss and the penetration depth decreased. The study shows also that empirical formulae used for the penetration depth overestimated it, and therefore further experiments are needed to create formulae that show good results for UHPFRC. Concrete reinforced with steel fibers has been investigated for the impact of projectiles with different caliber sizes and muzzle energies [22]. This research shows that the failure modes depend on the fiber content and panel thickness, while increasing panel thickness caused the failure modes to change.
However, no simulation or experimental work has yet reported on the geometrical and shape consideration of the projectile in damage evolution in reinforced concrete components. Specifically, there is no research available that considers the angle of attack (AoA) with different projectile contours. As a matter of fact, the evolution of damage is a function of deformation and strain development in the component, and the AoA and the geometry of the projectile tip play a significant role in the determination of strain components and, consequently, damage due to a high-speed impact that induces instantaneous large deformations (i.e., high strain rate deformation). Accordingly, this work brings novelty and advances the boundaries of knowledge by taking the first steps towards considering the effects of geometrical and shape factors in damage resistance of reinforced concrete targets resisting large projectiles. To address the corresponding gap in the knowledge, this research uses FEM to simulate the damage and depth of penetration in reinforced concrete, as well as the results of the impact of the projectile with different tip contours hitting the concrete body at different angles, which makes this work novel.
2. Materials and Methods
The main investigation was how the change of specific parameters would affect the projectile impact into a concrete target. The first parameter that was varied was the tip contour of the projectile. It changed from 35° up to a flat tip (i.e., 180°), and a round tip was also included, which can be seen in Figure 1 along with the dimensions of the projectile. In total, six different tip contours were investigated. The second parameter that was varied was the angle of attack (AoA), which is the angle between the surface of the target and the trajectory of the projectile. The range of variation was between 30° to 90°.
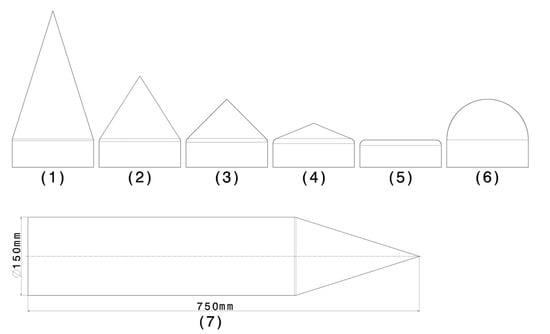
Figure 1.
Tip contours: (1) 35°, (2) 65°, (3) 90°, (4) 135°, (5) flat, (6) round and (7) projectile dimensions.
As a target for the simulation, a concrete block with steel reinforcement was used. The block had the dimensions of 2750 × 1000 × 750 mm (width × height × depth) with three layers of steel reinforcement that had a diameter of 20 mm. The target geometry can be seen in Figure 2.
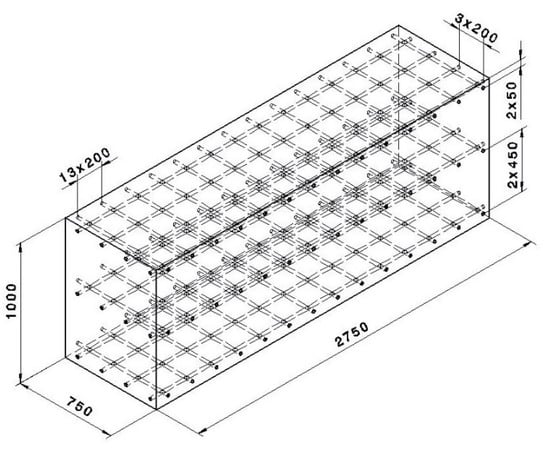
Figure 2.
Target geometry with measurements in mm and a reinforcement diameter of 20 mm.
The target in Figure 2 is a half model, as symmetry was applied to it to keep the simulative effort at a computationally lower cost. After conducting a mesh convergence study using the maximal penetration depth of the projectile tip, as Figure 3 shows, a mesh size of 35 mm was chosen to conduct all of the simulations. For the convergence study, an AoA of 45° with a tip angle of 35° was used, and a maximal penetration after 0.01 s has been reported. According to Figure 3, a mesh size of 35 mm provides an optimal relationship between the simulation time and penetration. Additionally, it is evident that changing the element size from 75 mm to 40 mm changed the results by 57%, while element sizes below 40 mm had a maximum of 9% difference; which is in the range of normal fluctuations of an Explicit FEA solver. Furthermore, an element size of 35 mm led to a simulation time for one case of 7.35 min, which is reasonable for the number of simulations performed.
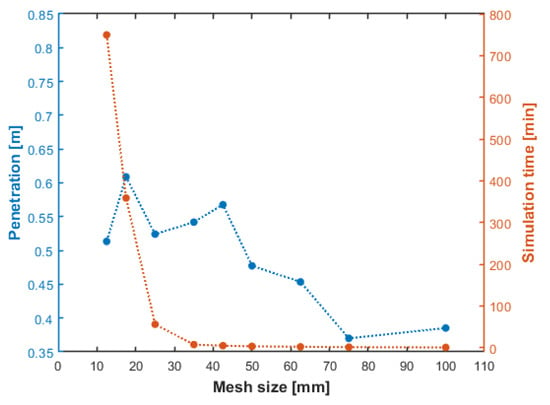
Figure 3.
Mesh convergence study results.
To model the concrete material of the target the Ansys material, CONC-35 MPA was used, which has also been applied in other research [23]. It uses the RHT concrete failure model to predict damage. The material parameters can be found in Table 1. These material properties, as described in detail elsewhere [23], govern stress, strain, strain rate, and damage parameter correlations, which are used in the calculations by the FEA software.

Table 1.
Material parameters CONC-35MPA [23].
The reported damage in the results is only for the concrete part of the target, and is based on the RHT concrete failure model. The RHT concrete failure model has the capability of pressure hardening, strain hardening, strain rate hardening, third invariant dependence of compressive and tensile meridians, damage effects (strain softening), and crack softening associated with brittle materials [24]. The factors that influenced the penetration of the projectile in the RHT model are the pressure and strain rate in compression. The damage of the material was determined through the factor D, which can be seen in Equation (1).
Here, Δεp is the accumulated plastic strain and εf is the failure strain given by Equation (2).
Parameters D1 and D2 in the failure strain are the material constants, while p is the pressure, pspall is the spall strength, and fc’ is the unconfined compression strength.
The steel used for reinforcement was AISI 4340 steel, which has also been used by independent research [23]. The material properties are listed in Table 2. The projectile had the material property of the AISI 4340 steel, but for the impact, a rigid behavior was assumed.

Table 2.
Material parameters AISI 4340 Steel [23].
The simulation was performed in Ansys® (ANSYS Inc., Canonsburg, PA, USA) using the Explicit Dynamics solver. The simulation setup assumed the projectile was a rigid body, so as to focus on the target without any change in the projectile. The initial velocity was set to 400 m/s for every tip contour and AoA. A body interaction was assigned to appropriately connect the reinforcement of the concrete. The contact between the projectile and the target was defined also through a body interaction that was set to frictionless. The mesh element order was set to linear and using a mesh size of 35 mm, as mentioned above, the number of elements for the target was 55,317. For the results, the penetration of the projectile tip was reported for the different tip contours over varying AoA. Furthermore, the damage was also reported for the concrete target. For the damage, a nodal threshold of 0.01 was used to define a damaged node; therefore, every node with a damage of >0.01 was reported as damaged.
3. Results
3.1. Penetration
Figure 4 illustrates the penetration over the AoA of the projectile tip for the different tip contours. As evident, a value for the penetration of 1 m (1000 mm) is equivalent to reaching that depth or to penetrating all the way through the target, as the height/thickness of the target is 1 m. What becomes clear is that the steeper the AoA, the deeper the penetration, independent of the tip contour.
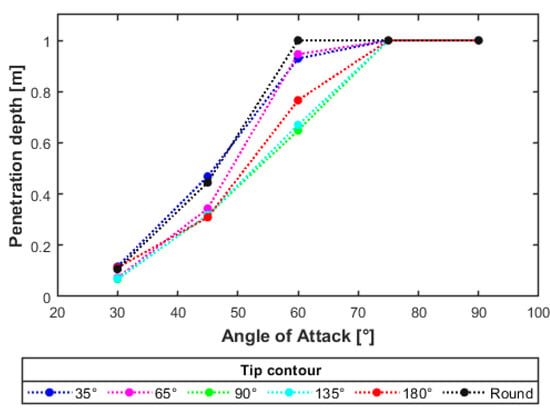
Figure 4.
Penetraion vs. AoA.
The different tip contours show the same trend of penetration over the variation of AoA. An AoA of 90° shows that full penetration of the target is present for all tips. On the other side, an AoA of 30° shows only little penetration, as this AoA leads to the projectile bouncing off of the target after damaging the surface and reaching the reinforcement. A significant decrease in penetration can be seen when comparing the penetration of reinforced with non-reinforced concrete. This was studied for a tip contour of 90° and is demonstrated in Figure 5. It is worthy of attention that similar to other literature reports, such as [20], the possible behavior with the change in velocity can be estimated. The penetration depth and crater for non-fully-penetration projectiles would increase when increasing the velocity, and a reduction in velocity would see the opposite trend. An increased speed would possibly, especially for a low AoA, increase the damage as the possibility of the projectile penetrating the target becomes higher.
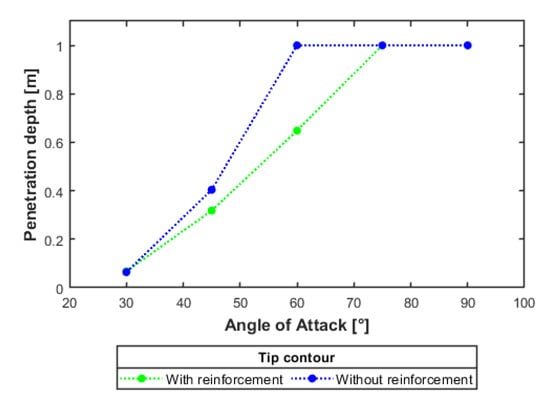
Figure 5.
Penetration of reinforced vs. non-reinforced concrete.
3.2. Damage
In Figure 6, the percent of damage of the concrete part of the target for the different tip contours over a variation of AoA can be seen.
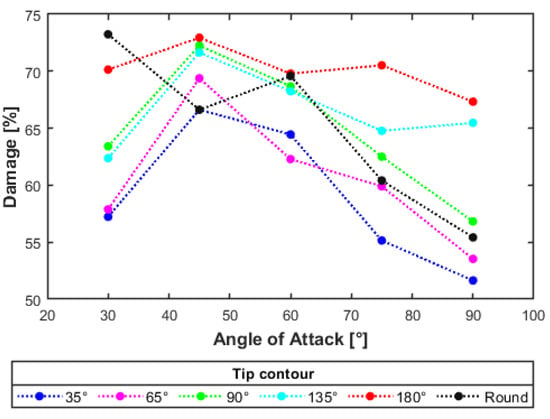
Figure 6.
Damage vs. AoA.
From the figure, it can be seen that most of the projectiles show a similar trend of the percent of damage they cause on the concrete part of the target. The lower damage at an AoA of 30° is caused by the bouncing off of the target, therefore not causing too much damage on the target. An example of the extent of damage for an AoA of 30° with a tip angle of 35° can be seen in Figure 7.
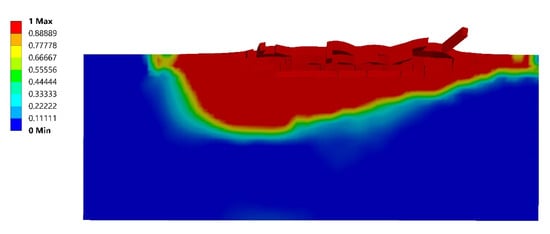
Figure 7.
Damage of a 35° tip angle AoA 30° projectile bouncing off of the target.
The decrease in damage at a higher AoA, like 90°, is caused by the fact that the extent of damage, in this case, is limited to the area around the path the projectile created when passing through the target, which can be seen in Figure 8.
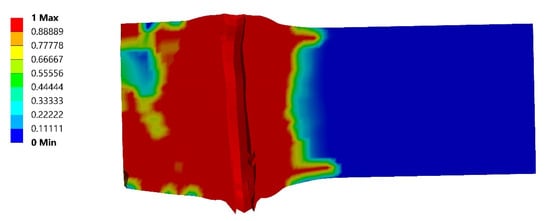
Figure 8.
Damage—35° tip angle-AoA 90°, projectile passing through the target.
For this case, the 180° tip shows the highest value, which can be concluded through the fact that a flat tip creates more damage than a sharp tip, which passes easier through the material. The data for a round tip does not really follow the trend of the other tip contours for a low AoA. This can be explained by this tip being able to dig in slightly under the top surface of the target and penetrating further through the target, more than the other tip contours, before also leaving the target towards the top. As there is no published research on how the variation of AoA and tip contour influence the penetration and damage, an AoA of 90°, which is often reported in the literature, works best for comparing the findings of this work against the published reports. Additionally, projectiles fired by handguns are mostly used, while this work looks at bigger projectiles (i.e., missiles) and their impact on a reinforced concrete wall, thus deepening the current understanding of the behavior of reinforced concrete structures. Comparing the damage results from an AoA of 90° with the simulated damage results found in [25], the contour plots of the damage, deformation, and material separation of the target shows the same pattern at the impact area, which leads to the conclusion that the results of this research are valid. Additionally, comparing the results of the damage to [3] (both simulations and experiments), the scabbing and the projectile path generation are essentially the same, which are both simulative and experimental. Furthermore, comparing the penetrating behavior damage of a projectile with AoA of 90° with the results of the physical tests of [12], where a bigger projectile was studied, it can be concluded that the impact crater and deformation pattern reported by this work and [12] are the same.
4. Conclusions
The penetration of a projectile with different tip contours and the damage in a reinforced concrete target have been reported over different AoAs. Damage of the concrete target was obtained using an RHT concrete failure model. The results show the following:
- The penetration had a similar behavior for all tip contours and mostly depended on the AoA. A flat AoA caused bouncing off of the target and therefore a low penetration.
- A similar tendency for penetration could be also seen in unreinforced concrete. However, the penetration depth for a specific case was significantly reduced with reinforced compared with unreinforced concrete.
- The damage had a similar, but less significant, behavior over all tip contours, while the lowest damage was mostly caused for a flat AoA because of bouncing off of the projectile. A flat tip of the projectile caused the highest damage on the target overall.
- A round tip had a significant difference in damage for an AoA of 30°, which was caused by the projectile digging it into the target right below the surface.
Future investigations should look at deformable projectiles and also look into the comparison of different failure models for the target.
Author Contributions
Conceptualization, A.T.; methodology, A.T.; software, S.P.J.; validation, A.T. and S.P.J.; formal analysis, S.P.J.; investigation, S.P.J.; resources, A.T.; writing—original draft preparation, S.P.J.; writing—review and editing, A.T.; visualization, S.P.J.; supervision, A.T.; project administration, A.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be available by request to authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, S.; Kong, X.; Fang, Q.; Chen, L.; Wang, Y. Numerical Prediction of Dynamic Failure in Concrete Targets Subjected to Projectile Impact by a Modified Kong-Fang Material Model. Int. J. Impact Eng. 2020, 144, 103633. [Google Scholar] [CrossRef]
- Kong, X.; Fang, Q.; Li, Q.M.; Wu, H.; Crawford, J.E. Modified K&C Model for Cratering and Scabbing of Concrete Slabs under Projectile Impact. Int. J. Impact Eng. 2017, 108, 217–228. [Google Scholar] [CrossRef]
- Rajput, A.; Iqbal, M.A.; Gupta, N.K. Ballistic Performances of Concrete Targets Subjected to Long Projectile Impact. Thin-Walled Struct. 2018, 126, 171–181. [Google Scholar] [CrossRef]
- Xu, X.; Ma, T.; Ning, J. Failure Mechanism of Reinforced Concrete Subjected to Projectile Impact Loading. Eng. Fail. Anal. 2019, 96, 468–483. [Google Scholar] [CrossRef]
- Feng, J.; Gao, X.; Li, J.; Dong, H.; He, Q.; Liang, J.; Sun, W. Penetration Resistance of Hybrid-Fiber-Reinforced High-Strength Concrete under Projectile Multi-Impact. Constr. Build. Mater. 2019, 202, 341–352. [Google Scholar] [CrossRef]
- Tabei, A.; Li, D.S.; Lavender, C.A.; Garmestani, H. Investigation of Precipitate Refinement in Mg Alloys by an Analytical Composite Failure Model. Mech. Mater. 2015, 89, 59–71. [Google Scholar] [CrossRef]
- Tabei, A.; Ahzi, S.; Li, D.S.; Lavender, C.A.; Garmestani, H. Effects of Morphology and Geometry of Inclusions on Two-Point Correlation Statistics in Two Phase Composites. Int. J. Theor. Appl. Multiscale Mech. 2014, 3, 1–17. [Google Scholar] [CrossRef]
- Lyons, C.K.; Tabei, A.; Sobhani, S. Energy Absorbing Cab Guards for Log Trucks. Int. J. For. Eng. 2021, 1–8. [Google Scholar] [CrossRef]
- Wu, C.T.; Wu, Y.; Crawford, J.E.; Magallanes, J.M. Three-Dimensional Concrete Impact and Penetration Simulations Using the Smoothed Particle Galerkin Method. Int. J. Impact Eng. 2017, 106, 1–17. [Google Scholar] [CrossRef]
- Oucif, C.; Kalyana Rama, J.S.; Shankar Ram, K.; Abed, F. Damage Modeling of Ballistic Penetration and Impact Behavior of Concrete Panel under Low and High Velocities. Def. Technol. 2021, 17, 202–211. [Google Scholar] [CrossRef]
- Blasone, M.; Saletti, D.; Baroth, J.; Forquin, P.; Bonnet, E.; Delaplace, A. Ultra-High Performance Fibre-Reinforced Concrete under Impact of an AP Projectile: Parameter Identification and Numerical Modelling Using the DFHcoh-KST Coupled Model. Int. J. Impact Eng. 2021, 152, 103838. [Google Scholar] [CrossRef]
- Ning, J.; Meng, F.; Ma, T.; Xu, X. Failure Analysis of Reinforced Concrete Slab under Impact Loading Using a Novel Numerical Method. Int. J. Impact Eng. 2020, 144, 103647. [Google Scholar] [CrossRef]
- Abdel-Kader, M. Modified Settings of Concrete Parameters in RHT Model for Predicting the Response of Concrete Panels to Impact. Int. J. Impact Eng. 2019, 132, 103312. [Google Scholar] [CrossRef]
- Liu, J.; Wu, C.; Su, Y.; Li, J.; Shao, R.; Chen, G.; Liu, Z. Experimental and Numerical Studies of Ultra-High Performance Concrete Targets against High-Velocity Projectile Impacts. Eng. Struct. 2018, 173, 166–179. [Google Scholar] [CrossRef]
- Hu, F.; Wu, H.; Fang, Q.; Liu, J.C. Impact Resistance of Concrete Targets Pre-Damaged by Explosively Formed Projectile (EFP) against Rigid Projectile. Int. J. Impact Eng. 2018, 122, 251–264. [Google Scholar] [CrossRef]
- Chen, X.; Lu, F.; Zhang, D. Penetration Trajectory of Concrete Targets by Ogived Steel Projectiles–Experiments and Simulations. Int. J. Impact Eng. 2018, 120, 202–213. [Google Scholar] [CrossRef]
- Wu, J.; Ning, J.; Ma, T. The Dynamic Response and Failure Behavior of Concrete Subjected to New Spiral Projectile Impacts. Eng. Fail. Anal. 2017, 79, 547–564. [Google Scholar] [CrossRef]
- Pavlovic, A.; Fragassa, C.; Disic, A. Comparative Numerical and Experimental Study of Projectile Impact on Reinforced Concrete. Compos. Part B Eng. 2017, 108, 122–130. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Rajput, A.; Gupta, N.K. Performance of Prestressed Concrete Targets against Projectile Impact. Int. J. Impact Eng. 2017, 110, 15–25. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, X.; Chen, H.; Wang, J.; Wei, H.; Xiong, W. Experimental and Theoretical Study on Steel Long-Rod Projectile Penetration into Concrete Targets with Elevated Impact Velocities. Int. J. Impact Eng. 2020, 138, 103482. [Google Scholar] [CrossRef]
- Mina, A.L.; Petrou, M.F.; Trezos, K.G. Resistance of an Optimized Ultra-High Performance Fiber Reinforced Concrete to Projectile Impact. Buildings 2021, 11, 63. [Google Scholar] [CrossRef]
- Jamnam, S.; Maho, B.; Techaphatthanakon, A.; Sonoda, Y.; Yoo, D.-Y.; Sukontasukkul, P. Steel Fiber Reinforced Concrete Panels Subjected to Impact Projectiles with Different Caliber Sizes and Muzzle Energies. Case Stud. Constr. Mater. 2020, 13, e00360. [Google Scholar] [CrossRef]
- Elhozayen, A.E.; Lassi, M.Y.; Attia, W.A. Numerical modeling of high-velocity, projectile penetrating concrete blocks reinforced by teflon sheets. WIT Trans. Eng. Sci. 2019, 125, 15–25. [Google Scholar] [CrossRef]
- Leelavanichkul, S.; Brannon, R.M. Survey of Four Damage Models for Concrete; SAND2009-5544, 993922; Sandia National Laboraotories: Albuquerque, NM, USA, 2009. [Google Scholar] [CrossRef][Green Version]
- Tham, C.Y. Numerical and Empirical Approach in Predicting the Penetration of a Concrete Target by an Ogive-Nosed Projectile. Finite Elem. Anal. Des. 2006, 42, 1258–1268. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).