Author Contributions
Conceptualization, M.S. and F.A.; methodology, M.S.; software, M.S., M.P. and M.H.; validation, M.S., F.A. and M.P.; formal analysis, M.S. and F.A; investigation, M.S., F.A. and M.P.; resources M.S., F.A., M.P. and M.H.; data curation, M.S., F.A., M.P. and M.H; writing—original draft preparation, M.S.; writing—review and editing, M.S., F.A., M.P. and M.H.; visualization, M.S.; supervision, F.A. and M.P.; project administration, M.S. and F.A.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Figure 1.
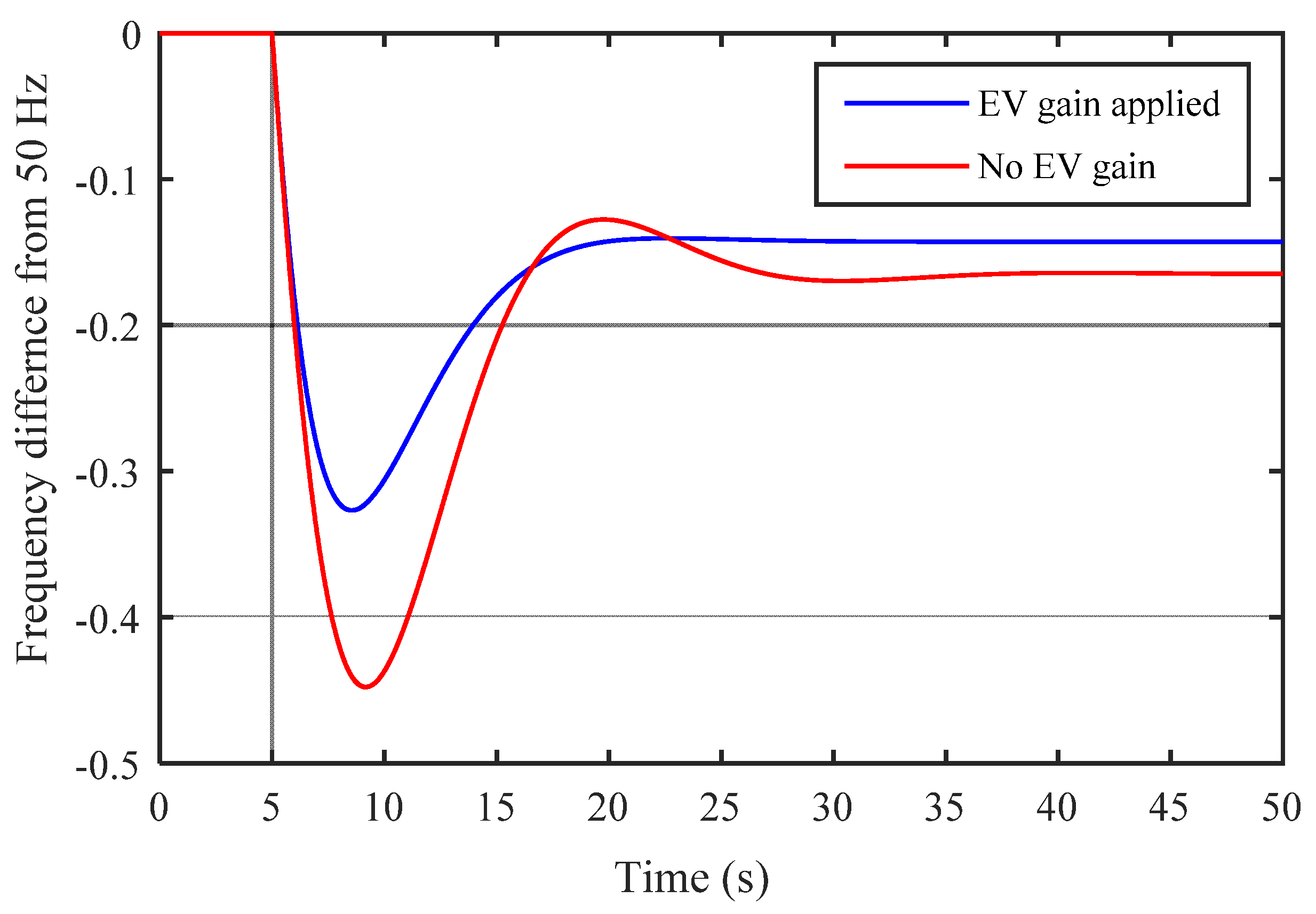
Frequency fluctuations following the loss of generation up to 1800 MW [
1].
Figure 1.
Frequency fluctuations following the loss of generation up to 1800 MW [
1].
Figure 2.
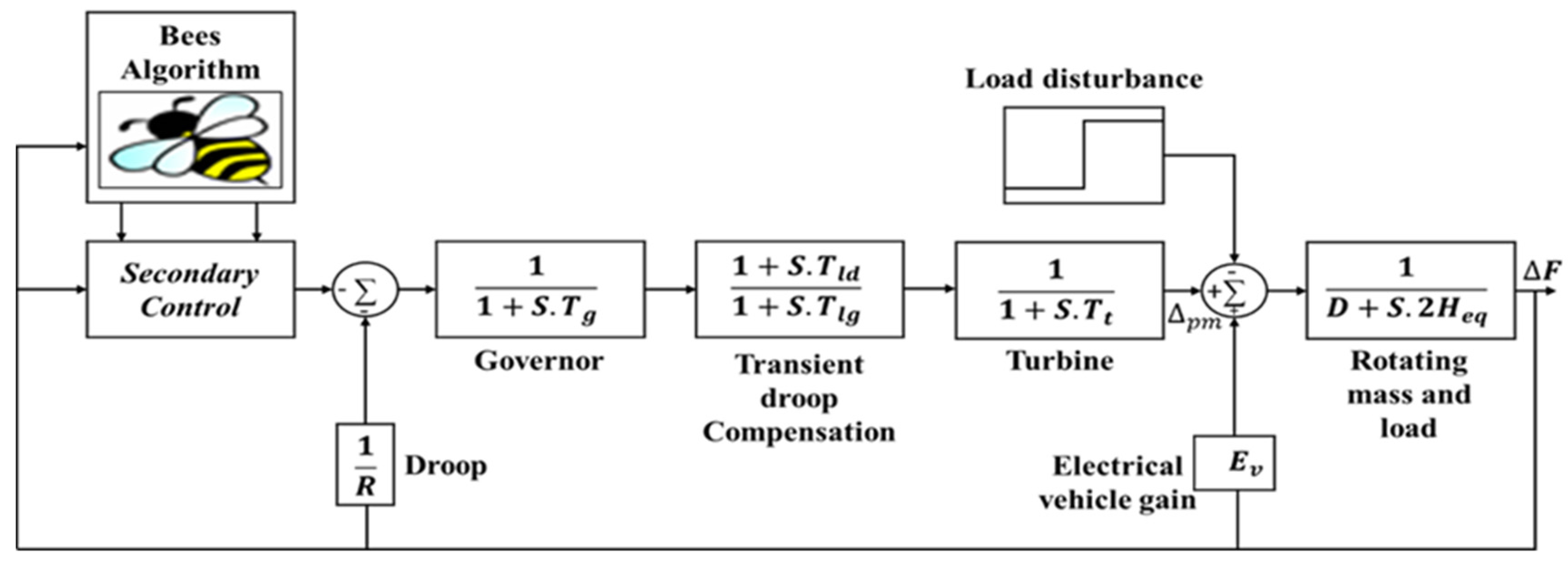
GB simplified power system.
Figure 2.
GB simplified power system.
Figure 3.
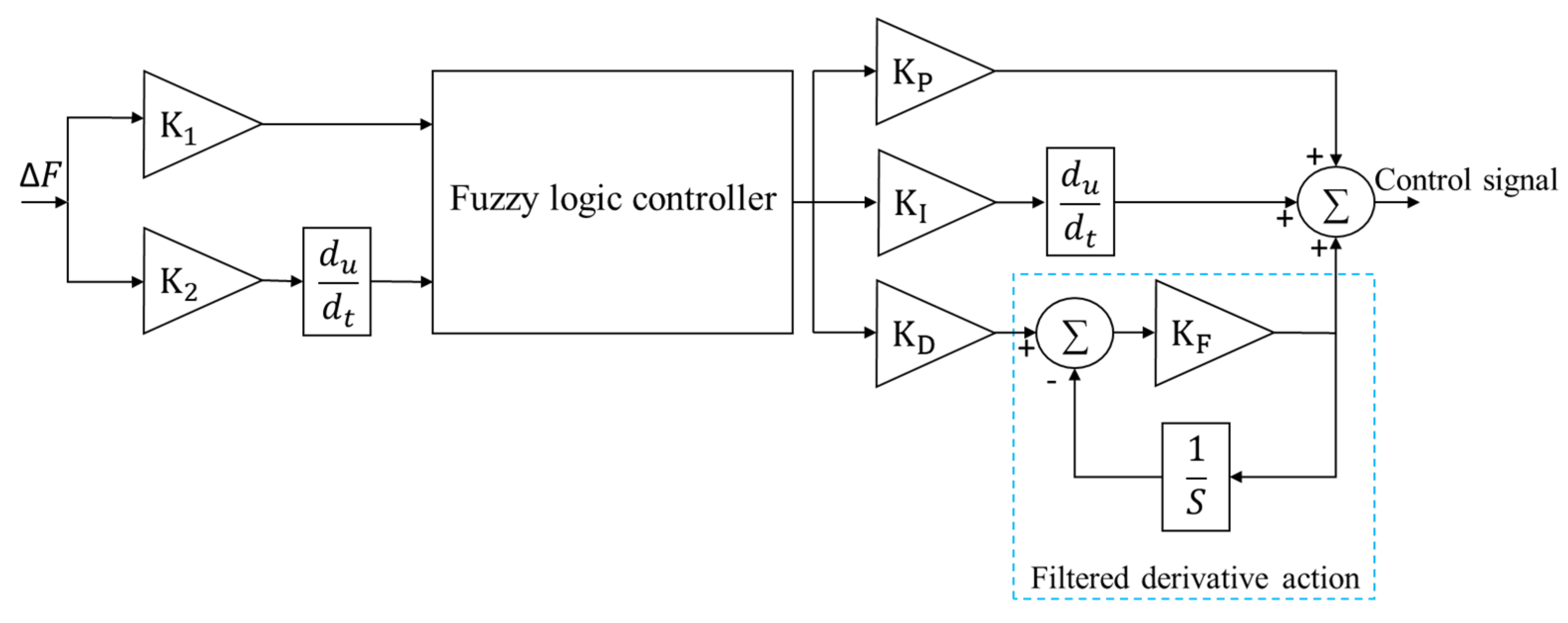
Structural diagram of fuzzy PIDF controller.
Figure 3.
Structural diagram of fuzzy PIDF controller.
Figure 4.
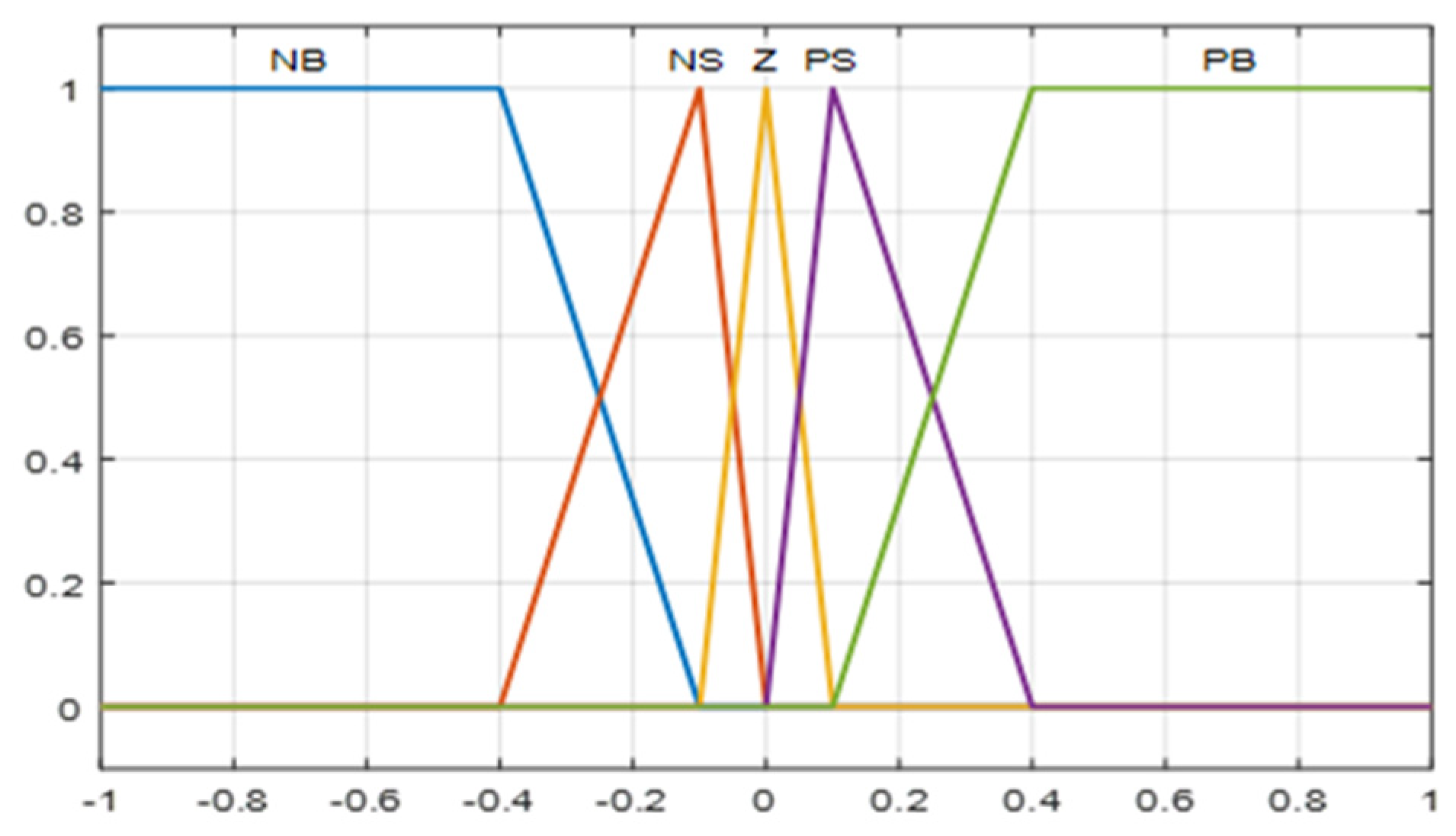
Membership functions of the two inputs and output.
Figure 4.
Membership functions of the two inputs and output.
Figure 5.
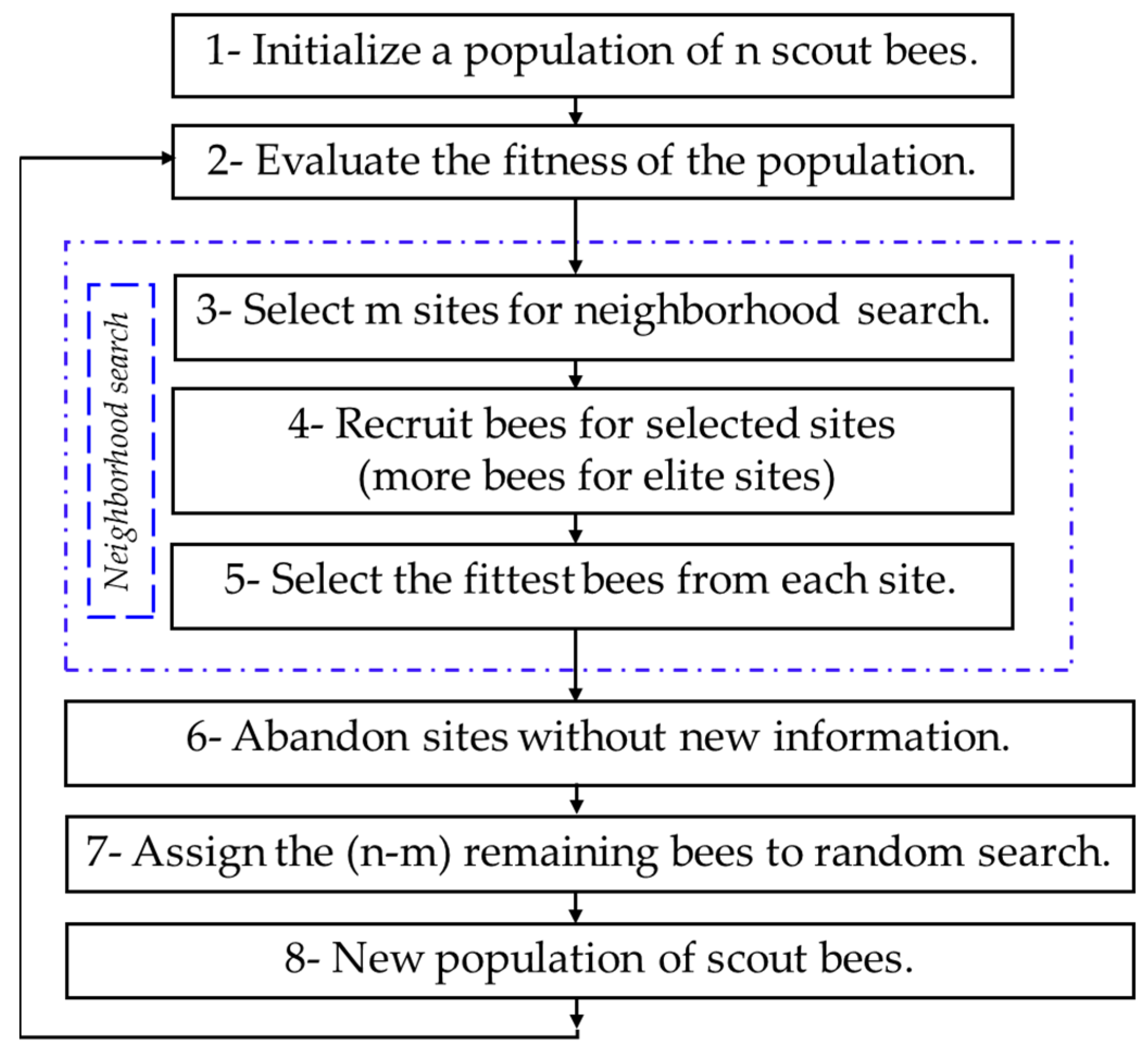
The Bees Algorithm flowchart.
Figure 5.
The Bees Algorithm flowchart.
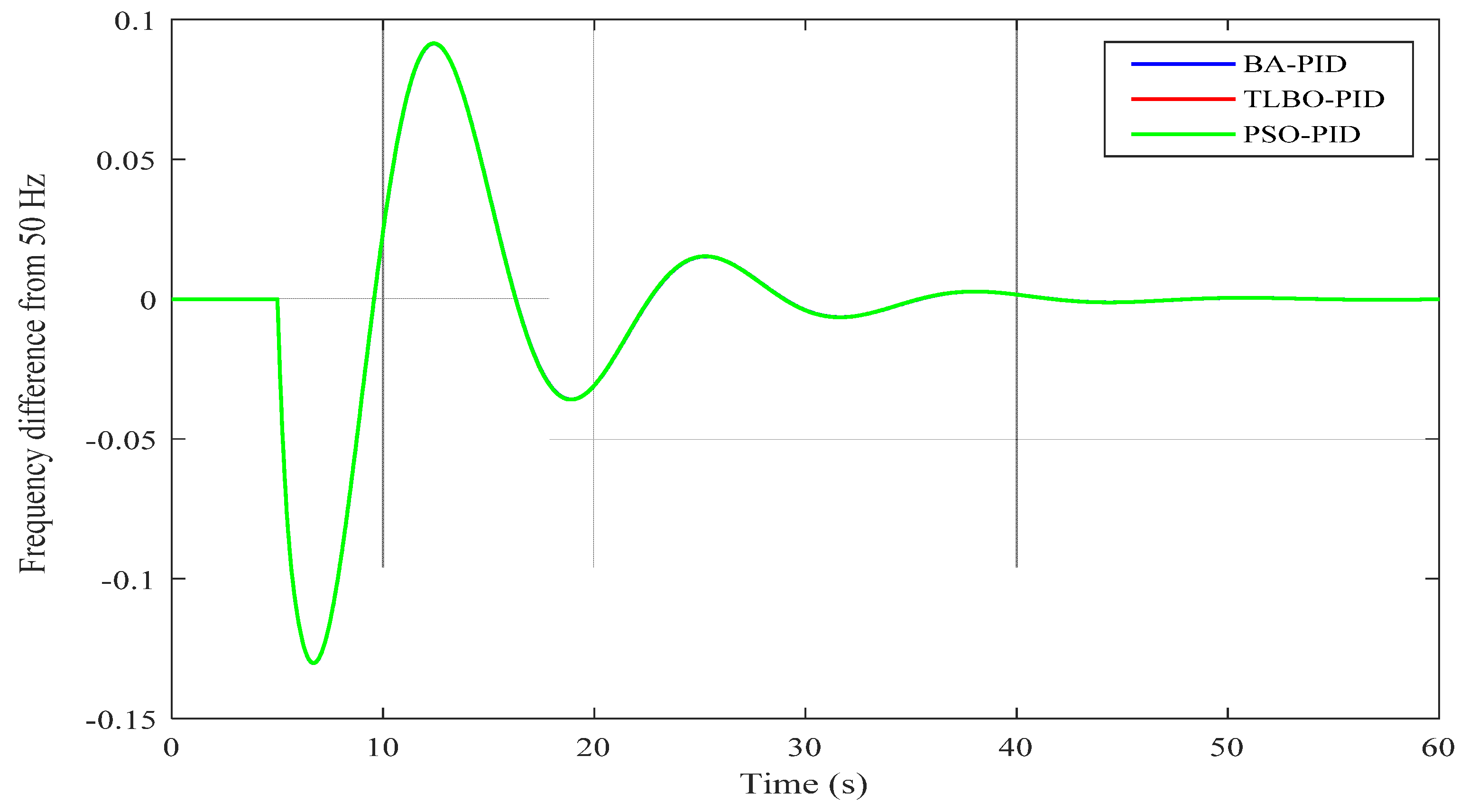
Figure 6.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned PID-based ISE.
Figure 6.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned PID-based ISE.
Figure 7.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned PID-based ITAE.
Figure 7.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned PID-based ITAE.
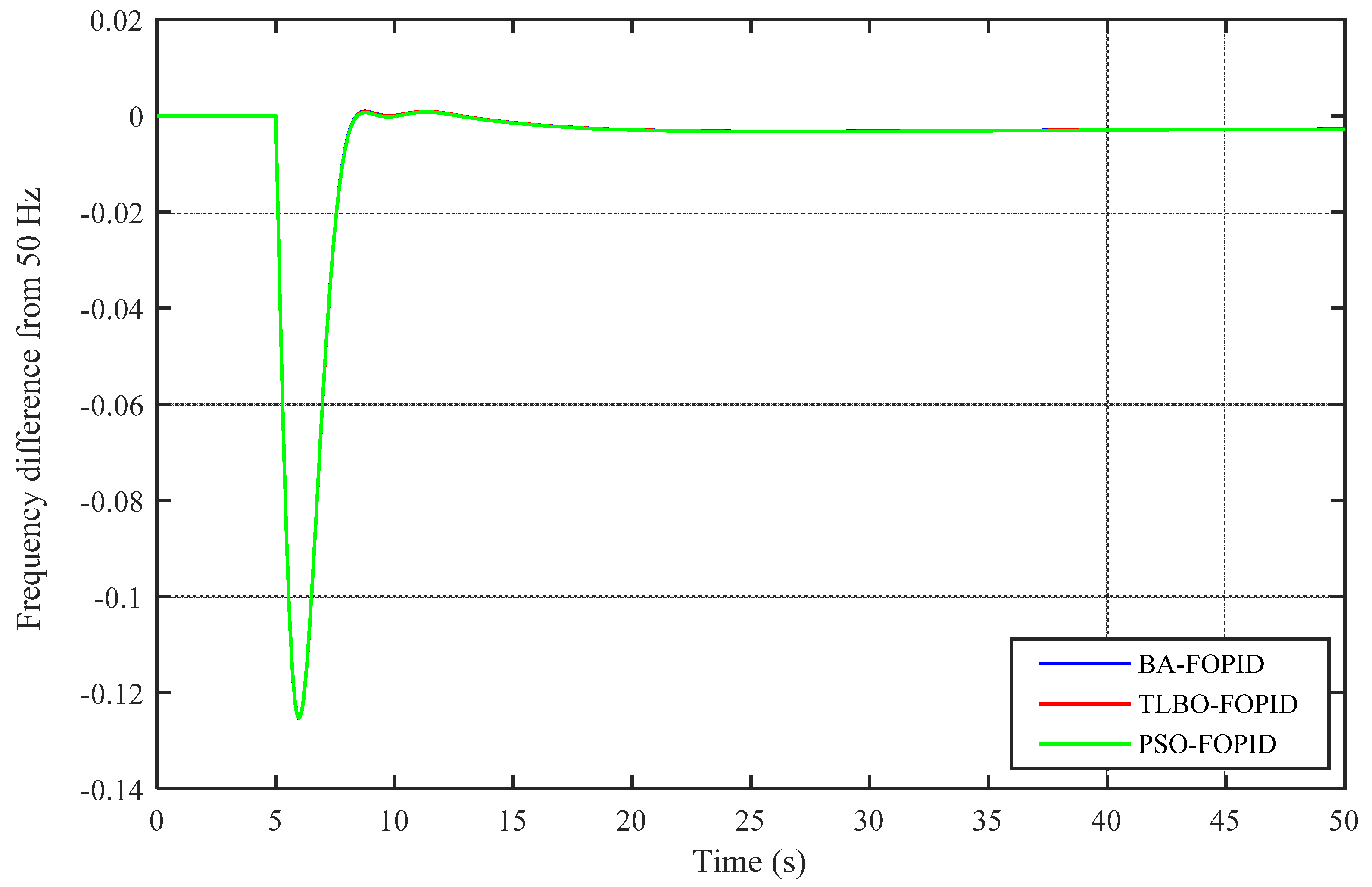
Figure 8.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned FOPID-based ISE.
Figure 8.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned FOPID-based ISE.
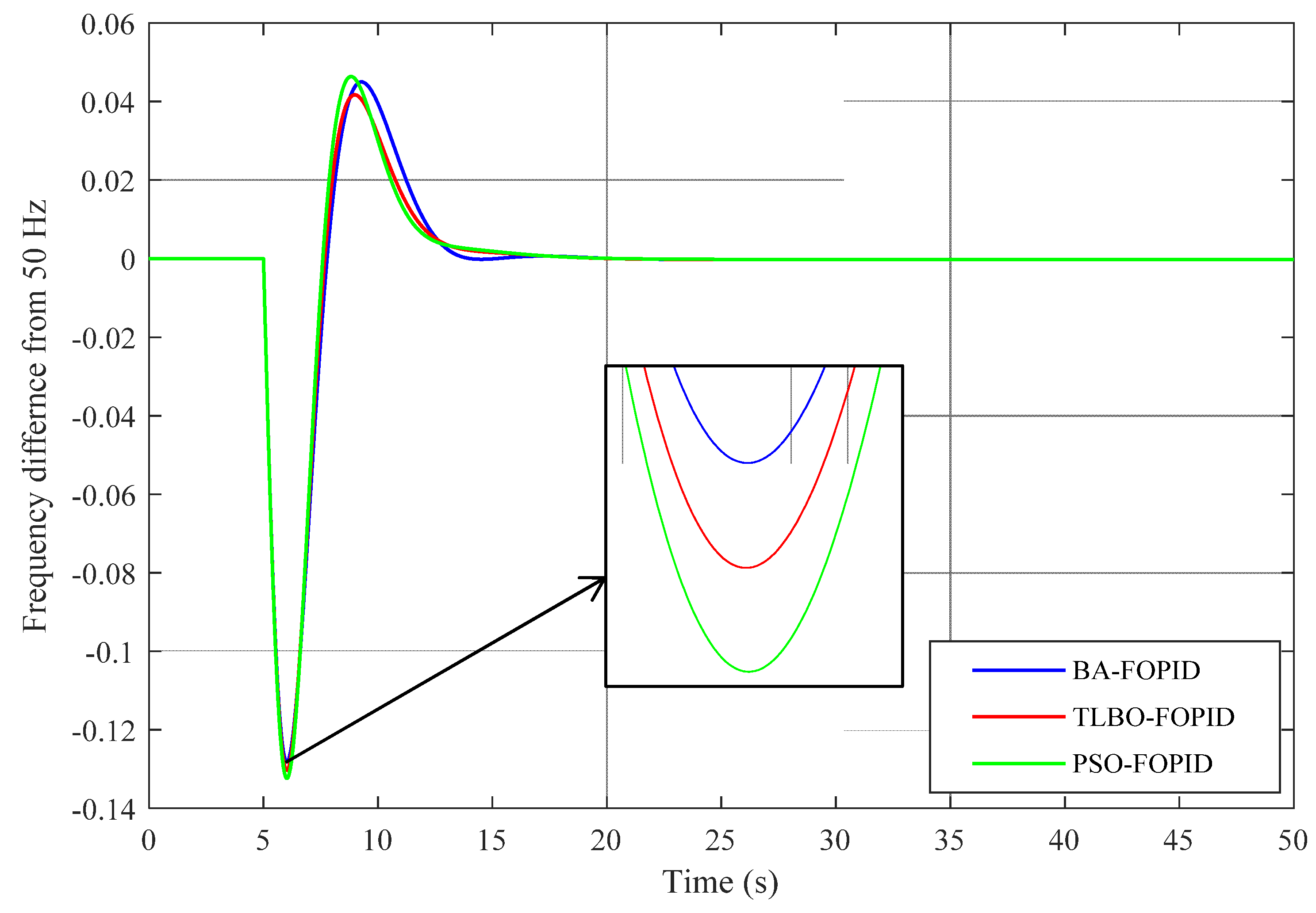
Figure 9.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned FOPID-based ITAE.
Figure 9.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned FOPID-based ITAE.
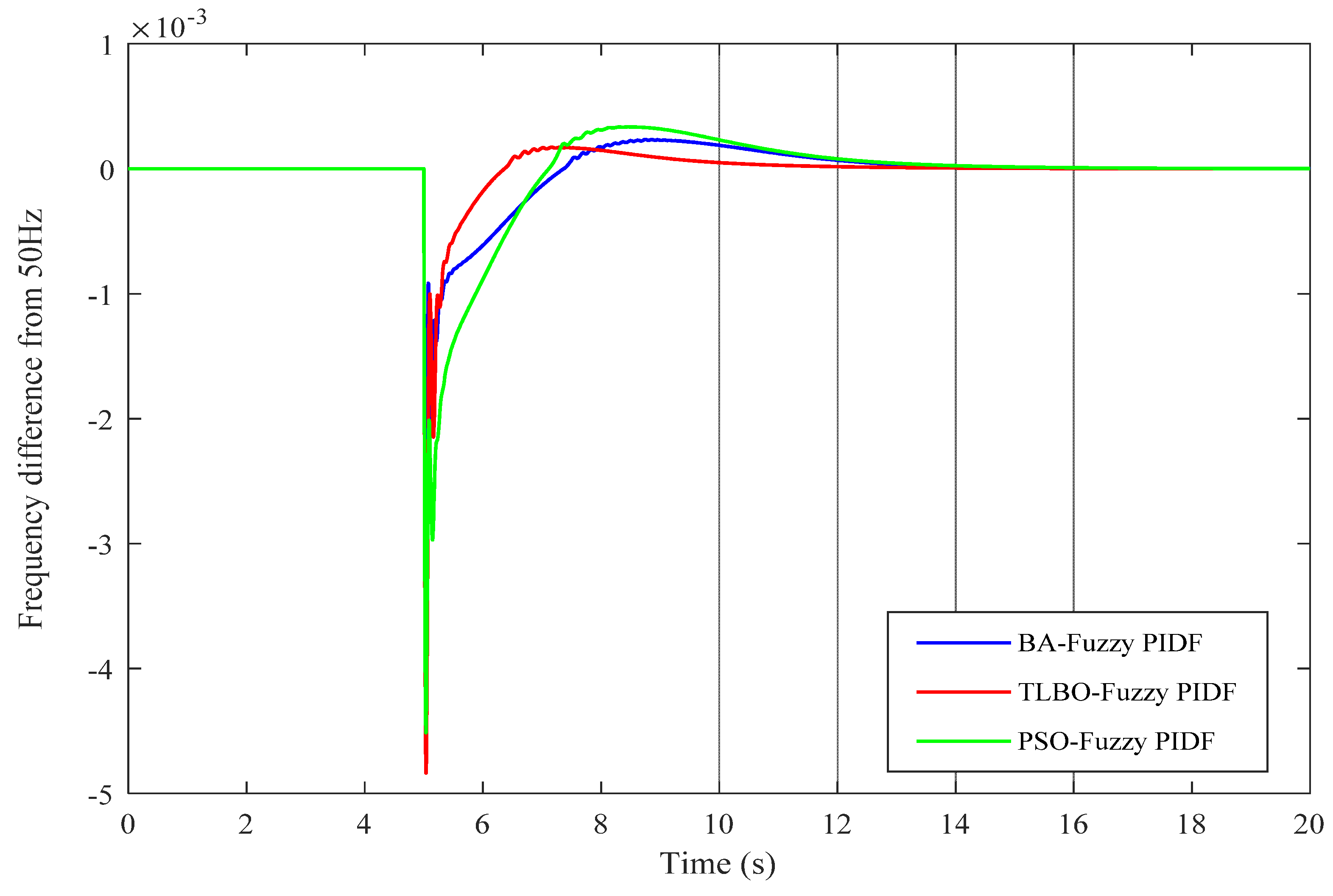
Figure 10.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned Fuzzy PIDF-based ISE.
Figure 10.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned Fuzzy PIDF-based ISE.
Figure 11.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned Fuzzy PIDF-based ITAE.
Figure 11.
Change in frequency in the GB power system for 0.035 pu load disturbance with tuned Fuzzy PIDF-based ITAE.
Figure 12.
Comparison of the dynamic response of GB power model with parameter uncertainties of scenarios 1 and 2 with no secondary control loop.
Figure 12.
Comparison of the dynamic response of GB power model with parameter uncertainties of scenarios 1 and 2 with no secondary control loop.
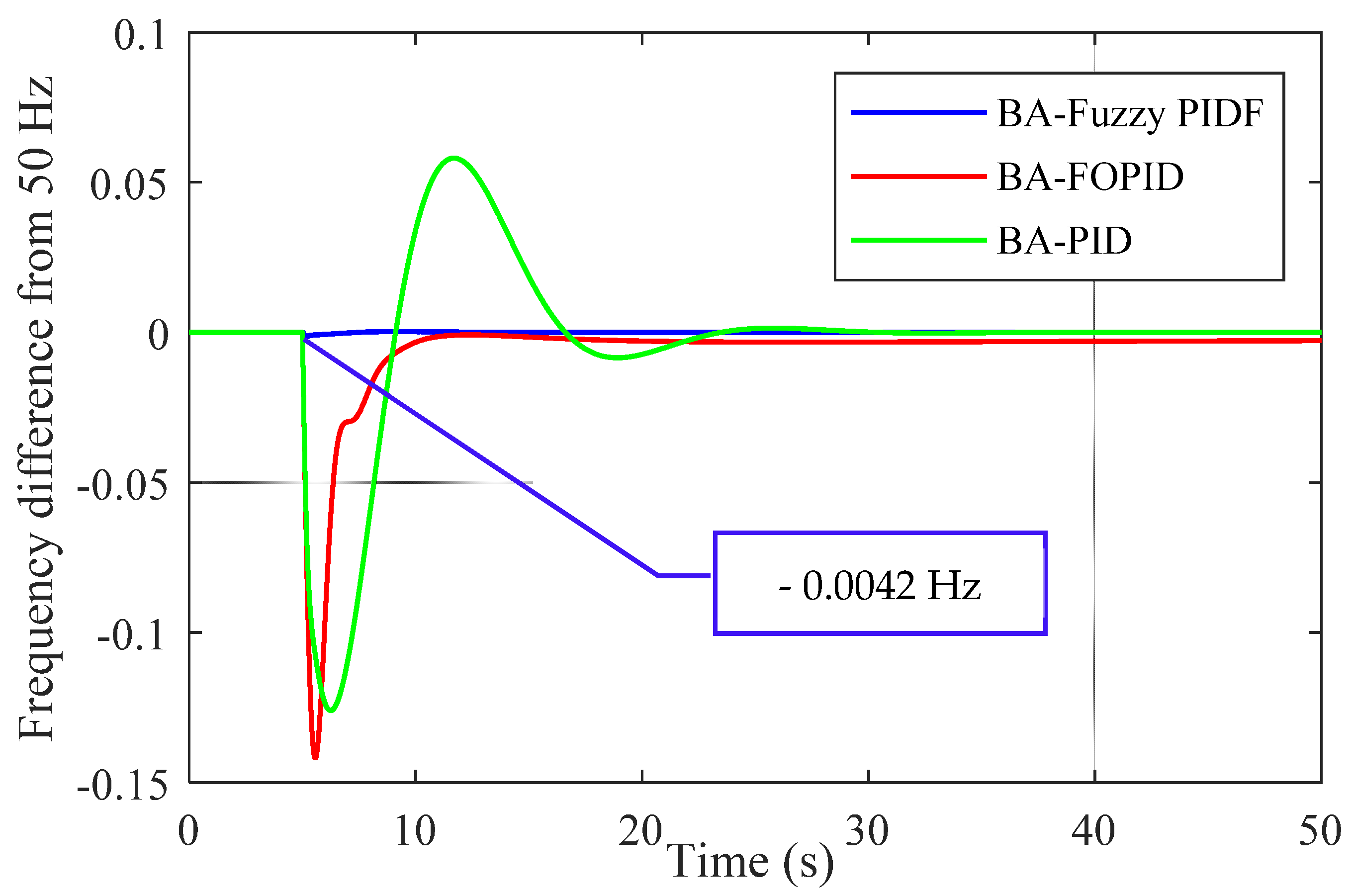
Figure 13.
Comparison of three controllers tuned by BA based on ISE for scenario 2.
Figure 13.
Comparison of three controllers tuned by BA based on ISE for scenario 2.
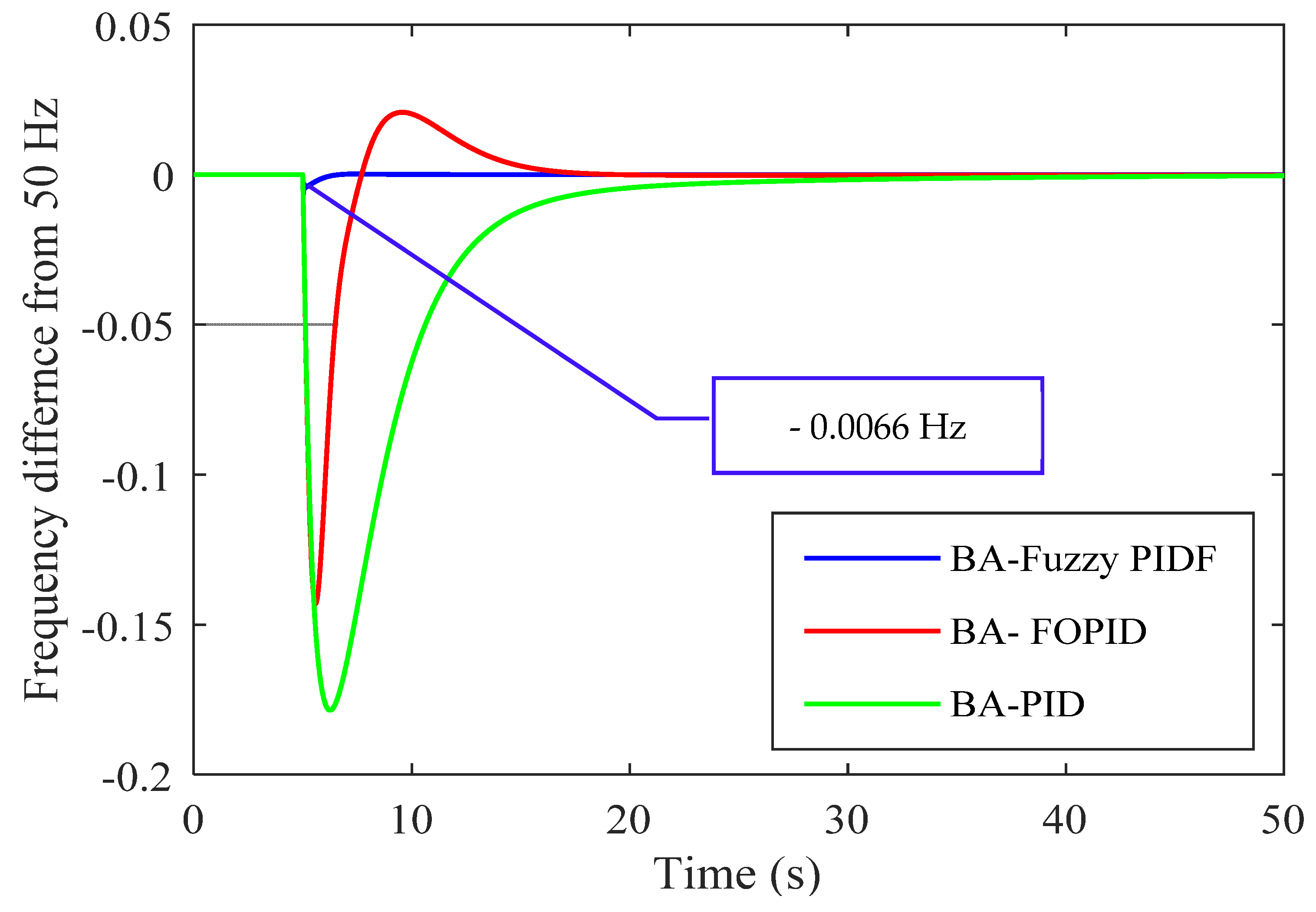
Figure 14.
Comparison of three controllers tuned by BA based on ITAE for scenario 2.
Figure 14.
Comparison of three controllers tuned by BA based on ITAE for scenario 2.
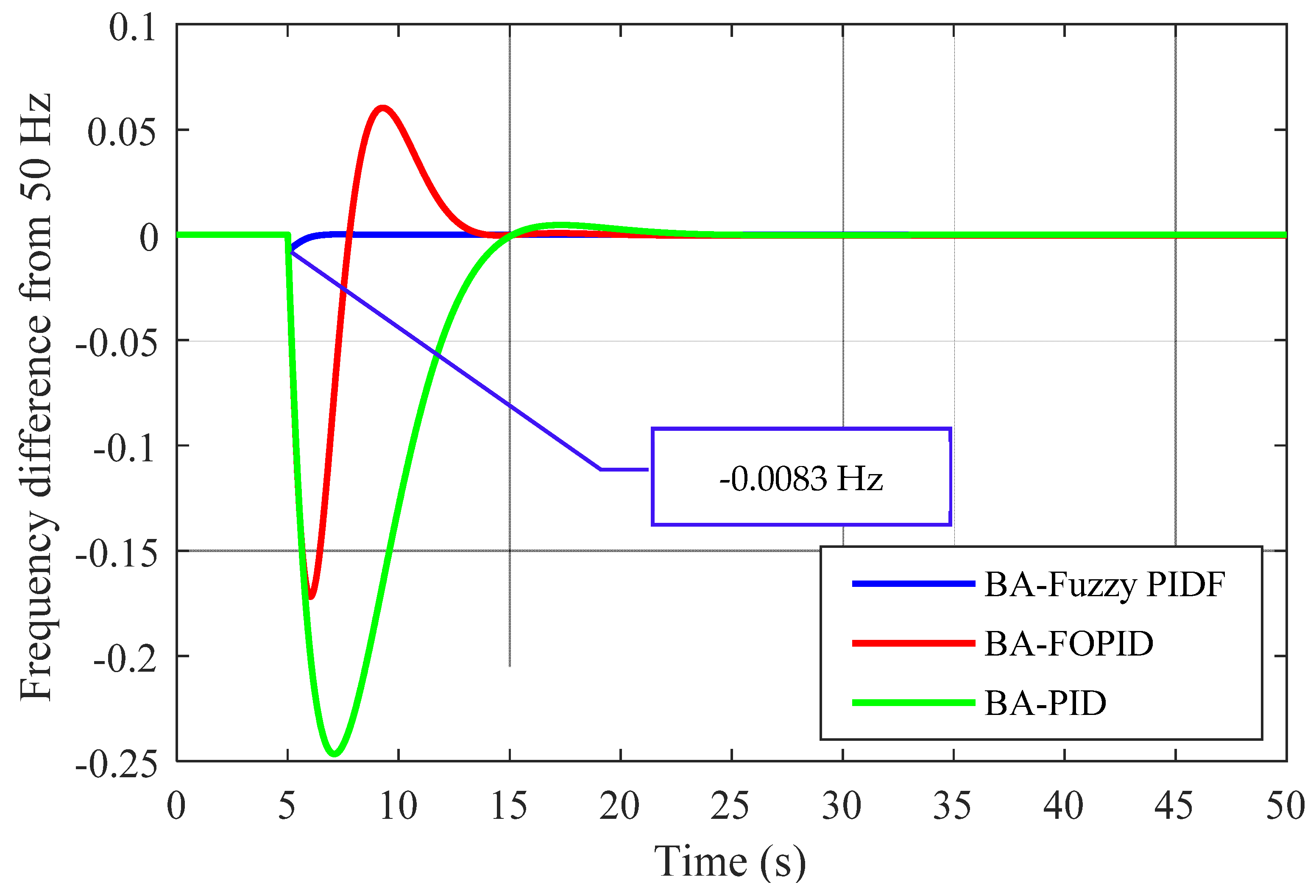
Figure 15.
Comparison of three controllers tuned by BA based on ITAE for LFC of the GB system in the nominal scenario with 0.053 pu load disturbance.
Figure 15.
Comparison of three controllers tuned by BA based on ITAE for LFC of the GB system in the nominal scenario with 0.053 pu load disturbance.
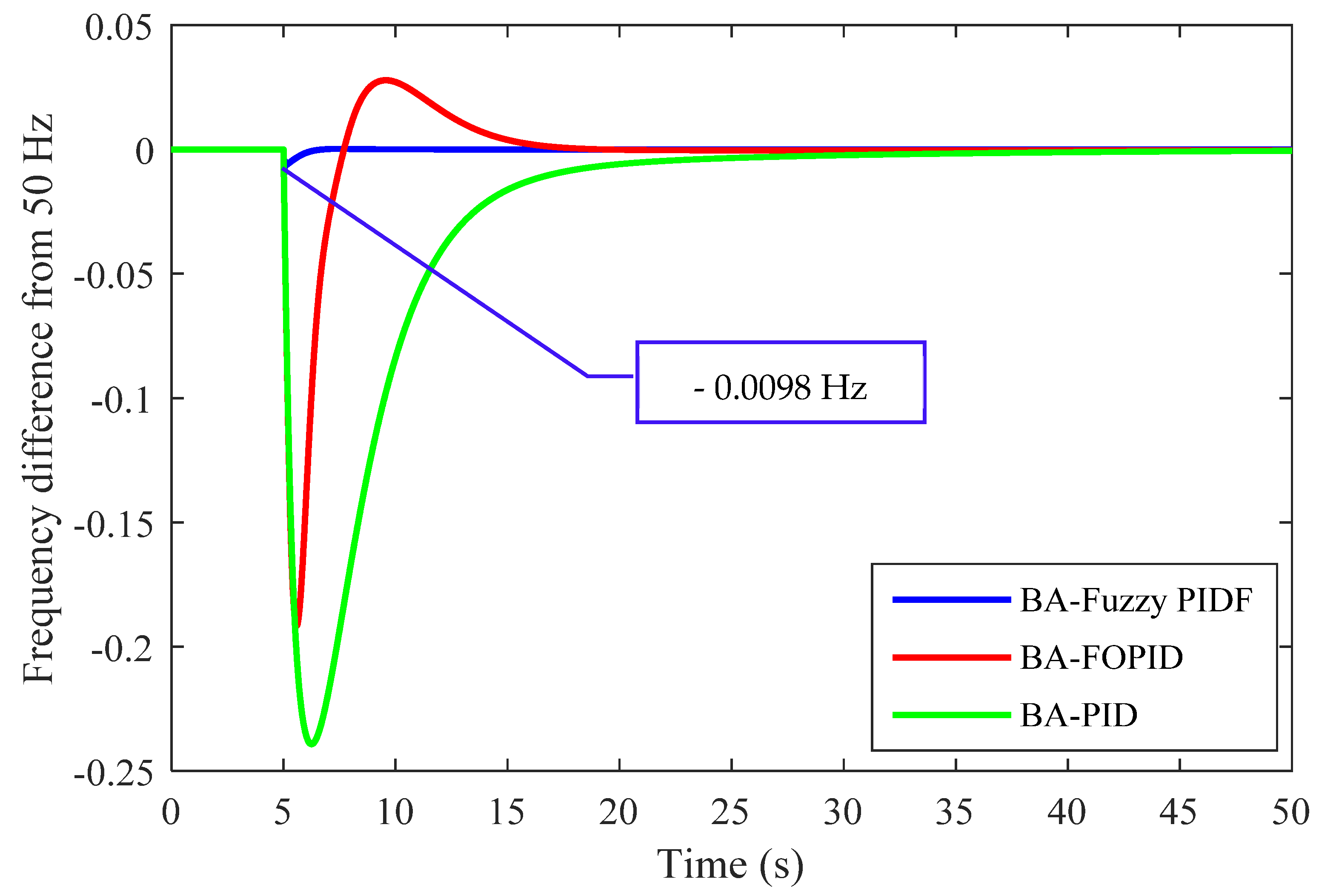
Figure 16.
Comparison of three controllers tuned by BA based on ITAE for LFC of the GB system in scenario 2 with 0.053 pu load disturbance.
Figure 16.
Comparison of three controllers tuned by BA based on ITAE for LFC of the GB system in scenario 2 with 0.053 pu load disturbance.
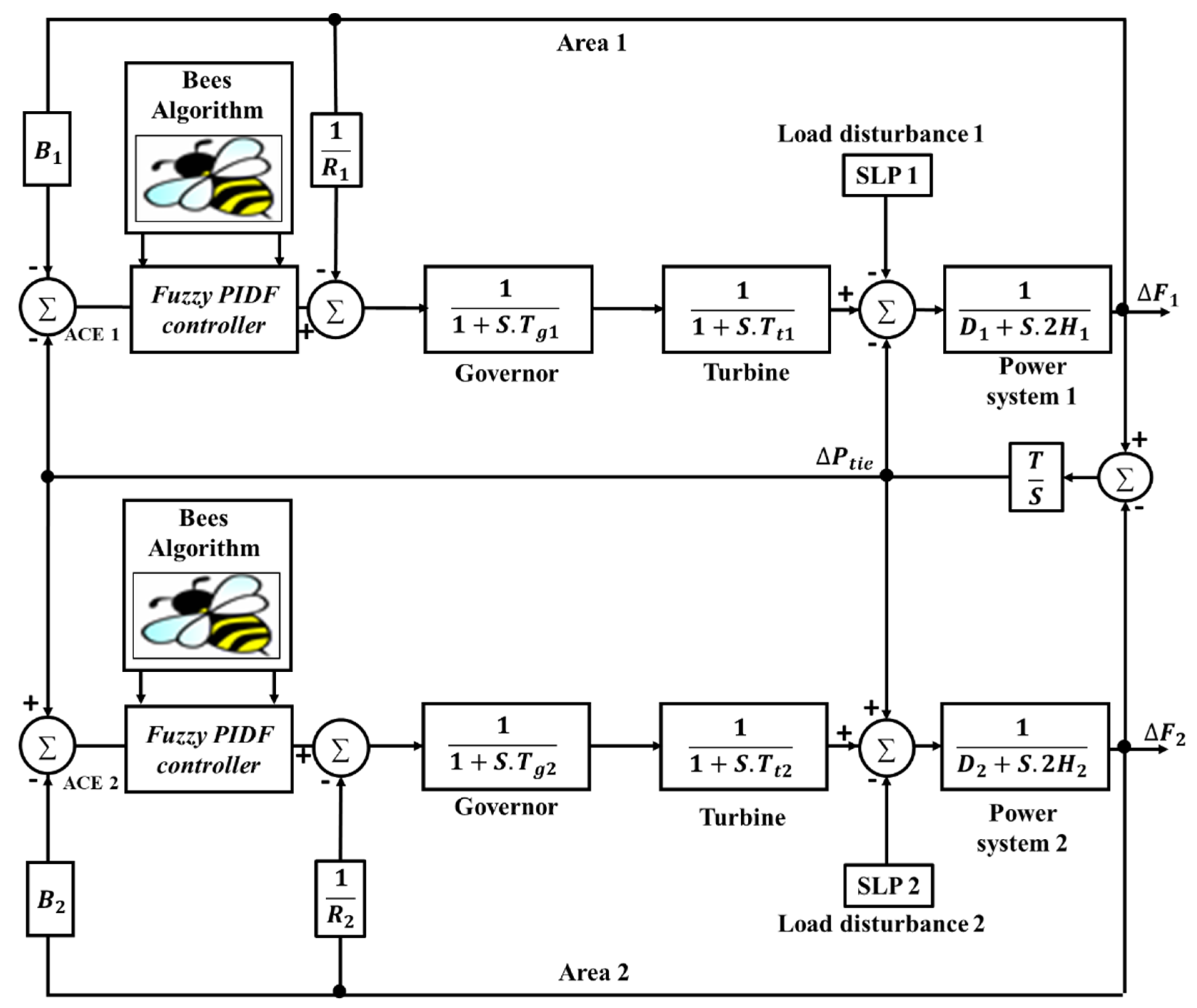
Figure 17.
Transfer function model of the investigated dual-area power system.
Figure 17.
Transfer function model of the investigated dual-area power system.
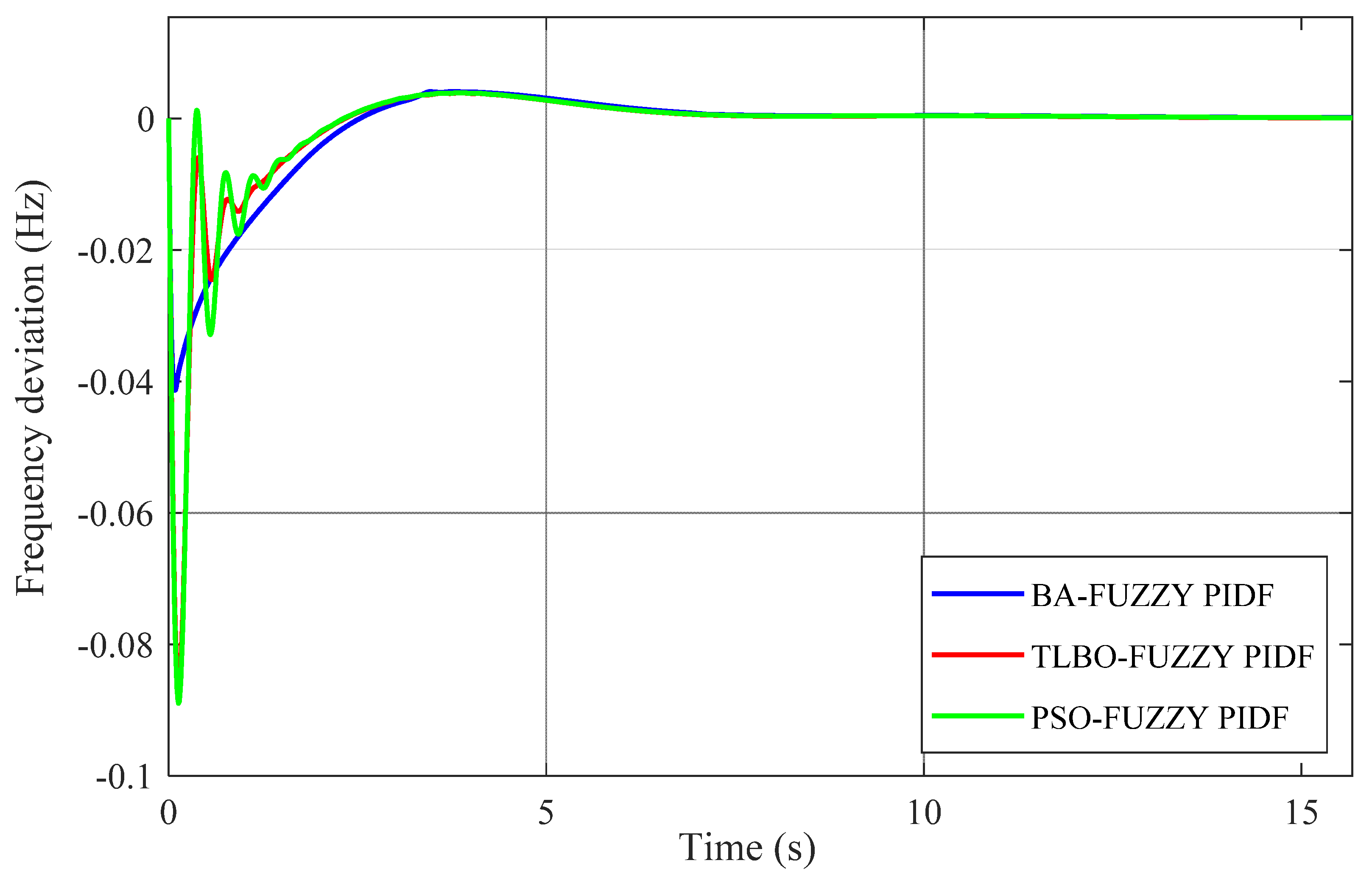
Figure 18.
Frequency deviation in area 1 (∆F1).
Figure 18.
Frequency deviation in area 1 (∆F1).
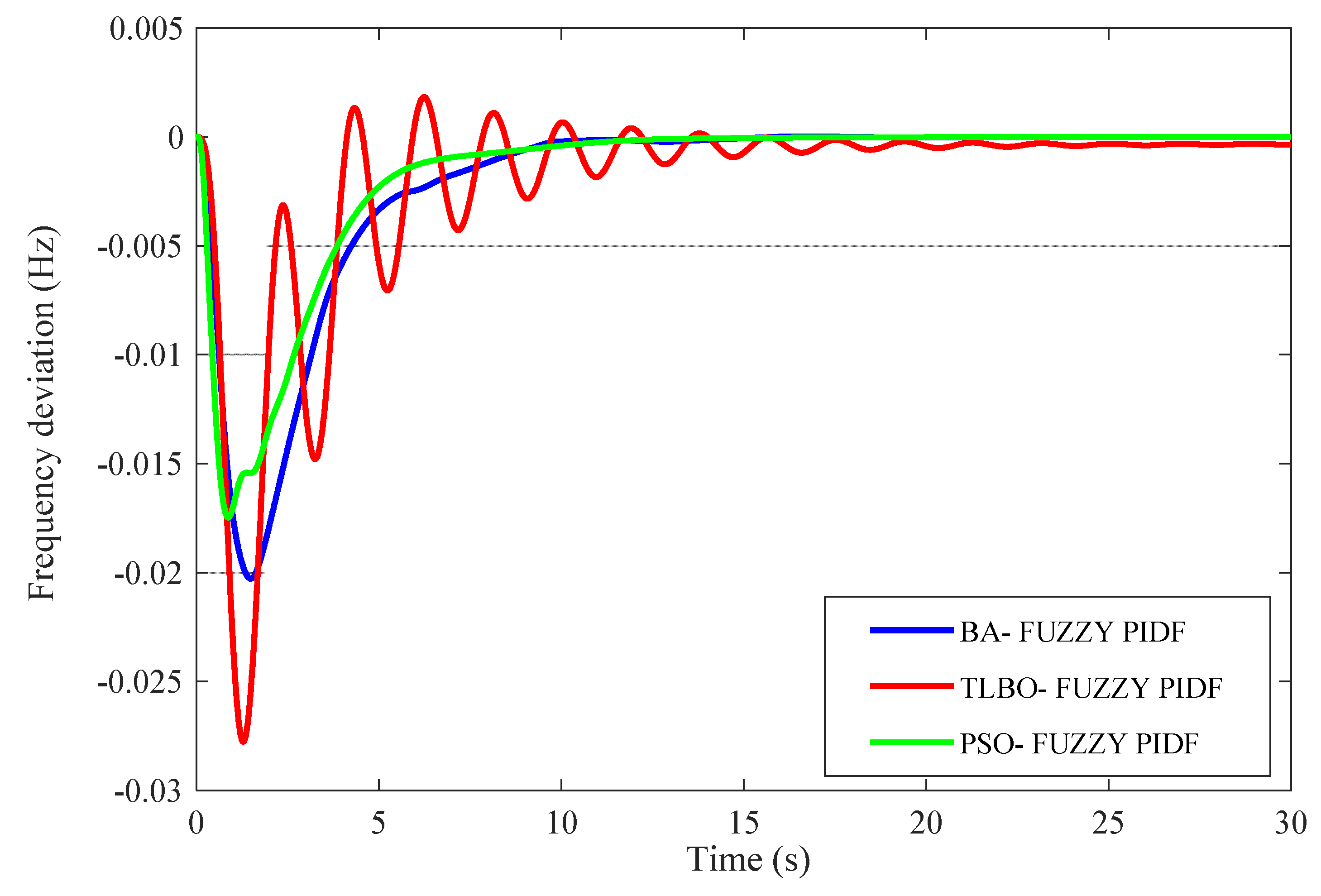
Figure 19.
Frequency deviation in area 2 (∆F2).
Figure 19.
Frequency deviation in area 2 (∆F2).
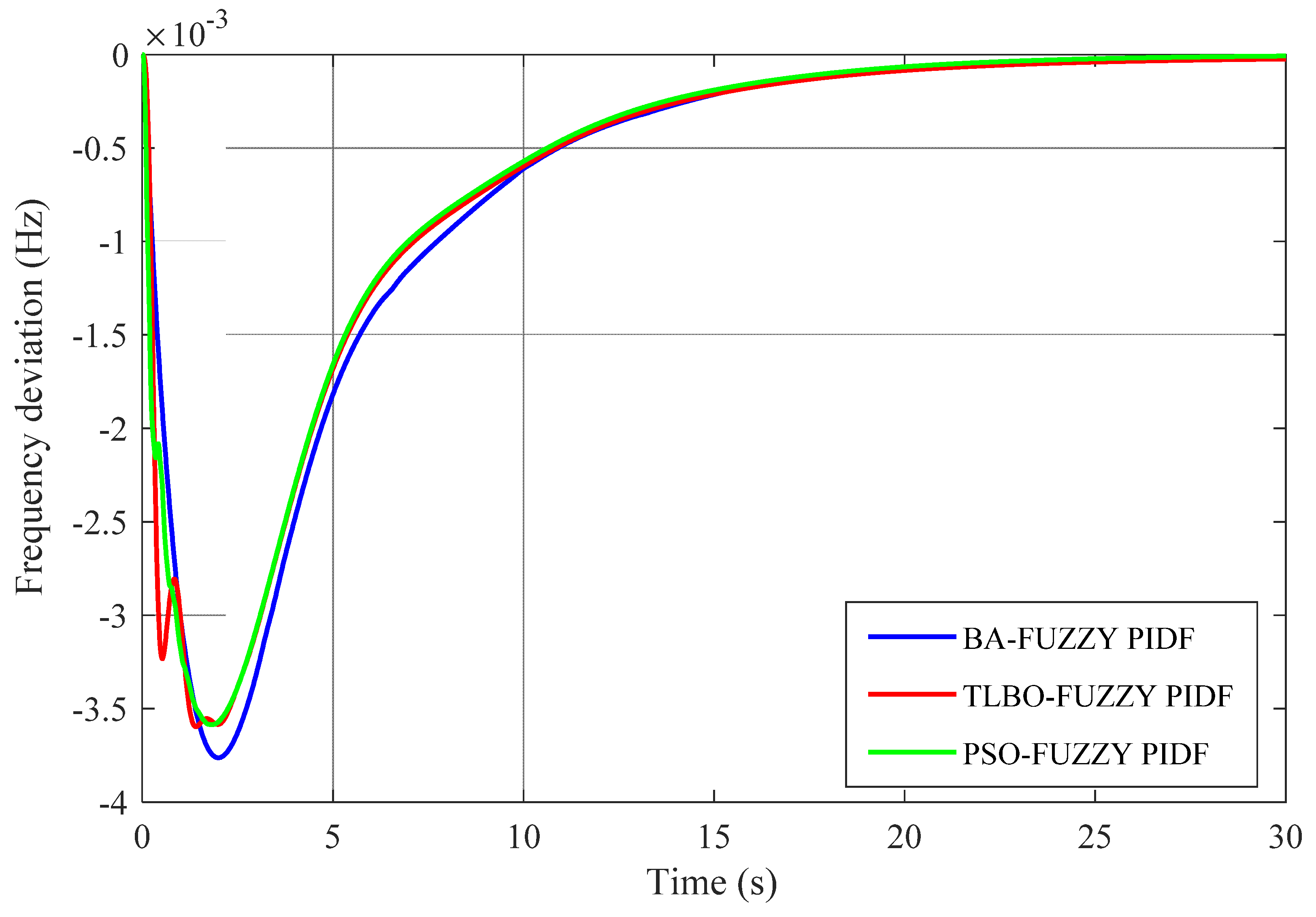
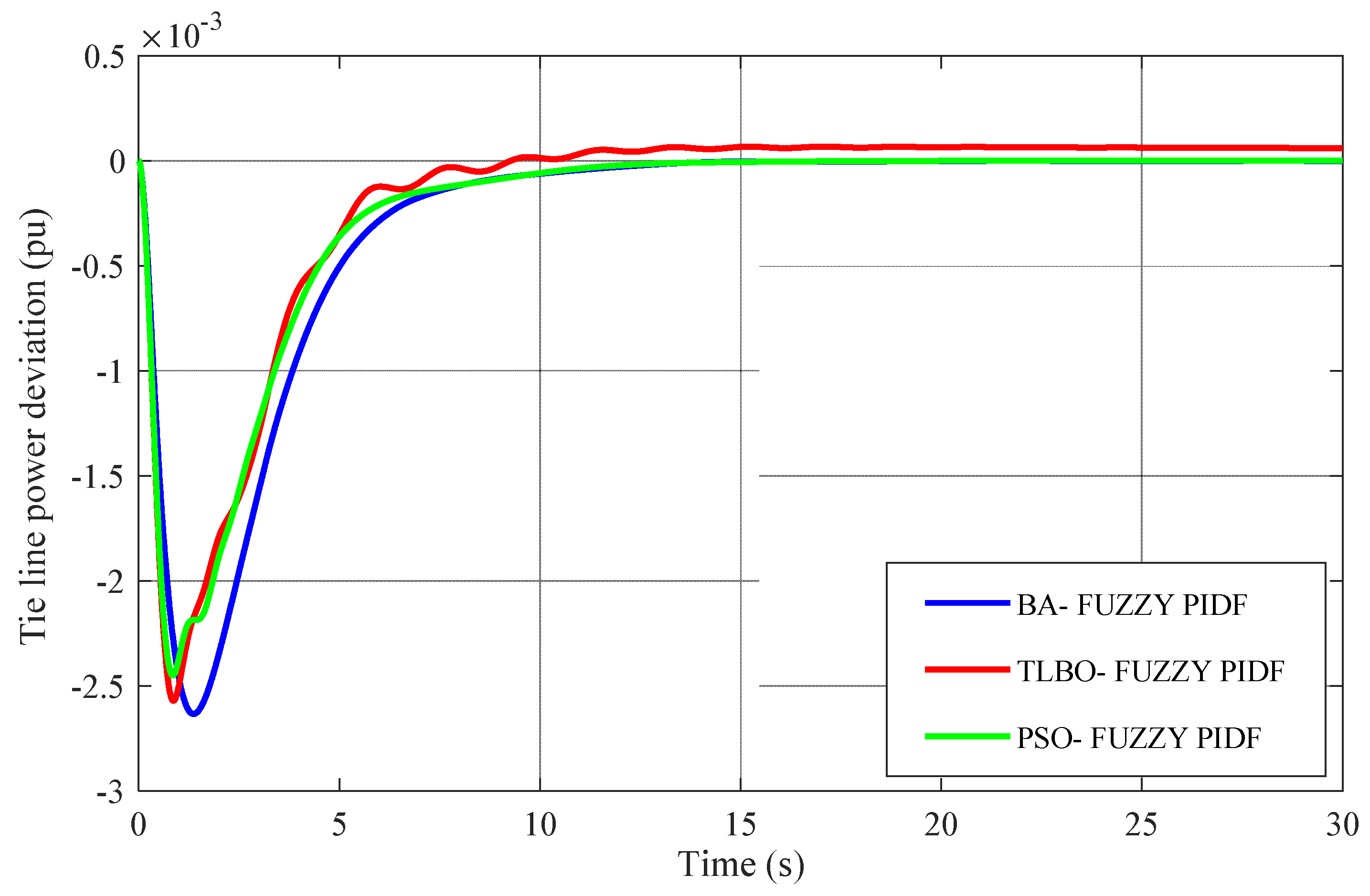
Figure 20.
Tie-line power deviation (∆Ptie).
Figure 20.
Tie-line power deviation (∆Ptie).
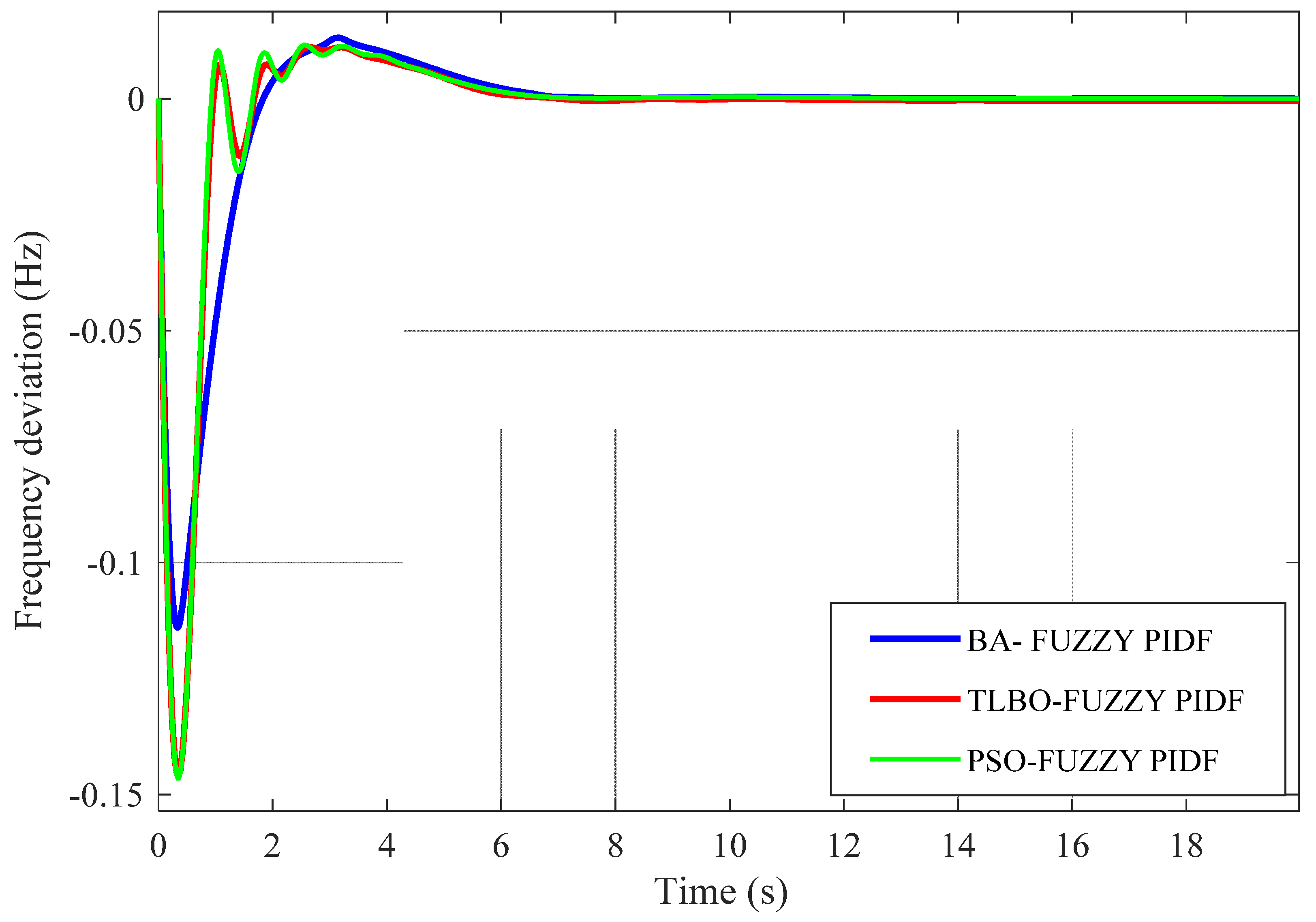
Figure 21.
Frequency deviation in area 1 (∆F1) under parametric uncertainties.
Figure 21.
Frequency deviation in area 1 (∆F1) under parametric uncertainties.
Figure 22.
Frequency deviation in area 1 (∆F2) under parametric uncertainties.
Figure 22.
Frequency deviation in area 1 (∆F2) under parametric uncertainties.
Figure 23.
Tie-line power deviation (∆Ptie) under parametric uncertainties.
Figure 23.
Tie-line power deviation (∆Ptie) under parametric uncertainties.
Table 1.
Frequency limits for the GB power system.
Table 1.
Frequency limits for the GB power system.
| Frequency Constraints (Hz) | Case Description |
|---|
| ±0.2 | System frequency in normal operational conditions and the acceptable frequency deviation following a generation loss or connecting demand to ±300 MW. |
| ±0.5 | The maximum deviation in frequency when generation units over 300 MW and of up to 1320 MW is lost. |
| −0.8 | The maximum deviation in frequency following a generation loss over 1320 MW and up to 1800 MW, requiring restoration of frequency to a minimum of 49.5 Hz in 60 s. |
Table 2.
Parameters for the simplified model of the power system.
Table 2.
Parameters for the simplified model of the power system.
| R | Tg | T1d | T1g | Tt | Heq | D | Ev |
|---|
| −0.09 pu | 0.2 s | 2 s | 12 s | 0.3 s | 8.88 s | 1 pu | 1.35 pu |
Table 3.
Fuzzy rule base of the proposed controller.
Table 3.
Fuzzy rule base of the proposed controller.
| ∆F | ∆F |
|---|
| NB | NS | Z | PS | PB |
|---|
| NB | NB | NB | NB | NS | Z |
| NS | NB | NB | NS | Z | PS |
| Z | NB | NS | Z | PS | PB |
| PS | NS | Z | PS | PB | PB |
| PB | Z | PS | PB | PB | PB |
Table 4.
The BA parameters.
Table 4.
The BA parameters.
| n | m | e | nep | nsp | ngh |
|---|
| 30 | 12 | 6 | 11 | 7 | 0.011 |
Table 5.
The PSO parameters.
Table 5.
The PSO parameters.
| No. Particles | Wmin | Wmax | C1 | C2 | CR |
|---|
| 30 | 0.4 | 0.9 | 2 | 2 | 0.65 |
Table 6.
Optimal gains of PID and FOPID with different algorithms for GB power system.
Table 6.
Optimal gains of PID and FOPID with different algorithms for GB power system.
| Proposed | Optimization Algorithms/Controller Parameters |
|---|
| Controller | Parameters | BA | TLBO | PSO |
|---|
| | KP | 40 | 40 | 40 |
| PID-ISE | KI | 18.61 | 18.6373 | 18.6347 |
| | KD | 40 | 40 | 40 |
| | KP | 40 | 40 | 40 |
| PID-ITAE | KI | 2.3044 | 2.383 | 2.3129 |
| | KD | 16.1483 | 14.523 | 15.1724 |
| | KP | 40 | 40 | 40 |
| | KI | 40 | 40 | 40 |
| FOPID-ISE | KD | 40 | 40 | 40 |
| | λ | 0.5584 | 0.55805 | 0.5562 |
| | μ | 0.3441 | 0.3450 | 0.3439 |
| | KP | 40 | 40 | 40 |
| | KI | 40 | 40 | 40 |
| FOPID-ITAE | KD | 40 | 40 | 40 |
| | λ | 0.89 | 0.872 | 0.8953 |
| | μ | 0.388 | 0.3184 | 0.236 |
Table 7.
Frequency response performances with PID tuned by different algorithms and designed by minimizing ISE.
Table 7.
Frequency response performances with PID tuned by different algorithms and designed by minimizing ISE.
| Controller | Ush in Hz | Osh in Hz | Ts in s | Error | ISE × 10−5 |
|---|
| BA-PID | −0.1301 | 0.09148 | 33.777 | 0 | 2.891 |
| PSO-PID | −0.1301 | 0.09148 | 33.793 | 0 | 2.891 |
| TLBO-PID | −0.1301 | 0.09143 | 33.794 | 0 | 2.891 |
Table 8.
Frequency response performances with PID tuned by different algorithms and designed by minimizing ITAE.
Table 8.
Frequency response performances with PID tuned by different algorithms and designed by minimizing ITAE.
| Controller | Ush in Hz | Osh in Hz | Ts in s | Error | ITAE |
|---|
| BA-PID | −0.1840 | 3.51 × 10−3 | 9.4256 | 0 | 0.1515 |
| PSO-PID | −0.1859 | 3.71 × 10−3 | 9.2792 | 0 | 0.1508 |
| TLBO-PID | −0.1870 | 5 × 10−3 | 13.8580 | 0 | 0.1553 |
Table 9.
Frequency response performances with FOPID tuned by different algorithms and designed by minimizing ISE.
Table 9.
Frequency response performances with FOPID tuned by different algorithms and designed by minimizing ISE.
| Controller | Ush in Hz | Osh in Hz × 10−4 | Ts in s | Error | ISE × 10−6 |
|---|
| BA-PID | −0.12 | 8.91 | 8.0145 | 2.72 | 7.8 |
| PSO-PID | −0.12 | 7.8 | 7.9536 | 2.76 | 7.8 |
| TLBO-PID | −0.12 | 8.82 | 8.0137 | 2.73 | 7.8 |
Table 10.
Frequency response performances with FOPID tuned by different algorithms and designed by minimizing ITAE.
Table 10.
Frequency response performances with FOPID tuned by different algorithms and designed by minimizing ITAE.
| Controller | Ush in Hz | Osh in Hz | Ts in s | Error | ITAE |
|---|
| BA-PID | −0.1282 | 0.045 | 8.045 | 0 | 0.0581 |
| PSO-PID | −0.1324 | 0.0463 | 9.0826 | 0 | 0.0558 |
| TLBO-PID | −0.1303 | 0.0417 | 8.7397 | 0 | 0.0566 |
Table 11.
Optimal gains of Fuzzy PIDF with different algorithms for GB power system.
Table 11.
Optimal gains of Fuzzy PIDF with different algorithms for GB power system.
| Proposed | Optimization Algorithms/Controller Parameters |
|---|
| Controller | Parameters | BA | TLBO | PSO |
|---|
| | K1 | 3.41 | 2.99 | 3.88 |
| | K2 | 40 | 40 | 29.72 |
| Fuzzy PIDF | KP | 29.91 | 40 | 26.60 |
| ISE | KI | 18.59 | 39.99 | 17.82 |
| | KD | 20.93 | 14.998 | 14.59 |
| | KC | 40 | 40 | 40 |
| | K1 | 20.37 | 3.955 | 7.1590 |
| | K2 | 38.12 | 14.997 | 24.2973 |
| Fuzzy PIDF | KP | 19.25 | 39.996 | 18.83 |
| ITAE | KI | 38.14 | 40 | 7.68 |
| | KD | 4.29 | 14.995 | 3.889 |
| | KC | 40 | 40 | 40 |
Table 12.
Frequency response performance with Fuzzy PIDF controllers designed via ISE.
Table 12.
Frequency response performance with Fuzzy PIDF controllers designed via ISE.
| Controller | Ush in Hz | Osh in Hz | Ts in s | Error | ISE × 10−10 |
|---|
| BA-Fuzzy PIDF | −0.0028 | 2.37 × 10−4 | 11.7941 | 0 | 6.71 |
| PSO-Fuzzy PIDF | −0.0045 | 2.8 × 10−4 | 11.7689 | 0 | 15.2 |
| TLBO-Fuzzy PIDF | −0.0048 | 1.75 × 10−4 | 8.8523 | 0 | 6.88 |
Table 13.
Frequency response performance with Fuzzy PIDF controllers designed via ITAE.
Table 13.
Frequency response performance with Fuzzy PIDF controllers designed via ITAE.
| Controller | Ush in Hz | Osh in Hz | Ts in s | Error | ITAE |
|---|
| BA-Fuzzy PIDF | −0.0057 | 2.15 × 10−4 | 8.3776 | 0 | 0.000391 |
| PSO-Fuzzy PIDF | −0.00793 | 3.7 × 10−4 | 13.6303 | 0 | 0.001065 |
| TLBO-Fuzzy PIDF | −0.0043 | 4.9 × 10−4 | 10.9389 | 0 | 0.000495 |
Table 14.
The variation range of the parameters in the two scenarios.
Table 14.
The variation range of the parameters in the two scenarios.
| Scenarios | Parameters | Nominal Value | Variation Range | New Value |
|---|
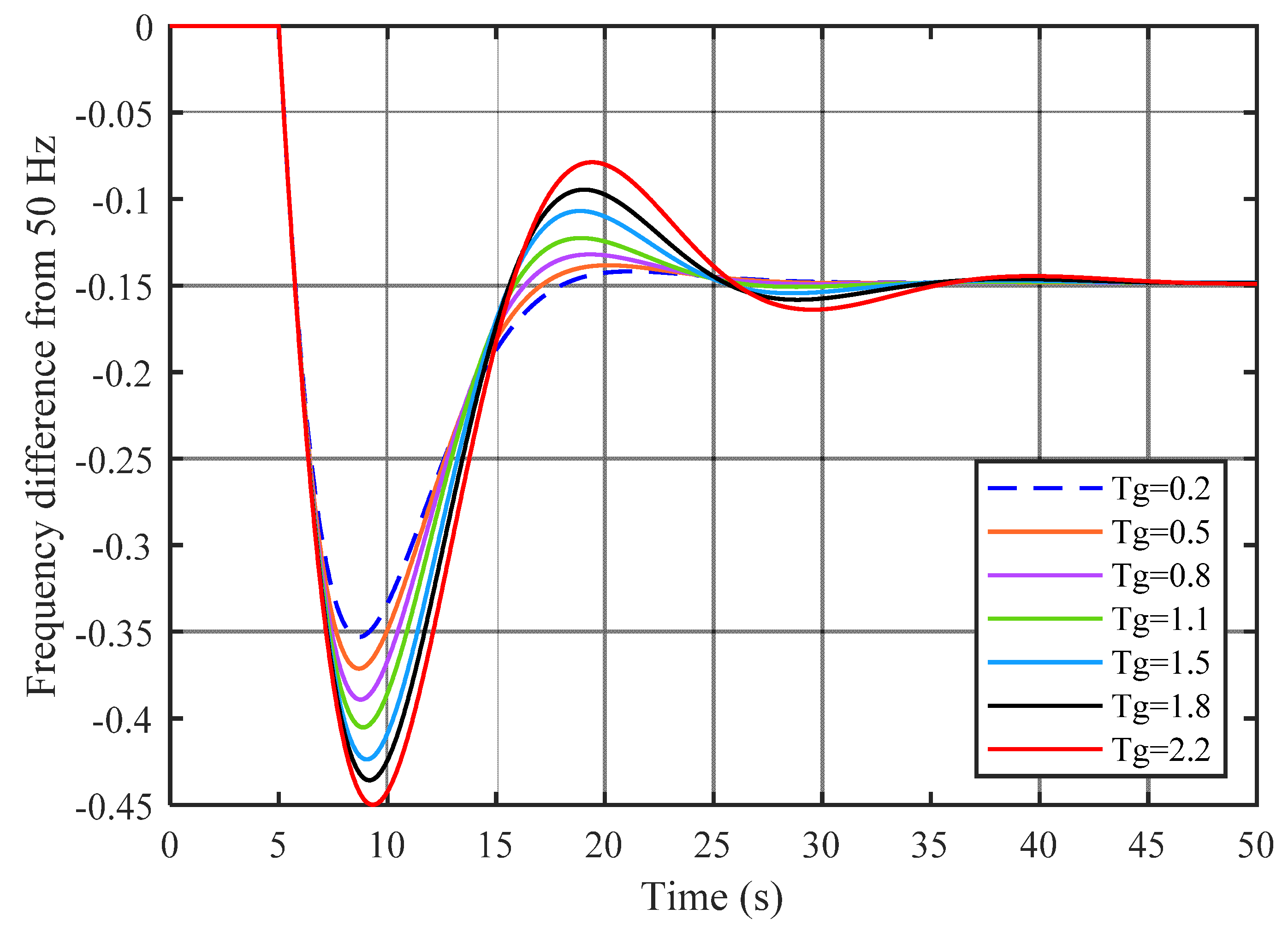
| Scenario1 | Tg | 0.2 | +50% | 0.3 |
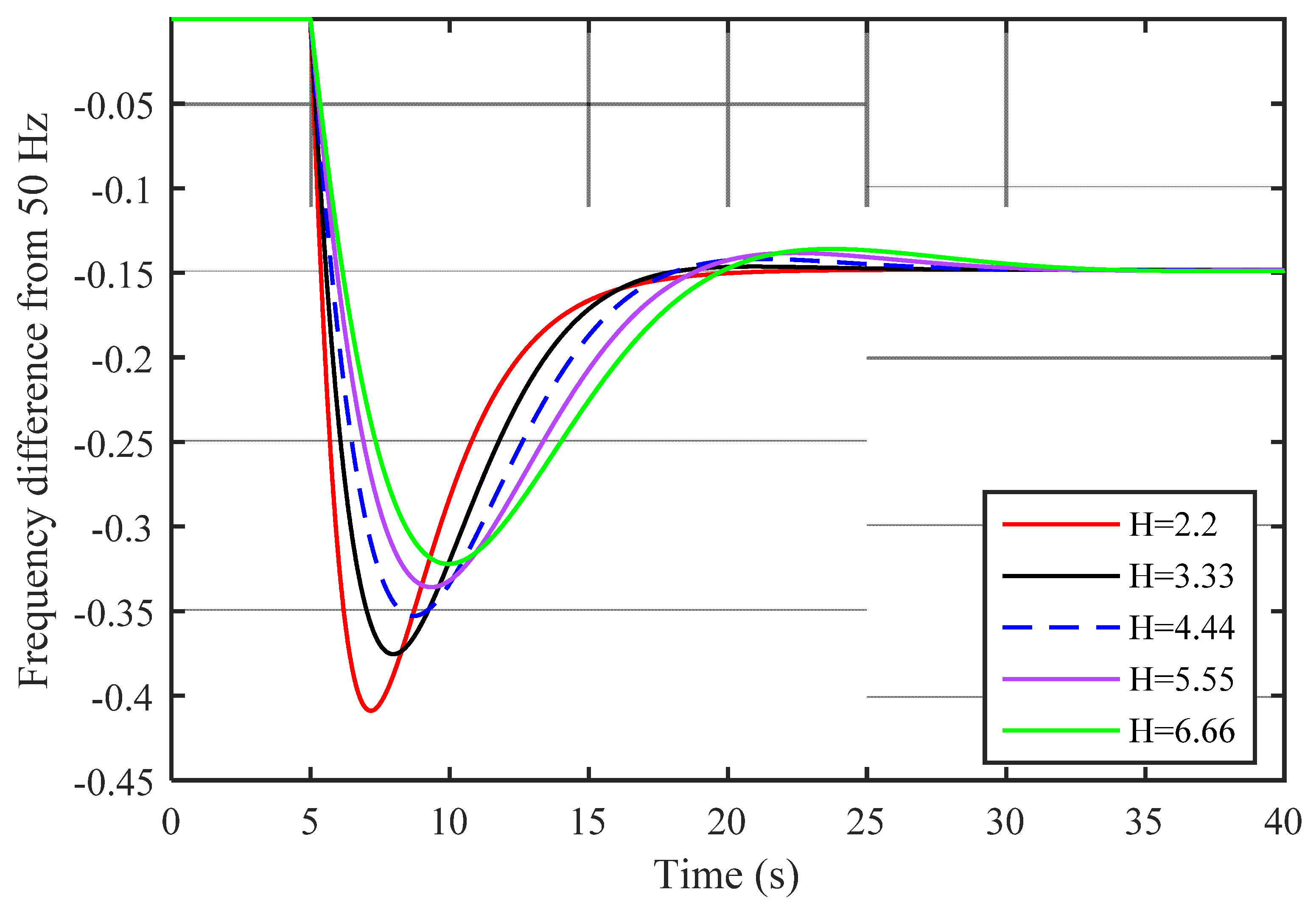
| Heq | 4.44 | +50% | 6.66 |
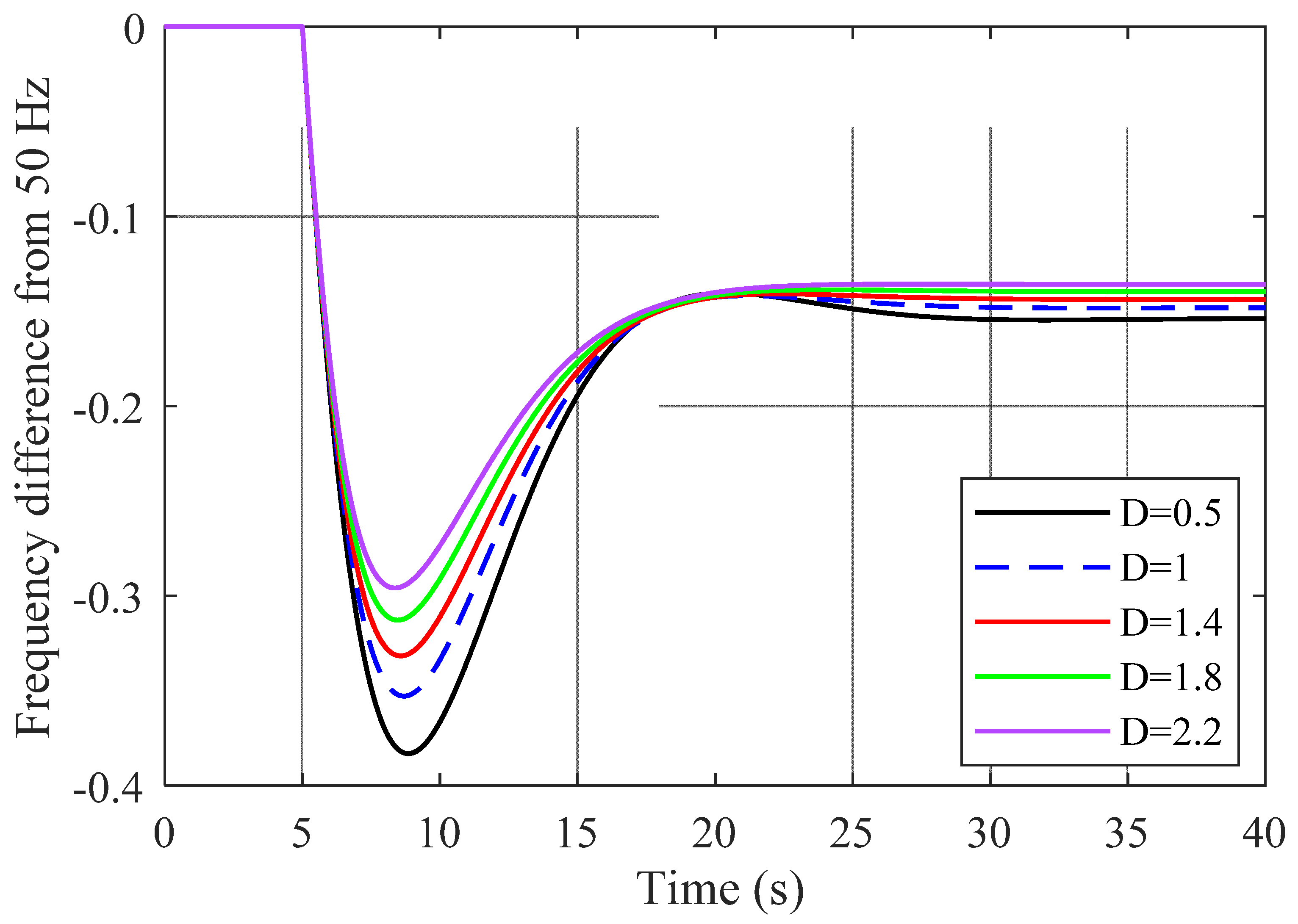
| D | 1 | −50% | 0.5 |
| R | −0.09 | −50% | 0.045 |
| Scenario2 | Tg | 0.2 | −50% | 0.1 |
| Heq | 4.44 | −50% | 2.22 |
| D | 1 | +50% | 1.5 |
| R | −0.09 | +50% | 0.135 |
Table 15.
Frequency response performances with different BA-tuned controllers designed via ISE for scenario 2.
Table 15.
Frequency response performances with different BA-tuned controllers designed via ISE for scenario 2.
| Controller | Ush in Hz | Osh in Hz | Ts in s | Error | ISE |
|---|
| BA-Fuzzy PIDF | −0.0042 | 2.68 × 10−4 | 12.61 | 0 | 6.77 × 10−10 |
| BA-FOPID | −0.141 | 0 | 9.40 | −2.75 × 10−3 | 0.0454 |
| BA-PID | −0.126 | 0 | 22.09 | 0 | 0.1643 |
Table 16.
Frequency response performance with different BA-tuned controllers designed via ITAE for scenario 2.
Table 16.
Frequency response performance with different BA-tuned controllers designed via ITAE for scenario 2.
| Controller | Ush in Hz | Osh in Hz | Ts in s | Error | ITAE |
|---|
| BA-Fuzzy PIDF | −0.006 | 2.68 × 10−4 | 8.22 | 0 | 0.0004 |
| BA-FOPID | −0.143 | 0.020 | 15.16 | 0 | 0.0454 |
| BA-PID | −0.178 | 0 | 20.75 | −4 × 10−3 | 0.1643 |
Table 17.
Frequency response performance with BA tuned different controllers designed via ITAE for scenario 2.
Table 17.
Frequency response performance with BA tuned different controllers designed via ITAE for scenario 2.
| Controller | Ush in Hz | Osh in Hz | Ts in s | Error | ITAE |
|---|
| BA-Fuzzy PIDF | −0.0083 | 2.8 × 10−4 | 8.22 | 0 | 0.00056 |
| BA-FOPID | −0.171 | 0.0603 | 13.04 | −3 × 10−4 | 0.0779 |
| BA-PID | −0.246 | 5 × 10−3 | 14.42 | 0 | 0.203 |
Table 18.
Frequency response performances with BA-tuned controllers designed via minimizing ITAE in scenario 2 with 0.053 pu load disturbance.
Table 18.
Frequency response performances with BA-tuned controllers designed via minimizing ITAE in scenario 2 with 0.053 pu load disturbance.
| Controller | Ush in Hz | Osh in Hz | Ts in s | Error | ITAE |
|---|
| BA-Fuzzy PIDF | −0.0098 | 2.7 × 10−4 | 8.021 | 0 | 0.00058 |
| BA-FOPID | −0.191 | 0.028 | 15.16 | −3.1 × 10−4 | 0.06096 |
| BA-PID | −0.239 | 0 | 20.75 | −5.5 × 10−4 | 0.22020 |
Table 19.
Frequency response performances with different controllers.
Table 19.
Frequency response performances with different controllers.
| Controller | Controller Gains of Area 1 | Controller Gains of Area 2 |
|---|
| K1 | K2 | KP1 | KI1 | KD1 | KF1 | K3 | K4 | KP2 | KI2 | KP2 | KF2 |
|---|
| Fuzzy PIDF-BA | 0.403 | 2 | 2 | 2 | 2 | 98.4841 | 0.2648 | 1.0081 | 0.9133 | 1.9730 | 1.9889 | 93.8922 |
| Fuzzy PIDF-TLBO | 0.035 | 1.9992 | 1.9986 | 1.99868 | 1.9995 | 99.0606 | 1.9602 | 0.03707 | 0.4435 | 1.3003 | 0.019 | 99.7446 |
| Fuzzy PIDF-PSO | 0.02 | 2 | 2 | 2 | 2 | 100 | 2 | 2 | 2 | 0.015 | 1.4035 | 11.21 |
Table 20.
Frequency response performances with different controllers.
Table 20.
Frequency response performances with different controllers.
| Controller | Frequency in Area 1 | Frequency in Area 2 | Tie-Line Power Deviation | ITAE |
|---|
| Ush in Hz | Osh in Hz | Ts in s | Ush in Hz | Osh in Hz | Ts in s | Ush in pu | Osh in pu | Ts in s |
|---|
| Fuzzy PIDF-BA | 0.0414 | 0.0041 | 6.9401 | 0.0038 | 0 | 19.2991 | 0.0010 | 0 | 19.360 | 0.0361 |
| Fuzzy PIDF-TLBO | 0.0868 | 0.0040 | 5.7544 | 0.0036 | 0 | 19.3273 | 0.00099 | 0 | 18.893 | 0.0304 |
| Fuzzy PIDF-PSO | 0.0890 | 0.0040 | 5.7175 | 0.0036 | 0 | 19.1020 | 0.0010 | 0 | 19.154 | 0.0330 |
Table 21.
The parameters of the testbed system under parametric uncertainties.
Table 21.
The parameters of the testbed system under parametric uncertainties.
| Parameters | Nominal Values | Variation Range | New Values |
|---|
| Area 1 | Area 2 | Area 1 | Area 2 |
|---|
| Tg | 0.2 | 0.3 | +50% | 0.3 | 0.45 |
| Tt | 0.5 | 0.6 | +50% | 0.75 | 0.9 |
| B | 20.6 | 16.9 | −50% | 10.3 | 8.45 |
| D | 0.6 | 0.9 | −50% | 0.3 | 0.45 |
| H | 5 | 4 | +50% | 7.5 | 6 |
Table 22.
Frequency response performances with different controllers.
Table 22.
Frequency response performances with different controllers.
| Controller | Frequency in Area 1 | Frequency in Area 2 | Tie-Line Power Deviation | ITAE |
|---|
| Ush in Hz | Osh in Hz | Ts in s | Ush in Hz | Osh in Hz | Ts in s | Ush in pu | Osh in pu | Ts in s |
|---|
| Fuzzy PIDF-BA | 0.1140 | 0.0131 | 5.9858 | 0.0203 | 0 | 9.3781 | 0.0026 | 0 | 10.453 | 0.03094 |
| Fuzzy PIDF-TLBO | 0.1458 | 0.0111 | 5.4378 | 0.0278 | 0.00183 | 14.818 | 0.0026 | 0.000065 | 9.3769 | 0.0511 |
| Fuzzy PIDF-PSO | 0.1465 | 0.0115 | 5.4468 | 0.0175 | 0 | 10.269 | 0.0024 | 0 | 10.421 | 0.02535 |