Reduction in the Computational Complexity of Calculating Losses on Eddy Currents in a Hydrogen Fuel Cell Using the Finite Element Analysis
Abstract
:1. Introduction
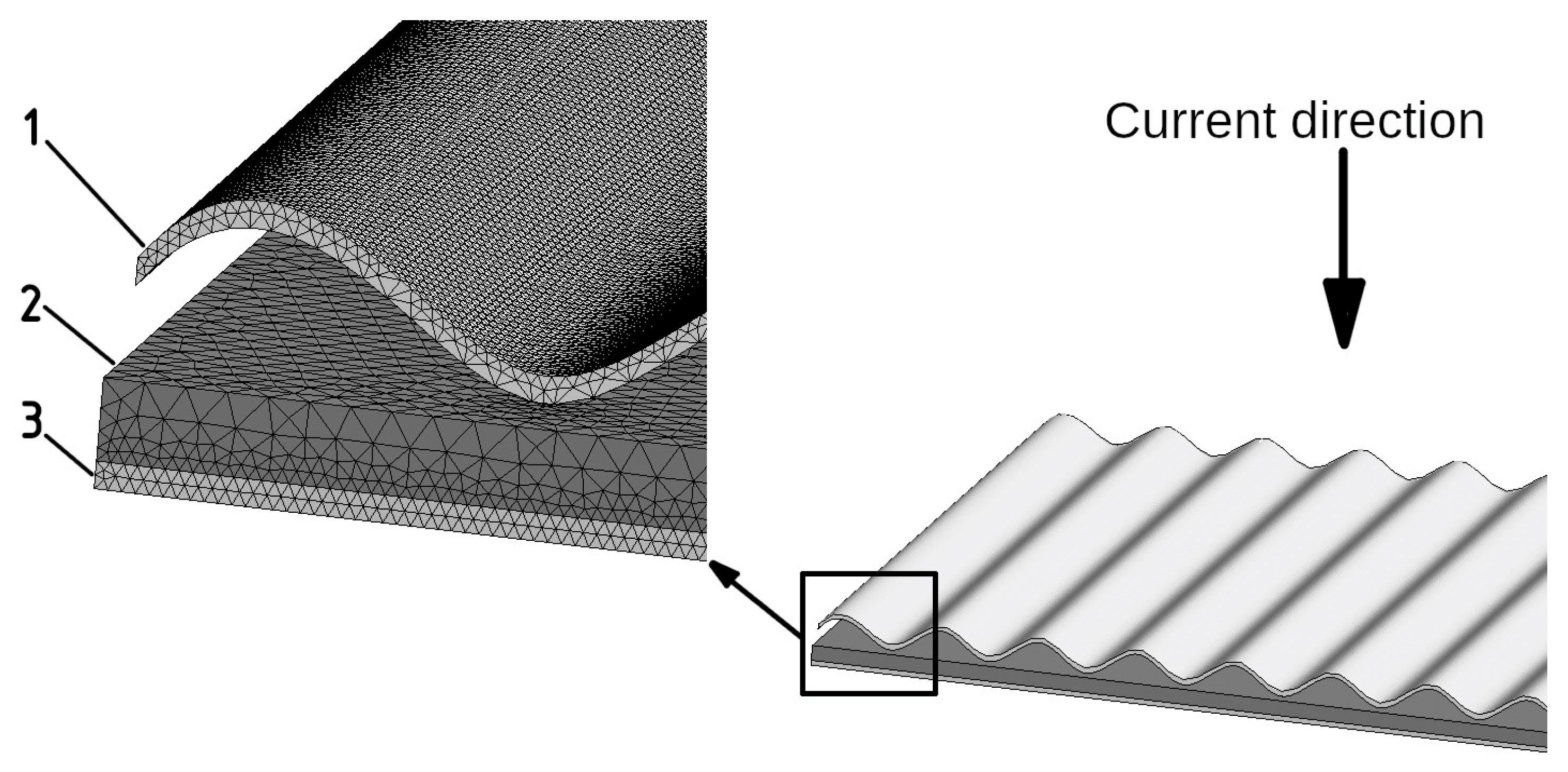
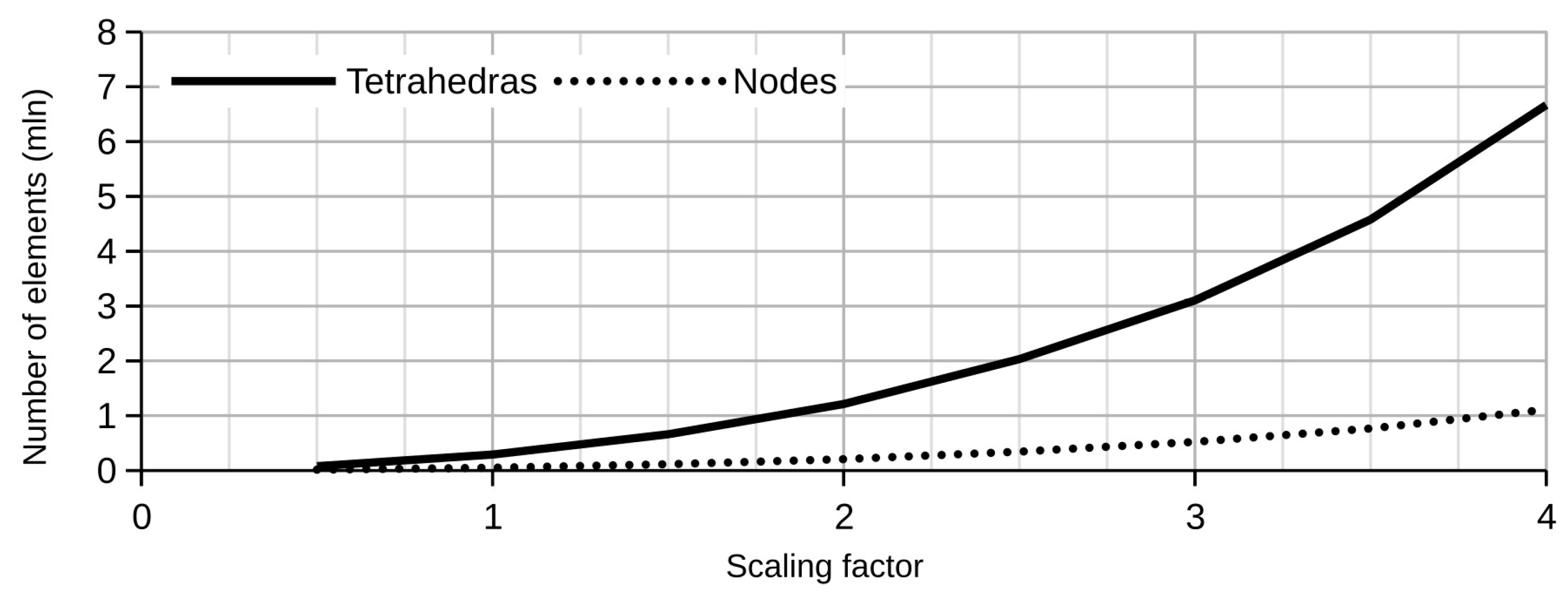
2. Geometric and Finite Element Models
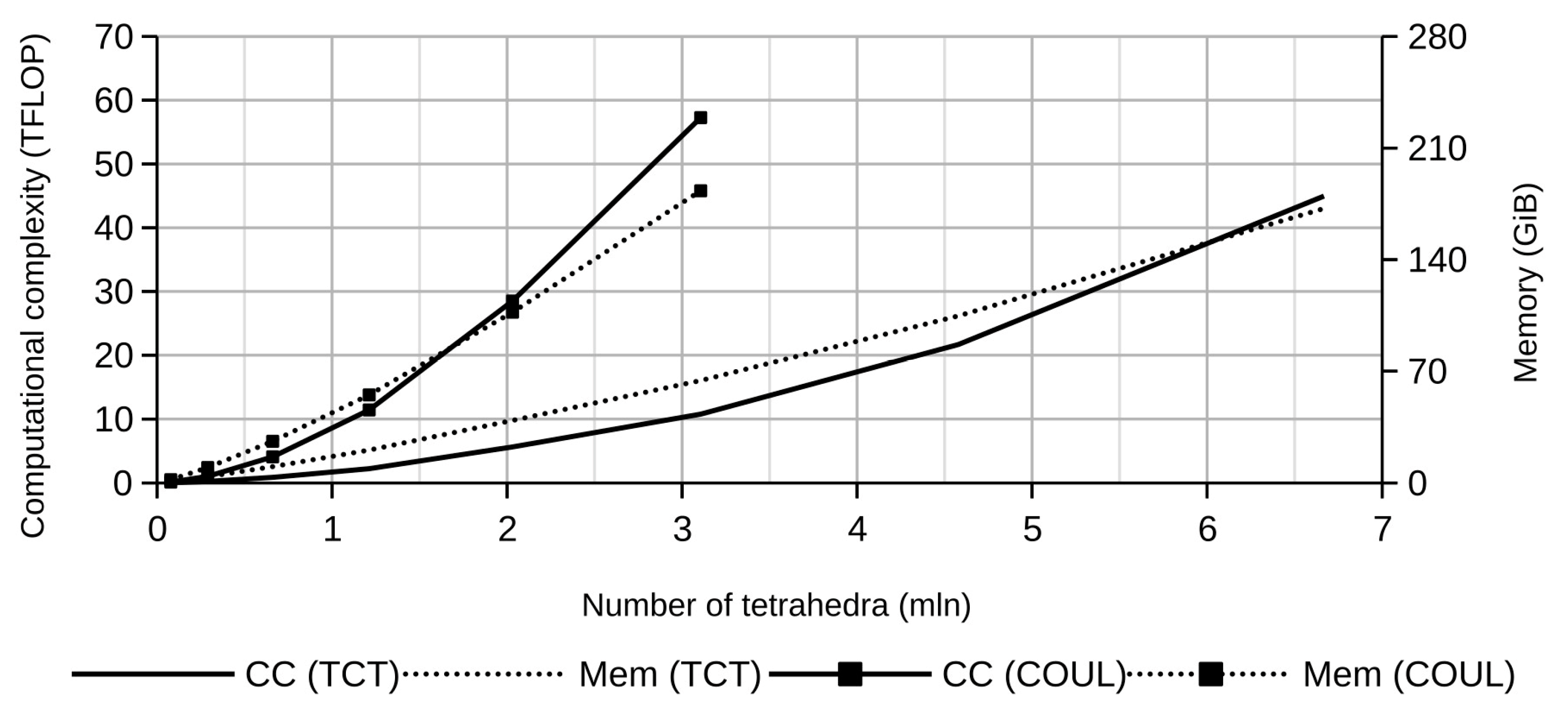
3. Mathematical Model
(σ∂tA, gradV′)Ωσ + (σgradV, gradV′)Ωσ = ∑ IiUi(V′),
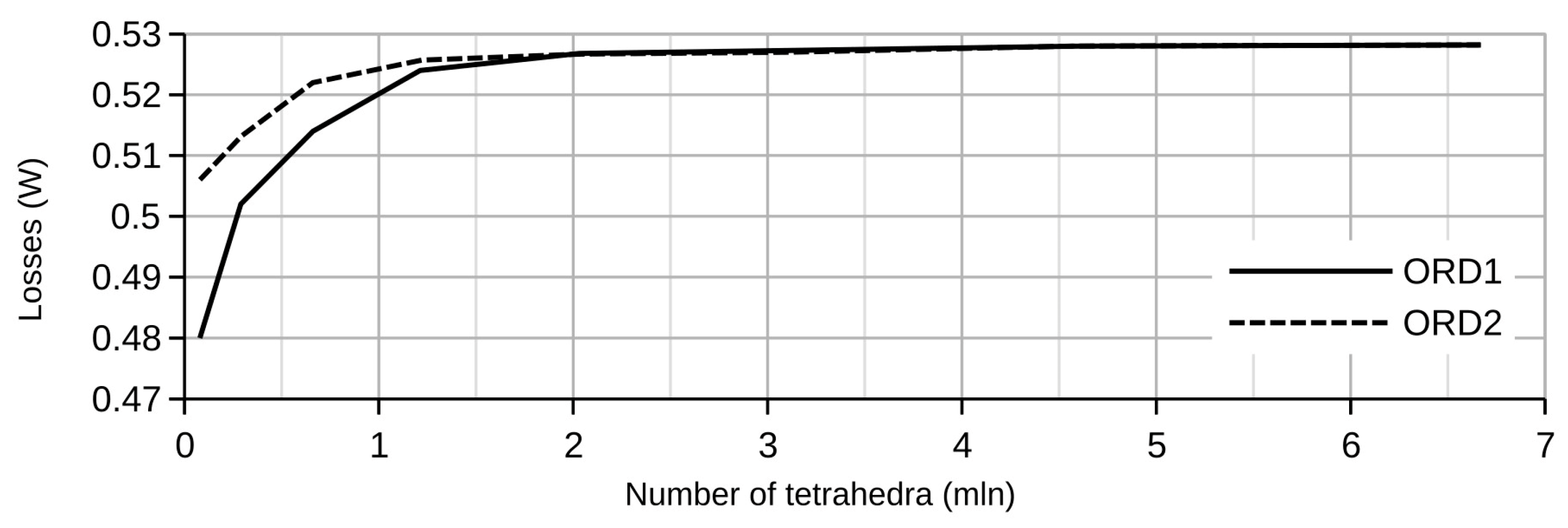
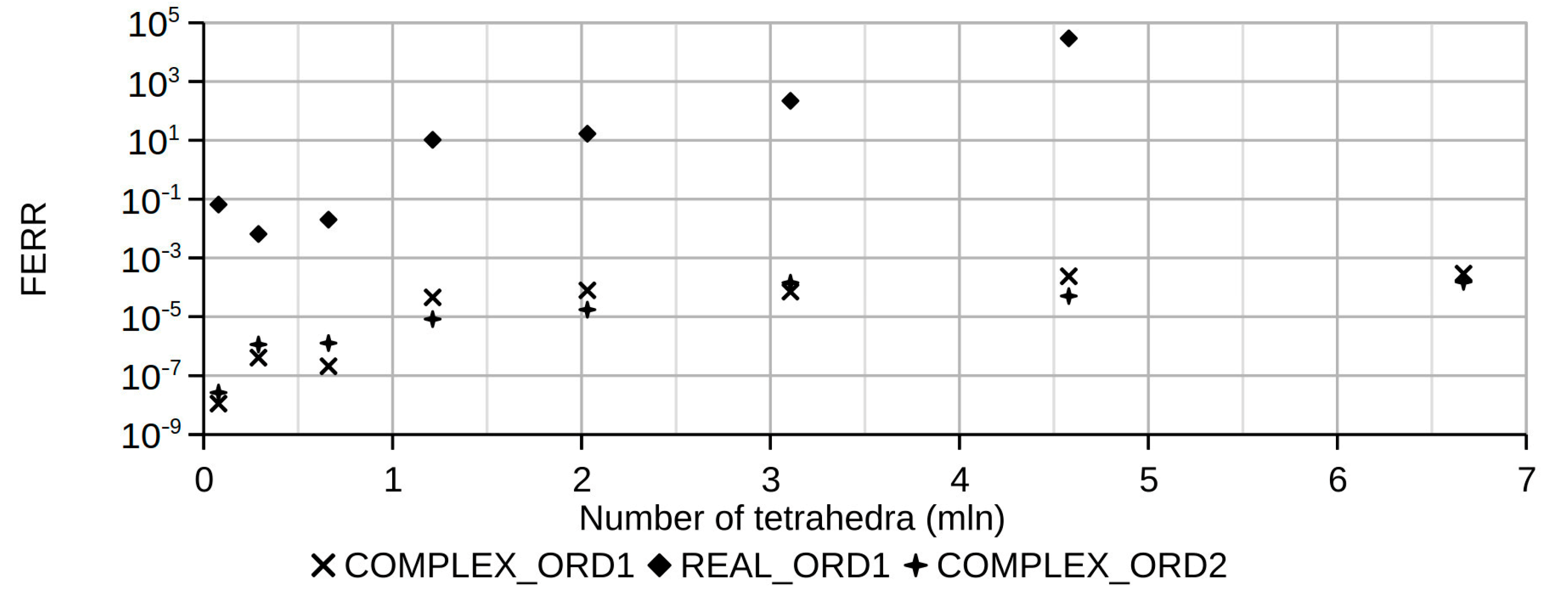
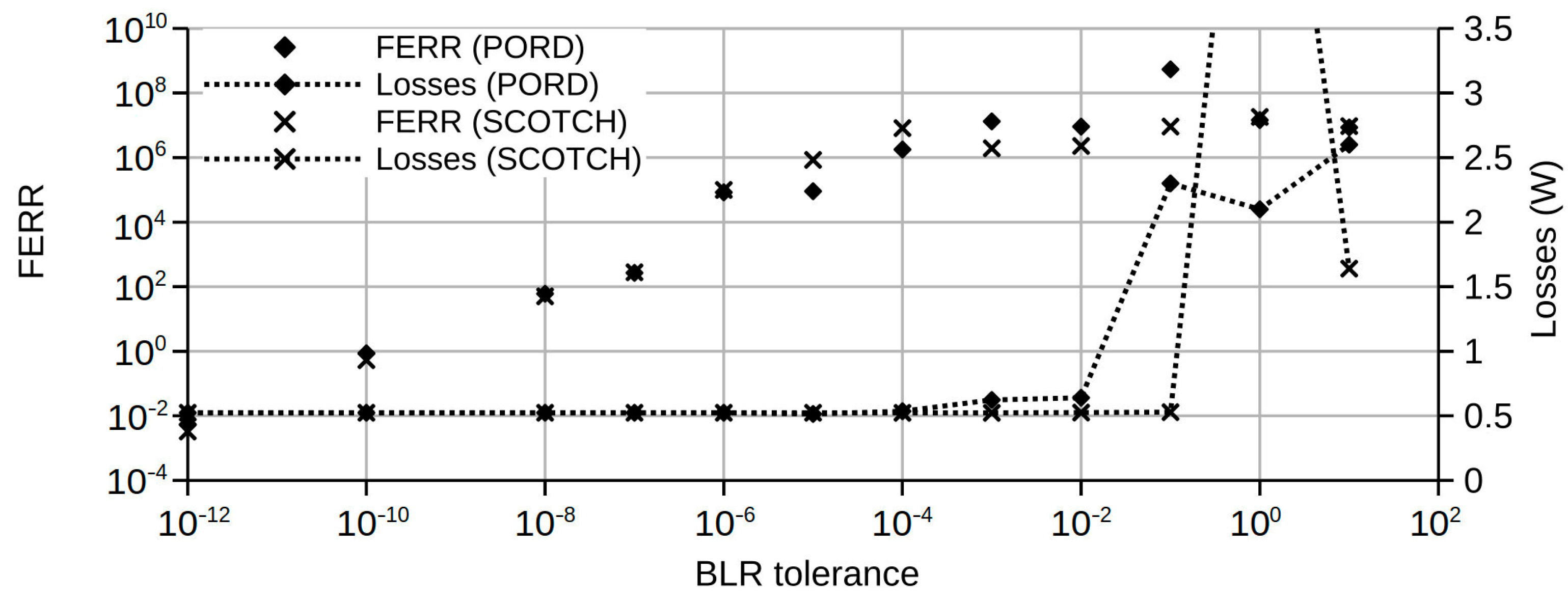
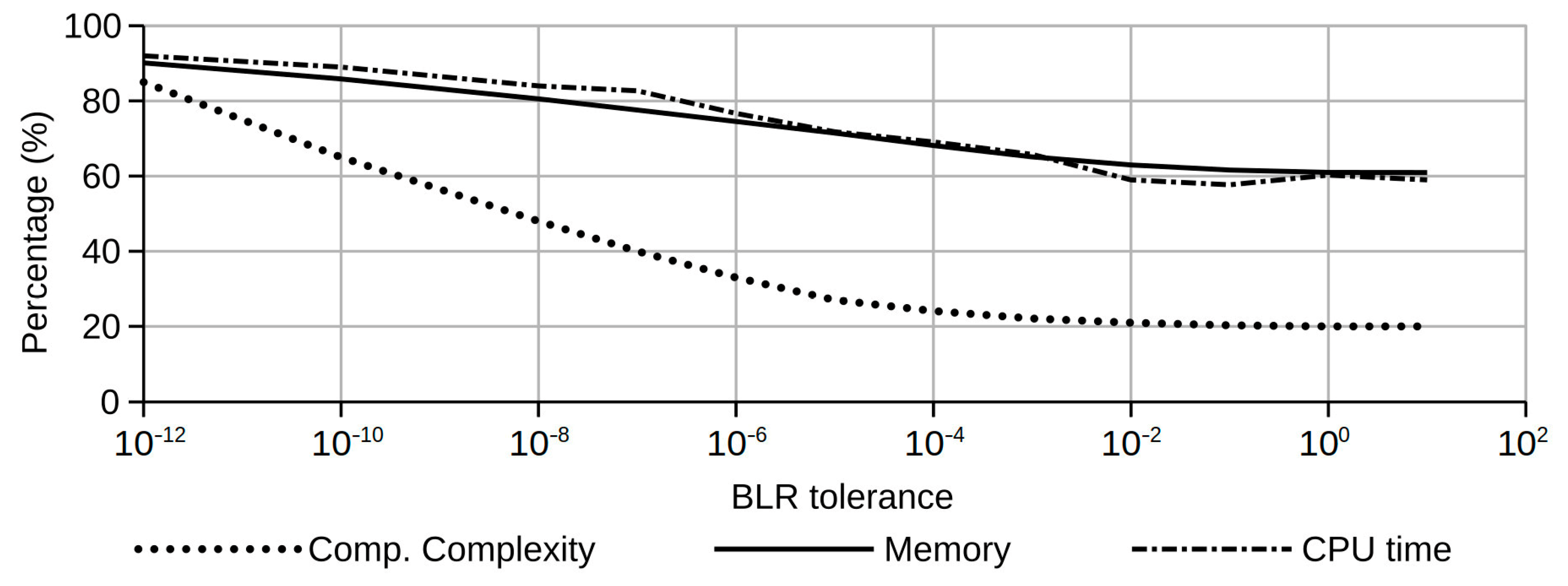
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pfeif, E.; Jones, Z.; Lasseigne, A.; Koenig, K.; Krzywosz, K.; Mader, E.; Yagnik, S.; Mishra, B.; Olson, D. Submerged Eddy Current Method of Hydrogen Content Evaluation of ZIRCALOY4 Fuel Cladding. AIP Conf. Proc. 2011, 1335, 1168. [Google Scholar] [CrossRef]
- Felt, W. Electromagnetic Excitation Methods for Thermographic Defect Detection in Fuel Cell Materials; Technical report; National Renewable Energy Laboratory: Golden, CO, USA, 2012. [Google Scholar]
- Elia, G. Characterization of Voltage Loss for Proton Exchange Membrane Fuel Cell. Bachelor’s Thesis, Polytechnic University of Catalonia (UPC), Barcelona, Spain, 2015. [Google Scholar]
- Gou, B.; Na, W.; Diong, B. Linear and Nonlinear Models of Fuel Cell Dynamics. Dynamic Modeling and Control with Power Electronics Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Hirschfeld, J. Tomographic Problems in the Diagnostics of Fuel Cell Stacks, PGI-1/IAS-1; Berichte des Forschungszentrums Jülich: Jülich, Germany, 2009. [Google Scholar]
- Burtsev, Y.A.; Pavlenko, A.V.; Vasyukov, I.V. A step-down converter of a power plant based on fuel cells for an unmanned aerial vehicle. Electr. Eng. 2021, 10, 81–85. [Google Scholar]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Lu, Q.; Shephard, M.S.; Tendulkar, S.; Beall, M.W. Parallel mesh adaptation for high-order finite element methods with curved element geometry. Eng. Comput. 2014, 30, 271–286. [Google Scholar] [CrossRef]
- Marot, C.; Pellerin, J.; Remacle, J.F. One machine, one minute, three billion tetrahedra. Int. J. Numer. Methods Eng. 2018, 117, 967–990. [Google Scholar] [CrossRef]
- Bastos, J.; Sadowski, N. Electromagnetic Modelling by Finite Element Methods, 1st ed.; M. Dekker: New York, NY, USA, 2003. [Google Scholar]
- Geuzaine, C.; Remacle, J.-F. (Eds.) Gmsh Reference Manual; The documentation for Gmsh 4.8.4; Belgium, 2022. [Google Scholar]
- Dular, P.; Geuzaine, C.; Henrotte, F.; Legros, W. A general environment for the treatment of discrete problems and its application to the finite element method. IEEE Trans. Magn. 1998, 34, 3395–3398. [Google Scholar] [CrossRef]
- Biro, O.; Paul, C.; Preis, K. “The use of a reduced vector potential A-r formulation for the calculation of iron induced field errors”, ROXIE: Routine for the Optimization of Magnet X-Sections, Inverse Field Calculation and Coil End Design. In Proceedings of the First International Roxie Users Meeting and Workshop CERN, Geneva, Switzerland, 16–18 March 1998; pp. 31–47. [Google Scholar]
- Biro, O. Edge element formulations of eddy current problems. Comput. Methods Appl. Mech. Eng. 1999, 169, 391–405. [Google Scholar] [CrossRef]
- Geuzaine, C. High Order Hybrid Finite Element Schemes for Maxwell Equations Taking Thin Structures and Global Quantities into Account. Ph.D. Thesis, Université de Liège, Liège, Belgium, 2001; pp. 71–80. [Google Scholar]
- Krähenbühl, L.; Muller, D. Thin layers in electrical engineering. Example of shell models in analysing eddy-currents by boundary and finite element methods. IEEE Trans. Magn. 1993, 29, 1450–1455. [Google Scholar] [CrossRef]
- Khoroshev, A.S.; Pavlenko, A.V.; Batishchev, D.V.; Puzin, V.S.; Shevchenko, E.V.; Bolshenko, I.A. Verification of the GMSH GetDP software package for finite element modeling of electromagnetic fields. Proc. High. Educ. Inst. North Cauc. Region. Ser. Tech. Sci. 2013, 6, 74–78. [Google Scholar]
- Balay, S.; Abhyankar, S.; Adams, M.F.; Adams, M.-F.; Benson, S.; Brown, J.; Brune, P.; Buschelman, K.; Constantinescu, E.-M.; Dalcin, L.; et al. PETSc Web Page. 2020. Available online: http://www.mcs.anl.gov/petsc (accessed on 1 November 2022).
- Gregoire, R. Coupling MUMPS and Ordering Software; CERF ACS Report; WN/PA/02/24; CERFAC: Toulouse, France, 2002. [Google Scholar]
- Pellegrini, F. SCOTCH and LIBSCOTCH 5.1 User’s Guide; Technical Report; LaBRI, Université Bordeaux I: Talence, France, 2008; p. 128. [Google Scholar]
- Schulze, J. Towards a tighter coupling of bottom-up and top-down sparse matrix ordering methods. Comput. Sci. BIT Numer. Math. 2001, 41, 800–841. [Google Scholar] [CrossRef]
- Arioli, M.; Demmel, J.; Duff, I.S. Solving sparse linear systems with sparse backward error. SIAM J. Matrix Anal. Appl. 1989, 10, 165–190. [Google Scholar] [CrossRef]
- Belov, S.A.; Zolotykh, N.Y. Numerical Methods of Linear Algebra; Laboratory practice; Publishing House of the Nizhny Novgorod State University. N.I. Lobachevsky: Nizhny Novgorod, Russia, 2005; p. 235. [Google Scholar]
- MUltifrontal Massively Parallel Solver (MUMPS 5.4.0) User’s Guide; Mumps Technologies SAS; Laboratoire de l’informatique du Parallélisme: Lyon, France, 2021.
- Khoroshev, A.S.; Pavlenko, A.V.; Puzin, V.S.; Shchuchkin, D.A.; Batishchev, D.V.; Bolshenko, I.A.; Kramarov, A.S. The Influence of Gauge Conditions on Process and Result of Solving 3-D Problems of Computational Electromagnetism by the Finite Element Method. IEEE Trans. Magn. 2022, 58, 1–11. [Google Scholar] [CrossRef]
- Saad, Y. Iterative methods for sparse linear systems. Soc. Ind. Appl. Math 2003, 541, 41–42. [Google Scholar]
- Khoroshev, A.S. Modeling of nonlinear magnetic systems by the finite element method using BLR factorization. Proc. High. Educ. Institutions. Elektromekhanika 2021, 64, 14–19. [Google Scholar] [CrossRef]
- Bebendorf, M. Hierarchical Matrices: A Means to Eciently Solve Elliptic Boundary Value Problems; Lect. Notes. Comput. Sci. Eng 63; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Amestoy, P.R.; Ashcraft, C.; Boiteau, O.; Buttari, A.; L’Excellent, J.-Y.; Weisbecker, C. Improving Multifrontal Methods by Means of Block Low-Rank Representations. SIAM J. Sci. Comput. Soc. Ind. Appl. Math. 2015, 37, 1451–1474. [Google Scholar] [CrossRef]
- Dachuan, Y.; Yuvarajan, S. Electronic circuit model for proton exchange membrane fuel cells. J. Power Sources 2005, 142, 238–242. [Google Scholar]
- Pavlenko, A.; Burtsev, Y.; Vasyukov, I.; Puzin, V.; Gummel, A. Equivalent Scheme of the Fuel Cell Taking into Account the Influence of Eddy Currents and A Practical Way to Determine Its Parameters. Inventions 2022, 7, 72. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoroshev, A.; Vasyukov, I.; Pavlenko, A.; Batishchev, D. Reduction in the Computational Complexity of Calculating Losses on Eddy Currents in a Hydrogen Fuel Cell Using the Finite Element Analysis. Inventions 2023, 8, 38. https://doi.org/10.3390/inventions8010038
Khoroshev A, Vasyukov I, Pavlenko A, Batishchev D. Reduction in the Computational Complexity of Calculating Losses on Eddy Currents in a Hydrogen Fuel Cell Using the Finite Element Analysis. Inventions. 2023; 8(1):38. https://doi.org/10.3390/inventions8010038
Chicago/Turabian StyleKhoroshev, Artem, Ivan Vasyukov, Alexander Pavlenko, and Denis Batishchev. 2023. "Reduction in the Computational Complexity of Calculating Losses on Eddy Currents in a Hydrogen Fuel Cell Using the Finite Element Analysis" Inventions 8, no. 1: 38. https://doi.org/10.3390/inventions8010038
APA StyleKhoroshev, A., Vasyukov, I., Pavlenko, A., & Batishchev, D. (2023). Reduction in the Computational Complexity of Calculating Losses on Eddy Currents in a Hydrogen Fuel Cell Using the Finite Element Analysis. Inventions, 8(1), 38. https://doi.org/10.3390/inventions8010038





