A Generalized Framework for Adopting Regression-Based Predictive Modeling in Manufacturing Environments
Abstract
1. Introduction
- Formulation of a generalized framework for predictive modeling in manufacturing environments using data collected from real-time manufacturing processes.
- Validation of the proposed generalized framework by applying several regression learning techniques to undertake predictive modeling using an open-source multi-stage continuous-flow manufacturing process data set.
- Summarized inference-based and statistically verified rankings for the adoption and selection of regression learning techniques to potentially invent predictive modeling-based paradigms for typical manufacturing processes.
2. Materials and Methods
2.1. Relevant Related Work
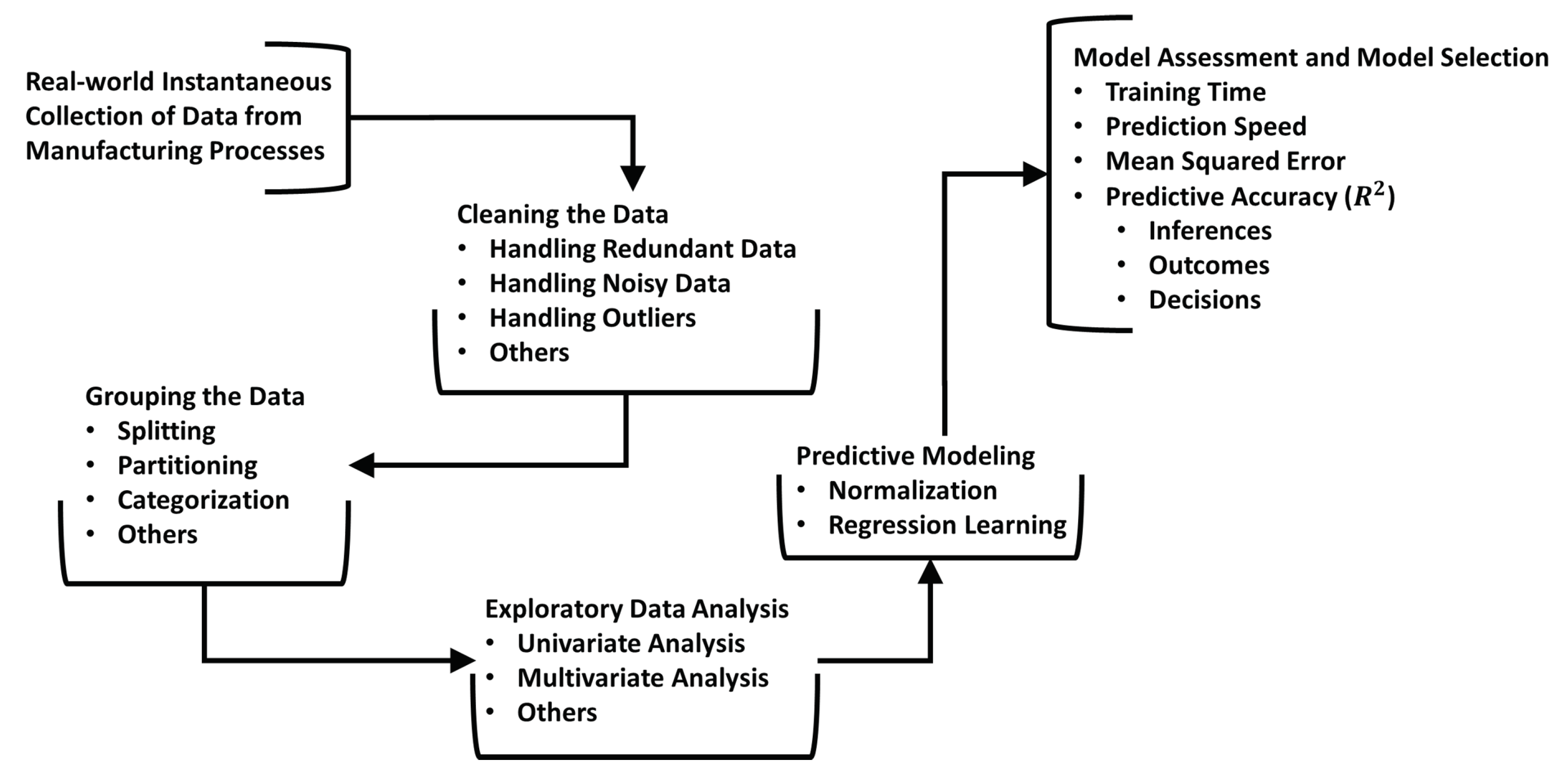
2.2. The Proposed Framework
- Step 1: Data is collected instantaneously and/or recursively from critical manufacturing processes of interest. The collected data is used to create a database, .
- Step 2: Metrics for all explanatory and response variables in , and , respectively, are passed through purpose-built functions to generate a clean database, = [, ], where unwanted observations or data (e.g., redundant data) are handled correctly and robustly. See Section 2.3.1 for more details on the custom functions adopted in this work.
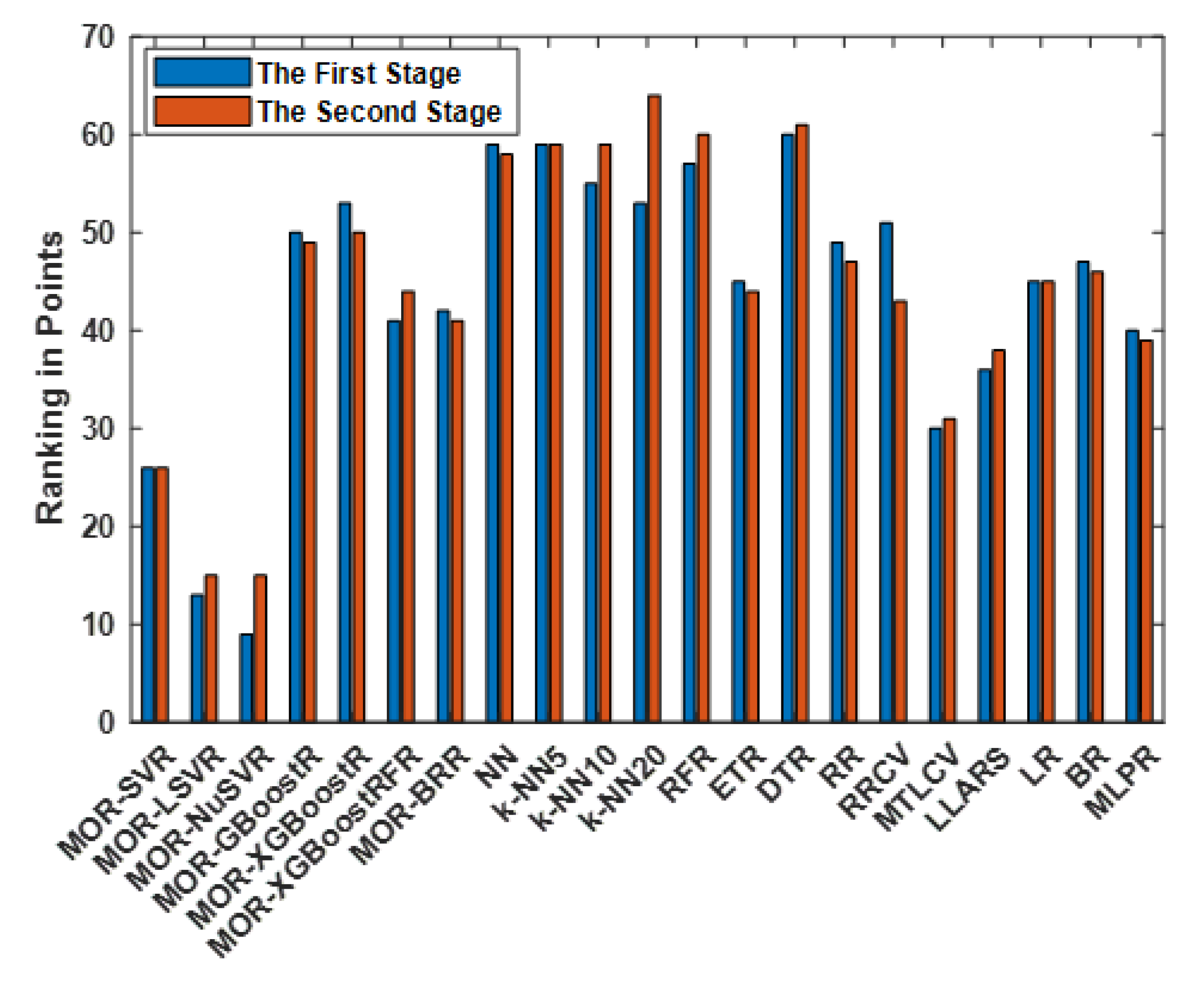
- Step 3: Since the metrics in are expected to be from the continuous-flow stages of manufacturing processes, is grouped to ensure metrics collected from the same stage of the manufacturing process are collocated. For example, (first stage) and (second stage) for a two-stage continuous-flow manufacturing process as we have investigated in this work (See Section 2.3).
- Step 4: Exploratory data analysis techniques are employed for the univariate analysis and multivariate analysis of the metrics in to establish their descriptive statistics and relationships. In this work, only descriptive statistics are presented.
- Step 5: The explanatory metrics in (i.e., ) are then normalized for regression learning to have a new database (i.e., as carried out in this work (See Section 2.4)).
- Step 6: Predictive modeling is carried out by applying several regression learning techniques to [, ] to ascertain the most suitable ones in terms of the mean squared error (), predictive accuracy (R-squared value ()), prediction speed (), and training time ().
- Step 7: To rank all methods, some inferences are drawn a posteriori based on the assessment of the outcomes from Step 6.
- Step 8: The inference-based rankings from Step 7 are statistically verified to determine the best regression learning technique(s) to select and adopt for the given manufacturing process data set.
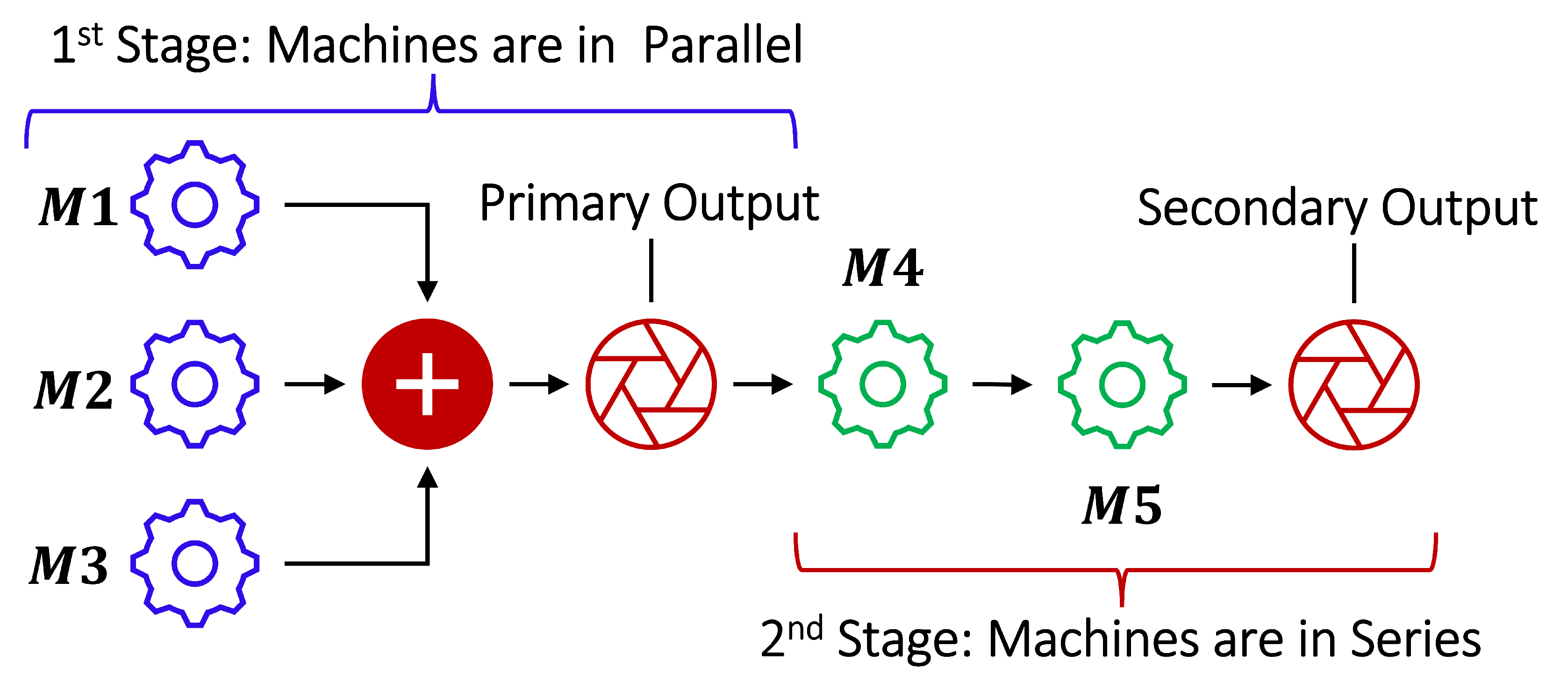
2.3. Case Study of a Multi-Stage Continuous-Flow Manufacturing Process
2.3.1. Data Set Description
- 1
- For every observation in , select all the columns for the explanatory variables to have an array or matrix and select all the columns for the response variables to have an array or matrix .
- 2
- For every column vector () in , perform the following operations:
- 3
- For every column vector () in , perform the following operations:
Feature Scaling of the Data Set
2.4. The Machine Learning Problem and Investigated Methods
2.4.1. Predictive Modeling Problem Definition for the Case Study
2.4.2. Regression Learning for the Case Study
3. Experimental Setup
4. Results and Discussion
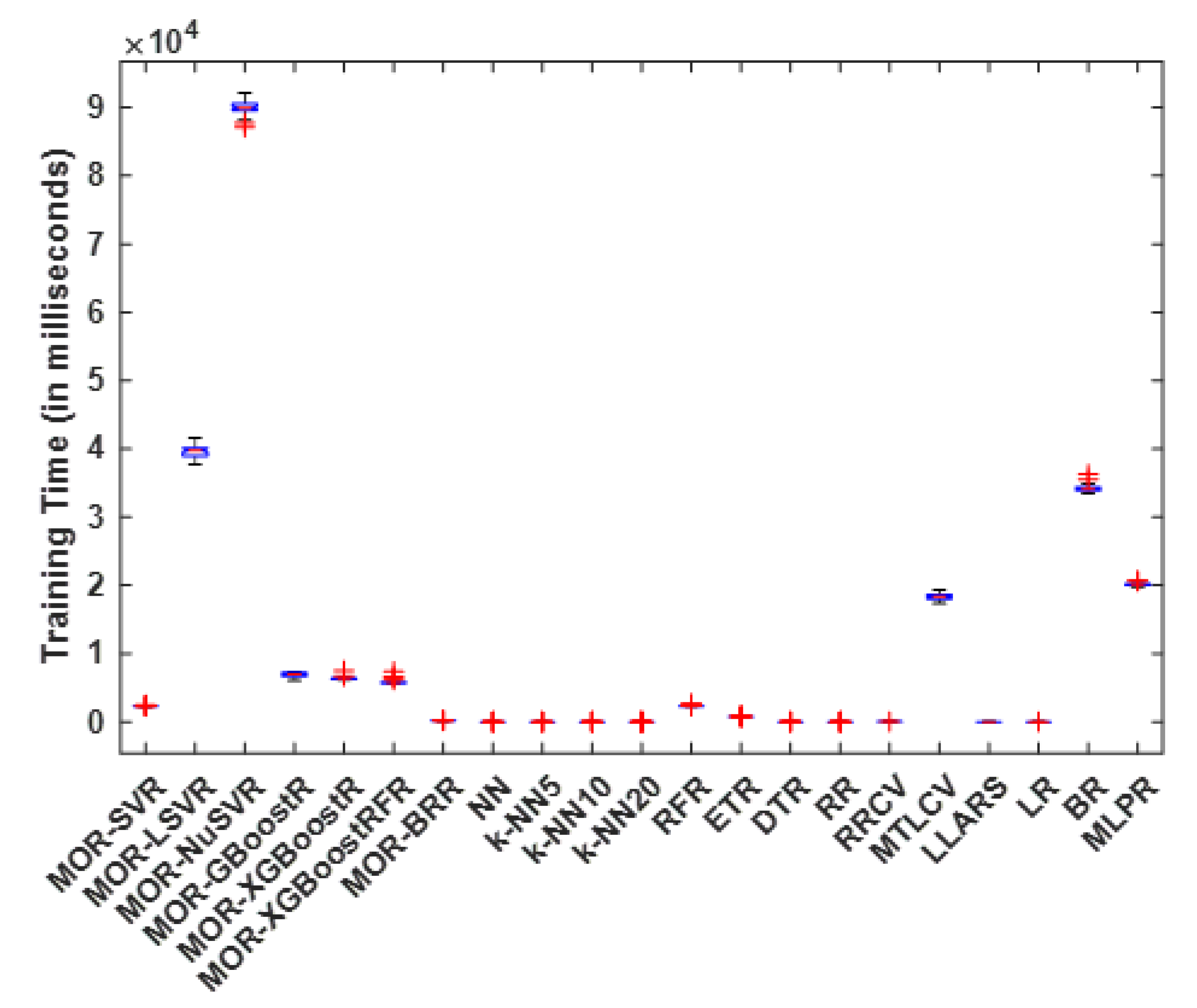
4.1. Training Time
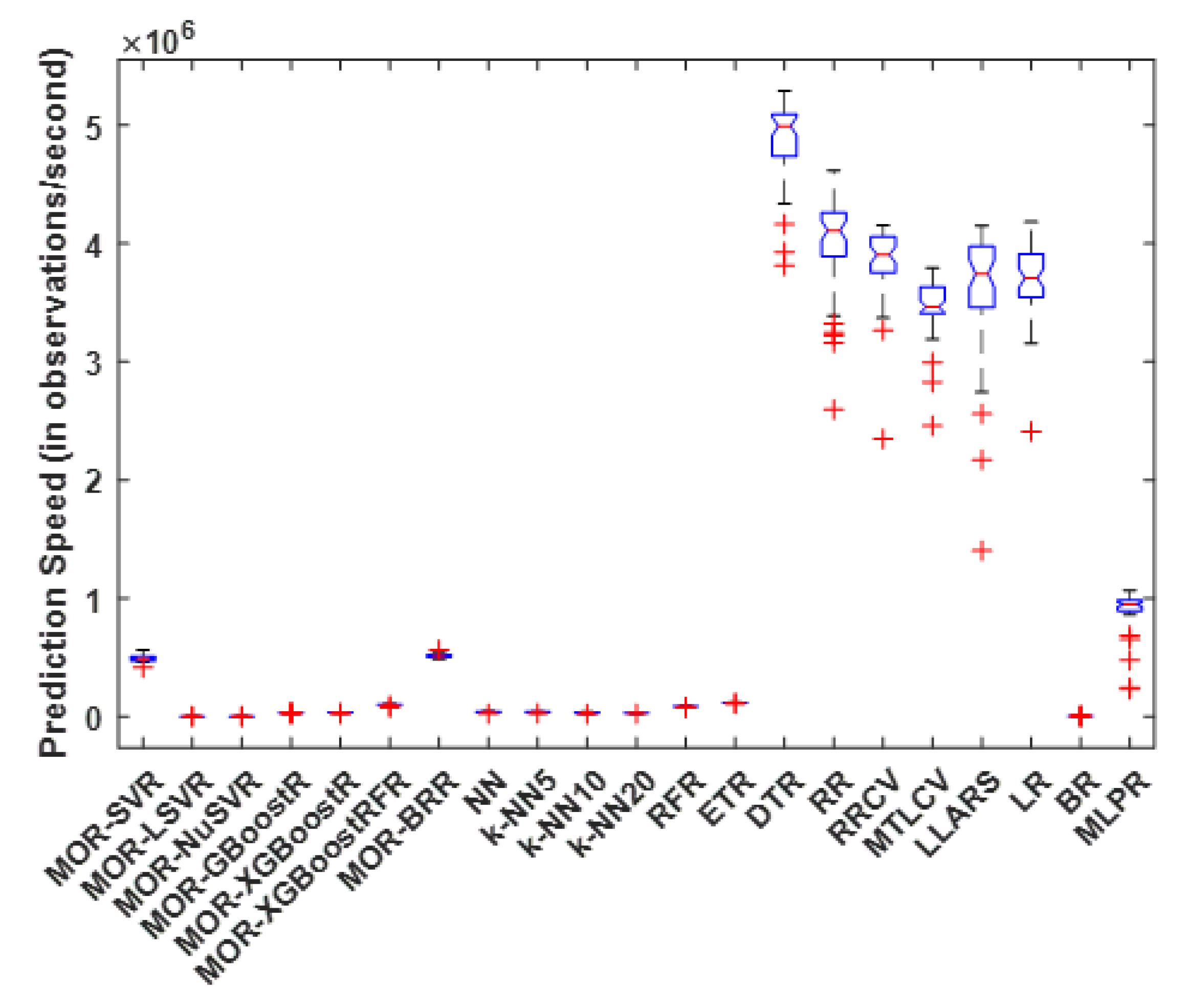
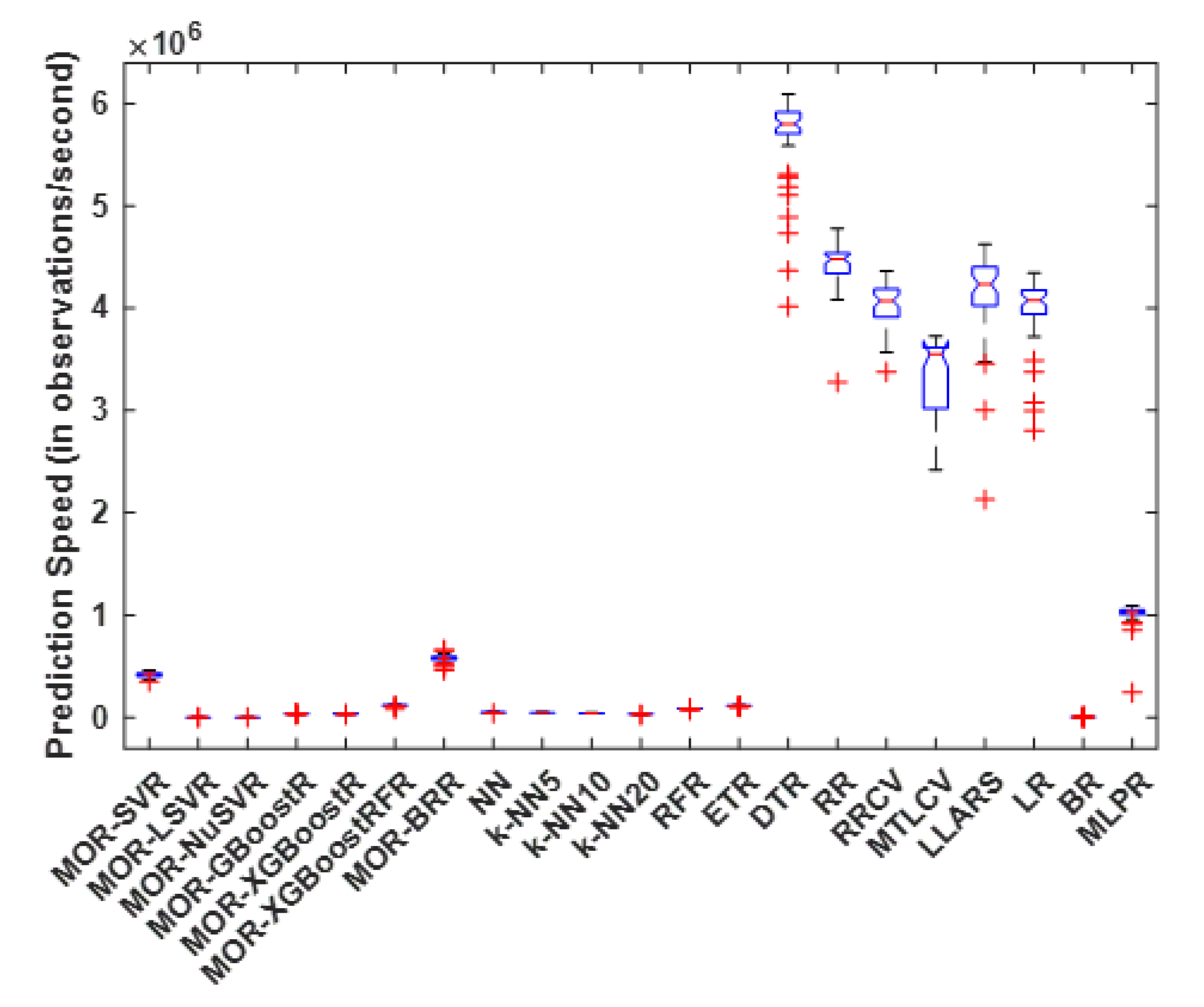
4.2. Prediction Speed
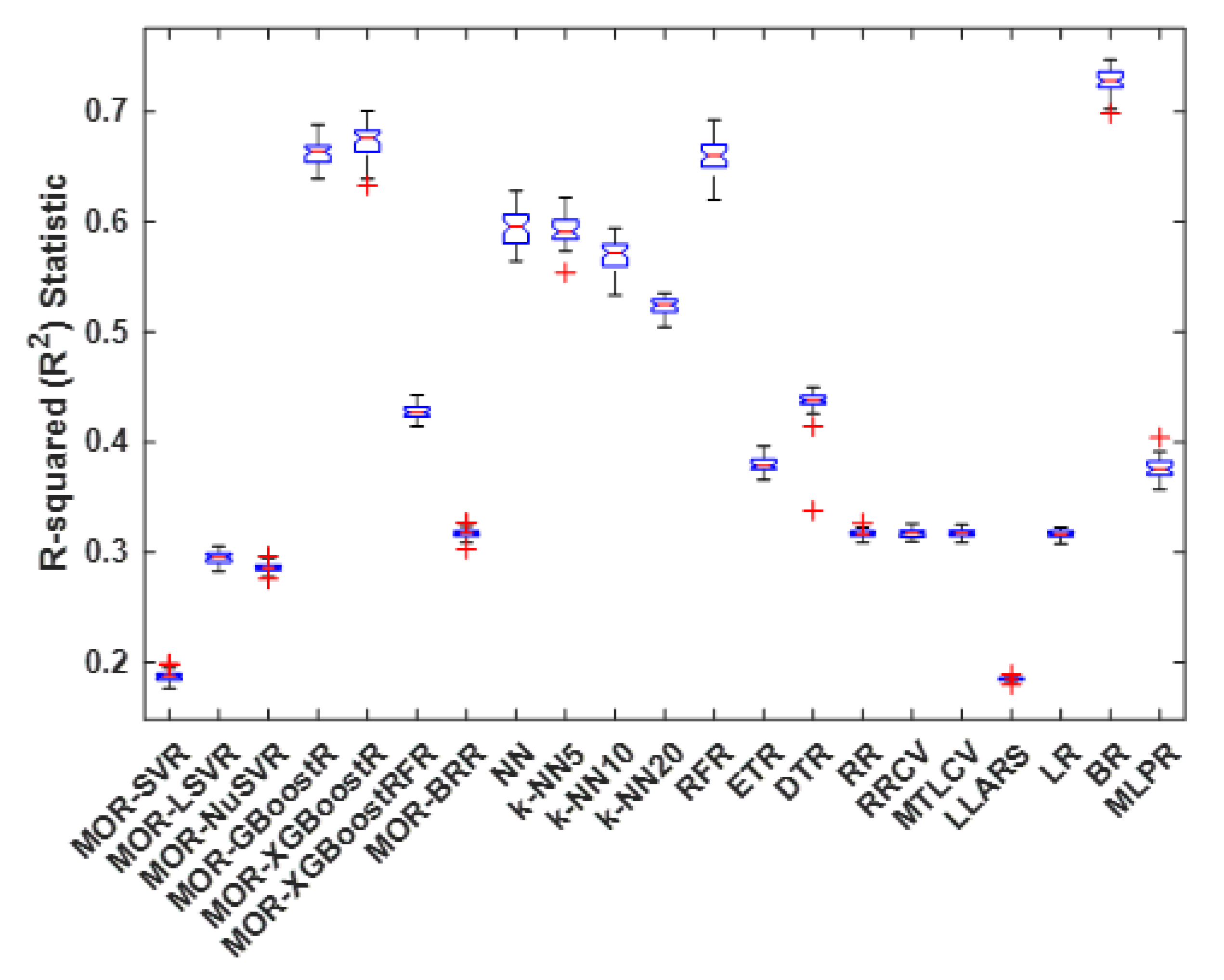
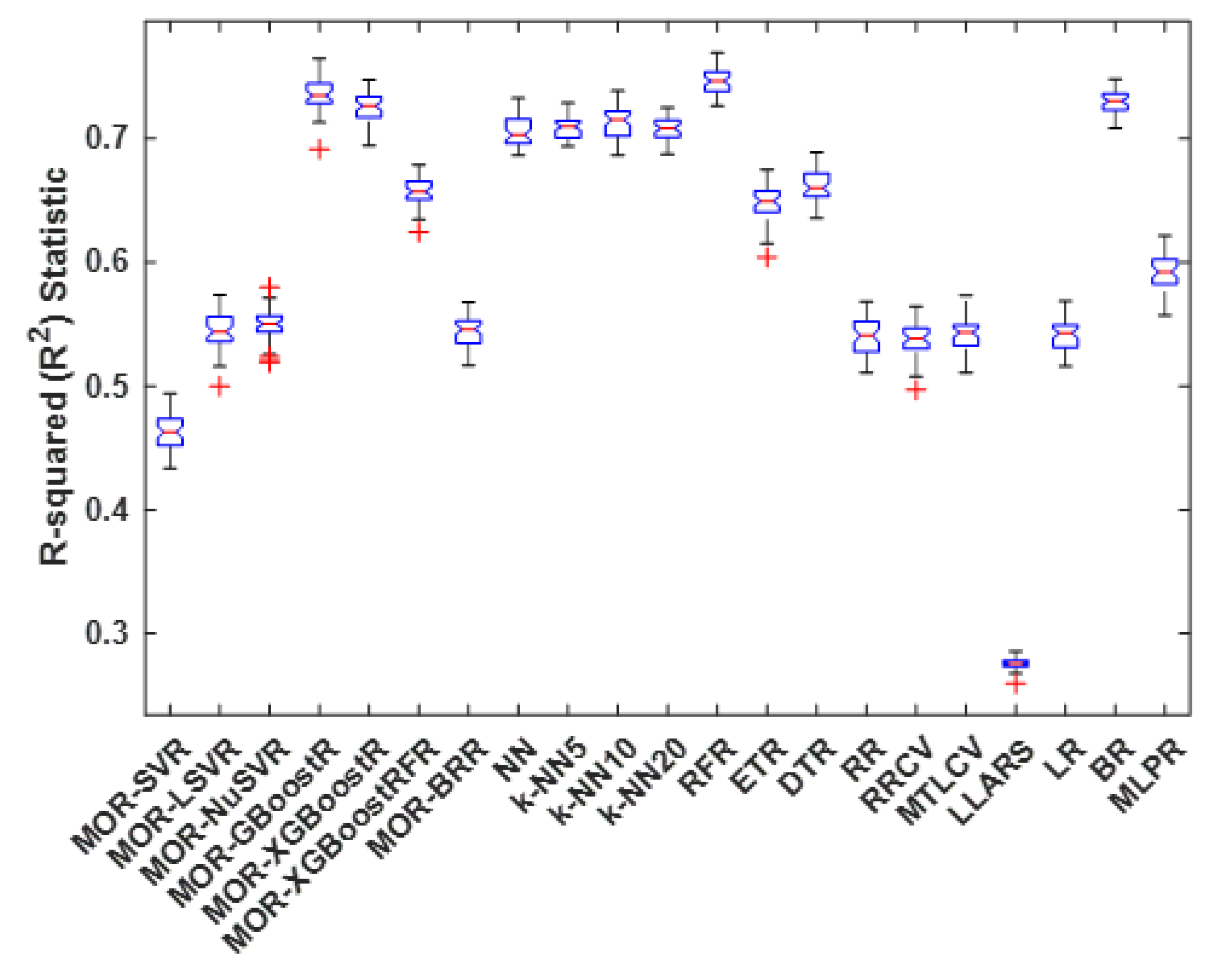
4.3. R-Squared Statistic
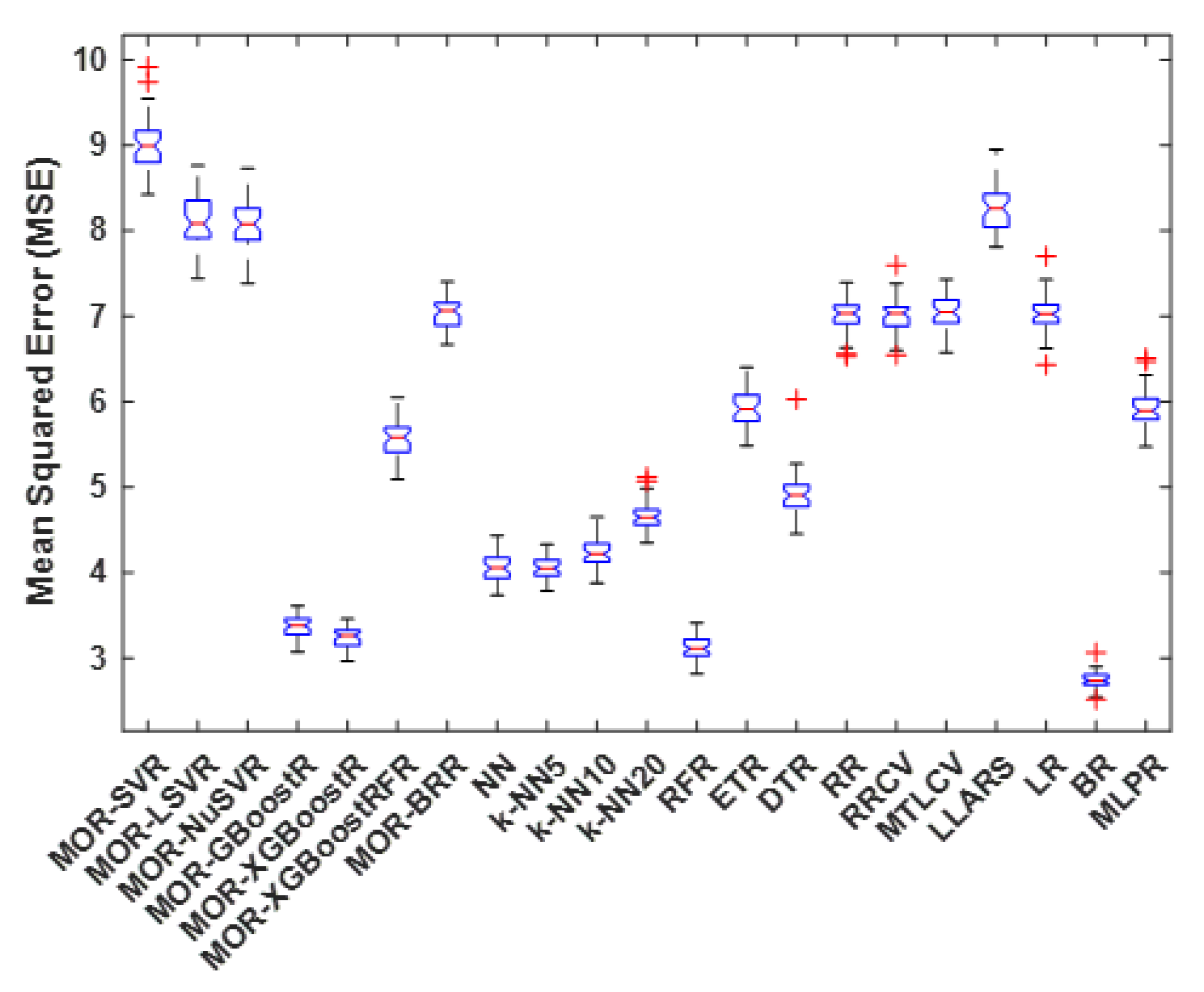
4.4. Mean Squared Error
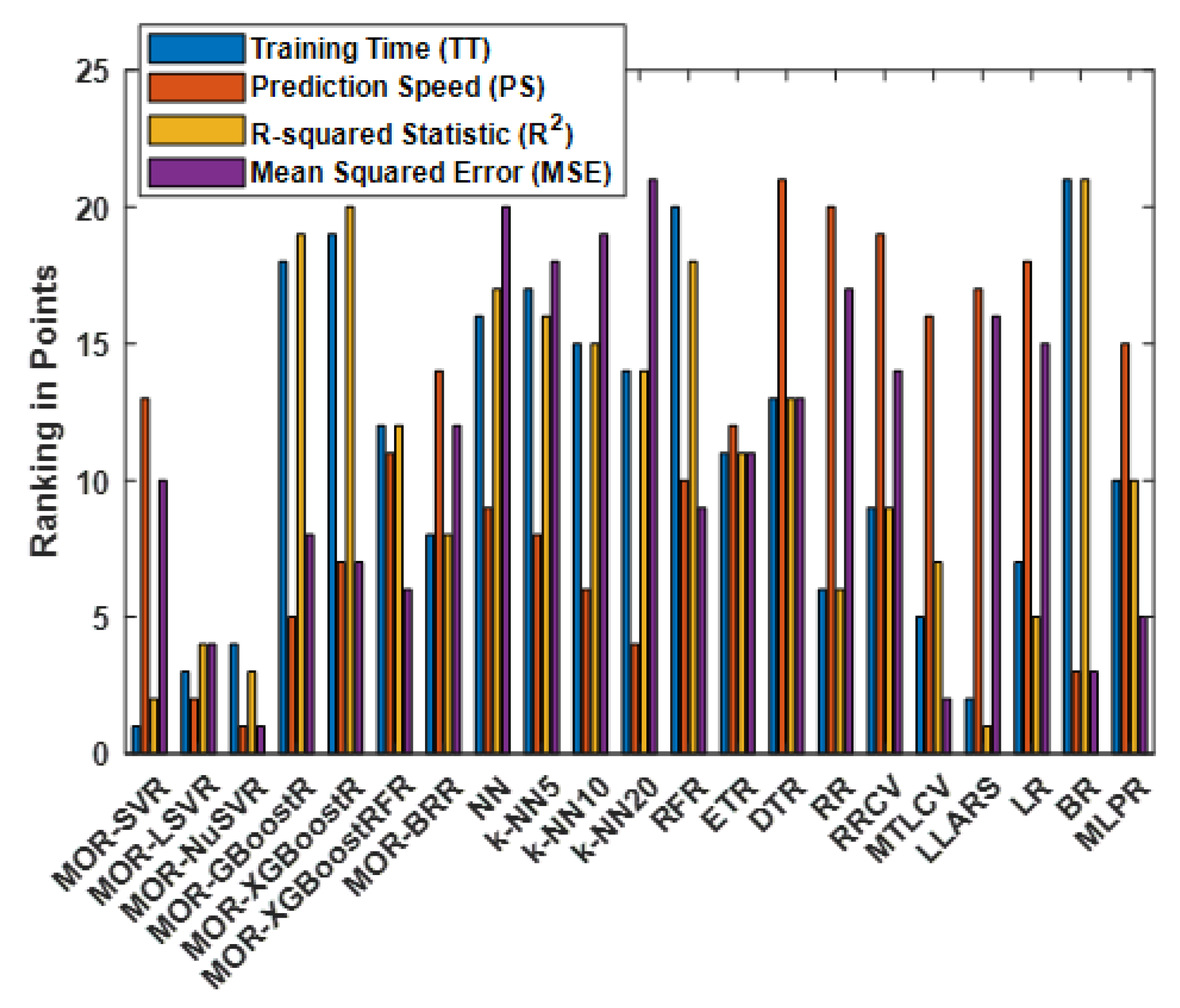
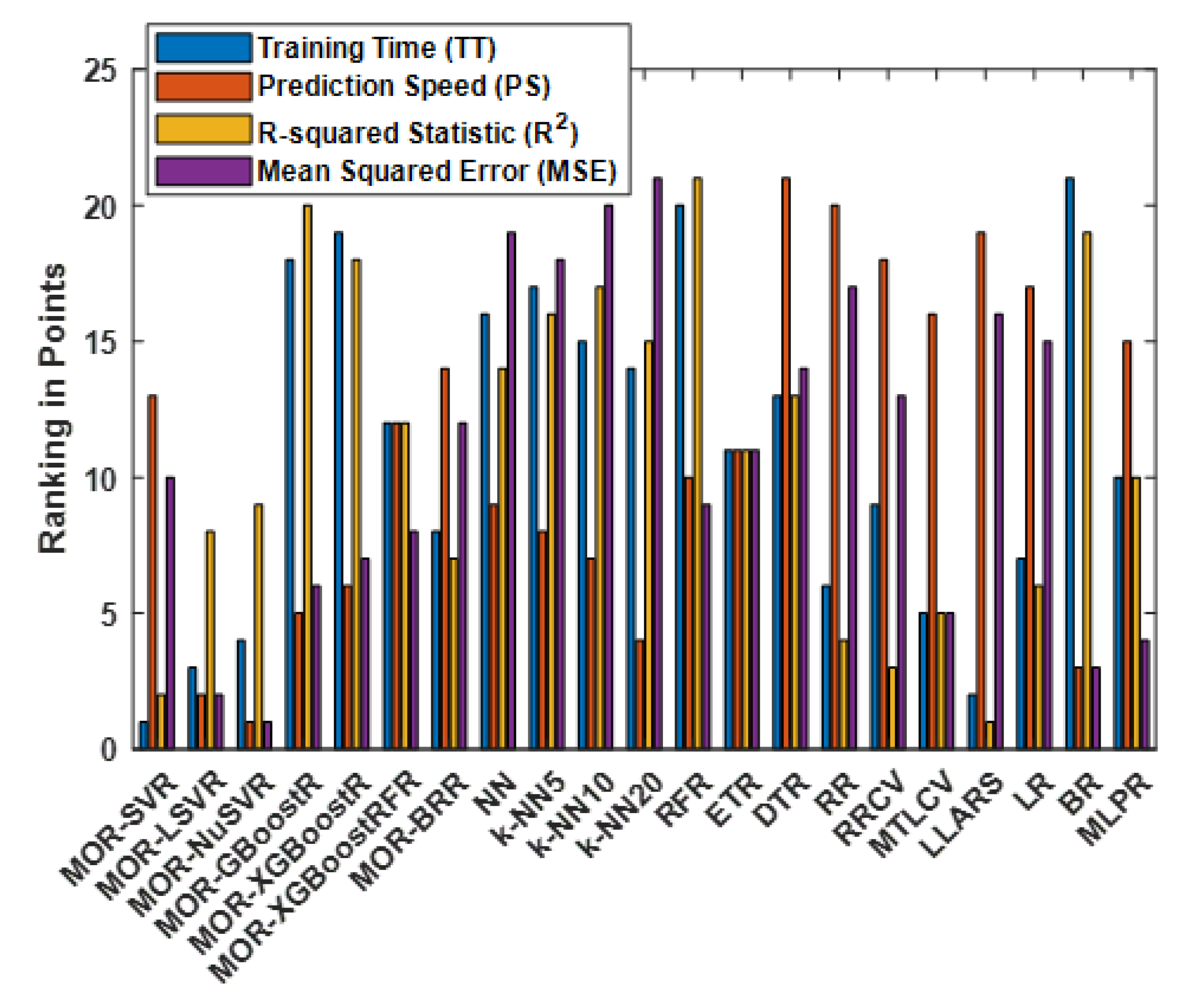
4.5. Ranking of All Methods
4.6. Hypothesis Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bajic, B.; Rikalovic, A.; Suzic, N.; Piuri, V. Industry 4.0 Implementation Challenges and Opportunities: A Managerial Perspective. IEEE Syst. J. 2021, 15, 546–559. [Google Scholar] [CrossRef]
- Shiroishi, Y.; Uchiyama, K.; Suzuki, N. Society 5.0: For Human Security and Well-Being. Computer 2018, 51, 91–95. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A. Critical components of Industry 5.0 towards a successful adoption in the field of manufacturing. J. Ind. Integr. Manag. 2020, 5, 327–348. [Google Scholar] [CrossRef]
- Malige, A.; Korcyl, G.; Firlej, M.; Fiutowski, T.; Idzik, M.; Korzeniak, B.; Lalik, R.; Misiak, A.; Molenda, A.; Moroń, J.; et al. Real-Time Data Processing Pipeline for Trigger Readout Board-Based Data Acquisition Systems. IEEE Trans. Nucl. Sci. 2022, 69, 1765–1772. [Google Scholar] [CrossRef]
- Akinsolu, M.O. Applied Artificial Intelligence in Manufacturing and Industrial Production Systems: PEST Considerations for Engineering Managers. IEEE Eng. Manag. Rev. 2022, 51, 1–8. [Google Scholar] [CrossRef]
- Miller, W.J.; Poole, M. Advanced CIM environment for manufacturing data analysis. IEEE Trans. Semicond. Manuf. 1993, 6, 128–133. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Li, J.; Gao, H. A generic data analytics system for manufacturing production. Big Data Min. Anal. 2018, 1, 160–171. [Google Scholar] [CrossRef]
- Zhang, C.; Ji, W. Big Data Analysis Approach for Real-Time Carbon Efficiency Evaluation of Discrete Manufacturing Workshops. IEEE Access 2019, 7, 107730–107743. [Google Scholar] [CrossRef]
- Cui, Y.; Kara, S.; Chan, K.C. Manufacturing big data ecosystem: A systematic literature review. Robot.-Comput.-Integr. Manuf. 2020, 62, 101861. [Google Scholar] [CrossRef]
- Feng, M.; Li, Y. Predictive Maintenance Decision Making Based on Reinforcement Learning in Multistage Production Systems. IEEE Access 2022, 10, 18910–18921. [Google Scholar] [CrossRef]
- Costello, J.J.A.; West, G.M.; McArthur, S.D.J. Machine Learning Model for Event-Based Prognostics in Gas Circulator Condition Monitoring. IEEE Trans. Reliab. 2017, 66, 1048–1057. [Google Scholar] [CrossRef]
- Ayodeji, A.; Wang, Z.; Wang, W.; Qin, W.; Yang, C.; Xu, S.; Liu, X. Causal augmented ConvNet: A temporal memory dilated convolution model for long-sequence time series prediction. ISA Trans. 2022, 123, 200–217. [Google Scholar] [CrossRef] [PubMed]
- Boyes, H.; Hallaq, B.; Cunningham, J.; Watson, T. The industrial internet of things (IIoT): An analysis framework. Comput. Ind. 2018, 101, 1–12. [Google Scholar] [CrossRef]
- Aebersold, S.A.; Akinsolu, M.O.; Monir, S.; Jones, M.L. Ubiquitous Control of a CNC Machine: Proof of Concept for Industrial IoT Applications. Information 2021, 12, 529. [Google Scholar] [CrossRef]
- Siva Vardhan, D.S.V.; Narayan, Y.S. Development of an automatic monitoring and control system for the objects on the conveyor belt. In Proceedings of the 2015 International Conference on Man and Machine Interfacing (MAMI), Bhubaneswar, India, 17–19 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Çınar, Z.M.; Abdussalam Nuhu, A.; Zeeshan, Q.; Korhan, O.; Asmael, M.; Safaei, B. Machine learning in predictive maintenance towards sustainable smart manufacturing in industry 4.0. Sustainability 2020, 12, 8211. [Google Scholar] [CrossRef]
- Djurdjanovic, D.; Lee, J.; Ni, J. Watchdog Agent—An infotronics-based prognostics approach for product performance degradation assessment and prediction. Adv. Eng. Inform. 2003, 17, 109–125. [Google Scholar] [CrossRef]
- Liu, C.; Tang, D.; Zhu, H.; Nie, Q. A Novel Predictive Maintenance Method Based on Deep Adversarial Learning in the Intelligent Manufacturing System. IEEE Access 2021, 9, 49557–49575. [Google Scholar] [CrossRef]
- Liu, H.; Yuan, R.; Lv, Y.; Li, H.; Gedikli, E.D.; Song, G. Remaining Useful Life Prediction of Rolling Bearings Based on Segmented Relative Phase Space Warping and Particle Filter. IEEE Trans. Instrum. Meas. 2022, 71, 1–15. [Google Scholar] [CrossRef]
- He, J.; Cen, Y.; Alelaumi, S.; Won, D. An Artificial Intelligence-Based Pick-and-Place Process Control for Quality Enhancement in Surface Mount Technology. IEEE Trans. Components Packag. Manuf. Technol. 2022, 12, 1702–1711. [Google Scholar] [CrossRef]
- Dogan, A.; Birant, D. Machine learning and data mining in manufacturing. Expert Syst. Appl. 2021, 166, 114060. [Google Scholar] [CrossRef]
- Cui, P.H.; Wang, J.Q.; Li, Y. Data-driven modelling, analysis and improvement of multistage production systems with predictive maintenance and product quality. Int. J. Prod. Res. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Liveline Technologies. Multi-Stage Continuous-Flow Manufacturing Process. 2019. Available online: https://www.kaggle.com/datasets/supergus/multistage-continuousflow-manufacturing-process (accessed on 15 October 2022).
- Liveline Technologies. Convert Your Manufacturing Assets into an Intelligent, Autonomous System Using AI-Based Process Controls. 2022. Available online: https://www.liveline.tech/ (accessed on 5 December 2022).
- Pach, F.; Feil, B.; Nemeth, S.; Arva, P.; Abonyi, J. Process-data-warehousing-based operator support system for complex production technologies. IEEE Trans. Syst. Man Cybern.- Part A Syst. Hum. 2006, 36, 136–153. [Google Scholar] [CrossRef]
- LJ Create. PETRA II Advanced Industrial Control Trainer. 2023. Available online: https://ljcreate.com/uk/engineering/petra-ii-advanced-industrial-control-trainer/ (accessed on 7 January 2023).
- Nargesian, F.; Samulowitz, H.; Khurana, U.; Khalil, E.B.; Turaga, D.S. Learning Feature Engineering for Classification. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence (IJCAI-17), Melbourne, Australia, 19–25 August 2017; pp. 2529–2535. [Google Scholar]
- Wan, X. Influence of feature scaling on convergence of gradient iterative algorithm. J. Phys. Conf. Ser. 2019, 1213, 032021. [Google Scholar] [CrossRef]
- Sangodoyin, A.O.; Akinsolu, M.O.; Pillai, P.; Grout, V. Detection and Classification of DDoS Flooding Attacks on Software-Defined Networks: A Case Study for the Application of Machine Learning. IEEE Access 2021, 9, 122495–122508. [Google Scholar] [CrossRef]
- Akinsolu, M.O.; Sangodoyin, A.O.; Uyoata, U.E. Behavioral Study of Software-Defined Network Parameters Using Exploratory Data Analysis and Regression-Based Sensitivity Analysis. Mathematics 2022, 10, 2536. [Google Scholar] [CrossRef]
- Sangodoyin, A.O.; Akinsolu, M.O.; Awan, I. A deductive approach for the sensitivity analysis of software defined network parameters. Simul. Model. Pract. Theory 2020, 103, 102099. [Google Scholar] [CrossRef]
- Liu, P.; Lv, N.; Chen, K.; Tang, L.; Zhou, J. Regression Based Dynamic Elephant Flow Detection in Airborne Network. IEEE Access 2020, 8, 217123–217133. [Google Scholar] [CrossRef]
- Shohani, R.B.; Mostafavi, S.A. Introducing a New Linear Regression Based Method for Early DDoS Attack Detection in SDN. In Proceedings of the 2020 6th International Conference on Web Research (ICWR), Tehran, Iran, 22–23 April 2020; pp. 126–132. [Google Scholar] [CrossRef]
- Borchani, H.; Varando, G.; Bielza, C.; Larranaga, P. A survey on multi-output regression. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2015, 5, 216–233. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Support Vector Machines and Support Vector Regression. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer: Cham, Switzerland, 2022; pp. 337–378. [Google Scholar]
- scikit-learn. scikit-learn Machine Learning in Python. 2022. Available online: https://scikit-learn.org/stable/ (accessed on 15 October 2022).
- Platt, J. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Adv. Large Margin Classif. 1999, 10, 61–74. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Dudani, S.A. The Distance-Weighted k-Nearest-Neighbor Rule. IEEE Trans. Syst. Man Cybern. 1976, SMC-6, 325–327. [Google Scholar] [CrossRef]
- An efficient instance selection algorithm for k nearest neighbor regression. Neurocomputing 2017, 251, 26–34. [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Xu, M.; Watanachaturaporn, P.; Varshney, P.K.; Arora, M.K. Decision tree regression for soft classification of remote sensing data. Remote Sens. Environ. 2005, 97, 322–336. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- McDonald, G.C. Ridge regression. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 93–100. [Google Scholar] [CrossRef]
- Nokeri, T.C. Advanced Parametric Methods. In Data Science Revealed; Apress: Berkley, CA, USA, 2021; pp. 45–53. [Google Scholar]
- Liu, K.; Xu, B.; Kim, C.; Fu, J. Well performance from numerical methods to machine learning approach: Applications in multiple fractured shale reservoirs. Geofluids 2021, 2021, 3169456. [Google Scholar] [CrossRef]
- Hesterberg, T.; Choi, N.H.; Meier, L.; Fraley, C. Least angle and ℓ1 penalized regression: A review. Stat. Surv. 2008, 2, 61–93. [Google Scholar] [CrossRef]
- Cohen, P.; West, S.G.; Aiken, L.S. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 2003. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Negnevitsky, M. Artificial Intelligence: A Guide to Intelligent Systems; Pearson Education: Harlow, UK, 2005. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Google Research. Colaboratory. 2022. Available online: https://colab.research.google.com/ (accessed on 15 October 2022).
- Isabona, J.; Imoize, A.L.; Kim, Y. Machine Learning-Based Boosted Regression Ensemble Combined with Hyperparameter Tuning for Optimal Adaptive Learning. Sensors 2022, 22, 3776. [Google Scholar] [CrossRef] [PubMed]
- Passos, D.; Mishra, P. A tutorial on automatic hyperparameter tuning of deep spectral modelling for regression and classification tasks. Chemom. Intell. Lab. Syst. 2022, 223, 104520. [Google Scholar] [CrossRef]
- Chicco, D. Ten quick tips for machine learning in computational biology. BioData Min. 2017, 10, 1–17. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar]


| Explanatory Variable | Mean | Median | Minimum | Maximum | S.D. |
|---|---|---|---|---|---|
| First Condition: | 15.3 | 15.1 | 13.8 | 17.2 | 1.2 |
| Second Condition: | 23.8 | 23.9 | 23.0 | 24.4 | 0.4 |
| First Stage: | 1242.8 | 1264.4 | 231.3 | 1331.8 | 95.8 |
| First Stage: | 72.0 | 72.0 | 71.9 | 72.5 | 0.1 |
| First Stage: | 72.0 | 72.0 | 71.3 | 72.7 | 0.4 |
| First Stage: | 70.3 | 72.0 | 44.4 | 88.5 | 5.5 |
| First Stage: | 11.1 | 10.7 | 10.4 | 12.2 | 0.6 |
| First Stage: | 409.0 | 417.0 | 359.5 | 487.2 | 20.5 |
| First Stage: | 81.5 | 81.3 | 76.3 | 83.9 | 0.9 |
| First Stage: | 76.0 | 75.0 | 69.7 | 80.0 | 2.1 |
| First Stage: | 202.6 | 203.3 | 0.0 | 266.5 | 15.1 |
| First Stage: | 69.0 | 69.0 | 68.7 | 69.7 | 0.1 |
| First Stage: | 69.1 | 69.1 | 67.8 | 69.9 | 0.1 |
| First Stage: | 73.4 | 73.4 | 71.6 | 74.4 | 0.4 |
| First Stage: | 13.9 | 13.9 | 13.8 | 14.0 | 0.0 |
| First Stage: | 226.1 | 226.1 | 218.9 | 250.6 | 3.1 |
| First Stage: | 76.8 | 77.0 | 68.8 | 77.4 | 0.9 |
| First Stage: | 60.0 | 60.0 | 59.6 | 60.5 | 0.2 |
| First Stage: | 202.4 | 202.9 | 0.0 | 259.1 | 15.7 |
| First Stage: | 78.0 | 78.0 | 77.3 | 78.7 | 0.1 |
| First Stage: | 78.0 | 78.0 | 77.7 | 78.6 | 0.1 |
| First Stage: | 345.1 | 342.9 | 321.2 | 374.3 | 9.1 |
| First Stage: | 13.3 | 13.4 | 12.0 | 14.0 | 0.4 |
| First Stage: | 246.8 | 247.5 | 235.1 | 263.7 | 6.1 |
| First Stage: | 74.1 | 75.1 | 65.3 | 75.5 | 2.1 |
| First Stage: | 65.0 | 65.0 | 64.8 | 65.2 | 0.1 |
| First Stage: | 108.9 | 105.5 | 45.3 | 118.9 | 5.7 |
| First Stage: | 84.9 | 74.8 | 53.3 | 115.2 | 18.6 |
| First Stage: | 80.0 | 80.0 | 79.6 | 80.3 | 0.1 |
| Second Stage: | 360.1 | 360.0 | 298.0 | 393.0 | 2.3 |
| Second Stage: | 360.1 | 360.0 | 284.0 | 396.0 | 3.0 |
| Second Stage: | 17.2 | 17.0 | 14.0 | 25.0 | 0.9 |
| Second Stage: | 322.6 | 324.0 | 268.0 | 327.0 | 3.7 |
| Second Stage: | 17.2 | 17.0 | 14.0 | 25.0 | 0.9 |
| Second Stage: | 309.8 | 311.0 | 260.0 | 326.0 | 2.9 |
| Second Stage: | 187.1 | 192.0 | 35.0 | 216.0 | 23.7 |
| Second Stage: | 310.0 | 310.0 | 309.4 | 310.3 | 0.0 |
| Second Stage: | 290.0 | 290.0 | 289.7 | 290.3 | 0.1 |
| Second Stage: | 269.7 | 270.0 | 263.8 | 270.0 | 1.0 |
| Second Stage: | 242.7 | 242.7 | 237.6 | 245.0 | 1.6 |
| Second Stage: | 245.0 | 245.0 | 242.9 | 245.7 | 0.1 |
| Second Stage: | 63.4 | 63.4 | 62.8 | 66.1 | 0.4 |
| Second Stage: | 154.0 | 155.6 | 45.4 | 159.2 | 10.3 |
| Response Variable | Mean | Median | Minimum | Maximum | S.D. |
|---|---|---|---|---|---|
| First Stage: | 12.9 | 13.0 | 0.0 | 20.9 | 0.9 |
| First Stage: | 8.1 | 13.2 | −3.1 | 19.1 | 6.9 |
| First Stage: | 11.4 | 11.3 | −4.9 | 23.5 | 1.1 |
| First Stage: | 21.3 | 21.5 | 0.0 | 26.2 | 2.1 |
| First Stage: | 32.9 | 33.5 | −7.7 | 34.8 | 3.9 |
| First Stage: | 0.1 | 0.0 | −0.6 | 5.0 | 0.6 |
| First Stage: | 1.3 | 1.6 | −0.8 | 7.0 | 1.1 |
| First Stage: | 1.1 | 0.0 | −0.8 | 5.2 | 1.4 |
| First Stage: | 19.8 | 20.9 | 22.5 | 4.8 | |
| First Stage: | 18.0 | 18.9 | 20.4 | 4.2 | |
| First Stage: | 7.7 | 7.8 | 13.1 | 1.1 | |
| First Stage: | 1.5 | 0.0 | 7.5 | 2.5 | |
| First Stage: | 1.2 | 1.5 | 4.0 | 0.7 | |
| First Stage: | 2.9 | 3.2 | −1.2 | 6.9 | 0.9 |
| First Stage: | 9.9 | 15.0 | −6.6 | 22.3 | 7.4 |
| Second Stage: | 11.7 | 12.8 | 19.1 | 3.6 | |
| Second Stage: | 6.3 | 6.5 | 12.9 | 1.6 | |
| Second Stage: | 10.3 | 10.9 | 16.5 | 2.3 | |
| Second Stage: | 19.3 | 20.6 | 25.2 | 4.7 | |
| Second Stage: | 2.9 | 0.0 | 34.3 | 9.2 | |
| Second Stage: | 2.7 | 2.7 | 8.1 | 0.4 | |
| Second Stage: | 0.5 | 0.6 | 3.3 | 0.2 | |
| Second Stage: | 2.9 | 3.0 | 7.4 | 0.5 | |
| Second Stage: | 18.4 | 19.7 | 24.8 | 5.0 | |
| Second Stage: | 11.6 | 16.6 | 18.4 | 7.6 | |
| Second Stage: | 7.5 | 7.9 | 8.6 | 1.6 | |
| Second Stage: | 5.4 | 5.6 | 6.3 | 1.2 | |
| Second Stage: | 2.0 | 2.1 | 5.2 | 0.4 | |
| Second Stage: | 3.5 | 3.5 | 8.0 | 0.5 | |
| Second Stage: | 7.5 | 7.9 | −3.4 | 14.3 | 2.1 |
| Method | References |
|---|---|
| MOR-based Support Vector Regression (MOR-SVR) | [34,35,36] |
| MOR-based Linear Support Vector Regression (MOR-LSVR) | [34,35,36] |
| MOR-based Support Vector Regression (MOR-NuSVR) | [34,36,37] |
| MOR-based Gradient Boosting Regression (MOR-GBoostR) | [34,36,38] |
| MOR-based Extreme Gradient Boosting Regression (MOR-XGBoostR) | [34,36,38,39] |
| MOR-based Extreme Gradient Boosting Random Forest Regression (MOR-XGBoostRFR) | [34,36,40] |
| MOR-based Bayesian Ridge Regression (MOR-BRR) | [34,36,41] |
| k-Nearest Neighbors (k-NN) | [36,42,43] |
| Random Forest Regressor (RFR) | [36,40,44] |
| Decision Trees Regressor (DTR) | [36,45] |
| Extra-Trees Regressor (ETR) | [36,46] |
| Ridge Regression (RR) | [36,47] |
| Ridge Regression with Built-In Cross-Validation (RRCV) | [36,48] |
| Multi-Task Least Absolute Shrinkage and Selection Operator with Cross-Validation (MTLCV) | [36,49] |
| Least Absolute Shrinkage and Selection Operator Model Fit Least Angle Regression (LLARS) | [36,50] |
| Linear Regression (LR) | [36,51] |
| Bagging Regressor (BR) | [36,52] |
| Multilayer Perceptron Regressor (MLPR) | [36,53] |
| Method | Best | Worst | Average | Median | S.D. |
|---|---|---|---|---|---|
| MOR-SVR | 4575.9 | 6671.0 | 4827.9 | 4727.1 | 400.7 |
| MOR-LSVR | 40,305.4 | 48,648.8 | 42,700.9 | 42,682.0 | 1434.7 |
| MOR-NuSVR | 113,936.0 | 123,388.0 | 117,689.1 | 117,561.5 | 1963.4 |
| MOR-GBoostR | 11,168.3 | 14,176.8 | 13,158.5 | 13,318.5 | 673.0 |
| MOR-XGBoostR | 13,315.4 | 16,089.9 | 13,712.1 | 13,588.3 | 533.6 |
| MOR-XGBoostRFR | 14,293.3 | 15,382.8 | 14,749.8 | 14,687.6 | 239.4 |
| MOR-BRR | 319.4 | 344.6 | 331.8 | 331.3 | 5.5 |
| NN | 1.8 | 6.3 | 4.9 | 5.0 | 0.5 |
| k-NN5 | 3.5 | 5.8 | 5.1 | 5.2 | 0.4 |
| k-NN10 | 3.8 | 5.4 | 5.0 | 5.1 | 0.3 |
| k-NN20 | 3.6 | 5.4 | 4.8 | 4.9 | 0.4 |
| RFR | 7006.4 | 7704.1 | 7206.6 | 7170.0 | 158.5 |
| ETR | 1200.7 | 1245.8 | 1213.4 | 1211.5 | 8.5 |
| DTR | 57.4 | 71.6 | 60.2 | 58.6 | 3.6 |
| RR | 5.5 | 7.7 | 5.9 | 5.8 | 0.4 |
| RRCV | 37.2 | 55.1 | 44.2 | 43.7 | 3.5 |
| MTLCV | 56,858.4 | 65,233.8 | 60,883.6 | 60,837.8 | 2035.8 |
| LLARS | 13.3 | 61.7 | 15.9 | 14.3 | 7.1 |
| LR | 22.9 | 33.3 | 26.8 | 26.4 | 2.4 |
| BR | 57,496.6 | 61,163.2 | 58,489.6 | 58,287.5 | 806.4 |
| MLPR | 21,222.5 | 25,145.9 | 22,101.6 | 22,172.1 | 571.8 |
| Method | Best | Worst | Average | Median | S.D. |
|---|---|---|---|---|---|
| MOR-SVR | 2255.4 | 2489.4 | 2288.4 | 2281.9 | 33.8 |
| MOR-LSVR | 37,700.3 | 41,578.9 | 39,647.9 | 39,768.1 | 983.8 |
| MOR-NuSVR | 87,112.3 | 92,142.7 | 90,015.0 | 89,941.3 | 967.9 |
| MOR-GBoostR | 6050.4 | 7306.2 | 6888.9 | 6994.2 | 364.5 |
| MOR-XGBoostR | 6132.9 | 7488.9 | 6348.6 | 6313.3 | 191.8 |
| MOR-XGBoostRFR | 5589.7 | 7371.5 | 5808.3 | 5720.9 | 297.4 |
| MOR-BRR | 180.9 | 201.1 | 186.4 | 185.5 | 4.0 |
| NN | 1.6 | 5.6 | 4.5 | 4.5 | 0.5 |
| k-NN5 | 3.7 | 4.8 | 4.5 | 4.5 | 0.2 |
| k-NN10 | 3.5 | 4.7 | 4.4 | 4.4 | 0.2 |
| k-NN20 | 3.1 | 4.8 | 4.2 | 4.3 | 0.4 |
| RFR | 2258.4 | 2584.2 | 2308.9 | 2282.4 | 72.5 |
| ETR | 740.5 | 845.3 | 756.7 | 752.0 | 16.3 |
| DTR | 19.6 | 22.6 | 20.2 | 20.0 | 0.6 |
| RR | 4.5 | 6.2 | 4.8 | 4.7 | 0.3 |
| RRCV | 25.6 | 32.3 | 28.0 | 27.5 | 1.6 |
| MTLCV | 17,352.7 | 19,314.4 | 18,337.5 | 18,385.4 | 384.9 |
| LLARS | 9.9 | 13.7 | 11.3 | 11.1 | 0.8 |
| LR | 13.8 | 20.9 | 16.3 | 15.9 | 1.7 |
| BR | 33,483.8 | 36,263.5 | 34,183.6 | 34,043.4 | 495.9 |
| MLPR | 19,726.4 | 20,654.0 | 20,127.9 | 20,117.5 | 220.0 |
| Method | Best | Worst | Average | Median | S.D. |
|---|---|---|---|---|---|
| MOR-SVR | |||||
| MOR-LSVR | 5.9448 | ||||
| MOR-NuSVR | 2.1876 | ||||
| MOR-GBRoostR | |||||
| MOR-XGBoostR | |||||
| MOR-XGBoostRFR | |||||
| MOR-BRR | |||||
| NN | |||||
| k-NN5 | |||||
| k-NN10 | |||||
| k-NN20 | |||||
| RFR | |||||
| ETR | |||||
| DTR | |||||
| RR | |||||
| RRCV | |||||
| MTLCV | |||||
| LLARS | |||||
| LR | |||||
| BR | |||||
| MLPR |
| Method | Best | Worst | Average | Median | S.D. |
|---|---|---|---|---|---|
| MOR-SVR | |||||
| MOR-LSVR | 5.6600 | ||||
| MOR-NuSVR | 2.7050 | ||||
| MOR-GBoostR | |||||
| MOR-XGBoostR | |||||
| MOR-XGBoostRFR | |||||
| MOR-BRR | |||||
| NN | |||||
| k-NN5 | |||||
| k-NN10 | |||||
| k-NN20 | |||||
| RFR | |||||
| ETR | |||||
| DTR | |||||
| RR | |||||
| RRCV | |||||
| MTLCV | |||||
| LLARS | |||||
| LR | |||||
| BR | |||||
| MLPR |
| Method | Best | Worst | Average | Median | S.D. |
|---|---|---|---|---|---|
| MOR-SVR | 0.199 | 0.176 | 0.188 | 0.188 | 0.005 |
| MOR-LSVR | 0.305 | 0.283 | 0.295 | 0.295 | 0.005 |
| MOR-NuSVR | 0.296 | 0.276 | 0.286 | 0.286 | 0.004 |
| MOR-GBoostR | 0.688 | 0.639 | 0.663 | 0.664 | 0.011 |
| MOR-XGBoostR | 0.701 | 0.633 | 0.673 | 0.676 | 0.016 |
| MOR-XGBoostRFR | 0.443 | 0.414 | 0.428 | 0.427 | 0.006 |
| MOR-BRR | 0.327 | 0.303 | 0.317 | 0.317 | 0.004 |
| NN | 0.628 | 0.564 | 0.594 | 0.596 | 0.016 |
| k-NN5 | 0.622 | 0.554 | 0.592 | 0.591 | 0.013 |
| k-NN10 | 0.594 | 0.533 | 0.570 | 0.572 | 0.015 |
| k-NN20 | 0.535 | 0.505 | 0.523 | 0.524 | 0.007 |
| RFR | 0.693 | 0.620 | 0.661 | 0.660 | 0.015 |
| ETR | 0.397 | 0.366 | 0.380 | 0.379 | 0.006 |
| DTR | 0.450 | 0.338 | 0.436 | 0.438 | 0.015 |
| RR | 0.327 | 0.309 | 0.317 | 0.317 | 0.003 |
| RRCV | 0.326 | 0.310 | 0.317 | 0.317 | 0.004 |
| MTLCV | 0.325 | 0.309 | 0.317 | 0.317 | 0.003 |
| LLARS | 0.189 | 0.180 | 0.185 | 0.185 | 0.002 |
| LR | 0.323 | 0.308 | 0.317 | 0.316 | 0.003 |
| BR | 0.747 | 0.698 | 0.728 | 0.728 | 0.010 |
| MLPR | 0.404 | 0.357 | 0.376 | 0.375 | 0.009 |
| Method | Best | Worst | Average | Median | S.D. |
|---|---|---|---|---|---|
| MOR-SVR | 0.494 | 0.434 | 0.463 | 0.463 | 0.015 |
| MOR-LSVR | 0.574 | 0.500 | 0.544 | 0.544 | 0.015 |
| MOR-NuSVR | 0.580 | 0.519 | 0.549 | 0.55 | 0.013 |
| MOR-GBoostR | 0.765 | 0.691 | 0.736 | 0.735 | 0.013 |
| MOR-XGBoostR | 0.748 | 0.694 | 0.726 | 0.726 | 0.013 |
| MOR-XGBoostRFR | 0.679 | 0.625 | 0.657 | 0.657 | 0.012 |
| MOR-BRR | 0.568 | 0.517 | 0.544 | 0.546 | 0.012 |
| NN | 0.733 | 0.686 | 0.706 | 0.703 | 0.012 |
| k-NN5 | 0.729 | 0.694 | 0.709 | 0.710 | 0.009 |
| k-NN10 | 0.739 | 0.686 | 0.713 | 0.715 | 0.013 |
| k-NN20 | 0.725 | 0.687 | 0.708 | 0.708 | 0.010 |
| RFR | 0.769 | 0.726 | 0.746 | 0.746 | 0.010 |
| ETR | 0.675 | 0.604 | 0.648 | 0.649 | 0.014 |
| DTR | 0.689 | 0.635 | 0.662 | 0.660 | 0.012 |
| RR | 0.568 | 0.511 | 0.540 | 0.541 | 0.015 |
| RRCV | 0.564 | 0.497 | 0.538 | 0.539 | 0.014 |
| MTLCV | 0.573 | 0.511 | 0.541 | 0.543 | 0.013 |
| LLARS | 0.286 | 0.260 | 0.275 | 0.276 | 0.005 |
| LR | 0.569 | 0.516 | 0.542 | 0.543 | 0.012 |
| BR | 0.748 | 0.709 | 0.730 | 0.730 | 0.010 |
| MLPR | 0.621 | 0.557 | 0.592 | 0.592 | 0.014 |
| Method | Best | Worst | Average | Median | S.D. |
|---|---|---|---|---|---|
| MOR-SVR | 8.4 | 9.9 | 9.0 | 9.0 | 0.3 |
| MOR-LSVR | 7.4 | 8.8 | 8.1 | 8.1 | 0.3 |
| MOR-NuSVR | 7.4 | 8.7 | 8.1 | 8.1 | 0.3 |
| MOR-GBoostR | 3.1 | 3.6 | 3.4 | 3.4 | 0.1 |
| MOR-XGBoostR | 3.0 | 3.5 | 3.2 | 3.3 | 0.1 |
| MOR-XGBoostRFR | 5.1 | 6.0 | 5.6 | 5.6 | 0.2 |
| MOR-BRR | 6.7 | 7.4 | 7.0 | 7.1 | 0.2 |
| NN | 3.7 | 4.4 | 4.1 | 4.1 | 0.2 |
| k-NN5 | 3.8 | 4.3 | 4.1 | 4.0 | 0.1 |
| k-NN10 | 3.9 | 4.6 | 4.2 | 4.2 | 0.1 |
| k-NN20 | 4.3 | 5.1 | 4.7 | 4.6 | 0.2 |
| RFR | 2.8 | 3.4 | 3.1 | 3.1 | 0.1 |
| ETR | 5.5 | 6.4 | 5.9 | 5.9 | 0.2 |
| DTR | 4.4 | 6.0 | 4.9 | 4.9 | 0.2 |
| RR | 6.5 | 7.4 | 7.0 | 7.0 | 0.2 |
| RRCV | 6.5 | 7.6 | 7.0 | 7.0 | 0.2 |
| MTLCV | 6.6 | 7.4 | 7.0 | 7.0 | 0.2 |
| LLARS | 7.8 | 8.9 | 8.3 | 8.3 | 0.2 |
| LR | 6.4 | 7.7 | 7.0 | 7.0 | 0.2 |
| BR | 2.5 | 3.1 | 2.7 | 2.7 | 0.1 |
| MLPR | 5.5 | 6.5 | 5.9 | 5.9 | 0.2 |
| Method | Best | Worst | Average | Median | S.D. |
|---|---|---|---|---|---|
| MOR-SVR | 10.3 | 11.6 | 10.9 | 10.9 | 0.3 |
| MOR-LSVR | 9.6 | 10.8 | 10.2 | 10.2 | 0.3 |
| MOR-NuSVR | 9.5 | 10.9 | 10.3 | 10.3 | 0.3 |
| MOR-GBoostR | 3.3 | 3.9 | 3.6 | 3.7 | 0.1 |
| MOR-XGBoostR | 3.4 | 4.0 | 3.7 | 3.7 | 0.1 |
| MOR-XGBoostRFR | 5.7 | 6.3 | 6.0 | 6.0 | 0.1 |
| MOR-BR | 8.0 | 9.1 | 8.5 | 8.5 | 0.2 |
| NN | 3.7 | 4.3 | 4.1 | 4.1 | 0.1 |
| k-NN5 | 3.9 | 4.4 | 4.1 | 4.0 | 0.1 |
| k-NN10 | 3.8 | 4.3 | 4.1 | 4.0 | 0.1 |
| k-NN20 | 4.0 | 4.6 | 4.3 | 4.3 | 0.1 |
| RFR | 3.2 | 3.8 | 3.5 | 3.5 | 0.1 |
| ETR | 5.6 | 6.4 | 6.0 | 6.0 | 0.2 |
| DTR | 5.0 | 5.7 | 5.3 | 5.3 | 0.2 |
| RR | 8.0 | 8.9 | 8.5 | 8.5 | 0.2 |
| RRCV | 8.0 | 9.0 | 8.5 | 8.5 | 0.2 |
| MTLCV | 8.1 | 9.0 | 8.5 | 8.5 | 0.2 |
| LLARS | 8.6 | 9.8 | 9.2 | 9.2 | 0.2 |
| LR | 8.1 | 8.9 | 8.5 | 8.5 | 0.2 |
| BR | 3.2 | 3.8 | 3.5 | 3.5 | 0.1 |
| MLPR | 6.8 | 7.9 | 7.3 | 7.3 | 0.2 |
| Method | Overall | ||||
|---|---|---|---|---|---|
| MOR-SVR | 1 | 13 | 2 | 10 | 26 |
| MOR-LSVR | 3 | 2 | 4 | 4 | 13 |
| MOR-NuSVR | 4 | 1 | 3 | 1 | 9 |
| MOR-GBoostR | 18 | 5 | 19 | 8 | 50 |
| MOR-XGBoostR | 19 | 7 | 20 | 7 | 53 |
| MOR-GBoostRFR | 12 | 11 | 12 | 6 | 41 |
| MOR-BR | 8 | 14 | 8 | 12 | 42 |
| NN | 16 | 9 | 17 | 20 | 59 |
| k-NN5 | 17 | 8 | 16 | 18 | 59 |
| k-NN10 | 15 | 6 | 15 | 19 | 55 |
| k-NN20 | 14 | 4 | 14 | 21 | 53 |
| RFR | 20 | 10 | 18 | 9 | 57 |
| ETR | 11 | 12 | 11 | 11 | 45 |
| DTR | 13 | 21 | 13 | 13 | 60 |
| RR | 6 | 20 | 6 | 17 | 49 |
| RRCV | 9 | 19 | 9 | 14 | 51 |
| MTLCV | 5 | 16 | 7 | 2 | 30 |
| LLARS | 2 | 17 | 1 | 16 | 36 |
| LR | 7 | 18 | 5 | 15 | 45 |
| BR | 21 | 3 | 21 | 3 | 47 |
| MLPR | 10 | 15 | 10 | 5 | 40 |
| Method | Overall | ||||
|---|---|---|---|---|---|
| MOR-SVR | 1 | 13 | 2 | 10 | 26 |
| MOR-LSVR | 3 | 2 | 8 | 2 | 15 |
| MOR-NuSVR | 4 | 1 | 9 | 1 | 15 |
| MOR-GBoostR | 18 | 5 | 20 | 6 | 49 |
| MOR-XGBoostR | 19 | 6 | 18 | 7 | 50 |
| MOR-XGBoostRFR | 12 | 12 | 12 | 8 | 44 |
| MOR-BRR | 8 | 14 | 7 | 12 | 41 |
| NN | 16 | 9 | 14 | 19 | 58 |
| k-NN5 | 17 | 8 | 16 | 18 | 59 |
| k-NN10 | 15 | 7 | 17 | 20 | 59 |
| k-NN20 | 14 | 4 | 15 | 21 | 64 |
| RFR | 20 | 10 | 21 | 9 | 60 |
| ETR | 11 | 11 | 11 | 11 | 44 |
| DTR | 13 | 21 | 13 | 14 | 61 |
| RR | 6 | 20 | 4 | 17 | 47 |
| RRCV | 9 | 18 | 3 | 13 | 43 |
| MTLCV | 5 | 16 | 5 | 5 | 31 |
| LLARS | 2 | 19 | 1 | 16 | 38 |
| LR | 7 | 17 | 6 | 15 | 45 |
| BR | 21 | 3 | 19 | 3 | 46 |
| MLPR | 10 | 15 | 10 | 4 | 39 |
| Method | (p-Values) | (p-Values) | (p-Values) | (p-Values) |
|---|---|---|---|---|
| MOR-SVR | ||||
| MOR-LSVR | ||||
| MOR-NuSVR | ||||
| MOR-GBoostR | ||||
| MOR-XGBoostR | ||||
| MOR-XGBoostRFR | ||||
| MOR-BRR | ||||
| NN | ||||
| k-NN5 | ||||
| k-NN10 | ||||
| k-NN20 | ||||
| RFR | ||||
| ETR | ||||
| RR | ||||
| RRCV | ||||
| MTLCV | ||||
| LLARS | ||||
| LR | ||||
| BR | ||||
| MLPR |
| Method | (p-Values) | (p-Values) | (p-Values) | (p-Values) |
|---|---|---|---|---|
| MOR-SVR | ||||
| MOR-LSVR | ||||
| MOR-NuSVR | ||||
| MOR-GBoostR | ||||
| MOR-XGBoostR | ||||
| MOR-XGBoostRFR | ||||
| MOR-BRR | ||||
| NN | 0.2385 | |||
| k-NN5 | 0.7512 | |||
| k-NN10 | 0.0013 | 0.0223 | ||
| RFR | ||||
| ETR | ||||
| DTR | ||||
| RR | ||||
| RRCV | ||||
| MTLCV | ||||
| LLARS | ||||
| LR | ||||
| BR | ||||
| MLPR |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akinsolu, M.O.; Zribi, K. A Generalized Framework for Adopting Regression-Based Predictive Modeling in Manufacturing Environments. Inventions 2023, 8, 32. https://doi.org/10.3390/inventions8010032
Akinsolu MO, Zribi K. A Generalized Framework for Adopting Regression-Based Predictive Modeling in Manufacturing Environments. Inventions. 2023; 8(1):32. https://doi.org/10.3390/inventions8010032
Chicago/Turabian StyleAkinsolu, Mobayode O., and Khalil Zribi. 2023. "A Generalized Framework for Adopting Regression-Based Predictive Modeling in Manufacturing Environments" Inventions 8, no. 1: 32. https://doi.org/10.3390/inventions8010032
APA StyleAkinsolu, M. O., & Zribi, K. (2023). A Generalized Framework for Adopting Regression-Based Predictive Modeling in Manufacturing Environments. Inventions, 8(1), 32. https://doi.org/10.3390/inventions8010032







