Abstract
Rotary drum dryers operating in co-current mode are commonly used for drying food and feed in leaf form, reducing the damage caused by the high air temperatures typical of these dryers, as well as providing advantages including reduced drying times and increased energy efficiency. However, drying control to ensure a desirable product exit moisture content is strongly based on empirical practices, which are usually jealously guarded by producers and users, grounded in simplified mathematical modelling. To overcome these uncertainties, in this work, a more complete mathematical modelling approach, based on the solution of ordinary differential equations (ODEs), is developed. The ODEs describe the drying process in the drum dryer, where the air is continuously cooled and humidified as the product dries. The mathematical model developed was experimentally verified in a drum dryer by drying alfalfa, and the maximum relative error was found to be only 2.4%. Finally, a comparison between the complete model proposed here and a simplified model was conducted, using both for drying control to keep the product exit moisture content constant (i.e., at 0.111). The results indicated that the simplified model provided values of air inlet temperatures erroneously higher, up to +8.2%, with a consequent higher energy consumption, lower dried alfalfa quality, and a greater risk of fire, given that the product exit temperature was dangerously increased.
1. Introduction
In the food and feed industry, co-current operating rotary drum dryers are commonly used for drying thin and fibrous products, such as leaves and stems. These products accept the high air inlet temperatures (often higher than 500 °C) used in rotary drum dryers [1] with minimal damage, facilitating rapid drying. Many studies have focused on this positive characteristic and, therefore, on the reduction in residence time of the products in rotary drum dryers [2,3,4,5,6,7,8,9], thus allowing for a reduced risk of fire [10]. It should also be noted that higher air inlet temperatures result in higher energy efficiency [11,12].
Considering design guidelines regarding the thermal–hygrometric aspects of rotary drum dryers, the classic ones proposed by Perry et al. (2019) [13] are well known, based on equations of the thermal–hygrometric exchange, and simplified and integrated by empirical indications. Again, with regard to the design, computational methods based on finite element analysis have also recently been proposed [14,15,16]. These methods are very useful for analysing and verifying the thermal–hygrometric and fluid dynamic phenomena inside the rotary drum after the dimensions, flow rates, and temperatures have been set. However, finite element methods do not allow for a direct design with which, after having decided on the performance of the dryer, the dimensions, the air-drying inlet temperatures and the mass flow rates can be directly calculated.
Instead, in order to obtain the desired final moisture content of the product, various data and empirical habits are used for drying control, which are often jealously guarded by producers and users. However, this empiricism rests on some simplified thermal–hygrometric exchange equations, such as those indicated by Perry et al. (2019) [13].
To date, the limits of the simplified equations proposed by Perry et al. (2019) [13] have been partially overcome through corrections, as the result of experience which, however, are typically kept hidden for commercial reasons.
In this work, in an attempt to overcome this limitation, ordinary differential equations (ODEs) describing the drying process inside the drum—where the air continuously cools and humidifies while the product dries—are set. The solution of these ODEs will provide equations that will constitute a more complete mathematical model than that used by Perry et al. (2019) [13].
These equations contain variables such as temperatures and moisture contents, where some will be the unknowns to obtain and others will be data to input; however, the equations will also contain two characteristic quantities of the product/process: the thermal energy and the coefficient of the convective heat transfer, combined with the transverse dimension of the product. Given the complexity of the phenomena underlying drying, such as the diffusion of water inside the product, the complex geometric shape of the product, the Dufour effect, and so on, these two quantities must be estimated, either experimentally (e.g., in a pilot plant) or directly from a real dryer. Regarding the objective of this work, which is to propose a complete mathematical model which is useful for process control to obtain the desired exit moisture content of the product, as a real dryer was available to us, it was used to determine these two quantities.
Consequently, the experimental activity—performed with alfalfa—serves a dual purpose: (1) to create an experimental protocol using the equations of the complete mathematical model to determine the values of the thermal energy and the convective heat transfer coefficient, a protocol that can also be used for other products; (2) to evaluate the accuracy of the complete mathematical model.
Finally, by performing simulations of drying control with two mathematical models—an older simplified one and the proposed complete one—the differences between the two will be highlighted. The most interesting advantages of the proposed complete mathematical model are the reduction in energy consumption and lower fire risk.
2. Materials and Methods
2.1. The Complete Mathematical Model
In this section, a complete mathematical model for the continuous drying process inside a rotary drum dryer is developed. Figure 1 shows the schematic of a rotary drum. A typical diagram indicating the temperatures of the air TA and the product TP inside the dryer is also shown. Two zones can be identified in the dryer: in the first, long LI−C, the product reduces its moisture content from the initial value XI to the critical value XC; in the second, long LC−E, the product reaches the final moisture content XE.
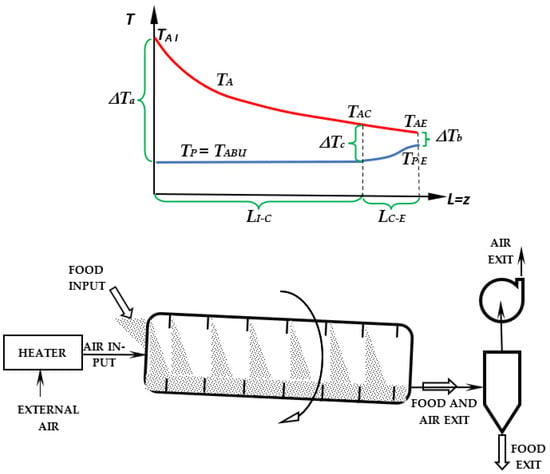
Figure 1.
Rotary drum dryer mass flows and diagram of the temperature of the air (red line) and the product (blue line). The product has final moisture content XE < XC.
In Figure 2, the temperature inside the dryer is presented. The thermal–hygrometric exchange surface A, instead of just the length z = L of the dryer, is shown. The diagram is completed with the identification of an elemental area dA of the product, which can be defined as the infinitesimal length dz of the drum multiplied by a quantity f, which is the sum of the perimeters of the sections of the product elements present in the generic section of the drum, as shown in Figure 3.
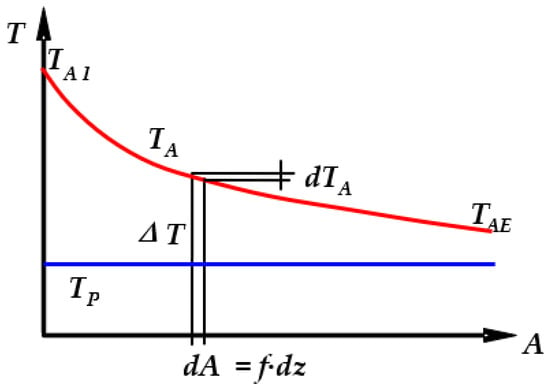
Figure 2.
Diagram of the temperature of the air TA (red line) and product TP (blue line) vs. the exchange surface A. The elemental area dA is equal to the product of elemental length dz and the quantity f (see Figure 3).
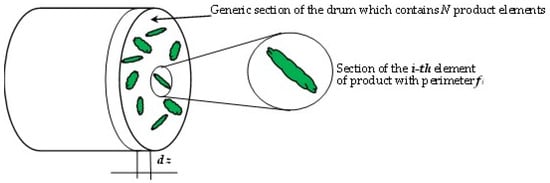
Figure 3.
Generic section of the drum containing N product elements. In the foreground, the i-th element with perimeter fi is shown. The average value of the sum of the perimeters fi of all elements in the generic drum section constitutes the “transverse dimension,” which is multiplied by the infinitesimal axial length dz to give the elemental area dA = f·dz.
2.1.1. First Zone of the Dryer (LI−C)
In the first zone, long LI−C, the moisture content X of the product is higher than the critical content XC; therefore, the temperature TP is constant and equal to the wet-bulb temperature TWB [17,18].
Through the infinitesimal area dA, the infinitesimal heat transfer rate, dq, is transmitted from the air to the product, as shown in Figure 2. This heat transfer rate can be written as follows:
where α is the convective heat transfer coefficient; dA is the infinitesimal area equal to f·dz (Figure 2); f is a quantity transverse dimension (see Figure 3); TA is the air temperature meeting the area dA; and TWB is the product temperature, which is assumed to be equal to the wet-bulb temperature of the air.
Assuming an adiabatic dryer, the infinitesimal heat transfer rate dq in Equation (1) is equal to that released by the air when it meets the infinitesimal area dA which, therefore, lowers its temperature by an infinitesimal quantity dTA:
where GDAI is the mass flow rate of dry air coinciding with the mass flow rate of hot air entering the dryer, as the air humidity at the inlet is very low (only 0.01 kg/kgD.A.); cA and cV are the specific heat of dry air and of vapor, respectively; dTA is the infinitesimal variation of the air temperature when it touches the area dA; and GEV is the mass flow rate of the vapor that originates from the product, which increases along the first zone of the dryer.
To produce the infinitesimal mass flow rate of vapor dGEV from the elemental area dA of the product, it must receive the infinitesimal heat transfer rate dq from Equations (1) and (2). The relationship between the elemental mass flow rate and infinitesimal heat transfer rate is
where rI−C is the thermal energy, in the first zone I − C of the dryer (Figure 1), required to produce 1 kg of superheated steam at the air temperature TA. It is considered to be a constant.
By combining Equations (2) and (3), the following ordinary differential equation (ODE) is obtained:
The easy solution, obtained by separation of variables, is
where TAI is the air temperature at the inlet of the dryer; TAC is the air temperature at the end of the first zone, where z = LI−C corresponds to the critical moisture content of the product (Figure 1); and GEV(I−C) is the total mass flow rate produced by the product along the first zone I − C.
Finally, by combining Equations (1) and (2), the following second ODE is obtained:
From Equation (5), the term was obtained and introduced into Equation (6). Therefore, the solution to Equation (6), obtained by separation of variables and under condition TA = TAC at the point C where the length of the drum is LI−C, becomes
where the function Ei is called Exponential integral. It is clear that the total thermal–hygrometric exchange surface of the first zone is , where f is the transverse dimension (shown in Figure 3), and LI−C is the length of the I − C zone of the dryer (see Figure 1).
The values of Ei(−x) can be calculated using the following series [19]:
where γ = 0.5772… is Euler’s constant. Relative to the rotary drum dryers, which present typical values of the argument , Ei(−x) function is approximable as with an error lower than 1%.
Therefore, Equation (7) becomes
Inserting Equation (5) into Equation (8), we obtain
To complete the mathematical modelling of the first zone of dryer, the relationship between the total mass flow rate of vaporized water and that of the product at the dryer inlet, , can be written as
where XI is the moisture content of the product at the inlet, and XC is the critical moisture content of the product at the end of the I − C zone (Figure 1).
The equations for calculating the wet-bulb temperature are written using the laws of thermodynamics for air–water mixtures:
where is the enthalpy of the air at the dryer inlet; is the enthalpy of the air at the wet-bulb point, reached under the isenthalpic humidification process; λ is the latent heat; TWB is the temperature of the air at the wet-bulb condition; is the absolute humidity of air at the dryer inlet, with its value of 0.01 kg/kgD.A. considered constant, due to the external air temperature of 25 °C and at 50% relative humidity also being considered constant; xWB is the absolute humidity of the saturated air (i.e., in the wet-bulb condition); pSWB is the vapor pressure in the wet-bulb condition (saturated air); and patm is the atmospheric pressure, as the dryer operates at this pressure.
The solution to the system of Equations (11)–(13) furnish the values of TWB with respect to the air inlet temperature TAI.
2.1.2. Second Zone of the Dryer (LC−E)
With the same mathematical approach as that for the first zone I − C, the Equation for the second zone C − E (Figure 1), equivalent to Equations (5), (8), (9) and (10), can be obtained, respectively, as
where the new quantities, with respect to Equations (5), (8), (9), and (10), are , which is the mass flow rate generated from the product into the entire second zone C − E; , which is the mass flow rate of the product at the point C, where the critical moisture content occurs; XE, which is the product moisture content at the exit of dryer; , which is the length of the second zone of the drum dryer; TPE, the product temperature at the exit of the dryer, which is greater than the wet-bulb temperature TWB [20]; and , which is the thermal energy necessary to produce 1 kg of superheated vapor at the air temperature TA (Figure 1), and is equal to the difference in enthalpy [21] between the superheated vapor at TA and the water contained in the product to be dried at the temperature TP. The value of rC−E will be greater than that of rI−C for the first zone with X > XC as, below a certain value of the moisture content X (i.e., lower than the critical one XC), evaporation of the bound water requires thermal energy greater than that for free-form water.
Therefore, Equations (14)–(17) constitute the mathematical model of the C – E drying zone, in which the product moisture content is lower than the critical one; that is, X < XC (Figure 1).
2.2. The Simplified Mathematical Model
In this section, a simplified mathematical model for the continuous drying process inside a rotary drum dryer is discussed.
If, in Equation (2), we neglect the presence of vapor in the drying air—that is, if we consider that the superheated steam (at temperature TA) coming from the product does not participate in the production of dq, due to the lowering of the temperature equal to dTA—then the ODE can be simplified, and its solution provides the following equation:
By recombining the terms and multiplying the left and right sides by , we obtain the total heat transfer rate qI−C in the I − C zone as
Ultimately, we obtain the total heat transfer rate in the first zone of the dryer:
as the ratio (see Figure 1) is the logarithmic mean temperature difference ΔTmL(I−C) in the I − C zone.
Equation (20), derived from Equation (18), has also been suggested by Perry et al. (2019) [13] for the design of the rotary drum dryers. However, if we compare the results of the application of Equation (18) and the more complete Equation (9) obtained here, we find that the difference is negligible only for air inlet temperatures below about 150 °C. Unfortunately, rotary drum dryers commonly use much higher temperatures TAI—often over 500 °C [1]—for which the error with Equation (18)—and, therefore, Equation (20)—is not negligible, as demonstrated in Section 3.5. The same Equation (20) has been used in [17,19,20], precisely because the conveyor belt dryers presented and studied used air inlet temperatures TAI below 150 °C.
This equation is similar to Equation (16) of the complete mathematical model. Equations (18) and (21) can be combined, thus obtaining
where is the total length of the drum (Figure 1).
As the wet-bulb temperature TWB depends on the air inlet temperature, according to Equations (11)–(13), and as the product exit temperature TPE must remain limited to avoid fire risks (particularly, within 5–10 °C above the TWB) in Equation (22), only two unknowns remain: the air temperature TAI and TAE.
To find a second equation, a balance is made between the heat transfer rate required by evaporation and that transferred by the dry air:
Combining Equations (22) and (23), we obtain
As the mass flow rates GEV(I−C) and GEV(C−E) depend on the moisture content of the product at the inlet XI and exit XE of the drum, according to Equations (10) and (17), Equation (24) provides the value of the air inlet temperature which ensures the achievement of the required moisture content XE, based on simplified mathematical modelling.
2.3. The Rotary Drum Dryer and the Product
The experimental study was carried out in a rotary drum dryer used to dry alfalfa, which has been previously prepared by chopping the stems into 5 cm-long pieces. The characteristics of the dryer are provided in Table 1. The alfalfa used was the Italian variety “Delta,” grown in the Delta Po Regional Park (Veneto). The product was cut and pre-dried naturally in the field. It was then harvested, and the stems were chopped to 5 cm in length. Depending on the degree of pre-drying in the field, a range of moisture values was possible. Five moisture values were chosen, in order to have a wide range, from a minimum of 0.41 to a maximum of 2.03 kg/kg (Table 2). The product was then immediately taken to the dryer, without other treatments.

Table 1.
Geometric and operational data of the rotary drum dryer.

2.4. The Mass Flow Rate of the Product GPI
The rotary drum dryer was fed the alfalfa by a rotary loader, which kept the volume of product per revolution constant. Thus, the volumetric flow rate of the alfalfa was regulated according to the speed of rotation of the loader. Usually, the plant operator [22] adjusts the mass flow rate empirically, based on experience, in order to avoid flooding of the drum; however, to improve this adjustment, an experiment was conducted to highlight the limiting values of the alfalfa mass flow rate which produce flooding.
As, with the same volumetric flow rate introduced into the drum, the mass flow rate of alfalfa increases as the moisture content increases, the experiment was conducted in alfalfa at 5 different moisture content values. For each of these moisture levels, the test consisted of gradually increasing the rotation speed of the loader until flooding occurred, and then established the limit of the mass flow rate GPI as equal to 90% of that measured at the moment of flooding.
To establish the relationship between the volumetric flow rate and the mass flow rate of the alfalfa, three repeated samples of unit volume (m3/revolution) were taken and weighed, in order to measure the unit mass mT (kg/revolution) from the loader for each of the five moisture values (XI). Considering the relationship between the dry mass mD and the moisture content and wet mass mT of alfalfa, , it was found that mD is equal to 3.8 kg/revolution and is invariant with respect to moisture content. Therefore, the mass flow rate of alfalfa at the dryer inlet GPI was calculated using the following equation:
where NC denotes the loader’s rotation (rps).
2.5. The Mass Flow Rate of the Dry Air GDAI
The volumetric flow rate of air QA was measured at the intake of the heater (Figure 1) by means of orifice plates—one on the primary air for combustion and one on the secondary air. Therefore, the air was at the external condition, with an average temperature Text = 25 °C, an average absolute humidity 0.01 kg/kgD.A., and with density ρext = 1.18 kg/m3 assumed to be constant. Considering the vapor component (xext only 0.01) of this external humid air mixture to be negligible, and considering the mass conservation law, the mass flow rate of the hot dry air GDAI at the inlet of the drum is given by
2.6. Experimental Assessment of the Thermal Energy rI−C and of the Convective Heat Transfer Coefficient α·f
As mentioned above, the dryer was fed with alfalfa at five different moisture levels. Therefore, for each of these moisture contents, after carrying out the experiment described in the previous section to determine the relative optimal mass flow rate of alfalfa, GPI, an experiment was also carried out to determine the values of the thermal energy rI−C of the first zone, where X > XC, and of the convective heat transfer coefficient multiplied by the transverse dimension α·f.
For this purpose, Equations (5) and (9) were used; the use of which was, however, conditioned by the final moisture content . For this reason, reduced temperatures of the hot air at the inlet TAI were chosen, such that the reduced heat transfer rate supplied by the air to the product did not allow the exit moisture content XE to be lower than the critical moisture content XC. Equation (5) was used to calculate the thermal energy rI−C, while Equation (9) was used for the convective heat transfer coefficient α·f, both with the foresight to replace the length LI−C with that of the drum LTOT. Using the two equations to obtain these two quantities, rI−C and α·f, involves measuring the inlet and exit temperatures, the alfalfa and air mass flow rates, and the alfalfa moisture content at inlet XI and exit XE. PT100 resistance thermometers and data loggers were used to measure and register the TAI and TAE air temperatures, and the alfalfa temperature at the exit of the dryer, TPE, was measured using an infrared thermometer. The mass flow rates were obtained according to the measurements and calculations described in Section 2.4 and Section 2.5. Finally, the moisture content of the alfalfa at the inlet XI and exit XE was measured using a thermobalance.
2.7. Experimental Assessment of the Thermal Energy rC−E and Evaluation of the Accuracy of Mathematical Modelling
Starting again from the alfalfa at the five different moisture levels, the dryer was regulated with air temperatures at the inlet TAI, increased by 170 °C compared to the previous experiment. Thus, they turned out to be similar to those suggested in [1] and similar to those adopted by the operator of the dryer, by virtue of his personal experience. In this way, there was certainty that the exit moisture content of the alfalfa would be lower than the critical one and a high probability that the commercial moisture content expected for the storage of the alfalfa (XE = 0.111) would be reached.
For each of the available alfalfa moisture levels XI, the following were measured: the air temperatures at the inlet TAI and exit TAE; the temperature of the alfalfa at the exit TPE; the moisture content of the alfalfa at the exit XE. The mass flow rates for the alfalfa GPI were those obtained from the tests on the flooding risks (see Section 2.4) and mass flow rates of the air GDAI were those calculated using the method indicated in Section 2.5.
Furthermore, we adopted the values of the thermal energy of the first zone rI−C and of the convective heat transfer coefficient α·f determined with the method indicated in Section 2.6.
Knowing all the values of the quantities listed above, it was possible to use the mathematical model proposed in Section 2.1. Using Equation (5), the air temperature was calculated at point C of the drum TAC, where the product assumes the critical moisture content XC. With Equation (8), the distance of point C with respect to the inlet was calculated, following which the length of the drum of the second zone, LC−E = LTOT − LI−C, was calculated. With Equation (14), the value of the thermal energy rC−E corresponding to the second zone C − E was calculated (Figure 1).
Finally, through Equation (15), the temperatures TPE of the alfalfa at the exit of the dryer were calculated. These values were compared with the measured ones, allowing us to verify the accuracy of the proposed mathematical model.
3. Results
3.1. Product Mass Flow Rate GPI
The results of the tests carried out to identify the optimum mass flow rate values GPI to avoid product blockage in the drum (flooding), as indicated in Section 2.4, are provided in Table 2, together with the five moisture values of the products XI introduced into the drum dryer. By applying non-linear regression (R2 = 0.994), the following relationship between the optimal mass flow rate of the product GPI and the moisture content XI was obtained:
3.2. Thermal Energy rI−C and Convective Heat Transfer Coefficient α·f
For each of the five tests conducted, each with different product moisture content XI, Table 2 shows the hot air inlet temperatures TAI chosen with reduced values, according to the criterion indicated in Section 2.6 (i.e., to have an exit moisture content of the product XE higher than the critical one; also shown in Table 2). Clearly, the temperatures TAI increased with the moisture content of the product at the inlet XI, given that, as the amount of water to be evaporated increases, it is necessary to increase the heat transfer rate from the air to the product. As the (logarithmic) mean temperature difference between the air and the product must also increase, there is also an increase in the air exit temperature TAE. Table 2 shows these measured temperatures TAE and the wet-bulb temperatures TWB calculated using Equations (11)–(13). These were found to be superimposable on the measured product exit temperatures TPE, confirming that, with X > XC, the presence of water on the surface of the product allows it to remain at TWB.
Furthermore, Table 2 shows the mass flow rate of the external air GDAext introduced into the heater, measured as indicated in Section 2.5. As already mentioned, for the law of conservation of mass, neglecting the contribution of that of the fuel, it is equal to the mass flow rate of the dry air entering the drum GDAI. Note that GDAI decreased with an increase in the air inlet temperature TAI and, therefore, in the air exit temperature TAE. This fact can be explained by the decrease in the density of the air at the intake of the centrifugal fan (Figure 1). In fact, this turbomachine should keep the volumetric flow rate constant, as it depends on the diameter of the impeller, the inclination of the blades, and the rotation speed, which are fixed. Therefore, if the fan intake air is hotter, a reduction in density and, therefore, in the mass flow rate of the air at the drum exit follows. This is reflected in a reduction in the mass flow rate GDAI at the drum inlet. However, it appears that with warmer and less dense air, the pressure drop in the drum is reduced. Therefore, the fan shifts the operating point towards a partial increase in the volumetric flow rate, according to the characteristic curve, but which is not sufficient to keep the mass flow rate GDAI constant.
Table 2 presents the values of the thermal energy rI−C obtained by Equation (5), introducing into it: the measured temperatures TAI and TAE, the latter in place of TAC; cA and cV, as shown in Table 1; and the air and vapor mass flow rates GDAI and GEV, presented in Table 2. GEV was calculated using Equation (10).
The quantity rI−C turned out to be higher than that obtained in previous experience on a conveyor belt dryer [17]. In fact, it should be noted that thermal energy includes the latent heat, the heat to overheat the steam generated up to the temperature TA, and the heat losses from the walls of the drum. In the rotary drum dryer, these latter two contributions are clearly higher than that in a conveyor belt dryer, due to the much higher TA temperature and the rotation, which increases the convective heat transfer coefficient. By applying non-linear regression (R2 = 0.935), the following relationship was found between the thermal energy in the first zone, where X > XC, rI−C, and the product inlet moisture content XI:
Finally, Table 2 also shows the values of the convective heat transfer coefficient multiplied by the transverse dimension α·f, obtained by applying Equation (8) or (9). Applying non-linear regression (R2 = 0.945), the following relationship between the convective heat transfer coefficient multiplied by the transverse dimension α·f and the moisture content XI was determined:
3.3. Thermal Energy rC−E and Evaluation of the Accuracy of the Mathematical Model
The results of the tests carried out with alfalfa at the same inlet moisture content in order to identify the values of the thermal energy rC−E in the second zone C − E of the drum (Figure 1) where X < XC, are shown in Table 3. The rC−E was calculated by applying Equation (14), which required the knowledge of other quantities, such as the following:

Table 3.
Experimental and calculated data from tests described in Section 2.7.
- -
- -
- The air exit temperatures TAE, which were measured and shown in Table 3;
- -
- The product exit moisture contents XE, which were measured and shown in Table 3;
- -
- The wet-bulb temperatures TWB, calculated using Equations (11)–(13);
- -
- The air temperatures TAC at point C, where the alfalfa was at critical moisture content, calculated by means of Equation (5);
- -
- The air inlet mass flow rates GDAI, measured as indicated in Section 2.5;
- -
- The vapor mass flow rates of the first zone I − C (Figure 1) GEV(I−C), calculated by means of Equation (10);
- -
- The vapor mass flow rates of the second zone C − E (Figure 1) GEV(C−E), calculated by means of Equation (17).
Finally, the obtained values of the thermal energy rC−E of the second zone (Figure 1) were inserted into Equation (15), in order to calculate the values of the product exit temperature TPE, which are shown in Table 3 together with those measured during the tests. The maximum relative error was 2.4% and, in all cases, the differences were not statistically significant. Therefore, we found the complete mathematical modelling results from these first experimental tests to be accurate.
By applying linear regression (R2 = 0.164), the following relationship was found between the thermal energy in the second zone, where X < XC, rC−E, and the product inlet moisture content XI:
Applying another linear regression (R2 = 0.996), the following relationship was found between the air inlet mass flow rate GDAI and the air inlet temperature TAI:
3.4. Drying Control Using Complete Mathematical Modelling
Next, the equations of the complete mathematical model, presented in Section 2.1, were used to simulate the control of the drying process.
The rotary drum dryer (Table 1) used to carry out the experiments described in Section 2.3, Section 2.4, Section 2.5, Section 2.6, Section 2.7, was used to perform a simulation of the drying process control. The experiment made it possible to determine the values of (the convective heat transfer coefficient · transverse dimension) α·f, the thermal energies rI−C and rC−E, and the product inlet mass flow rate GPI, all as a function of the product inlet moisture content XI, based on the relationships presented in Equations (29), (28), (30) and (27), respectively.
The objective of the drying control was to maintain the product exit moisture content XE as a constant, equal to the commercial value of 0.111 (10% w.b.). It is important that XE remains constant and equal to the commercial value as if XE < 0.111, then the energy consumption and the risk of fire are both increased. Meanwhile, if XE > 0.111, then the shelf-life and the quality of the alfalfa may be reduced.
In order for the product exit moisture content XE to be constant and equal to 0.111, it is necessary to act on the air inlet temperature; that is, it is necessary to calculate TAI using the modelling equations after setting the desired value of XE. The equations are the following:
- -
- Equation (10), to obtain the mass flow rate of evaporated water GEV(I−C) from the first zone I − C (Figure 1), knowing the product moisture content XI and XC;
- -
- Equation (17), to obtain the mass flow rate of evaporated water GEV(C−E) from the second zone C − E (Figure 1), knowing the product moisture content XI, XC, and XE (as it is forced to be equal to 0.111);
- -
- Equations (5), (8), (14), and (15), to obtain the four unknowns (i.e., the three temperatures TAI, TAE, and TAC, as well as the length of the first zone of the drum LI−C). The wet-bulb temperature TWB and the air mass flow rate GDAI also appear in the system of equations. However, TWB can be determined through Equations (11)–(13), in which the unknown TWB is a function of the temperature TAI. The air mass flow rate GDAI is a function of TAI through Equation (31). The system of Equations (5), (8), (14), (15), (11), (12), (13), and (31) must be solved with a recursive procedure, which is easily conducted in spreadsheets, as the equations implicitly contain the unknowns.
The simulation results are shown in Table 4. It is interesting to note that the temperature differences between the exit product TPE and the wet-bulb TWB were between 5 and 8.7 °C, thus reducing the risk of fire.

Table 4.
Data simulated from the complete mathematical model used for drying control to maintain the product exit moisture content XE at a constant level (=0.111).
3.5. Drying Control Using Simplified Mathematical Model
Next, the equations of the simplified mathematical model presented in Section 2.2 were used to simulate the control of the drying process. The results were compared with those obtained in the previous Section 3.4 by applying the equations of the complete mathematical model.
The simplified mathematical model presented in Section 2.2 was the same one that led Perry et al. (2019) [13] to propose Equation (20) for the design of rotary drum dryers.
Table 5 shows the simulation results; in particular, note that the air inlet temperature TAI is higher than that obtained by the complete mathematical model, which is also presented in Table 5 for a direct comparison. The simplified model matches the results of the complete model for TAI below about 150 °C, while it becomes less accurate at the higher temperatures essential for drying products with higher inlet moisture XI. For example, in test no. 5, the simplified model suggested a TAI of 604 °C, compared to the 558 °C derived by the complete model, presenting a difference of +8.2%.

Table 5.
Comparison between the air and product temperatures simulated with the complete mathematical model and the simplified one. The goal is to control the dryer, through the air inlet temperature value, to keep the product exit moisture content XE constant (at 0.111). The last line shows the exit moisture content calculated with the complete model after having implemented the air inlet temperatures simulated using the simplified model.
Therefore, the simplified mathematical model caused the dryer to operate at temperatures TAI higher than those required to achieve the expected product exit content XE. This means that the product will exit with a lower content than expected. To estimate this, the TAI of 604 °C was implemented in the complete mathematical model in the case of test no. 5, and it was found that XE was 0.076, compared to the desired 0.111. This excessive product drying leads to a waste of energy (+8.2%) and, above all, a higher product exit temperature TPE which, in test no. 5, was found to be 17 °C higher than the TWB (i.e., about 82 °C), thus increasing the risk of fire.
4. Discussion and Conclusions
In the food and feed industry, drying operations are frequently carried out, due to the increased shelf life and low storage costs. Among the many drying systems available, rotary drum dryers have the highest energy efficiency and the shortest process times, especially those operating in co-current mode, which can reduce the thermal damage to the product. Rotary drum dryers achieve these advantages by operating at high temperatures—often higher than 500 °C—but this means that the product to be dried must be thin and fibrous, such as the leaves and stems of the alfalfa; this is the only way to limit the thermal alterations of the product components.
Drying control to obtain the desired product exit moisture content is typically based on the use of empirical data, which are often jealously guarded by producers, integrated with the equations of a simplified mathematical model proposed by Perry et al. (2019) [13].
This uncertain situation prompted the present study, motivating us to develop a more complete mathematical model. This model was based on ordinary differential equations (ODEs) describing the drying process inside the drum, where the air cools and humidifies continuously as the product dries. The solution of these ODEs appeared to be complicated, due to the presence of the Integral Exponential function. Fortunately, using its series expansion and truncation from the third term of the series, which was acceptable due to the low values assumed by the function argument, the ODEs could be solved, and the consequent mathematical model became easier to use. The variables contained in the solution, such as air and product temperatures and product moisture content, are partly unknowns to be obtained from the complete mathematical model, and partly data to be implemented.
However, this complete mathematical model, like the simplified one proposed by Perry et al. (2019) [13], in order to be applied as a tool for process control, requires the values of three quantities characterizing the product/process: the two thermal energies (of the first and second zones of the dryer; see Figure 1) and the convective heat transfer coefficient. The values of these quantities are influenced by aspects that are difficult to determine, such as the complex shape of the product, the water diffusion from inside it (especially in the second area of the dryer), the Dufour effect, and so on. Therefore, the values of these three quantities were found through an experiment carried out directly in the real dryer which operates by drying alfalfa.
Therefore, after having developed the complete mathematical model, an experiment was conducted according to a double procedure: the first for the determination of the thermal energy of the first zone and the coefficient of convective thermal transfer multiplied by the transversal dimension, and the second for the thermal energy of the second zone of the dryer.
With the second experimental procedure, it was also possible to verify the accuracy of the complete mathematical model, as evaluated according to the predicted values of the product exit temperatures TPE, which resulted in a maximum relative error of only 2.4%, compared to the experimental values.
Finally, using the two mathematical models—that is, the simplified one and the proposed complete one—drying control simulations were carried out for five different inlet moisture values XI of alfalfa (from a minimum of about 0.4 to a maximum of about 2). In all cases, the mathematical models were required to maintain the product exit moisture content XE constant and equal to 0.111, which is precisely the drying control task. The simplified model provided higher air inlet temperatures TAI than the complete model. The TAI differences were found to be negligible for reduced XI values (i.e., when the air entered with a TAI lower than 150 °C), but they gradually became more marked at higher XI. For XI equal to 2 (in the fifth simulation test), the two TAI temperatures were 604 °C and 558 °C, respectively, with a difference of +8.2% for the simplified model, notably reflected in an equal increase in energy consumption.
This higher energy consumption was, in turn, reflected in a reduction in the product exit moisture content XE. To determine the actual value of the moisture content XE with the TAI temperatures proposed by simplified mathematical model, these temperatures were implemented in the complete mathematical model, thus obtaining, in the extreme case of the fifth test, an XE of 0.076 and, above all, a product exit temperature of 82 °C (17 °C higher than the wet-bulb temperature)—a very high value, increasing the risk of fire and reducing the quality of the product. This fact indicates the good opportunity provided by the proposed model, in order to better realize drying control.
The next step in our research will be evaluation of the mathematical model under different operating conditions, such as varied drum rotation speeds and air flow rates, as well as with different products.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are contained within the article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Rezaei, H.; Lim, C.J.; Sokhansanj, S. A computational approach to determine the residence time distribution of biomass particles in rotary drum dryers. Chem. Eng. Sci. 2022, 247, 116931. [Google Scholar] [CrossRef]
- Perazzini, H.; Freire, F.B.; Freire, J.T. Prediction of Residence Time Distribution of Solid Wastes in a Rotary Dryer. Dry. Technol. 2014, 32, 428–436. [Google Scholar] [CrossRef]
- Thibault, J.; Alvarez, P.I.; Blasco, R.; Vega, R. Modeling the Mean Residence Time in a Rotary Dryer for Various Types of Solids. Dry. Technol. 2010, 28, 1136–1141. [Google Scholar] [CrossRef]
- Hamawand, I.; Yusaf, T. Particles motion in a cascading rotary drum dryer. Can. J. Chem. Eng. 2014, 92, 648–662. [Google Scholar] [CrossRef]
- Huang, Z.-G.; Weng, Y.-X.; Fu, N.; Fu, Z.-Q.; Li, D.; Chen, X.D. Modeling the Total Residence Time in a Rotary Dryer. Int. J. Food Eng. 2015, 11, 405–410. [Google Scholar] [CrossRef]
- Lee, A.; Sheehan, M.E. Development of a geometric flight unloading model for flighted rotary dryers. Powder Technol. 2010, 198, 395–403. [Google Scholar] [CrossRef]
- Song, Y.; Thibault, J.; Kudra, T. Dynamic Characteristics of Solids Transportation in Rotary Dryers. Dry. Technol. 2003, 21, 755–773. [Google Scholar] [CrossRef]
- Sokhansanj, S.; Rezaei, H. Dual objectives of forage drying and insect disinfestation. Dry. Technol. 2022, 40, 2510–2518. [Google Scholar] [CrossRef]
- Fernandes, N.J.; Ataíde, C.H.; Barrozo, M.A.S. Modeling and experimental study of hydrodynamic and drying characteristics of an industrial rotary dryer. Braz. J. Chem. Eng. 2009, 26, 331–341. [Google Scholar] [CrossRef]
- Rezaei, H.; Yazdanpanah, F.; Lim, C.J.; Lau, A.; Sokhansanj, S. How to Lower the Chance of Rotary Drum Dryer Fires. Canadian Biomass Magazine. Available online: https://www.canadianbiomassmagazine.ca/how-to-lower-the-chance-of-rotary-drum-dryer-fires/ (accessed on 11 March 2020).
- Mafart, P. Genie Industriel Alimentaire, 2nd ed.; Lavoisier Tec & Doc: Paris, France, 1996; p. 253. [Google Scholar]
- Friso, D. Energy saving with total energy system for cold storage in Italy: Mathematical modeling and simulation, exergetic and economic analysis. Appl. Math. Sci. 2014, 8, 6529–6546. [Google Scholar] [CrossRef]
- Perry, R.H. Chemical Engineers Handbook, 9th ed.; McGraw-Hill International: Singapore, 2019; pp. 12–53. [Google Scholar]
- Xie, L.; Yang, L.; Su, L.; Xu, S.; Zhang, W. A Novel Rotary Dryer Filled with Alumina Ceramic Beads for the Treatment of Industrial Wastewaters: Numerical Simulation and Experimental Study. Processes 2021, 9, 862. [Google Scholar] [CrossRef]
- Scherer, V.; Mönnigmann, M.; Berner, M.O.; Sudbrock, F. Coupled DEM–CFD simulation of drying wood chips in a rotary drum—Baffle design and model reduction. Fuel 2016, 184, 896–904. [Google Scholar] [CrossRef]
- Havlík, J.; Dlouhý, T. Indirect Dryers for Biomass Drying—Comparison of Experimental Characteristics for Drum and Rotary Configurations. ChemEngineering 2020, 4, 18. [Google Scholar] [CrossRef]
- Friso, D. Conveyor-belt dryers with tangential flow for food drying: Mathematical modeling and design guidelines for final moisture content higher than the critical value. Inventions 2020, 5, 22. [Google Scholar] [CrossRef]
- Friso, D. Conveyor-Belt Dryers with Tangential Flow for Food Drying: Development of Drying ODEs Useful to Design and Process Adjustment. Inventions 2021, 6, 6. [Google Scholar] [CrossRef]
- Friso, D. A New Mathematical Model for Food Thermal Process Prediction. Model. Simul. Eng. 2013, 2013, 569473. [Google Scholar] [CrossRef]
- Friso, D. Mathematical modelling of conveyor-belt dryers with tangential flow for food drying up to final moisture content below the critical value. Inventions 2021, 6, 43. [Google Scholar] [CrossRef]
- Geankopolis, C.J. Transport Process Unit Operations, 3rd ed.; Prentice-Hall International: Englewood Cliffs, NJ, USA, 1993; pp. 528–562. [Google Scholar]
- Cerruto, E.; Balsari, P.; Oggero, G.; Friso, D.; Guarella, A.; Raffaelli, M. Operator safety during pesticide application in greenhouses: A survey on Italian situation. Acta Hortic. 2008, 801, 1507–1514. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).