A Cloud-Edge-Based Framework for Electric Vehicle Emergency Energy Trading

Abstract

The number of electric vehicles (EVs) is increasingly growing day by day and the charging infrastructure for covering this growing number of EVs should be developed. The construction of charging stations is one of the main solutions for supporting EVs while it costs huge investments for installation. Thus, this is not financially logical to invest in charging stations in remote areas with lower demands. An alternative way of constructing charging stations is to provide a peer-to-peer (P2P) energy exchange system in order to support out-of-charge EVs. In this paper, a private cloud-edge emergency energy trading framework is proposed to facilitate energy exchange among consumers and providers. Furthermore, a bidding system is suggested to encourage EVs with extra charges to exchange their energy. Moreover, a matching strategy for pairing consumers and providers is suggested in this paper that considers the benefit of both consumers and providers. In the proposed matching system, a measurement strategy is also suggested for considering the effect of the reliability and punctuality of the providers. To develop the accuracy and efficiency of the proposed framework, employing deep learning methods is also suggested in different layers of the framework. The performance of the proposed framework is evaluated on several case studies in the presence of EVs with realistic features to prove its efficiency, feasibility, and scalability.

1. Introduction

1.1. Background

The transportation system has been one of the main sources of environmental pollution for years. By increasing the concerns about carbon dioxide emissions, greenhouse gases and environmental pollution caused by burning fossil fuels, the transportation industries are encouraged to develop electric vehicles (EVs). With clean charging sources, EVs can deeply decrease the environmental concerns related to burning fossil fuels [1]. On the other hand, by increasing the number of EVs in the urban and interurban transportation system, providing charging stations would be a challenging issue. To construct a public charging station, in addition to costs for equipment, support from the main utility company is also needed. To bring electricity to the desired point, up to tens of thousands of millions of dollars is required to plan and install a 480-volt charging station [2]. Due to that, it is not financially logical to install stations in low-traffic areas. Alternatively, the vehicle-to-vehicle (V2V) energy trading system is suggested to fill this gap in charging stations as a subcategory of peer-to-peer (P2P) energy exchange. A P2P energy trading system is defined as the electricity exchange between end-users equipped with energy resources. However, V2V trading system is defined specifically for energy exchange between EVs. In a P2P energy exchange of EVs, EVs not only are considered as vehicles but also as moving energy storage units [3]. EVs directly exchange energy with each other using special connectors constructed by DC/DC converters [4]. Regarding information sharing among EVs, there are two main concepts as P2P-based and V2V-based communication schemes. The V2V-based communication facilitates local communications and P2P-based communication with a wider coverage area can be utilized for vehicles that are far from each other [5].

1.2. Literature Review and Discussion

Recent papers in V2V energy exchange have been published on presenting ways to facilitate P2P trading of EVs in two main research areas: (1) inventing fast and efficient power electronic-based connectors for V2V charging [6], (2) optimizing the way of matching EVs that need energy (consumers) and EVs with extra charge in their storage (providers) in an area [7]. The focus of the paper is on the second area of research. The studies in this regard try to find the best answer to the following question: “Which provider should provide energy to which consumer and in which location?”. Technically, there are two infrastructure-dependent and infrastructure-free ways of charging demanding EVs. In infrastructure-dependent systems, it is assumed that the energy transfer is performed in pre-installed stations, i.e., grid-connected stations or swapping stations without connection to the grid. On the other hand, in infrastructure-free systems, EVs connect to each other using the DC/DC converters at any desired location [8].

In the review of recent articles in the presented research area, [9] suggests a P2P energy exchange system in which EVs not only provide energy to their peers but also behave as ancillary services to help the energy deficiency of the smart grid. The P2P price of energy in the paper is assumed to be as the time of use price of the grid and the transactions are assumed to be executed through smart contracts to save their reliability. In [10], mobile charging stations as ultracapacitors are suggested to be implemented in the system in two on-grid and off-grid modes. In this idea, the charging stations are special cars with the duty to charge the consumers. In [11], the Stackelberg algorithm is employed to match the consumers with providers by increasing the incentives considering the profit of consumers, providers and the system. In [12], the Stackelberg and genetic algorithms are utilized to optimize the energy trading between smart grid and EVs. Authors in [13] use a non-cooperative game method that takes into account the linked limitation to solve the parking-lot EV charging scheduling problem. In [14], the Stackelberg game model is suggested to optimize the utility of consumers and providers by making a competitive environment. Furthermore, the security and privacy of transactions are assumed to be preserved by blockchain technology. In [15], a blockchain-based strategy is suggested to make the transactions and authentication of vehicles in V2V trading reliable and safe. The Bayesian game approach is utilized in [16] for the optimization of social welfare for consumers and providers to trade with the utility or with each other. In [17], a V2V trading system is proposed considering the quality of service for parties. In addition, smart contracts are also suggested for making the exchange operation more transparent and reliable. The scheduling problem of charging stations with EVs using the benders decomposition method is solved in [18] to minimize the social costs.

By elaborating on the recent pieces of research, the common features of the studies and the research gaps can be summarized as follows:

Research gap 1 

There are a great number of studies on using blockchain technology to protect the reliability of transactions among EVs. However, there is not a comprehensive framework for energy exchange covering locating service, pricing and matching EVs.

Research gap 2 

There are a lot of studies trying to optimize the V2V exchange in a centralized manner that needs to disclose the private features of the EVs such as their battery state of charge (SoC), battery consumption rate and driving behaviors. However, these approaches do not protect the privacy of EVs.

Research gap 3 

Moreover, few studies are performed on maximizing the benefit of consumers based on realistic features such as monetary time value for consumers, the driving behavior and punctuality of the optional providers.

Research gap 4 

Most of the researchers strive toward maximizing the benefits of the consumers and several researchers work on the benefit of both sides of the energy exchange and they consider a competitive game among parties to acquire the maximum welfare through a competitive environment. However, few researchers consider the pricing strategy based on the realistic benefit of the providers containing their vehicle features and the monetary value of time for them.

1.3. Contributions and Paper Organization

Based on the reviewed literature and existing research gaps, in this paper, a comprehensive framework based on cloud-edge architecture is designed for P2P emergency energy exchange for out-of-charge vehicles stopped in the middle of their way. The paper provides the following contributions:

Contribution to fill gap 1 

To fill the research gap in providing a comprehensive framework, a cloud-edge structure is tailored in this paper for the proposed P2P emergency energy trading system to match the providers and consumers in a fair behavior. This aim is reached in this paper by a matching game inspired by the stable Gale-Shapely matching strategy that resolves the equality assumption in stable matching.

Contribution to fill gap 2 

To have a framework that protects the EVs’ privacy, the proposed framework provides a communication system in which both consumers and providers keep the private features of their EVs such as energy consumption, driving behavior, and remaining electric charge safe from exchanging with other parties.

Contribution to fill gap 3 

To have a more realistic trading system with realistic features, a reliability measurement unit is defined in this paper. Due to that, the reliability and punctuality of the providers are considered as a decisive role in their winning chance. In other words, providers who do not keep their promises in previous trades have a lower chance of winning the game.

Contribution to fill gap 4 

The benefits of providers and the utility of consumers are considered in the matching algorithm simultaneously considering the realistic features of providers’ vehicles. That means both consumers and providers are deciders in the proposed energy exchange game. The performance of the proposed framework is also evaluated on several case studies considering realistic car features to show its feasibility and scalability.

The remainder of the paper is organized as follows: In Section 2, the problem statement and the proposed methodology are presented. After that, the proposed cloud edge framework and the matching strategy are completely explained. Next, the simulation results and discussion are analyzed in Section 3 and Section 4. Finally, the conclusion is described in Section 5.

2. Materials and Methods

The main aim of this paper is to propose a private P2P matching emergency trading system for those EVs that run out of charge in the middle of their way with no charging station close to them. This system would descend the burden on the huge government investments in the construction of charging stations in remote areas with less charging demands. The considered EVs in the paper can be from both types of battery EVs (BEVs) and plug-in EVs (PHEVs) however BEVs are more likely to join the trade. Since BEV consumers are in danger of needing emergency charge since their only energy source is electricity in comparison with PHEVs with two energy resources (electricity and fuel). Furthermore, as a provider vehicle to provide emergency energy, BEVs have the more proper capacity. However, if a PHEV has extra capacity and based on its features wins in the matching process, there is no other limitation for them. In the following, the abovementioned system is presented and formularized to match the most proper consumers and providers.

Take Figure 1 as an example that illustrates a schematic view of an imaginary system with several demandant EVs to purchase energy (consumers) and several EVs as volunteers to sell their extra charge (providers) on the Aarhus city Google Earth. It is assumed that consumers have run out of charge and stopped in their location with no charging station near them. This paper aims to design a model to match them with the most proper providers, considering the benefits to both consumers and providers. Both consumers and providers want to maximize their benefits in this system. In other words, consumers want to purchase energy at a low price during the lowest possible time. Furthermore, the providers prefer to sell their extra energy at the maximum price with the lowest degradation of their vehicle during the minimum possible time.

To this aim, the next subsection describes all the objective functions and constraints related to the proposed problem. Next, a matching strategy is devised to solve the problem. Furthermore, a cloud-fog structure is also designed for the practicality of the proposed system.

2.1. Problem Statement

The main goal of the matching system is to help EVs that need emergency energy (called consumers) in their location by other EVs with extra energy (called providers) considering the utility of both sides. Therefore, the proposed problem is a stable matching problem to obtain the best match of consumers and providers based on their utility function. We match the providers to the consumers considering their location, available time and energy exchange costs. Thus, the decision variables are binary that show whether a match is established between a consumer and provider (1) or not (0). Furthermore, several variables in types of equality and inequality should be calculated before the matching process as the initial values to be considered in the matching process. In the following, the utility functions of the consumers and providers are explained. Next, the required constraints to be considered for the trade are presented.

2.1.1. Utility Functions

In the proposed framework, the utility functions of both consumers and providers are taken into consideration [19]. The consumer utility function is maximized by trying to maximize the reliability of the matched provider and minimize the delivery time and the total payable price for the requested energy. Thus, the utility function of the i-th consumer in trading with the j-th presenting provider can be formularized as follows:

$$U_i^C({\mathrm{EV}}_j^P)=r_i·R_j-\left({\lambda }_i{T}_{i,j}^{exchange}+B_{i,j}^{P2P}{E}_i^{req}\right)$$

(1)

which is a function of the provider’s features as follows:

$${\mathrm{EV}}_j^P=\left\{{\alpha }_j,{\eta }_j^{veh},{\eta }_j^{conv},{\theta }_j,{\tau }_j,{\varphi }_j^y,x_j,R_j,v_j^P,{\mathrm{SoC}}_j^{\min },{\mathrm{SoC}}_j^{\max },{\mathrm{SoC}}_j\right\}$$

(2)

where $r_i·R_j$ is the reliability variable of the optional provider with a coefficient that specifies the importance of the provider’s punctuality for the consumer. Furthermore, ${\lambda }_i{T}_{i,j}^{exchange}$ presents the exchange operation time with the coefficient that demonstrates the monetary value of every unit of time for the intended consumer. The payable price is also calculated by multiplying the P2P bid by the amount of requested energy as $B_{i,j}^{P2P}{E}_i^{req}$. Since the second and third terms in (1) are tried to be decreased, they are appeared in the function with a minus sign before them while the first term is shown with a positive sign to show the consumer’s willingness to its increase [20].

The provider utility function is maximized by trying to maximize the received payment from the optional consumer and minimize the actual costs of the charging process for the provider [21]. The utility function of the j-th provider in trade with the i-th consumer is presented as follows:

$$U_j^P({\mathrm{EV}}_i^C)=B_{i,j}^{P2P}{E}_i^{req}-\left(C_{i,j}^{delivery}+C_{i,j}^{trans}+C_{i,j}^{\varphi }+{\lambda }_j{T}_{i,j}^{exchange}\right)$$

(3)

which is a function of the consumer-related variables as follows:

$${\mathrm{EV}}_i^C=\left\{E_i^{req},x_i\right\}$$

(4)

The payment that the provider acquires is shown by $B_{i,j}^{P2P}{E}_i^{req}$ that appears with a positive sign because the provider intends it to be increased. However, due to the willingness of the consumer to minimize the cost of energy that the provider needs to travel to the consumer ($C_{i,j}^{delivery}$), energy transmission cost ($C_{i,j}^{trans}$), the battery degradation cost ($C_{i,j}^{\varphi }$), and the monetary value of the whole exchange process time (including delivery and energy exchange time) for the provider (${\lambda }_j{T}_{i,j}^{exchange}$), these amounts are shown by the negative sign in the provider utility function in summation of.

2.1.2. Inequality Constraints

The j-th provider needs to have a minimum amount of energy as ${\mathrm{E}}_{i,j,t}^{P,\min }$ in its battery to be able to attend to the trade with the i-th consumer. The amount of the stored energy in the provider’s battery ($E_j^P$) must be more than this minimum amount, as follows [22]:

$${\mathrm{E}}_{i,j}^{P,\min }\le E_j^P$$

(5)

To calculate ${\mathrm{E}}_{i,j,t}^{P,\min }$, we should consider the nominal minimum (${\mathrm{E}}_j^{P,\min }$) battery charge of the provider’s EV, the required energy of the provider to travel to the optional consumer location ($E_{i,j}^{delivery}$), transmitted energy ($E_{i,j}^{trans}$) to charge the consumer battery in the amount of the consumer requested energy and the extra energy that the provider want to remain in its battery (other than the nominal minimum) after the process. The extra remaining energy is assumed to be obtained in two ways in this paper. One is to obtain it by a predefined percentage of the maximum battery capacity as ${\gamma }_j·Ca{p}_j$. The other is to calculate it based on the required energy to travel to the second destination (k) after the energy exchange process. The following equations present the mentioned ways to calculate ${\mathrm{E}}_{i,j,t}^{P,\min }$:

$$\begin{array}{l}{\mathrm{E}}_{i,j}^{P,\min }={\mathrm{E}}_j^{P,\min }+E_{i,j}^{delivery}+E_{i,j}^{trans}+{\gamma }_j·Ca{p}_j\\ or\\ {\mathrm{E}}_{i,j}^{P,\min }={\mathrm{E}}_j^{P,\min }+E_{i,j}^{delivery}+E_{i,j}^{trans}+E_{i,k}^{delivery}\end{array}$$

(6)

The maximum capacity of EV batteries decreases from the nominal capacity $Ca{p}_j^n$ over time. The current capacity of an EV is obtained as follows [6]:

$$Ca{p}_j=Ca{p}_j^n-{\displaystyle \sum _{y=0}^{LF}\left({\theta }_j{\tau }_j+{\varphi }_j^y\right)}$$

(7)

in which ${\theta }_j$ is the number of the operating cycles of the EV’s battery, ${\tau }_j$ is a constant coefficient, LF is the lifetime of the battery (in years) and ${\varphi }_j^y$ indicates the yearly capacity degradation independent from the operating cycles. This formula shows the capacity of the provider’s battery at a particular time (the time of energy exchange). That is calculated based on the degradation indices including the number of operating cycles (charges and discharges) that is calculated based on the average utilization of the battery in a year and the degradation caused by the battery age after the manufacturing date. In other words, the total degradation of the capacity of the providers’ battery is calculated based on the summation of the battery degradation in each year of battery lifespan after its manufacturing date until the time of energy exchange based on usage and aging degradation factors.

Another constraint that is considered in the proposed exchange problem is the available time of the providers ($T_j^{\max }$). In other words, the time length of energy exchange must not exceed the provider’s time limit, as is demonstrated as follows [23]:

$$T_{i,j}^{exchange}\le T_j^{\max }$$

(8)

The exchange process length of time simply can be obtained using the distance between the optional match of the consumer and provider ($D_{i,j}$), the average velocity of the provider to travel the distance ($v_j^P$) and the required time to transmit the requested energy to the provider which is obtained based on the velocity of transmission per energy unit (${\omega }_{i,j}$) and the transmission efficiency (${\eta }_j^{trans}$). Hence, the total energy exchange time is obtained as follows [22]:

$$T_{i,j}^{exchange}=\frac{D_{i,j}}{v_j^P}+\frac{{\omega }_{i,j}{E}_i^{req}}{{\eta }_j^{trans}}$$

(9)

However, the authors suggest a deep learning-based method in which providers calculate the exchange time based on the elaborated factors as follows: the driving behavior of the provider, the type of the streets toward the destination, and the weather.

2.1.3. Bidding

The price of the P2P energy exchange should be in a way that the provider would be encouraged to attend the exchange program. To this aim, in this paper, a share of the total price would be considered as the pure benefit for the provider as a reward called the percentage of benefit as ${\alpha }_j$. Furthermore, the bidding price of P2P trading is offered based on the total exchange cost plus a percentage of benefit as calculated in (10). That means, the provider sells energy to the consumer with the energy price calculated by summation of the total cost of exchange (summation of the cost of traveling of the provider toward the consumer ($C_{i,j}^{delivery}$), the transmission cost of the requested energy by the consumer ($C_{i,j}^{trans}$) and the battery degradation cost ($C_{i,j}^{\varphi }$) and a benefit calculated by a percentage of the total cost of exchange, per each unit of exchanged energy. Thus, the P2P energy price and the pure benefit of the provider for the pair of the i-th consumer and the j-th provider is obtained as follows:

$$B_{i,j}^{P2P}=\left(1+{\alpha }_j\right)\left(C_{i,j}^{delivery}+C_{i,j}^{trans}+C_{i,j}^{\varphi }\right)/E_i^{req}$$

(10)

$$P{B}_{ij}^P={\alpha }_j\left(C_{i,j}^{delivery}+C_{i,j}^{trans}+C_{i,j}^{\varphi }\right)$$

(11)

2.1.4. Exchange Costs for the Provider

The cost of traveling is determined based on the following factors: the provider’s car model, the driving behavior of the driver, the distance between the consumer and provider, and the weather. Simply, the traveling energy and the related cost can be modeled as follows [22]:

$$E_{i,j}^{delivery}=D_{i,j}/{\eta }_j^{veh}$$

(12)

$$C_{i,j}^{delivery}=B·E_{i,j}^{delivery}$$

(13)

However, we suggest a deep learning-based approach to predict $E_{i,j}^{delivery}$ for each provider with the input factors mentioned above as an interesting area for future work.

The transmission energy to provide the requested energy for the consumer is determined based on the efficiency of the connector that performs the exchange operation. Thus, the transmission energy and the related cost are obtained as follows:

$$E_{i,j}^{trans}=\frac{E_i^{req}}{{\eta }^{conv}}$$

(14)

$$C_{i,j}^{trans}=B·\frac{E_i^{req}}{{\eta }_j^{trans}}$$

(15)

The cost of the provider’s battery degradation to attend the exchange with the i-th consumer is calculated based on the battery replacement cost (as $\sigma$, containing the capital cost to replace the battery plus the labor costs) and the coefficient of battery capacity degradation ($\phi$), as follows:

$$C_{i,j}^{\varphi }=\sigma ·\phi ·E_i^{req}$$

(16)

2.1.5. Reliability

In this paper, the reliability of a provider is defined as a factor that is specified based on the precedent history of the provider in attending the previous exchanges. This factor is calculated based on the punctuality of the provider after winning an exchange. If the provider appears in the meeting after winning, the variable $l$ would be set to 1 and one point be added to its reliability factor. Otherwise, the variable $l$ is 0 and the reliability factor loses two points. Furthermore, in this paper, we assumed the importance of being on time for the meeting. In other words, to the extent that the provider meets the consumer sooner or later in comparison with the promised exchange time, the reliability factor increased or decreased by a constant coefficient ($\beta$). The reliability factor for the next time interval is updated after the exchange operation as follows:

$$R_j⟵\left\{\begin{array}{l}{R}_j+1+\beta (T_{i,j}^{exchange}-T^{real})\hspace{1em}\hspace{1em}if\hspace{1em}\hspace{1em}l=1\\ R_j-2\hspace{1em}\hspace{1em}if\hspace{1em}\hspace{1em}l=0\end{array}\right.$$

(17)

Another factor worth considering in a P2P trade of EVs is the reliability of the transactions. To this aim in [24], authors define innovative transactive control frameworks for energy communities with independent energy storage systems that facilitate energy storage sharing in a reliable manner. They offer algorithms based on a game theoretical control formulation that determine the best time to allocate the energy activities of a group of prosumers, who were defined by their own demand and renewable generation, and a group of energy storage service providers, who were able to store the surplus energy produced by the prosumers and release it after receiving payment.

2.2. The Proposed Cloud-Edge Framework

A private cloud-edge computing framework is designed in this paper, to efficiently solve the P2P energy trading problem. In this section, we propose a matching system to match the providers with the minimum possible consumption cost for providers and the lowest energy price for the consumers at the most efficient timespan that tries to increase the pure benefit for the provider, simultaneously. Next, a cloud-edge architecture is designed based on the proposed matching strategy as a private infrastructure to make the proposed strategy feasible to be practically implemented. The proposed matching algorithm supported by the particular cloud-edge architecture would design a feasible framework for a private energy trading system. In the suggested framework, providers and consumers are determiners of their exchange while keeping the particular features of their EVs and driving behaviors private. Furthermore, the providers in the proposed system have the right to specify their benefits based on their situation. A supervisory unit is also devised to determine the reliability of the EVs and the system’s security. Figure 2 illustrates a general view of the proposed cloud-edge P2P energy exchange system.

2.2.1. Matching Consumers to Providers

In general, we have two sets of EVs, i.e., consumers and providers that want to maximize their own benefits in the energy exchange system. To match the consumers with the optimal providers considering the benefit of providers, the proposed matching strategy inspired by the Gale-Shapely algorithm is presented after an introduction to the Gale-Shapely method.

(a)

Gale-Shapely algorithm

The Gale-Shapley algorithm is an efficient algorithm that is devised to solve matching problems stably. To elaborate on stable matching, the stable marriage problem is a common example. Take two sets of people as an example. The first set contains N females and the second set contains N males. Each member in the group has a list of preferences to be paired with the other group. The aim is to match these men and women based on their preferences somehow there is no other pair where both participants prefer each other as their partners (stable matching) [25]. David Gale and Lloyd Shapley proved that, for an equal number of males and females, it always exists a stable solution to pair them stably [26]. The Gale-Shapely algorithm is as follows:

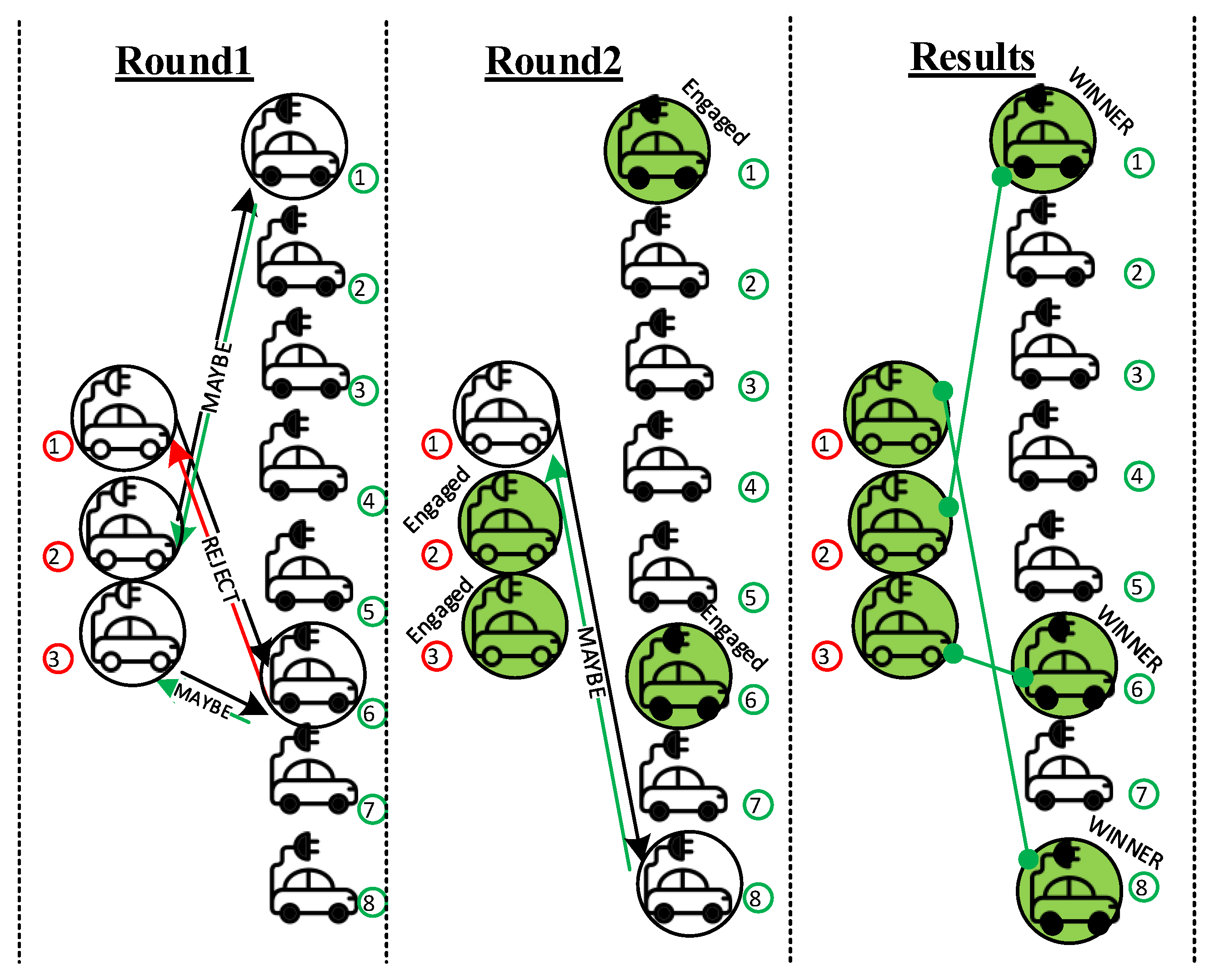
In the first round, every man proposes to the woman at the first rank on his preference list. Next each woman replies ‘Maybe’ to the most preferable suitor based on her predefined list and ‘Reject’ the other suitors. Now, she is temporarily engaged with the suitor she preferred.

In each following round, each unengaged man proposes to the first woman on his list to whom he is not yet proposed regardless of the engagement status of the woman. Afterward, each woman replies ‘Maybe’ to the most-preferable man among all suitors and his probable partner. If the woman prefers a suitor over her current partner, she is engaged with the new preferred suitor and ‘Reject’ his partner who will be unengaged then. This round is repeated until everyone is engaged.

(b)

The proposed matching strategy

In the proposed energy exchange problem, we have unequal sets of consumers and providers to optimally match utilizing the extended version of Gale-Shapely. Each member has its own preference list based on its utility function calculated by the imaginary trade with members of the other group. In this paper, to have a fair matching strategy for both consumers and providers with unequal numbers we try to consider the benefit of both consumers and providers. The stable Gale-Shapely algorithm is for problems with an equal number of participants in both sets. However, this assumption is not rational in the proposed system.

To establish justice among providers and consumers, the bidding right is conferred to providers, and the right to propose using the extended Gale-Shapely strategy and acquire a more-optimal partner is given to the consumers, in return. Thus, in this matching strategy, the consumers behave similar to the suitors in the stable marriage example mentioned above who propose to their preferred providers based on their utility function. Next the providers provisionally engage with the best proposers based on their utility function. The proposal rounds are repeated until all the members of either consumers or providers find their pairs.

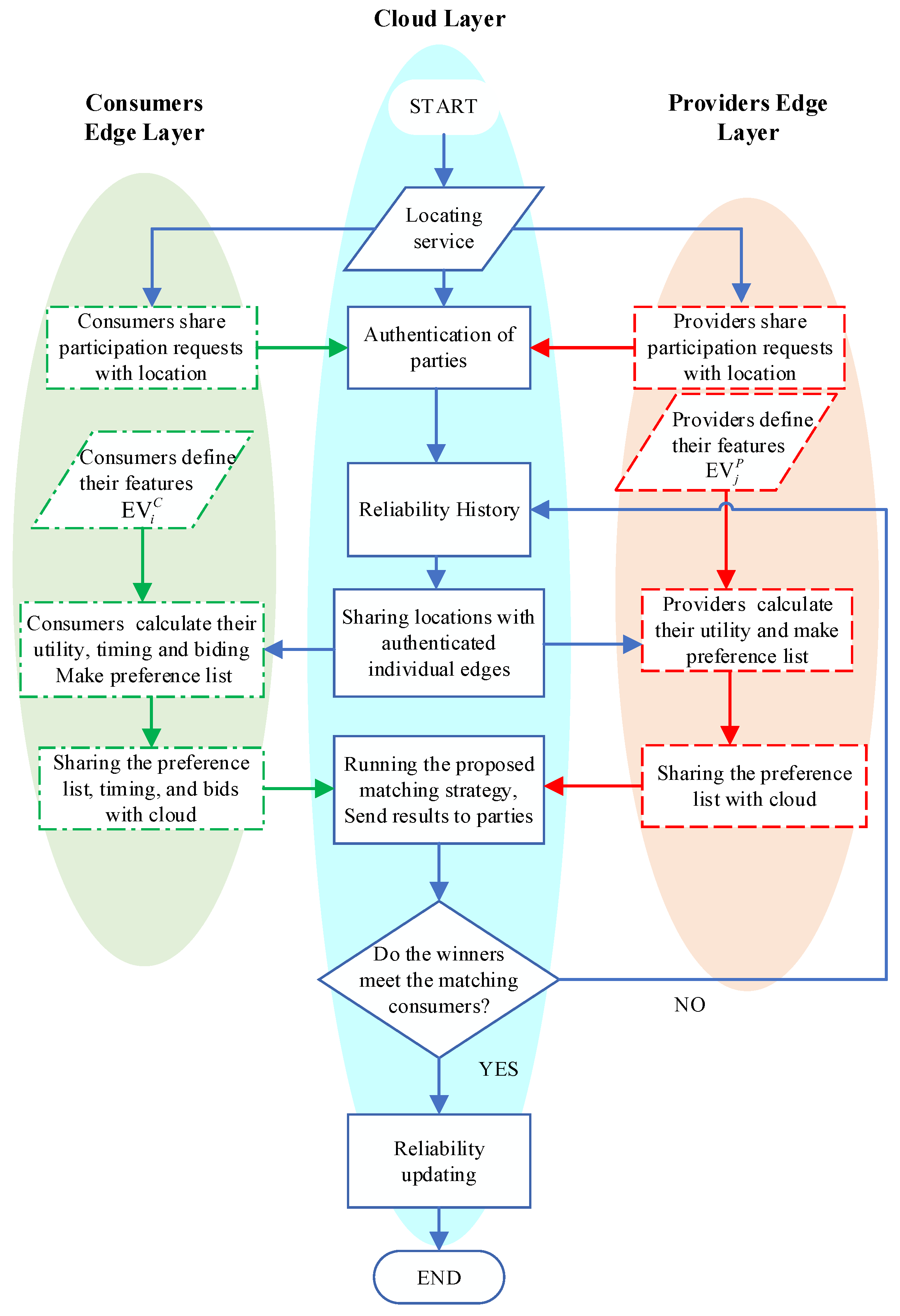
2.2.2. Cloud Layer

To facilitate the implementation of the proposed matching program, a two-layer architecture based on cloud and edge computing is designed and tailored for the proposed exchange system. The cloud layer is the upper layer using cloud computing technology that brings remote computing and storage resources for users who are distributed in different locations [27]. Several duties are assigned to the cloud layer in the proposed framework which is illustrated in a flowchart in Figure 3 and described as follows:

Supervisory and Security

The cloud layer is responsible for supervising the functionality of the system and conserving its security. This layer is in charge of identity recognition of the participating providers and consumers to preserve the system and participants safe from malicious attacks. Furthermore, financial transactions are performed under the control of this layer for their safety. Moreover, the responsibilities of making and enforcing rules and regulations are all allocated to the cloud layer.

Reliability Updating System

As mentioned in Section 2.1.5, the reliability of the providers should be determined using (17). That means a supervisory utility should observe the functionality of the providers in order to determine and render them to the consumer that is assigned to the cloud layer as well.

Locating Service

In order to have more optimal routing, timing and energy consumption results, the locating service system is devised to be performed in the cloud layer containing positioning of the participants, weather prediction, i.e., wind speed and raining status, street traffic and slide modeling, and driving rules in different streets. This information is provided in the cloud layer for a better decision-making process for consumers and providers.

Communication Interface

A telecommunication bridge is assumed to be constructed between consumers and providers using cloud computing. That means, after the identity recognition of consumers and providers, the cloud layer makes an interface between these two groups by connecting the confirmed ones.

2.2.3. Deep Learning-Enabled Edge Layer for Providers

The edge layer using the edge technology brings computing and storage sources close to the application [28]. That helps the proposed system to be more private. Since the calculation needs private features of EVs as inputs are assumed to be privately calculated in the edge layer by each participant. Here, two different edge layers are described for providers and consumers that are suggested to be equipped with deep learning algorithms to higher their functionality.

Routing

Routing is one of the main duties of the providers’ edge layer. Finding the most proper route to meet the consumer is executed on the individual provider’s edge using the gathered data from the cloud locating service of the cloud layer and is suggested to be performed by deep learning methods.

Timing

Providers timing to travel toward the consumers is a determinative factor in the calculation of utility functions. This factor also affects the reliability of providers due to their punctuality at meeting times. This timing is assumed to be calculated based on the locating service data gathered from the cloud layer and is suggested to be calculated based on the behavior of the driver and the type of his EV.

Energy Consumption

The energy consumption of an EV per distance depends on several factors such as the EV model, speed of driving, weather situation and wind speed, and slope of the ways. The energy consumption can be estimated based on the precedent data of the EV using deep learning algorithms. In the edge layer, the energy consumption prediction is calculated for determining the consumption used for traveling to the consumer or to specify the required energy to drive toward the third destination after the exchange operation.

Bidding and Preference List

Finally, to calculate the utility function and provide bidding for each consumer using (10), the edge layer performs the related computation using the information of the consumers’ location and their requested energy which are gathered by the infrastructure that the cloud layer provides for participants’ communication. After bidding, the providers set their preference list based on the gained utility.

Communication with the Other Layers

Each provider needs information about other consumers and the locating service information of the cloud layer. Thus, its edge communicates with the cloud layer and consumers’ edge to acquire this non-sensitive information conserving the privacy of all the participants.

2.2.4. Deep Learning-Enabled Edge Layer for Consumers

Consumers also are assumed to have their individual edge layers to perform their calculations privately near their location. The responsibilities of the consumers’ edge layer are as follows:

Energy Consumption

Each consumer needs to calculate the required energy to continue their way to the new destination. This consumption is suggested to be performed by having the information of the EV and the desired route features by having the cloud locating service using the deep learning method in the consumers’ edge layer.

Preference List

Calculating the consumers’ utility to set a preference list by having the timing, bidding, and reliability factor of the providers is also operated in the edge layer.

Communication with the Other Layers

To have the global features of the providers and location service of the cloud layer, the consumer communicates with the providers’ edge and the main cloud layer through its edge layer.

3. Results

The performance of the proposed cloud-edge energy exchange framework is evaluated using MATLAB simulation. The simulation is firstly performed on a toy example to show the stages of the work, winning and losing participants’ benefits and bids, and the effect of the reliability variable on the output matching rounds and pairs. Next, the performance of the proposed work is examined on a larger scale to observe the scalability of the framework. The toy example contains a system shown in Figure 1 with three consumers and eight providers. Their locations are randomly selected in a special area on the Aarhus map.

The features of the EVs are gathered from realistic cars which are listed in

Table 1. Consumers initial data.

EV Model	${\mathit{\lambda }}_{\mathit{i}}$ $/h	$\mathit{S}\mathit{o}{\mathit{C}}_{\mathit{i}}^{\mathit{r}\mathit{e}\mathit{q}}$ %	$\mathit{C}\mathit{a}{\mathit{p}}_{\mathit{i}}$ kWh
Opel Corsa-e	10	7	50
Renault Zeo R110	12	5	52
Volkswagon e-UP	15	10	36.8

and

Table 2. Providers initial data.

EV Model	${\mathit{\eta }}_{\mathit{j}}^{\mathit{v}\mathit{e}\mathit{h}}$ kWh/ km	$\mathit{\sigma }$ $/kwh	${\mathbf{SoC}}_{\mathit{j}}$ %	${\mathbf{SoC}}_{\mathit{j}}^{\mathbf{min}}$ %	${\mathit{R}}_{\mathit{j}}$	$\mathit{\alpha }$ %	${\mathit{\lambda }}_{\mathit{j}}$ $/h	$\mathit{C}\mathit{a}{\mathit{p}}_{\mathit{j}}$ kWh
Audi e-tron	4.167	150	57	5	10	40	11	95
BMW i3 2018	5.55	145	47	18	8	45	12	42.2
Chevrolet Bolt	5.55	271	52	5	0	25	10	65
Tesla Model X 75	4.35	137	34	17	5	50	10	75
VW e-Golf 2017	5.55	654	25	11	1	50	15	35.8
VW e-Golf 2020	5.55	137	79	20	6	35	11	35.8
Tesla Model X 90	4.35	135	31	5	−2	45	13	90
Nissan Leaf 2018	0.19	187	53	9	5	25	14	40

in addition to other related initial data for consumers and providers separately. It is noteworthy that the requested energy of the consumer, the current energy of the provider, and the provider’s minimum needed energy are calculated as $E_i^{req}=So{C}_i^{req}·Ca{p}_i$, ${\mathrm{E}}_j={\mathrm{SoC}}_j·Ca{p}_j$ and ${\mathrm{E}}_j^{\min }={\mathrm{SoC}}_j^{\min }·Ca{p}_j$. Furthermore, the bid of each kWh ($B_t$) energy in common charging stations is assumed to be the average electricity price of the unites states 10.42 ¢/kWh, and the other initial values are gathered from [22] as ${\omega }_{i,j}$ = 0.025, $\phi$ = 0.27%, and ${\eta }_j^{conv}$ = 2.7%.

In the first case study, the reliability coefficient r is assumed to be fixed on 1. The order of the proposals and answers for this case can be observed in Figure 4. First, consumers send their location, the monetary value of time for them and requested energy to the cloud. Providers send their location and monetary value of time for them to the cloud as well. Cloud also identifies the reliability of the providers based on their precedent exchanges. After the identity recognition process, the cloud layer shares the data of two sets with private edges of the other sets. Having this data, provider edges compute the P2P bid, required timing, and their utility for each consumer and send them into the cloud. Next, the cloud layer based on these non-private and non-sensitive data runs the matching algorithm to find the best matches in two rounds as is illustrated in Figure 4. In the first round, consumer1 and 3 send their proposal to their best optional match which is provider 6 and consumer 2 proposes to provider 1. Thus, provider 1 engaged with its only proposer and provider 6 choose its best optional consumer which is consumer 3. Next, the only unengaged consumer proposes to provider 8 which is currently unengaged too. Now, all the consumers are engaged and the pairs are defined by the cloud.

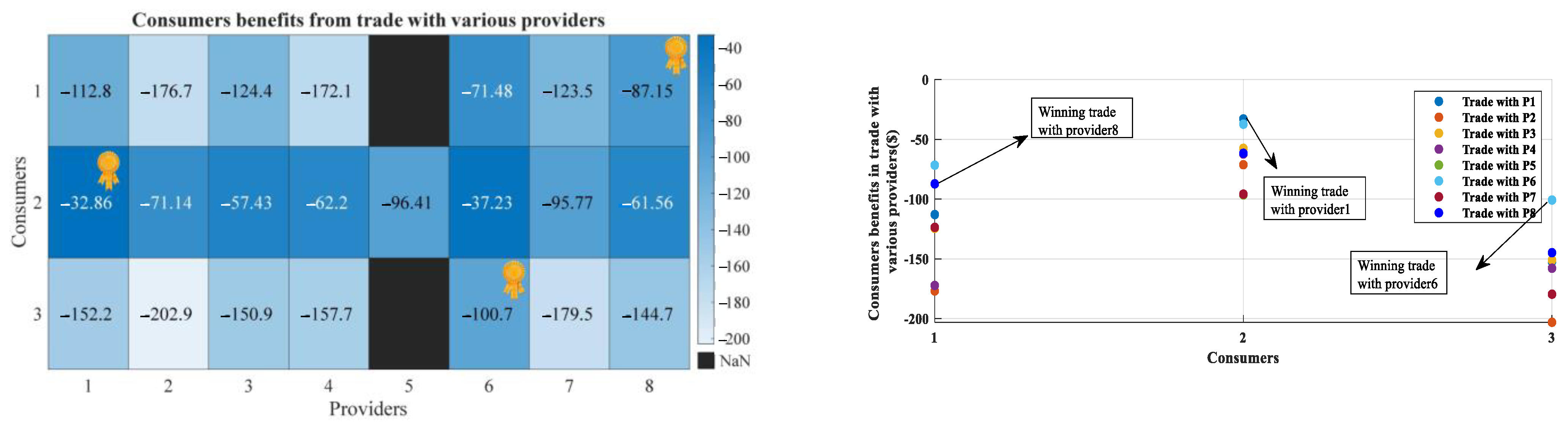
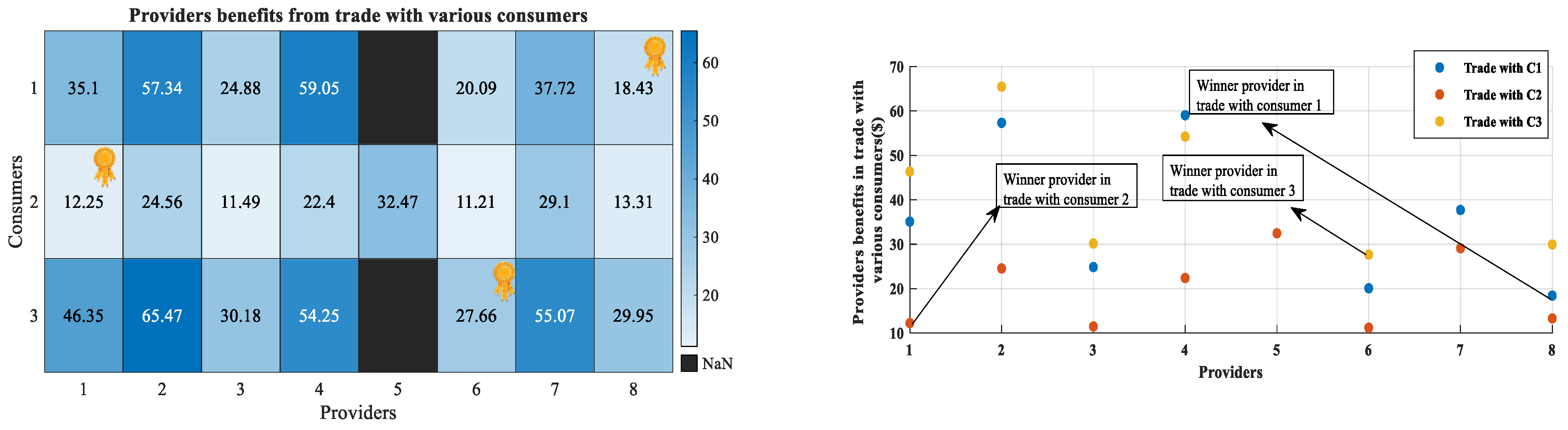
The final results are shared with the winners’ edges for the exchange operation. Optional consumers’ and providers’ benefits in trade with each other are demonstrated in Figure 5 and Figure 6, respectively. By elaborating on these figures, we can conclude that the proposed matching system tries to maximize the consumers’ benefit. This is fair for both sides of the game in the proposed work since the providers also predefined their percentage of benefit for participating in the game as a privilege to providers. Furthermore, in the situation of confronting two or several consumers to match with one provider, the provider is the final decider of the game. The consumers’ payable bids calculated by providers’ edge are also shown for different consumers in Figure 7.

Now, to evaluate the effect of reliability on the results, the reliability coefficient is increased from one to 100, one by one. The results of matching and the required rounds to acquire these results can be observed in

Table 3. Required rounds and winning providers using the proposed strategy calculated with different reliability coefficients.

r	Rounds	Winning Providers in Trade with (C1, C2, C3)
1 ≤ r ≤6	2	8, 1, 6
7 ≤ r ≤ 11	4	1, 2, 6
12 ≤ r ≤ 13	3	1, 2, 6
13 ≤ r ≤ 17	3	6, 2, 1
18 ≤ r ≤ 53	2	6, 2, 1
54 ≤ r ≤ 100	3	2, 6, 1

. As can be observed, the reliability of the EVs and their coefficient can have an essential impact on the final matches and even the number of required rounds.

To evaluate the scalability, the proposed example is extended for different numbers of providers and consumers. In

Table 4. Required rounds of running the proposed method with different numbers of providers and consumers as (N^p, N^c).

(Np, Nc)	(200, 10)	(200, 50)	(200, 100)	(200, 150)	(350, 200)
Average required rounds	3.31	21.58	61.12	160.97	135.44
(Np, Nc)	(10, 200)	(50, 200)	(100, 200)	(150, 200)	(200, 350)
Average required rounds	2.33	20.29	52.54	134.26	114.24

, the average number of required rounds to acquire the final matches are listed. In the table, the first two rows are dedicated to the situations in which the number of providers (N^p) is more than the number of consumers (N^c) and the second two rows are vice versa. The table shows that the convergence will happen even with a large number of participants in the limited but scale-related number of rounds.

4. Discussion

The main problem of the paper is to match EVs with extra charge to consumers with emergency energy requirements in their location. A matching strategy in a cloud-fog architecture is proposed in this paper that considers both consumer’s and provider’s utility. In this scheme, the effect of the reliability of the providers in their previous trades is also considered. The parties’ privacy is protected in the suggested framework. This means thanks to the cloud-fog architecture, both customers and suppliers maintain their EVs’ private characteristics, such as their energy usage, driving style, and remaining electric charge, hidden from the other EVs. To evaluate the proposed framework, several numerical examinations were performed. First, the performance of the method on a toy example is evaluated. The results demonstrate that the suggested matching system aims to maximize the benefit to the consumers. This is appropriate for the planned task because the suppliers also agreed to a predetermined percentage of benefit as a privilege for participating in the game. In addition, the provider is the ultimate decider of the game when two or more consumers are pitted against one supplier. After that, the effect of the reliability index on the final results is evaluated by changing the value of the reliability coefficient. The outcome demonstrates that this index directly influences the final winners in the system. This can help the more reliable providers with more punctuality have a better chance to win in the trades. This fact helps us to have a more reliable trading system that encourages providers to be more punctual and responsible. Next, the performance of the proposed framework on larger scales is analyzed. The data indicate that even with a large number of participants in the limited yet scale-related rounds, convergence will occur.

Several areas for future improvement of the manuscript can be as follows: The performance of the proposed framework can be improved by working on the scalability of the matching strategy somehow the required round of convergence become irrelated to the scale of the number of participants. Furthermore, recharging costs after the trade for the providers can also be considered in future related works. Furthermore, the transactions settlement of the P2P trades would be a future research area to amend the practical aspect of the trading system.

5. Conclusions

In this paper, a cloud-edge framework for a fair P2P emergency energy trading system is proposed. The proposed framework considers the reliability of providers and their punctuality based on the precedents that the cloud layer defines. It conserves the privacy of participants from the disclosure of their private features such as their EV battery consumption, their current battery charge, etc. using a private edge layer. Furthermore, the proposed framework makes a fair exchange environment to exchange energy that considers the utility of both consumers and providers at the same time. The proposed framework functionality is examined in several case studies. The privacy of the parties remained safe from disclosure using the suggested cloud-edge structure through the simulation. Furthermore, it is observed that by changing the coefficient of reliability, a clear change occurred in the final winners. In addition, by increasing the number of participants, the number of required rounds increases but the convergence occurs in limited rounds. In conclusion, the simulation results prove the privacy-preserving, reliability-conserving, and scalable nature of the proposed matching framework. Furthermore, the framework performance is suggested to be developed using deep learning algorithms in various mentioned layers of the system.