Abstract
The processing of the piece surfaces involves the transformation of the blank into a piece, the defining characteristics of the surfaces (the form, dimensions, deviations, etc.), depending to a large extent on the parameters of the generated processes of the surfaces. Generating surfaces by enveloping represents a complex problem, this mode of generating being a constant concern of researchers due to its advantages. A very important issue is the cutting edge profiling of the future tool, which will generate the wanted profile of the piece. Throughout time, researchers have studied the problems of enveloping surfaces and stated theorems related to them, based on which practical solutions have been conceive to determine the generating and generated surfaces form. The paper presents an overview on study methods for reciprocally enwrapping surfaces, as well as methods for profiling tools for generating helical surfaces by the kinematic method and by the method of decomposing the helical movement. This review can represent a basis for future research articles and projects.
1. Introduction
The processing of the surfaces of the pieces assume transforming the blank into a piece, having the shape and dimensions prescribed in the design stage.
According to well-known authors such as Radzevich [1], the purpose of machining processes is to obtain the functional surfaces of the pieces. The defining characteristics of the surfaces of the processed pieces, such as their shape, dimensions, deviations, roughness, etc., largely depend on the parameters of the surface generating processes [1].
The generating of surfaces by enwrapping is a problem of utmost importance, both in the case of cutting processes and in the case of plastic deformation processes. This mode of generating has been a continuing concern of researchers and technologists due to the advantages of this mode of generating. Among these advantages are: high productivity and increased machining accuracy, due to the fact that the profile errors of the tool are greatly reduced on the profile of the generated piece [1,2].
According to Cioară [3], a piece can be obtained by various manufacturing processes, in accordance with different requirements such as: dimensional accuracy, surface quality or productivity. The shape of that part is characterized by the generating and directing curves, which can be obtained by copying, kinematically or can be materialized by the cutting edges of the tools.
In his work, Cioară [3] presents the cases of generating the surfaces characterized by the director obtained kinematically, in the form of the envelope of a family of curves.
Since the 19th century, there have been concerns about improving the profiles of the active surfaces of the gears. George Biddell Airy [4] performed research in this field, starting from previous studies conducted by Euler in 1760.
Concerns about changing the shape of teeth in order to improve their bearing capacity are still relevant, as evidenced by research [5,6,7,8].
Profiling the tools that generate by enveloping often requires an analytical representation of the surfaces of the pieces. In addition, the analytical representation of surfaces is used for processing on computer numerical control (CNC) machines and for computer-aided inspection processes (CAD, CAM) [9,10].
The generating of surfaces by enwrapping involves their processing by cutting, in which case, obviously, the quality of the surfaces obtained depends mainly on the geometry of the cutting tool.
A particularly important problem is the profiling of the edge of the future tool, which will generate the desired profile of the piece. This implies the existence of adequate methodologies, which allow us to solve the problem of profiling the tools that generate by enwrapping.
Over time, researchers have studied the aspects of surface enwrapping and stated theorems related to them, based on which practical solutions have been devised to determine the shape of generating and generated surfaces [1,2,11,12].
Initially, the issue of generating surfaces by enveloping had a graphical approach, due to the difficulties related to the analytical calculation, often very laborious, necessary to solve such problems.
The geometrical methods used in this regard are: the Camus theorem [13], a method based on the fundamental properties of enwrapping curves [5], the Poncelet method (1827) and the Rouleaux method (1842).
Subsequently, based on geometric methods, analytical methods for tool profiling were developed, which generate by enwrapping, in particular, by the rolling method [2,12].
According to the definition accepted in the theory of enwrapping surfaces, rolling is the relative movement of two curves that are constantly in contact.
It can be of two types: rolling without slipping and rolling with slipping. In the case of rolling without slipping, the relative speeds between the two curves have the direction of the common tangent. In the case of rolling with slipping, the curves have the same direction of the common tangent at the point of contact and the relative speeds are of opposite directions.
Theodore Olivier (1842) developed two fundamental theorems, which bear his name, for the case of generating enveloping surfaces with linear contact and, respectively, with point contact [2,14].
Subsequently, these theorems are reviewed by the mathematician Gohman (1896), who approaches a method that simplifies the way of analyzing the contact of enwrapping surfaces with linear contact and point contact [2,14].
In 1843, the normal theorem, also known as the Willis theorem, was developed for reciprocally enwrapping profiles associated with rolling centrodes [15].
The Nikolaev method (1950) is also another method specific to the profiling of surfaces, reciprocally enveloping, cylindrical or revolutionary [2].
Based on this fundamental method, Guo Q. et al. [16] developed an analytical method for calculating the envelope of the tool profile at processing on a numerically controlled five-axis machine.
In paper [17], based on the normal to the generating surface and the relative velocity vector between the tool and the blank, the analytical expression of the enwrapping of the cutting edge positions of the tool is obtained, during its movement according to the programmed trajectory. The method is validated by exemplifying it when processing on a machine tool with five axes numerically controlled and there is a wide discussion on the influence of geometric errors of the tool on the generated surface.
Complementary methods, such as the minimum distance method (1992), method of substituting circles (1998), the tangent method (2000) and the planar trajectory method (2002), are methods that use the direct way of expressing the enwrapping conditions and treat problems specific to the generating of reciprocally enveloping surfaces [18].
The development of industrial systems, as well as the increasing use of computer numerical controlled (CNC) machine tools, have allowed the generating of complex-shaped surfaces, which use circular or rectilinear generating tools. They describe complex trajectories, involving the development of applications for the study of enveloping surfaces made through graphic design programs, such as CATIA, AutoCAD, SolidEdge, etc. [16,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36].
Albu [18] studied the possibility of simulating the milling processing with the front cylinder tool of the helical surfaces of a conveyor screw. In the respective paper, the possibility of obtaining a conical helical surface of variable pitch is analyzed.
Teodor V.G., Popa I. and Oancea N. (2010) created an algorithm to replace the plane generators of surfaces discreetly known by Bezier curves [37,38].
As a result of the development of computing systems and the evolution of graphic design media, graphic methods could be imagined and developed to solve the problems of tool profiling, which generate by enwrapping thus providing solutions to problems related to the study of reciprocally enveloping surfaces [21,37,39,40,41,42,43,44].
A number of authors have used the theory of enwrapping surfaces to study the effect of deviations of the tool from the programmed trajectory on the geometric shape of the generated surface [9,16,45,46,47,48,49].
2. Materials and Methods
2.1. Olivier Method
This method is based on Olivier’s two fundamental theorems, namely:
- -
- Theorem I—generating of surfaces with linear contact for conjugated surfaces that depend on a single parameter [11,14];
- -
- Theorem II—generating of surfaces with point contact for conjugated surfaces that depend on two independent parameters [2,11].
In the case of Olivier’s first theorem, in a straight orthogonal system, a family of surfaces that depends on a parameter is described by equations of form:
or, in a vectorial expression:
where, u and v are independent variable parameters of the current point belonging to the Σ surface and α is the parameter that determines the family of surfaces [11,14].
Observation: The characteristic curve on a surface Σ, Figure 1, which performs a movement in relation to a fixed part, depending on a single variable parameter, is the geometric place of the points on the surface, where the normal to it is perpendicular to the velocity vector, in the absolute movement of the surface in relation to the fixed part (fixed reference system) [50].
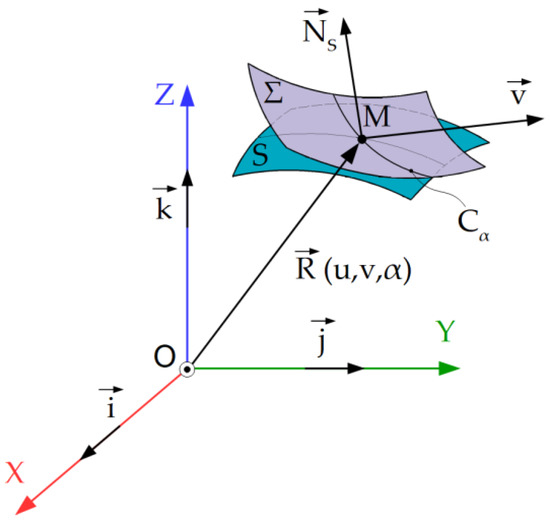
Figure 1.
Characteristic curve.
Olivier’s first theorem can be expressed, for a value of the variable parameter Σ, depending on the variable parameters u and v of the surface, by the analytical forms [50]:
or by a vectorial form equation:
In the case of a family of surfaces described by two independent parameters α and β, it will have the parametric equations of the form [2]:
or:
According to Olivier’s second theorem [2], if the function admits partial derivatives after all arguments, in a domain D, of variation of the parameters u and v, for a defined domain of the independent parameters α and β, then the envelope of the family can be determined from the system of equations:
where and are partial derivatives of the vector.
2.2. Gohman Theorem
Olivier’s theorems allowed the mathematician Gohman (1896) to develop a method for determining the characteristic curve on a moving surface.
The theorem states that: “a point on the S surface will belong to the characteristic curve only if, at that point, the normal to the S surface is perpendicular to the velocity vector in the absolute movement executed by the surface” [2,51].
Figure 2 shows the S surface and the two reference systems.
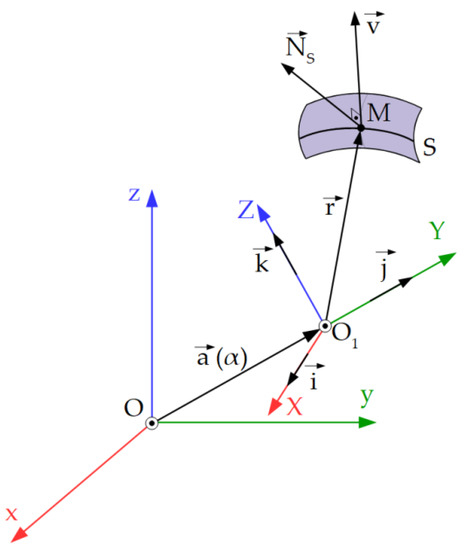
Figure 2.
Reference systems: xyz—fixed reference system, XYZ—mobile reference system.
The S surface, in the reference system XYZ, can be expressed as:
The S surface executes a movement, depending on a single parameter τ. In this movement, the S surface describes the family of surfaces in the fixed system xyz in the form:
Gohman’s theorem can define the characteristic curve C given by the system of equations:
The equation can be seen as the scalar product of two vectors, obviously representing the normal at the S surface, and the vector representing the absolute velocity (relative to the fixed system) in the movement of the surface.
Therefore, the condition can be written as which allows the enunciation of Gohman’s theorem.
The Gohman method can easily solve the problem of generating surfaces (surface vortexes) associated with a couple of rolling centrodes (the case of rack tool generating, gear shaped cutter tool generating or the generating of cylindrical helical surfaces with rotary cutter tools) [9].
Based on Gohman’s theorem, Dooner [15] applies the theory of enwrapping surfaces to cylindrical, conical and hypoid gears.
Dooner and Griffis present the application of the first gear law to the study of worm and hypoid gears, in which, in general, normal at the flank of the tooth does not intersect the instantaneous rotation axis [52]. In the same paper, the second law of gearing is applied for the study of hyperboloid gears, noting that: “the spiral profile of the flank of the tooth, in these gears, is generated so as to allow any pressure angle with the conjugate profile” [52].
2.3. Normals Method (Willis Theorem)
The “gearing” theorem, also known as the “normals method” or “Willis theorem” (1843) [2,51] or sometimes as “Euler–Savary theorem” [52], can be stated as follows: “two profiles associated with rolling centrodes, which transmit rotational movement between two parallel axes, are reciprocally enveloping if, in the process of rolling the centrodes, the contact points of the profiles admit a common normal, which passes through the gearing pole”.
Two enwrapping profiles are considered, Figure 3, having the two centrodes C1 and C2 tangent at the contact point, P. The centrodes rotate around the axes O1 and O2 having the velocities expressed by the parameters ω1 and ω2.
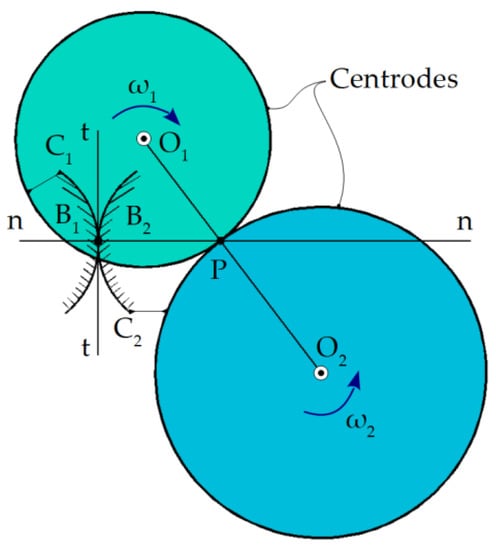
Figure 3.
Conjugated profiles.
In these circumstances, the transmission ratio may be established:
The relative velocity of points B1 and B2 will have the direction of the common tangent to the C1 and C2 curves at the contact point (line t-t). As a result, the instantaneous radius of rotation PB1 = PB2 has the direction of the common normal at the two conjugate profiles (line n-n).
2.4. Minimum Distance Method
Minimum distance method is an analytical method for the study of enwrapping surfaces based on a specific theorem [2,12]: “the envelope of a family of plane curves that performs a movement joined with a couple of rolling centrodes is the geometrical locus of the points belonging to the family for which, in the different rolling positions, the distance to the gearing pole is minimal”, Figure 4.
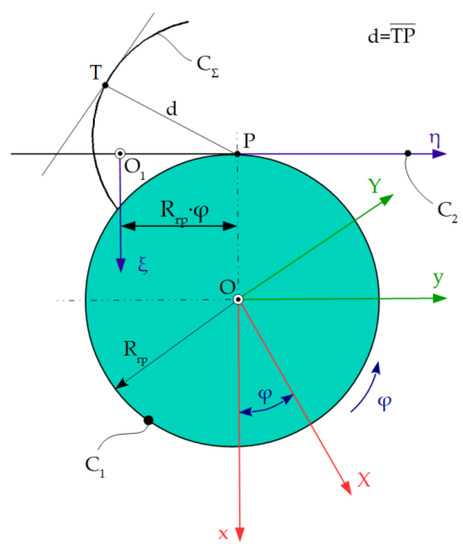
Figure 4.
Minimum distance method applied to rack tool generating [12].
The following are defined:
- -
- Centrode associated with the vortex of the blank profiles—C1 (radius circle Rrp);
- -
- Centrode associated with the flank of the generating rack—C2 (line superimposed on the η axis);
- -
- Reference systems: xy—fixed reference system; XY—mobile reference system, joined with the blank; and ξη—mobile reference system, joined with the generating rack.
If the parametric equations of the CΣ profile are defined:
and the relative movement in relation to the rack system, ξη, in form:
then, the family of profiles, CΣ, in the system ξη, is described by the transformation:
The distance from the current point of the family of curves to the gearing pole P, in the system ξη of the rack is:
The minimum condition of distance d becomes:
representing the enwrapping condition according to this method.
The set of Equations (15) and (17) represents, in the ξη system, the enveloping surface of the family —the profile of the rack conjugated to the family
2.5. Method of Substituting Circles
This method is based on a new principle, namely the family of substituting surfaces (curves) [2,12,51,53] and can be stated as follows: “the envelope of a curve associated with a couple of rolling centrode is the family of substituting circles transposed, in the rolling movement, on the conjugate centrode”, Figure 5.
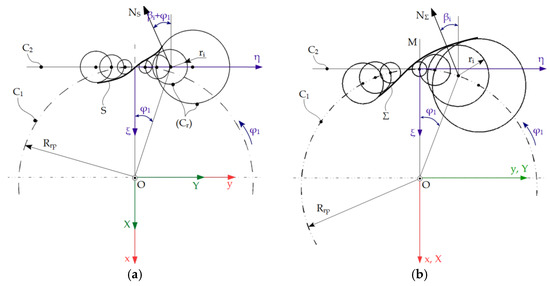
Figure 5.
Family of substituting circles associated: (a) with a centrode; (b) Σ profile.
In the XY system, the family of substituting circles has the equations:
The enwrapping condition is, in this case:
with and
The equations of the envelope S result:
The method of substituting circles has applicability in solving the problem of profiling the tools that generate by enwrapping and allows a suggestive graphic expression, thus preventing the avoidance of major errors. Applications of the method are presented in [54,55].
2.6. Trajectory Method
Trajectory method is a complementary method which is based on determining the enwrapping condition by identifying the trajectories of the points in the tool space, the trajectories tangent to the profile to be generated [12,56].
The trajectory method can be expressed as follows: “the enveloping of a profile associated with a centrode, belongs to a couple of rolling centrodes, is the enveloping of the trajectories described by the point of this profile in the space associated with the rolling centrode” [12].
Figure 6 shows a detail of the tool profile and the plane trajectories of the points belonging to the piece’s profile in the tool’s space.
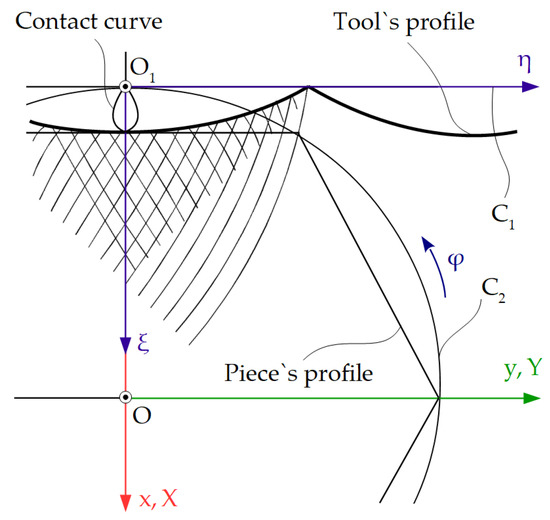
Figure 6.
Tool’s profile and the in-plane trajectories of piece [12].
The parametric equations of the characteristic curve, CΣ, are given by Equation (12), u being a variable parameter.
Therefore, the rolling condition is:
The family of trajectories is expressed by the form:
Relation (22), along with the condition:
allows us to determine the profile of the envelope, CS, which represents the enwrapping curve of the in-plane trajectories of the points belonging to the curve CΣ, in the rolling movement of the centrode [2,12].
2.7. Comparative Study on Specific Forms of Enwrapping Condition
In the case of analytical methods, in order to determine the profiles of the tools that generate by enwrapping, by the rolling method, a typical algorithm is followed, consisting of the following steps:
- (1)
- Establishing the parametric equations of the profile to be generated;
- (2)
- Determining the form of the rolling condition, which determines that the lengths traversed by the instantaneous centers of rotation, on each of the two centrodes, are equal;
- (3)
- Determining the absolute movements of the piece and the tool;
- (4)
- Based on the absolute movements, the relative movements between the tool and the piece are determined;
- (5)
- Considering the fixed tool, the family of curves generated by the profile of the piece is determined, during the relative movement that it has towards the tool;
- (6)
- Determining the specific form of the enwrapping condition;
- (7)
- Associating to the family of curves, determined in step 5, the enwrapping condition obtained in step 6, the profile of the generating tool is determined; practically, the enwrapping condition allows that, from the points belonging to the family of curves, only those belonging to the envelope, and, therefore, to the tool profile, to be selected.
- (8)
- The parametric equations of the gearing curve can be obtained; this represents the geometric locus, in the fixed space, in which the tangency between the two reciprocally enveloping profiles takes place, that of the piece-known and that of the tool-determined.
2.7.1. Rack Tool Profiling—Gohman’s Theorem
The rolling condition, according to the Gohman’s Theorem [11,41,57,58], see Figure 7, of the centrode C1 (circle of radius Rrp), associated with the profile Σ and of the centrode C2, associated with the rack tool S is given by the Equation (21).
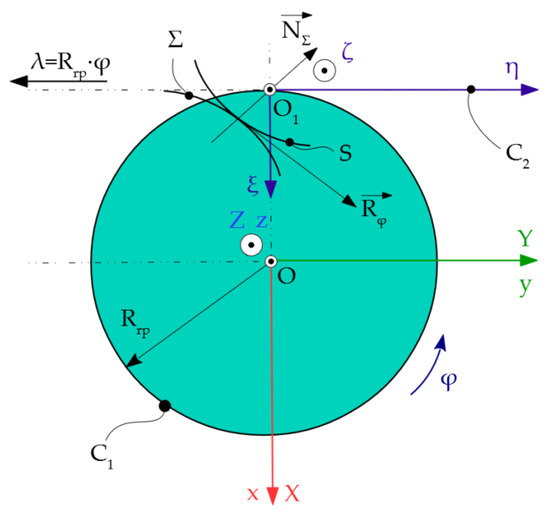
Figure 7.
Reference systems for generating with rack tool, xyz is the fixed reference system, XYZ—mobile reference system, joined with the Σ profile, ξηζ—mobile reference system, joined with the rack tool.
The reference systems, in this case, are presented in Figure 7.
The relative movement of the existing point in the mobile reference system joined with the Σ profile towards to the mobile system joined with the rack tool is given by Equations (13) and (14).
The parametric equations of the Σ profile are defined, depending on the variable parameter u:
The envelope of the surface family in the reference system ξηζ is determined, which represents the flank of the generating rack, from (13) and (14):
According to Gohman’s theorem, for profiling rack tools, the enwrapping condition will be [2]:
where represents the normal at the Σ profile:
and
2.7.2. Gear Shaped Cutter Tools Profiling—Gohman’s Theorem
In the case of gear shaped cutter tools [11,28,55,59,60], the rolling without sliding movement is at the contact between two rotating cylindrical surfaces. The radii of the two surfaces are denoted as follows: Rrp—for blank and Rrs—for tool. Figure 8 also shows the centrodes associated with the tool and the blank, C2, respectively, C1.
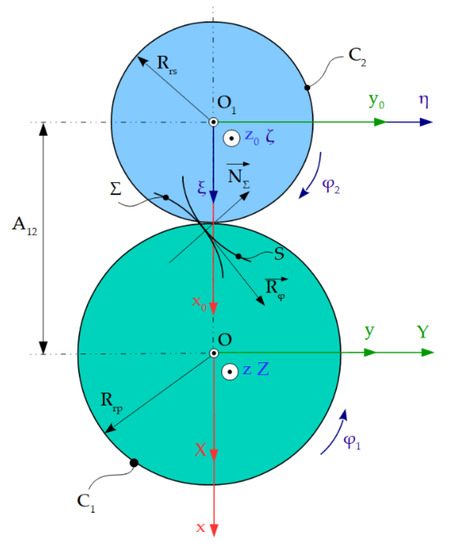
Figure 8.
Generating with gear shaped cutter tool.
From the rolling condition, the transmission ratio expressed by the form is defined:
with φ1 and φ2 angular parameters belonging to the two rotational movements.
The parametric equations in the mobile reference system XYZ that define the Σ profile are similar to Equation (24).
The relative movements of the mobile reference systems are:
The family of surfaces, in the mobile reference system ξηζ is given by the equation:
A12 representing the distance measured between the z and z0 axes.
The enwrapping condition, in the case of gear shaped cutter tools, has the form:
2.7.3. Rotary Cutter Tools Profiling—Gohman’s Theorem
In the case of generating with the rotary cutter tool [11,12,41,54], Figure 9, the plane of the blank will roll on the tool cylinder of radius Rrs. The centrodes are represented: C1—the centrode associated with the blank, and C2—the centrode of the rotary cutter.
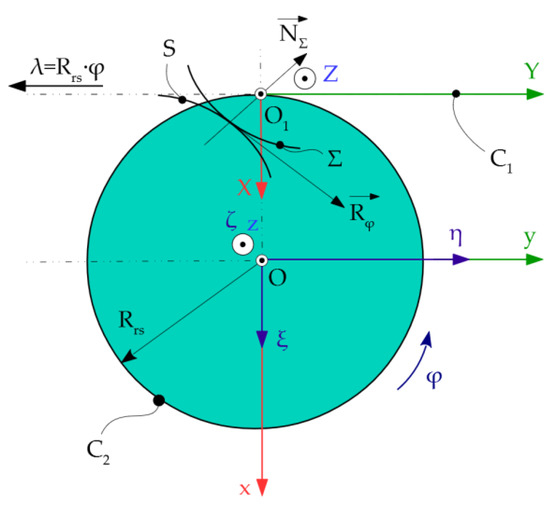
Figure 9.
Generating with rotary cutter tool.
The rolling condition is:
The relative movement of the blank relative to the ξη system is:
The parametric equations in the mobile reference system are of the form (24). The enwrapping condition becomes, in this case:
2.7.4. Rack Tool Profiling—Minimum Distance Method
Knowing the curve CΣ of the profile to be generated by the equation of type (24), with u variable parameter, as well as the relative movement in the mobile reference system of the generating rack ξη, (13), the family of profiles can be determined with the Equation (15) [12,61], with Rrp—rolling radius of the blank centrode.
Therefore, the enwrapping condition according to the minimum distance method is give by (17).
2.7.5. Gear Shaped Cutter Tool Profiling—Minimum Distance Method
Figure 10 shows the minimum distance method applied at generating with the gear shaped cutter tool [12,61].
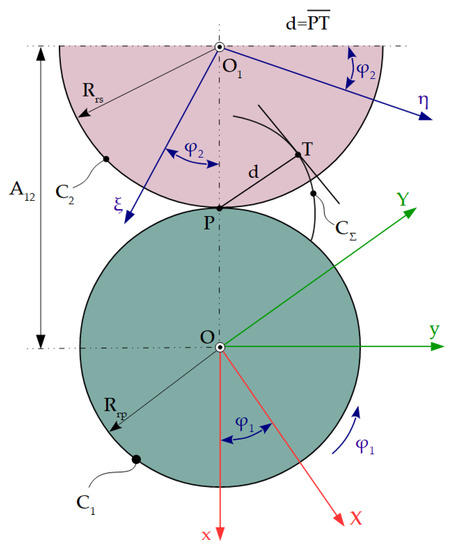
Figure 10.
The minimum distance method applied at generating with the gear shaped cutter tool [2].
The relative movements of the mobile reference systems are given by Equation (30). Equation (30) represents the relative movement of the blank in the reference system of the tool, the relative movement of the tool towards the piece being expressed in the form:
The enwrapping condition, according to the minimum distance method, is given by the relation:
2.7.6. Rotary Cutter Tool Profiling—Minimum Distance Method
Figure 11 shows the profiling of the rotary cutter tool [12,61], according to the minimum distance method.
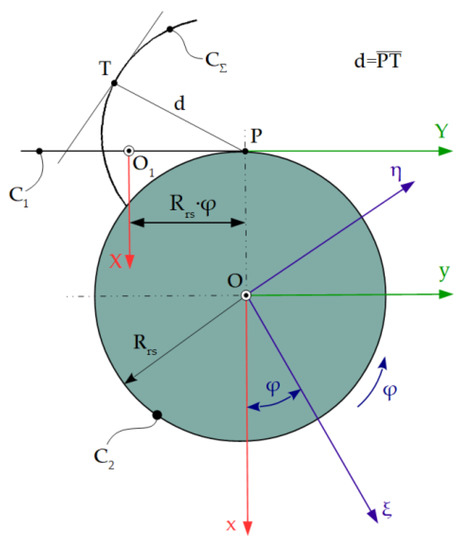
Figure 11.
The minimum distance method applied at generating with rotary cutter tool [2].
The relative movement of the piece in the tool space is given by Equation (34).
The enwrapping condition is:
By combining Equations (34) and (38), the profile of the rotary cutter tool is obtained.
To ensure the generation of the active surface of the pump screw [62,63], it is necessary that the two helical surfaces, the tool and the blank, have opposite directions and have the same inclination to their own axes on the rolling circles.
2.8. Profile of Tools for Generating of Helical Surfaces by Kinematic Method
2.8.1. Profiling of the Disk Tool for the Generating of Helical Surfaces—Profiling Algorithm
The generating of helical surfaces with disc tools has a wide spread, both in mass production (processing of helical drill channels), large series production (in the case of milling of machine tool screws) [64,65,66,67] as well as in the production of unique [68].
Determining the form of the primary peripheral surface of the tool involves determining the axial section of the rotating surface—the most commonly used case in practice is when the clearance angle of the tool teeth is zero, therefore the axial section of the rotating surface is given by the cutting edge configuration of the tool teeth [2,69].
Thus, with the helical surface Σ being known, of axis and parameter p, the rotation surface S can be determined, this being reciprocally enveloping with the surface Σ.
The reference systems are defined according to Figure 12.
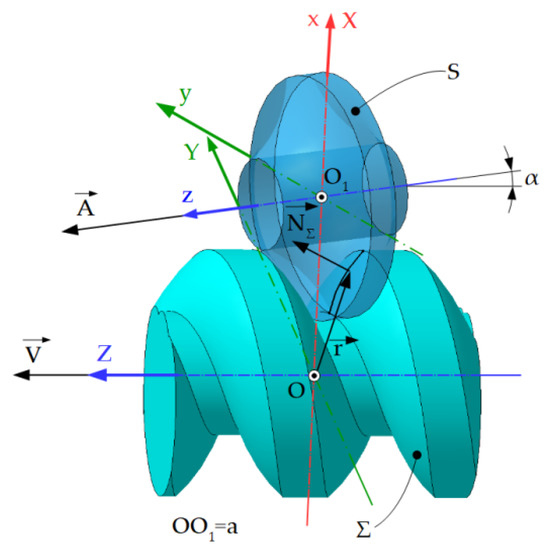
Figure 12.
Disc tool-reference systems: xyz—fixed reference system, the z axis being superimposed on the axis of the rotation surface S; X—mobile reference system, integral with the Σ surface, the Z axis being superimposed on the axis at the initial moment, with the plane ZO1Y the mobile reference system is parallel to the plane zOy.
The axis of the S surface, the axis is at a distance a from the axis of the helical surface and, together with it, forms the angle of inclination, α. This angle is determined by the pitch of the helical surface being processed.
If the surfaces S and Σ are reciprocally enveloping, the surface S is considered to be the family envelope (Σ), in the absolute movement performed by the surface.
Although the surface Σ performs a compound movement: a rotational movement about the axis and a helical movement about the axis and parameter p, the characteristic of the Σ surface depends only on the first mentioned movement (rotational movement), because in the case of the helical movement, Σ self-generates.
Thus, the movement of the Σ surface, being joined with the mobile reference system, XYZ, will be known from the transformation of coordinates:
where:
- -
- α represents the transformation matrix between the versors of the XYZ and xyz systems and is given by the relation:
- -
- A-the matrix formed by the coordinates of point O1, compared to the fixed coordinate system.
Given that the parameter φ is a function of time, after development, the relationship
represents the movement law of a point of space XYZ towards to the fixed reference system.
The characteristic curve is determined by calculating, in the first step, the velocity vector in movement of a point in the space XYZ towards to the fixed reference system, xyz:
From Equation (41), it results:
or
The result is the matrix:
or, in vector form:
In the mobile coordinate system, XYZ, the parametric equations of the helical surface Σ are known:
with u and v independent variables.
The vector of the normal at the Σ surface, is established:
The enwrapping condition is, according to Gohman’s theorem, given by
The condition requires that the vectors and be defined in the same reference system.
Therefore, the vector will be defined according to the fixed coordinate system, xyz, by the transformation:
The director parameters of the normal are:
where Nx, Ny and Nz represent the director parameters of normal at the Σ surface in the fixed coordinate system, xyz.
Thus, for a certain value of parameter φ, the expression of the condition for determining the characteristic curve is obtained, which allows the determination of a connection between the parameters u and v, of the form v = v(u). Taking into account the Equations (26), (45) and (50), the condition is:
The condition (51) and the expression of the parametric equations of the helical surface Σ (47) determine the equations of the characteristic curve, C:
The axial section of the rotating surface, S, is, in fact, the primary peripheral surface of the tool, which, by means of the equations of the characteristic curve, C, at the fixed coordinate system, xyz, results in the transformation of coordinates:
By replacing in Equation (52) the parameters X, Y and Z determine the parametric equations of the characteristic curve, C, in the coordinate system, xyz:
The characteristic curve has a rotational movement around the axis , thus generating the S surface, simplifying the determination of the axial section of the surface.
The points M and N on the characteristic curve, C and the generator, G, are on the same parallel circle, in the same plane perpendicular to the tool axis, Figure 13.
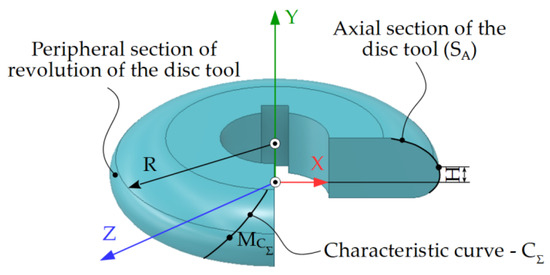
Figure 13.
Axial section of the rotating surface [12].
The radius of the parallel circle is determined by the relation:
The equations of the axial section of the SA surface are given by the relation:
The axis of the tool is defined by the axis defined by the parameters a and α, and is perpendicular to the helix of minimum inclination of the helical surface—Figure 14.
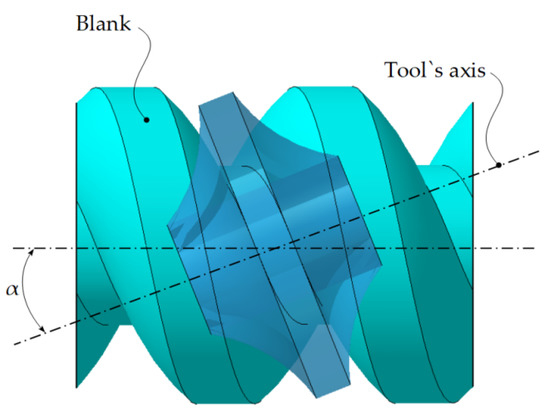
Figure 14.
Axial section of the rotating surface.
Figure 15 shows the generating kinematics, namely the relative position of the tool (milling disc) and the blank (trapezoidal thread).
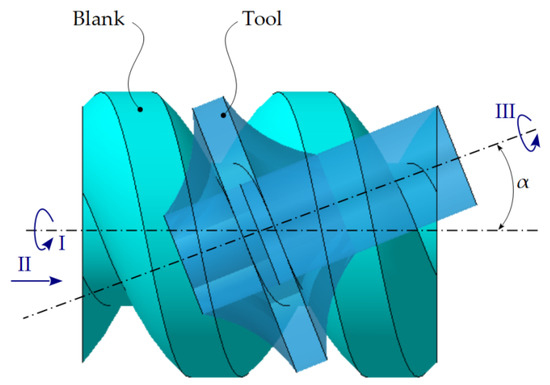
Figure 15.
Generating kinematics with disc tool: movement I—rotational movement of the blank around its own axis, II—translational movement, along the same axis; III—cutting movement.
If D is the diameter of the cylinder, corresponding to the helical line, which belongs to the surface to be processed and PE represents the pitch of the helical surface, the angle of inclination, α, can be determined as follows:
2.8.2. Profiling of Cylindrical-Front Tools (Finger Cutter Tools) for the Generating of Helical Surfaces—Profiling Algorithm
For technological or economic reasons, in some cases (for example zig-zag or V-teeth), the use of disc tools is not possible and it is necessary to use a tool with a smaller size for profiling helical surfaces [18,40,70].
Therefore, the disc tool is replaced with a finger cutter tool or a cylinder-front tool.
To determine the primary peripheral surface of the tool, a rotating surface is determined, perpendicular to the axis of the helical surface, Σ, already known and reciprocally enveloping with it [28,40].
The helical surface, Σ, performs a combined movement: a helical movement, of axis and parameter p and a rotational movement around the axis The surface envelope Σ, depends only on the rotational movement, because, in the helical movement, it self-generates.
Coordinate systems are defined according to Figure 16.
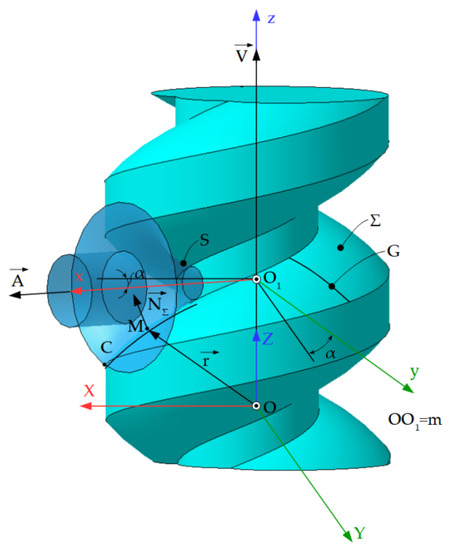
Figure 16.
Generating of the helical surface with the finger cutter tool, reference systems: XYZ represents the mobile coordinate system, solid with the surface Σ, xyz—fixed reference system, having the x-axis superimposed on the tool axis, .
The movement of the helical surface is described by the transformation of coordinates:
where:
The parameter m is a constant that depends on the relative position of the reference systems presented above. Usually, to simplify the calculations, it is consider m = 0.
The characteristic curve, C, of the Σ surface is determined by the equation:
for the parameter φ = constant.
The vector is calculated as follows:
which, after development, has the form:
In the mobile coordinate system, XYZ, the parametric equations of the helical surface Σ are known by equations of type (47).
The normal is defined with Equation (48), which, in the xyz coordinate system, has the director parameters:
The condition for determining the characteristic curve, for φ = 0, is obtained from Equation (26):
which, associated with Equation (47), allows to obtain the parametric equations of the characteristic curve in form (52).
The Equation (63) is equivalent to the coplanarity condition of the vectors and is described by an equation of form, with X, Y and Z defined by (52):
being known as “Nicolaev condition”.
From a technological point of view, it is necessary to determine the axial section of the finger cutter tool, Figure 17.
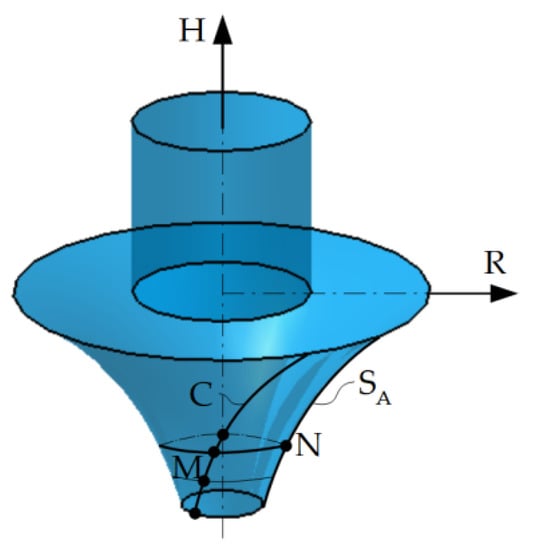
Figure 17.
The axial section of the finger cutter tool.
The parametric equations of the characteristic curve are related to the coordinate system, xyz, by the transformation:
with C given by (54).
The parametric equations of the axial section are:
Figure 18 shows the kinematic principle when processing helical surfaces with finger cutter tools [1,18].
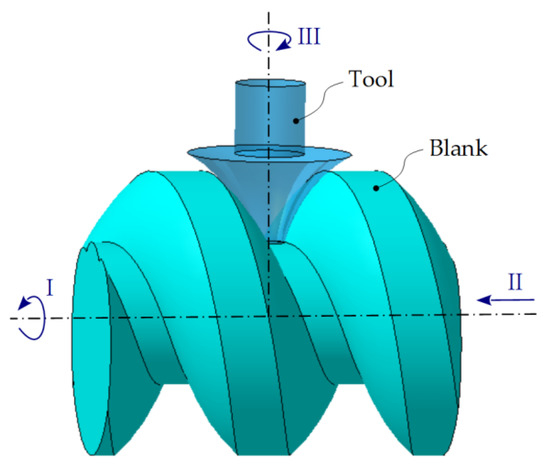
Figure 18.
Kinematic principle.
Movement I represents the rotation of the blank around its own axis. This is correlated with the translational movement II, along the same axis, to ensure the helical movement.
Movement III, represents the rotational movement of the tool, being ensured by a special kinematic chain. The velocity with which the generator travels through the helical direction is conditioned by the possibilities of the technological process used.
2.8.3. Profiling of Cylindrical Generating Tools (Slotting Tools) for Generating of Helical Surfaces—Profiling Algorithm
Slotting is the process of generating helical surfaces, [7,53], most often used in the case of tools with cutting edges that belong to cylindrical surfaces or which, in relative movement to the blank, generates a cylindrical surface [1].
Although the processing productivity is relatively low, the operation of a slotting tool is simpler, due to the ease of its profiling process.
Figure 19 shows the relative position of the cylindrical (generating) and helical surfaces. The cylindrical surface is determined, reciprocally enveloping with the given surface.
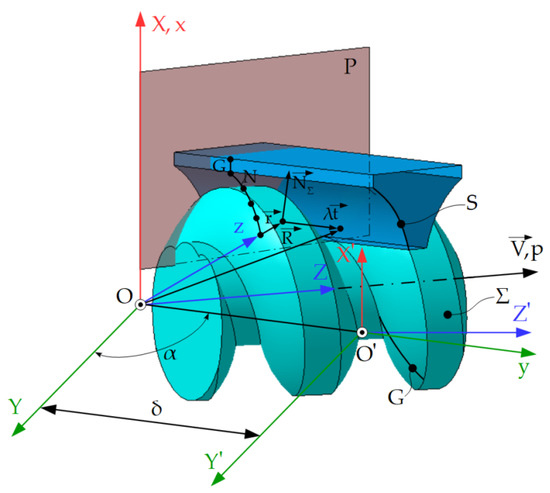
Figure 19.
The relative position of the cylindrical (generating) and helical surfaces. Reference systems: XYZ represents the mobile reference system, joined with the helical surface; xyz—fixed coordinate system; the y-axis is parallel to the direction of the cylindrical surface generators; X’Y’Z’—mobile reference system resulting from the movement of the XYZ system with the variable parameter δ.
To generate the helical surface, S tool performs two movements:
- -
- Translational movement, along the own generators, determining the main cutting movement;
- -
- Helical movement of the axis and helical parameter p, determining the generating movement of Σ surface.
As in the previous cases, the characteristic of the Σ surface does not depend on the helical movement, in which the surface self-generates.
Reference systems are defined according to Figure 19.
In the mobile reference system, the equations of the helical surface are known by equations of type (47), with u and v independent variables.
The movement of the XYZ system and of the Σ surface, along the generators of the cylindrical surface, is given by the relation:
where:
with δ variable parameter.
The director parameters of the normal, are expressed as follows:
In the xyz coordinate system, the director parameters of the normal are:
The vector is calculated as follows:
Thus, the condition for determining the characteristic curve, is expressed as follows:
condition that allows the expression of the parametric equations of the characteristic curve of the form:
In the xyz coordinate system, the equations of the characteristic curve are determined from:
having the form:
Thus, the equation of the S surface will be:
where:
- -
- represents the vector of a current point on the cylindrical surface;
- -
- —the vector of a current point on the characteristic curve;
- -
- λ—variable parameter;
- -
- —the versor of the cylindrical surface generators.
Equation (76) is transcribed, in analytical form, as follows:
From (77), the condition results, representing the section Y = 0:
that allows the determination of the cross section equations, ST:
Figure 20 shows the kinematic principle of generating in the processing of helical surfaces with slotting tools.
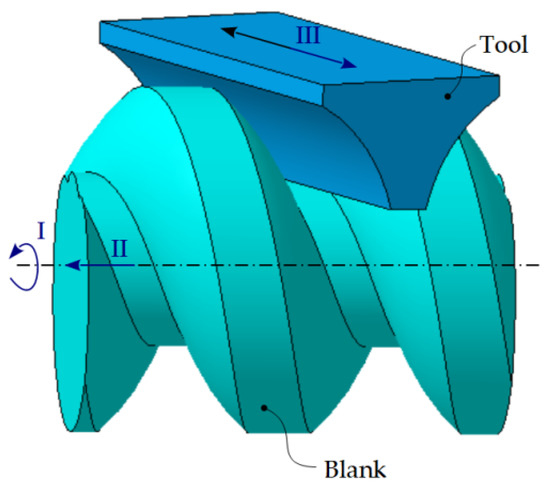
Figure 20.
The kinematic principle of generating: I represents the rotational movement of the blank, II—the translational movement of the blank along its own axis, III—the cutting movement performed by the tool.
According to Figure 20, the movements are defined.
Movements I and II represent the helical movements of definition of the helical surface Σ.
2.9. Generating of Helical Surfaces by the Method of Decomposing the Helical Movement—Nikolaev Condition
2.9.1. Generating of Helical Surfaces with Disc Tools—Profiling Algorithm
The Nikolaev condition [2] is also known as the method of decomposing helical movement according to which: “the characteristic of a revolution surface, reciprocally enveloping a cylindrical and constant pitch helical surface, is the geometric locus of the points belonging to the helical surface for which the normal at this intersects the axis of the revolution surface” [2].
According to Figure 21, the problem involves determining the rotation surface S, the helical surface, Σ, being obtained by means of the helical movement of the generator, G.
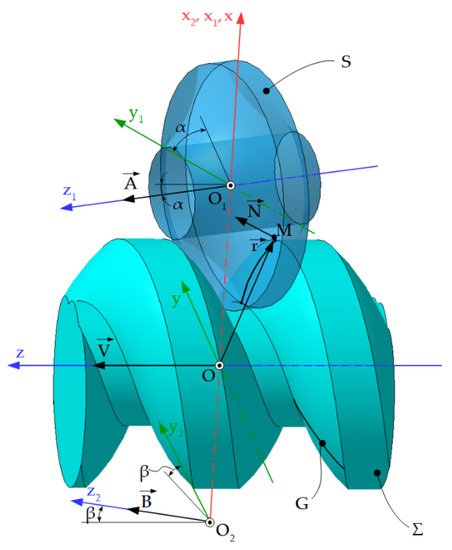
Figure 21.
Generating with disc-tool.
The axis of the rotation surface— forms, together with the axis of the Σ surface— the angle of inclination α, the distance between the axes being determined by the scalar parameter a [2,12].
Reference systems are defined:
- -
- xyz represents the fixed reference system, the z axis being superimposed on the surface axis Σ;
- -
- x1y1z1—fixed coordinate system with z1 axis being superimposed on the axis
- -
- x2y2z2—fixed coordinate system, z2 axis being superimposed on the axis of rotation
The determination of the S surface results from the determination of its characteristic curve C, in the helical movement (V, ω, p).
In the helical movement of the characteristic curve C, the curve generates the Σ surface and, if rotational movement is applied around the axis the S surface is generated.
The helical movement of the rotating surface is decomposed into rotational movements of axes and , their sum being equivalent to the helical movement [2].
If the normal is required to intersect the axis therefore, according to the properties of the helical radii, the normal also intersects the second conjugated axis.
The movement of the point M, corresponding to the S surface, represents a sum of rotations around the axes and the normal being perpendicular to the velocity vector of this point. Therefore, the normal determines the characteristic curve.
The parametric equations of the helical surface Σ are known:
The position vector of the point M is given by:
The following are defined:
- -
- Axis of rotation surface S:
- -
- The vector joining the origin of the fixed coordinate system, x1y1z1 with the point M:
The characteristic curve, C, is determined from the coplanarity condition of the vectors and the condition being of the form:
or, taking into account the Equations (80)–(83):
Nx, Ny and Nz being the guiding parameters of the normal at the Σ surface.
By developing the Equation (85) the condition can be rewritten in the form:
Thus, the parametric equations of the characteristic curve, C, can be determined in form given by Equation (54), associating to the Σ surface equations the enwrapping condition (86).
To determine the axial section of the S surface, the characteristic curve is transposed into the fixed coordinate system, x1y1z1, by transforming the coordinates:
or, after development:
If the parameters x, y and z from Equations (54) and (88) are replaced, in the fixed coordinate system, x1y1z1, the equations of the characteristic curve C will be obtained:
By the rotational movement of the characteristic curve C around the axis the searched surface S can be generated.
Figure 22 shows the axial section of the disc tool.
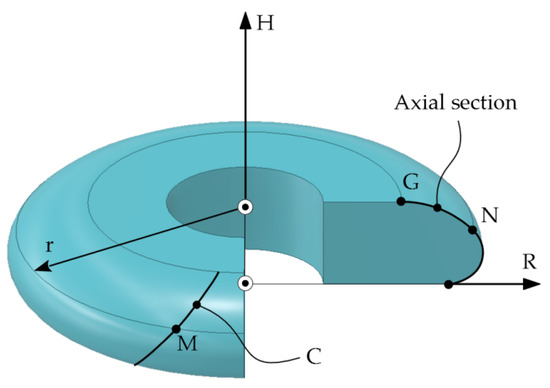
Figure 22.
Axial section of the disc tool.
The points M and N on the characteristic curve C and the generator G are on the same parallel circle. The radius of the circle is determined by the relation:
Therefore, the parametric equations of the generator G are determined:
2.9.2. Generating of Helical Surfaces with Cylindrical-Front Tool—Profiling Algorithm
According to Figure 23, the helical surface Σ is known, this being determined in the helical movement (V, ω, p) of the generating curve, G, [2].
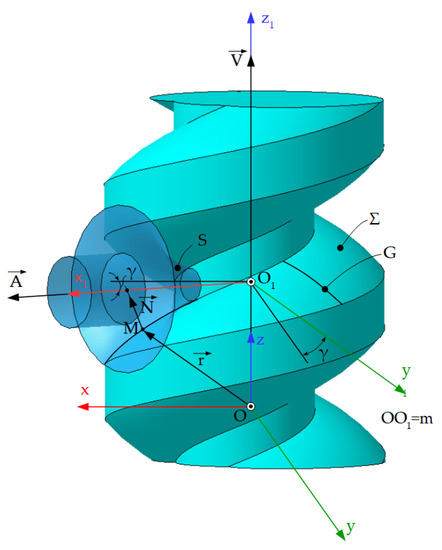
Figure 23.
Generating with cylinder-front surface; reference systems: z represents the fixed reference system, with the z axis superimposed on the surface axis Σ; xz1—fixed reference system, the x1 axis being superimposed on the axis of the searched surface, S.
It is required to determine a rotation surface, S, with the axis perpendicular to the axis of the Σ surface. This surface is obtained from the condition that the Σ surface is the envelope of the (S) family in the helical movement and admits a common characteristic with the helical surface, Σ.
The S surface performs the following movements:
- -
- Rotational movement around its own axis, constituting the cutting movement;
- -
- Helical movement of the axis and parameter p (the movement of generating the helical surface).
The normal to the Σ surface is perpendicular to the velocity vector and must be in the axial plane of the S surface.
Thus, for determination of the characteristic curve common to the reciprocally enveloping surfaces, the definition can be accepted: “the characteristic of a rotating surface, having the axis perpendicular to the axis of the helical surface with which it is reciprocally enveloping, represents the geometric locus of the points on the helical surface, where its normal intersects the axis of the rotating surface” [2].
According to Figure 23, the coordinate systems are defined.
In the xyz coordinate system, the parametric equations of the Σ surface are known in for given by Equation (80).
The position of the axis of the rotation surface of axis is also known:
The vector of the current point on the Σ surface is determined by the relation (81).
At the same point, the normal to the helical surface Σ is given by (69).
The vector is calculated as follows:
where the m parameter is arbitrary and establishes a convenient position of the axis towards to the Σ surface.
The condition of coplanarity is given by (84), or, after replacement:
By development, it results the condition for determining the characteristic curve of form:
Equations (54) and (95) define the equations of the characteristic curve C, common to the surfaces S and Σ.
If it is chosen that the origins O and O1 of the reference systems coincide and that the axis is parallel, for example, with the x-axis, then the relation (95) becomes:
If a connection is established between the parameters u and v, of form u = u(v), then the equations of the characteristic curve will be in form (52):
By relating the equations from the relation (97) to the reference system x1y1z1, joined with the S surface, the transformation of coordinates is obtained:
Thus, the parametric equations of the characteristic curve will be brought, in principle, to the form:
The peripheral surface of the finger cutter tool is obtained by rotating the characteristic around the axis
According to Figure 24, the points M and N on the characteristic curve and on the generator are at the same distance from the surface axis x1 (with x1 axis superimposed on the H axis).
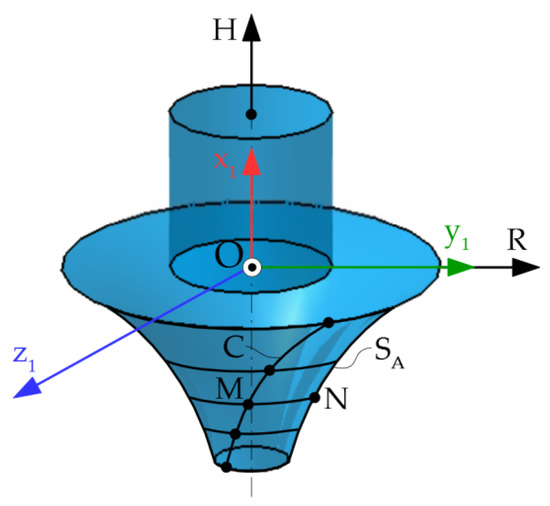
Figure 24.
Axial section.
The radius of the parallel circle is determined by the equation:
where y1(v) and z1(v) have the meanings given by the Equation (99).
Therefore, the parametric equations of the axial section, SA, are given by the relation:
2.9.3. Generating of Helical Surfaces with Cylindrical Tools—Profiling Algorithm
The problem involves knowing the helical surface Σ, obtained by the helical movement of the generating curve, G and determining a cylindrical surface, S, generated in the directional movement by the edge of a planing tool, Figure 25 [2,12].
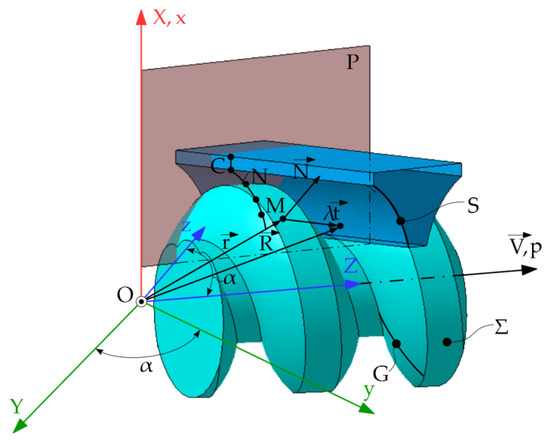
Figure 25.
Generating with cylindrical tools.
The S surface is determined from the condition that the surface is the envelope of the (S) family, in the helical movement of axis and parameter p. Therefore, the S surface admits a contact curve with the helical surface, this curve being the characteristic curve, C.
Therefore, the cylindrical tool must perform the following movements:
- -
- Translational movement along the own generators, which constitutes the cutting movement;
- -
- Helical movement, identical with the movement of generating the helical surface by the generator, G.
The determination of the characteristic curve assumes that the normal to the Σ surface is perpendicular to the direction of velocity, in the translational movement along the generators of the S surface, therefore the condition for determining the characteristic curve of the reciprocally enveloping surfaces, Σ and S can be stated as follows: “the characteristic of the helically enwrapping surface with a cylindrical surface is the geometric locus of the points on the helical surface, where the normal to it is perpendicular to the direction of the cylindrical surface generators”.
In the xyz coordinate system, the Σ surface is known in form (80), the direction versor of the generators of the cylindrical surface is expressed in the form
where α represents the angle that the generators make with the axis
If denoted by the normal at the current point on the helical Σ surface, having the Equation (69), then, taking into account the Equations (80) and (81), the condition for determining the characteristic C, is expressed in the form:
or, after replacing:
Equations (80) and (103) represent the parametric equations of the characteristic curve C on the helical surface, Σ.
The Equation (103) determines a connection between the parameters u and v of the form u = u(v), so that the parametric equations of the characteristic C can be expressed as in (97).
Characteristic C from Figure 25 together with the versor generates the S surface, which is in fact the searched surface.
The equation of the S surface, in vector form, is where λ is a variable parameter and the vector of a point on the characteristic curve.
The parametric equations of the cylindrical surface, S, are:
The cross section, ST, of the S surface determines the form of the template with which the profile of the planing cutter is controlled.
Therefore, it is considered a plane containing the x-axis and is perpendicular to the direction of the versor denoted by P.
The equation of the P plane is:
where represents the position vector of a current point in the P plane calculated by the relation:
After replacing the vectors, it results:
Equations (104) and (107) represent the parametric equations of the cross section of the cylindrical surface, S, the G curve:
By coordinate transformation, changing the reference system, from xyz to x1y1z1, the equations of the cross section take the form:
Taking into account the equation in relation (109), the parametric equations of the cross section, S are determined:
Equation (110) is the profile of the planing cutter that performs a translational movement, representing the cutting movement, according to the direction of the versor
3. Conclusions
The generating of surfaces by enwrapping presupposes the existence of specific methodologies for solving the problem of profiling generating tools.
The profiling of the tools for generating by enwrapping can be done using the fundamental theorems, applied in the conditions in which the surfaces are considered non-deformable.
These theorems have a high degree of generality and mathematical rigor, but can sometimes be difficult to apply. The way of expressing the enwrapping conditions leads, in many of the practical cases, to laborious analytical calculations and to complicated analytical forms of expression of the equations of the enwrapping surfaces.
This led to the development of complementary methods, characterized by a simpler expression of the enwrapping conditions.
Complementary methods are methods that use the direct way of expressing the enwrapping conditions and treat problems specific to the generating of reciprocally enwrapping surfaces.
These methods have a simpler form of expression, but a lower degree of generality.
The paper presented a review on study methods for reciprocally enwrapping surfaces, as well as methods for profiling tools for generating helical surfaces by the kinematic method and by the Nicolaev condition, forming a basis for future research papers and projects.
Author Contributions
Conceptualization, N.O., V.G.T. and N.B.; methodology, N.O. and V.G.T.; validation, N.B., V.G.T., N.O. and V.P.; formal analysis, N.O.; investigation, G.A.M.; resources, N.O., V.P., V.G.T. and N.B.; writing—original draft preparation, G.A.M.; writing—review and editing, G.A.M.; visualization, N.B. and V.G.T.; supervision, N.O.; project administration, V.G.T. and N.B.; funding acquisition, G.A.M. All authors have read and agreed to the published version of the manuscript.
Funding
Academic excellence and entrepreneurial values—scholarship system to ensure opportunities for training and development of entrepreneurial skills of doctoral and postdoctoral students—ANTREPRENORDOC, POCU project/380/6/13, contract number 36355/23.05.2019 HRD OP /380/6/13 SMIS Code: 123847 http://www.antreprenordoc.ugal.ro/index.php/ro/ (accessed on 1 December 2021).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work is supported by the project ANTREPRENORDOC, in the framework of Human Resources Development Operational Programme 2014–2020, financed from the European Social Fund under the contract number 36355/23.05.2019 HRD OP /380/6/13–SMIS Code: 123847.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Radzevich, S.P. Kinematics Geometry of Surface Machining; CRC Press: London, UK, 2008. [Google Scholar]
- Oancea, N. Surfaces Generation through Winding, Vol. I–III; Galati University Press: Galati, Romania, 2004. [Google Scholar]
- Cioară, R. Kinematic Structures for Processing of Surfaces with a Circle Directrix and a Straight Line Generatrix (Part IV). IOP Conf. Ser. Mater. Sci. Eng. 2016, 161, 1–8. [Google Scholar]
- Airy, G.B. On the Forms of the Teeth of Wheels. Trans. Camb. Philos. Soc. 1827, 2, 277–286. [Google Scholar]
- Figliolini, G.; Stachel, H.; Angeles, J. Kinematic Properties of Planar and Spherical Logarithmic Spirals: Applications to the Synthesis of Involute Tooth Profiles. Mech. Mach. Theory 2019, 136, 14–26. [Google Scholar] [CrossRef]
- He, F.; Shi, Z.; Yu, B. Effects of Tooth Surface Modification on Planar Double-Enveloping Hourglass Worm Gear Drives. J. Adv. Mech. Des. Syst. Manuf. 2018, 12, 1–13. [Google Scholar] [CrossRef]
- Stanieck, R. Shaping of Face Toothing in Flat Spiroid Gears. J. Mech. Eng. 2011, 57, 47–54. [Google Scholar] [CrossRef]
- Totolici, S.; Teodor, V.G.; Baroiu, N.; Oancea, N. A New Profile for the Worm Gear Drive of a Spiral Gear. IOP Conf. Ser. Mater. Sci. Eng. 2018, 400, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Carmo, M.P. Differential Geometry of Curves and Surfaces; Courier Dover Publications: New York, NY, USA, 2016. [Google Scholar]
- Phillips, J. General Spatial Involute Gearing; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2003. [Google Scholar]
- Litvin, F.L. Theory of Gearing, Reference Publication 1212; NASA, Scientific and Technical Information Division: Washington, DC, USA, 1984. [Google Scholar]
- Teodor, V.G. Contributions to the Elaboration of a Method for Profiling Tools. Tools Which Generate by Enwrapping; Lambert Academic Publishing: Saarbrücken, Germany, 2010. [Google Scholar]
- Chan, C.L.; Ting, K.L. Extended Camus Theory and Higher Order Conjugated Curves. J. Mech. Robot. 2019, 11, 1–9. [Google Scholar] [CrossRef]
- Dana-Picard, T.; Zehavi, N. Automated study of envelopes of one-parameter families of surfaces. Springer Proc. Math. Stat. 2017, 198, 29–44. [Google Scholar]
- Dooner, D.B. On the Third Law of Gearing: A Study on Hypoid Gear Tooth Contact. Mech. Mach. Theory 2019, 134, 224–248. [Google Scholar] [CrossRef]
- Guo, Q.; Qing, G.G.; Jiang, Y. An Analytic Method of Computing the Envelope Surface of General Cutter with Runout in 5-axis Machining for Manufacturing Systems. J. Chin. Soc. Mech. Eng. 2017, 38, 403–412. [Google Scholar]
- Ding, H.; Zhou, Y.S.; Tang, J.Y.; Zhong, J.; Zhou, Z.; Wan, G. A Novel Operation Approach to Determine Initial Contact Point for Tooth Contact Analysis with Errors of Spiral Bevel and Hypoid Gears. Mech. Mach. Theory 2017, 109, 155–170. [Google Scholar] [CrossRef]
- Albu, S.C. Simulation of Processing of a Helical Surface with the Aid of a Frontal-Cylindrical Milling Tool. Procedia Manuf. 2019, 32, 36–41. [Google Scholar] [CrossRef]
- Huai, C.; Zhao, Y. Meshing Theory and Tooth Profile Geometry of Toroidal Surface Enveloping Conical Worm Drive. Mech. Mach. Theory. 2019, 134, 476–498. [Google Scholar] [CrossRef]
- Jia, K.; Zheng, S.; Guo, J.; Hong, J. A Surface Enveloping-Assisted Approach on Cutting Edge Calculation and Machining Process Simulation for Skiving. Int. J. Adv. Manuf. Technol. 2019, 100, 1635–1645. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, H.; Yu, G.; Wang, S. A Novel CNC Machining Method for Enveloping Surface. Int. J. Adv. Manuf. Technol. 2016, 85, 779–790. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, Q.; Liu, N.; Song, J. A Profile Error Compensation Method in Precision Grinding of Screw Rotors. Int. J. Adv. Manuf. Technol. 2019, 100, 2557–2567. [Google Scholar] [CrossRef]
- Meng, Q.; Zhao, Y.; Yang, Z. Meshing Limit Line of the Conical Surface Enveloping Conical Worm Pair. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 693–703. [Google Scholar] [CrossRef]
- Meng, Q.; Zhao, Y.; Yang, Z.; Cui, J. Meshing Theory and Error Sensitivity of Mismatched Conical Surface Enveloping Conical Worm Pair. Mech. Mach. Theory 2020, 145, 103681. [Google Scholar] [CrossRef]
- Yang, J.; Li, H.; Rui, C.; Wei, W.; Dong, X. A Method to Generate the Spiral Flutes of an Hourglass Worm Gear Hob. J. Mech. Des. Trans. ASME 2018, 140, 1–12. [Google Scholar] [CrossRef]
- Zhao, Y.; Kong, X. Meshing Principle of Conical Surface Enveloping Spiroid Drive. Mech. Mach. Theory 2018, 123, 1–26. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, Y.; Wang, L.; Tang, J.; Ouyang, H. A New Closed-Form Calculation of Envelope Surface for Modeling Face Gears. Mech. Mach. Theory 2019, 137, 211–226. [Google Scholar] [CrossRef]
- Berbinschi, S.; Teodor, V.G.; Baroiu, N.; Oancea, N. The Substitutive Circles Family Method-Graphical Aproach in CATIA Design Environment. Ann. Dunarea Jos Univ. Galati Fascicle V Technol. Mach. Build. 2013, 1, 53–66. [Google Scholar]
- Baroiu, N.; Berbinschi, S.; Teodor, V.G.; Oancea, N. Comparative Study of Drill’s Flank Geometry Developed with the CATIA Software. Ann. Dunarea Jos Univ. Galati Fascicle V Technol. Mach. Build. 2012, 1, 27–32. [Google Scholar]
- Baroiu, N.; Berbinschi, S.; Teodor, V.G.; Susac, F.; Oancea, N. The Complementary Graphical Method used for Profiling Side Mill for Generation of Helical Surface. In Proceedings of the IOP Conf. Series: Materials Science and Engineering, 2017, 227, ModTech International Conference Modern Technologies in Industrial Engineering, Sibiu, Romania, 14–17 June 2017. [Google Scholar]
- Baroiu, N.; Baroiu, L.; Teodor, V.G.; Ciocan, T.L. Graphical Method for Profiling the Side Mill which Generate Helical Flute of Tungsten Carbide Dental Cross Cut Bur. Rom. J. Mater. 2018, 48, 131–139. [Google Scholar]
- Berbinschi, S.; Teodor, V.G.; Oancea, N. 3D Graphical Method for Profiling Gear Hob Tools. Int. J. Adv. Manuf. Technol. 2013, 64, 291–304. [Google Scholar] [CrossRef]
- Berbinschi, S.; Teodor, V.G.; Baroiu, N.; Oancea, N. Enwrapping Surfaces with Point Contact-Comparison between CATIA Method and Analytical One. Ann. Dunarea Jos Univ. Galati Fascicle V Technol. Mach. Build. 2011, 2, 117–122. [Google Scholar]
- Berbinschi, S.; Teodor, V.G.; Frumuşanu, G.R.; Oancea, N. Graphical Method for Profiling the Tools which Generate Internal Surfaces by Rolling. Acad. J. Manuf. Eng. 2014, 12, 12–17. [Google Scholar]
- Berbinschi, S.; Teodor, V.G.; Oancea, N. A Graphical Method Developed in CATIA Design Environment for the Modeling of Generation by Enveloping. Ann. Dunarea Jos Univ. Galati Fascicle V Technol. Mach. Build. 2011, 1, 25–30. [Google Scholar]
- Berbinschi, S.; Baroiu, N.; Teodor, V.G.; Oancea, N. Profiling Method of Side Mill for Threading Screw for Dental Implants. Adv. Mater. Res. 2014, 837, 22–27. [Google Scholar] [CrossRef]
- Teodor, V.G.; Popa, I.; Oancea, N. The profiling of End Mill and Planing Tools to Generate Helical Surfaces Known by Sampled Points. Int. J. Adv. Manuf. Technol. 2010, 51, 439–452. [Google Scholar] [CrossRef]
- Teodor, V.G.; Popa, I.; Popa, C.; Dura, G.; Oancea, N. Algorithm for Gear Hub Tool Profiling by Bezier Polynomial Approximation. The Rotary Helical Screw Compressor Case. In Proceedings of the 8th WSEAS International Conference on System Science and Simulation in Engineering (ICOSSSE’09), Genova, Italy, 17–19 October 2009. [Google Scholar]
- Baroiu, N.; Teodor, V.G.; Susac, F.; Oancea, N. Hob mill for trilobed rotor-Graphical method in CATIA. IOP Conf. Ser. Mater. Sci. Eng. 2018, 448, 1–17. [Google Scholar] [CrossRef]
- Teodor, V.G.; Baroiu, N.; Berbinschi, S.; Susac, F.; Oancea, N. A Graphical Solution in CATIA for Profiling End Mill Tool which Generates a Helical Surface. IOP Conf. Ser. Mater. Sci. Eng. 2017, 227, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Teodor, V.G.; Baroiu, N.; Susac, F. The Synthesis of New Algorithms for CAD Profiling of Cutting Tools; Lambert Academic Publishing: Saarbrücken, Germany, 2018. [Google Scholar]
- Baroiu, N.; Teodor, V.G.; Susac, F.; Oancea, N. Hob Mill Profiling Method for Generation of Timing Belt Pulley. In Proceedings of the 5th International Conference on Advanced Manufacturing and Technologies (NewTech), Belgrade, Serbia, 6–9 June 2017; pp. 13–26. [Google Scholar]
- Hong, X.; Hong, R.; Lin, X. Tool Orientations’ Generation and Nonlinear Error Control based on Complex Surface Meshing. Int. J. Adv. Manuf. Technol. 2019, 105, 4279–4288. [Google Scholar] [CrossRef]
- Wang, Q.; Feng, Y.; Gao, Y.; Li, Z.; Tan, J. Smooth Fillet-End Cutter Tool Path Generation Method on Triangular-Mesh Surface Based on Modified Butterfly Subdivision. Int. J. Adv. Manuf. Technol. 2018, 98, 2831–2847. [Google Scholar] [CrossRef]
- Cera, M.; Pennestrì, E. The Mechanical Generation of Planar Curves by Means of Point Trajectories, Line and Circle Envelopes: A Unified Treatment of the Classic and Generalized Burmester Problem. Mech. Mach. Theory 2019, 142, 103580. [Google Scholar] [CrossRef]
- Cera, M.; Pennestrì, E. Higher-order curvature analysis of planar curves enveloped by straight-lines. Mech. Mach. Theory 2019, 134, 213–223. [Google Scholar] [CrossRef]
- Gouchao, L.; Sun, J.; Jianfeng, L. Process Modeling of End Mill Groove Machining Based on Boolean Method. Int. J. Adv. Manuf. Technol. 2014, 57, 959–966. [Google Scholar]
- Guo, Q.; Sun, Y.; Jiang, Y.; Yan, Y.; Zhao, B.; Ming, P. Tool Path Optimization for Five-Axis Flank Milling with Cutter Runout Effect Using the Theory of Envelope Surface Based on CL Data for General Tools. J. Manuf. Syst. 2016, 38, 87–97. [Google Scholar] [CrossRef]
- Liu, G.; Wei, W.; Dong, X.; Rui, C.; Liu, P.; Li, H. Relief Grinding of Planar Double-Enveloping Worm Gear Hob Using a Four-Axis CNC Grinding Machine. Int. J. Adv. Manuf. Technol. 2016, 89, 9–12. [Google Scholar] [CrossRef]
- Nieszporek, T.; Boral, P.; Gołȩbski, R. Particular Solution of Cutting Tool Path Applied on Helical Surface with Circular Profile. Teh. Vjesn. 2019, 26, 22–28. [Google Scholar]
- Oancea, N. Méthode numérique pour l’étude des surfaces enveloppées. Mech. Mach. Theory 1996, 31, 957–972. [Google Scholar]
- Dooner, D.B.; Griffis, M.W. On spatial Euler-Savary Equations for Envelopes. J. Mech. Des. Trans. ASME 2007, 129, 865–875. [Google Scholar] [CrossRef]
- Berbinschi, S.; Teodor, V.G.; Oancea, N. A 3D Method for Profiling the Shaping Tool for the Generation of Helical Surfaces. Ann. Dunarea Jos Univ. Galati Fascicle V Technol. Mach. Build. 2011, 1, 19–24. [Google Scholar]
- Baroiu, N.; Teodor, V.G.; Oancea, N. A New Form of Plane Trajectories Theorem. Generation with Rotary Cutter. Bull. Polytech. Inst. Iasi 2015, 3, 27–36. [Google Scholar]
- Baroiu, N.; Teodor, V.G.; Popa, C.; Oancea, N. Gear Shaped Cutter–A Profiling Method Developed in Graphical Form. Ann. Dunarea Jos Univ. Galati Fascicle V Technol. Mach. Build. 2015, 33, 9–16. [Google Scholar]
- Teodor, V.G.; Baroiu, N.; Susac, F.; Oancea, N. The Modelling of Involute Teeth Generation with the Relative Generating Trajectories Method. Acad. J. Manuf. Eng. 2016, 14, 126–131. [Google Scholar]
- Teodor, V.G.; Baroiu, N.; Susac, F.; Oancea, N. The Rack-Gear Tool Generation Modelling. Non-Analytical Method Developed in CATIA, Using the Relative Generating Trajectories Method. IOP Conf. Ser. Mater. Sci. Eng. 2016, 161, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Teodor, V.G.; Păunoiu, V.; Berbinschi, S.; Baroiu, N.; Oancea, N. The Method of ”In-Plane Generating Trajectories” for Tools Which Generate By Enveloping-Application in CATIA. J. Mach. Eng. 2015, 15, 69–80. [Google Scholar]
- Berbinschi, S.; Frumuşanu, G.; Teodor, V.G.; Oancea, N. The method of substitutive circles family. Application in CATIA design environment for gear shaped tool profiling. Adv. Mater. Res. 2014, 1036, 370–375. [Google Scholar] [CrossRef]
- Berbinschi, S.; Teodor, V.G.; Frumușanu, G.R.; Oancea, N. The pinion cutter for profiled holes-Graphical method in CATIA. Appl. Mech. Mater. 2014, 657, 720–724. [Google Scholar] [CrossRef]
- Teodor, V.G.; Berbinschi, S.; Baroiu, N.; Oancea, N. Study of the Enwrapping Profiles Associated with Rolling Centrodes by the Minimum Distance Method. Graphical Solution Developed in the CATIA Design Environment. Appl. Mech. Mater. 2014, 656, 181–191. [Google Scholar] [CrossRef]
- Popa, L.C.; Popa, I.; Teodor, V.G.; Baroiu, N. Profiling Tool Generating Method using the Profile Measurement of Rotor of Screw Compressor Components. Ann. Dunarea Jos Univ. Galati Fascicle V Technol. Mach. Build. 2011, 2, 123–128. [Google Scholar]
- Baroiu, N.; Moroșanu, G.A.; Teodor, V.G.; Oancea, N. Roller Profiling for Generating the Screw of a Pump with Progressive Cavities. Inventions 2021, 6, 34. [Google Scholar] [CrossRef]
- Bo, P.; Bartoň, M.; Plakhotnik, D.; Pottmann, H. Towards efficient 5-axis flank CNC machining of free-form surfaces via fitting envelopes of surfaces of revolution. Comput. -Aided Des. 2016, 79, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Wang, D. Curvature Theory of Envelope Curve in Two-Dimensional Motion and Envelope Surface in Three-Dimensional Motion. J. Mech. Robot. 2015, 7, 1–9. [Google Scholar] [CrossRef]
- Zanger, F.; Sellmeier, V.; Klose, J.; Bartkowiak, M.; Schulze, V. Comparison of Modeling Methods to Determine Cutting Tool Profile for Conventional and Synchronized Whirling. Procedia CIRP 2017, 58, 222–227. [Google Scholar] [CrossRef]
- Hu, P.; Chen, L.; Tang, K. Efficiency-Optimal Iso-Planar Tool Path Generation for Five-Axis Finishing Machining of Freeform Surfaces. Comput. -Aided Des. 2018, 83, 33–50. [Google Scholar] [CrossRef]
- Berbinschi, S.; Teodor, V.G.; Baroiu, N.; Oancea, N. Profiling Methodology for Side Mill Tools for Generation of Helical Compressor Rotor Using Reverse Engineering. Ann. Dunarea Jos Univ. Galati Fascicle V Technol. Mach. Build. 2011, 2, 111–116. [Google Scholar]
- Berbinschi, S.; Teodor, V.G.; Oancea, N. 3D Graphical Method for Profiling Tools that Generate Helical Surfaces. Int. J. Adv. Manuf. Technol. 2012, 60, 505–512. [Google Scholar] [CrossRef]
- Berbinschi, S.; Baroiu, N.; Teodor, V.G.; Oancea, N. End Mill Tool Profiling by CAD Method. Indian J. Eng. Mater. Sci. 2014, 21, 296–302. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).