Efficient Model for Accurate Assessment of Frequency Support by Large Populations of Plug-in Electric Vehicles
Abstract
:1. Introduction
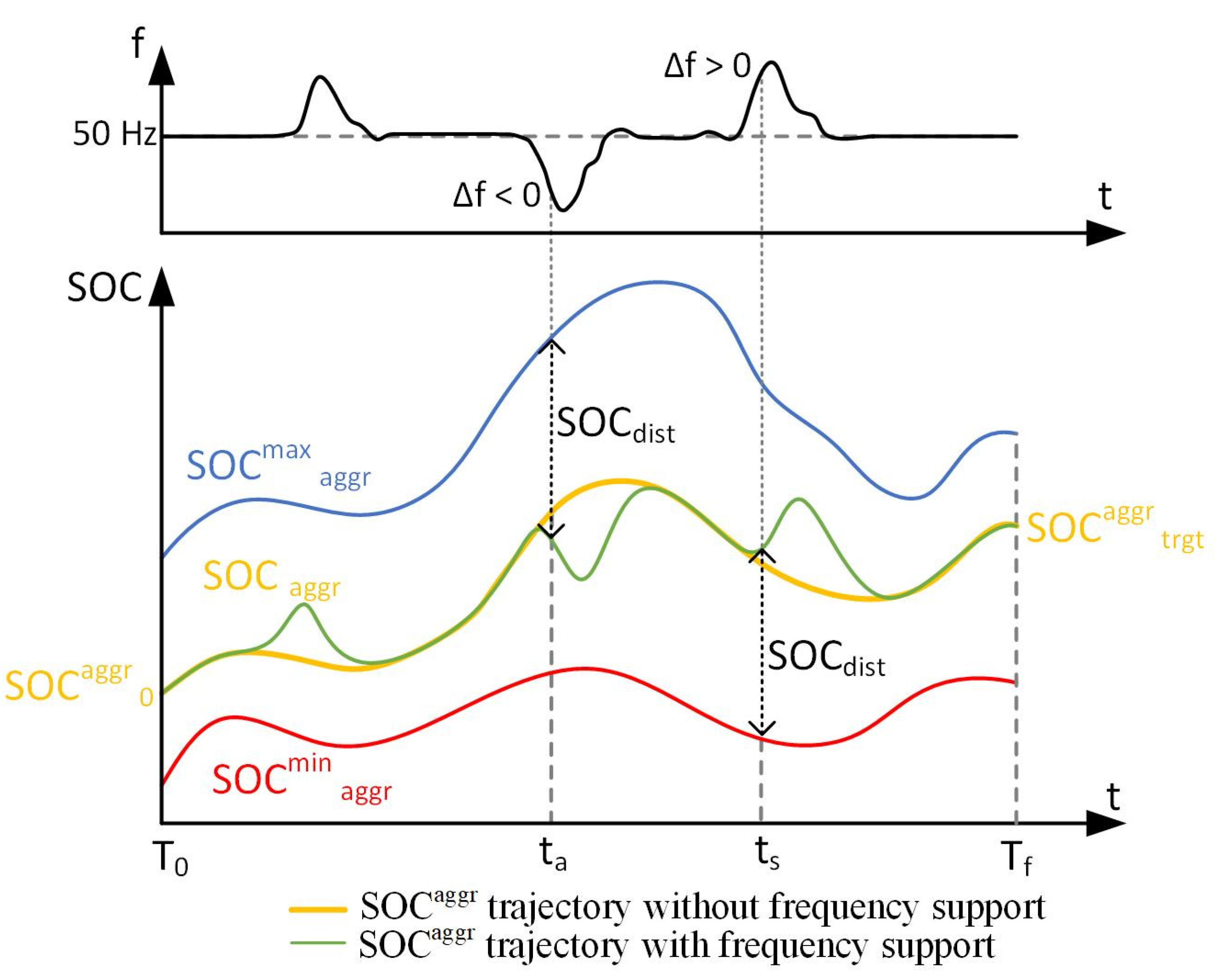
2. Formulation of the Aggregate Battery Model
- (1)
- Minimum and maximum power constraints,
- (2)
- Minimum and maximum SOC constraints,
- (3)
- Desired SOC at the end of the day,
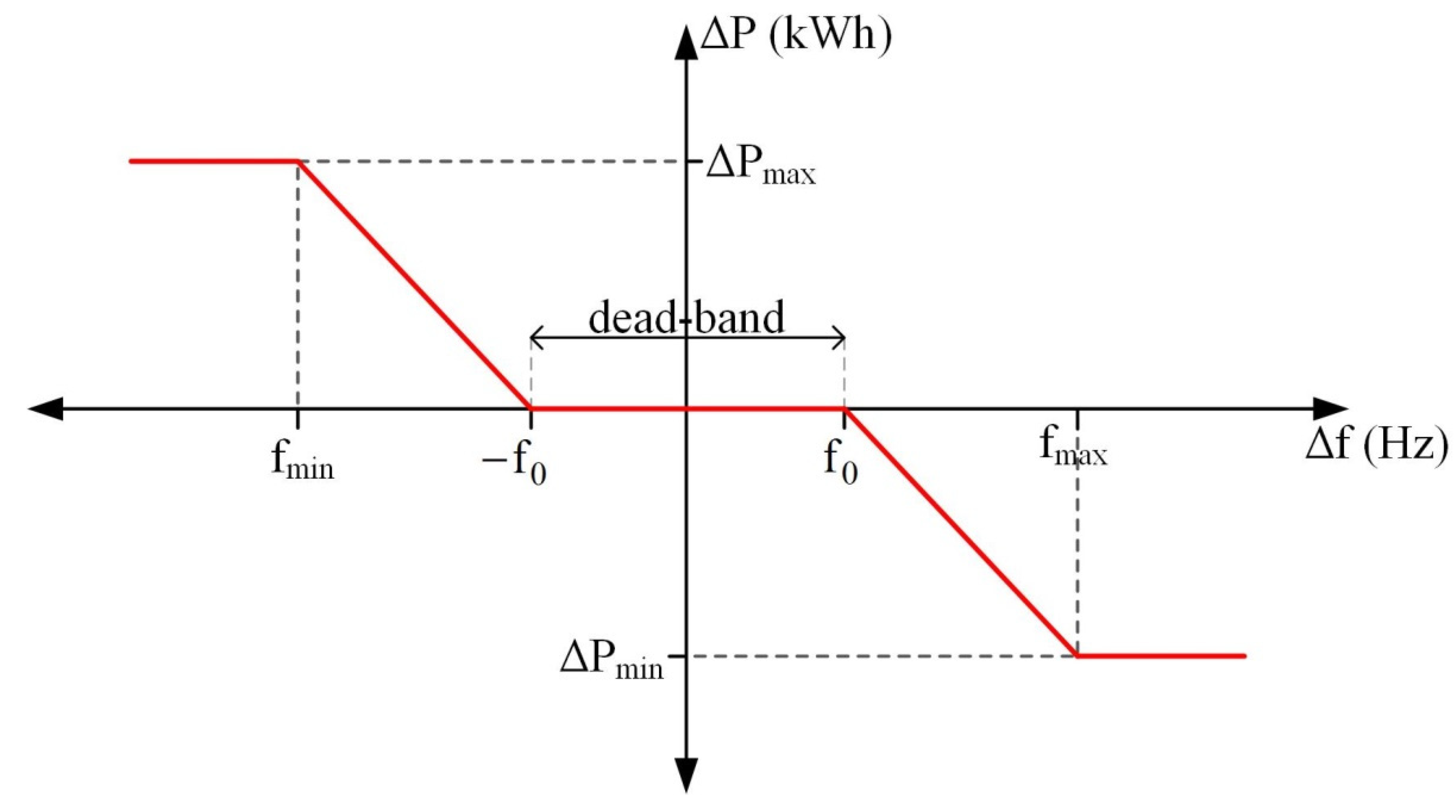
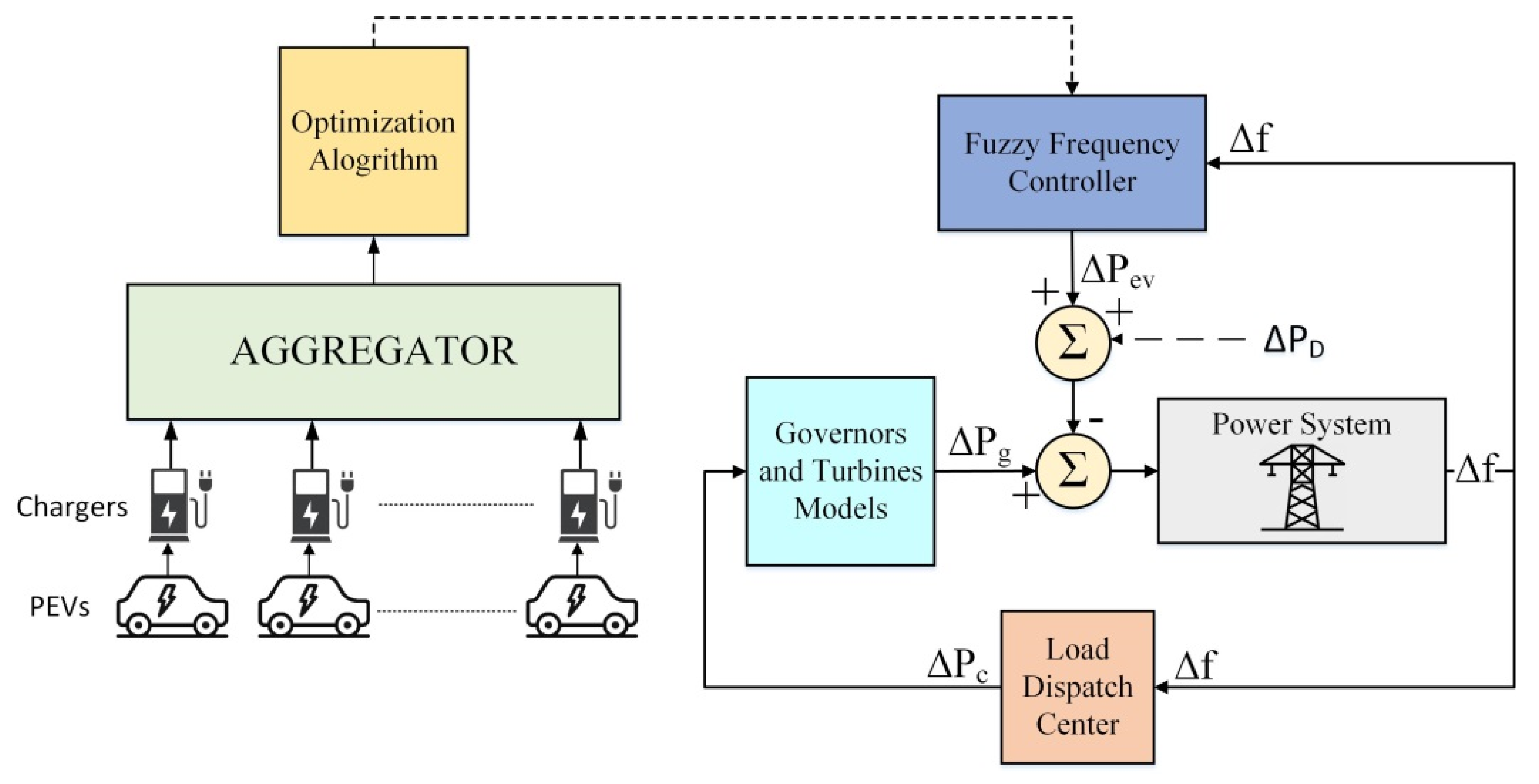
3. Frequency Support Implementation
4. Description of Power System Model
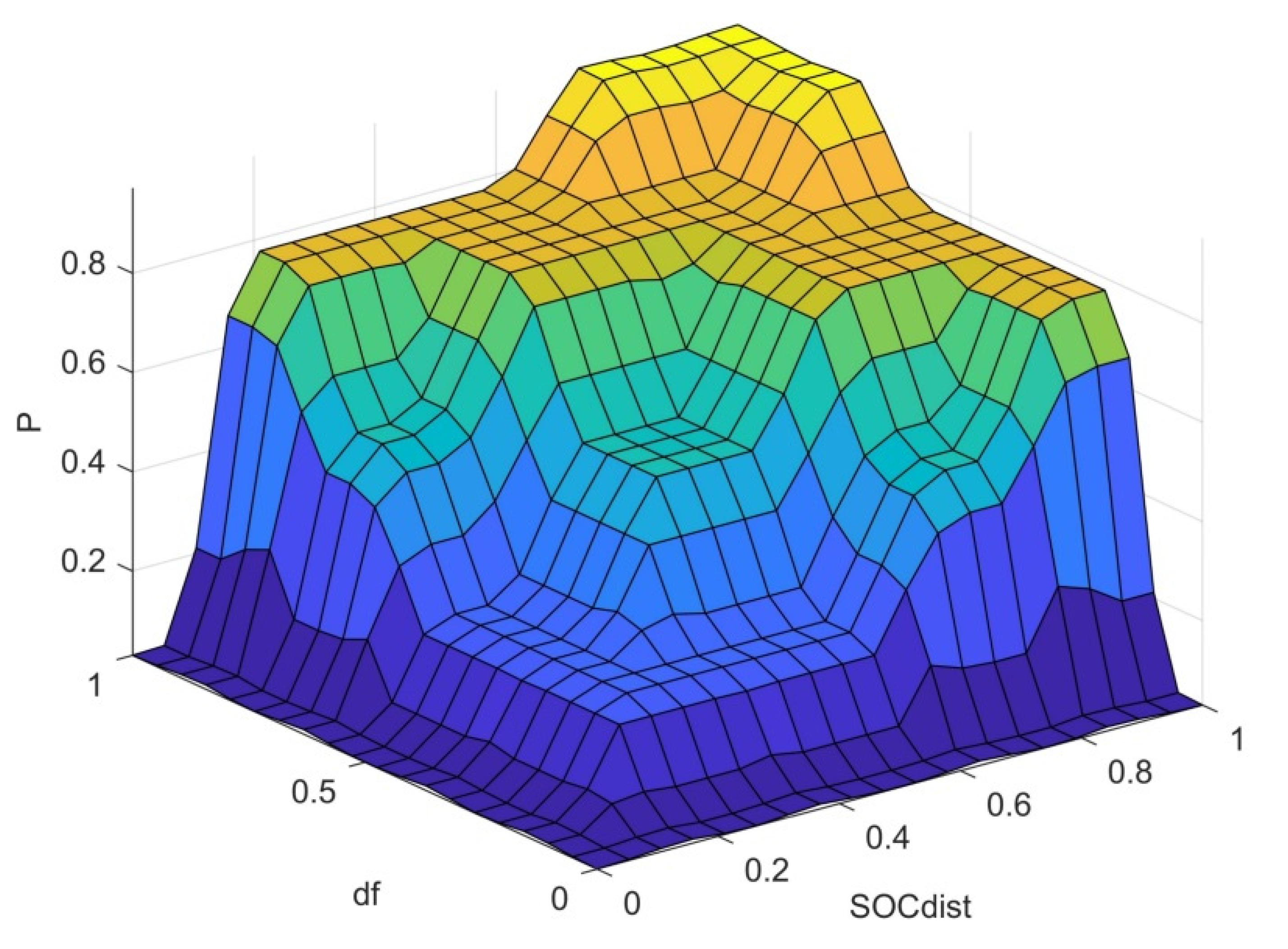
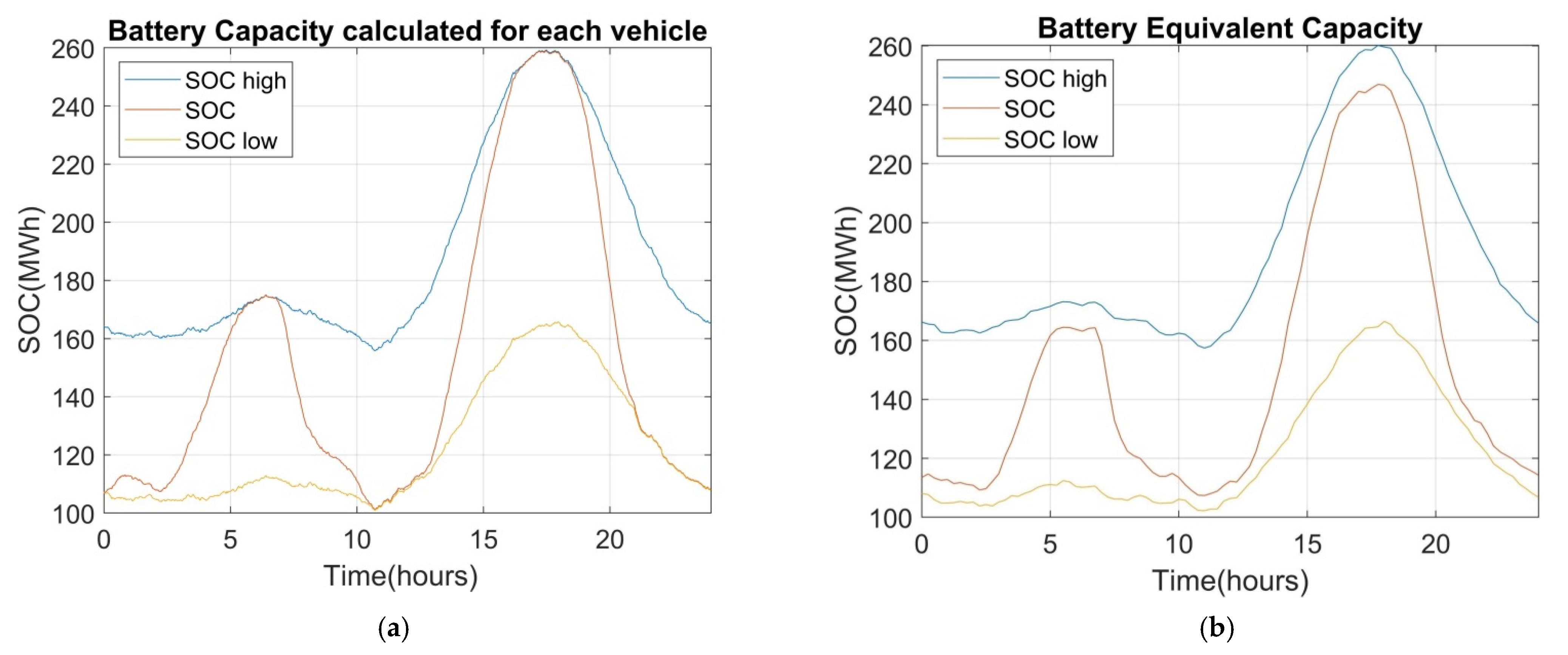
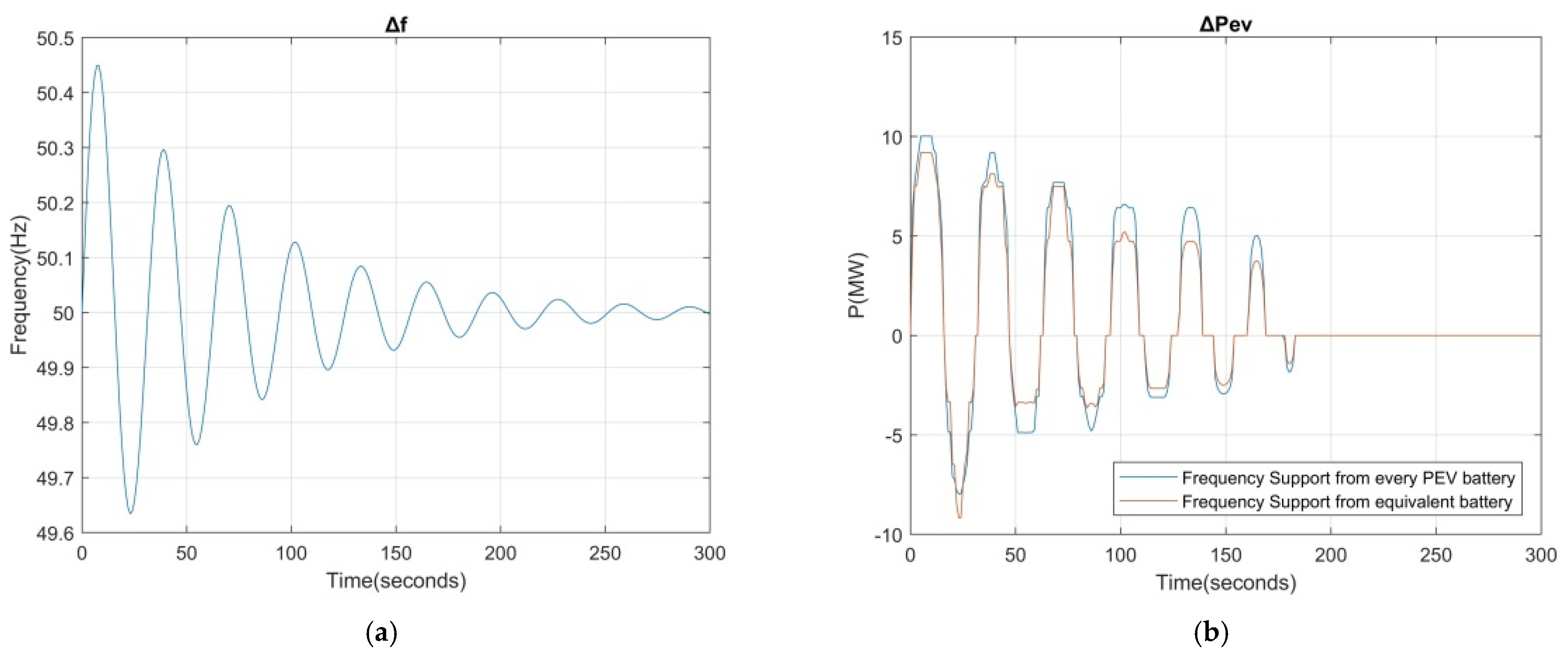
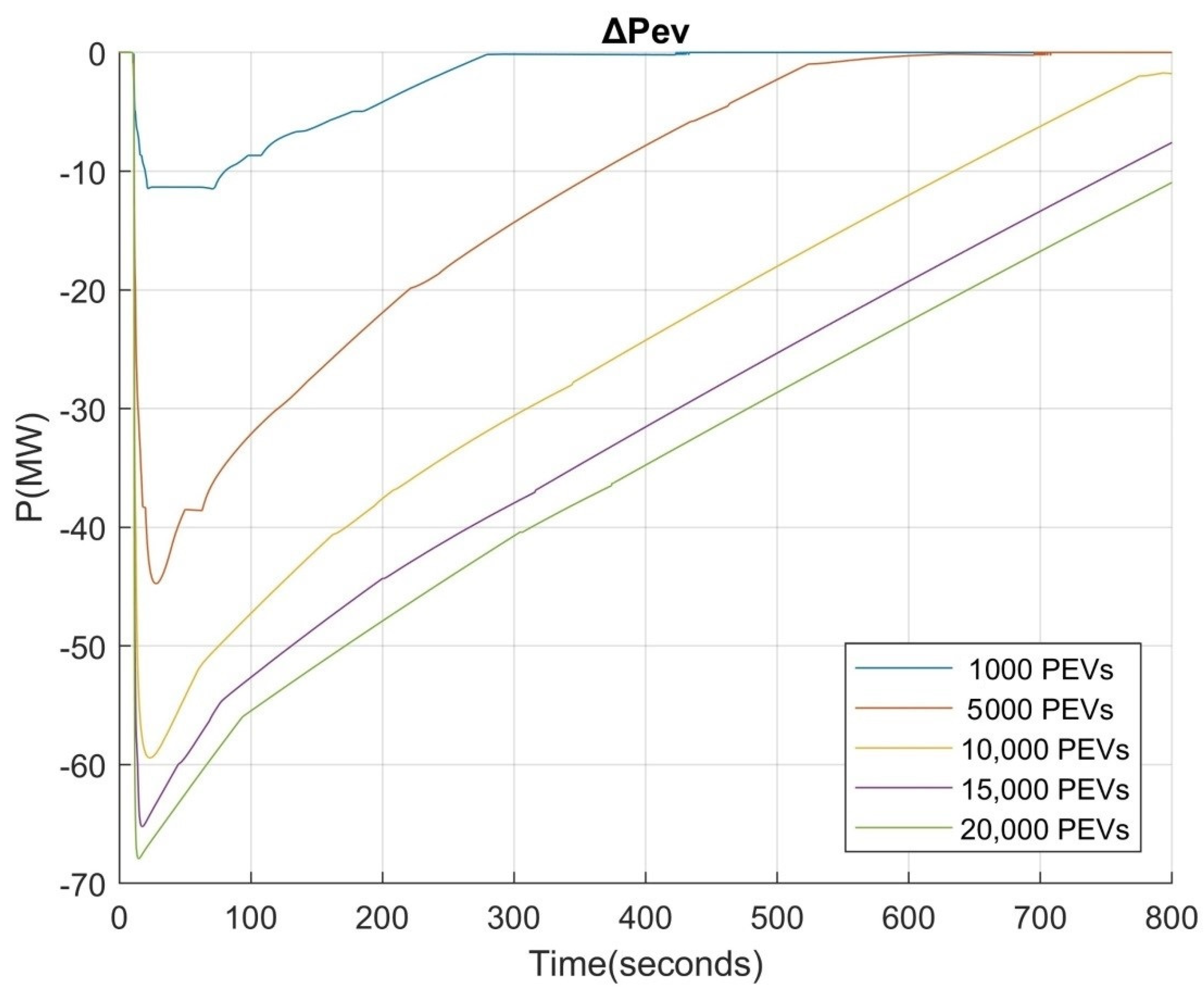
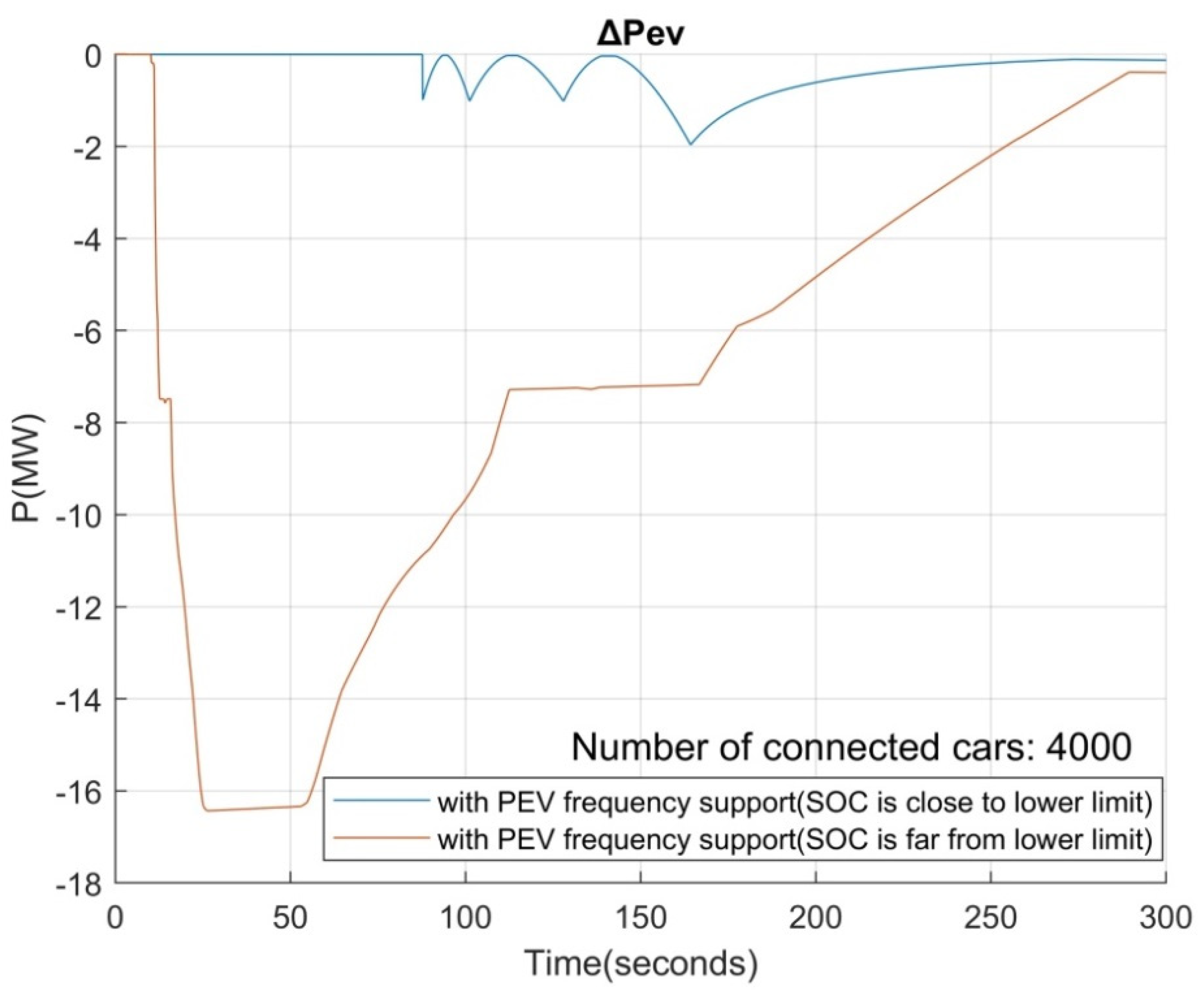
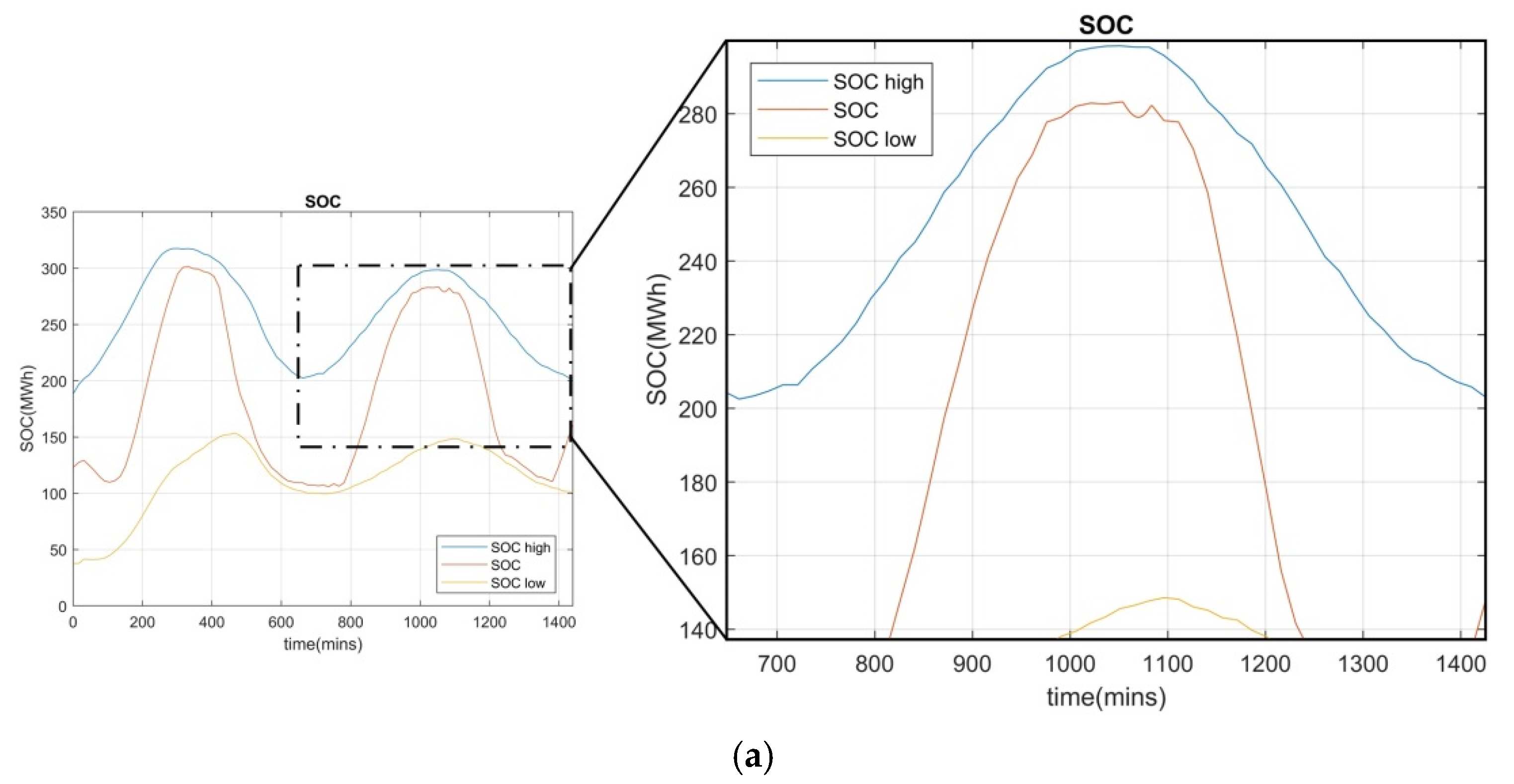
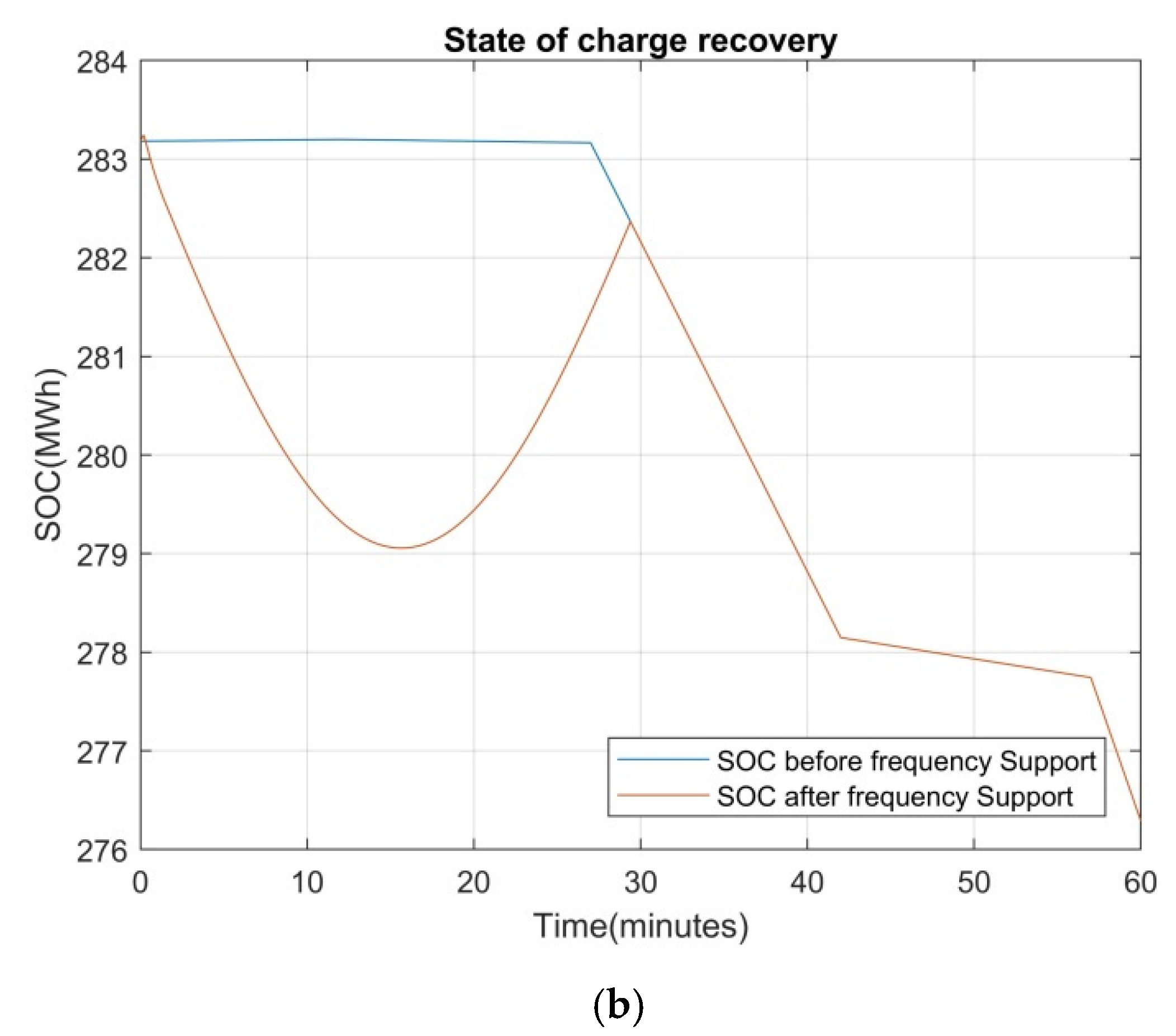
5. Case Study
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| The current time of simulation (min) | |
| The arrival time of the vehicle (min) | |
| The departure time of the vehicle (min) | |
| State of charge of PEV’s battery (kWh) | |
| Initial state of charge | |
| The maximum of PEV’s battery (kWh) | |
| The minimum of PEV’s battery (kWh) | |
| The desired at PEV’s departure time (kWh) | |
| The dynamic upper limit of PEV’s (kWh) | |
| The dynamic lower limit of PEV’s (kWh) | |
| The time that starts to converge to target or (min) | |
| The time that starts to converge to target or (min) | |
| The maximum power the PEV can exchange with the grid (kW) | |
| The minimum power the PEV can exchange with the grid (kW) | |
| The power that PEV exchanges with the grid (kW) | |
| Electricity price (EUR/kWh) | |
| Time step (min) | |
| The number of PEVs | |
| Total power change of PEVs during frequency support mode of operation (ΜW) | |
| Power demand change (ΜW) | |
| Generation power change during frequency support mode of operation (ΜW) |
References
- U.S. Energy Information Administration. Use of Energy Explained. Energy Used for Transportation. May 2019. Available online: https://www.eia.gov/energyexplained/use-of-energy/transportation.php (accessed on 10 November 2021).
- Mori, D.; Hirose, K. Recent challenges of hydrogen storage technologies for fuel cell vehicles. Int. J. Hydrogen Energy 2009, 34, 4569–4574. [Google Scholar] [CrossRef]
- Clean Energy Minestrial: EV30@30 Campaign. Available online: https://www.cleanenergyministerial.org/campaign-clean-energy-ministerial/ev3030-campaign (accessed on 10 November 2021).
- Galus, M.D.; Vaya, M.G.; Krause, T.; Andersson, G. The role of electric vehicles in smart grids. Wiley Interdiscip. Rev. Energy Environ. 2013, 2, 384–400. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of the impact of vehicle-to-grid technologies on distribution systems and utility interfaces. IEEE Trans. Power Electron. 2013, 28, 5673–5689. [Google Scholar] [CrossRef]
- Kalaitzakis, I.; Dakanalis, M.; Kanellos, F.D. Optimal Power Management for Residential PEV Chargers with Frequency Support Capability. In Proceedings of the 10th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 5–7 July 2021; pp. 1–4. [Google Scholar]
- Markel, A.J.; Bennion, K.; Kramer, W.; Bryan, J.; Giedd, J. Field Testing Plug-In Hybrid Electric Vehicles with Charge Control Technology in the Xcel Energy Territory; No. NREL-TP-550-46345; National Renewable Energy Laboratory: Golden, CO, USA, 2009.
- Energy Information Administration. Inventory of Electric Utility Power Plants in the United States 2000; DOE/EIA-0095 (2000), Table I; U.S. Department of Energy: Washington, DC, USA, 2002.
- Liu, H.; Hu, Z.; Song, Y.; Lin, J. Decentralized vehicle-to-grid control for primary frequency regulation considering charging demands. IEEE Trans. Power Syst. 2013, 28, 3480–3489. [Google Scholar] [CrossRef]
- Mu, Y.; Wu, J.; Ekanayake, J.; Jenkins, N.; Jia, H. Primary frequency response from electric vehicles in the Great Britain power system. IEEE Trans. Smart Grid 2013, 2, 1142–1150. [Google Scholar] [CrossRef]
- Kempton, W.; Tomic, J. Vehicle-to-grid power implementation: From stabilizing the grid to supporting large-scale renewable energy. J. Power Sources 2005, 1, 280–294. [Google Scholar] [CrossRef]
- Liu, H.; Qi, J.; Wang, J.; Li, P.; Wei, H. EV Dispatch Control for Supplementary Frequency Regulation Considering the Expectation of EV Owners. IEEE Trans. Smart Grid 2018, 4, 3763–3772. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Hu, Z.; Song, Y.; Wang, J.; Xie, X. Vehicle to Grid Control for Supplementary Frequency Regulation Considering charging demands. IEEE Trans. Power Syst. 2015, 6, 3110–3119. [Google Scholar] [CrossRef]
- Konstantinidis, G.; Kanellos, F.D.; Kalaitzakis, K. A simple multi-parameter method for efficient charging scheduling of electric vehicles. Appl. Syst. Innov. 2021, 4, 58. [Google Scholar] [CrossRef]
- Escudero-Garzas, J.J.; Garcia-Armada, A.; Seco-Granados, G. Fair Design of Plug-in Electric Vehicles Aggregator for V2G Regulation. IEEE Trans. Veh. Technol. 2012, 61, 3406–3419. [Google Scholar] [CrossRef] [Green Version]
- Sung, D.K.; Ko, K.S. The Effect of EV Aggregators With Time-Varying Delays on the Stability of a Load Frequency Control System. IEEE Trans. Power Syst. 2018, 1, 669–680. [Google Scholar]
- Zhang, H.; Hu, Z.; Xu, Z.; Song, Y. Evaluation of Achievable Vehicle-to-Grid Capacity Using Aggregate PEV Model. IEEE Trans. Power Syst. 2017, 1, 784–794. [Google Scholar] [CrossRef]
- Han, S.; Han, S.; Sezaki, K. Development of an optimal vehicle-to grid aggregator for frequency regulation. IEEE Trans. Smart Grid 2010, 1, 65–72. [Google Scholar]
- Wang, M.; Mu, Y.; Shi, Q.; Jia, H.; Li, F. Electric Vehicle Aggregator Modeling and Control for Frequency Regulation Considering Progressive State Recovery. IEEE Trans. Smart Grid 2020, 5, 4176–4189. [Google Scholar] [CrossRef]
- Almeida, P.R.; Soares, F.; Lopes, J.P. Electric vehicles contribution for frequency control with inertial emulation. Electr. Power Syst. Res. 2015, 127, 141–150. [Google Scholar] [CrossRef] [Green Version]
- Datta, M. Fuzzy Logic Based Frequency Control by V2G Aggregators. In Proceedings of the IEEE 5th International Symposium on Power Electronics for Distributed Generation Systems, Galway, Ireland, 24–27 June 2014. [Google Scholar]
- Falahati, S.; Taher, S.A.; Shahidehpour, M. Grid frequency control with electric vehicles by using of an optimized fuzzy controller. Appl. Energy 2016, 178, 918–928. [Google Scholar] [CrossRef]
- Lee, K.A.; Yee, H.; Teo, C. Self-tuning algorithm for automatic generation control in an interconnected power system. Electr. Power Syst. Res. 1991, 2, 157–165. [Google Scholar] [CrossRef]
- Altas, I.H.; Neyens, J. A fuzzy logic decision maker and controller for reducing load frequency oscillations in multi-area power systems. In IEEE Power Engineering Society General Meeting; IEEE: Montreal, QC, Canada, 2006. [Google Scholar]
- Kanellos, F.D. Multiagent-System-Based Operation Scheduling of Large Ports’ Power Systems with Emissions Limitation. IEEE Syst. J. 2019, 2, 1831–1840. [Google Scholar] [CrossRef]
- Dulau, M.; Bica, D. Simulation of Speed Steam Turbine Control System. In Proceedings of the 7th International Conference Interdisciplinarity in Engineering, Tirgu Mures, Romania, 10–11 October 2013; pp. 716–722. [Google Scholar]
- Caballero, R.; Duhé, J.-F. Comparative Analysis for the Load Frequency Control Problem in Steam and Hydraulic Turbines using Integral Control, Pole Placement and Linear Quadratic Regulator. Global Partnerships for Development and Engineering Education. In Proceedings of the 15th LACCEI International Multi-Conference for Engineering, Education and Technology, Boca Raton, FL, USA, 19–21 July 2017. [Google Scholar]
- Surianu, F.D. Mathematical Modelling and Numerical. Simulation of the Dynamic Behavior of Thermal and Hydro Power Plants; INTECH Open Access Publisher: Timisoara, Romania, 2012. [Google Scholar]
- Karnavas, Y.L.; Papadopoulos, D.P. Power generation control of a wind-diesel system using fuzzy logic and pi-sigma networks. In Proceedings of the 12th International Conference on Intelligent Systems Application to Power Systems (ISAP ’03), Lemnos Island, Greece, 31 August–3 September 2003. [Google Scholar]
- Wagle, R.; Pariyar, B. Mathematical Modeling of Isolated Wind-Diesel-Solar Photo Voltaic Hybrid Power System for Load Frequency Control. Int. J. Sci. Res. 2018, 7, 960–966. [Google Scholar]
- Krpan, M.; Kuzle, I. The Mathematical Model of a Wind Power Plant and a Gas Power Plant. Master’s Thesis, University of Zagreb, Faculty of Electrical Engineering and Computing, Zagreb, Croatia, September 2016. [Google Scholar]
- Barisal, A.K. Comparative performance analysis of teaching learning-based optimization for automatic load frequency control of multi-source power systems. Int. J. Electr. Power Syst. Res. 2015, 66, 67–77. [Google Scholar] [CrossRef]
- Kanellos, F.D. Optimal Scheduling and Real-Time Operation of Distribution Networks With High Penetration of Plug-In Electric Vehicles. IEEE Syst. J. 2021, 15, 3938–3947. [Google Scholar] [CrossRef]
- Santos, A.; McGuckin, N.; Nakamoto, H.Y.; Gray, D.; Liss, S. Summary of Travel Trends: 2009 National Household Travel Survey. Available online: https://nhts.ornl.gov/2009/pub/stt.pdf (accessed on 13 September 2021).
- Ramakrishna, K.S.S.; Sharma, P.; Bhatti, T.S. Automatic generation control of interconnected power system with diverse sources of power generation. Int. J. Eng. Sci. Technol. 2010, 5, 51–65. [Google Scholar] [CrossRef]

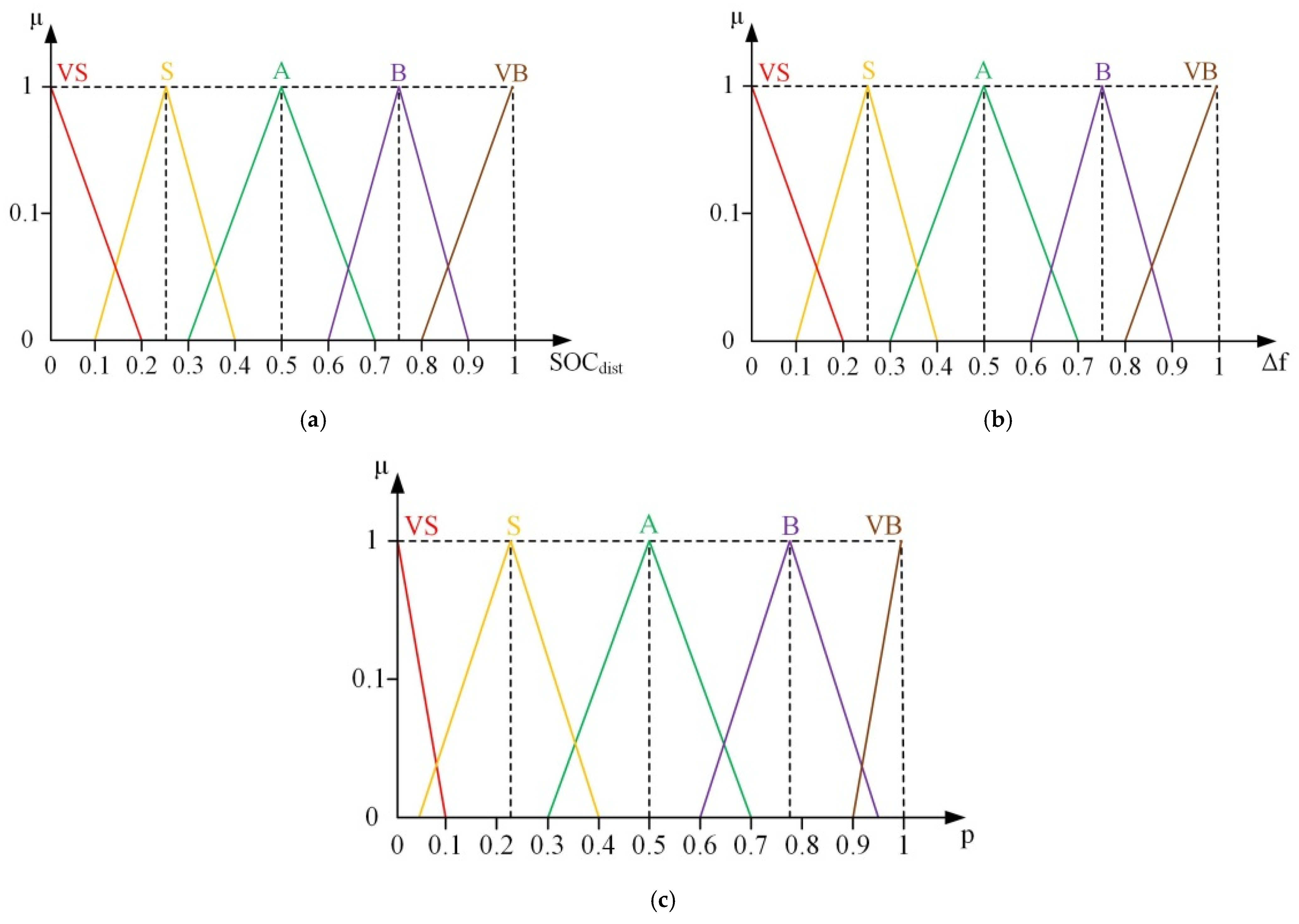




| VS | S | A | B | VB | ||
| VS | VS | VS | VS | VS | VS | |
| S | VS | S | S | M | B | |
| A | VS | S | M | B | B | |
| B | VS | M | B | B | VB | |
| VB | VS | B | B | VB | VB | |
| Price | Battery Capacity (kWh) | Nominal Power (kW) |
|---|---|---|
| Low | 35.3 | 7.3 |
| Low–medium | 51.5 | 10.25 |
| Medium | 63.9 | 9.5 |
| High–medium | 83.6 | 10.8 |
| High | 95.6 | 12.8 |
| Power Plant | Gas Turbine | Steam Turbine | Diesel Turbine | Installed Power (MW) |
|---|---|---|---|---|
| Heraklion | 118.47 | 105 | 49.12 | 272.59 |
| Chania | 302.69 | 42.5 | - | 345.19 |
| Lasithi | - | 100 | 102.24 | 202.24 |
| Total (MW) | 421.16 | 205 | 151.36 | 820.02 |
| Steam Turbine Parameters | ||
| Steam turbine governor time constant | 0.1 s | |
| Steam turbine time constant | 0.4 s | |
| Coefficient of reheat steam turbine | 0.5 | |
| Reheat time constant | 10.0 s | |
| Steam speed governor regulation parameter | 0.6 p.u. | |
| Steam turbine integral controller gain | 1 p.u. | |
| Hydraulic Turbine Parameters | ||
| Water time constant | 1 s | |
| Main servo time constant | 0.2 s | |
| Speed governor rest time | 5.0 s | |
| Transient droop time constant | 28.75 s | |
| Hydro speed governor regulation parameter | 0.25 p.u. | |
| Hydro turbine integral controller gain | 0.3 p.u. | |
| Diesel Turbine Parameters | ||
| Equivalent speed governor time constant 1 | 1.0 s | |
| Equivalent speed governor time constant 2 | 2.0 s | |
| Equivalent speed governor time constant 3 | 0.025 s | |
| Diesel turbine power generation time constant | 3.0 s | |
| Diesel turbine governor gain | 1.0 | |
| Diesel speed governor regulation parameter | 0.2 p.u. | |
| Diesel turbine integral controller gain | 0.1 p.u. | |
| Gas Turbine Parameters | ||
| Speed governor lead time constant | 0.6 s | |
| Speed governor lag time constant | 1.0 s | |
| Valve positioner constant | 1.0 | |
| Valve positioner constant | 0.05 | |
| Valve positioner constant | 1.0 | |
| Combustion reaction time delay | 0.3 s | |
| Fuel time constant | 0.23 s | |
| Compressor discharge volume time constant | 0.2 s | |
| Gas speed governor regulation parameter | 0.1 p.u. | |
| Gas turbine integral controller gain | 0.2 p.u. | |
| Power System Parameters | ||
| Power system gain | 0.06 p.u. | |
| Power system time constant | 20.0 s | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dakanalis, M.; Kanellos, F.D. Efficient Model for Accurate Assessment of Frequency Support by Large Populations of Plug-in Electric Vehicles. Inventions 2021, 6, 89. https://doi.org/10.3390/inventions6040089
Dakanalis M, Kanellos FD. Efficient Model for Accurate Assessment of Frequency Support by Large Populations of Plug-in Electric Vehicles. Inventions. 2021; 6(4):89. https://doi.org/10.3390/inventions6040089
Chicago/Turabian StyleDakanalis, Michail, and Fotios D. Kanellos. 2021. "Efficient Model for Accurate Assessment of Frequency Support by Large Populations of Plug-in Electric Vehicles" Inventions 6, no. 4: 89. https://doi.org/10.3390/inventions6040089
APA StyleDakanalis, M., & Kanellos, F. D. (2021). Efficient Model for Accurate Assessment of Frequency Support by Large Populations of Plug-in Electric Vehicles. Inventions, 6(4), 89. https://doi.org/10.3390/inventions6040089






