Determining the Initial Orientation for Navigation and Measurement Systems of Mobile Apparatus in Reforestation

Abstract

This paper considers the method of determining the initial orientation of the navigation and measuring complexes of mobile objects. The method is based on analytical gyrocompassing, using angular velocity sensors whose measurements are distorted by additive noise, with a priori uncertain statistical characteristics. The proposed approach requires small computational costs and can be effectively used in the development of high-precision systems of initial orientation of navigation–measurement systems of various mobile objects.

1. Introduction

Currently, one of the promising tendencies of contemporary reforestation is the use of Unmanned Mobile Apparatus (UMA) [1] for both ground [2] and aerial seeding [3], as well as for other reforestation operations. When used for seeding, the effectiveness of UMA depends to a significant extent on the accuracy of its positioning and spatial orientation, determined by the corresponding scheme of seeding. At the same time, accuracy of modern systems for UMA spatial orientation is largely determined by their most important component, the initial orientation systems, which is designed to provide high accuracy in determining the initial spatial orientation of the UMA’s navigation–measuring complex [4,5].

Development of a system for determining the initial azimuth of the navigation system, especially in the conditions of unavoidable interference of measurements of its Sensitive Elements (SE), represents the main problem in the construction of initial orientation systems. One of the most promising ways to solve this problem is the development of algorithms for processing measurements of inertial SE, which are part of the UMA’s navigation–measuring complex, in particular, Angular Velocity Sensors (AVS). To date, various ways of using AVS for solving the problem of azimuthal orientation have been developed [6,7], with gyrocompassing as one of the most effective methods. Currently, there are various options for implementing this method using AVS. The first group of methods consisting of a sequential change in the orientation of the AVS, with subsequent measurements of various parameters of its output signal, are described in [8,9,10]. Their significant disadvantages are the complexity of measurements and the possibility of using only gyroscopic AVS. The second group of gyrocompassing methods using AVS consists of a reverse change in the AVS sensitivity axis relative to the plane of the local meridian, followed by summation of the measurement signals [11,12]. The problem with these methods is the impossibility of compensation for broadband random noise measurements and low accuracy of determining the direction of the local meridian. Finally, there is a gyrocompassing method consisting of the sequential rotation, the axis of sensitivity of the AVS relative to the direction of the local meridian for the specified angles [13], with subsequent determination of the direction of the local meridian to the maximum of the output signal. The disadvantage of this method is the low accuracy due to the difficulty in determining the true maximum caused by unsteady random noise, with a priori uncertain statistical characteristics in the output AVS signal.

2. Task Definition

This paper aims to offer a new approach for solving the problem of developing a gyrocompassing algorithm using AVS, which provides high accuracy in determining the initial azimuth of the UMA’s navigation–measuring complex in conditions of unavoidable interference of angular velocity measurements, with a priori uncertain statistical characteristics.

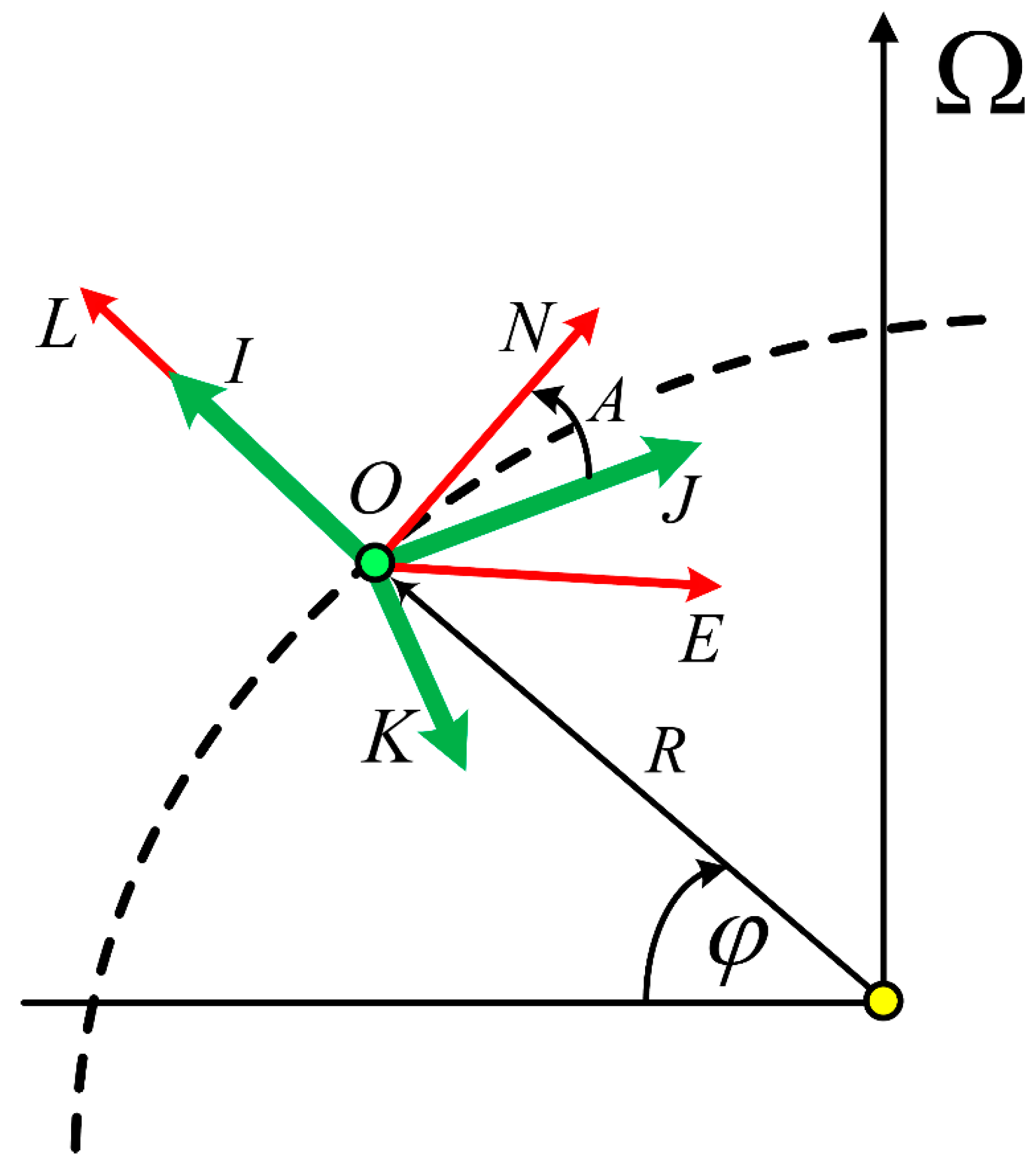
To solve this problem, we use the following Coordinate Systems (CS) presented in Figure 1:

• The local geographical CS OLNE is Earth-related, the beginning of which coincides with the UMA’s center of mass, located at latitude φ. The axis OL is directed along the radius R of the sphere of the Earth from its center, the axis ON lies in the plane of the local meridian (towards the north), and the axis OE complements the CS to the right (towards the east). In Figure 1, the OLNE CS axes are marked in red.
• The dash CS OIJK, the beginning of which coincides with the UMA’s center of mass. The axes OI, OJ, and OK, prior to the implementation of the system, deployed an initial orientation relative to the axes of CS OLNE unknown angles. In Figure 1, the OIJK CS axes are marked in green.

Under such general initial conditions for the possibility of solving the problem of azimuthal orientation (determining the angle of rotation A (see Figure 1), axis OJ relative to the plane of the local meridian), which was previously carried out by the exhibition of the AVS sensitivity axis, the axis of sensitivity which coincides with the axis OJ in the plane of the local horizon. Placing in the horizontal plane is carried out with the required accuracy (2.4 · 10⁻⁶ – 4.8 · 10⁻⁶ rad) using precision accelerometers. Measurement errors lie within 1 · 10⁻⁴ – 1 · 10⁻⁵ m s^-2, and the axis of sensitivity is oriented respectively long the axes OJ and OK. Thus, this stage is implemented by the combination of the axis A with the axis OL. The final solution initial orientation—the definition of the azimuthal angle A of dash CS—given the inevitable AVS interference measurements is implemented next, using the gyrocompassing algorithm described below.

The output signal Z of most modern angular velocity sensors (gyroscopic, laser, fiber-optic, etc.) in gyrocompassing mode can be represented as follows:

Z = ω + S + W,

(1)

where

• ω = Ω cosφ cosA—the Earth’s angular velocity projection on the AVS sensitivity axis;
• Ω—the angular velocity of the Earth’s rotation (see Figure 1);
• φ—the latitude;
• A—the azimuthal angle of the AVS sensitivity axis;
• S—the constant random interference, with a priori uncertain statistical characteristics;
• W—the broadband random interference, with a priori uncertain statistical characteristics.

To implement the proposed method of gyrocompassing after the initial exhibition of the AVS sensitivity axis in the plane of the local horizon (the orientation of sensitivity axis relative to the local meridian plane is a priori unknown), a sequential discrete rotation of the AVS sensitivity axis by a given angle Δ relative to the local meridian plane of the (n − 1) time is carried out. In each next i-th (i = 1, 2, ..., n) position of the AVS sensitivity axis, low-frequency filtering of the AVS output signal Z is performed (for example, using a high-order Butterworth filter). Filtering for a fixed time interval depends on the frequency of removal of AVS measurements. At the end of the filtration process, the AVS output signal in the i-th position Z_i becomes equal to:

Z_i = ω_i + S,

(2)

where ω_i = Ω cosφ cosA_i, A_i—the unknown azimuthal angle of the AVS sensitivity axis in the i-th position.

Next, by pairwise subtraction of the signals Z_i obtained in the neighboring angular positions of the AVS sensitivity axis (the rotation angles which are different with respect to the local meridian on Δ value), the difference δ_i is

δ_i = Z_i+1 − Z_i = ω_i+1 − ω_i = Ω cosφ (cosA_i+1 − cosA_i)

(3)

Assuming for certain that the rotation of the AVS sensitivity axis in the plane of the local meridian is carried out in the direction of increasing the value of Z_i, the termination of rotation is determined either by reaching a given value of n, or by changing the sign of the difference δ_i. The difference of the cosines (cosA_i+1 − cosA_i) is calculated before the gyrocompassing process for all possible values of angles A_n in a given interval of their change with the required accuracy. The maximum values of the boundaries of the interval here will be equal to [0, π/2]—for example, when calculating the angles A_n with a sampling step d = 10″, the maximum size of the calculated values array of cosines difference will be only 32,400 values, which is not difficult for modern computers. In addition, to begin the gyrocompassing process, the reference array calculates accurate values of ${\mathsf{\delta }}_i^{Et}$ for a particular latitude of gyrocompassing by multiplying the values of the array computed cosines difference on the Ω cosφ.

After the formation of (n − 1) δ_i values, because of the measurements carried out, the selection of a series (n − 1) of consecutive δ_i^Et values from the reference array of exact values that coincide as much as possible with the series (n–1) of δ_i values is carried out by brute force. The comparison is based on the specified matching criteria, for example:

$${{\displaystyle \sum }}_{i=1}^{n-1}\left|{\mathsf{\delta }}_i^{Et}-{\mathsf{\delta }}_i\right|\le \alpha ,{{\displaystyle \sum }}_{i=1}^{n-1}{\left({\mathsf{\delta }}_i^{Et}-{\mathsf{\delta }}_i\right)}^2\le {\alpha }_1,$$

(4)

where α and α₁—set values,$min{{\displaystyle \sum }}_{i=1}^{n-1}\left|{\mathsf{\delta }}_i^{Et}-{\mathsf{\delta }}_i\right|\forall A_n$, $min{{\displaystyle \sum }}_{i=1}^{n-1}{\left({\mathsf{\delta }}_i^{Et}-{\mathsf{\delta }}_i\right)}^2\forall A_n$ etc.

The formation of an etalon series of the consistent accuracy values (n − 1), determined by the angle A_n, corresponds to the value ${\mathsf{\delta }}_{n-1}^{Et}$. The angle A_n, with high precision (due to independence of the values δ_i from the above-mentioned interference), is the azimuth angle of the n-th position of the AVS sensitivity axis.

To test the effectiveness of the proposed method, a computational experiment was conducted, the results of which are shown below.

3. Results

In the numerical simulation of the developed method, the noise of the AVS measurement was modelled as the sum of the constant random drift S with zero expectation, a dispersion of (0.01)² °/hour and a broadband noise of W (Gaussian random sequence with zero expectation and dispersion of (0.15)² °/hour), generated with a time step of 0.01 s for the number of implementations equal to 90. The azimuth of the initial position of the AVS sensitivity axis, relative to the plane of the local meridian (with latitude 47°35′), was chosen to be 28°–29°, and the sampling step d to calculate all possible values of angles A_n in the range [0, π/2] was chosen to be 10″. The rotation of the AVS sensitivity axis was carried out in 60 steps and a time of each step of 1 s. At each step, the AVS output signal was filtered using a sixth-order Butterworth filter. Following the determination of differences δ_i using Equation (3), the choice of a number of values of δ_i^Et from the reference array of exact values that coincide as much as possible with a number of obtained values of δ_i was carried out by criterion ${{\displaystyle \sum }}_{i=1}^{n-1}\left|{\mathsf{\delta }}_i^{Et}-{\mathsf{\delta }}_i\right|\le \alpha$, where parameter α was selected to be 5″. The minimum values of errors in determining the azimuth AVS sensitivity axis at different azimuths of its initial position, obtained after processing the δ_i^Et values for all implementations, are presented in

Table 1. Errors in determining the azimuth of the Angular Velocity Sensors (AVS) sensitivity axis.

Number	Initial Azimuth	Error
1	28°10′	7.3″
2	28°30′	9.6″
3	28°50′	6″

.

As shown in Table 1, the minimum value of the error in determining the azimuth of the AVS sensitivity axis was 6″, and the maximum did not exceed the 10″. The results of the numerical experiment indicate the possibility of the effective practical use of the proposed approach.

4. Conclusions

In addition to high accuracy, the advantage of the proposed algorithm for solving the problem of determining the initial azimuth of the UMA’s navigation–measuring complex in the conditions of interference of the AVS measurements, with a priori uncertain statistical characteristics, is the lack of significant computational costs for its implementation. Indeed, when calculating all possible values of the angles A_n with a sampling step d = 10″ (corresponding to the modern requirements of the accuracy of the azimuth of the UMA’s navigation–measuring complex) in the interval [0, π/2] limits the maximum size of the array of the calculated values of the difference of the cosines to just 32,400 values (π/2d)—if the bitness of the computer is equal to 64, then it only requires 2592 Kbyte of RAM. For an exhaustive search of the array data within a time-step of AVS rotation axis sensitivity (at least one second in modern requirements of speed systems for the initial orientation), this does not pose difficulties for modern computers.

The algorithm is invariant to the type of AVS used, which provides the possibility of its effective practical application in the development of high-precision systems of initial orientation of various navigation and measuring complexes of mobile apparatus.