Mixed Logic Dynamic Models for MPC Control of Wind Farm Hydrogen-Based Storage Systems
Abstract
:1. Introduction
Nomenclature
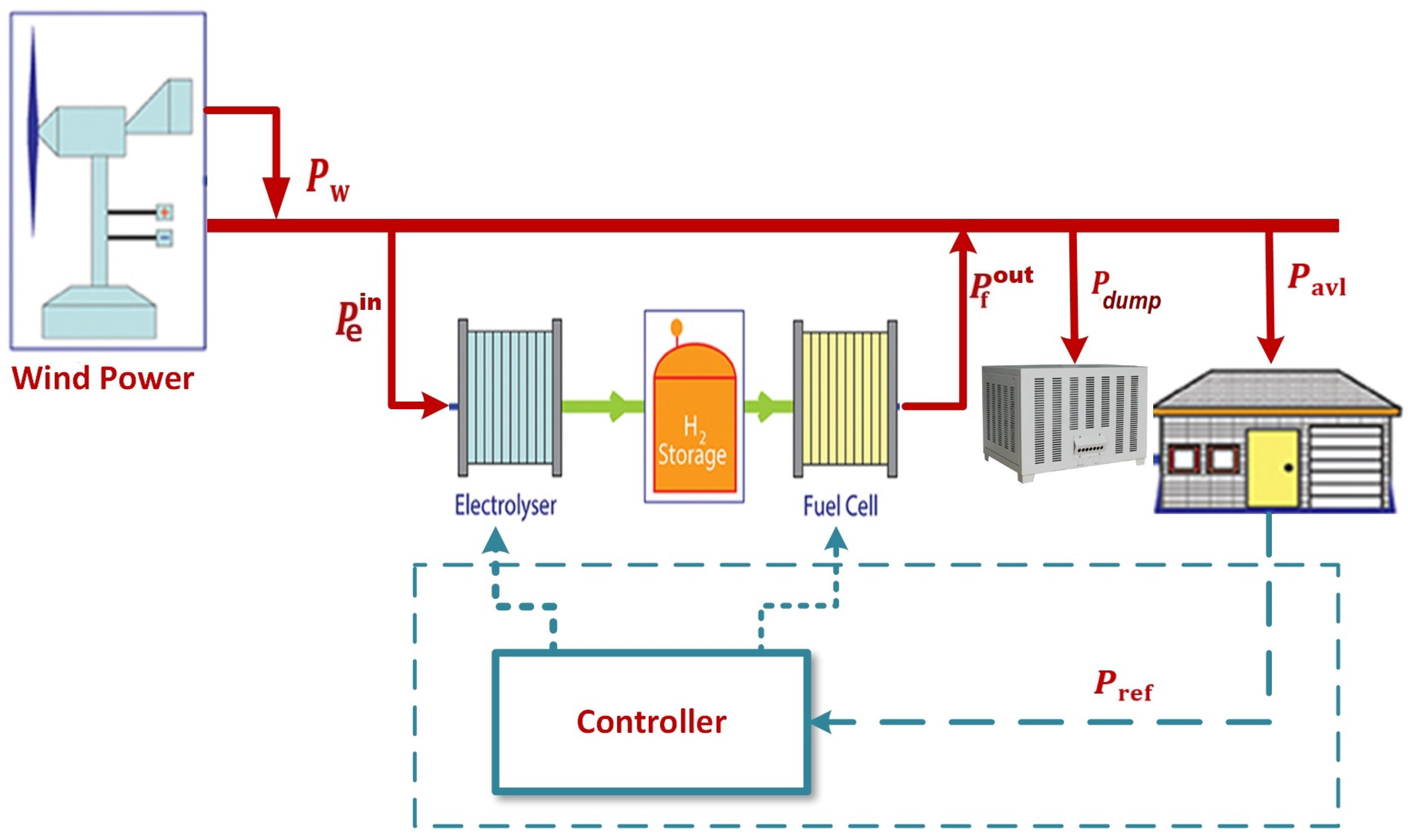
2. System Description and Modeling
2.1. Power Demand Reference Model
2.2. Electrolyzer and Fuel Cell Models
2.3. Hydrogen Storage Model
2.4. Feasibility and Operating Constraints
2.5. Power Balance Constraint
3. Implementation of the Proposed MPC Controller
3.1. Electrolyzer and Fuel cell Cost Functions
3.2. Load Tracking Cost Function
3.3. MPC Formulation
- protection of the hydrogen storage tank from excessive discharging and overcharging;
- limitation of the power rate of the fuel cell and of the electrolyzer to protect them;
- tracking of the power reference request according to the forecasted conditions;
- in case an expected event occurs, the fuel cell is employed as a contingent energy storage system to satisfy the power demand.
4. Case Study
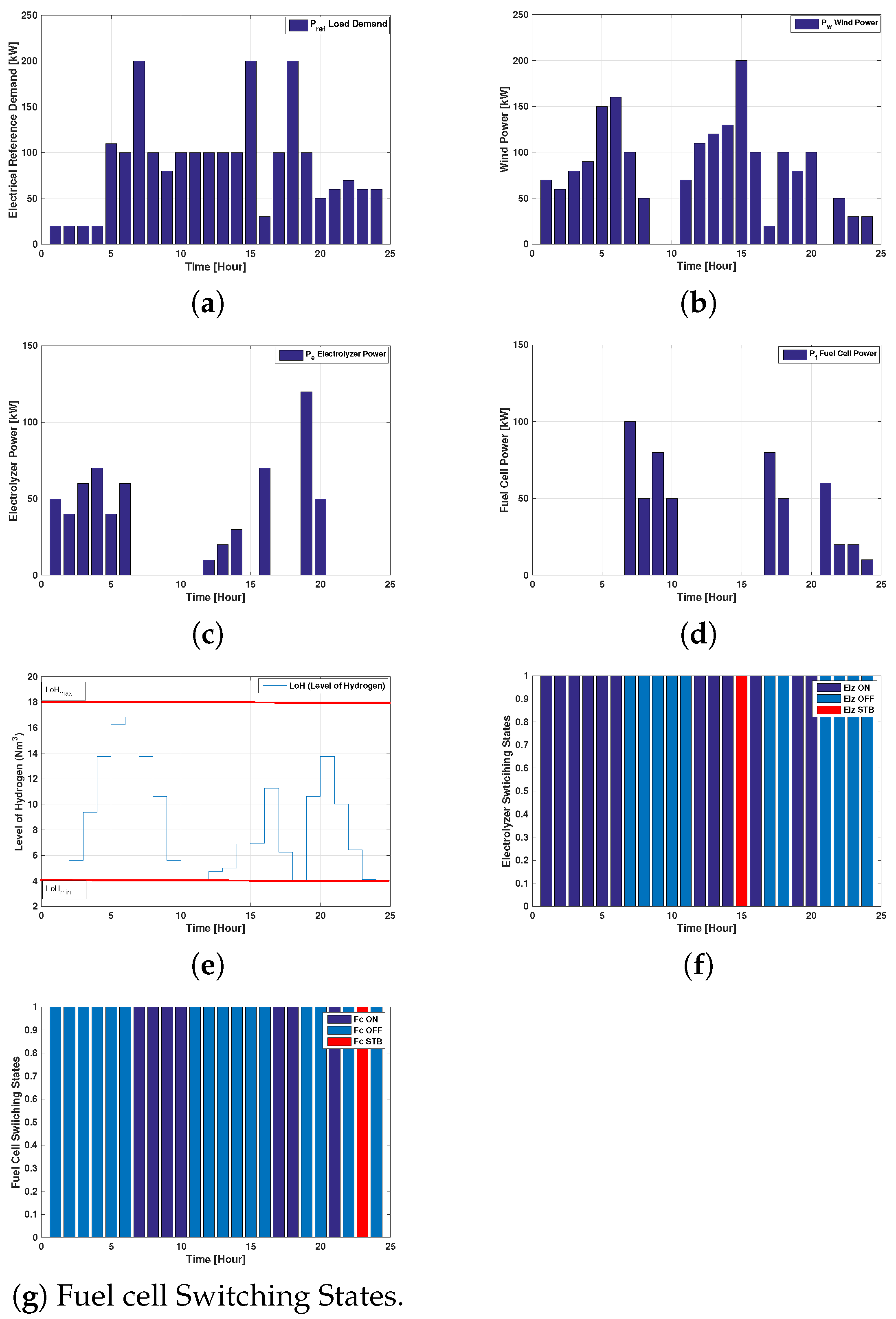
5. Simulations and Numerical Results
5.1. Example 1
5.2. Example 2
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A.
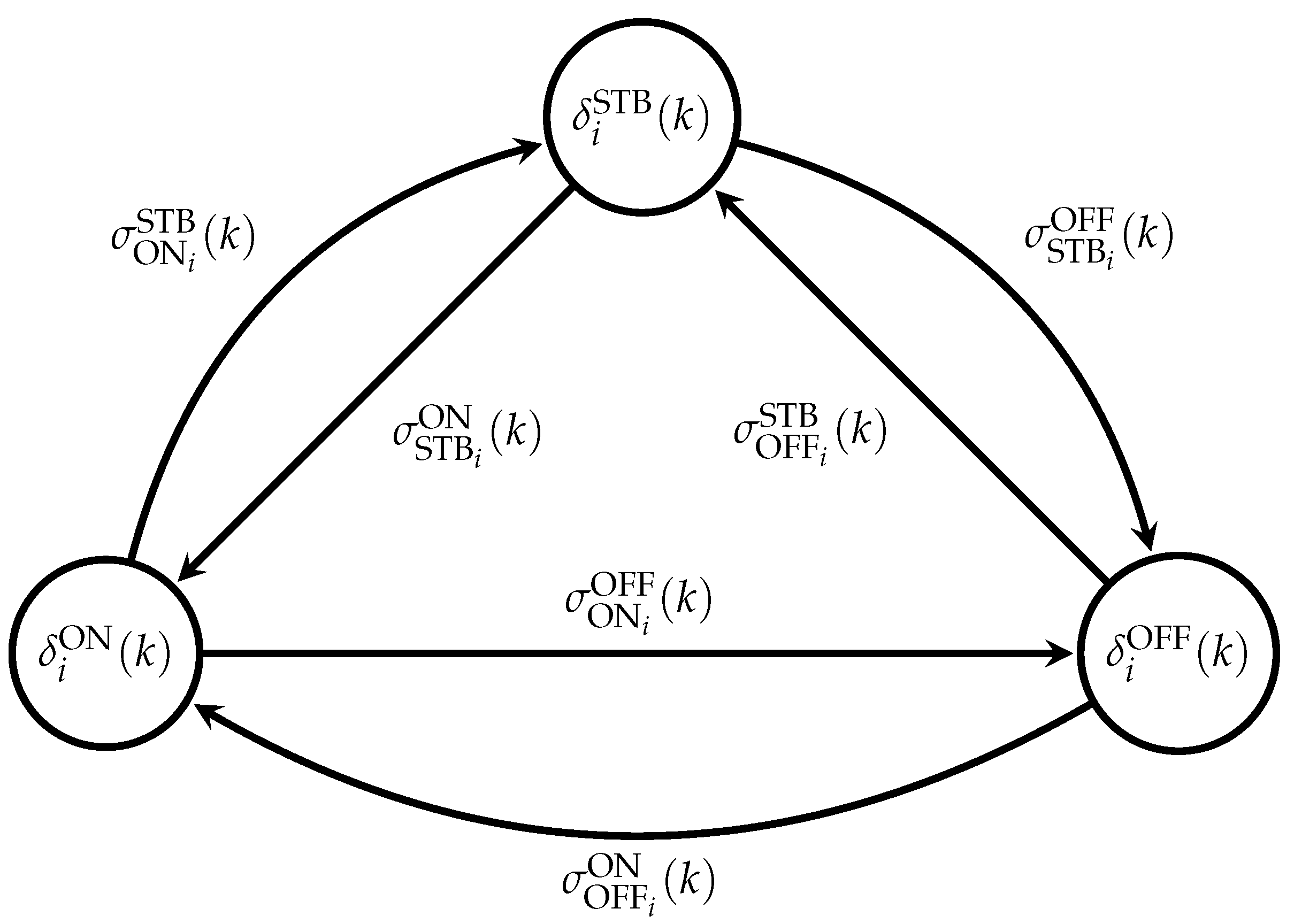
Appendix A.1. Constraints Formulation of the Logical States
Appendix A.2. Mathematical Model and Constraints Formulation of the State Transitions
References
- Hosseini, S.E.; Wahid, M.A. Hydrogen production from renewable and sustainable energy resources: Promising green energy carrier for clean development. Renew. Sustain. Energy Rev. 2016, 57, 850–866. [Google Scholar] [CrossRef]
- Tande, J.O.G. Exploitation of wind-energy resources in proximity to weak electric grids. Appl. Energy 2000, 65, 395–401. [Google Scholar] [CrossRef]
- Akinyele, D.; Rayudu, R. Review of energy storage technologies for sustainable power networks. Sustain. Energy Technol. Assess. 2014, 8, 74–91. [Google Scholar] [CrossRef]
- Schoenung, S.M. Characteristics and Technologies for Long-vs. Short-Term Energy Storage; United States Department of Energy, Sandia National Laboratories: Albuquerque, NM, USA, 2001.
- Carapellucci, R.; Giordano, L. Modeling and optimization of an energy generation island based on renewable technologies and hydrogen storage systems. Int. J. Hydrogen Energy 2012, 37, 2081–2093. [Google Scholar] [CrossRef]
- Uzunoglu, M.; Onar, O.; Alam, M. Modeling, control and simulation of a PV/FC/UC based hybrid power generation system for stand-alone applications. Renew. Energy 2009, 34, 509–520. [Google Scholar] [CrossRef]
- Castaneda, M.; Cano, A.; Jurado, F.; Sánchez, H.; Fernandez, L.M. Sizing optimization, dynamic modeling and energy management strategies of a stand-alone PV/hydrogen/battery-based hybrid system. Int. J. Hydrogen Energy 2013, 38, 3830–3845. [Google Scholar] [CrossRef]
- Valverde, L.; Bordons, C.; Rosa, F. Power management using model predictive control in a hydrogen-based microgrid. In Proceedings of the IECON 38th Conference on Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 5669–5676. [Google Scholar]
- Trifkovic, M.; Sheikhzadeh, M.; Nigim, K.; Daoutidis, P. Hierarchical control of a renewable hybrid energy system. In Proceedings of the IEEE 51st Conference on Decision and Control (CDC), Grand Wailea, Maui, HI, USA, 16 August 2012; pp. 6376–6381. [Google Scholar]
- Serna, Á.; Yahyaoui, I.; Normey-Rico, J.E.; de Prada, C.; Tadeo, F. Predictive control for hydrogen production by electrolysis in an offshore platform using renewable energies. Int. J. Hydrogen Energy 2017, 42, 12865–12876. [Google Scholar] [CrossRef]
- De Angelis, F.; Boaro, M.; Fuselli, D.; Squartini, S.; Piazza, F.; Wei, Q. Optimal home energy management under dynamic electrical and thermal constraints. IEEE Trans. Ind. Inform. 2013, 9, 1518–1527. [Google Scholar] [CrossRef]
- Jiang, Q.; Xue, M.; Geng, G. Energy management of microgrid in grid-connected and stand-alone modes. IEEE Trans. Power Syst. 2013, 28, 3380–3389. [Google Scholar] [CrossRef]
- Yang, P.; Nehorai, A. Joint optimization of hybrid energy storage and generation capacity with renewable energy. IEEE Trans. Smart Grid 2014, 5, 1566–1574. [Google Scholar] [CrossRef]
- Malysz, P.; Sirouspour, S.; Emadi, A. An optimal energy storage control strategy for grid-connected microgrids. IEEE Trans. Smart Grid 2014, 5, 1785–1796. [Google Scholar] [CrossRef]
- Vahidi, A.; Greenwell, W. A decentralized model predictive control approach to power management of a fuel cell-ultracapacitor hybrid. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 11–13 July 2017; pp. 5431–5437. [Google Scholar]
- Greenwell, W.; Vahidi, A. Predictive control of voltage and current in a fuel cell–ultracapacitor hybrid. IEEE Trans. Ind. Electron. 2009, 57, 1954–1963. [Google Scholar] [CrossRef]
- Bergen, A.P. Integration and Dynamics of a Renewable Regenerative Hydrogen Fuel Cell System. Ph.D. Thesis, University of Victoria, Victoria, BC, Canada, 25 April 2008. [Google Scholar]
- Ferrari-Trecate, G.; Gallestey, E.; Letizia, P.; Spedicato, M.; Morari, M.; Antoine, M. Modeling and control of co-generation power plants: A hybrid system approach. IEEE Trans. Control Syst. Technol. 2004, 12, 694–705. [Google Scholar] [CrossRef]
- Ferrari-Trecate, G.; Gallestey, E.; Letizia, P.; Spedicato, M.; Morari, M.; Antoine, M. Modeling and Control of Co-Generation Power Plants: A Hybrid System Approach; Tomlin, C.J., Greenstreet, M.R., Eds.; Hybrid Systems: Computation and Control; Springer: Berlin/Heidelberg, Germany, 2002; pp. 209–224. [Google Scholar]
- Stevens, M. Hybrid Fuel Cell Vehicle Power Train Development Considering Power Source Degradation. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2009. [Google Scholar]
- Vazquez, S.; Lukic, S.M.; Galvan, E.; Franquelo, L.G.; Carrasco, J.M. Energy storage systems for transport and grid applications. IEEE Trans. Ind. Electron. 2010, 57, 3881–3895. [Google Scholar] [CrossRef]
- Tani, A.; Camara, M.B.; Dakyo, B. Energy management based on frequency approach for hybrid electric vehicle applications: Fuel-cell/lithium-battery and ultracapacitors. IEEE Trans. Veh. Technol. 2012, 61, 3375–3386. [Google Scholar] [CrossRef]
- Wang, L.; Li, H. Maximum fuel economy-oriented power management design for a fuel cell vehicle using battery and ultracapacitor. IEEE Trans. Ind. Appl. 2010, 46, 1011–1020. [Google Scholar] [CrossRef]
- Liu, W.S.; Chen, J.F.; Liang, T.J.; Lin, R.L.; Liu, C.H. Analysis, design, and control of bidirectional cascoded configuration for a fuel cell hybrid power system. IEEE Trans. Power Electron. 2010, 25, 1565–1575. [Google Scholar]
- Garcia-Torres, F.; Valverde, L.; Bordons, C. Optimal load sharing of hydrogen-based microgrids with hybrid storage using model-predictive control. IEEE Trans. Ind. Electron. 2016, 63, 4919–4928. [Google Scholar] [CrossRef]
- Kalinci, Y.; Hepbasli, A.; Dincer, I. Techno-economic analysis of a stand-alone hybrid renewable energy system with hydrogen production and storage options. Int. J. Hydrogen Energy 2015, 40, 7652–7664. [Google Scholar] [CrossRef]
- Geer, T.; Manwell, J.; McGowan, J. A feasibility study of a wind/hydrogen system for Martha’s Vineyard, Massachusetts. In Proceedings of the American Wind Energy Association Windpower 2005 Conference; Massachusetts Technology Corporation (MTC): Brighton, MA, USA, 2005; Volume 37. [Google Scholar]
- Korpas, M. Distributed Energy Systems with Wind Power and Energy Storage. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2004. [Google Scholar]
- Hydrogen-Aeolic Energy with Optimized Electrolysers Upstream of Substatio Project. 2018. Available online: http://www.haeolus.eu/ (accessed on 20 July 2019).
- Hydrogenics—Innovators in Hydrogen Technology & Solutions. 1995. Available online: http://www.hydrogenics.com/ (accessed on 2 September 2019).
- Parisio, A.; Rikos, E.; Glielmo, L. A model predictive control approach to microgrid operation optimization. IEEE Trans. Control Syst. Technol. 2014, 22, 1813–1827. [Google Scholar] [CrossRef]
- Alessandra, P.; Glielmo, L. Energy Efficient Microgrid Management using Model Predictive Control. In Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC), Orlando, FL, USA, 12–15 Decemeber 2011. [Google Scholar]
- Alavi, F.; Lee, E.P.; van de Wouw, N.; De Schutter, B.; Lukszo, Z. Fuel cell cars in a microgrid for synergies between hydrogen and electricity networks. Appl. Energy 2017, 192, 296–304. [Google Scholar] [CrossRef] [Green Version]
- Petrollese, M.; Valverde, L.; Cocco, D.; Cau, G.; Guerra, J. Real-time integration of optimal generation scheduling with MPC for the energy management of a renewable hydrogen-based microgrid. Appl. Energy 2016, 166, 96–106. [Google Scholar] [CrossRef]
- Khalid, M.; Savkin, A. A model predictive control approach to the problem of wind power smoothing with controlled battery storage. Renew. Energy 2010, 35, 1520–1526. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Ismail, M.; Moghavvemi, M. Energy management strategies in hybrid renewable energy systems: A review. Renew. Sustain. Energy Rev. 2016, 62, 821–835. [Google Scholar] [CrossRef]
- Núñez-Reyes, A.; Rodríguez, D.M.; Alba, C.B.; Carlini, M.Á.R. Optimal scheduling of grid-connected PV plants with energy storage for integration in the electricity market. Sol. Energy 2017, 144, 502–516. [Google Scholar] [CrossRef]
- Spendelow, J.; Marcinkoski, J.; Satyapal, S. Doe hydrogen and fuel cells program record 14012. Dep. Energy (DOE) 2014, 125. Available online: https://www.hydrogen.energy.gov/pdfs/14012_fuel_cell_system_cost_2013.pdf (accessed on 13 June 2014).
- Howel, D. Battery status and cost reduction prospects. In EV everywhere grand challenge battery workshop. Dep. Energy (DOE) 2012, 125. Available online: https://www1.eere.energy.gov/vehiclesandfuels/pdfs/ev_everywhere/5_howell_b.pdf (accessed on 26 July 2012).
- Bemporad, A.; Morari, M. Control of systems integrating logic, dynamics, and constraints. Automatica 1999, 35, 407–427. [Google Scholar] [CrossRef]


| Parameters | Description |
|---|---|
| Hydrogen level in the storage unit [Nm3] | |
| Maximum level of the hydrogen storage unit [Nm3] | |
| Minimum level of the hydrogen storage unit [Nm3] | |
| Maximum power level of the electrolyzer [] | |
| Standby power of the electrolyzer [] | |
| Minimum power level of the electrolyzer [] | |
| Maximum power level of the fuel cell [] | |
| Minimum power level of the fuel cell [] | |
| Standby power of the fuel cell [] | |
| Number of life hours of the electrolyzer | |
| Number of life hours of the fuel cell | |
| Number of per year life hours of the electrolyzer | |
| Number of per year life hours of the fuel cell | |
| Degradation rate of the electrolyzer at maximum input power and over the number of yearly life hours | |
| Degradation rate of the fuel cell at maximum output power and over the number of yearly life hours | |
| Electrolyzer stack replacement cost [€/] | |
| Fuel cell stack replacement cost [€/] | |
| Sampling period [] | |
| T | Simulation horizon [] |
| Forecasts | Description |
|---|---|
| Wind power production [] | |
| Electrical load demand [] |
| Variables | Description |
|---|---|
| On state of the electrolyzer | |
| Off state of the electrolyzer | |
| Standby state of the electrolyzer | |
| On state of the fuel cell | |
| Off state of the fuel cell | |
| Standby state of the fuel cell | |
| Electrical power of the electrolyzer [] | |
| Electrical power of the fuel cell [] | |
| Available system electrical power [] | |
| Dumped electrical power [] | |
| z | Electric power formulated as mixed logic dynamic (MLD) variables for the electrolyzer and the fuel cell [] |
| Logical variables ON/OFF/STB states for the electrolyzer and the fuel cell | |
| Electrolyzer degradation rate [Nm3/] | |
| Fuel cell degradation rate [/Nm3] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shehzad, M.F.; Abdelghany, M.B.; Liuzza, D.; Mariani, V.; Glielmo, L. Mixed Logic Dynamic Models for MPC Control of Wind Farm Hydrogen-Based Storage Systems. Inventions 2019, 4, 57. https://doi.org/10.3390/inventions4040057
Shehzad MF, Abdelghany MB, Liuzza D, Mariani V, Glielmo L. Mixed Logic Dynamic Models for MPC Control of Wind Farm Hydrogen-Based Storage Systems. Inventions. 2019; 4(4):57. https://doi.org/10.3390/inventions4040057
Chicago/Turabian StyleShehzad, Muhammad Faisal, Muhammad Bakr Abdelghany, Davide Liuzza, Valerio Mariani, and Luigi Glielmo. 2019. "Mixed Logic Dynamic Models for MPC Control of Wind Farm Hydrogen-Based Storage Systems" Inventions 4, no. 4: 57. https://doi.org/10.3390/inventions4040057





