Homotopy Semi-Numerical Modeling of Non-Newtonian Nanofluid Transport External to Multiple Geometries Using a Revised Buongiorno Model
Abstract
1. Introduction
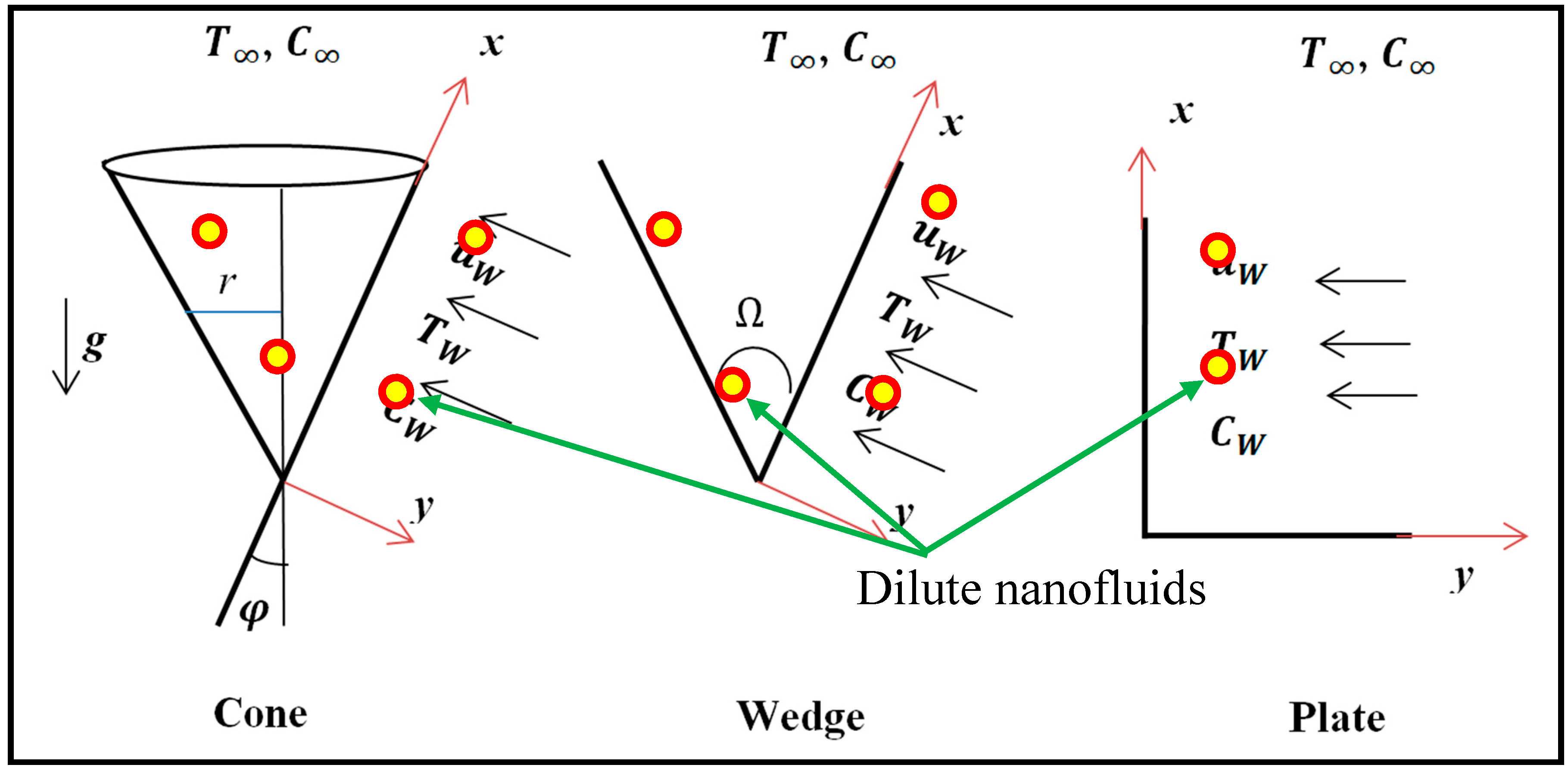
2. Mathematical Modeling
- (a)
- and : cone
- (b)
- and : wedge
- (c)
- and : plate
3. Solution Using Homotopy Analysis Method
Convergence of Homotopy Series Solution
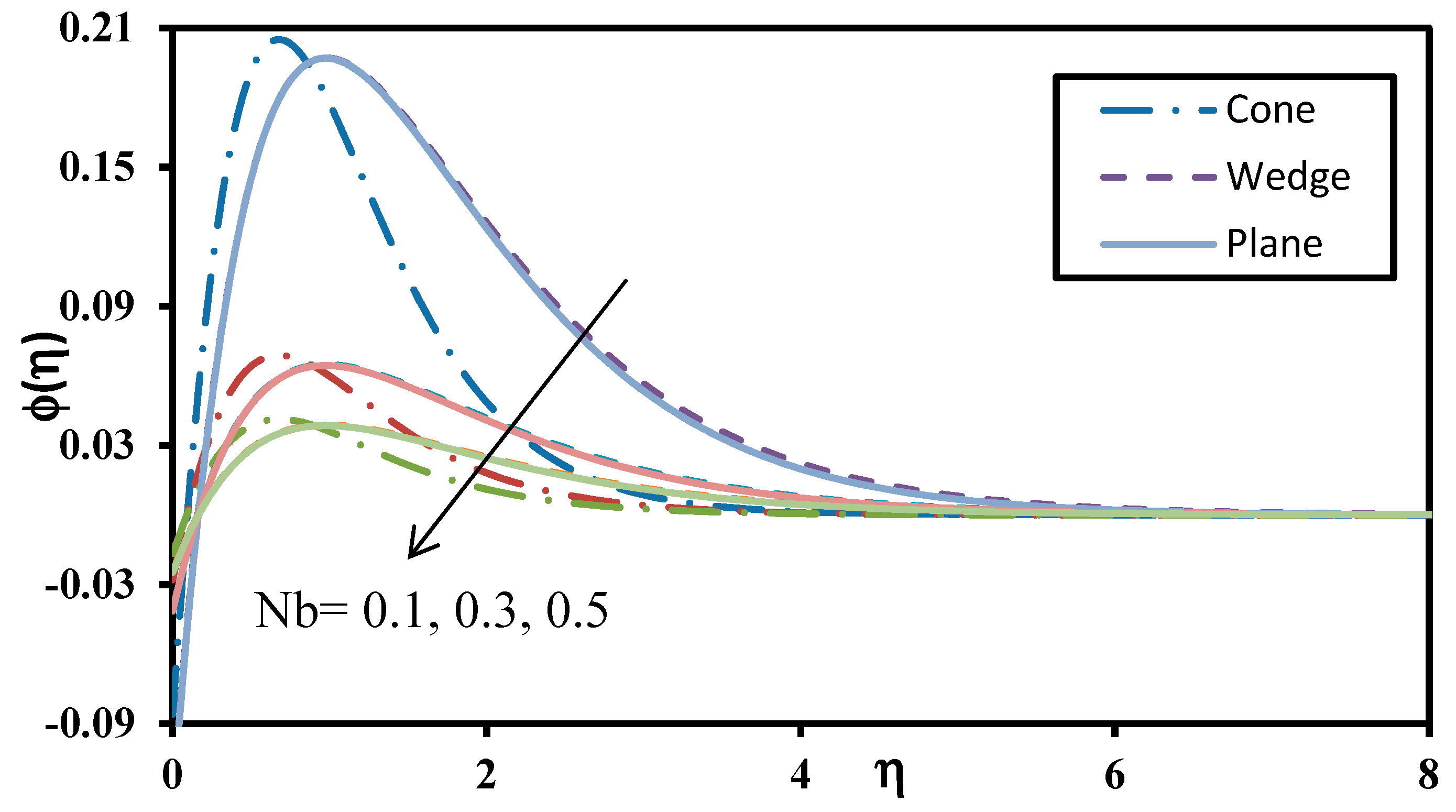
4. Results and Discussion
5. Conclusions
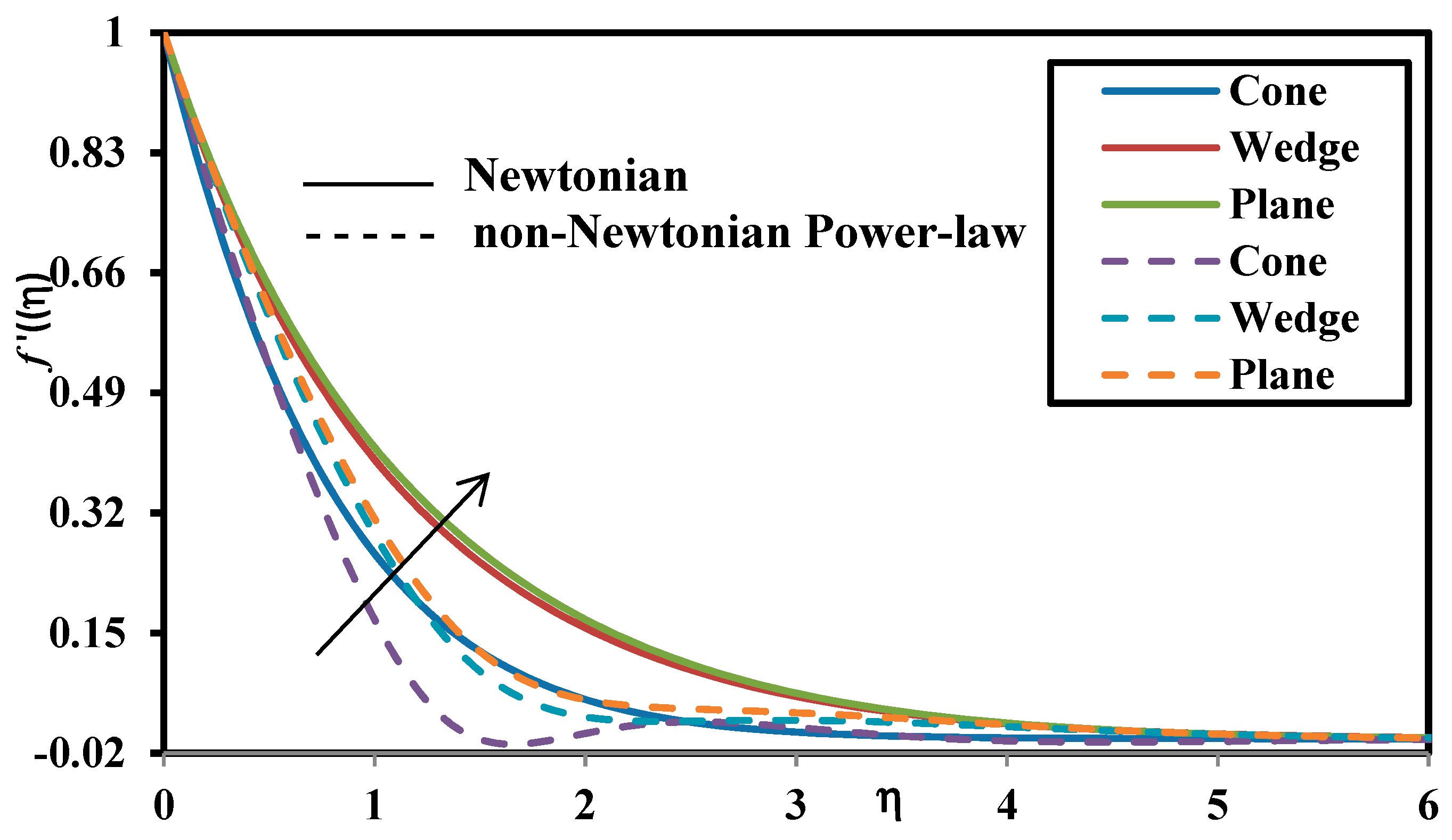
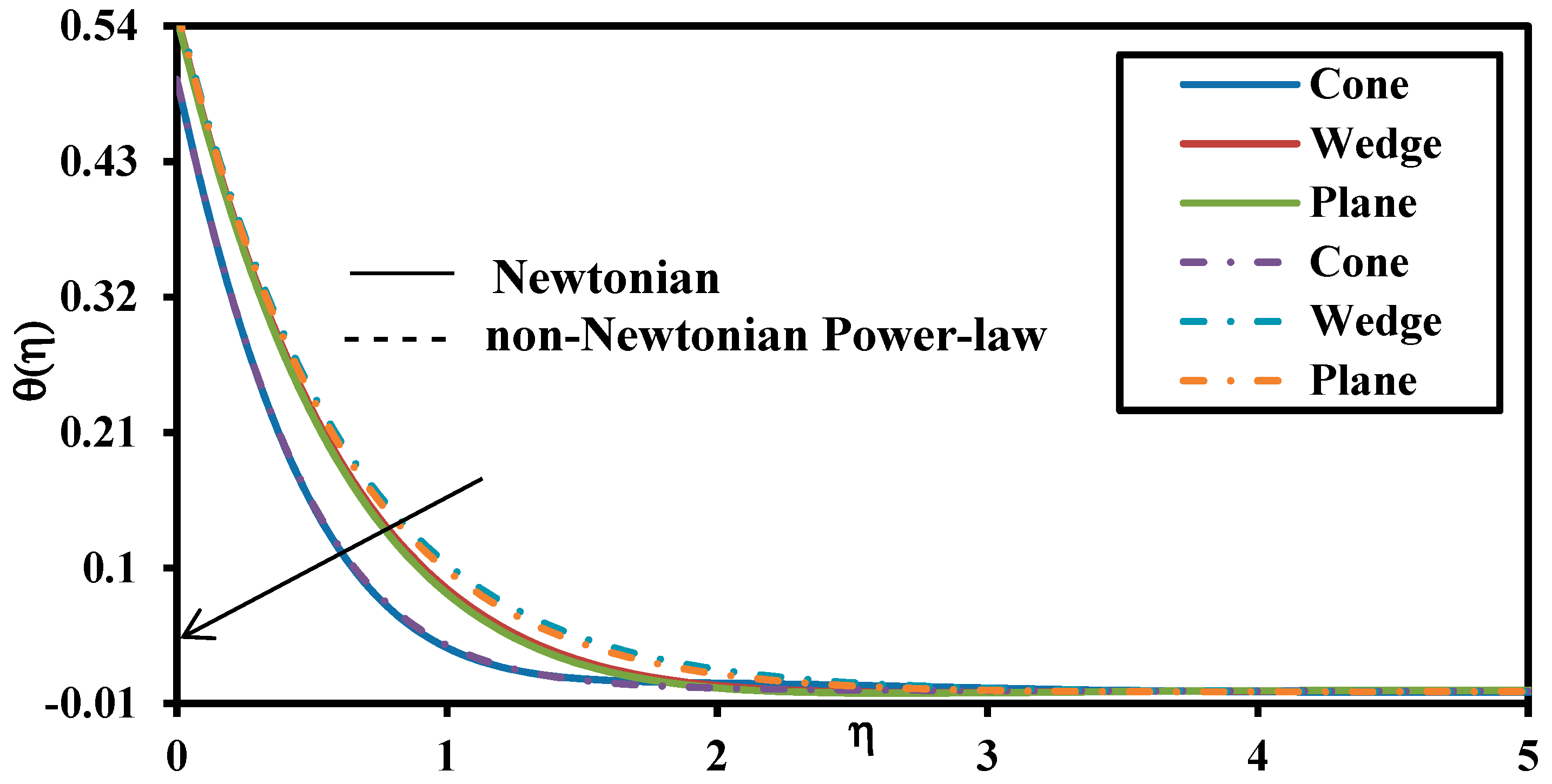
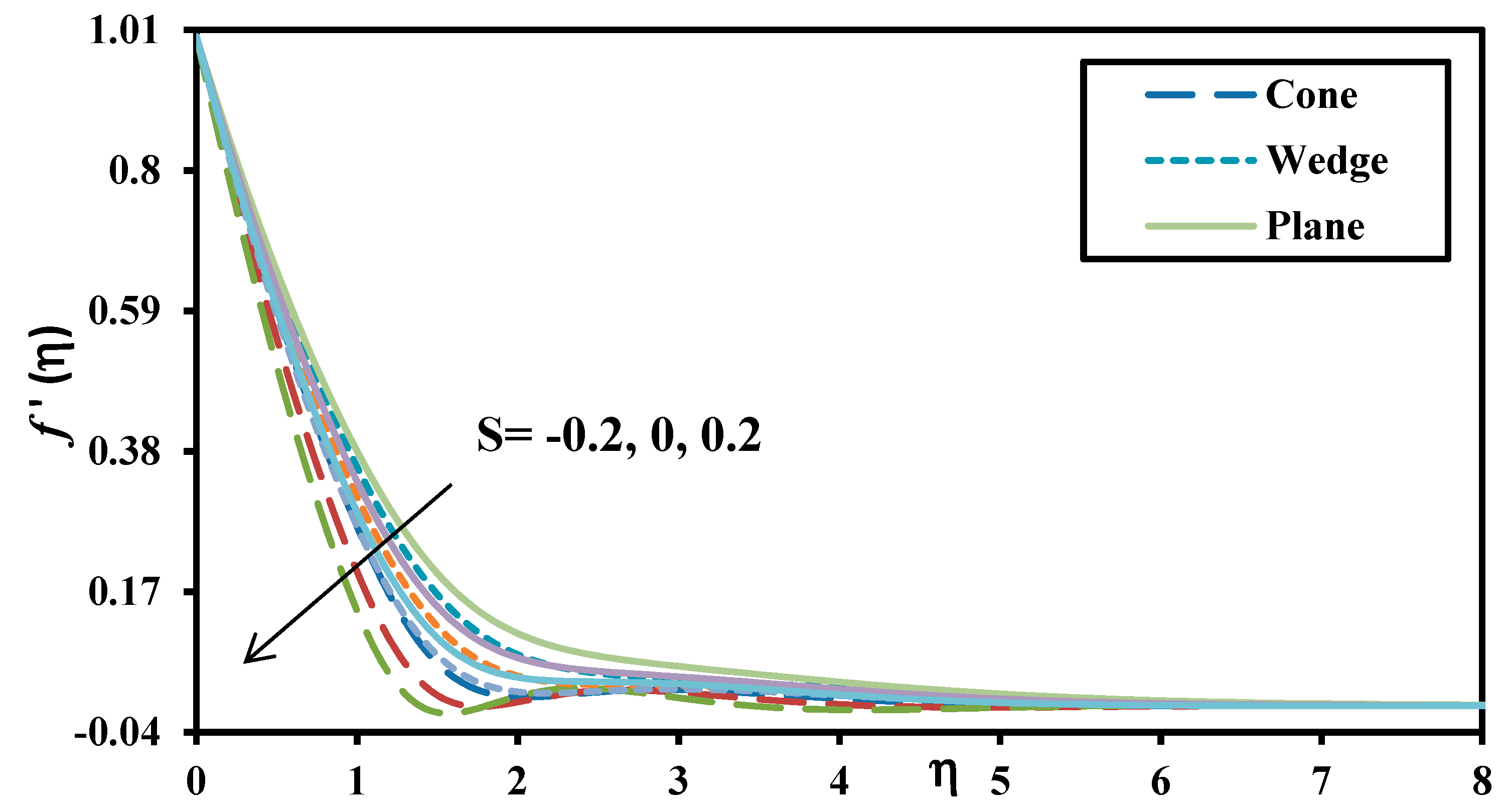
- Momentum boundary layer thickness is more significantly modified for the plate compared to the cone and wedge whereas thermal and concentration boundary layer is more significantly altered for the wedge geometry.
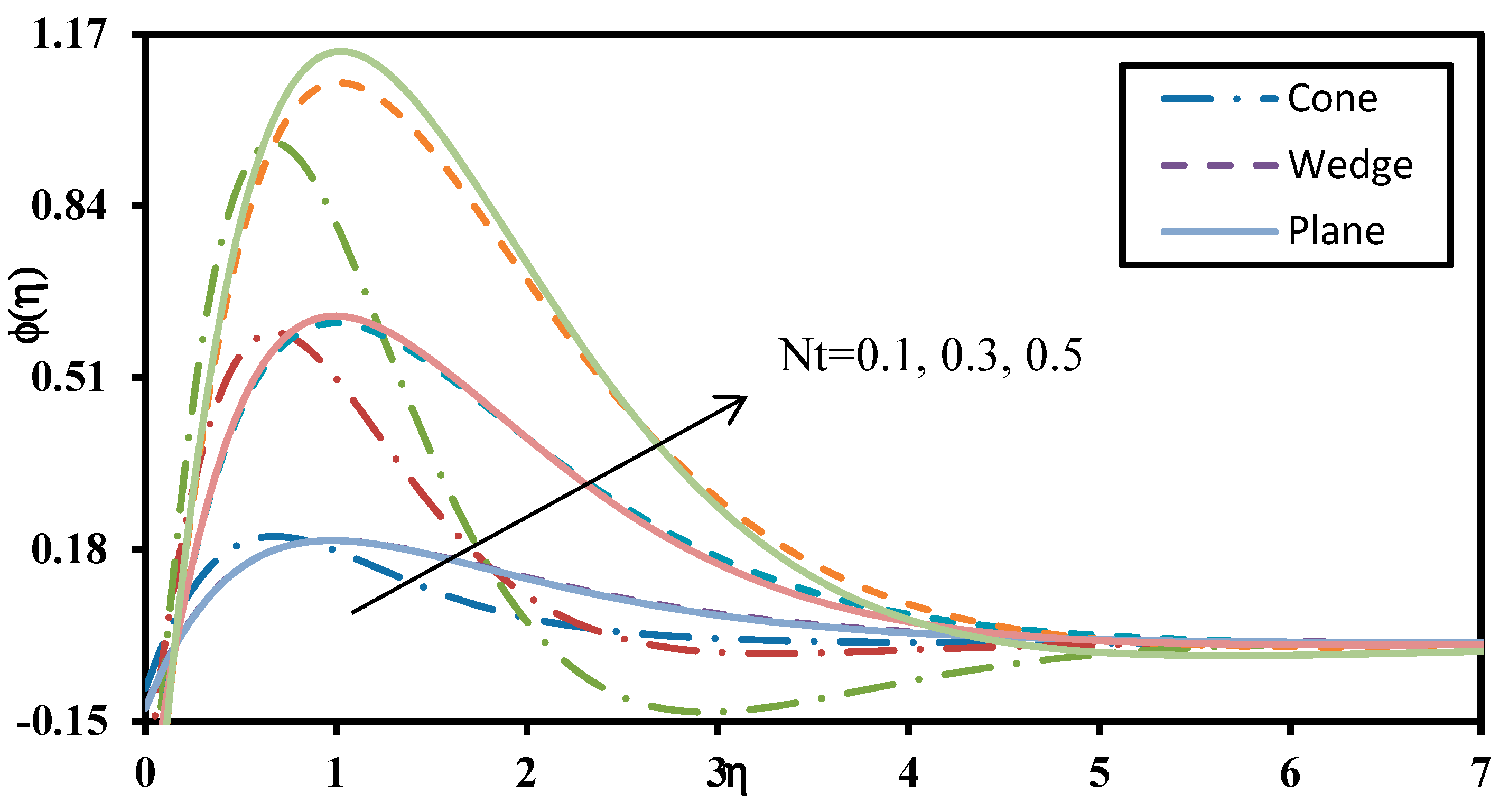
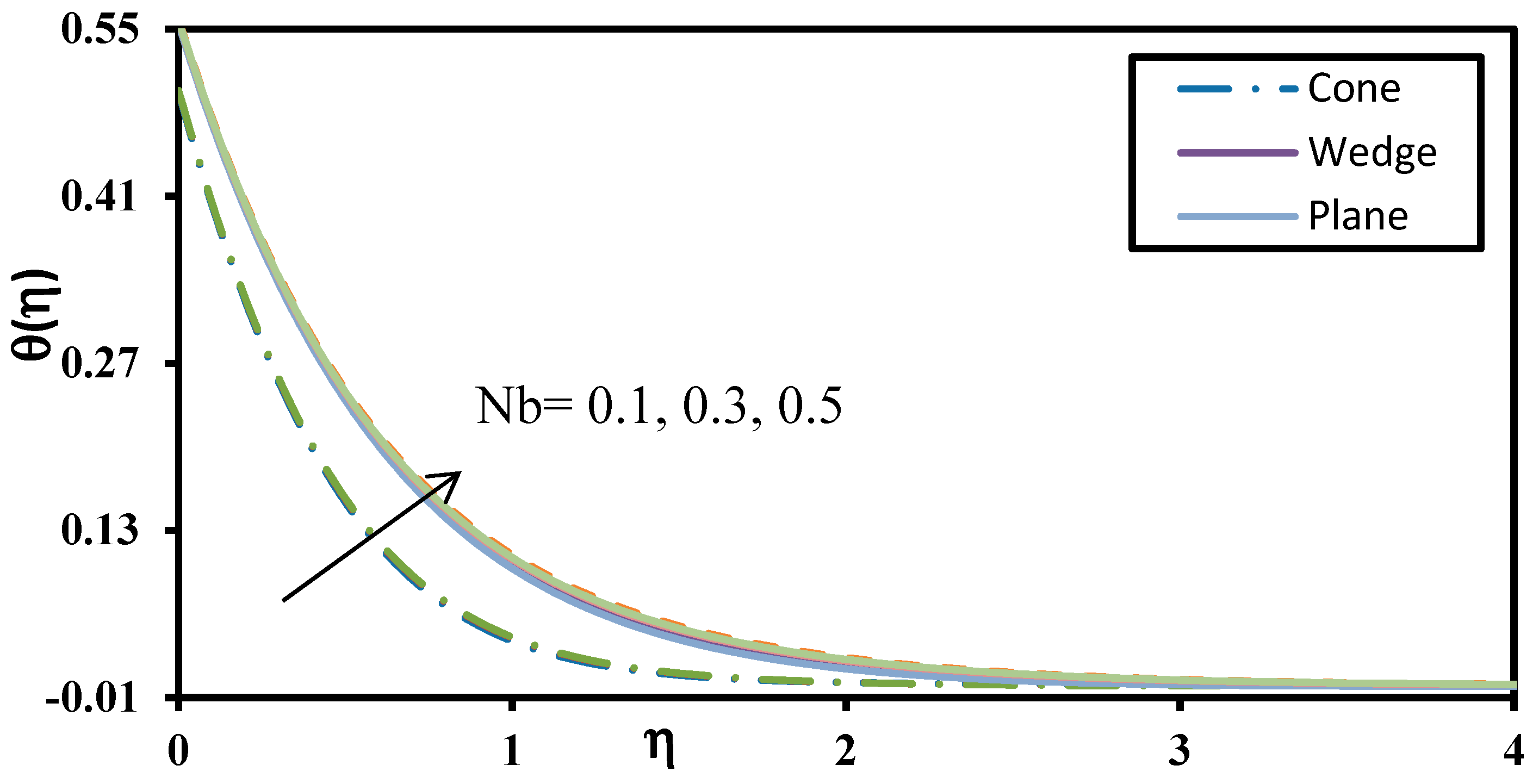
- Due to the boundary condition defined by modified Buongiorno model, the mass transfer rate (Sherwood number) decreases with increase in thermophoresis parameter and increases with increase in Brownian motion parameter for all the geometries.
- Brownian motion exerts a stronger influence on mass transfer rates (Sherwood numbers) for all the geometries when compared to heat transfer rates (Nusselt numbers).
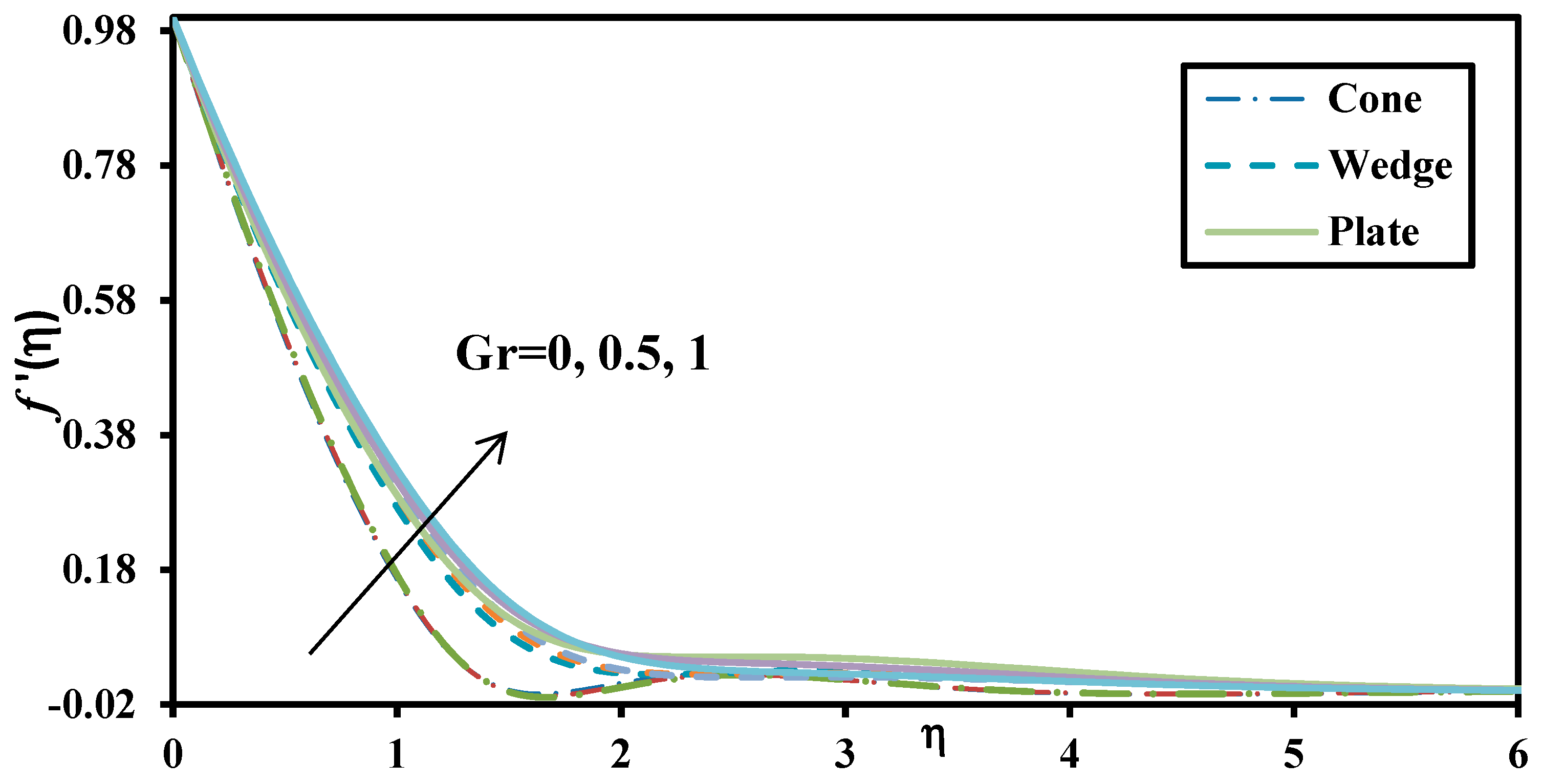
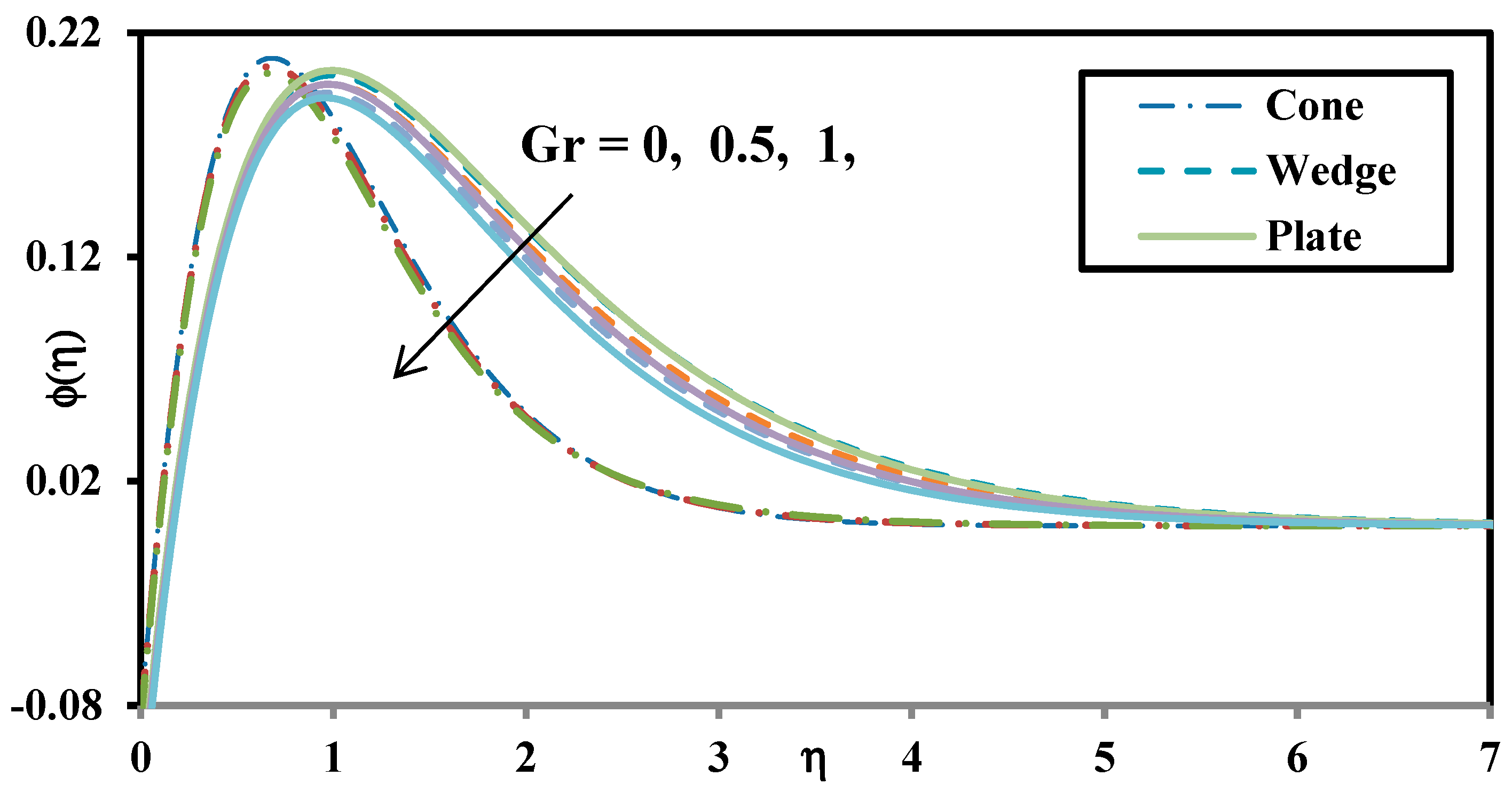
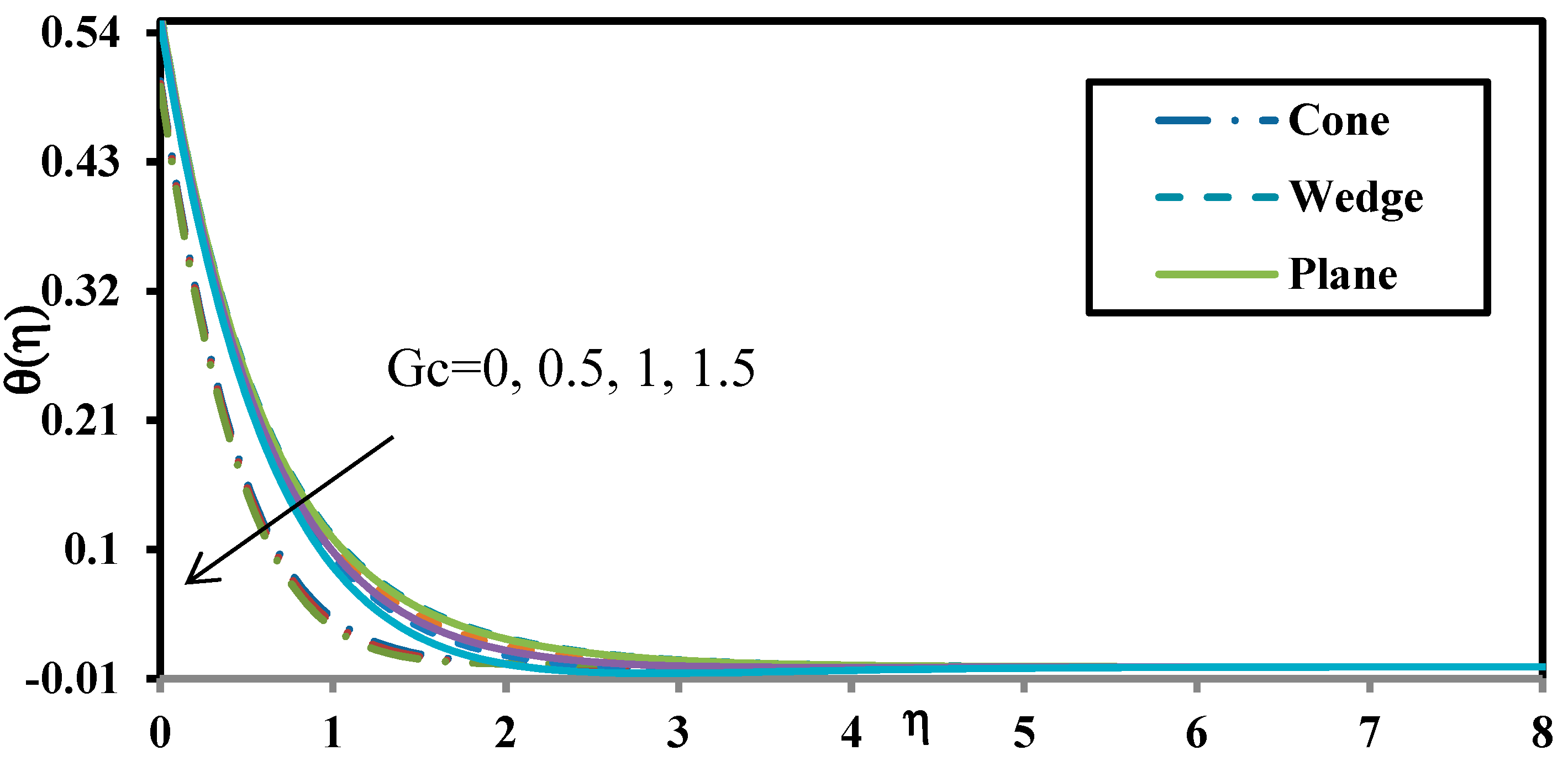
- Increasing thermal Grashof number and solutal (nanoparticle) Grashof number reduce temperature and enhance wall heat transfer rates (Nusselt numbers).
- Increasing thermal Grashof number and solutal (nanoparticle) Grashof number both elevate the skin friction factor for all geometries considered (cone, wedge and plate).
- The Nusselt number for the cone is in excess of that for either a plate or wedge.
- The convective boundary condition parameter, i.e., Biot number, controls the thermal and concentration boundary layer significantly and improves the heat transfer rates (Nusselt numbers) and in particular achieves high magnitudes for the wedge (Falkner–Skan case).
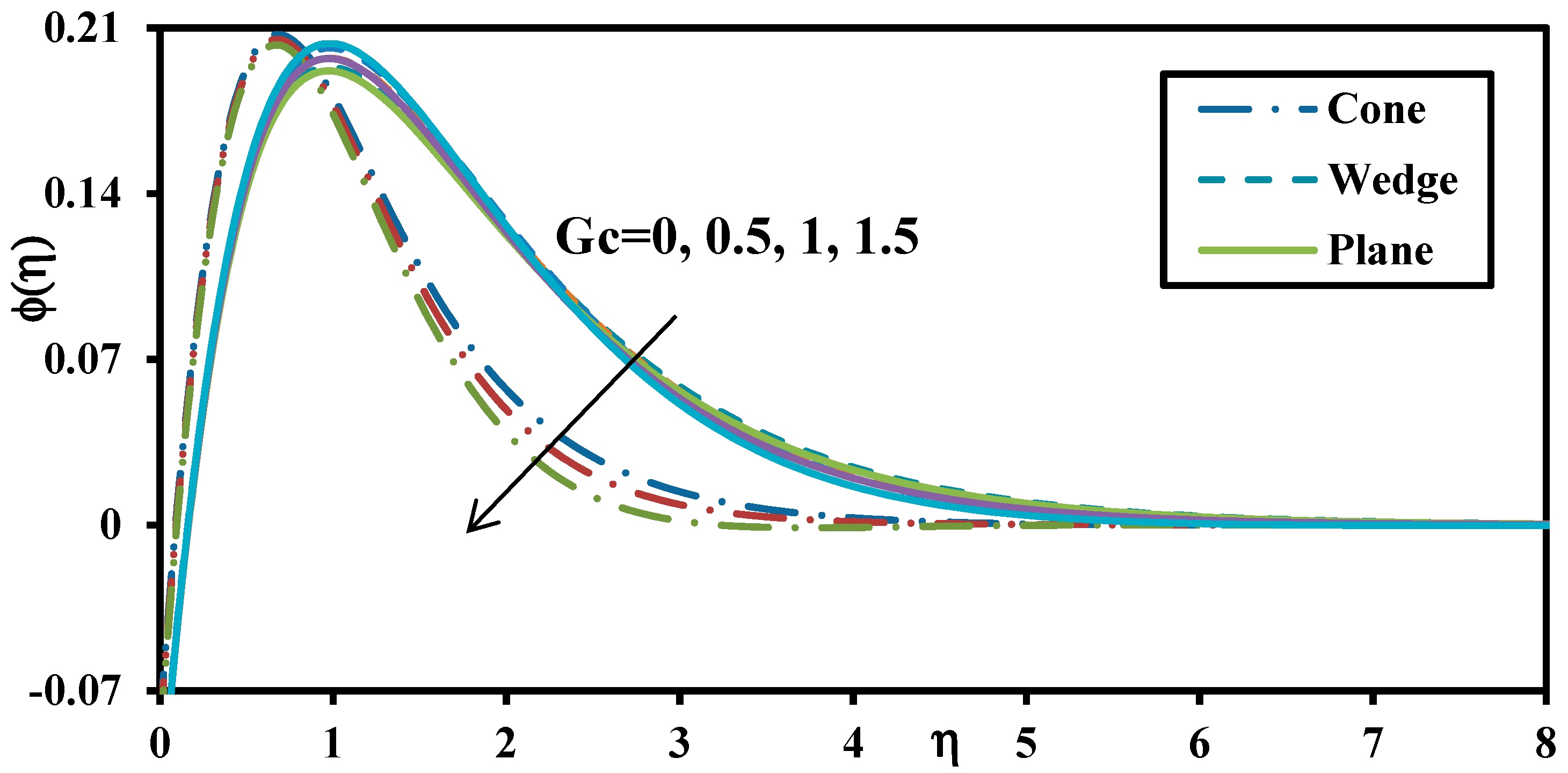
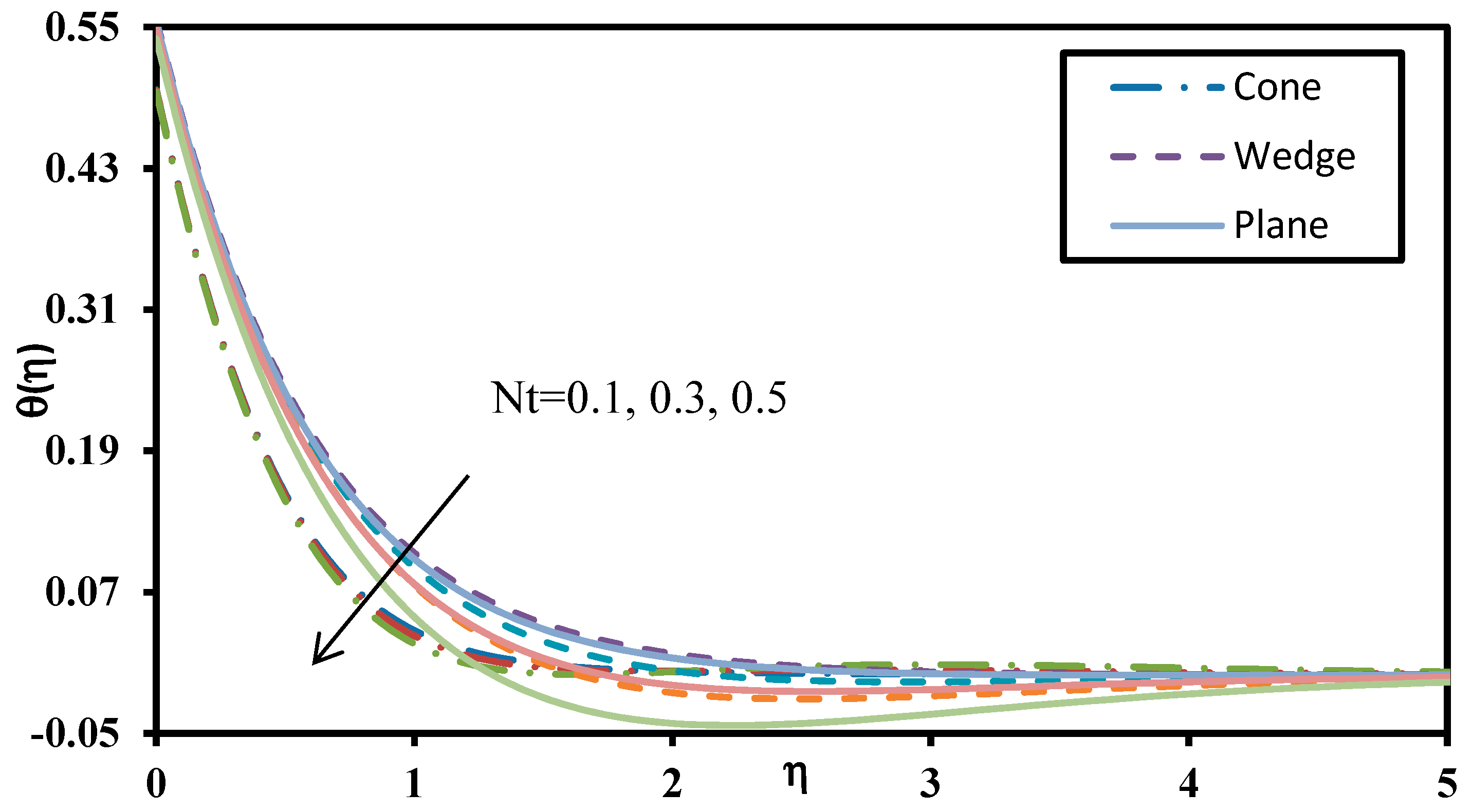
- Increasing non-isothermal behaviour (rising value of wall temperature parameter) and non-iso-solutal effect (greater wall concentration parameter) magnifies the heat transfer and mass transfer rates (i.e., Nusselt and Sherwood numbers) for all geometries.
- Thermal and solute Grashof number enhances the momentum boundary layer and suppresses the thermal and concentration boundary layer for all geometries. Both thermal and species buoyancy force therefore increase the rate of heat and nanoparticle mass transfer to the wall.
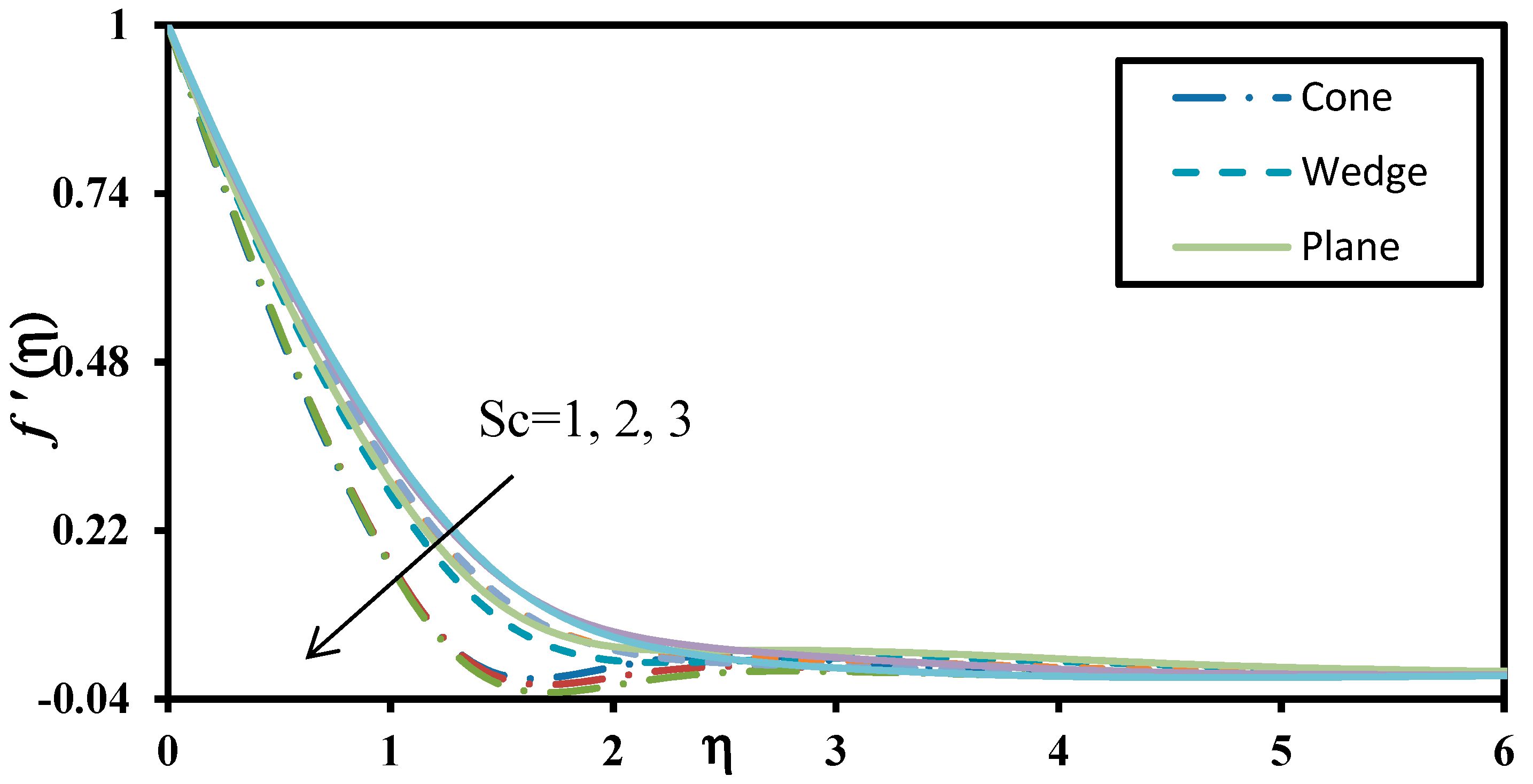
- The dominant effect of increasing Schmidt number is to lessen the heat transfer rate and enhance skin friction and nanoparticle mass transfer rate for all geometries.
- Increasing Schmidt number, Brownian motion and non-iso-solutal wall parameter deplete the Nusselt numbers, i.e., reduce heat transfer rates at the walls of all the geometries studied.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roy, S. Free convection from a vertical cone at high Prandtl number. J. Heat Transf. 1974, 96, 115–117. [Google Scholar]
- Vajravelu, K.; Nayfeh, J. Hydromagnetic convection at a cone and a wedge. Int. Commun. Heat Mass Transf. 1992, 19, 701–710. [Google Scholar]
- Ramanaiah, G.; Malarvizhi, G. Free convection about a wedge and a cone subjected to mixed thermal boundary conditions. Acta Mech. 1992, 93, 119–123. [Google Scholar]
- Watanabe, T.; Funazaki, K.; Taniguchi, H. Theoretical analysis on mixed convection boundary layer flow over a wedge with uniform suction or injection. Acta Mech. 1994, 105, 133–141. [Google Scholar]
- Fang, T.; Lee, C.F. A moving-wall boundary layer flow of a slightly rarefied gas free stream over a moving flat plate. Appl. Math. Lett. 2005, 18, 487–495. [Google Scholar]
- Xu, H.; Liao, S.J. Laminar flow and heat transfer in the boundary-layer of non-Newtonian fluids over a stretching flat sheet. Comput. Math. Appl. 2009, 57, 1425–1431. [Google Scholar]
- Cheng, C.Y. Natural convection heat and mass transfer from a vertical truncated cone in a porous medium saturated with a non-Newtonian fluid with variable wall temperature and concentration. Int. Commun. Heat Mass Transf. 2009, 36, 585–589. [Google Scholar]
- Gorla, R.S.R.; Chamkha, A.J.; Rashad, A.M. Mixed convective boundary layer flow over a vertical wedge embedded in a porous medium saturated with a nanofluid: Natural convection dominated regime. Nanoscale Res. Lett. 2011, 6, 207–216. [Google Scholar]
- Rahman, M.M.; Lawatia, M.A.A.; Eltayeb, I.A.; Salti, N.A. Hydromagnetic slip flow of water based nanofluids past a wedge with convective surface in the presence of heat generation or absorption. Int. J. Therm. Sci. 2012, 57, 172–182. [Google Scholar]
- Chamkha, A.J.; Rashad, A.M. Unsteady heat and mass transfer by MHD mixed convection flow from a rotating vertical cone with chemical reaction and Soret and Dufour effects. Can. J. Chem. Eng. 2014, 92, 758–767. [Google Scholar]
- Rashidi, M.M.; Rastegari, M.T.; Asadi, M.; Bég, O.A. A study of non-Newtonian flow and heat transfer over a non-isothermal wedge using the homotopy analysis method. Chem. Eng. Commun. 2012, 199, 231–256. [Google Scholar]
- Vasu, B.; Kumar, M. Transient boundary layer laminar free convective flow of a nanofluid over a vertical cone/plate. Int. J. Appl. Comput. Math. 2015, 1, 427–448. [Google Scholar]
- Vasu, B.; Gorla, R.S.R. Two-phase laminar mixed convection Al2O3 water nanofluid in elliptic duct. Nanoscale Flow Adv. Model. Appl. 2015, 4, 101–120. [Google Scholar]
- Vasu, B.; Gorla, R.S.R.; Murthy, P.V.S.N. Thermophoresis on boundary layer heat and mass transfer flow of Walters-B fluid past a radiate plate with heat sink/source. Heat Mass Transf. 2017, 53, 1553–1570. [Google Scholar]
- Vasu, B.; Gorla, R.S.R.; Murthy, P.V.S.N.; Bég, O.A.; Prasad, V.R.; Kadir, A. Unsteady flow of a nanofluid over a sphere with non-linear Boussinesq approximation. AIAA J. Thermophys. Heat Transf. 2018. [Google Scholar] [CrossRef]
- Ray, A.K.; Vasu, B.; Bég, O.A.; Gorla, R.S.R.; Murthy, P.V.S.N. Magneto-bioconvection flow of a Casson thin film with nanoparticles over an unsteady stretching sheet. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Sreenivasulu, P.; Vasu, B.; Tamalapakula, P.; Reddy, N.B. Inclined Lorentzian force effect on tangent hyperbolic radiative slip flow imbedded carbon nanotubes: Lie group analysis. J. Comput. Appl. Res. Mech. Eng. 2018. [Google Scholar] [CrossRef]
- Irgens, F. Rheology and Non-Newtonian Fluids; Springer International Publishing: New York, NY, USA, 2014. [Google Scholar]
- Prasad, V.R.; Vasu, B.; Bég, O.A.; Parshad, R. Unsteady free convection heat and mass transfer in a Walters-B viscoelastic flow past a semi-infinite vertical plate: A numerical study. Therm. Sci. 2011, 15, 291–305. [Google Scholar]
- Ray, A.K.; Vasu, B. Hydrodynamics of non-Newtonian Spriggs fluid flow past an impulsively moving plate. In Applications of Fluid Dynamics; Springer: Singapore, 2018; pp. 95–107. [Google Scholar]
- Chhabra, R.P.; Richardson, J. Non-Newtonian Flow and Applied Rheology: Engineering Applications, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2008. [Google Scholar]
- Acrivos, A.; Shah, M.J.; Petersen, E.E. Momentum and heat transfer in laminar boundary-layer flows of non-Newtonian fluids past external surfaces. AIChE J. 1960, 6, 312–317. [Google Scholar]
- Schowalter, W.R. The application of boundary-layer theory to power-law pseudoplastic fluids: Similar solutions. AIChE J. 1960, 6, 24–28. [Google Scholar]
- Gorla, R.S.R.; Kumari, M. Non-similar solutions for mixed convection in non-Newtonian fluids along a vertical plate in a porous medium. Transp. Porous Med. 1998, 33, 295–307. [Google Scholar]
- Ikbal, M.A.; Chakravarty, S.; Wong, K.K.; Mazumdar, J.; Mandal, P.K. Unsteady response of non-Newtonian blood flow through a stenosed artery in magnetic field. J. Comput. Appl. Math. 2009, 230, 243–259. [Google Scholar]
- Mahapatra, T.R.; Nandy, S.K.; Gupta, A.S. Heat transfer in the magneto hydrodynamic flow of a power-law fluid past a porous flat plate with suction or blowing. Int. Commun. Heat Mass Transf. 2012, 39, 17–23. [Google Scholar]
- Qi, Z.; Kuang, S.; Rong, Y.A. Lattice Boltzmann investigation of the wake effect on the interaction between particle and power-law fluid flow. Powder Technol. 2018, 326, 208–221. [Google Scholar]
- Vasu, B. MHD free convection flow of power-law nanofluid film along an inclined surface with viscous dissipation and joule heating. World J. Eng. 2019, 16, 115–124. [Google Scholar]
- Bég, O.A.; Malleque, K.A.; Islam, M.N. Modelling of Ostwald-deWaele non-Newtonian flow over a rotating disk in a non-Darcian porous medium. Int. J. Appl. Math. Mech. 2012, 8, 46–67. [Google Scholar]
- Choi, U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Transf. 2006, 128, 240–250. [Google Scholar]
- Minkowycz, W.J.; Sparrow, E.M.; Abraham, J.P. Nanoparticle Heat Transfer and Fluid Flow; CRC press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar]
- Godson, L.; Raja, B.; Lal, D.M.; Wongwises, S. Enhancement of heat transfer using nanofluids—An overview. Renew. Sustain. Energy Rev. 2010, 14, 629–641. [Google Scholar]
- Yacob, N.A.; Ishak, A.; Nazar, R.; Pop, I. Falkner-Skan problem for a static and moving wedge with prescribed surface heat flux in a nanofluid. Int. Commun. Heat Mass Transf. 2011, 38, 149–153. [Google Scholar]
- Kuznetsov, A.V.; Nield, D.A. Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 2010, 49, 243–247. [Google Scholar]
- Bachok, N.; Ishak, A.; Pop, I. Boundary-layer flow of nanofluids over a moving surface in a flowing fluid. Int. J. Therm. Sci. 2010, 49, 1663–1668. [Google Scholar]
- Bég, O.A.; Prasad, V.R.; Vasu, B. Numerical study of mixed bioconvection in porous media saturated with nanofluid containing oxytactic microorganisms. J. Mech. Med. Biol. 2013, 13, 1350067. [Google Scholar]
- Kuznetsov, A.V.; Nield, D.A. Natural convective boundary-layer flow of a nanofluid past a vertical plate: A revised model. Int. J. Therm. Sci. 2014, 77, 126–129. [Google Scholar]
- Malvandi, A.; Ganji, D.D. Brownian motion and thermophoresis effects on slip flow of alumina/water nanofluid inside a circular microchannel in the presence of a magnetic field. Int. J. Therm. Sci. 2014, 84, 196–206. [Google Scholar]
- Moshizi, S.A.; Malvandi, A.; Ganji, D.D.; Pop, I. A two-phase theoretical study of Al2O3–water nanofluid flow inside a concentric pipe with heat generation/absorption. Int. J. Therm. Sci. 2014, 84, 347–357. [Google Scholar]
- Kameswaran, P.K.; Vasu, B.; Murthy, P.V.S.N.; Gorla, R.S.R. Mixed convection from a wavy surface embedded in a thermally stratified nanofluid saturated porous medium with non-linear Boussinesq approximation. Int. Commun. Heat Mass 2016, 77, 78–86. [Google Scholar]
- Bég, O.A.; Basir, M.F.M.; Uddin, M.J.; Ismail, A.M. Numerical study of slip effects on unsteady asymmetric bioconvective nanofluid flow in a porous microchannel with an expanding/contracting upper wall using Buongiorno’s model. J. Mech. Med. Biol. 2017, 17, 1750059. [Google Scholar]
- Liao, S. Homotopy Analysis Method in Nonlinear Differential Equations; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Bataineh, A.S.; Noorani, M.S.M.; Hashim, I. Approximate analytical solutions of systems of PDEs by homotopy analysis method. Comput. Math Appl. 2008, 55, 2913–2923. [Google Scholar]
- Sheikholeslami, M.; Nimafar, M.; Ganji, D.D. Analytical approach for the effect of melting heat transfer on nanofluid heat transfer. Eur. Phys. J. Plus 2017, 132, 385. [Google Scholar]
- Mabood, F.; Khan, W.A.; Ismail, A.M. MHD flow over exponential radiating stretching sheet using homotopy analysis method. J. King Saud Univ. Eng. Sci. 2017, 29, 68–74. [Google Scholar]
- Sravanthi, C.S.; Gorla, R.S.R. Effects of heat source/sink and chemical reaction on MHD Maxwell nanofluid flow over a convectively heated exponentially stretching sheet using homotopy analysis method. Int. J. Appl. Mech. Eng. 2018, 23, 137–159. [Google Scholar]
- Hayat, T.; Kiran, A.; Imtiaz, M.; Alsaed, A. Unsteady flow of carbon nanotubes with chemical reaction and Cattaneo-Christov heat flux model. Nonlinear Anal. Real World Appl. 2009, 10, 2346–2356. [Google Scholar]
- Bég, O.A.; Tasveer, A.; Rashidi, M.M.; Asadi, M. Homotopy semi-numerical modelling of nanofluid convection flow from an isothermal spherical body in a permeable regime. Int. J. Microscale Nanoscale Therm. Fluid Transp. Phenom. 2012, 3, 237–266. [Google Scholar]
- Bég, O.A.; Rashidi, M.M.; Rahimzadeh, N.; Tasveer, A.; Hung, T.K. Homotopy semi-numerical simulation of two-phase thermal haemodynamics in a high permeability blood purification device. J. Mech. Med. Biol. 2013, 13, 1350066. [Google Scholar]
- Ray, A.K.; Vasu, B.; Gorla, R.S.R. Homotopy simulation of non-Newtonian spriggs fluid flow over a flat plate with oscillating motion. Int. J. Appl. Mech. Eng. 2019, 24, 359–385. [Google Scholar]
- Hassanien, I.A.; Abdullah, A.A.; Gorla, R.S.R. Flow and heat transfer in a power-law fluid over a non-isothermal stretching sheet. Math. Comput. Model. 1998, 28, 105–116. [Google Scholar]
- Shukla, R.K.; Dhir, V.K. Effect of Brownian motion on thermal conductivity of nanofluids. ASME J. Heat Transf. 2008, 130, 042406. [Google Scholar]
- Vasu, B.; Ray, A.K. Numerical study of Carreau nanofluid flow past vertical plate with the Cattaneo–Christov heat flux model. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 702–723. [Google Scholar]
- Mishra, S.R.; Shamshuddin, M.; Bég, O.A.; Kadir, A. Numerical study of heat transfer and viscous flow in a dual rotating extendable disk system with a non-Fourier heat flux model. Heat Transf. Asian Res. 2018. [Google Scholar] [CrossRef]





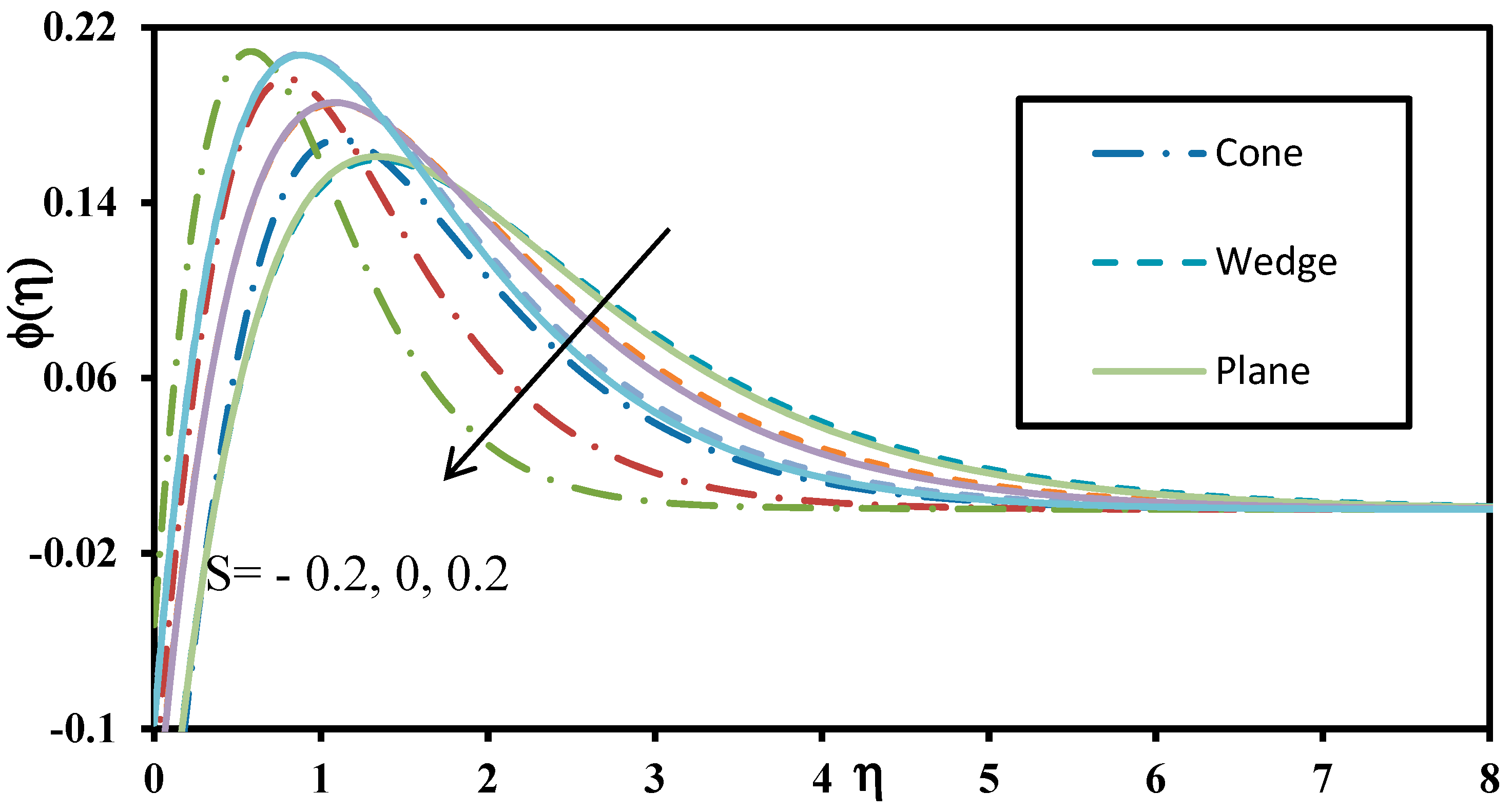
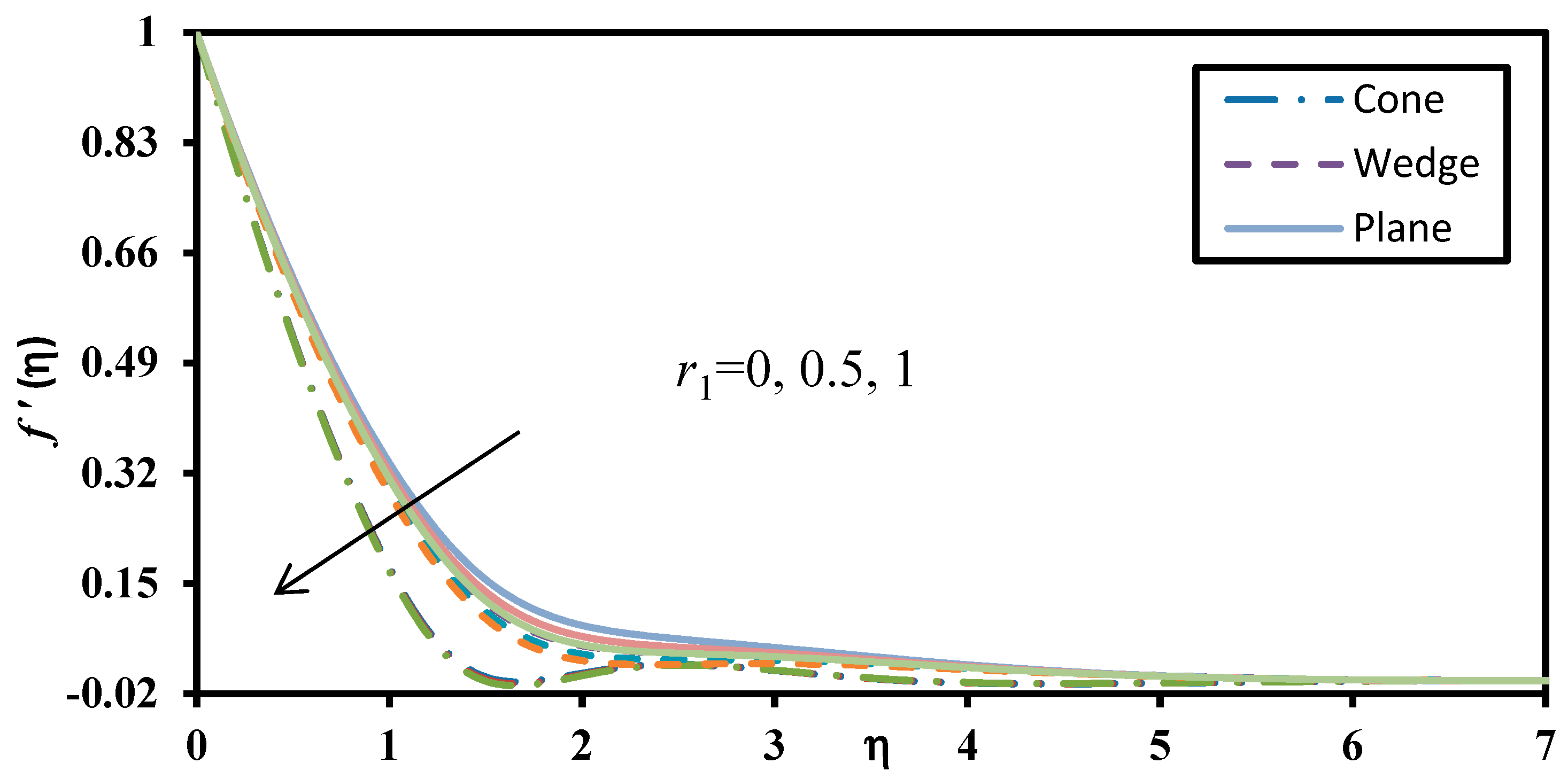
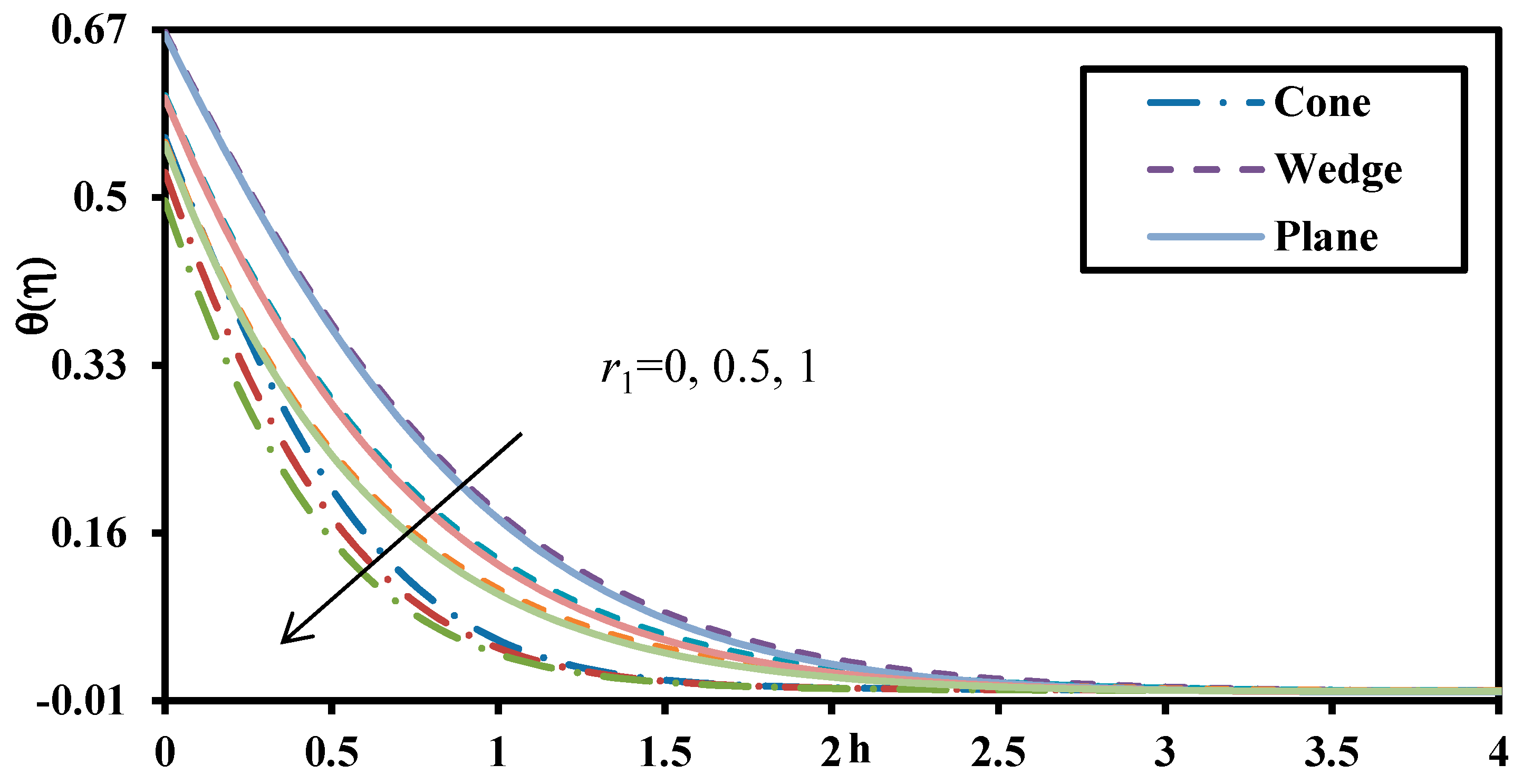
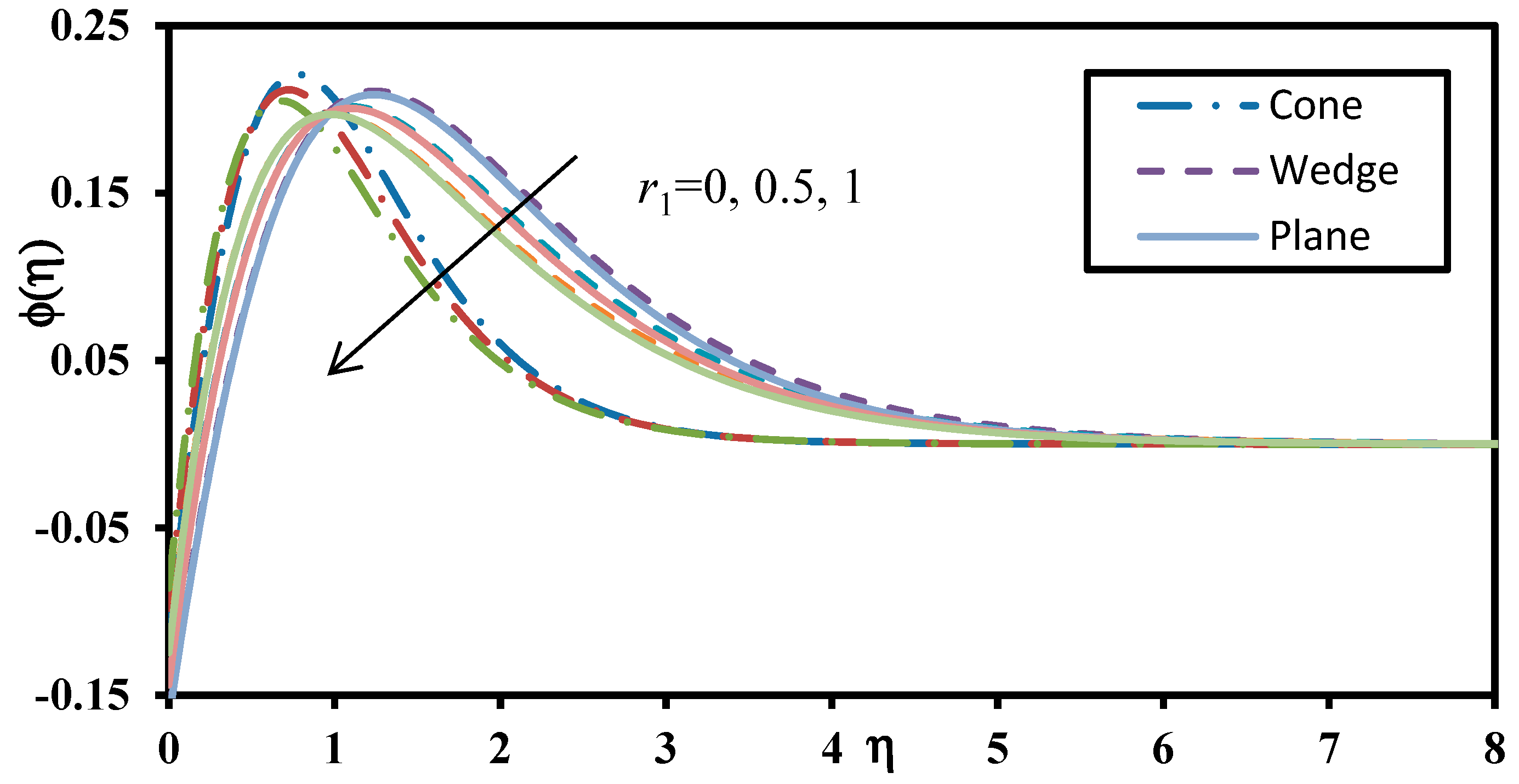


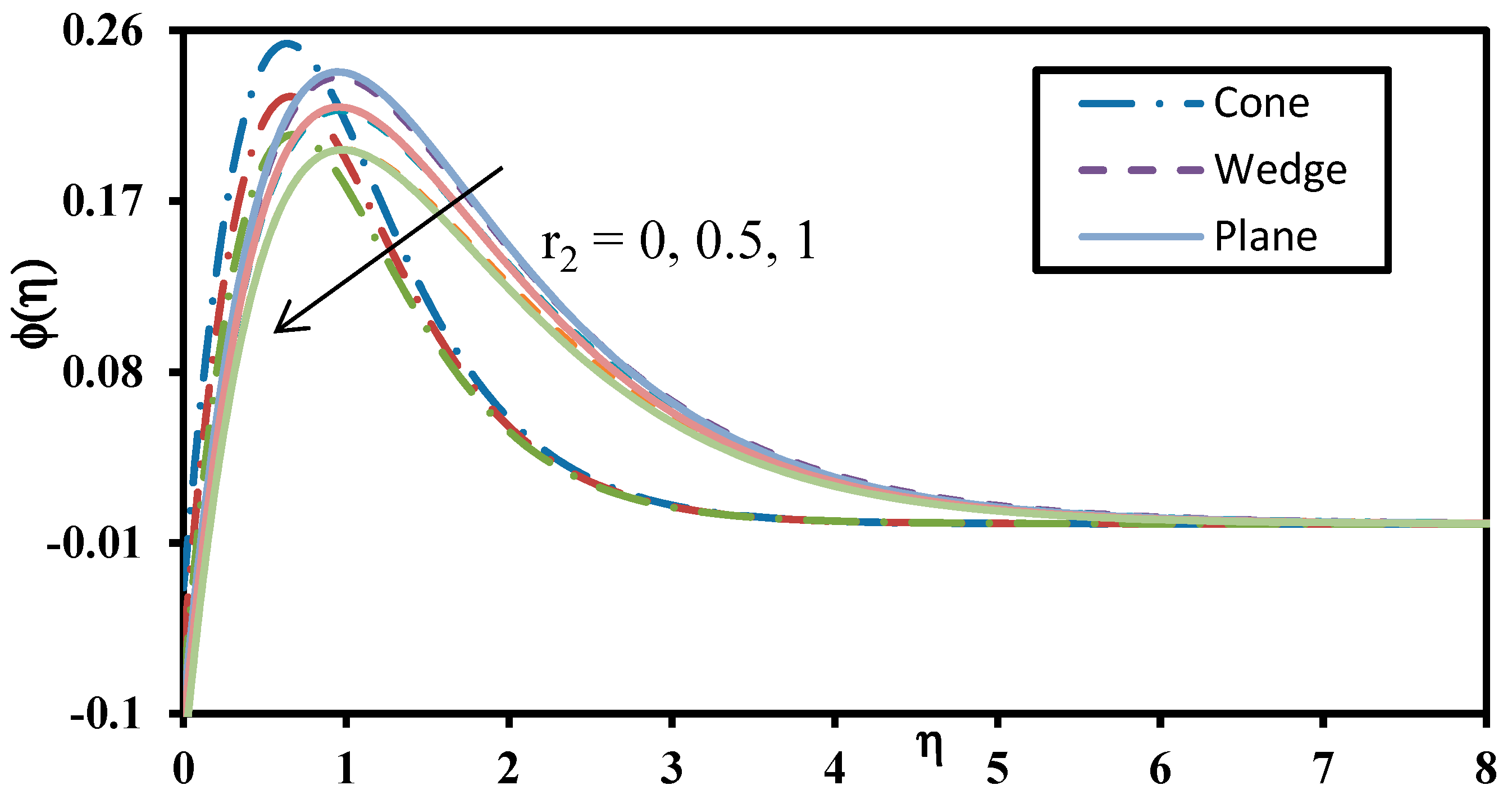
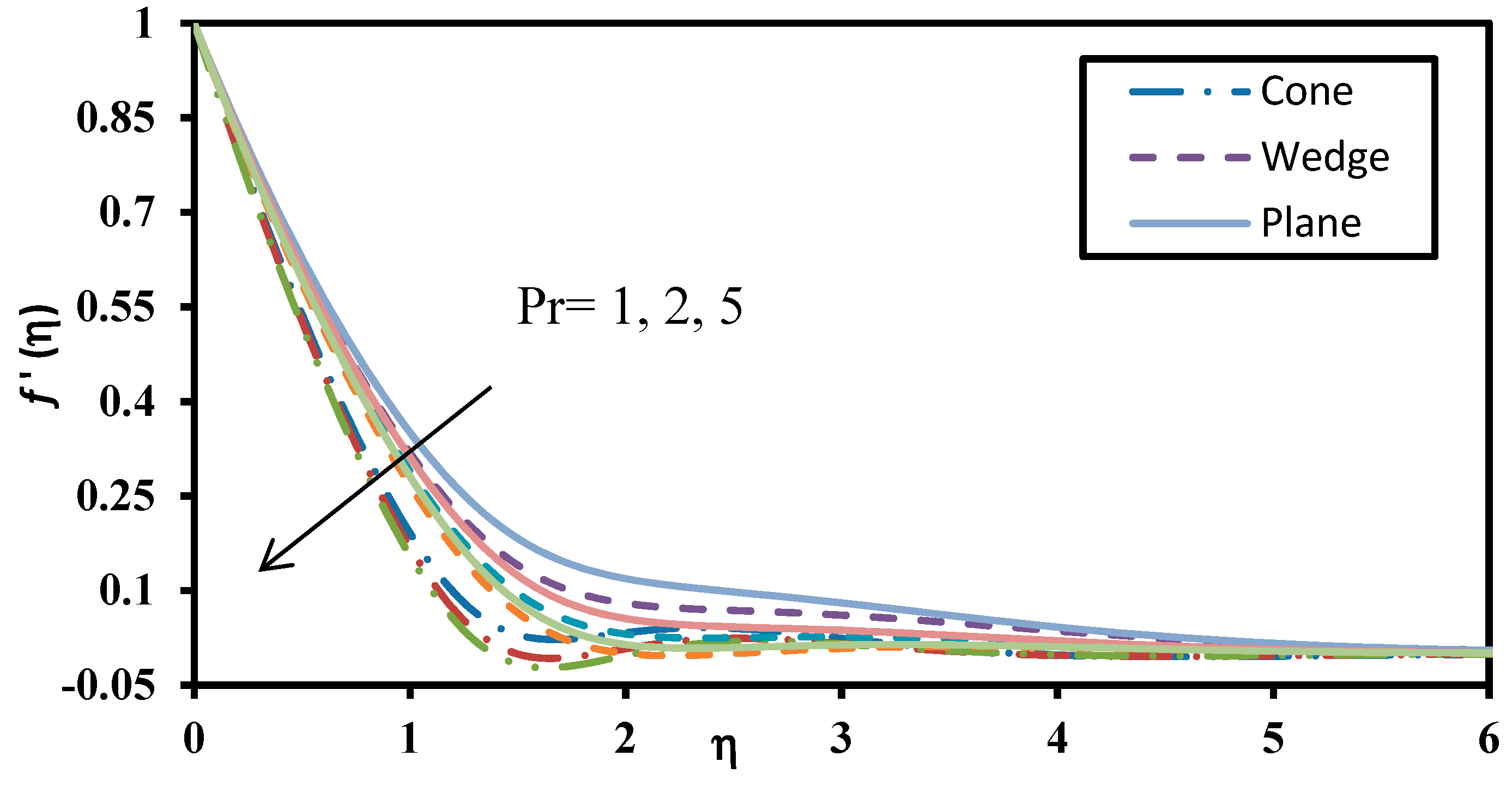

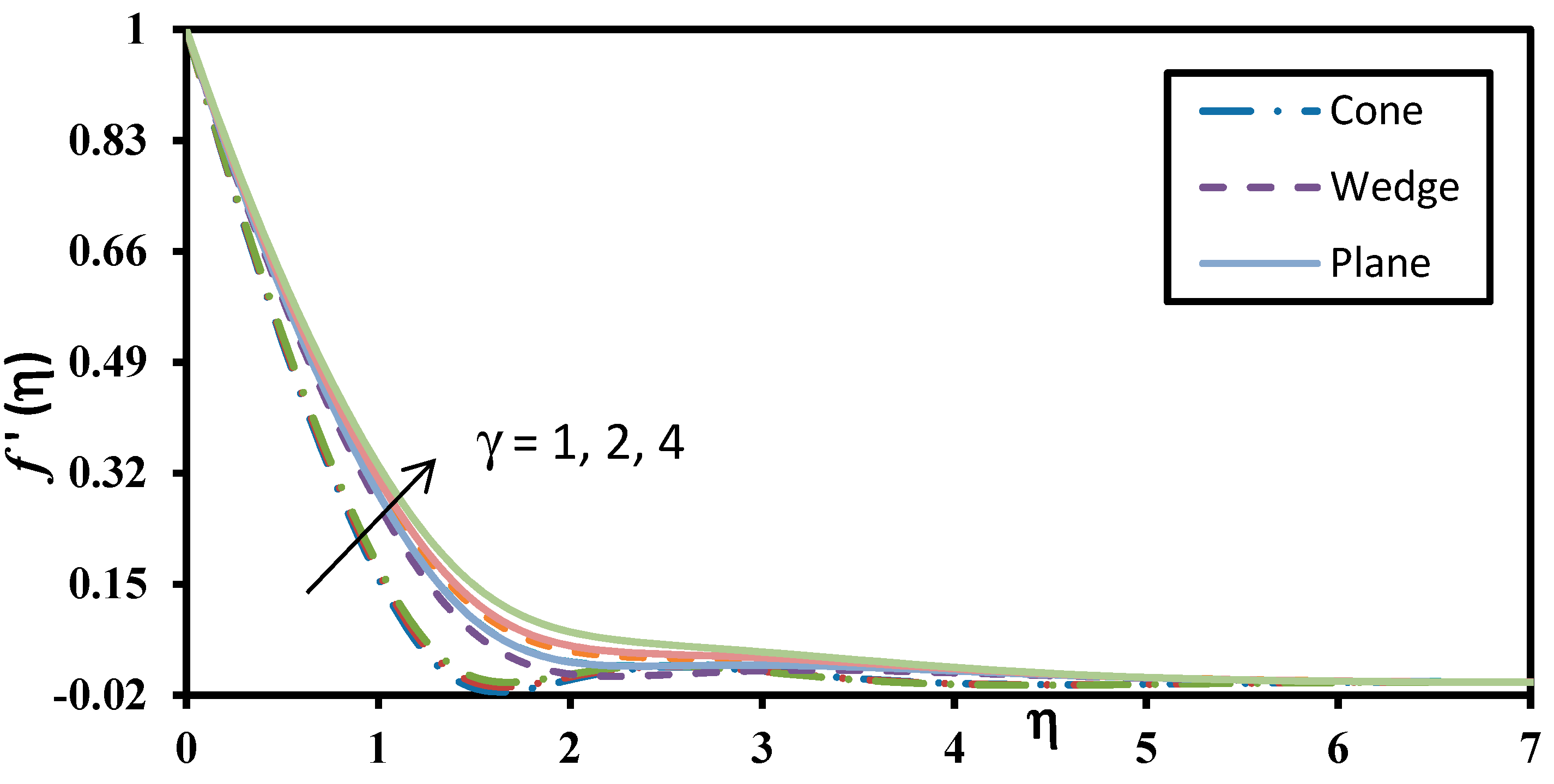

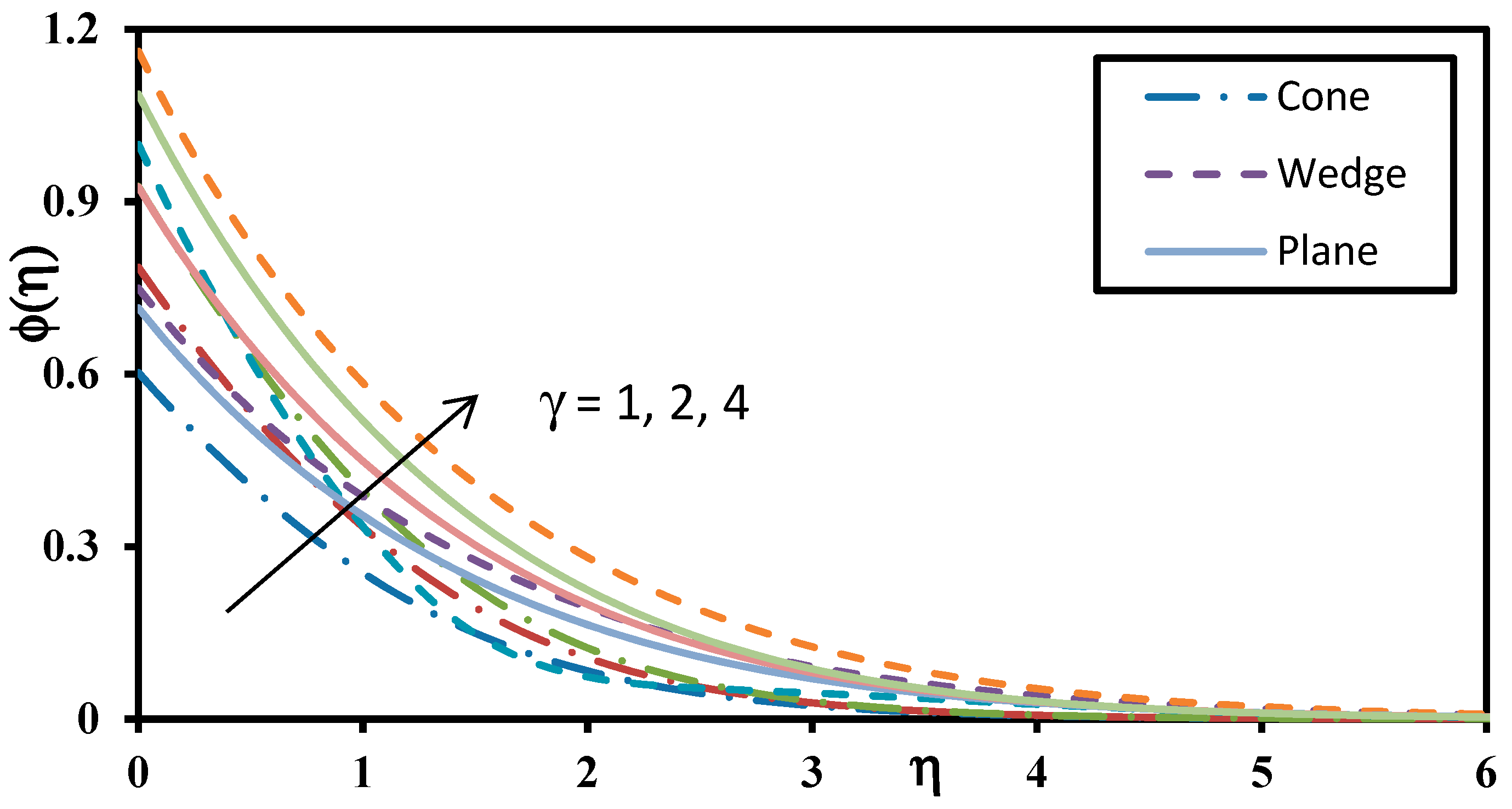

| m (Order) | f″(0) | θ′(0) | ϕ′(0) |
|---|---|---|---|
| 4 | −1.03007 | −0.89245 | 0.89245 |
| 8 | −1.03696 | −0.97244 | 0.97244 |
| 10 | −1.03724 | −0.98955 | 0.98955 |
| 12 | −1.03712 | −0.99906 | 0.99906 |
| 16 | −1.03673 | −1.00664 | −1.00665 |
| 20 | −1.03651 | −1.00822 | 1.00822 |
| 22 | −1.03658 | −1.00829 | 1.00829 |
| S | Exact [53] | Hassanien et al. [53] | Present |
|---|---|---|---|
| −1.5 | 0.500005 | 0.500005 | 0.500093 |
| −1 | 0.618042 | 0.618042 | 0.6179949 |
| −0.5 | 0.780781 | 0.780781 | 0.7807835 |
| 0 | 1.00000 | 1.00000 | 1.000000 |
| 0.5 | 1.280777 | 1.280777 | 1.280275 |
| 1 | 1.618034 | 1.618034 | 1.616967 |
| 1.5 | 2.00000 | 2.00000 | −1.99857 |
| Geometries | Residual Error | Order | Computational Time (in Seconds) |
|---|---|---|---|
| Cone | 10−3 | 4 | 4.1638 |
| 10−5 | 6 | 10.8407 | |
| 10−7 | 12 | 76.2564 | |
| Wedge | 10−3 | 2 | 0.758698 |
| 10−5 | 6 | 8.5965 | |
| 10−7 | 12 | 67.8979 | |
| Plate | 10−3 | 2 | 0.75515 |
| 10−5 | 4 | 3.2184 | |
| 10−7 | 10 | 41.0949 |
| 1 | 1.0483845 | 0.780282 | −0.78028 | |||||||||
| 2 | 1.1143002 | 1.00665 | −1.00665 | |||||||||
| 5 | 1.164296 | 1.26109 | −1.26109 | |||||||||
| 1 | 0 | 1.1701714 | 1.006335 | −1.00634 | ||||||||
| 0.5 | 1.1143002 | 1.00665 | −1.00665 | |||||||||
| 1 | 1.0579479 | 1.007142 | −1.00714 | |||||||||
| 0.5 | 0 | 1.188345 | 1.002249 | −1.00225 | ||||||||
| 0.5 | 1.1143002 | 1.00665 | −1.00665 | |||||||||
| 1 | 1.0463852 | 1.011312 | −1.01131 | |||||||||
| 0.5 | 0 | 0.9553758 | 0.942301 | −0.9423 | ||||||||
| 0.2 | 1.2824339 | 1.06812 | −1.06812 | |||||||||
| 0.4 | 1.6362823 | 1.178777 | −1.17878 | |||||||||
| 0.1 | 0 | 1.0942366 | 0.878849 | −0.87885 | ||||||||
| 0.5 | 1.1053063 | 0.949277 | −0.94928 | |||||||||
| 1 | 1.1143002 | 1.00665 | −1.00665 | |||||||||
| 0 | 1.096399 | 1.007789 | −1.00779 | |||||||||
| 0.5 | 1.1065814 | 1.007163 | −1.00716 | |||||||||
| 1 | 1.1143002 | 1.00665 | −1.00665 | |||||||||
| 1 | 1.1424273 | 1.007178 | −1.00718 | |||||||||
| 2 | 1.0713618 | 1.00337 | −1.00337 | |||||||||
| 3 | 1.0576191 | 1.000187 | −1.00019 | |||||||||
| 1.2 | 0.1 | 1.1143002 | 1.00665 | −1.00665 | ||||||||
| 0.3 | 0.9815406 | 1.007427 | −3.02228 | |||||||||
| 0.5 | 0.8671823 | 1.0101 | −5.0505 | |||||||||
| 0.1 | 0.1 | 1.1143002 | 1.00665 | −1.00665 | ||||||||
| 0.3 | 1.1629507 | 1.003694 | −0.33456 | |||||||||
| 0.5 | 1.1730216 | 1.003114 | −0.20062 | |||||||||
| 0.1 | 1 | 1.1577563 | 0.670264 | −0.67026 | ||||||||
| 2 | 1.1143002 | 1.00665 | −1.00665 | |||||||||
| 4 | 1.072742 | 1.341994 | −1.34199 |
| 1 | 0.673389 | 0.682206 | −0.682206 | |||||||||
| 2 | 0.731789 | 0.888087 | −0.888087 | |||||||||
| 5 | 0.784382 | 1.128502 | −1.128502 | |||||||||
| 1 | 0 | 0.821404 | 0.883647 | −0.883647 | ||||||||
| 0.5 | 0.731789 | 0.888087 | −0.888087 | |||||||||
| 1 | 0.647859 | 0.891888 | −0.891888 | |||||||||
| 0.5 | 0 | 0.796872 | 0.88223 | −0.88223 | ||||||||
| 0.5 | 0.731789 | 0.888087 | −0.888087 | |||||||||
| 1 | 0.670713 | 0.894365 | −0.894365 | |||||||||
| 0.5 | 0 | 0.662437 | 0.852889 | −0.852889 | ||||||||
| 0.2 | 0.805917 | 0.923339 | −0.923339 | |||||||||
| 0.4 | 0.96738 | 0.993094 | −0.993094 | |||||||||
| 0.1 | 0 | 0.692245 | 0.665117 | −0.665117 | ||||||||
| 0.5 | 0.715419 | 0.79364 | −0.79364 | |||||||||
| 1 | 0.731789 | 0.888087 | −0.888087 | |||||||||
| 0 | 0.727855 | 0.888483 | −0.888482 | |||||||||
| 0.5 | 0.72746 | 0.888416 | −0.888416 | |||||||||
| 1 | 0.731789 | 0.888087 | −0.888087 | |||||||||
| 1 | 0.769299 | 0.886881 | −0.886881 | |||||||||
| 2 | 0.66277 | 0.888964 | −0.888963 | |||||||||
| 3 | 0.631357 | 0.888297 | −0.88829 | |||||||||
| 1.2 | 0.1 | 0.731789 | 0.888087 | −0.888087 | ||||||||
| 0.3 | 0.611019 | 0.893689 | −2.681066 | |||||||||
| 0.5 | 0.5012 | 0.901164 | −4.505822 | |||||||||
| 0.1 | 0.1 | 0.731789 | 0.888087 | −0.888087 | ||||||||
| 0.3 | 0.774666 | 0.884138 | −0.294713 | |||||||||
| 0.5 | 0.783482 | 0.88337 | −0.176674 | |||||||||
| 0.1 | 1 | 0.777708 | 0.614742 | −0.614742 | ||||||||
| 2 | 0.731789 | 0.888087 | −0.888087 | |||||||||
| 4 | 0.691919 | 1.141768 | −1.141768 |
| 1 | 0.5967038 | 0.689775 | −0.68978 | |||||||||
| 2 | 0.6719077 | 0.892232 | −0.89223 | |||||||||
| 5 | 0.7421422 | 1.130564 | −1.13056 | |||||||||
| 1 | 0 | 0.7925617 | 0.886282 | −0.88628 | ||||||||
| 0.5 | 0.6719077 | 0.892232 | −0.89223 | |||||||||
| 1 | 0.5608891 | 0.896999 | −0.897 | |||||||||
| 0.5 | 0 | 0.7587574 | 0.883975 | −0.88398 | ||||||||
| 0.5 | 0.6719077 | 0.892232 | −0.89223 | |||||||||
| 1 | 0.5926799 | 0.901358 | −0.90136 | |||||||||
| 0.5 | 0 | 0.6056181 | 0.857314 | −0.85731 | ||||||||
| 0.2 | 0.7435705 | 0.927157 | −0.92716 | |||||||||
| 0.4 | 0.9023529 | 0.996141 | −0.99614 | |||||||||
| 0.1 | 0 | 0.619437 | 0.669709 | −0.66971 | ||||||||
| 0.5 | 0.6656502 | 0.892576 | −0.89258 | |||||||||
| 1 | 0.6719077 | 0.892232 | −0.89223 | |||||||||
| 0 | 0.666216 | 0.892418 | −0.89242 | |||||||||
| 0.5 | 0.6656502 | 0.892576 | −0.89258 | |||||||||
| 1 | 0.6719077 | 0.892232 | −0.89223 | |||||||||
| 1 | 0.7220157 | 0.890116 | −0.89012 | |||||||||
| 2 | 0.5816218 | 0.894629 | −0.89463 | |||||||||
| 3 | 0.5412732 | 0.894543 | −0.89454 | |||||||||
| 1.2 | 0.1 | 0.6719077 | 0.892232 | −0.89223 | ||||||||
| 0.3 | 0.5166001 | 0.904096 | −2.71229 | |||||||||
| 0.5 | 0.3788474 | 0.920086 | −4.60043 | |||||||||
| 0.1 | 0.1 | 0.6719077 | 0.892232 | −0.89223 | ||||||||
| 0.3 | 0.7287665 | 0.886638 | −0.29555 | |||||||||
| 0.5 | 0.7406224 | 0.885563 | −0.17711 | |||||||||
| 0.1 | 1 | 0.7334558 | 0.616243 | −0.61624 | ||||||||
| 2 | 0.6719077 | 0.892232 | −0.89223 | |||||||||
| 4 | 0.6192847 | 1.149904 | −1.1499 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ray, A.K.; Vasu, B.; Bég, O.A.; Gorla, R.S.R.; Murthy, P.V.S.N. Homotopy Semi-Numerical Modeling of Non-Newtonian Nanofluid Transport External to Multiple Geometries Using a Revised Buongiorno Model. Inventions 2019, 4, 54. https://doi.org/10.3390/inventions4040054
Ray AK, Vasu B, Bég OA, Gorla RSR, Murthy PVSN. Homotopy Semi-Numerical Modeling of Non-Newtonian Nanofluid Transport External to Multiple Geometries Using a Revised Buongiorno Model. Inventions. 2019; 4(4):54. https://doi.org/10.3390/inventions4040054
Chicago/Turabian StyleRay, Atul Kumar, Buddakkagari Vasu, O. Anwar Bég, Rama S.R. Gorla, and P.V.S.N. Murthy. 2019. "Homotopy Semi-Numerical Modeling of Non-Newtonian Nanofluid Transport External to Multiple Geometries Using a Revised Buongiorno Model" Inventions 4, no. 4: 54. https://doi.org/10.3390/inventions4040054
APA StyleRay, A. K., Vasu, B., Bég, O. A., Gorla, R. S. R., & Murthy, P. V. S. N. (2019). Homotopy Semi-Numerical Modeling of Non-Newtonian Nanofluid Transport External to Multiple Geometries Using a Revised Buongiorno Model. Inventions, 4(4), 54. https://doi.org/10.3390/inventions4040054





