An Innovative Stochastic Multi-Agent-Based Energy Management Approach for Microgrids Considering Uncertainties
Abstract
1. Introduction
1.1. State-of-the-Art
1.2. Artificial Intelligence (AI) Techniques in Microgrid Energy Management
- UncertaintyThe wind and solar generation uncertainty, as well as the load uncertainty, and the interaction of the load and the generation are considered simultaneously in a multi-agent based microgrid energy management approach.
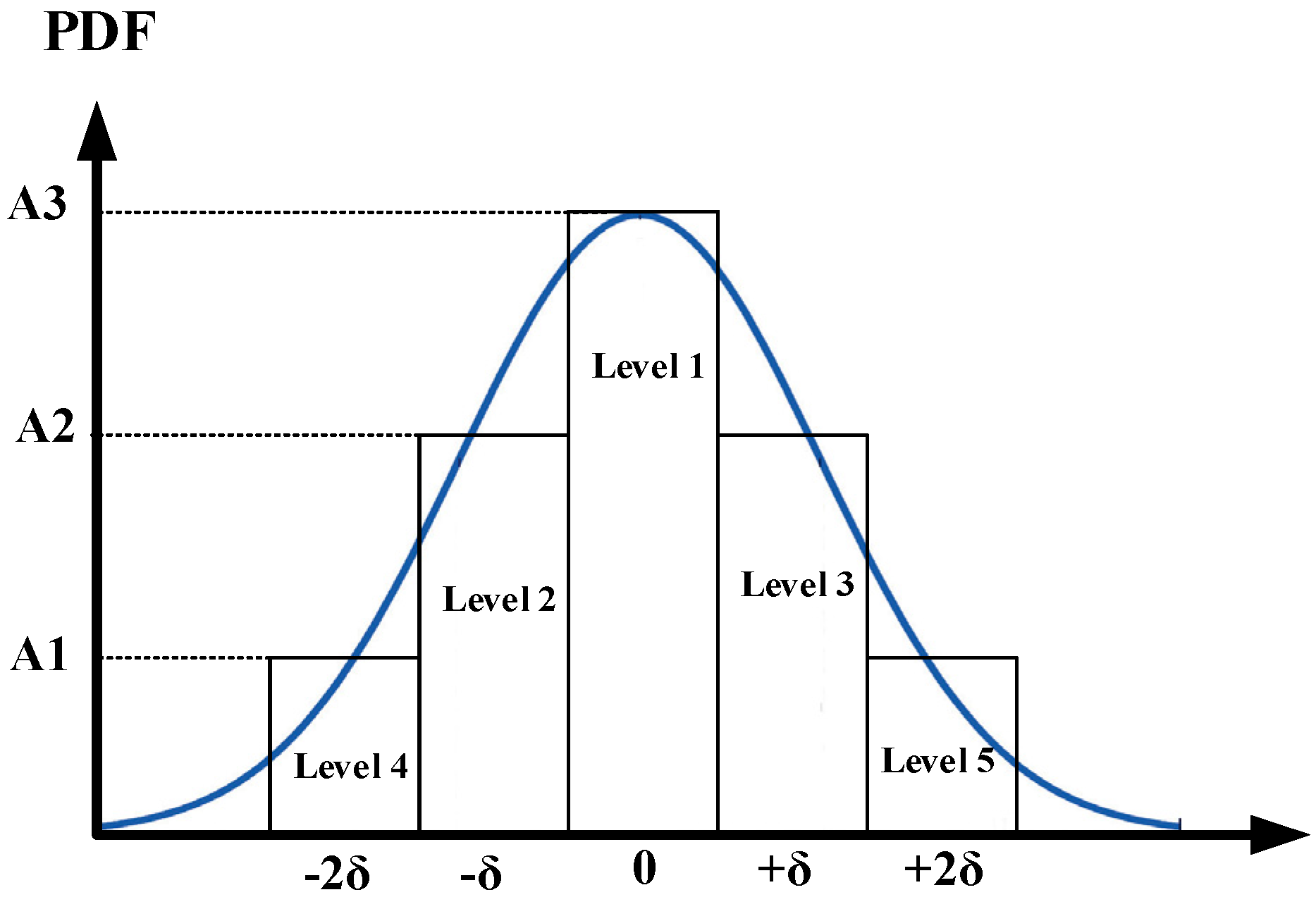
- Weighted Objective FunctionA new weighted objective function is proposed for the microgrid energy management in which each contingency influences the objective function in terms of its own probability coefficient obtained from the deployed Probability Density Function.
- Metaheuristic Optimization MethodA modified version of the Lightning Search Algorithm is presented for the energy management problem. Having higher accuracy than its previous version, the modified algorithm permits a more precise energy management of a microgrid under uncertainty.
2. Problem Formulation
2.1. Proposed Objective Function
2.2. Constraints
3. Uncertainties in the Proposed Model
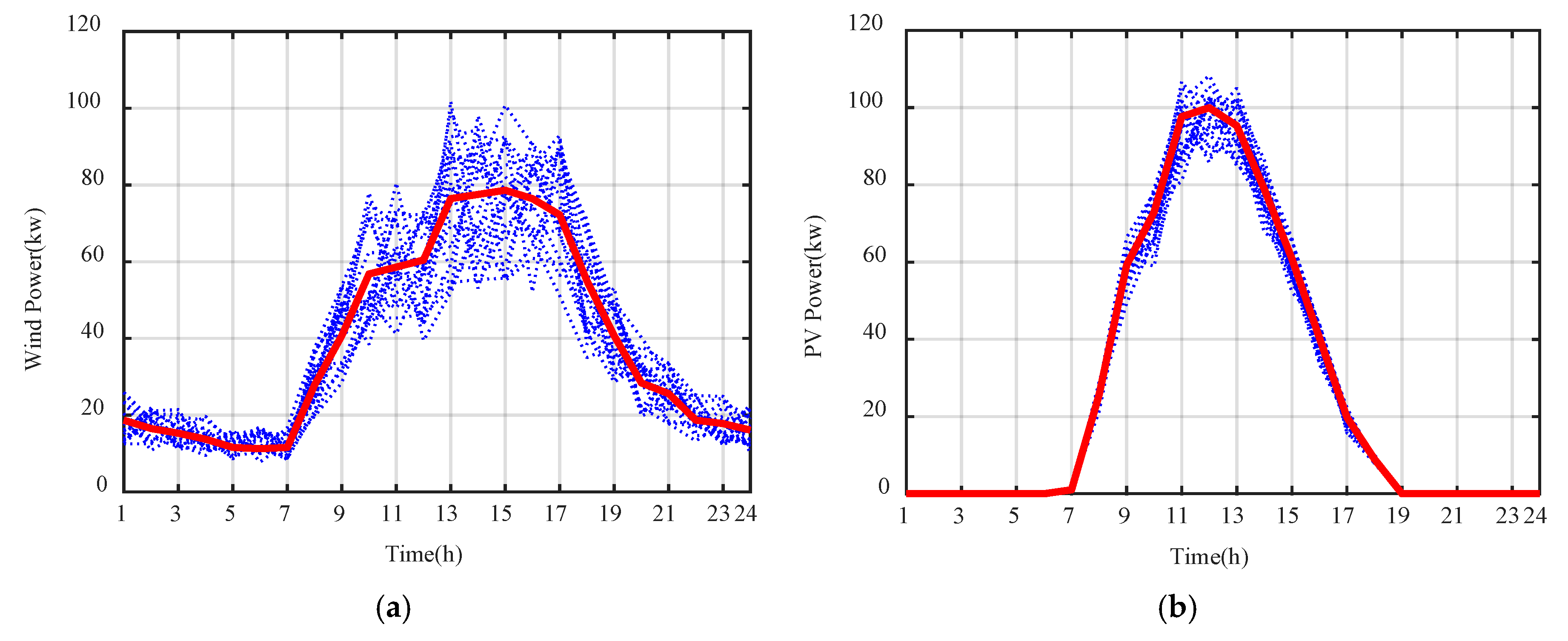
3.1. Photovoltaic (PV) System Model
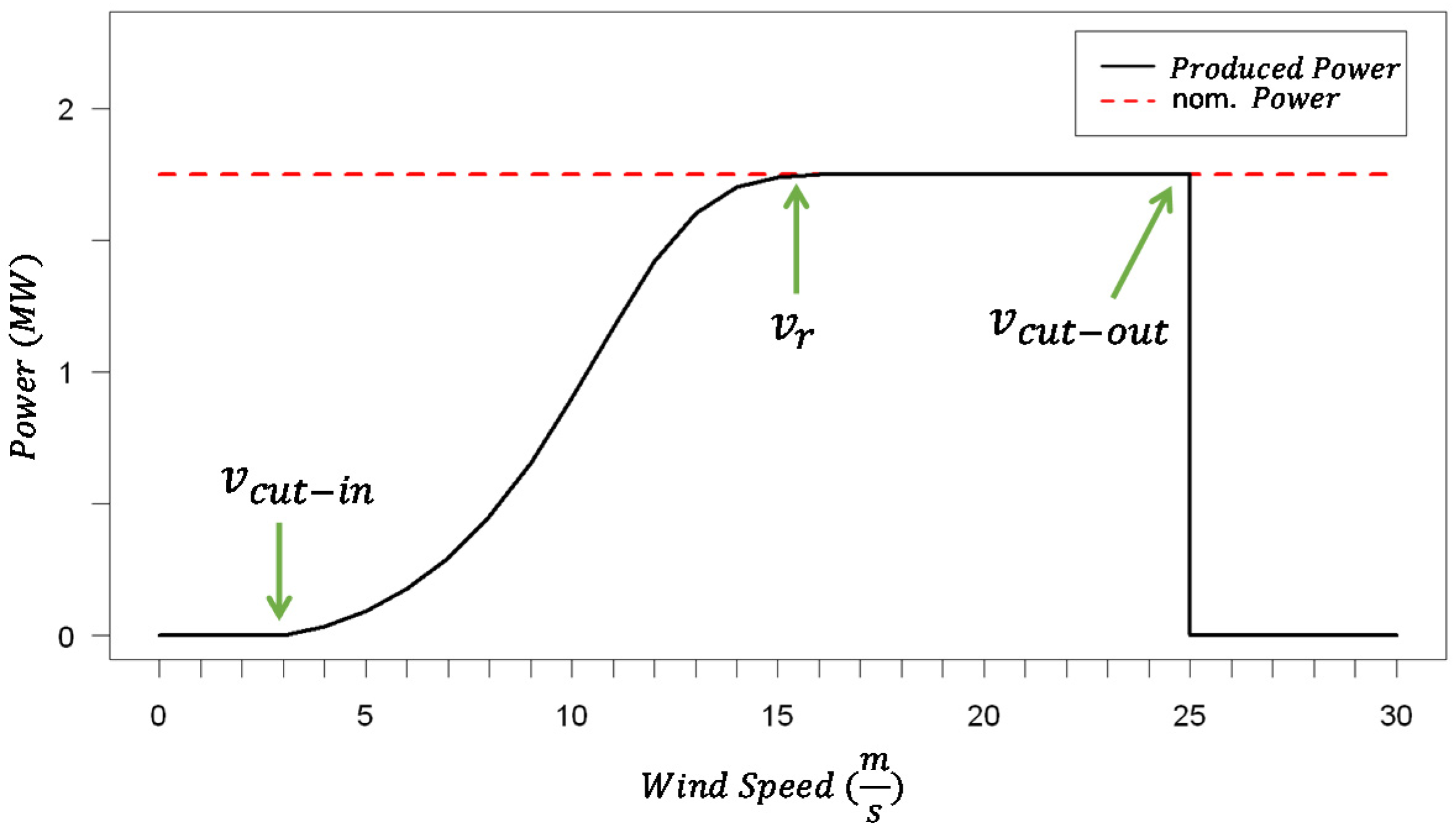
3.2. Wind Turbine (WT) System Model
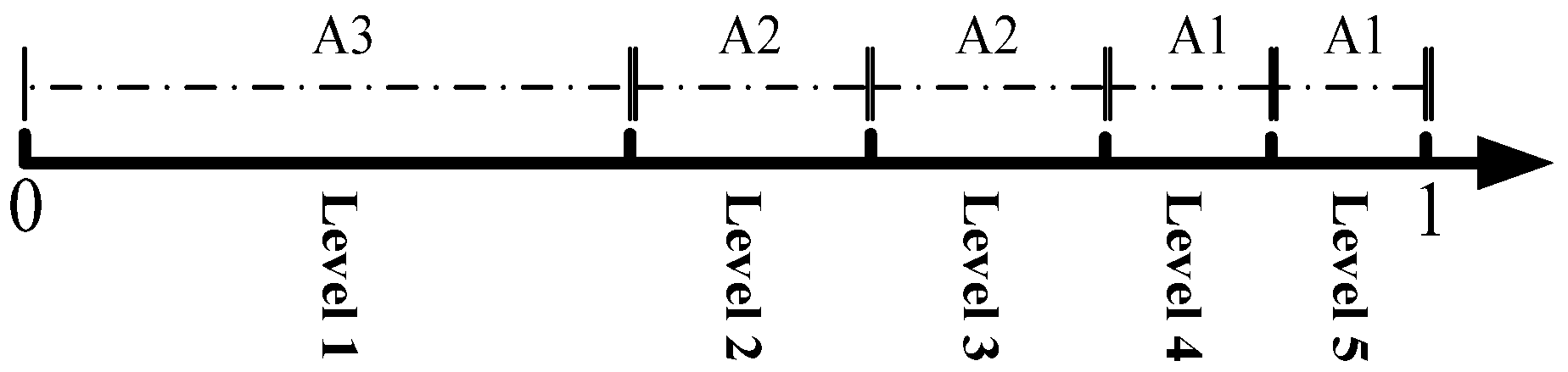
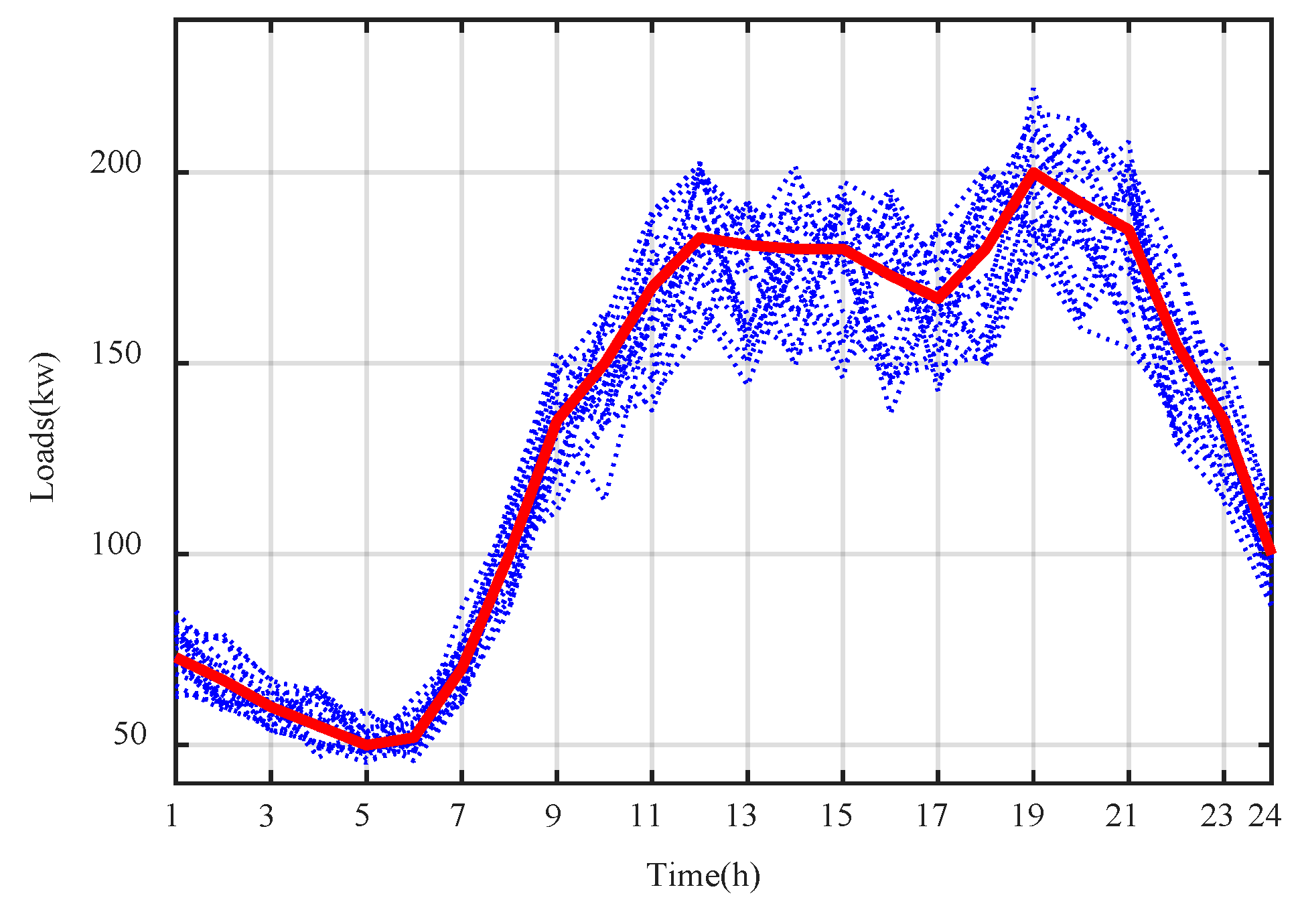
3.3. Scenario Generation
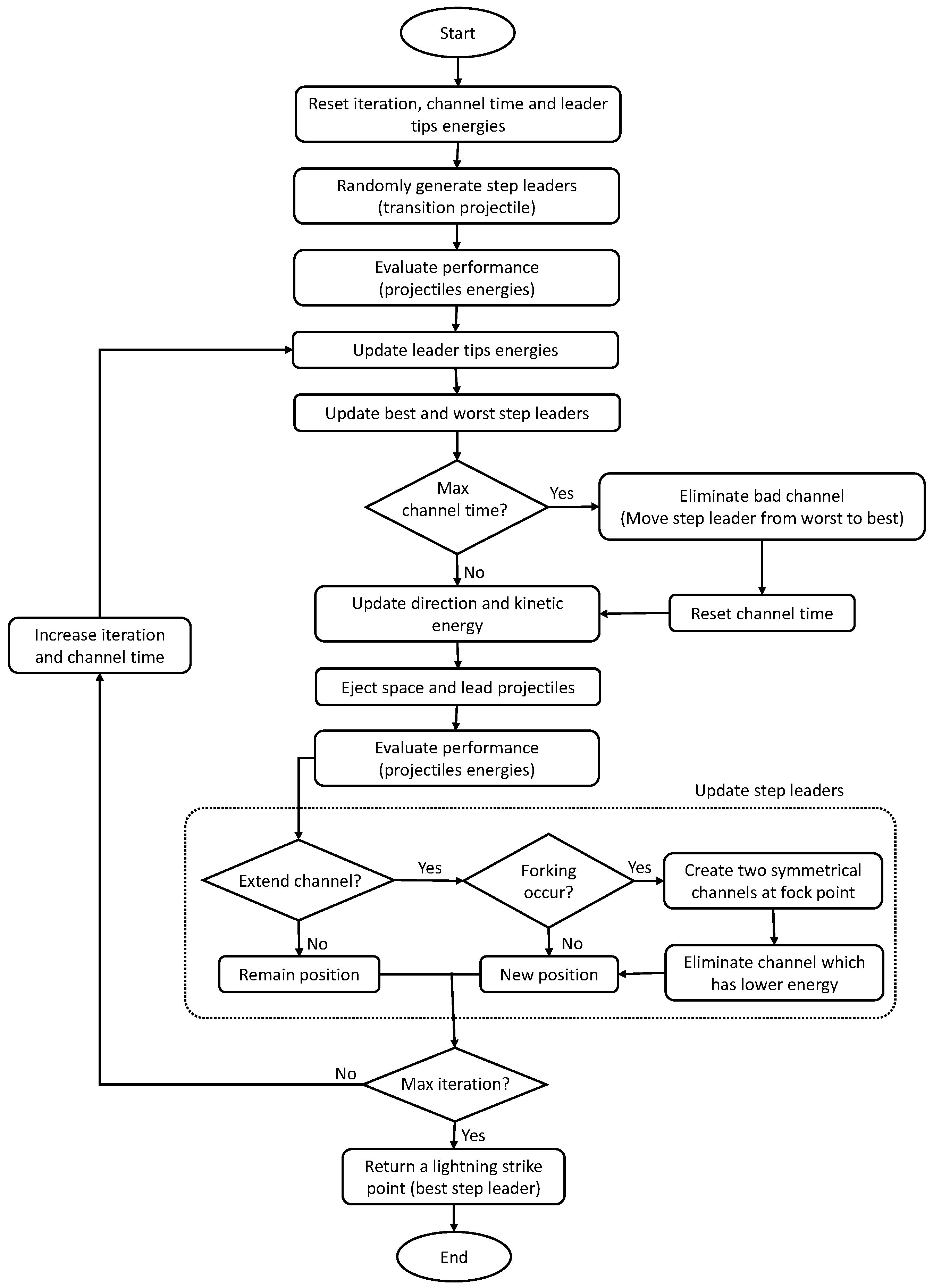
4. Lightning Search Algorithm (LSA)
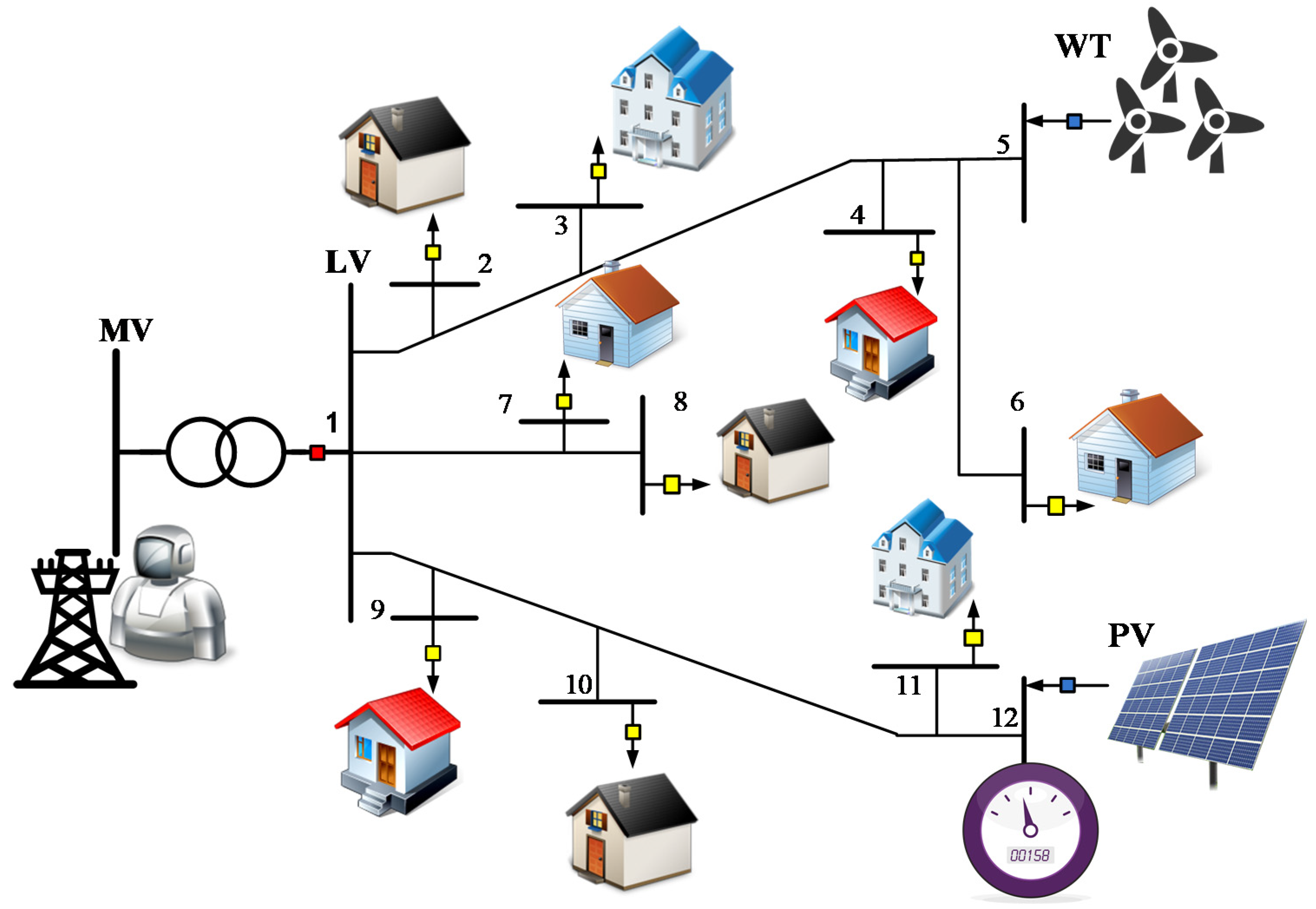
5. Case Study: Microgrid System Model
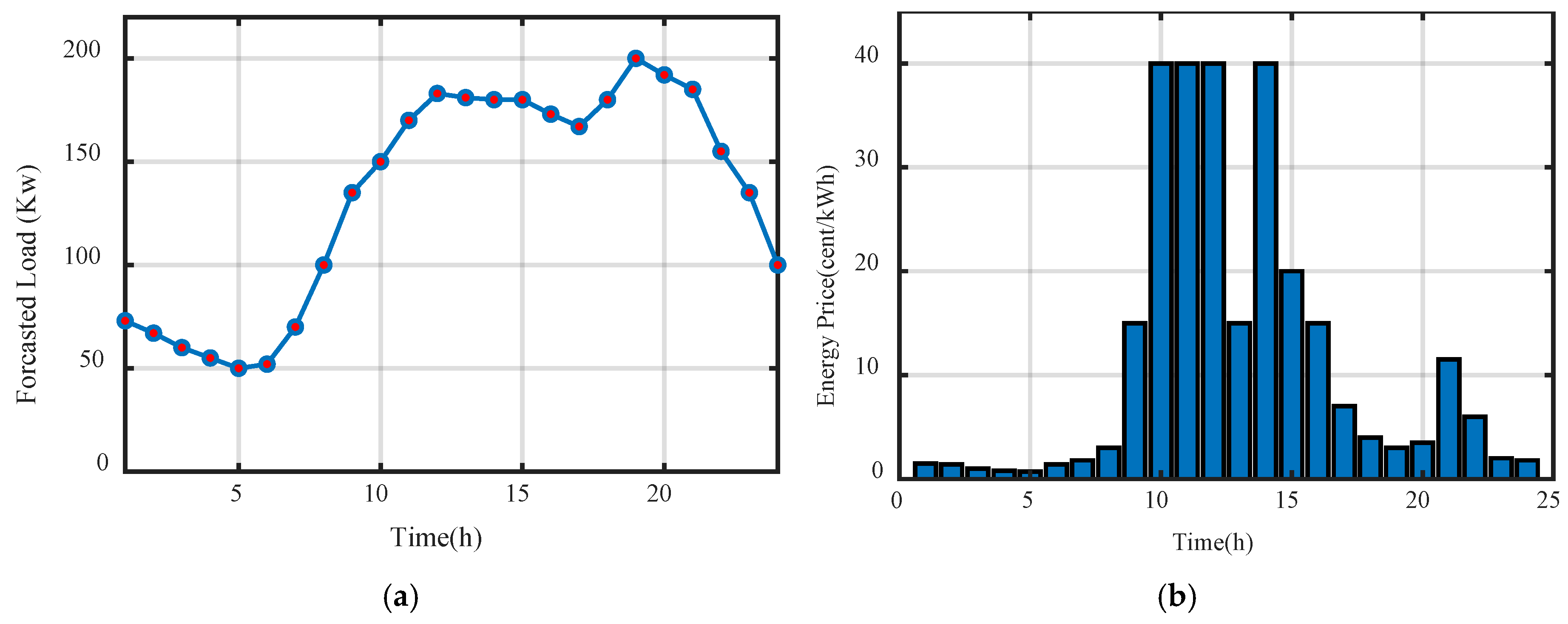
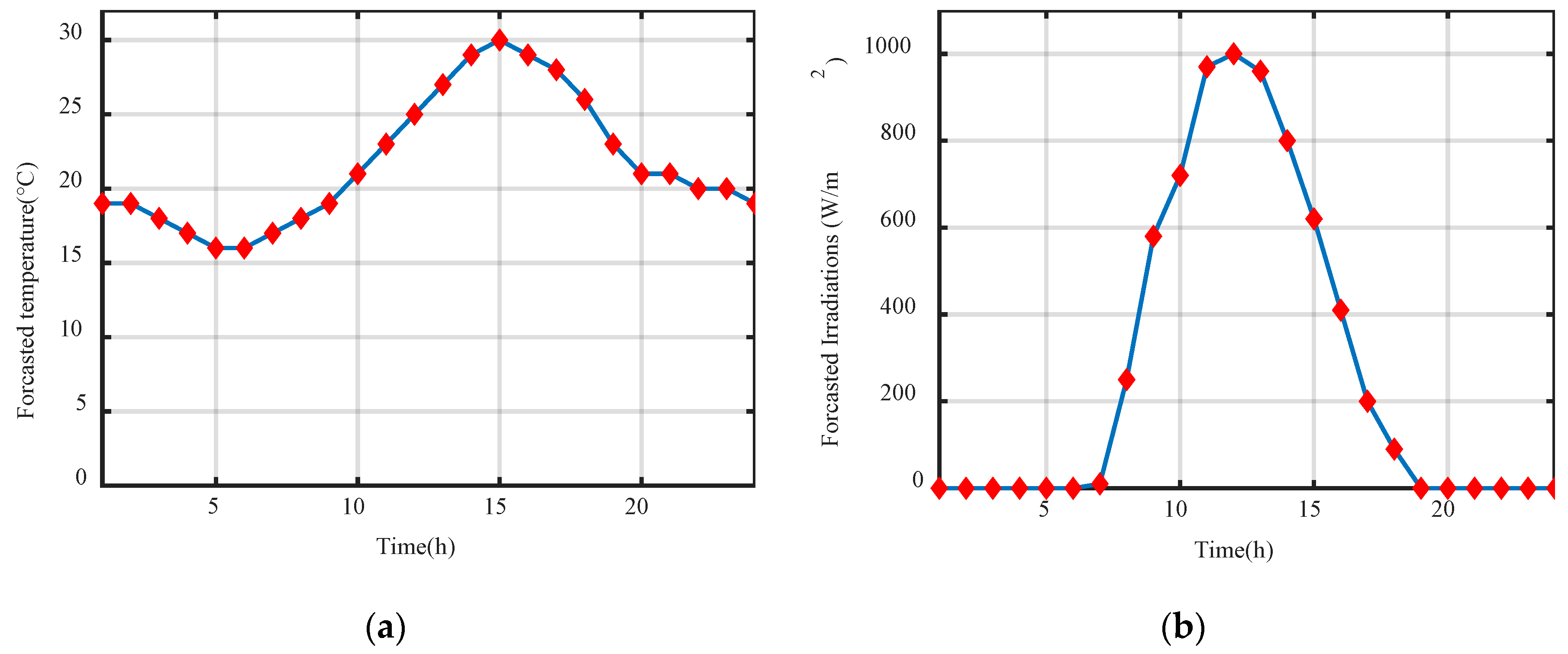
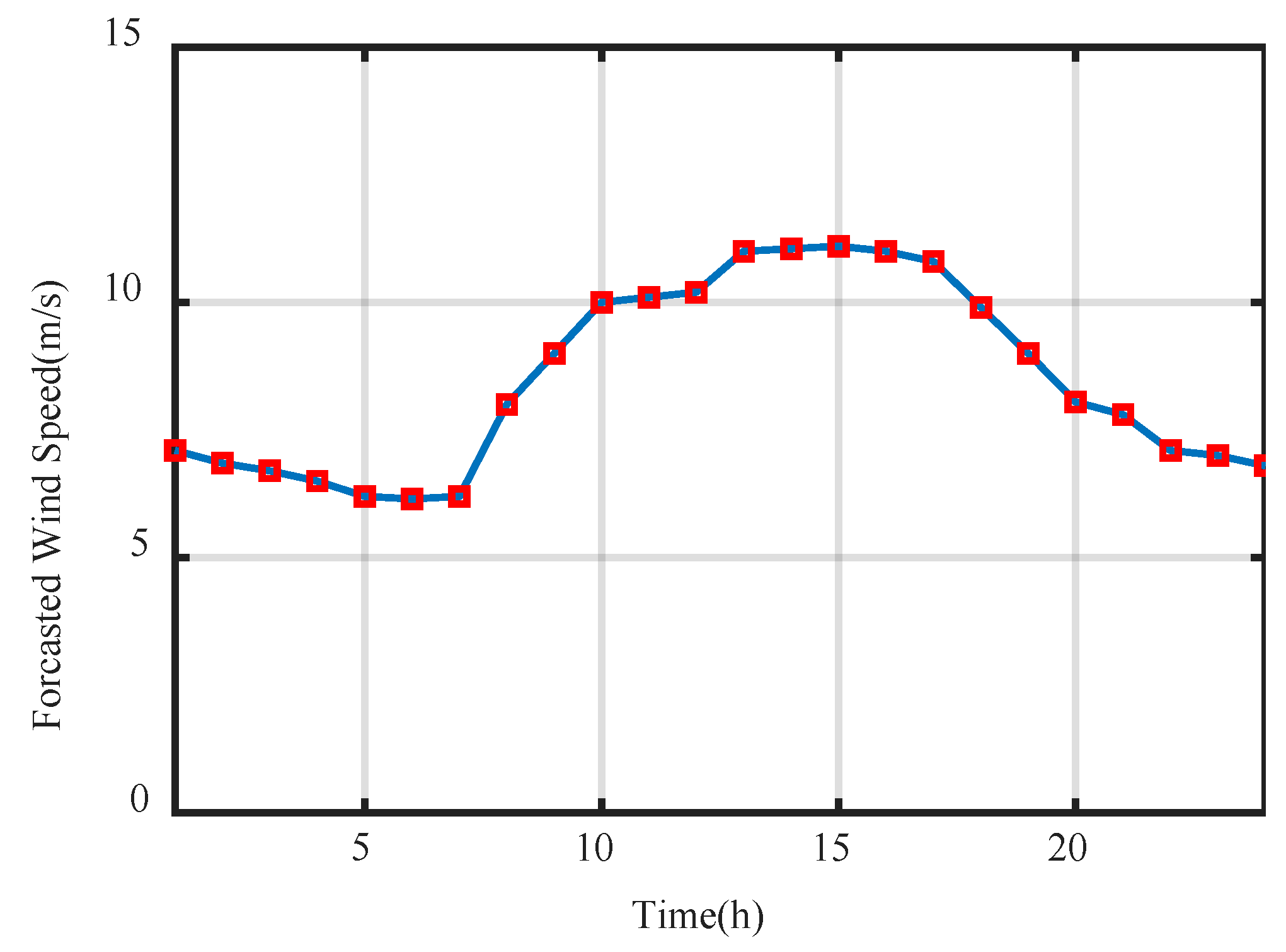
6. Simulation Result
- Step 1:
- Collecting the solar radiation, the wind speed and the load data in the microgrid.
- Step 2:
- Selecting the appropriate PDF for the variables (irradiation, wind speed and load) using the values obtained in step one.
- Step 3:
- Generating random data for the irradiations, the wind speed, and the load using the PDFs designed in step two.
- Step 4:
- Selecting scenarios using the roulette wheel mechanism.
- Step 5:
- Calculating the optimal microgrid energy management by deploying the modified version of LSA algorithm and using the proposed objective function.
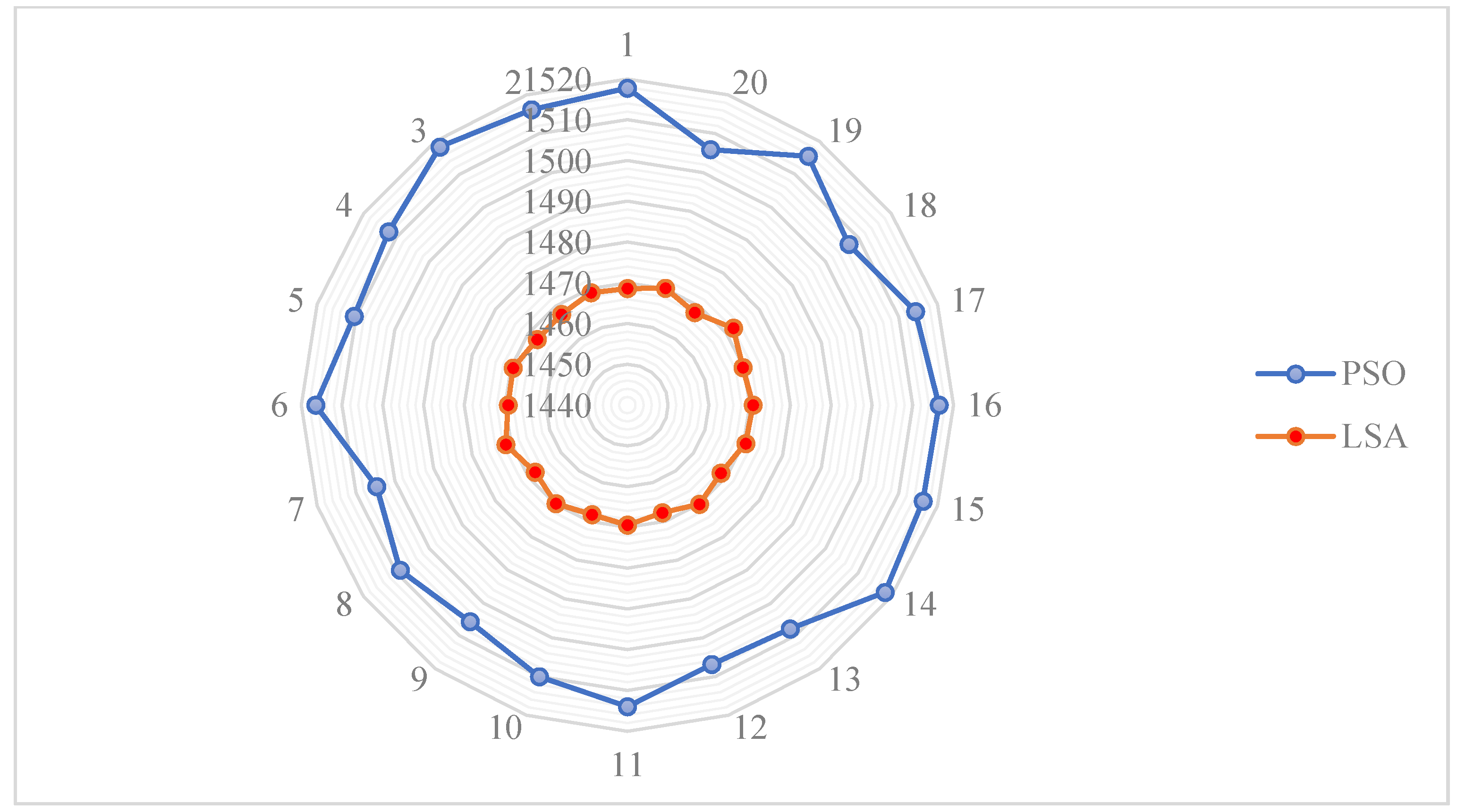
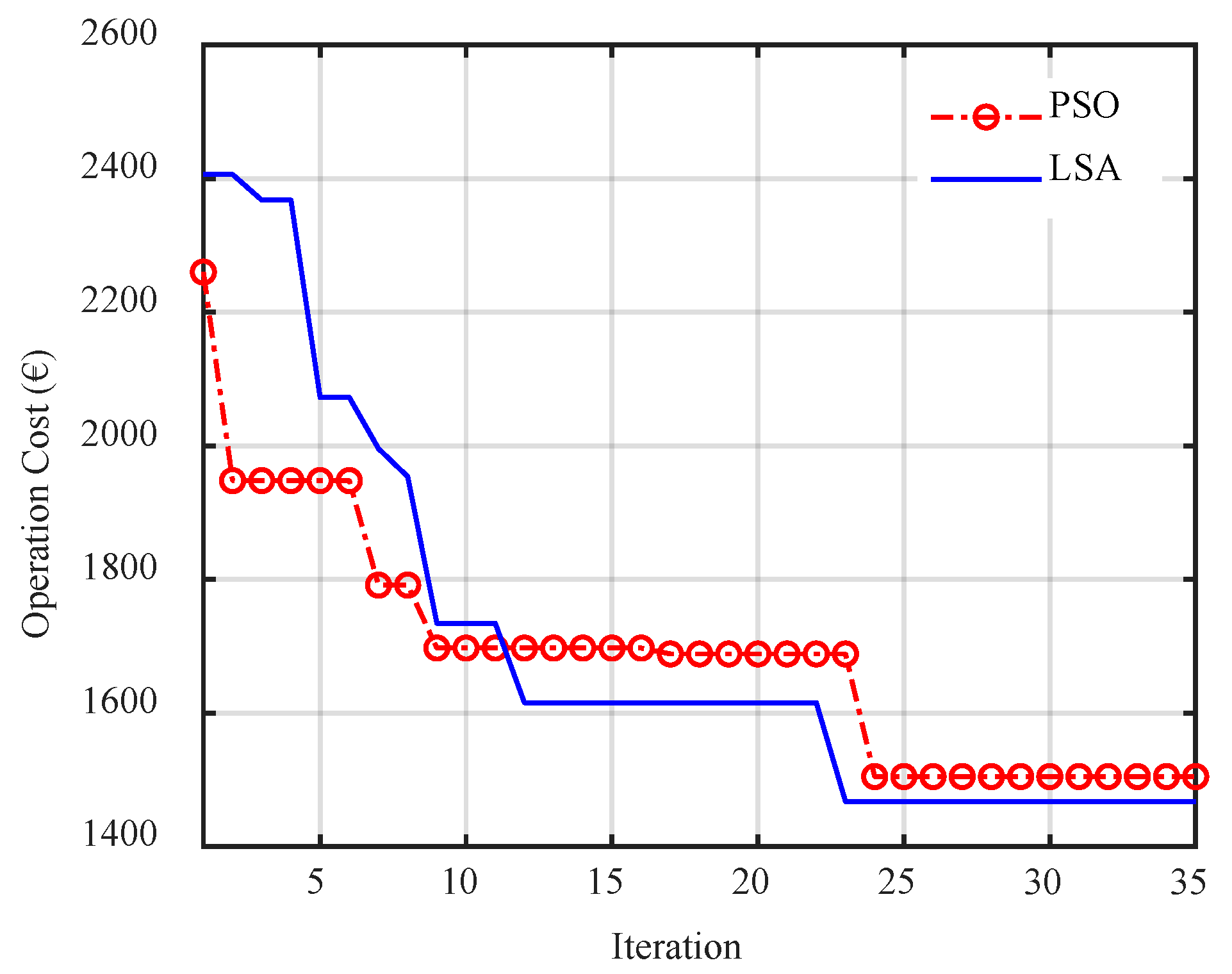
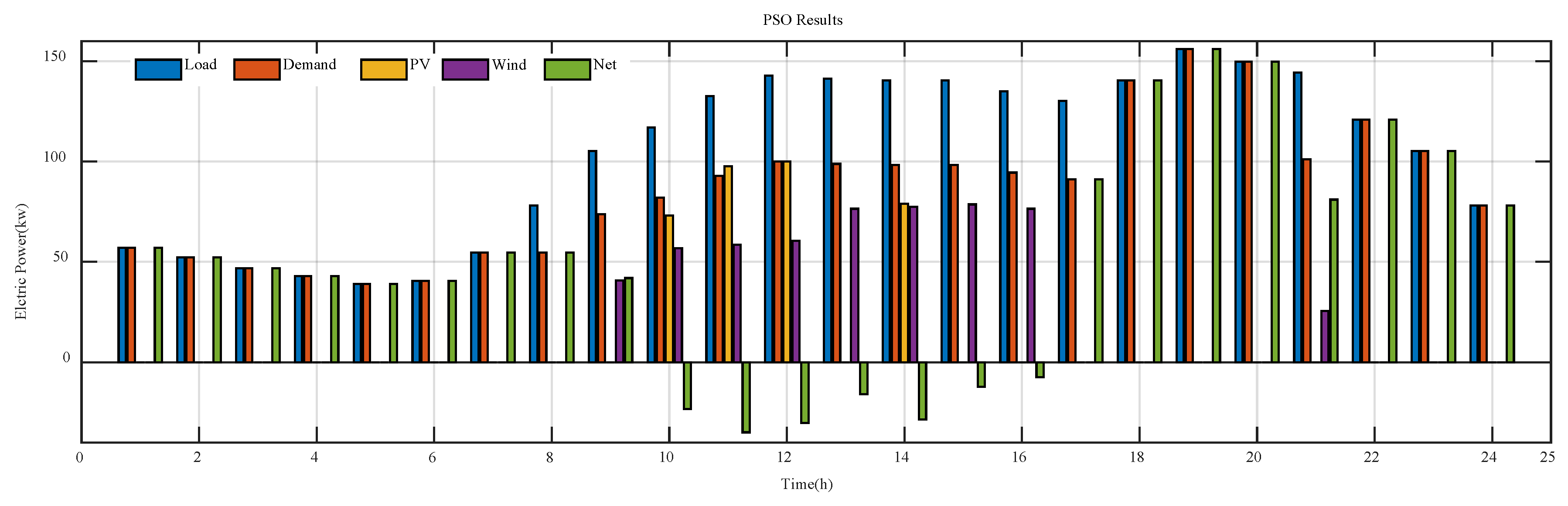
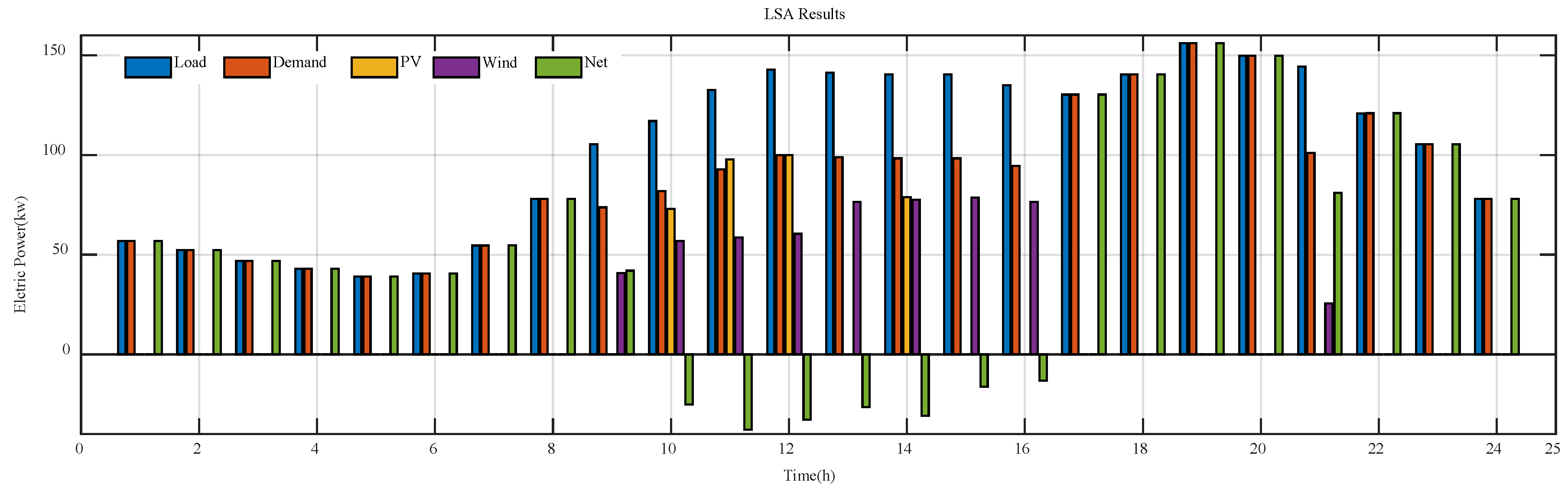
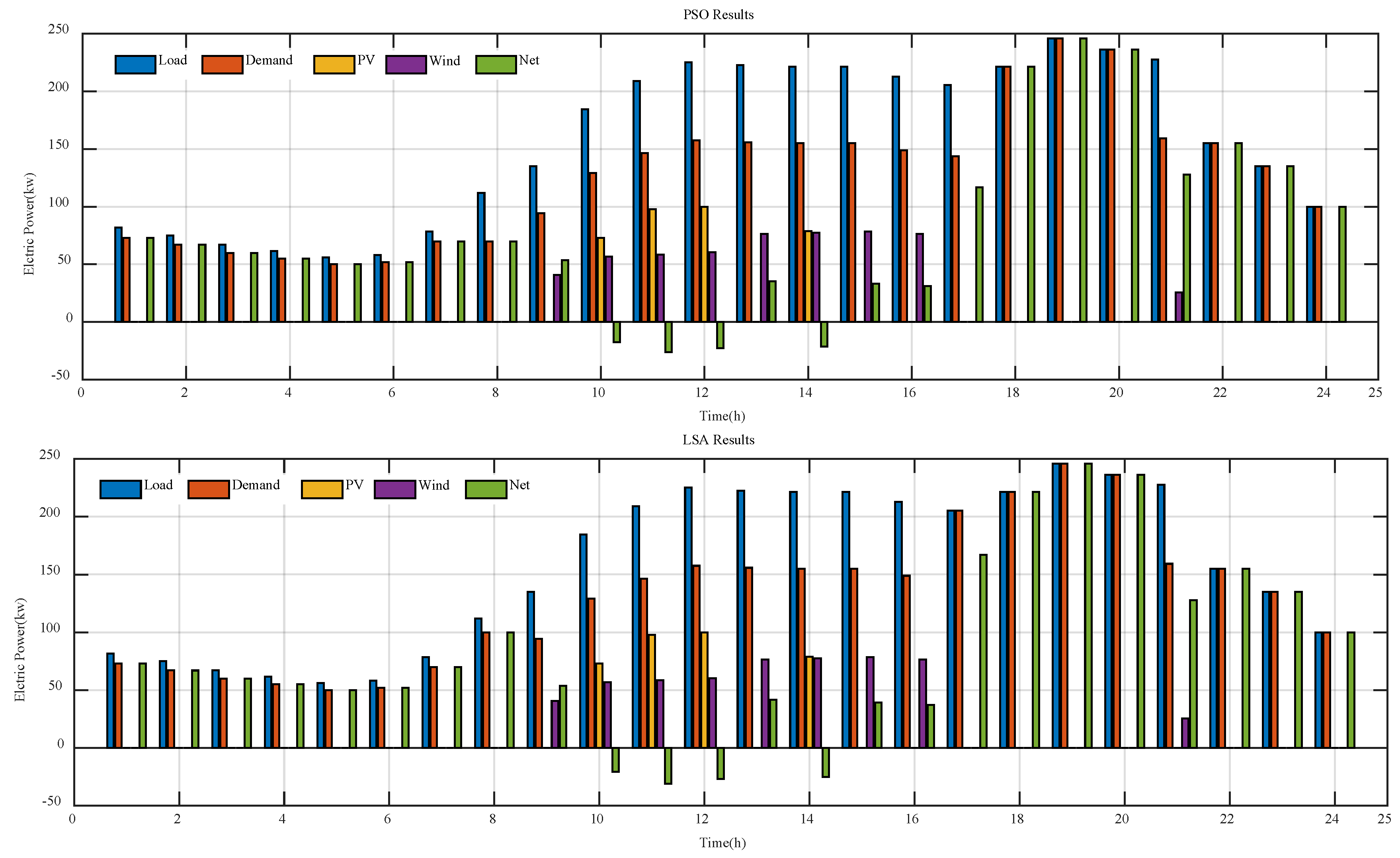
6.1. Part One: Optimization Regardless of Uncertainty
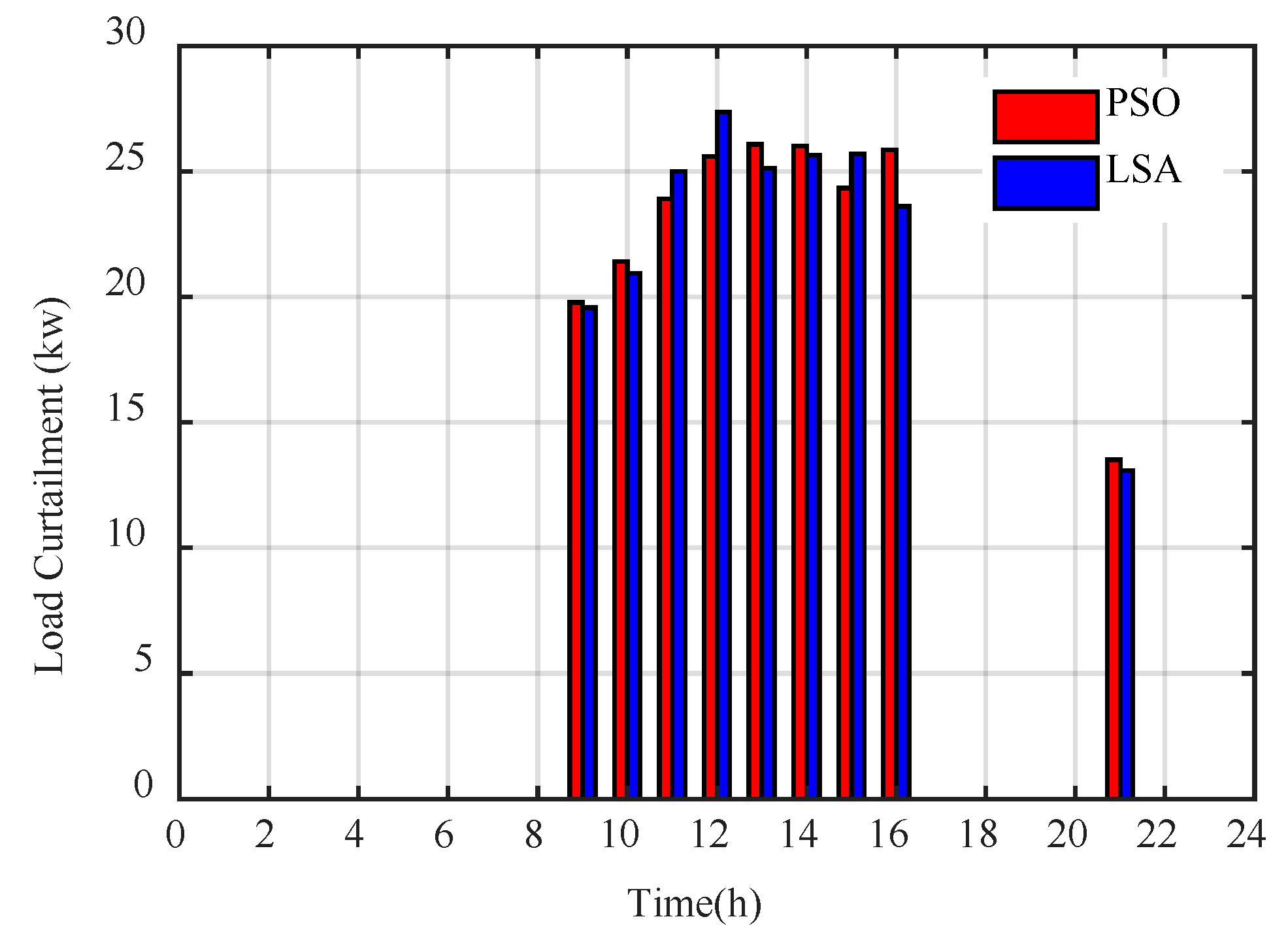
6.2. Part Two: Optimization Considering Uncertainties
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid. 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Khan, A.A.; Naeem, M.; Iqbal, M.; Qaisar, S.; Anpalagan, A. A compendium of optimization objectives, constraints, tools and algorithms for energy management in microgrids. Renew. Sustain. Energy Rev. 2016, 58, 1664–1683. [Google Scholar] [CrossRef]
- Feng, W.; Jin, M.; Liu, X.; Bao, Y.; Marnay, C.; Yao, C.; Yu, J. A review of microgrid development in the United States—A decade of progress on policies, demonstrations, controls, and software tools. Appl. Energy 2018, 228, 1656–1668. [Google Scholar] [CrossRef]
- Pourbehzadi, M.; Niknam, T.; Aghaei, J.; Mokryani, G.; Shafie-khah, M.; Catalão, J.P. Optimal operation of hybrid AC/DC microgrids under uncertainty of renewable energy resources: A comprehensive review. Int. J. Electr. Power Energy Syst. 2019, 109, 139–159. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy. 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Dong, G.; Chen, Z. Data-driven energy management in a home microgrid based on bayesian optimal algorithm. IEEE Trans. Ind. Inform. 2019, 15, 869–877. [Google Scholar] [CrossRef]
- Ju, C.; Wang, P.; Goel, L.; Xu, Y. A two-layer energy management system for microgrids with hybrid energy storage considering degradation costs. IEEE Trans. Smart Grid 2018, 9, 6047–6057. [Google Scholar] [CrossRef]
- Moradi, H.; Esfahanian, M.; Abtahi, A.; Zilouchian, A. Optimization and energy management of a standalone hybrid microgrid in the presence of battery storage system. Energy 2018, 147, 226–238. [Google Scholar] [CrossRef]
- Ghorbani, S.; Unland, R. A Holonic Multi-Agent Control System for Networks of Micro-Grids. In Proceedings of the German Conference on Multiagent System Technologies, Klagenfurt, Austria, 27–30 September 2016; Springer: Cham, Switzerland, 2016; pp. 231–238. [Google Scholar]
- Meng, L.; Sanseverino, E.R.; Luna, A.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Microgrid supervisory controllers and energy management systems: A literature review. Renew. Sustain. Energy Rev. 2016, 60, 1263–1273. [Google Scholar] [CrossRef]
- Vrba, P.; Mařík, V.; Siano, P.; Leitão, P.; Zhabelova, G.; Vyatkin, V.; Strasser, T. A review of agent and service-oriented concepts applied to intelligent energy systems. IEEE Trans. Ind. Inform. 2014, 10, 1890–1903. [Google Scholar] [CrossRef]
- Esfahani, M.M.; Hariri, A.; Mohammed, O.A. A multiagent-based game-theoretic and optimization approach for market operation of multimicrogrid systems. IEEE Trans. Ind. Inform. 2019, 15, 280–292. [Google Scholar] [CrossRef]
- Liu, W.; Gu, W.; Wang, J.; Yu, W.; Xi, X. Game Theoretic Non-Cooperative Distributed Coordination Control for Multi-Microgrids. IEEE Trans. Smart Grid 2018, 9, 6986–6997. [Google Scholar] [CrossRef]
- Arcos-Aviles, D.; Guinjoan, F.; Pascual, J.; Marroyo, L.; Sanchis, P.; Gordillo, R.; Ayala, P.; Marietta, M.P. A review of fuzzy-based residential grid-connected microgrid energy management strategies for grid power profile smoothing. In Energy Sustainability in Built and Urban Environments; Springer: Cham, Switzerland, 2019; pp. 165–199. [Google Scholar]
- Hettiarachchi, H.; Hemapala, K.U.; Jayasekara, A.B.P. Review of applications of fuzzy logic in multi-agent-based control system of ac-dc hybrid microgrid. IEEE Access 2019, 7, 1284–1299. [Google Scholar] [CrossRef]
- Faisal, M.; Hannan, M.A.; Ker, P.J.; Hussain, A.; Mansor, M.B.; Blaabjerg, F. Review of energy storage system technologies in microgrid applications: Issues and challenges. IEEE Access 2018, 6, 35143–35164. [Google Scholar] [CrossRef]
- Morsali, R.; Ghorbani, S.; Kowalczyk, R.; Unland, R. On battery management strategies in multi-agent microgrid management. In Proceedings of the International Conference on Business Information Systems, Poznan, Poland, 28–30 June 2017; Springer: Cham, Switzerland, 2017; pp. 191–202. [Google Scholar]
- Haider, H.T.; See, O.H.; Elmenreich, W. A review of residential demand response of smart grid. Renew. Sustain. Energy Rev. 2016, 59, 166–178. [Google Scholar] [CrossRef]
- Strüker, J. Blockchain-based management of shared energy assets using a smart contract ecosystem. In Proceedings of the Business Information Systems Workshops: BIS 2018 International Workshops, Seville, Spain, 26–28 June 2019; Revised Papers. Springer: Cham, Switzerland, 2019; p. 217. [Google Scholar]
- Imani, M.H.; Ghadi, M.J.; Ghavidel, S.; Li, L. Demand response modeling in microgrid operation: A review and application for incentive-based and time-based programs. Renew. Sustain. Energy Rev. 2018, 94, 486–499. [Google Scholar] [CrossRef]
- Ghorbani, S.; Rahmani, R.; Unland, R. Multi-agent Autonomous Decision Making in Smart Micro-Grids’ Energy Management: A Decentralized Approach. In Proceedings of the German Conference on Multiagent System Technologies, Leipzig, Germany, 23–26 August 2017; Springer: Cham, Switzerland, 2017; pp. 223–237. [Google Scholar]
- Ghorbani, S.; Morsali, R.; Unland, R.; Kowalczyk, R. Distributed multi-agent based energy management of smart micro-grids: Autonomous participation of agents in power imbalance handling. In Proceedings of the International Conference on Practical Applications of Agents and Multi-Agent Systems, Toledo, Spain, 20–22 June 2018; Springer: Cham, Switzerland, 2018; pp. 321–332. [Google Scholar]
- Gholami, K.; Dehnavi, E. A modified particle swarm optimization algorithm for scheduling renewable generation in a micro-grid under load uncertainty. Appl. Soft Comput. 2019, 78, 496–514. [Google Scholar] [CrossRef]
- Indragandhi, V.; Logesh, R.; Subramaniyaswamy, V.; Vijayakumar, V.; Siarry, P.; Uden, L. Multi-objective optimization and energy management in renewable based AC/DC microgrid. Comput. Electr. Eng. 2018, 70, 179–198. [Google Scholar]
- Roy, K.; Mandal, K.K.; Mandal, A.C. Ant-Lion Optimizer algorithm and recurrent neural network for energy management of micro grid connected system. Energy 2019, 167, 402–416. [Google Scholar] [CrossRef]
- Xu, M.; Gu, T.; Qin, J.; Zheng, W. GA Based Multi-Objective Operation Optimization of Power Microgrid. In Proceedings of the 2019 IEEE International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Changsha, China, 12–13 January 2019; pp. 103–107. [Google Scholar]
- Shan, H.; Hongjing, L.; Linlin, W.; Feng, Z.; Wang, M.; Yang, L.; Jie, G. Economic optimisation of microgrid based on improved quantum genetic algorithm. J. Eng. 2019, 2019, 1167–1174. [Google Scholar] [CrossRef]
- Agüera-Pérez, A.; Palomares-Salas, J.C.; de la Rosa, J.J.G.; Florencias-Oliveros, O. Weather forecasts for microgrid energy management: Review, discussion and recommendations. Appl. Energy 2018, 228, 265–278. [Google Scholar] [CrossRef]
- Maleki, A.; Khajeh, M.G.; Ameri, M. Optimal sizing of a grid independent hybrid renewable energy system incorporating resource uncertainty, and load uncertainty. Int. J. Electr. Power Energy Syst. 2016, 83, 514–524. [Google Scholar] [CrossRef]
- Roy, A.; Kedare, S.B.; Bandyopadhyay, S. Optimum sizing of wind-battery systems incorporating resource uncertainty. Appl. Energy 2010, 87, 2712–2727. [Google Scholar] [CrossRef]
- Fazlalipour, P.; Ehsan, M.; Mohammadi-Ivatloo, B. Optimal participation of low voltage renewable micro-grids in energy and spinning reserve markets under price uncertainties. Int. J. Electr. Power Energy Syst. 2018, 102, 84–96. [Google Scholar] [CrossRef]
- Aien, M.; Hajebrahimi, A.; Fotuhi-Firuzabad, M. A comprehensive review on uncertainty modeling techniques in power system studies. Renew. Sustain. Energy Rev. 2016, 57, 1077–1089. [Google Scholar] [CrossRef]
- Mohseni-Bonab, S.M.; Rabiee, A.; Mohammadi-Ivatloo, B. Voltage stability constrained multi-objective optimal reactive power dispatch under load and wind power uncertainties: A stochastic approach. Renew. Energy 2016, 85, 598–609. [Google Scholar] [CrossRef]
- Shargh, S.; Mohammadi-Ivatloo, B.; Seyedi, H.; Abapour, M. Probabilistic multi-objective optimal power flow considering correlated wind power and load uncertainties. Renew. Energy 2016, 94, 10–21. [Google Scholar] [CrossRef]
- Yang, Y.; Li, S.; Li, W.; Qu, M. Power load probability density forecasting using Gaussian process quantile regression. Appl. Energy 2018, 213, 499–509. [Google Scholar] [CrossRef]
- Koohi-Kamali, S.; Rahim, N.A.; Mokhlis, H. Smart power management algorithm in microgrid consisting of photovoltaic, diesel, and battery storage plants considering variations in sunlight, temperature, and load. Energy Convers. Manag. 2014, 84, 562–582. [Google Scholar] [CrossRef]
- Teng, J.-H.; Luan, S.-W.; Lee, D.-J.; Huang, Y.-Q. Optimal charging/discharging scheduling of battery storage systems for distribution systems interconnected with sizeable PV generation systems. IEEE Trans. Power Syst. 2012, 28, 1425–1433. [Google Scholar] [CrossRef]
- Tito, S.; Lie, T.; Anderson, T. Optimal sizing of a wind-photovoltaic-battery hybrid renewable energy system considering socio-demographic factors. Sol. Energy 2016, 136, 525–532. [Google Scholar] [CrossRef]
- Fan, X.; Wang, W.; Shi, R.; Cheng, Z. Hybrid pluripotent coupling system with wind and photovoltaic-hydrogen energy storage and the coal chemical industry in Hami, Xinjiang. Renew. Sustain. Energy Rev. 2017, 72, 950–960. [Google Scholar] [CrossRef]
- Kayal, P.; Chanda, C. Optimal mix of solar and wind distributed generations considering performance improvement of electrical distribution network. Renew. Energy 2015, 75, 173–186. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, D.; Chan, K.W.; Li, C.; Cao, Y.; Bu, S. A two-stage framework for multiobjective energy management in distribution networks with a high penetration of wind energy. Energy 2017, 135, 754–766. [Google Scholar] [CrossRef]
- Lipowski, A.; Lipowska, D. Roulette-wheel selection via stochastic acceptance. Phys. A Stat. Mech. Appl. 2012, 391, 2193–2196. [Google Scholar] [CrossRef]
- Shareef, H.; Ibrahim, A.A.; Mutlag, A.H. Lightning search algorithm. Appl. Soft Comput. 2015, 36, 315–333. [Google Scholar] [CrossRef]
- Shareef, H.; Mutlag, A.H.; Azah, M. A novel approach for fuzzy logic PV inverter controller optimization using lightning search algorithm. Neurocomputing 2015, 168, 435–453. [Google Scholar] [CrossRef]
- Islam, M.M.; Shareef, H.; Mohamed, A.; Wahyudie, A. A binary variant of lightning search algorithm: BLSA. Soft Comput. 2017, 21, 2971–2990. [Google Scholar] [CrossRef]
- Wang, M.Q.; Gooi, H.B. Spinning reserve estimation in microgrids. IEEE Trans. Power Syst. 2011, 26, 1164–1174. [Google Scholar] [CrossRef]

| LSA | Population | Iteration | α | β | γ | |
| 100 | 50 | 0.2 | 0.8 | 0.2 | ||
| PSO | Population | Iteration | C1 = C2 | Vmax | Vmin | W |
| 100 | 50 | 2 | 0.4 | 0.9 | 0.7 |
| Best (€) | Worst (€) | Average (€) | SD | |
|---|---|---|---|---|
| PSO | 1504.7 | 1518.3 | 1509.7 | 6.67 |
| LSA | 1467.4 | 1472.1 | 1470.6 | 2.41 |
| Scenario | Algorithm | Best (€) | Worst (€) | Average (€) | SD | Simulation Time (s) |
|---|---|---|---|---|---|---|
| S1 | PSO | 1546.3 | 1572.7 | 1564.6 | 5.43 | 64.33 |
| LSA | 1534.4 | 1543.1 | 1537.2 | 2.82 | 57.41 | |
| S2 | PSO | 1764.2 | 1791.3 | 1778.2 | 6.43 | 67.24 |
| LSA | 1758.1 | 1771.2 | 1765 | 2.72 | 59.23 | |
| S3 | PSO | 1521.6 | 1546.5 | 1534.9 | 5.14 | 65.84 |
| LSA | 1507.5 | 1518.4 | 1512.2 | 2.63 | 58.26 | |
| S4 | PSO | 1842.6 | 1876.9 | 1864.7 | 7.77 | 65.56 |
| LSA | 1833.4 | 1842.2 | 1837.9 | 3.13 | 57.44 | |
| S5 | PSO | 1661.7 | 1686.3 | 1674.3 | 6.23 | 65.72 |
| LSA | 1632.1 | 1638 | 1635.5 | 2.34 | 58.69 | |
| S6 | PSO | 1573.2 | 1597.4 | 1589.4 | 5.89 | 66.82 |
| LSA | 1560.2 | 1569.7 | 1565.3 | 2.38 | 53.67 | |
| S7 | PSO | 1612.6 | 1646.5 | 1638.3 | 7.21 | 67.42 |
| LSA | 1601.7 | 1612.2 | 1607.2 | 2.89 | 56.48 | |
| S8 | PSO | 1586.3 | 1612.8 | 1603.3 | 5.78 | 62.91 |
| LSA | 1552.2 | 1561.1 | 1556.9 | 2.42 | 58.32 | |
| S9 | PSO | 1723.4 | 1748.3 | 1737 | 7.86 | 68.22 |
| LSA | 1696.3 | 1708.4 | 1701.4 | 3.07 | 57.69 | |
| S10 | PSO | 1573.1 | 1598.6 | 1589.5 | 5.94 | 63.83 |
| LSA | 1541.9 | 1550.8 | 1546.8 | 2.63 | 54.76 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghorbani, S.; Unland, R.; Shokouhandeh, H.; Kowalczyk, R. An Innovative Stochastic Multi-Agent-Based Energy Management Approach for Microgrids Considering Uncertainties. Inventions 2019, 4, 37. https://doi.org/10.3390/inventions4030037
Ghorbani S, Unland R, Shokouhandeh H, Kowalczyk R. An Innovative Stochastic Multi-Agent-Based Energy Management Approach for Microgrids Considering Uncertainties. Inventions. 2019; 4(3):37. https://doi.org/10.3390/inventions4030037
Chicago/Turabian StyleGhorbani, Sajad, Rainer Unland, Hassan Shokouhandeh, and Ryszard Kowalczyk. 2019. "An Innovative Stochastic Multi-Agent-Based Energy Management Approach for Microgrids Considering Uncertainties" Inventions 4, no. 3: 37. https://doi.org/10.3390/inventions4030037
APA StyleGhorbani, S., Unland, R., Shokouhandeh, H., & Kowalczyk, R. (2019). An Innovative Stochastic Multi-Agent-Based Energy Management Approach for Microgrids Considering Uncertainties. Inventions, 4(3), 37. https://doi.org/10.3390/inventions4030037




