Development of a Fuzzy Economic Order Quantity Model of Deteriorating Items with Promotional Effort and Learning in Fuzziness with a Finite Time Horizon

Abstract

This study investigates an economic order quantity model of deteriorating items, where demand is fuzzy in nature and depends on promotional effort with full backorder for a given time horizon. The learning effect in the fuzzy environment is added in this model. A constant deterioration rate is assumed. Under these circumstances, a mathematical model is developed to curtail the total cost over a finite time horizon by determining the replenishment order quantity, number of replenishments, and the fraction of the replenishment cycle when inventory is positive. A solution algorithm is developed to find the optimal solutions. The applicability of the proposed model is illustrated through numerical examples. To get further insights, sensitivity analysis is carried out for the main parameters in crisp, fuzzy, and fuzzy-learning environments.

1. Introduction

In today’s highly competitive global era, most organizations face challenges to meet customer’s ever-changing demands and to earn a profit. Use of promotion has been a marketing strategy for years. Even smaller organizations and retailers have used promotion to increase sales for more revenue and higher market share. Various promotional strategies such as price discounts, free goods, free credit period, and after sale services are widely used. The importance of promotional efforts also attracts the attention of researchers and practitioners. On this note, a first of its kind study was done by Tsao and Sheen [1] regarding policies on dynamic pricing, promotion, and replenishment under permissible payment delay with time- and price-dependent demand for deteriorating items. Zhang et al. [2] developed a finite horizon periodic model for maximizing profit by jointly optimizing pricing, promotion, and stock replenishment policy, being considered a single item. Grewal et al. [3] studied the broad advancement in pricing and promotion in retail while putting three key research areas, targeting, models, and design, before the researchers. Among others, researchers (Maihami and Karimi [4], Palanivel and Uthayakumar [5], Priyan et al. [6], and Taleizadeh [7]) have undertaken different interesting studies related to promotional efforts with sensitive demand in the inventory systems. Recently, Soni and Suthar [8] studied replenishment policy for non-instantaneous deteriorating items for price- and promotional effort-dependent stochastic demand. It was found that deterioration is an important factor in deciding the optimal replenishment policy.

Deterioration is a manifestation that affects inventory systems. Risks, like obsolescence, pilferage, decay, damage, loss of the marginal value of a commodity, dryness, evaporation, or loss of utility, affect many items in inventory. In real-life situations, most manufacturing companies face challenges to protect items such as food items, pharmaceuticals, chemicals, blood, gasoline, radioactive chemicals, etc., which deteriorate with time. While deciding the economic order quantity, the loss from deterioration ought to be considered. Ghare and Schrader [9] were first to develop a deteriorating inventory model. Aggarwal and Jaggi [10] explored an EOQ model to obtain the optimal order quantity of deteriorating items under a permissible delay in payments. After that, Chang et al. [11], Sana and Chaudhiri [12], and Ouyang et al. [13] studied different forms of deteriorating items for different inventory models with time-dependent demand. Roy [14] and Sana [15] analyzed an EOQ model with various types of deteriorating items for time-dependent demand. Dye and Hsiesh [16] developed an EOQ inventory model by considering deteriorating items with price-dependent demand under inflation. Sarkar and Sarkar [17] analyzed an inventory model for time-varying deteriorating rate with stock-dependent demand by considering shortage and partial backlogging. Soni and Patel [18] discussed an inventory model for joint pricing and replenishment policies by considering time taking deteriorating products. Zhang et al. [19] pioneered an EOQ model for deteriorating items by considering a joint pricing and replenishment cycle decision-making problem. Geetha and Udayakumar [20] presented an EOQ inventory model by allowing shortages and partial backlogging for deteriorating items with price- and advertisement-dependent demand.

Apart from the promotional effort and deteriorating items, uncertainty in demand arises due to many unknown factors in the inventory model. Hence, to capture the uncertainty in a fuzzy sense, the articles authored by Park [21], Yao et al. [22], Yao and Chang [23], Chang et al. [24], Kar et al. [25], Rong et al. [26], Shah and Soni [27], Dutta et al. [28], Mondal et al. [29], Dey et al. [30], Sarkar and Mahapatra [31], and Soni et al. [32] are worth mentioning. Afterward, De and Sana [33] developed an optimal inventory policy for imprecise selling price and promotional effort where the decision variables are fuzzy random variables. De et al. [34] developed an EOQ model using the intuitionist fuzzy programming technique by considering selling price and promotional effort with full backlogging. De and Sana [35] also investigated the classical backorder EOQ model by considering the promotional effort and fuzzy unit selling price.

In terms of alleviating the impact of fuzziness, it might be said that uncertainty in demand can be reduced through a process of learning by a proper study of previous data concerning uncertainty in sales, promotion activities, and so forth. Therefore, this involves a gradual order of demand instead of a huge risk-taking venture, as is established in the elaborate works of Glock et al. [36] and Kazemi et al. [37]. Firstly, Wright [38] pioneered an innovative work on the effect of learning in a repetitive job. In this paper, the concept of the learning effect is applied to a continuous review inventory model with backorders under a fuzzy environment. There is a dearth of literature on this phenomenon, but a few researchers have worked on it recently. Jaber and Salameh [39] discussed the finite production inventory model under learning concepts and allowed shortages and backorders. Chen et al. [40] initiated an imperfect production system considering shortages for the unit production time using the learning effect. They minimized the total cost of the production system through optimal determination of the production quantity and the shortage level of each cycle. Kumar and Goswami [41] discussed the learning effect of the unit production time under a fuzzy random environment for an imperfect production process by taking shortages and partial backlogging. Kazemi et al. [37] investigated a fuzzy EOQ inventory model with backorders by considering the learning effect over the planning horizon. Recently, Shekarian et al. [42] considered an economic order quantity (EOQ) model for imperfect quality items based on two different holding costs and learning considerations, which was analyzed in a fuzzy sense.

In this study, the ideas proposed by Glock et al. [36] are explored further to examine the impact of learning to reduce fuzziness within a finite time horizon and also to study how this reduction in fuzziness affects the operating strategy to reduce the total cost of a continuous review inventory system in a fuzzy environment. The concept of learning is applied for the fuzzy demand of deteriorating items in the presence of promotional effort. Numerical analysis is performed for a crisp and fuzzy model of a continuous review EOQ model (with or without learning) and the impact of learning on the optimal policy analyzed. Results obtained in this study have a profound impact on the decision maker’s operation in an uncertain demand scenario and the total inventory cost gradually improving with the passage of time based on learning.

The rest of the paper is structured as follows: Section 2 presents a continuous review inventory system for the fuzzy demand of deteriorating items with promotional effort and learning in fuzziness for a finite time horizon. In Section 3, numerical analysis is done with an example, and sensitivity analysis is performed on a number of periods for the crisp, fuzzy, and fuzzy-learning scenario. Finally, conclusions and a possible extension of the model are presented in Section 4.

2. Mathematical Model

2.1. A Continuous Review Crisp Inventory Model (Model I)

Notation:

Parameters:

• H length of finite planning horizon
• T time interval between replenishment
• Q order quantity
• D annual demand
• A ordering cost ($/per order)
• h holding cost ($/per unit)
• c deteriorating cost ($/per unit)
• s shortage cost ($/per unit)
• $\varphi$ constant deterioration rate
• $\rho$ promotional effort
• k promotional cost for unit promotional effort
• $T_i$ total elapsed time; this also includes the $i^{\mathrm{th}}$ replenishment cycle where $T_0=0,T_1=T,T_n=H$
• $t_i$ time at which the level of the inventory system for the $i^{\mathrm{th}}$ replenishment cycle drops to zero
• $I(t)$ inventory level at time $\mathit{t}$
• $I_m$ maximum inventory level
• $I_b$ maximum shortage quantity
• $TC(n,F)$ total cost over the finite time horizon $\mathit{H}$

Decision variables:

• $\mathit{n}$ number of replenishments (integer) during the planing horizon $H=nT$
• $\mathit{F}$ fraction of period with a positive inventory in a replenishment cycle

Assumptions:

• The planning horizon and order size are finite.
• The customer demand rate is given by the following expression $D(\rho )=d_0+d_1\rho$, where $d_0$ is the initial demand rate, independent of the sales team’s effort $\rho$, and $d_1$ is a scale parameter of demand change, which varies with sales effort. Here, $d_0$ is a triangular fuzzy number $\widetilde{d_0}=(d_0-{\Delta }_l,d_0,d_0+{\Delta }_r)$ where $0<{\Delta }_l<d_0$ and $0<{\Delta }_r<d_0$, and ${\Delta }_l$ and ${\Delta }_r$ are determined by the decision maker.
• Shortage is allowed and is fully backlogged. The inventory model starts with shortage and ends with zero inventory.
• The replenishment rate is infinite, while the lead time is negligible.
• The deterioration rate is constant, and a fraction $\varphi$$(0\le \varphi \le 1)$ of inventory deteriorates per unit of time. No repair or replacement of deteriorated units is considered during the replenishment cycle.
• The promotional effort cost (PEC) is given by $k{\rho }^m$, where $k>0$ and m are constants, and values are selected from the best fit of the promotional cost function (Soni and Suthar [8]).
• Wright’s [38] explanation of the learning effect is considered to characterize the learning phenomenon, while placing orders over the finite horizon.

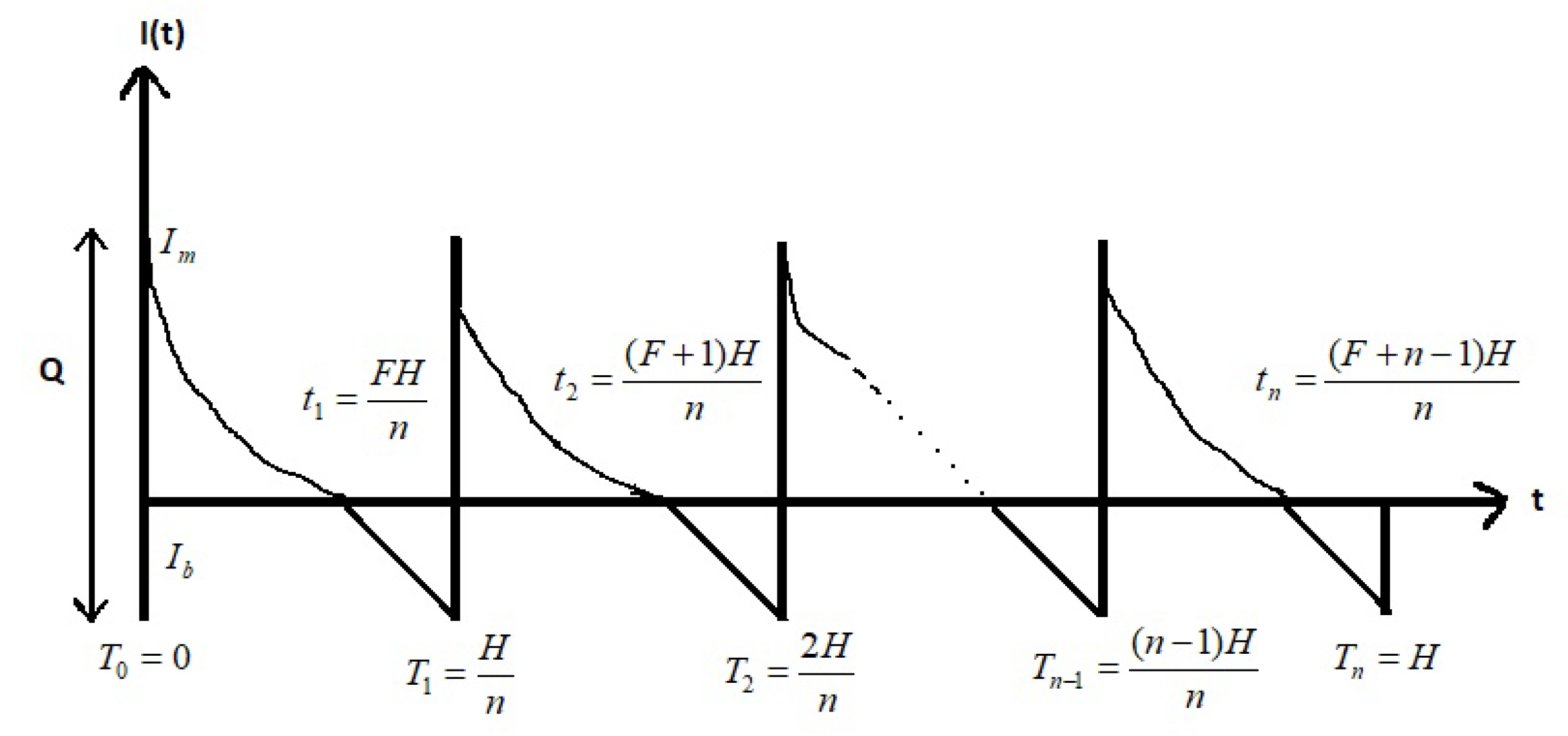
The length of the finite planning horizon $H=nT$, where $\mathit{n}$ represents an integer decision variable for the number of replenishments that has to be made during $\mathit{H}$, while $\mathit{T}$ represents the time between two replenishments, which is shown in Figure 1 (see Taleizadeh and Nematollahi [43]).

The inventory level $I(t)$ gradually decreases due to demand fulfillment and deterioration. Based on the aforementioned description, the inventory level in the system during the time interval $(0\le t\le T)$ can be expressed through the differential equation as described below:

$$\begin{array}{cc}\hfill \frac{dI(t)}{dt}+\varphi I(t)=& -D,0\le t\le t_1,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \frac{dI(t)}{dt}=& -D,t_1\le t\le T\hfill \end{array}$$

(2)

Solving the above Equation (1) using the boundary condition $I(t_1)=0$, the following solution can be found:

$$I(t)={\displaystyle \frac{D}{\varphi }}\left[e^{\varphi (t_1-t)}-1\right],0\le t\le t_1$$

(3)

Again, solving the second differential equation, one gets:

$$I(t)=-D(t-t_1),t_1\le t\le T$$

(4)

The maximum level of inventory and backorder can be found at $t=0$ and $t=T$ from Equations (3) and (4), respectively, and presented as follows:

$$\begin{array}{cc}\hfill I_m=I(0)=& {\displaystyle \frac{D}{\varphi }}\left[e^{\varphi t_1}-1\right]\hfill \\ \hfill I_b=I(T)=& -D(T-t_1)=-D\left({\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right)\hfill \end{array}$$

(5)

Therefore, the cost components of total inventory cost with n replenishments are computed as follows:

(a) The ordering cost is A for each replenishment.

Therefore, the total ordering cost (OC) is $(n+1)\times A$.

(b) Using Equation (3), the inventory holding cost during the first cycle is given by:

$$\begin{array}{c}\hfill HC=h{\int }_0^{t_1}I(t)dt=\frac{hD}{{\varphi }^2}\left[e^{\varphi t_1}-\varphi t_1-1\right]\end{array}$$

Hence, the total holding cost (HC) for the time horizon $\mathit{H}$ would be:

$$\begin{array}{cc}\hfill HC=& \frac{nhD}{{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]\hfill \end{array}$$

(c) The deterioration cost (DC) during the first cycle is given by ${\displaystyle \frac{cD}{\varphi }}\left[e^{\varphi t_1}-\varphi t_1-1\right]$.

Hence, the total deterioration cost for the time horizon $\mathit{H}$ is given by

$DC={\displaystyle \frac{ncD}{\varphi }}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]$.

(d) Using Equation (4), the shortage cost (SC) during the first cycle is given by $s{\int }_{t_1}^{T}D(t-t_1)dt={\displaystyle \frac{sD}{2}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2$.

Hence, the total shortage cost (SC) for the time horizon $\mathit{H}$ would be $SC={\displaystyle \frac{nsD}{2}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2$.

(e) The promotional effort cost (PEC) is given by $k{\rho }^m$. Therefore, the total promotional effort cost (PEC) for the time horizon $\mathit{H}$ is given by $nk{\rho }^m$

Hence, the total cost of the system over planning period $\mathit{H}$ would be:

$$\begin{array}{cc}\hfill TC(n,F)=& \mathrm{Ordering}\cos \mathrm{t}+\mathrm{Holding}\cos \mathrm{t}+\mathrm{Deterioration}\cos \mathrm{t}+\mathrm{Shortage}\cos \mathrm{t}+\mathrm{Promotional}\cos \mathrm{t}\hfill \\ \hfill =& OC+HC+DC+SC+PEC\hfill \\ \hfill =& (n+1)A+\frac{nhD}{{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]+{\displaystyle \frac{ncD}{\varphi }}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]+{\displaystyle \frac{nsD}{2}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2+nk{\rho }^m\hfill \\ \hfill =& (n+1)A+\frac{nD(h+\varphi c)}{{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]+{\displaystyle \frac{nsD}{2}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2+nk{\rho }^m\hfill \end{array}$$

(6)

The value of the deterioration rate is usually very small for real-world problems. The following expression can be used from a truncated Taylor series expansion by ignoring the higher order term (see Taleizadeh and Nematollahi [43]):

$$e^{\varphi x}=1+\varphi x+\frac{1}{2}{(\varphi x)}^2$$

(7)

Using the approximate value as per Equation (7), the total cost of the crisp model as per Equation (6) is rewritten as:

$$TC(n,F)=(n+1)A+\frac{nD(h+\varphi c)}{{\varphi }^2}\left[\frac{1}{2}{\left({\displaystyle \frac{\varphi FH}{n}}\right)}^2\right]+{\displaystyle \frac{nsD{H}^2}{2n^2}}{\left[1-F\right]}^2+nk{\rho }^m$$

(8)

Considering first and second order partial derivatives of $TC(n,F)$ with respect to $\mathit{n}$ and $\mathit{F}$ in Equation (8), one gets:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial TC(n,F)}{\partial n}}& =& A-\frac{D(h+\varphi c)H^2{F}^2}{2n^2}-{\displaystyle \frac{sD{H}^2}{2n^2}}{\left[1-F\right]}^2+k{\rho }^m\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial TC(n,F)}{\partial F}}& =& \frac{D(h+\varphi c)H^{2}F}{n}-\frac{sD{H}^2}{n}\left(1-F\right)\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{2}TC(n,F)}{\partial n^2}}& =& \frac{D{H}^2}{n^3}\left[(h+\varphi c)F^2+s{\left(1-F\right)}^2\right]\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{2}TC(n,F)}{\partial F^2}}& =& \frac{D{H}^2}{n}\left[(h+\varphi c)+s\right]\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{2}TC(n,F)}{\partial n\partial F}}& =& \frac{D{H}^2}{n^2}\left[-(h+\varphi c)F+s\left(1-F\right)\right]\hfill \end{array}$$

(13)

Therefore, from the classical EOQ model, we obtain the number of replenishments and the fraction of replenishment cycles by setting ${\displaystyle \frac{\partial TC(n,F)}{\partial F}}=0$ and ${\displaystyle \frac{\partial TC(n,F)}{\partial n}}=0$, and one gets:

$$\begin{array}{ccc}\hfill F_C& =& {\displaystyle \frac{s}{s+(h+\varphi c)}}\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill n_C& =& \mathrm{Integer} \mathrm{value} \mathrm{of} H\times \sqrt{{\displaystyle \frac{sD\left(h+\varphi c\right)}{2\left(A+k{\rho }^m\right)\left[s+(h+\varphi c)\right]}}}\hfill \end{array}$$

(15)

Hence, the optimal replenishment number $(n_C^{*})$ and fractional period of positive inventory $(F_C^{*})$ can be determined using the minimum total cost condition as follows:

$$\begin{array}{cc}\hfill TC(n_C^{*},F_C^{*})=& \min \{TC(n_C,F_C),TC((n_C+1),F_C)\}\hfill \end{array}$$

(16)

A sufficient condition for $TC(n,F)$ to be minimum is to prove the convexity with the Hessian matrix as positive definite at $(n,F)$. It can be shown as follows:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{2}TC(n,F)}{\partial n^2}}{\displaystyle \frac{{\partial }^{2}TC(n,F)}{\partial F^2}}-{\left[{\displaystyle \frac{{\partial }^{2}TC(n,F)}{\partial n\partial F}}\right]}^2& =& {\displaystyle \frac{s{D}^2{H}^4(h+\varphi c)}{n^4}}>0\hfill \\ \hfill {\displaystyle \frac{{\partial }^{2}TC(n,F)}{\partial n^2}}& =& \frac{D{H}^2}{n^3}\left[(h+\varphi c)F^2+s{\left(1-F\right)}^2\right]>0\hfill \end{array}$$

Therefore, the objective function $TC(n,F)$ is a convex function of $(n,F)$. Using the optimal replenishment number $(n_C^{*})$ and the fraction of the period with positive inventory $(F_C^{*})$, one can obtain the optimal order quantity $(Q_C^{*})$ as:

$$\begin{array}{cc}\hfill Q_C^{*}=I(0)+I_b=& {\displaystyle \frac{D}{\varphi }}\left[e^{{\displaystyle \frac{\varphi F_C^{*}H}{n_C^{*}}}}-1\right]+D\left[{\displaystyle \frac{H}{n_C^{*}}}-{\displaystyle \frac{F_C^{*}H}{n_C^{*}}}\right]\hfill \end{array}$$

(17)

2.2. A Fuzzy Continuous Review Inventory Model with an Imprecise Demand Rate (Model II)

In this section, the demand rate is assumed to follow $D(\rho )=d_0+d_1\rho$ where $d_0$ is considered as a fuzzy variable, so that real scenarios can be represented in a more suitable manner with its flexibility. $d_0$ is treated as a triangular fuzzy number (TFN), then the cost function in (8) also becomes TFN. Thus, the problem can be stated as:

$$\begin{array}{c}\hfill \mathrm{Minimize}\widetilde{TC}(n,F)\\ \hfill \mathrm{Subject}\mathrm{to}0\le F\le 1\\ \hfill n\ge 1,\mathrm{and}\mathrm{an}\mathrm{integer}\end{array}$$

where $\widetilde{TC}(n,F)=\left(T{C}_1(n,F),T{C}_2(n,F),T{C}_3(n,F)\right)$; here, $T{C}_i(n,F)(i=1,2,3)$ are real-valued functions satisfying the condition $T{C}_1(n,F)\le T{C}_2(n,F)\le T{C}_3(n,F)$.

Using the function principle (see Chen et al. [44]), the expressions for $T{C}_i(n,F),i=1,2,3$, are as follows:

$$\begin{array}{cc}\hfill T{C}_1(n,F)=& (n+1)A+\frac{n(D-{\Delta }_l)(h+\varphi c)}{{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]+{\displaystyle \frac{ns(D-{\Delta }_l)}{2}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2+nk{\rho }^m\hfill \\ \hfill T{C}_2(n,F)=& (n+1)A+\frac{nD(h+\varphi c)}{{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]+{\displaystyle \frac{nsD}{2}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2+nk{\rho }^m\hfill \\ \hfill T{C}_3(n,F)=& (n+1)A+\frac{n(D+{\Delta }_r)(h+\varphi c)}{{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]+{\displaystyle \frac{ns(D+{\Delta }_r)}{2}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2+nk{\rho }^m\hfill \end{array}$$

Applying the centroid formula, the estimation of the total variable cost over the planning horizon $\mathit{H}$ in the fuzzy case is given by:

$$\begin{array}{cc}\hfill M(\widetilde{TC}(n,F))=& {\displaystyle \frac{T{C}_1(n,F)+T{C}_2(n,F)+T{C}_3(n,F)}{3}}\hfill \\ \hfill =& (n+1)A+\frac{nD(h+\varphi c)}{{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]+{\displaystyle \frac{nsD}{2}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2+nk{\rho }^m\hfill \\ \hfill +& \frac{n(h+\varphi c)({\Delta }_r-{\Delta }_l)}{3{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]+{\displaystyle \frac{ns({\Delta }_r-{\Delta }_l)}{6}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2\hfill \\ \hfill =& TC(n,F)+\frac{n(h+\varphi c)({\Delta }_r-{\Delta }_l)}{3{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]+{\displaystyle \frac{ns({\Delta }_r-{\Delta }_l)}{6}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2\hfill \end{array}$$

(18)

Therefore, the total relevant cost over the finite horizon $\mathit{H}$ for the fuzzy model would be as per Equation (18), which can be rewritten using Equation (7) as:

$$M(\widetilde{TC}(n,F))=TC(n,F)+GC(n,F)$$

(19)

where

$$GC(n,F)=\frac{H^2({\Delta }_r-{\Delta }_l)}{6n}\left[(h+\varphi c)F^2+s{\left(1-F\right)}^2\right]$$

(20)

Again, considering the first and second order partial derivatives of $GC(n,F)$ with respect to $\mathit{n}$ and $\mathit{F}$ in Equation (20), one gets:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial GC(n,F)}{\partial n}}& =& -\frac{H^2({\Delta }_r-{\Delta }_l)}{6n^2}\left[(h+\varphi c)F^2+s{\left(1-F\right)}^2\right]\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial GC(n,F)}{\partial F}}& =& \frac{H^2({\Delta }_r-{\Delta }_l)}{3n}\left[(h+\varphi c)F-s\left(1-F\right)\right]\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{2}GC(n,F)}{\partial n^2}}& =& \frac{H^2({\Delta }_r-{\Delta }_l)}{3n^3}\left[(h+\varphi c)F^2+s{\left(1-F\right)}^2\right]\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{2}GC(n,F)}{\partial F^2}}& =& \frac{H^2({\Delta }_r-{\Delta }_l)}{3n}\left[(h+\varphi c)+s\right]\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{2}GC(n,F)}{\partial n\partial F}}& =& -\frac{H^2({\Delta }_r-{\Delta }_l)}{3n^2}\left[(h+\varphi c)F-s\left(1-F\right)\right]\hfill \end{array}$$

(25)

Therefore, the optimal replenishment number $(n_f^{*})$ and fraction of the cycle with positive inventory $(F_f^{*})$ in the fuzzy scenario can be obtained from the equations ${\displaystyle \frac{\partial M(\widetilde{TC}(n,F))}{\partial F}}=0$ and ${\displaystyle \frac{\partial M(\widetilde{TC}(n,F))}{\partial n}}=0$, which implies:

$$\begin{array}{ccc}\hfill F_f& =& {\displaystyle \frac{s}{s+(h+\varphi c)}}\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill n_f& =& \mathrm{Integer} \mathrm{value} \mathrm{of} \mathit{H}\times \sqrt{{\displaystyle \frac{s\left[3D+({\Delta }_r-{\Delta }_l)\right]\left(h+\varphi c\right)}{6\left(A+k{\rho }^m\right)\left[s+(h+\varphi c)\right]}}}\hfill \end{array}$$

(27)

Hence, the optimal replenishment number $(n_f^{*})$ and fraction of the period with positive inventory $(F_f^{*})$ can be determined from the minimum total cost condition as follows:

$$\begin{array}{cc}\hfill TC(n_f^{*},F_f^{*})=& \min \{TC(n_f,F_f),TC((n_f+1),F_f)\}\hfill \end{array}$$

(28)

Theorem 1.

The addition of two convex functions having the same interval would generate a convex function. If one of them is strictly convex, then the sum is also strictly convex.

It was already proven that $TC(n,f)$ is a convex function of $(n,F)$. Now, for the sufficient condition for $\mathit{n}$ and $\mathit{F}$ to obtain the convexity of $GC(n,F)$, its Hessian matrix must be positive definite at $(n,F)$, and that requires:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2}GC(n,F)}{\partial n^2}}{\displaystyle \frac{{\partial }^{2}GC(n,F)}{\partial F^2}}-{\left[{\displaystyle \frac{{\partial }^{2}GC(n,F)}{\partial n\partial F}}\right]}^2=& {\displaystyle \frac{s{H}^4(h+\varphi c){({\Delta }_r-{\Delta }_l)}^2}{9n^4}}>0\hfill \\ \hfill {\displaystyle \frac{{\partial }^{2}GC(n,F)}{\partial n^2}}=& \frac{H^2({\Delta }_r-{\Delta }_l)}{3n^3}\left[(h+\varphi c)F^2+s{\left(1-F\right)}^2\right]>0\hfill \end{array}$$

Hence, the function $GC(n,F)$ is a convex function of $(n,F)$. Therefore, from the above proposition, it can be verified that $M(\widetilde{TC}(n,F))$ is a convex function of $(n,F)$ under the fuzzy sense, as well.

Similar to the crisp model, using the optimal replenishment number $(n_f^{*})$ and fraction of period with positive inventory $(F_f^{*})$, the optimal order quantity $(Q_f^{*})$ for the fuzzy model can be derived as:

$$\begin{array}{cc}\hfill Q_f^{*}=& \left[{\displaystyle \frac{e^{{\displaystyle \frac{\varphi F_f^{*}H}{n_f^{*}}}}-1}{\varphi }}+{\displaystyle \frac{H}{n_f^{*}}}-{\displaystyle \frac{F_f^{*}H}{n_f^{*}}}\right]\left[D+{\displaystyle \frac{{\Delta }_r-{\Delta }_l}{3}}\right]\hfill \end{array}$$

(29)

2.3. Fuzzy Learning in a Continuous Review Inventory Model (Model III)

In this section, the fuzzy model developed in the previous section is extended to incorporate the effect of learning. In real-life situations, decision makers collect information about the customer demand through various modes of interaction before processing an order. Thus, it may be concluded that the estimation of the learning effect is depended on the number of orders instead of the quantity of the order. Learning in fuzziness is assumed to follow the mathematical relationship formulated by Wright [38] and also used by many researcher’s such as Yelle [45] and Jaber [46], which can be written as:

$$p_i=p_1{i}^{-l}$$

(30)

where $p_i$ represents the performance at the time of the $i^{\mathrm{th}}$ replenishment, $p_1$ is the performance at the starting of the planning period, the index i is the number of replenishments, and l is the learning exponent.

If learning occurs as a function of the number of orders placed and affects the fuzzy parameters ${\Delta }_l$ and ${\Delta }_r$ subject to the same learning rate, then the value of the fuzzy parameter j, for j = 1 and 2, at the time of the $i^{\mathrm{th}}$ order is given by the expression (Glock et al. [36]):

$${\Delta }_{j,i}=\left\{\begin{array}{cc}{\Delta }_{j,1},\hfill & \mathrm{for}i=1\hfill \\ {\Delta }_{j,1}{\left(\frac{(i-1)H}{n}\right)}^{-l},\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(31)

Therefore, the total cost for the $i^{\mathrm{th}}$ replenishment cycle with $1<i\le n$ and $n\ge 2$ is given as:

$$\begin{array}{cc}& A+\frac{D(h+\varphi c)}{{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]+{\displaystyle \frac{sD}{2}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2+k{\rho }^m\hfill \\ \hfill +& \frac{(h+\varphi c)}{3{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]\left[\left({\Delta }_{r,1}-{\Delta }_{l,1}\right){\left({\displaystyle \frac{(i-1)H}{n}}\right)}^{-l}\right]\hfill \\ \hfill +& {\displaystyle \frac{s}{6}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2\left[\left({\Delta }_{r,1}-{\Delta }_{l,1}\right){\left({\displaystyle \frac{(i-1)H}{n}}\right)}^{-l}\right]\hfill \end{array}$$

(32)

Thus, the total cost for $\mathit{n}$ replenishments amounts to:

$$\begin{array}{cc}\hfill M_{fL}(\widetilde{TC}(n,F))=& (n+1)A+\frac{nD(h+\varphi c)}{{\varphi }^2}\left[e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right]+{\displaystyle \frac{nsD}{2}}{\left[{\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right]}^2+nk{\rho }^m\hfill \\ \hfill +& \left[\frac{(h+\varphi c)}{3{\varphi }^2}\left(e^{\frac{\varphi FH}{n}}-\frac{\varphi FH}{n}-1\right)+{\displaystyle \frac{s}{6}}{\left({\displaystyle \frac{H}{n}}-{\displaystyle \frac{FH}{n}}\right)}^2\right]\left({\Delta }_{r,1}-{\Delta }_{l,1}\right)\hfill \\ \hfill \times & \left(1+\sum _{i=2}^n{\left({\displaystyle \frac{(i-1)H}{n}}\right)}^{-l}\right)\hfill \end{array}$$

(33)

To continue, using Equation (7), the total relevant cost for the fuzzy-learning model, Equation (33), can be rewritten as:

$$\begin{array}{cc}\hfill M_{fL}(\widetilde{TC}(n,F))=& (n+1)A+\frac{nD(h+\varphi c)}{{\varphi }^2}\left[\frac{1}{2}{\left({\displaystyle \frac{\varphi FH}{n}}\right)}^2\right]+{\displaystyle \frac{sD{H}^2}{2n}}{\left[1-F\right]}^2+nk{\rho }^m\hfill \\ \hfill +& \left[\frac{(h+\varphi c)}{3{\varphi }^2}\frac{1}{2}{\left({\displaystyle \frac{\varphi FH}{n}}\right)}^2+{\displaystyle \frac{s{H}^2}{6n^2}}{\left(1-F\right)}^2\right]\left({\Delta }_{r,1}-{\Delta }_{l,1}\right)\hfill \\ \hfill \times & \left(1+\sum _{i=2}^n{\left({\displaystyle \frac{(i-1)H}{n}}\right)}^{-l}\right)\hfill \\ \hfill =& TC(n,F)+\frac{H^2}{6n^2}\left[\left(h+\varphi c\right)F^2+s{\left(1-F\right)}^2\right]\left({\Delta }_{r,1}-{\Delta }_{l,1}\right)\hfill \\ \hfill \times & \left(1+\sum _{i=2}^n{\left({\displaystyle \frac{(i-1)H}{n}}\right)}^{-l}\right)\hfill \end{array}$$

(34)

The convex property of $M_{fL}(\widetilde{TC}(n,F))$ is difficult to establish analytically due to the complex expression in Equation (34).

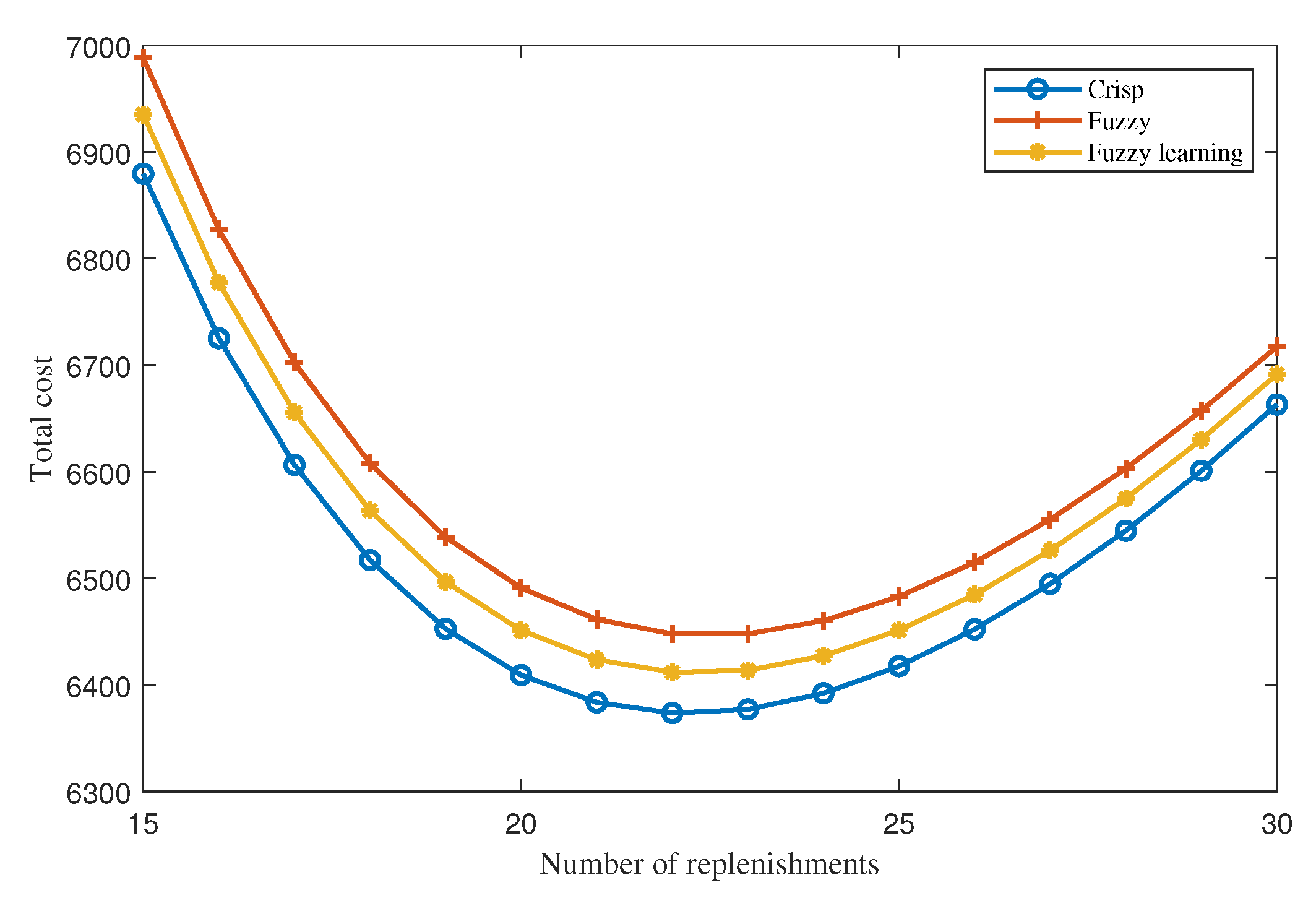
In such scenarios, numerical approaches are generally adopted. Therefore, we also ensured the convex nature of the objective function through a numerical process. It can be observed in Figure 2 that total cost functions for all the three models were convex in nature. We can observe that at $(n_{fL})=15$, the total cost for the fuzzy-learning model was $7136, and the total cost decreased with the increase in $(n_{fL})$. At $(n_{fL})=22$, the minimum cost for the fuzzy-learning model ($6412.73) was observed. Again, the total cost increased with the increase in $(n_{fL})$. Therefore, the cost function was found to be convex, and the developed algorithm would converge at the optimum number of replenishments. Hence, the following algorithm would ensure obtaining the optimal number of replenishments $(n_{fL}^{*}$ and the fraction of the period with positive inventory $F_{fL}^{*})$ for the fuzzy-learning model.

Algorithm.

Step 1

Input all the parameters.

Step 2

Choose an initial trial solution of $(n_{fL}^{*},F_{fL}^{*})$, say $(n,F)=(n_f^{*},F_f^{*})$, and compute $M_{fL}(\widetilde{TC}(n,F))$ and $M_{fL}(\widetilde{TC}(n-1,F))$.

Step 3

If $M_{fL}(\widetilde{TC}(n,F))\ge M_{fL}(\widetilde{TC}(n-1,F))$, then compute $M_{fL}(\widetilde{TC}(n-2,F))$, $M_{fL}(\widetilde{TC}(n-3,F))$,..., until the following inequality is satisfied $M_{fL}(\widetilde{TC}(u))<M_{fL}(\widetilde{TC}TC(u-1))$ or the number of replenishments becomes one. Accordingly, optimal values are set, i.e., $(n_{fL}^{*},F_{fL}^{*})=u$, or $n_{fL}^{*}=1$, and stop.

Step 4

If $M_{fL}(\widetilde{TC}(n,F))<M_{fL}(\widetilde{TC}(n-1,F))$, then compute $M_{fL}(\widetilde{TC}(n+1,F))$, $M_{fL}(\widetilde{TC}(n+2,F))$,..., until the following inequality is satisfied $M_{fL}(\widetilde{TC}(u))<M_{fL}(\widetilde{TC}(u+1))$. Set $(n_{fL}^{*},F_{fL}^{*})=u$, and stop.

Once the optimal number of replenishments ($n_{fL}^{*}$) and fraction of period of positive inventory ($F_{fL}^{*}$) are evaluated, the optimal order quantity for the fuzzy-learning model can be derived as:

$$\begin{array}{cc}\hfill Q_{fL}^{*}=& \left[{\displaystyle \frac{e^{{\displaystyle \frac{\varphi F_{fL}^{*}H}{n_{fL}^{*}}}}-1}{\varphi }}+{\displaystyle \frac{H}{n_{fL}^{*}}}-{\displaystyle \frac{F_{fL}^{*}H}{n_{fL}^{*}}}\right]\left[D+{\displaystyle \frac{({\Delta }_{r,1}-{\Delta }_{l,1})}{3}}{\left({\displaystyle \frac{\left(n_{fL}^{*}-1\right)F_{fL}^{*}H}{n_{fL}^{*}}}\right)}^{-l}\right]\hfill \end{array}$$

(35)

3. Numerical Analysis

In this section, the validity of the above models is examined with a continuous review inventory system. The annual customer demand rate is assumed to follow a linear function. With suitable units, the parameters for the three models are as follows: $A=80$, $H=12$, $h=0.4$, $d_0=1000$, $d_1=20$, $k=10$, $m=2$, $\rho =2.5$, $\varphi =0.15$, $c=6$, $s=3$, ${\Delta }_l=75$, ${\Delta }_r=150$, and $l=0.5$. The optimal solution for the number of replenishments $(n)$ and the fraction of the period with positive inventory $(F)$ for crisp, fuzzy, and fuzzy-learning models are presented with the corresponding optimal order quantity and total cost in

Table 1. Optimal solution of the crisp, fuzzy, and fuzzy-learning models.

Model	n	F	Q	Total Cost
Crisp	22	0.698	584.35	6373.67
Fuzzy	22	0.698	598.26	6447.88
Fuzzy Learning	22	0.698	589.27	6412.73

. The closed-form analytical solution approach and algorithm presented in Section 2.3 are applied to find these values.

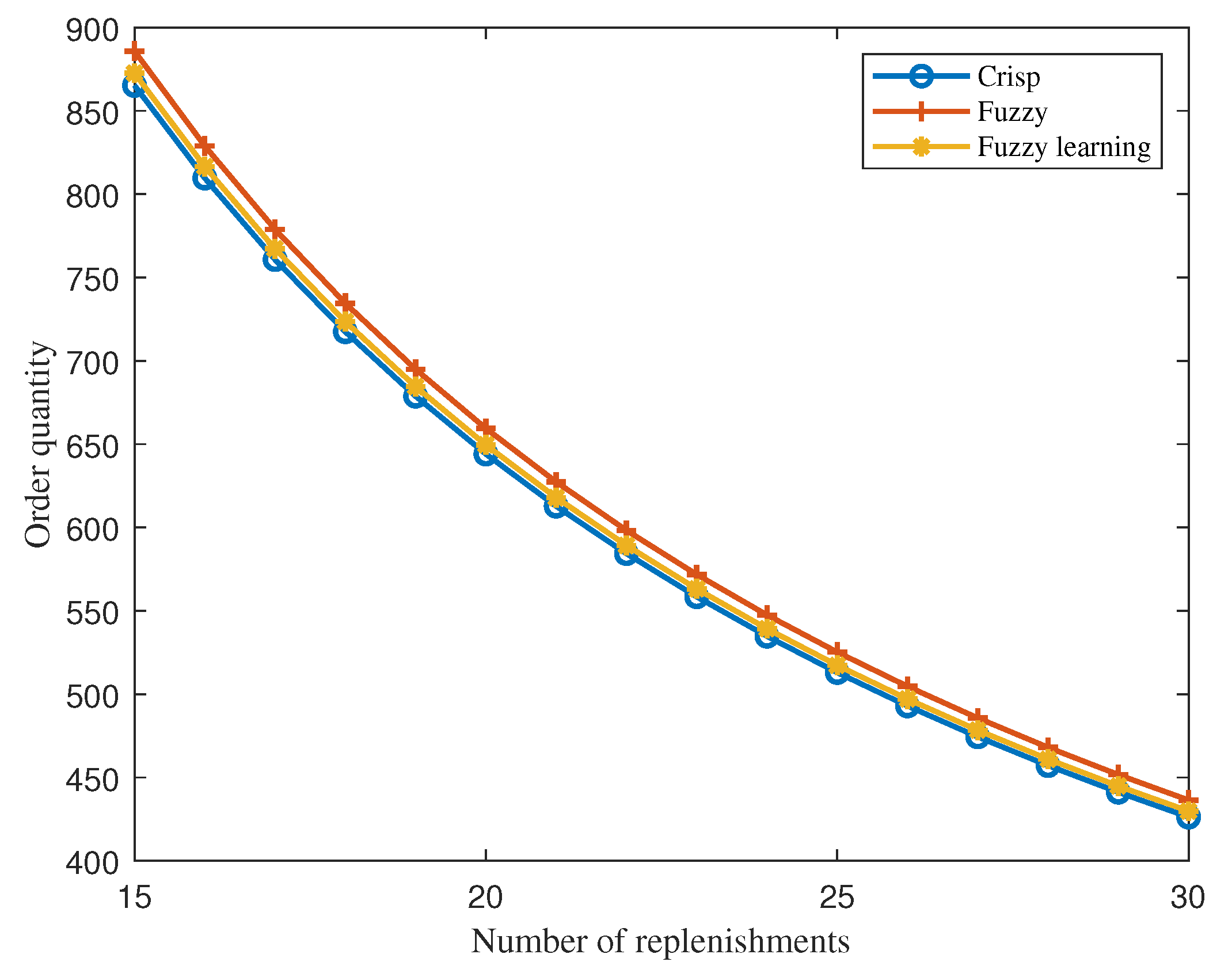
Based on the results presented in Table 1, it is observed that total cost and order quantity were lesser for the fuzzy-learning model in comparison with the fuzzy model. This signifies the importance of learning in decision making. It can also been observed in Figure 2 that the total cost was more sensitive to the lower number of replenishments than the higher number of replenishments. The difference of the total cost between the models reduced as the number of replenishments increased. However, the order quantity continuously reduced (see Figure 3) as the number of replenishments increased, but the rate of reduction decreased as number of replenishments increased.

To handle inaccuracy in customer demand estimation, it is beneficial to place a greater number of orders with a lesser order size in the initial period in spite of the high ordering cost, so that an adequate level of learning can be achieved in terms of process information, customer preference, organizational behavior, etc. Therefore, managers who work in erratic and unpredictable environments must take into account the impact of learning while selecting an optimal inventory policy.

Sensitivity analysis:

The sensitivity analysis was carried out on all the key parameters such as ordering cost $(A)$, unit holding cost $(h)$, deterioration rate $(\varphi )$, promotional effort $(\rho )$, amount of impreciseness $(\Delta )$, and the learning factor $(l)$ to get further insights. Ordering cost $(A)$ was found to be a significant factor not only for the optimal number of replenishments $(n)$, but also for the total cost $(TC)$ and optimal order quantity $(Q)$ (see

Table 2. Effect of ordering cost $(A)$ on the crisp, fuzzy, and fuzzy learning models.

Crisp					Fuzzy				Fuzzy Learning
A	${\mathit{n}}_{\mathit{C}}^{*}$	${\mathit{F}}_{\mathit{C}}^{*}$	${\mathit{Q}}_{\mathit{C}}^{*}$	$\mathit{TC}(\mathit{n},\mathit{F})$	${\mathit{n}}_{\mathit{f}}^{*}$	${\mathit{F}}_{\mathit{f}}^{*}$	${\mathit{Q}}_{\mathit{f}}^{*}$	$\mathit{M}(\widetilde{\mathit{TC}}(\mathit{n},\mathit{F}))$	${\mathit{n}}_{\mathit{fL}}^{*}$	${\mathit{F}}_{\mathit{fL}}^{*}$	${\mathit{Q}}_{\mathit{fL}}^{*}$	${\mathit{M}}_{\mathit{fL}}(\widetilde{\mathit{TC}}(\mathit{n},\mathit{F}))$
40	26	0.698	492.91	5372.19	26	0.698	504.65	5434.98	26	0.698	497.05	5405.32
50	25	0.698	512.98	5637.64	25	0.698	525.20	5702.95	25	0.698	517.29	5672.07
60	24	0.698	534.75	5892.20	24	0.698	547.48	5960.23	24	0.698	539.25	5928.05
70	23	0.698	558.45	6137.07	23	0.698	571.75	6208.05	23	0.698	563.15	6174.45
80	22	0.698	584.35	6373.67	22	0.698	598.26	6447.88	22	0.698	589.27	6412.73
90	22	0.698	584.35	6603.67	22	0.698	598.26	6677.88	22	0.698	589.27	6642.73
100	21	0.698	612.77	6823.71	21	0.698	627.36	6901.45	21	0.698	617.94	6864.61
110	20	0.698	644.09	7039.23	20	0.698	659.43	7120.86	20	0.698	649.53	7082.15
120	20	0.698	644.09	7249.23	20	0.698	659.43	7330.86	20	0.698	649.53	7292.15

). Low ordering cost $(A)$ led to a greater number of replenishments $(n)$ and a lesser order quantity $(Q)$, which resulted in a significant reduction of total cost $(TC)$. The number of replenishment $(n)$ was more sensitive to the lower value of ordering cost $(A)$ than a higher value, whereas the fraction of the period of positive inventory $(F)$ remained unchanged.

Low unit holding cost $(h)$ led to a lesser number of replenishments $(n)$ and thus more order quantity $(Q)$ (see

Table 3. Effect of holding cost $(h)$ on the crisp, fuzzy, and fuzzy-learning models.

Crisp					Fuzzy				Fuzzy Learning
h	${\mathit{n}}_{\mathit{C}}^{*}$	${\mathit{F}}_{\mathit{C}}^{*}$	${\mathit{Q}}_{\mathit{C}}^{*}$	$\mathit{TC}(\mathit{n},\mathit{F})$	${\mathit{n}}_{\mathit{f}}^{*}$	${\mathit{F}}_{\mathit{f}}^{*}$	${\mathit{Q}}_{\mathit{f}}^{*}$	$\mathit{M}(\widetilde{\mathit{TC}}(\mathit{n},\mathit{F}))$	${\mathit{n}}_{\mathit{fL}}^{*}$	${\mathit{F}}_{\mathit{fL}}^{*}$	${\mathit{Q}}_{\mathit{fL}}^{*}$	${\mathit{M}}_{\mathit{fL}}(\widetilde{\mathit{TC}}(\mathit{n},\mathit{F}))$
0.20	21	0.732	614.06	6015.09	21	0.732	628.68	6084.08	21	0.732	619.12	6051.38
0.25	21	0.723	613.72	6110.66	22	0.723	599.15	6181.08	21	0.723	618.80	6148.14
0.30	22	0.714	584.92	6202.05	22	0.714	598.84	6272.18	22	0.714	589.79	6238.96
0.35	22	0.706	584.63	6288.89	22	0.706	598.55	6361.08	22	0.706	589.52	6326.89
0.40	22	0.698	584.35	6373.67	22	0.698	598.26	6447.88	22	0.698	589.27	6412.73
0.45	23	0.690	558.21	6456.26	23	0.690	571.50	6529.12	23	0.690	562.93	6494.63
0.50	23	0.682	557.97	6533.61	23	0.682	571.26	6608.32	23	0.682	562.72	6572.95
0.55	23	0.674	557.74	6609.20	23	0.674	571.02	6685.70	23	0.674	562.52	6649.48
0.60	23	0.667	557.52	6683.07	24	0.667	546.61	6760.44	23	0.667	562.32	6724.28

). As a result, it also increased the value of the fraction of the period with positive inventory $(F)$. Similarly, a low deterioration rate $(\varphi )$ led to a lesser number of replenishments $(n)$ and total cost $(TC)$, but a higher value of the fraction of the period with positive inventory $(F)$ and order quantity $(Q)$ (see

Table 4. Effect of deterioration rate $(\varphi )$ on the crisp, fuzzy, and fuzzy-learning models.

Crisp					Fuzzy				Fuzzy Learning
$\mathit{\varphi }$	${\mathit{n}}_{\mathit{C}}^{*}$	${\mathit{F}}_{\mathit{C}}^{*}$	${\mathit{Q}}_{\mathit{C}}^{*}$	$\mathit{TC}(\mathit{n},\mathit{F})$	${\mathit{n}}_{\mathit{f}}^{*}$	${\mathit{F}}_{\mathit{f}}^{*}$	${\mathit{Q}}_{\mathit{f}}^{*}$	$\mathit{M}(\widetilde{\mathit{TC}}(\mathit{n},\mathit{F}))$	${\mathit{n}}_{\mathit{fL}}^{*}$	${\mathit{F}}_{\mathit{fL}}^{*}$	${\mathit{Q}}_{\mathit{fL}}^{*}$	${\mathit{M}}_{\mathit{fL}}(\widetilde{\mathit{TC}}(\mathit{n},\mathit{F}))$
0.03	16	0.838	793.76	4668.66	16	0.838	812.66	4723.34	16	0.838	799.92	4697.39
0.06	18	0.798	709.01	5213.60	18	0.798	725.89	5274.24	18	0.798	714.62	5245.46
0.09	20	0.761	640.00	5664.01	20	0.761	655.24	5728.42	20	0.761	645.17	5697.88
0.12	21	0.728	611.09	6044.45	21	0.728	625.64	6114.35	21	0.728	616.13	6081.23
0.15	22	0.698	584.35	6373.67	22	0.698	598.26	6447.88	22	0.698	589.27	6412.73
0.18	23	0.670	559.61	6661.57	23	0.670	572.93	6739.13	23	0.670	564.41	6702.41
0.21	24	0.644	536.69	6915.98	24	0.644	549.46	6996.13	24	0.644	541.38	6958.21
0.24	25	0.620	515.42	7143.16	25	0.620	527.70	7225.28	25	0.620	520.02	7186.46
0.27	26	0.598	495.67	7348.14	26	0.598	507.47	7431.71	26	0.598	500.17	7392.23

). Interestingly, order quantity $(Q)$ was found to be reduced step wise with the increase in $(h)$. It may be noted that the order quantity $(Q)$ for the fuzzy model was more than the crisp and fuzzy-learning models, except for a few values such as $(h)=0.25,0.60$. This is because, these values of the number of replenishments $(n)$ for the fuzzy model were greater than the other two models (see Table 3).

In the same way, it can be observed based on

Table 5. Effect of promotional effort $(\rho )$ on the crisp, fuzzy, and fuzzy-learning models.

Crisp					Fuzzy				Fuzzy Learning
$\mathit{\rho }$	${\mathit{n}}_{\mathit{C}}^{*}$	${\mathit{F}}_{\mathit{C}}^{*}$	${\mathit{Q}}_{\mathit{C}}^{*}$	$\mathit{TC}(\mathit{n},\mathit{F})$	${\mathit{n}}_{\mathit{f}}^{*}$	${\mathit{F}}_{\mathit{f}}^{*}$	${\mathit{Q}}_{\mathit{f}}^{*}$	$\mathit{M}(\widetilde{\mathit{TC}}(\mathit{n},\mathit{F}))$	${\mathit{n}}_{\mathit{fL}}^{*}$	${\mathit{F}}_{\mathit{fL}}^{*}$	${\mathit{Q}}_{\mathit{fL}}^{*}$	${\mathit{M}}_{\mathit{fL}}(\widetilde{\mathit{TC}}(\mathit{n},\mathit{F}))$
0.50	29	0.698	424.34	4769.98	29	0.698	434.84	4826.27	29	0.698	428.03	4799.73
1.00	28	0.698	444.09	5003.96	28	0.698	454.97	5062.27	28	0.698	447.92	5034.76
1.50	26	0.698	483.52	5361.39	26	0.698	495.26	5424.18	26	0.698	487.66	5394.52
2.00	24	0.698	529.66	5824.66	24	0.698	542.39	5892.68	24	0.698	534.15	5860.50
2.50	22	0.698	584.35	6373.67	22	0.698	598.26	6447.88	22	0.698	589.27	6412.73
3.00	20	0.698	650.23	6992.37	21	0.698	633.20	7070.49	21	0.698	623.77	7033.64
3.50	19	0.698	691.72	7662.53	19	0.698	707.88	7748.45	19	0.698	697.46	7707.69
4.00	17	0.698	782.49	8381.23	18	0.698	755.02	8473.53	18	0.698	744.01	8430.50
4.50	16	0.698	840.48	9131.54	16	0.698	859.76	9233.58	16	0.698	847.36	9185.15

that the increase in promotional effort $(\rho )$ reduced the number of replenishments $(n)$, remained insensitive to the fraction of the period of positive inventory $(F)$, and increased the order quantity $(Q)$ and total cost $(TC)$. As impreciseness in demand $(\Delta )$ increased, order quantity $(Q)$ and total cost $(TC)$ increased considerably for the fuzzy model, but the corresponding changes in the fuzzy-learning model were not significant (see

Table 6. Percentage of $\Delta$ changes on the fuzzy and fuzzy-learning models.

Fuzzy					Fuzzy Learning
$\Delta (\%)$	${\mathit{n}}_{\mathit{f}}^{*}$	${\mathit{F}}_{\mathit{f}}^{*}$	${\mathit{Q}}_{\mathit{f}}^{*}$	$\mathit{M}(\widetilde{\mathit{TC}}(\mathit{n},\mathit{F}))$	${\mathit{n}}_{\mathit{fL}}^{*}$	${\mathit{F}}_{\mathit{fL}}^{*}$	${\mathit{Q}}_{\mathit{fL}}^{*}$	${\mathit{M}}_{\mathit{fL}}(\widetilde{\mathit{TC}}(\mathit{n},\mathit{F}))$
−40	22	0.698	592.70	6418.20	22	0.698	587.30	6397.11
−30	22	0.698	594.09	6425.62	22	0.698	587.80	6401.01
−20	22	0.698	595.48	6433.04	22	0.698	588.29	6404.92
−10	22	0.698	596.87	6440.46	22	0.698	588.78	6408.83
0	22	0.698	598.26	6447.88	22	0.698	589.27	6412.73
10	22	0.698	599.66	6455.30	22	0.698	589.77	6416.64
20	22	0.698	601.05	6462.72	22	0.698	590.26	6420.54
30	22	0.698	602.44	6470.14	22	0.698	590.75	6424.45
40	22	0.698	603.83	6477.56	22	0.698	591.24	6428.35

). This reemphasizes the importance of learning while dealing with a fuzzy environment. It was also observed that the change in impreciseness in demand $(\Delta )$ remained insensitive to the number of replenishments $(n)$ and the fraction of the period of positive inventory $(F)$. The learning factor $(l)$ was also an important factor, as can be seen in

Table 7. Effect of l on the fuzzy-learning model.

l	${\mathit{n}}_{\mathit{fL}}^{*}$	${\mathit{F}}_{\mathit{fL}}^{*}$	${\mathit{Q}}_{\mathit{fL}}^{*}$	${\mathit{M}}_{\mathit{fL}}(\widetilde{\mathit{TC}}(\mathit{n},\mathit{F}))$
0.1	22	0.698	595.65	6437.88
0.2	22	0.698	593.53	6429.66
0.3	22	0.698	591.81	6422.89
0.4	22	0.698	590.41	6417.32
0.5	22	0.698	589.27	6412.73
0.6	22	0.698	588.35	6408.96
0.7	22	0.698	587.60	6405.86
0.8	22	0.698	586.99	6403.33

, and with the increase in the value of the learning factor $(l)$, order quantity $(Q)$ and total cost $(TC)$ decreased, but no change was observed in the number of replenishments $(n)$ and the fraction of the period of positive inventory $(F)$.

4. Conclusions

In this study, a continuous inventory control model was developed for the determination of the optimal number of replenishments, the fraction of the period with positive inventory, and their corresponding optimal order quantity for deteriorating items under promotional effort. The concept of the learning effect in a fuzzy environment was also addressed in this model. A promotional effort-dependent linear demand function was considered over the finite horizon. The model also considered shortage, and it was fully backlogged. Three separate models: crisp, fuzzy, and fuzzy-learning, were developed considering the above-mentioned features. A closed-form analytical solution was developed for the crisp and fuzzy model, whereas an algorithm was formulated for the fuzzy-learning model owing to the complex mathematical expression. Based on the optimal number of replenishments and the fraction of the period with positive inventory, the optimal order quantity was evaluated. Further, the proposed models were explained through a numerical example to emphasize the importance of the models. Sensitivity analysis was also carried out on key parameters to get further insights.

Developing a model to analyze the impact of preservation technology for deteriorating items and finding the optimal operational setup could be an interesting future work.