Abstract
Thermal storage system (TES) with phase change material (PCM) is an important device to store thermal energy. It works as a thermal buffer to reconcile the supply energy with the energy demand. It has a wide application field, especially for solar thermal energy storage. The main drawback is the low value of thermal conductivity of the PCM making the system useless for thermal engineering applications. A way to resolve this problem is to combine the PCM with a highly conductive material like metal foam and/or nanoparticles. In this paper a numerical investigation on the metal foam effects in a latent heat thermal energy storage system, based on a phase change material with nanoparticles (nano-PCM), is accomplished. The modelled TES is a typical 70 L water tank filled with nano-PCM with pipes to transfer thermal energy from a fluid to the nano-PCM. The PCM is a pure paraffin wax and the nanoparticles are in aluminum oxide. The metal foam is made of aluminum with assigned values of porosity. The enthalpy-porosity theory is employed to simulate the phase change of the nano-PCM and the metal foam is modelled as a porous media. Numerical simulations are carried out using the Ansys Fluent code. The results are shown in terms of melting time, temperature at varying of time, and total amount of stored energy.
1. Introduction
Thermal Energy Storage (TES) [1] is a device capable of storing excess energy by heating a storage medium. In base of the medium material, TES could be classified as sensible TES and latent TES. The latter has the best performance because it permits the storage of excess energy at a quasi-constant temperature. The base material of latent TES is the phase change material (PCM) that during the phase change process, adsorbs and then releases the thermal energy with small volume variation [2]. There are many types of PCM in literature [3], in particular, for a solid-liquid phase change process, paraffin [4] has many advantages such as high latent heat, non-toxicity, chemical stability, and small volume variation, but one of the worst drawbacks is the low value of thermal conductivity, making the application of pure PCM counterproductive for thermal storage application because it could behave as an insulated material. Therefore, different enhancement techniques are recommended in order to improve paraffin thermal conductivity such as putting highly-conductive nanoparticles [5] into the pure PCM or employing metal foam [6]. The addition of nanoparticles in the PCM creates a new class of material, called nano-PCM [7].
In the literature, there are few works about nano-PCM, for example Shin and Banerjee [7] have conducted some experimental works for enhancing the heat capacity of the PCM with the addition of nanoparticles. Chieruzzi [8] have experimentally investigated a PCM with nanoparticles concluding that the latent heat of the nano-PCM increased by 12%. Ercole [9] have found a robust correlation of the specific heat varying of temperature, nanoparticles’ diameters and volume concentration for PCM molten salt with silica nanoparticles using experimental data in literature. Bayat [10] numerically simulated the performance of a finned heat sink with phase change material with nanoparticles. Using the results, they showed that the nano-PCM has better performance even with a low concentration of nanoparticles, while for higher concentrations it seems that the heat sink has lower thermal performance.
The applications of an enhanced technique for PCM, especially using metal foam, have been broadly investigated in literature [11]. For example, Siahpush [12] have performed both a numerical and experimental study on a thermal energy storage system with PCM and metal foam, assuming the local thermal equilibrium hypothesis to simulate the heat transfer between PCM and metal foam. Tian and Zhao [13] have numerically investigated a TES system with paraffin RT58 as the PCM with aluminum metal foam assuming the local thermal non-equilibrium model. Fang [14] have proposed an index to characterize the effective energy storage capacity of a TES system with PCM. With relation to nano-PCM in metal foam, Hossain [15] have studied a numerical model with PCM with copper oxide nanoparticles in metal foam. The local thermal equilibrium is assumed between the PCM and the metal foam while the Darcy model is employed without the Forchheimer extension. The authors demonstrated that the nano-PCM melts at a faster rate inside the metal foam. Mahdi and Nsofor [16] experimentally worked on a triplex-tube storage system with nano-PCM in metal foam and they concluded that the metal foam has a predominant role in conduction phenomenon with respect to the convection of liquid PCM, and the nanoparticles slightly reduce the convection role but they do not eliminate it. Ren [17] have numerically investigated the melting process of the PCM of a TES system with nanoparticles and metal foam using the boundary-lattice Boltzmann method at pore-scale. The results have shown that metal foam is more effective with respect to the nanoparticles for the improvement of the PCM melting rate.
This work numerically studies the nano-PCM inside a metal foam. The volume concentration of nano-PCM is 1% of Al2O3 inside a paraffin wax with a melting point around 58 °C. A single-phase model is applied to evaluate the thermophysical properties of the nano-PCM. The metal foam is aluminum and the assigned porosity is set to 80%. The porous media assumption is considered to study the metal foam and the local thermal non-equilibrium (LTNE) assumption is employed to evaluate the heat transfer between the nano-PCM and the metal foam. The system is a typical 70 L water tank filled with nano-PCM in aluminum foam. The charging process is monitored in terms of liquid fraction, average temperature evolution, and stored energy.
2. Physical Model
The physical model of the TES system is a parallelepiped with the dimension of 785 × 120 × 710 mm filled with nano-PCM and a number of pipes where the heat transfer fluid (HTF), flows, passing throughout it. For the thermal and geometry symmetry the computational domain is only a part of the system and it is shown in Figure 1. During the charging operation, on the pipe surface a temperature value of 343.15 K is applied to take into account the heat exchange between the HTF and the TES system. The other surfaces are assumed adiabatic. Along the y-axis a gravitational acceleration is imposed and the Boussinesq approximation is considered to take into account the natural convection. The enthalpy-porosity method is employed [18], because the paraffin melts in a temperature range. In this method a non-dimensional parameter is introduced, called liquid fraction, indicated with Greek letter β, that describes the mixed zone during the phase change.
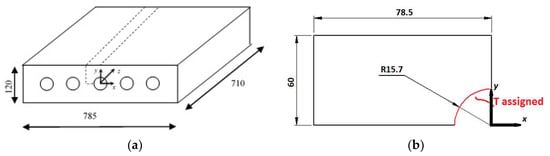
Figure 1.
Physical model of TES system. The dotted lines (a) represent the computational domain, frontal view of the computational domain (b).
This parameter is ranged from 0 to 1:
T is the local temperature, Tliquidus is the temperature over which the PCM is fully liquid while Tsolidus is the temperature under which it is fully solid. The mixed zone exists in a range of temperature between Tliquidus and Tsolidus.
The metal foam is modelled as a porous media subject to the Brinkman extended Darcy-Forchheimer model, therefore, a source term is added in the momentum equation. To simulate the heat transfer between PCM and metal foam, the local thermal non-equilibrium (LTNE) assumption is applied, where there are two functions of temperature in the porous media, one for the fluid phase (PCM) and the other for the solid phase (metal foam).
In order to simulate the thermophysical properties of the nano-PCM, the single-phase model is employed, therefore the Nano-PCM is considered as a homogeneous fluid without any dynamic difference between the nanoparticles and the base PCM. Using this approach, the thermophysical properties of the nano-PCM are a weighted average with respect to the volume concentration ψ between the property’s values of the nanoparticles and the pure PCM. The volume concentration of the nano-PCM ψ represents the ratio between the volume of the nanoparticles and the total volume of the domain:
To simulate the natural convection in the PCM/nano-PCM a Boussinesq approximation is considered:
where the subscripts PCM and 0 refer to the phase change material and the operating condition, respectively. The symbol ρ is the density while γ represents the thermal expansion faction. A value of 321 K is imposed for the operating temperature.
The governing equations [19] are the following:
In the local thermal non-equilibrium model, the equation of energy for PCM is [20]:
while for the metal foam it is [20]:
V is the velocity of the fluid phase (PCM or nano-PCM), ε is the porosity of the metal foam, t is the time, μ is the dynamic viscosity of the fluid phase, p the relative pressure, and S is a source term expressed in Equation (8). Therefore, the first term is the Boussinesq approximation, the second term models the mushy zone where Amush is the mushy zone constant, which represents the damping of the velocity to zero during the solidification [19]. In these simulations the value of the mushy zone constant is set to 105 kg/m3·s. In equation (8), K is the permeability of the porous media and CF is the inertial drag factor. The permeability and drag factor values are calculated with the following relations, by Calmidi [21]:
where df and dp are respectively the fiber diameter and the cell diameter of the porous media. Their value is taken from [21], in particular, for a metal foam of 20 pores per inch (ω = 20 PPI) and a porosity of 0.93, the values of dp and df are 1.12 × 10−3 m and 1.37 × 10−4 m, respectively.
In the energy equations, c is the specific heat, k is the thermal conductivity, HL is the latent heat of the PCM. The subscript foam indicates the physical characteristic of the metal foam. αsf and hsf are the specific surface area density and interfacial heat transfer coefficient, respectively. They are calculated by the following equations:
where Red is the Reynolds referring to the fiber diameter and Pr is the Prandtl number referring to the fluid phase (PCM)
Applying the single-phase model to calculate the values of the proprieties of the nano-PCM, the following relations [22] are used:
The subscripts NANOPCM, wax and Al2O3 refer to the nano-PCM, the base PCM (paraffin wax) and nanoparticles (aluminum oxide), respectively.
The dynamic viscosity of the nano-PCM is evaluated by [22]:
While for the thermal conductivity of the nano-PCM, the Maxwell equation is employed [23,24]:
Finally, for the latent heat the relation is taken from [24]:
The melting temperature is assumed independent from the volume concentration. The base PCM is RT58 paraffin wax [25], while the nanoparticles are oxide aluminum. The volume concentration of the nanoparticles is set to 1%. The porosity of the meal foam is set to 0.80.
All the thermal properties are expressed in Table 1.

Table 1.
Thermal properties of the materials.
3. Numerical Model
The finite volume approach using Ansys Fluent code is employed for the simulations. The SIMPLE algorithm is employed for the pressure-velocity coupling; the PRESTO algorithm is used for the pressure calculation. A transient analysis is performed with a time step size equal to 0.5 s. The convergence errors are assumed equal to 10−5 for the continuity and momentum equation and 10−8 for the energy equation. The boundary conditions and initial condition are:
- -
- Pipe Surface: assigned temperature Tw at 343.15 K.
- -
- The other surfaces are adiabatic.
Initial condition:
- -
- The system is assumed to be at 300 K.
Three types of meshes are evaluated for the mesh independent test: 27,630 nodes, 51,322 nodes and 104,556 nodes. A mesh with 27,630 nodes is chosen for the numerical study because it represents the best trade-off between the computational costs and accuracy.
The independence mesh test is represented in Table 2.

Table 2.
Independence mesh test.
The numerical model was validated by means of the comparison with the geometry and PCM given by Krishnan [26]. Table 3 shows the comparison between the results carried out by the present numerical model in the same geometry and PCM given by [26] and the ones carried out by Krishnan [26]. It is observed that the mean percentage deviation is about 2% with a maximum value at Fo number of 1.2 equals to 2.66%.

Table 3.
Model Validation.
T* is the non-dimensional temperature taken at the center of the domain and Fo is the Fourier number, defined as:
where Tw is the wall temperature and Ti is the initial temperature. L is a characteristic length of the system.
4. Results and Discussions
In Figure 2 there is a comparison in terms of average liquid fraction and average temperature of pure PCM and nano-PCM at 1%. During the time, it can be seen that the improvement of the nanoparticles has a small influence on the melting process because the two curves are nearly overlapped. The melting time is above 40,000 s and there is a smooth transition from solid to liquid phase during the time. In Figure 3 there is a comparison between the various improvements in terms of liquid fraction. The first important consideration is about the log scale of time, because when the metal foam is added, the melting process is very fast in a comparison of PCM or nano-PCM. The melting time for the pure PCM is 40,301 s, while for the nano-PCM it is 39,781 s. In the presence of the metal foam the melting time is 1321 s. This can be explained by the fact that the metal foam has a thermal conductivity higher than pure PCM of at least two orders of magnitude, leading a fast diffusion of heat inside the whole system reaching every point of the PCM thanks to its matrix structure. Moreover, in this figure there are three curves, but the nano-PCM and the PCM curves are overlapped because of the log scale, and the same consideration can be made in Figure 4 and Figure 5.
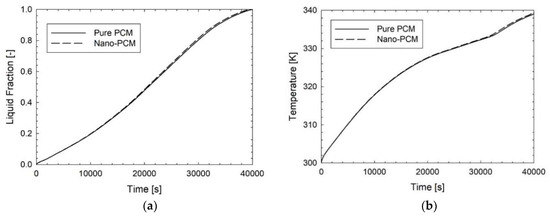
Figure 2.
Comparison of pure PCM and nano-PCM at 1% during the time in terms of (a) average liquid fraction and (b) average temperature evolution.
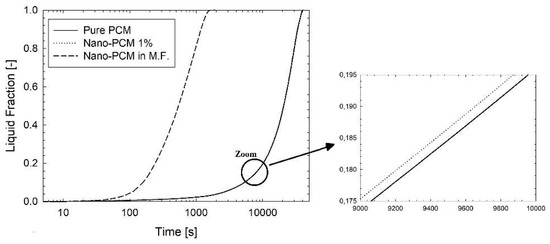
Figure 3.
Average liquid fraction evolution during the time for pure PCM, nano-PCM and nano-PCM in metal foam.
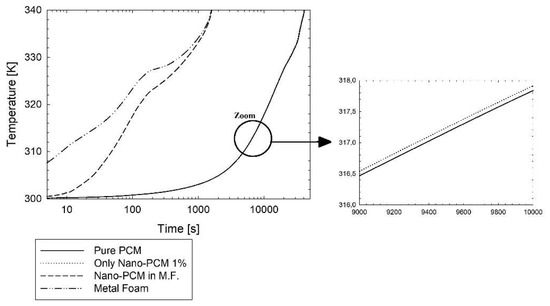
Figure 4.
Average temperature evolution during the time for pure PCM, nano-PCM, nano-PCM in metal foam (M.F.), and metal foam.
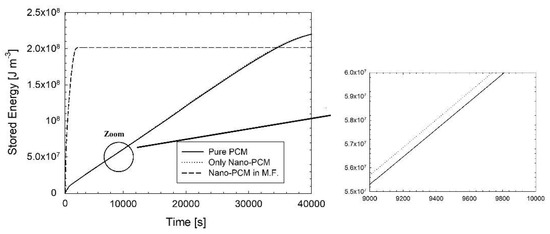
Figure 5.
Average stored energy per unit of mass evolution during the time for pure PCM, nano-PCM, and nano-PCM in metal foam.
In Figure 4 it is possible to see the temperature evolution of pure PCM, only nano-PCM without metal foam, and the temperature evolution of nano-PCM in metal foam and the metal foam temperature. The curves of the pure PCM and the nano-PCM at 1% are overlapped. With the addition of metal foam, even though the melting time is very low, 1321 s compared with 39,781 s, the stored energy is lower, and after the reaching of the thermal equilibrium the stored energy is constant. This aspect depends on the lower thermal capacity of the PCM with the metal foam, which is shown better in Figure 5.
Where the metal foam is not inserted, the temperature evolution curves are overlapped. In the presence of metal foam, the nano-PCM melts very fast; its melting time is nearly 2000 s. The evolution temperature curves of nano-PCM in metal foam and of metal foam reduce their temperature difference during the time until the whole nano-PCM is completely melted. Moreover, there is a shape change of the curves at about 330 K, because around that temperature the majority of the domain is melted, maintaining the temperature at nearly constant. It is possible to see that in the LTNE model, the nano-PCM in metal foam (M.F.) and the metal foam reached the temperature equilibrium when the liquid fraction is one, since the PCM is fully melted. In this Figure 4, the evolution of the average temperature is represented for three cases: the case with only pure PCM, the case with only nano-PCM at 1% and the case with the nano-PCM in metal foam. This last case uses the LTNE assumption, where there are two temperature functions, one for the nano-PCM and the other for the metal foam. Therefore, for this last case there are two temperature curves represented in Figure 4. In this last case the two temperature curves tend to reach the same point at the end of the charging operation. Furthermore, the metal foam temperature evolves more rapidly because the thermal diffusivity of the metal foam is greater than that of the PCM/nano-PCM. In fact, at the beginning, the thermal diffusion evolves very quickly inside the foam instead of inside the PCM. When the melting phenomenon increases, the temperature difference between the nano-PCM and the foam diminishes. It is worthy to note that during the melting phenomenon the foam gives more thermal energy to the PCM due to the phase change and so the average foam temperature curve has a minor slope with respect to the PCM.
Figure 5 shows the average stored energy per unit of volume. With the pure PCM it is possible to store more energy, while adding metal foams leads to a lower stored energy with respect to simple PCM and nano-PCM. The evaluation of the stored energy per unit of volume for pure PCM, nano-PCM, and nano-PCM in metal foam is obtained by the following equations:
In order to compare the effectiveness of this system, some comparison is accomplished in terms of melting time for different enhancement techniques. In Li and Wu [27] the charging time is about 220 with a similar geometry and with an inorganic PCM with fins. Another comparison is accomplished using the work of Ebadi [28] with a similar geometry but using only nano-PCM in terms of energy storage capacity. The stored energy is between 5000 and 30,000 J for different Rayleigh numbers and volume concentration, while the storage energy in this work is about 3 × 105 J, but the volume is larger. In Table 4 there are other comparisons in term of melting time with different enhancement.

Table 4.
Comparison of different enhancement in terms of melting time.
Obviously to compare the two storage systems an analysis in terms of non-dimensional number could be accomplished.
5. Conclusions
A numerical investigation on the metal foam effects in a latent heat thermal energy storage system, based on a phase change material with nanoparticles (nano-PCM), has been accomplished. The modelled TES was a typical 70 L water tank filled with nano-PCM and metal foam. The results have shown that metal foam is more effective than nano-PCM in terms of melting rate. Regarding the stored energy, the amount of stored energy is minor when the metal foam is applied. The melting time and the speed of charging are improved with the utilization of the metal foam; in fact, the ratios between the charging time of PCM/nano-PCM and PCM/nano-PCM in metal foam are 1.013 and 30.58, respectively. A comparison between different systems with different enhancements in literature has been done. The results are obviously different, and therefore, in the future, a comparison in terms of non-dimensional number could be accomplished. Moreover, the lack of information on nanoparticle diameter effect on thermophysical properties of nano-PCM limits the present results in a quantitative way. However, the effect of nanoparticle dimensions is an important issue that should be investigated.
Author Contributions
Conceptualization, B.B., D.E. and O.M.; Formal analysis, B.B., A.d.P. and D.E.; Methodology, B.B., A.d.P. and D.E.; Project administration, O.M.; Validation, A.d.P.; Writing–original draft, D.E.; Writing–review and editing, O.M.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| Amush | Mushy constant kg·m−3·s−1 |
| CF | drag factor coefficient |
| c | specific heat, J·kg−1·K−1 |
| df | fiber diameter, m |
| dp | cell diameter, m |
| hsf | interfacial heat transfer coefficient, W·m−2·K−1 |
| HL | latent heat, J·kg−1 |
| k | thermal conductivity, W·m−1·K−1 |
| K | porous permeability, m2 |
| L | Characteristic length, m |
| p | relative pressure, Pa |
| Pr | Prandtl number |
| r | radius tube, m |
| Re | Reynolds number |
| S | source term N·m−3 |
| t | time s |
| T | temperature, K |
| Vol | volume |
| V | velocity, m·s−1 |
| x | cartesian axis direction, m |
| y | cartesian axis direction, m |
| z | cartesian axis direction, m |
| Greek symbols | |
| αsf | specific surface area density, m−1 |
| β | liquid fraction |
| ε | porosity |
| γ | thermal expansion coefficient K−1 |
| μ | dynamic viscosity, kg·m−1·s−1 |
| ρ | density, kg·m−3 |
| ψ | volume concentration of nanoparticles |
| ω | number of pores per inch, m−1 |
| Subscripts | |
| 0 | operating condition |
| Al2O3 | Aluminium oxide |
| df | fiber diameter |
| Foam | metal foam |
| i | initial |
| Liquidus | liquidus temperature |
| NANOPCM | Nano-enhanced PCM |
| PCM | phase change material |
| Solidus | solidus temperature |
| TOTAL | whole domain |
| w | wall |
| Wax | paraffin wax RT58 |
References
- Alva, S.; Lin, Y.; Fang, G. An overview of thermal energy storage systems. Energy 2018, 144, 341–378. [Google Scholar] [CrossRef]
- Gil, A.; Medrano, M.; Martorell, I.; Lazaro, A.; Dolado, P.; Zalba, B.; Cabeza, L. State of the art on high temperature thermal energy storage for power generation. Part 1—Concepts, materials and modellization. Renew. Sustain. Energy Rev. 2010, 14, 31–55. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, Z.; Ghafoor, A. A review of performance enhancement of PCM based latent heat storage system within the context of materials, thermal stability and compatibility. Energy Convers. Manag. 2016, 115, 132–158. [Google Scholar] [CrossRef]
- Khyad, A.; Samrani, H.; Bargach, M.N. State of the art review of thermal energy storage systems using PCM operating with small temperature differences: Focus on Paraffin. J. Mater. Environ. Sci. 2016, 7, 1184–1192. [Google Scholar]
- Colla, L.; Ercole, D.; Fedele, L.; Mancin, S.; Manca, O.; Bobbo, S. Nano-phase change materials for electronics cooling applications. ASME J. Heat Transf. 2017, 139, 052406. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Lu, W.; Tian, Y. Heat transfer enhancement for thermal energy storage using metal foams embedded within phase change materials (PCMs). Sol. Energy 2010, 84, 1402–1412. [Google Scholar] [CrossRef]
- Shin, D.; Banerjee, D. Enhanced Specific Heat of Silica Nanofluid. ASME J. Heat Transf. 2010, 133, 024501. [Google Scholar] [CrossRef]
- Chieruzzi, M.; Cerritelli, G.F.; Miliozzi, A.; Kenny, J.M. Effect of nanoparticles on heat capacity of nanofluids based on molten salts as PCM for thermal energy storage. Nanoscale Res. Lett. 2013, 8, 448. [Google Scholar] [CrossRef] [PubMed]
- Ercole, D.; Manca, O.; Vafai, K. An investigation of thermal characteristics of eutectic molten salt-based nano fluids. Int. Comm. Heat Mass Transf. 2017, 87, 98–104. [Google Scholar] [CrossRef]
- Bayat, M.; Faridzadeh, M.R.; Toghraie, D. Investigation of finned heat sink performance with nano enhanced phase change material (NePCM). Therm. Sci. Eng. Prog. 2018, 5, 50–59. [Google Scholar] [CrossRef]
- Ibrahim, N.I.; Al-Sulaiman, A.F.; Rahmana, S.; Yilbas, B.S.; Sahinb, A.Z. Heat transfer enhancement of phase change materials for thermal energy storage applications: A critical review. Renew. Sustain. Energy Rev. 2017, 74, 26–50. [Google Scholar] [CrossRef]
- Siahpush, A.; O’Brien, J.; Crepeau, J. Phase change heat transfer enhancement using copper porous foam. ASME J. Heat Transf. 2008, 130, 082301. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, C.Y. A numerical investigation of heat transfer in phase change materials (PCMs) embedded in porous metals. Energy 2011, 36, 5539–5546. [Google Scholar] [CrossRef]
- Fang, Y.; Niu, J.; Deng, S. Numerical analysis for maximizing effective energy storage capacity of thermal energy storage systems by enhancing heat transfer in PCM. Energy Build. 2018, 160, 10–18. [Google Scholar] [CrossRef]
- Hossain, R.; Mahmud, S.; Dutta, A.; Pop, I. Energy storage system based on nanoparticle-enhanced phase change material inside porous medium. Int. J. Therm. Sci. 2015, 91, 49–58. [Google Scholar] [CrossRef]
- Mahdi, J.M.; Emmanuel, C.; Nsofor, E.C. Melting enhancement in triplex-tube latent heat energy storage system using nanoparticles-metal foam combination. Appl. Energy 2017, 191, 22–34. [Google Scholar] [CrossRef]
- Ren, Q.; Meng, F.; Guo, P. A comparative study of PCM melting process in a heat pipe-assisted LHTES unit enhanced with nanoparticles and metal foams by immersed boundary-lattice Boltzmann method at pore-scale. Int. J. Heat Mass Transf. 2018, 121, 1214–1228. [Google Scholar] [CrossRef]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Al-abidi, A.; Bin Mat, S.; Sopian, K.; Sulaiman, M.Y.; Mohammed, A.T. CFD application for latent heat thermal energy storage: A review. Renew. Sustain. Energy Rev. 2013, 20, 353–363. [Google Scholar] [CrossRef]
- Liu, Z.; Yao, Y.; Wu, H. Numerical modeling for solid–liquid phase change phenomena in porous media: Shell-and-tube type latent heat thermal energy storage. Appl. Energy 2013, 112, 1222–1232. [Google Scholar] [CrossRef]
- Calmidi, V.V. Transport Phenomena in High Porosity Metal Foams. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 2000. [Google Scholar]
- Sebti, S.S.; Mastiani, M.; Mirzaei, H.; Dadvand, A.; Kashani, S.; Hosseini, S.A. Numerical study of melting of nano-enhanced phase change material in a square cavity. Alex. Eng. J. 2013, 14, 307–316. [Google Scholar] [CrossRef]
- Maxwell, J.C. Treatise on Electricity and Magnetism; Clarendon: Oxford, UK, 1879. [Google Scholar]
- Khodadadi, J.M.; Hosseinizadeh, S.F. Nanoparticle-enhanced phase change materials (NEPCM) with great potential for improved thermal energy storage. Int. Commun. Heat Mass Transf. 2007, 34, 534–543. [Google Scholar] [CrossRef]
- Rubitherm GmBH. Available online: www.rubitherm.de (accessed on 25 October 2017).
- Krishnan, S.; Murthy, J.Y.; Garimella, S.V. A two-temperature model for solid–liquid phase change in metal foams. ASME J. Heat Transf. 2004, 127, 995–1004. [Google Scholar] [CrossRef]
- Wu, Z.G.; Li, Z. Analysis of HTFs, PCMs and fins effects on the thermal performance of shell-tube thermal energy storage units. Sol. Energy 2015, 122, 382–395. [Google Scholar] [CrossRef]
- Ebadi, S.; Tasnim, S.H.; Aliabadi, A.A.; Mahmud, S. Melting of nano-PCM inside a cylindrical thermal energy storage system: Numerical study with experimental verification. Energy Convers. Manag. 2018, 166, 241–259. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).