Current Trends and Challenges in Applying Metaheuristics to the Innovative Area of Weight and Structure Determination Neuronets

Abstract

The weights and structure determination (WASD) neuronet (or neural network) is a single-hidden-layer feedforward neuronet that exhibits an excellent approximation ability, despite its simple structure. Thanks to its strong generalization, fast speed, and ease of implementation, the WASD neuronet has been the subject of many modifications, including metaheuristics, and applications in a wide range of scientific fields. As it has garnered significant attention in the last decade, the aim of this study is to provide an extensive overview of the WASD framework. Furthermore, the WASD has been effectively used in numerous real-time learning tasks like regression, multiclass classification, and binary classification due to its exceptional performance. In addition, we present WASD’s applications in social science, business, engineering, economics, and medicine. We aim to report these developments and provide some avenues for further research.

1. Introduction

Artificial neuronets (ANs), also known as artificial neural networks, have been extensively studied and used in numerous scientific, engineering, and practical domains because of their exceptional characteristics, which include distributed storage, parallel processing, self-adaptive, and self-learning capabilities. With a history spanning more than 70 years, AN was initially proposed in the last century [1]. Neural network’s fundamental architecture resembles the nerve system in the human brain and was inspired by biological neuronets. A typical neuronet, which is a type of machine learning technique, is made up of neurons, connections, and weights. A neuron in a neuronet, often referred to as a perception [2], gives out output signals to subsequent neurons after receiving input signals from earlier neurons. A neuronet’s neurons are frequently arranged in multiple layers. The relationship between neurons in different layers was described as a connection. A neuron may be highly connected to neurons in both its former and subsequent layers. Additionally, weight is a crucial parameter that each connection provides. Note that weights are crucial because they determine how a neuron interprets input signals and generates output signals.

One of the most basic AN types ever created is the feed-forward neuronet, which is a universal approximator. The information moves forward through the input layer, multiple hidden layers, and a final layer of output nodes. The process of training a neuronet involves identifying the layer weights that optimize its ability to approximate data. One of the most well-known and significant feed-forward neuronet models, with numerous theoretical examinations and practical applications, is the one based on the error back-propagation (BP) training algorithm or its variations. BP-type neuronets, which were first proposed in the mid-1980s (or even earlier, in 1974), are a sort of multilayer feed-forward neuronet [3]. BP-type neuronets and their associated training methods remain widely used in several theoretical and practical applications to this day.

By adopting a gradient-based descent path, BP algorithms are essentially gradient-based iterative methods that modify the AN weights to bring the input/output behavior into a desired mapping. BP-type neuronets do, however, seem to have the following drawbacks: (i) the potential to become stuck in local minima; (ii) the challenge of selecting suitable learning rates (i.e., training speed); and (iii) the incapacity to deterministically create the smallest or optimal neuronet structure. Numerous enhanced BP-type algorithms have been suggested and studied as a result of the aforementioned intrinsic flaws [4]. There are generally two main categories of improvements. One could argue that the standard gradient-descent method could serve as a foundation for improving the BP-type algorithms [5]. On the other hand, the neuronet model might be trained using numerical optimization approaches. It is important to note that in an effort to enhance the performance of BP-type neuronets, many researchers typically concentrate on the learning algorithm itself. Still, nearly all of the enhanced BP-type algorithms are unable to overcome the aforementioned intrinsic flaws [6].

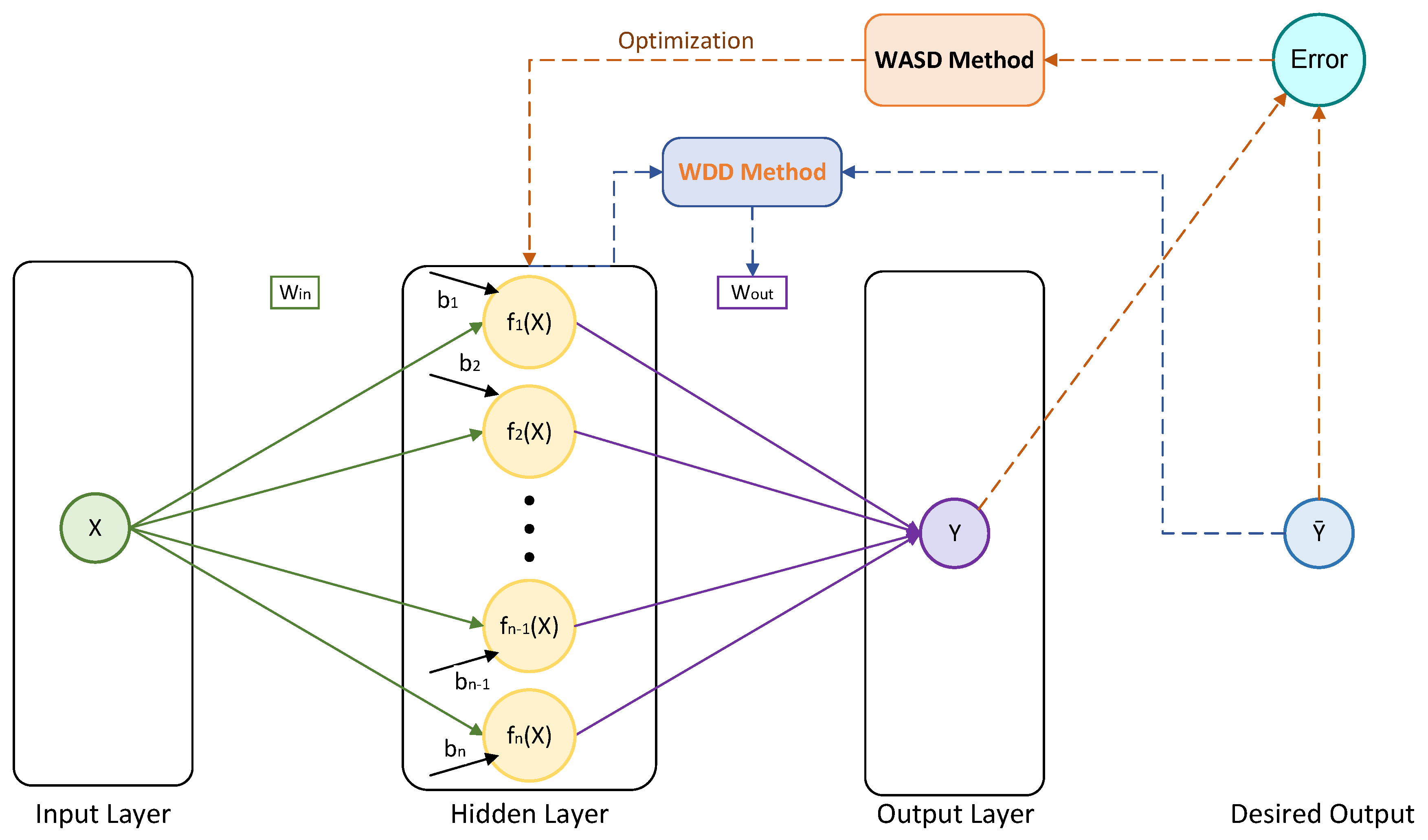
Deep neuronets were conceptualized with the aim of fixing the aforementioned problem of the traditional single-hidden-layer feedforward neuronet (SLFN), which has been the primary focus of research since the late 1990s. It should be noted that in order to create a neuronet model for any application, three main problems must be solved: (i) selecting the activation function; (ii) determining the required number of hidden-layer neurons; and (iii) computing the linking weights between two distinct layers. The preceding analysis indicates that finding the ideal number of hidden-layer neurons and linking weights for the neuronet is beneficial and significant as it can significantly lower the computational complexity and advance hardware realization. In other words, they increase the neuronets’ efficiency [7]. Several weights and structure determination (WASD) algorithms are presented in [8] as superior solutions to address the issues raised by the BP algorithms and to describe the ideal neuronet structure for more practical applications. The weights direct determination (WDD) subalgorithm is used by the WASD algorithm, which simultaneously determines the ideal neuronet structure during training and directly defines the optimal connecting weights between the hidden layer and output layer (i.e., only in one step). In this way, the WASD algorithm for feed-forward neuronets performs more accurately, deterministically, and efficiently than other algorithmic improvements on the training process.

In the last eighteen years, a great deal of research has been carried out on WASD with three goals in mind: reduced training time, increased classification accuracy, and less manual intervention. Investigations into the generalization and global approximation capabilities of WASD have also been conducted theoretically. It is important to bear in mind that WASD is often selected above other state-of-the-art approaches for artificial intelligence-related challenges across several disciplines due to its rapid speed, robust generalization, and ease of implementation.

We attempt to present a thorough overview of the evolution of WASD in this review, covering its theoretical analysis, variations, current developments, and practical applications. The remainder of the paper is structured as follows: We shall provide a thorough theoretical examination of the fundamental WASD in Section 2. Recent developments on WASD for regression and classification are presented in Section 3. In Section 4, the performance of WASD neuronets is evaluated. It specifically compares WASD to different machine learning methods and shows how well WASD neuronets perform across different application domains. Section 5 brings the review to a close.

2. WASD Neuronets

Figure 1 depicts the basic layout of the WASD neuronet, which is an example of a typical SLFN. All of the adjacent layers are connected; however, not all connections are shown in the diagram for simplicity’s sake. In this work, m, n, and k represent the number of neurons in the input layer, hidden layer, and output layer, respectively, whereas $W_{in}$ and $W_{out}$ represent the input and output weight matrices. $B=[b_1,\dots ,b_n]\in {\mathbb{R}}^n$ is the bias matrix; $f(·)$ is the activation function of the hidden layer neurons; and matrices $X\in {\mathbb{R}}^m$ and $Y,\overline{Y}\in {\mathbb{R}}^k$ are the neuronet’s input, output, and desired output (target), respectively. As a result, the neuronet produces the output shown in the equation below:

$$Y=f(X·W_{in}-B)·W_{out},$$

(1)

which is the target function approximation. $W_{in},W_{out},B$, and $f(·)$ in Equation (1) must be appropriately determined prior to its application. Typically, $f(·)$ is a manually chosen element-wise function. The WASD procedure sets $W_{in}$ and B as fixed or random values. The WDD approach described below can be used to obtain $W_{out}$ [9].

$$W_{out}=A^{†}·\overline{Y},$$

(2)

where the superscript ${(·)}^{†}$ denotes the pseudoinverse operator and $A=f(X·W_{in}-B)$.

The error function curve between Y and $\overline{Y}$ is typically used to automatically identify the neuronet structure, or the number n of hidden layer neurons, through the WASD approach. In particular, during the training phase, the number of hidden neurons is progressively increased, and the error on the validation set that corresponds to the current number is computed. Plotting of the error curve occurs concurrently with this increase. The optimal number of hidden neurons is determined by finding the number that corresponds to the lowest error point on the error curve, which generally shows an ascending trend after a declining trend. This idea is related to the SAD algorithm’s fundamental theory [9,10,11]. The method used to find the lowest point of error may vary significantly in practice, but the process ceases automatically when a sufficient level of accuracy is reached.

3. Modifications of WASD Neuronets

The fundamental framework of the WASD neuronet is shown in Section 2. In more useful applications, some enhanced versions have been developed.

In particular, the incorporation of Chebyshev polynomials as an activation function has improved the fundamental structure of the WASD neuronet. Using the WASD theory as a basis, ref. [12] employed fixed weights between the input layer and the hidden layer, rather than randomly generated points, a sequence of Chebyshev polynomials as the activation function of the hidden layer neurons, and the cross-validation approach to enhance the generalization. Thus, the Chebyshev polynomial feedforward neuronet with a single output (SOCPNN) and the multi-output Chebyshev polynomial feedforward neuronet with multiple outputs (MOCPNN) were presented. Additionally, the initial network model was trained using a subset technique in [13]; after that, the model was optimized, which enhanced the SOCPNN’s performance.

Furthermore, the random assignment of output weights has improved the fundamental structure of the WASD neuronet. An amended weights and structure determination neuronet (MWASDNN) model was created in [14,15], where the input weights were obtained in a single step by addressing the pseudoinverse issue and the output weights were allocated randomly. This means that in the MWASDNN, the input and output weight calculation techniques used in the original WASD neuronet were switched. Additionally, a model called the weights and structure determination neuronet assisted by double pseudoinversion (WASDNN-DP) was created in [16]. Prior to updating the output weight matrix, the WASDNN-DP randomly allocates the input weight matrix, solves the pseudoinverse’s problem to acquire the input weight matrix, and then solves the pseudoinverse’s problem once more.

A number of polynomials and power functions have been added to the WASD neuronet’s basic architecture as activation functions, along with pruning approaches to help the neuronet’s hidden-layer neurons be chosen during training. It is noteworthy to emphasize that less computational complexity is achieved in neuronet models by pruning neurons deemed less significant using pruning strategies. In particular, ref. [8] reintroduces the following neuronet models: a neuronet model with hidden layer neurons triggered by Legendre polynomials, which is trained using one of two WASD methods with varying growth rates to ascertain the ideal weights and configuration of the specific neuronet model [17]; a neuronet model that uses Chebyshev orthogonal polynomials of Class 1 to activate hidden-layer neurons, where the WASD technique involves pruning the given neuronet once it has grown [18]; a neuronet model where the structure automatic determination (SAD) subalgorithm of the WASD algorithm is used to identify the ideal number of hidden-layer neurons in the neuronet model, which is activated by a set of Chebyshev orthogonal polynomials of Class 2 [19,20]; a neuronet model with hidden-layer neurons activated by a power-activation function, where the WASD algorithm incorporates a growing and pruning technique for selecting the hidden-layer neurons of the neuronet through the training process [21]; a neuronet model with hidden-layer neurons activated by a group of Euler polynomials (MIEPN), where the WASD algorithm is equipped with the twice-pruning (TP) and pruning-while-growing (PWG) techniques for selecting the hidden-layer neurons of the neuronet during the training process [22]; a neuronet model with hidden-layer neurons activated by Bernoulli polynomials (MIBPN), which is trained by a WASD algorithm with TP [23]; a neuronet model with hidden-layer neurons activated by Hermite orthogonal polynomials (MIHPN), which has no weakness of dimension explosion [10]; a neuronet model with hidden-layer neurons activated by a sine function (MISAN), which is trained by a two-stage WASD (TS-WASD) algorithm [24]; and a neuronet model with hidden-layer neurons activated by tan-sigmoid functions, where the WASD algorithm is equipped with the PWG, TP, and Levenberg–Marquardt (LM) techniques for selecting the hidden-layer neurons of the neuronet during the training process [25]. It is important to mention that there are also some simplified versions of the aforementioned neuronet models included in [8].

Additionally, the K-Taylor polynomial-based power-activation functions have been added to the WASD neuronet’s fundamental architecture to improve it. In [26,27], the weights among the input layer and the hidden layer were fixed at 1 rather than being generated at random, and the hidden layer neurons were activated using the K-Taylor polynomial. Consequently, the power-activation feed-forward neuronet (PFN) and the speedy PFN were introduced. In [28], a multi-input WASD for time-series neuronet (MI-WASDTSN), along with three new power-activation functions based on the K-Taylor polynomial to train the initial network model, were developed. Moreover, ref. [29] used a subset approach in which a multi-function activated by a WASD for time series (MAWTS) was employed, along with four additional power-activation functions that can be used concurrently to train the initial network model. After that, the model was optimized, which enhanced the MAWTS’s performance. In [30], a two-input WASD based neuronet (2I-WASDBN) model was developed as an enhancement of the PFN under a power activation function, where the WASD algorithm is equipped with a pruning technique for selecting the hidden-layer neurons of the neuronet through the training process.

Power-activation functions in the output layer have improved the fundamental architecture of the WASD neuronet. In [24,31,32], three WASD neuronet models with hidden-layer neurons activated by a set of square wave, sine, and signum functions were introduced in [31], and a WASD neuronet model with hidden-layer neurons activated by a sine function was introduced. Using three distinct steps, ref. [33] develops a WASD neuronet model called FCI-WASD that uses Fresnel cosine integrals to determine its activation functions. These steps include adding enough neurons to the hidden layer, fine-tuning the resulting structure by cutting some neurons, and saving the relevant parts of the network so that it may be successfully recreated and used in the future. An enhanced version of FCI-WASD, the power Gaussian Error Linear Unit (GELU) activated WASD (PG-WASD) neuronet, was introduced in [34]. The PG-WASD outperforms the FCI-WASD in terms of overall performance. Another enhanced version of FCI-WASD, the multi-input trigonometrically activated WASD (MTA-WASD) neuronet, was introduced in [35]. The MTA-WASD performs better overall than the FCI-WASD and is based on the Bernstein polynomial. It also includes a pruning approach for choosing the neuronet’s hidden-layer neurons during training. An enhanced version of PG-WASD, the power Sigmoid Linear Unit (SiLU) activated WASD (SWASD) neuronet, was introduced in [36]. The SWASD outperforms the PG-WASD in terms of overall performance. In [37], a power softplus WASD (PS-WASD) model was introduced as an enhancement of the PFN under a power softplus activation function that includes a pruning technique for selecting the hidden-layer neurons of the neuronet through the training process. An enhanced version of PS-WASD, the multi-input multi-function activated WASD neuronet (MMA-WASDN), was developed in [38]. In order to overcome bias and avoid becoming trapped in local optima, the MMA-WASDN model employs cross-validation. In [39], a multi-input WASD for a time-series neuronet (MI-WASDTSN) with hidden-layer neurons activated by a power-activation function was introduced. A heuristic power-activation function in the output layer keeps the model’s predictions in a realistic domain, improving the prediction ability of the neuronet in this way. In [40], a WASD for multiclass classification (WASDMC) model with hidden-layer neurons activated by a power maxout activation function was introduced, which is not negatively impacted by dimension explosions.

The basic framework of the WASD neuronet has been enhanced with the use of metaheuristics and power-activation functions along with pruning techniques for selecting the hidden-layer neurons of the neuronet through the training procedure. In [41], a multi-input beetle antennae search WASD neuronet (MI-BASWASDN) model with hidden-layer neurons activated by a power sigmoid function was introduced. In order to determine the ideal number and powers of the hidden-layer neurons, the WASD model integrates a meta-heuristic optimization process called beetle antennae search (BAS). A bio-inspired WASD neuronet (BIWASDNN) model was introduced in [42] as an updated version of the MI-BASWASDN. This model improves the accuracy of the WDD technique and uses the cross-validation approach to increase the generalization.

The basic framework of the WASD neuronet has been enhanced with the addition of power-activation functions in the output layer along with fuzzy systems, metaheuristics, power-activation functions, and pruning techniques for selecting the hidden-layer neurons of the neuronet through the training process. A multi-input fuzzy WASD neuronet (MI-FUZWASDN) model was presented in [43] as an improvement of the PFN under a power softplus activation function for classification problems with no dimension explosion weakness. Furthermore, the WASD algorithm employs the cross-validation approach to increase the generalization and a fuzzy logic controller to map the input data into a specified interval that improves the accuracy of the WDD method. In [44], a bio-inspired WASD for multiclass classification tasks (BWASDC) neuronet model with hidden-layer neurons activated by a power maxout activation function was introduced. The BWASDC model uses the metaheuristic BAS algorithm to find the optimal number and the power activation function of the hidden-layer neurons, enhancing in this manner the WASD’s learning process. In [45], a bio-inspired WASD (BWASD) neuronet model with hidden-layer neurons activated by four power activation functions was introduced. The BWASD model uses the metaheuristic BAS algorithm to find the optimal number, powers, and activation function of the hidden-layer neurons, enhancing in this way the WASD algorithm’s learning process.

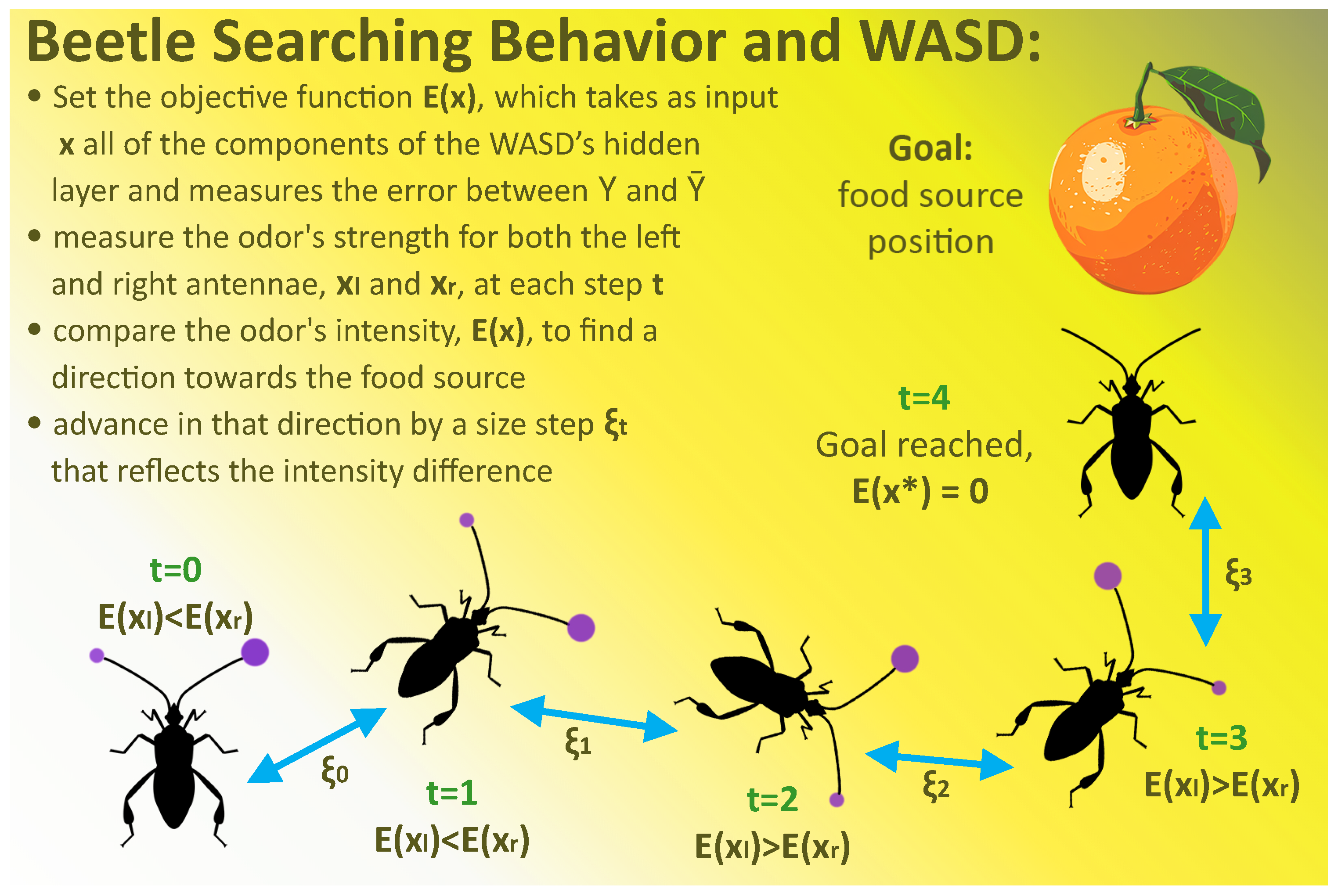
Notably, the BAS algorithm is incorporated into all of the previously stated bio-inspired WASD algorithms that train NN models [46]. Beetles typically utilize both antennae to find food, depending on the strength of the fragrance they detect (see Figure 2). The optimal solution finder of the BAS algorithm mimics this trend, and this approach enables the employment of cutting-edge optimization techniques [47]. To determine the ideal number of hidden layer neurons in a NN, its power values, and the ideal activation function for each hidden layer neuron, the aforementioned bio-inspired WASD algorithms specifically imitate the behavior of the beetle. Additionally, they optimize the ratio of the validation and fitting sets (also known as cross-validation auto-adjustment).

Table 1. Evolution of WASD across time.

Year	Ref.	Target Function Approx.	Task	Enhancement Methods	Application	Dataset Size
2008	[17]	Legendre polynomial	Regression	Two WASD method	Mathematical formulas approximation	4761 × 3
2009	[19]	Chebyshev polynomial	Regression	SAD subalgorithm	Mathematical formulas approximation	2116 × 3
2009	[22]	Euler polynomial	Regression	TP and PWG techniques	Mathematical formulas approximation	6000 × 4
2009	[23]	Bernoulli polynomial	Regression	TP	Mathematical formulas approximation	6561 × 4
2011	[21]	K-Taylor polynomial	Regression	Power-activation, growing,	Mathematical formulas approximation	1331 × 4
				and pruning techniques
2012	[18]	Chebyshev polynomial	Regression	Pruning technique	Mathematical formulas approximation	2116 × 3
2012	[10]	Hermite polynomial	Regression	Power-activation method	Mathematical formulas approximation	676 × 3
2013	[26]	K-Taylor polynomial	Regression	Power-activation method	Monthly time series forecast	129 × 1
2014	[32]	Polynomial	Binary Classif.	Power signum activation method	XOR logic prediction	100 × 2
2014	[20]	Chebyshev polynomial	Regression	Multi-fold cross-validation	Gray image denoising	65,536 × 1
2014	[25]	K-Taylor polynomial	Regression	Power tan-sigmoid activation,	Glomerular-filtration-rate estimation	1180 × 9
				PWG, TP, and LM methods
2014	[12]	Chebyshev polynomial	Binary Classif.	Power-activation method	Several real world datasets	4900 × 12
2016	[24]	K-Taylor polynomial	Regression	Power sine activation and	Mathematical formulas approximation	10,961 × 3
				two-stage WASD method
2019	[13]	Chebyshev polynomial	Binary Classif.	Subset method	Breast cancer	131 × 1926
2019	[14]	Linear	Binary Classif.	Monotonous nonlinear activation	Flatfoot diagnosis	611 × 83
				and k-fold cross-validation method
2019	[15]	Linear	Binary Classif.	Arctan activation and	Flatfoot diagnosis	611 × 83
				k-fold cross-validation method
2019	[16]	Linear	Binary Classif.	Arctan activation and	Flatfoot diagnosis	611 × 83
				double pseudoinversion method
2020	[31]	Multivalued	Binary Classif.	Periodic square wave activation	USA presidential parties predictions	42 × 2
2021	[27]	K-Taylor polynomial	Regression	Speedy power-activation method	Stock market forecast	180 × 1
2021	[43]	K-Taylor polynomial	Binary Classif.	Fuzzy controller and power	Breast Cancer classification	683 × 9
				softplus activation techniques
2022	[28]	K-Taylor polynomial	Regression	Multi-function activation method	Industrial indices forecast	262 × 1
2022	[29]	K-Taylor polynomial	Regression	Multi-function activation method	Stock market forecast	200 × 1
2022	[30]	K-Taylor polynomial	Regression	Multi-function activation	Stochastic exchange rate stabilization	1000 × 5
				and pruning techniques
2022	[38]	K-Taylor polynomial	Binary Classif.	Multi-function activation	Firm fraud and loan approval classif.	150,000 × 11
				and pruning techniques
2022	[41]	K-Taylor polynomial	Regression	BAS and power-activation method	European Central Bank publ. forecast	262 × 50
2022	[42]	K-Taylor polynomial	Regression	BAS and power-activation method	Feedback control systems stabilization	2000 × 3
2023	[33]	Bernstein polynomial	Binary Classif.	Power Fresnel cosine integral	Employee attrition classification	23,436 × 37
				activation and pruning techniques
2023	[37]	K-Taylor polynomial	Binary Classif.	Power softplus activation	Credit card attrition classification	10,127 × 34
				and pruning techniques
2023	[39]	K-Taylor polynomial	Regression	Multi-function activation	Gross domestic product forecast	109 × 1
				and pruning techniques
2023	[40]	K-Taylor polynomial	Multiclass classif.	Power maxout activation method	Occupations classification	1308 × 437
2024	[34]	K-Taylor polynomial	Binary Classif.	Power GELU activation	Customer churn classification	4228 × 22
				and pruning techniques
2024	[35]	Bernstein polynomial	Binary Classif.	Power activation and	Credit card attrition classification	10,127 × 34
				pruning techniques
2024	[44]	K-Taylor polynomial	Multiclass classif.	BAS and power maxout	Crosswalk of occupational classif.	3369 × 1124
				activation method
2024	[45]	K-Taylor polynomial	Binary Classif.	BAS and multi-function	Credit and loan approval classification	120,269 × 11
				activation method
2025	[36]	K-Taylor polynomial	Binary Classif.	Power SiLU activation	Credit approval classification	471 × 13
				and pruning techniques

provides a summary of the previously mentioned evolution of WASD over time. Specifically, it displays the year of introduction, the type of target function approximation, the task, the enhancement method, the application, and the greatest dataset size (samples × variables) for each neuronet model. Notably, WASD neuronets have only been evaluated on relatively small datasets. Remember that by “small dataset”, we mean datasets that are small enough to fit in a personal computer’s memory. The majority of WASD neuronet studies are carried out on Matlab on personal computers with the following hardware configurations: Windows operating system, Intel CPU, and less than 24 GB of RAM. Table 1 provides some significant dataset size instances. The inability of WASD neuronets to handle greater data sizes with excellent accuracy may be highlighted by the fact that they have not yet been tested on medium or large datasets. Future studies will have to determine this.

In light of the aforementioned, the most well-known WASD modifications are as follows:

• The favored option of the most recent WASD neuronets is that the input layer and the hidden layer were fixed as 1 rather than being produced at random;
• Power-activation functions based on K-Taylor polynomials seems to have the lowest time consumption during training, along with high accuracy levels;
• The pruning techniques for selecting the hidden-layer neurons of the neuronet through the training process seems to optimize the neuronet’s structure even more;
• Fuzzy logic controllers to map the input data into a specified interval seems to increase the accuracy of the WDD method even more;
• The cross-validation technique is typically applied to enhance the neuronet’s generalization;
• The use of heuristic algorithms, such as BAS, for finding the optimal number, powers, and the activation function of the hidden-layer neurons seems to enhance the WASD algorithm’s learning process even more;
• Power-activation functions in the output layer seem to be critical for the cross-domain adaptation of the WASD neuronets.

Finally, based on the different WASD neuronets discussed in this section, it is evident that certain combinations of the previous enhancements seem to improve the overall performance and accuracy of the WASD neuronets even more.

4. Performance of WASD Neuronets

Over the past eighteen years, a lot of research has been carried out on WASD analysis, particularly on how WASD compares to other cutting edge algorithms like Support Vector Machine (SVM), Gaussian process regression (GPR), K-nearest neighbors (KNN), Kernen Naive Bayes (KNB), Tree, and other deep learning techniques. As exemplary machine learning algorithms, these time-tested techniques reflect cutting-edge machine learning technologies in various eras. They have not only played a significant part in the history of machine learning development but are still actively engaged in the field today. We may more readily explore the significance of WASD in machine learning and more clearly detect WASD’s strength in related research by comparing it to these machine learning methods. In general, WASD is clearly faster than those techniques, and its variations are getting stronger and stronger. The accuracy performances of WASD are good when implemented simply.

It is important to mention that the accuracy, precision, mean absolute error (MAE), mean absolute percentage error (MAPE), symmetric MAPE (SMAPE), root mean square error (RMSE), time consumption (TC), mean directional accuracy (MDA), $R^2$ and F-score are the performance measures presented in the tables of this section. See [48,49] for more information and a thorough study of these measures.

4.1. Performance of WASD Versus SVM

Support Vector Machines (SVMs), one of the most well-known supervised methods for classification since the turn of the century, were introduced in 1995 by Cortes and Vapnik [50]. In general, given that data points are dispersed over space, there are several planes on which we might divide them into multiple classes. These planes are referred to as hyperplanes in SVMs. Among these hyperplanes, there is one that would optimize each data point’s distance to the plane. Thus, the easiest way to identify data points would be via this hyperplane. The goal of SVMs is to identify the optimal hyperplane, which also forms the foundation of the SVM concept.

In [28,29,41], three WASD neuronet models were compared with SVM models in time-series forecasting problems. In [33,35,37,38,39,43,45], six WASD neuronet models were compared with SVM models in binary classification problems. In [30], a WASD neuronet model was compared with SVM models in regression problems. All of these sources’ experimental findings showed that WASD was faster and had more accuracy than SVMs. Some performance metrics comparing WASD and SVMs are shown in

Table 2. Performance statistics: WASD versus SVM.

	Time-Series Forec. in [41]			Binary Classif. in [45]			Reg. Problem in [30]
Statistic	WASD	SVM	Statistic	WASD	SVM	Statistic	WASD	SVM
MAE	0.2541	736.9	MAE	0.1353	0.0768	MAE	0.0118	0.0249
RMSE	0.3183	887.5	Precision	0.5971	0.4281	RMSE	0.0146	0.0324
${\mathit{R}}^{\mathbf{2}}$	1	0.9959	Accuracy	0.8646	0.9231	${\mathit{R}}^{\mathbf{2}}$	0.9981	0.9899
TC	0.1 s	0.09 s	F-score	0.6935	0.5764	TC	0.03 s	0.06 s

and originate from the previously stated references. It follows that in the instances covered there, the WASD neuronets perform better than the SVM.

4.2. Performance of WASD Versus GPR

In statistics and machine learning, one powerful and versatile non-parametric regression technique is Gaussian process regression (GPR) [51]. When dealing with continuous data, where the relationship between the input and output variables may be complicated or unclear, it is quite useful. Time-series forecasting, optimization, and other fields can benefit greatly from the use of GPR, a Bayesian technique that can simulate prediction certainty [52]. The foundation of GPR is the idea of a Gaussian process, which is a group of random variables with a joint Gaussian distribution for any finite number of them. A distribution of functions can be used to conceptualize a Gaussian process.

In [27,28,29,41], four WASD neuronet models were compared with GPR models in time-series forecasting problems. In [39], a WASD neuronet models was compared with GPR models in a binary classification problem. In [30,42], two WASD neuronet models were compared with GPR models in regression problems. The experimental results from all of these sources demonstrated that WASD outperformed GPR in speed and accuracy. Some performance metrics comparing WASD and GPR are shown in

Table 3. Performance statistics: WASD versus GPR.

	Time-Series Forec. in [27]			Binary Classific. in [39]			Reg. Problem in [42]
Statistic	WASD	GPR	Statistic	WASD	GPR	Statistic	WASD	GPR
MAE	3.5	3.28	MAPE	6.63	11.17	MAPE	0.2115	0.2164
RMSE	4.36	5.1	SMAPE	3.1771	6.08	RMSE	0.1431	0.1438
${\mathit{R}}^{\mathbf{2}}$	0.91	0.88	${\mathit{R}}^{\mathbf{2}}$	0.6754	−4.0 × 10−3	${\mathit{R}}^{\mathbf{2}}$	0.9954	0.9954
TC	2.2 s	0.11 s	MDA	0.6842	0.1578	TC	0.1 s	6 s

and originate from the previously stated references. As a result, the WASD neuronets outperform the GPR in the cases discussed there.

4.3. Performance of WASD Versus KNN

Statistical pattern recognition frequently uses the k-nearest neighbor decision rule (KNN) as a classification technique [53]. Sample prototypes, or a training set of pattern vectors from that class, are provided for each class. To classify an unknown vector, its k nearest neighbors are selected from all prototype vectors, and a majority rule is used to determine the class label. The value of k should be odd in order to prevent ties on class overlap regions. Despite the simplicity and elegance of this rule, there is very little inaccuracy in its actual use. Theoretically, the asymptotic error rate approaches the optimal Bayes error rate and goes toward it as k increases, given a sufficiently high number of prototype samples [54]. Because of this, any new classifier, like neuronets, is compared to the KNN rule, which has become the industry standard.

The main issue with applying the KNN decision rule is its computing complexity, which arises from conducting a lot of distance calculations. Finding a variant of the rule that would be much lighter than the brute force method—which computes all the distances between the unknown pattern vector and the prototype vectors—is difficult for realistic pattern space dimensions [55]. As a result, numerous NN classifier improvements have been proposed; these are frequently based on editing or pruning approaches [53], which allow for a drop in prototype count without sacrificing accuracy.

In [34,35,36,37,38,43,45], seven WASD neuronet models were compared with KNN models in a binary classification problem. In [40,44], two WASD neuronet models were compared with KNN models in a multiclass classification problem. All of these sources’ experimental results showed that WASD performed faster and more accurately than KNN. Some performance metrics comparing WASD and KNN are shown in

Table 4. Performance statistics: WASD versus KNN.

	Binary Classific. in [35]			Binary Classific. in [43]			Multiclass Classific. in [44]
Statistic	WASD	KNN	Statistic	WASD	KNN	Statistic	WASD	KNN
MAE	0.0932	0.1501	MAE	0.4240	0.0424	MAE	0.4002	13.64
Precision	0.9706	0.9255	Precision	0.9835	0.9615	Precision	0.9327	0.8312
Accuracy	0.9067	0.8499	Accuracy	0.9576	0.9576	Accuracy	0.9327	0.8312
F-score	0.8018	0.7408	TC	0.05 s	2.1 s	F-score	0.9240	0.8126

and originate from the previously stated references. Consequently, in the instances covered there, the WASD neuronets perform better than the KNN.

4.4. Performance of WASD Versus KNB

One popular probabilistic classification algorithm is Naïve Bayes (NB). With many practical uses, this algorithm is straightforward but effective. In general, an algorithm for classification may be categorized as probabilistic or non-probabilistic. Distribution approximation is the cornerstone of probabilistic data classification. Probabilistic data classification techniques work well because the majority of connected feature distributions are probabilistic in nature. The basic topic of why the probabilistic approach performs well theoretically in a variety of real-world applications is addressed by Garg and Roth in [56]. A few of the probabilistic classifiers are multilayer perceptrons, logistic regression, and NB. Non-probabilistic classifiers include KNNs and SVMs.

NB holds a significant position in data categorization among the aforementioned methods for a variety of reasons. Two of the primary reasons are the algorithm’s accuracy and simplicity. The NB algorithm, as its name suggests, is a well-known probabilistic classification method used in data analytics and machine learning. It was founded on the widely-used Bayes theorem. The efficacy and resilience of the algorithm are contributing factors to NB’s appeal in addition to its simplicity [57]. The literature claims that NB is among the best algorithms for data mining [58].

In [33,34,35,37,38,45], six WASD neuronet models were compared with KNB models in binary classification problems. The experimental findings from all of these sources demonstrated that WASD outperformed KNB in terms of speed and accuracy. Some performance metrics comparing WASD and KNB are shown in

Table 5. Performance statistics: WASD versus KNB.

	Binary Classific. in [33]			Binary Classific. in [37]			Binary Classific. in [34]
Statistic	WASD	KNB	Statistic	WASD	KNB	Statistic	WASD	KNB
MAE	0.0945	0.1442	MAE	0.0529	0.1465	MAE	0.1835	0.1925
Precision	0.9089	0.8137	Precision	0.9860	1	Precision	0.5942	0.5695
Accuracy	0.9054	0.8557	Accuracy	0.9471	0.8535	Accuracy	0.8164	0.8074
F-score	0.9057	0.8494	F-score	0.8738	0.6743	F-score	0.6930	0.6722

and originate from the previously stated references. As a result, the WASD neuronets outperform the KNB in the cases discussed there.

4.5. Performance of WASD Versus Tree

An essential part of machine learning are tree-based algorithms, which provide human-like, intuitive decision-making processes. These algorithms build decision trees, with a prediction or classification at the end of each branch representing a decision based on features. Tree-based algorithms are widely used in many different applications because they produce transparent and interpretable models by recursively partitioning the feature space [59].

A type of supervised machine learning models, generally known as tree-based algorithms, build decision trees to divide the feature space into regions, allowing for the hierarchical representation of intricate relationships between input variables and output labels [60]. Classification trees refer specifically to tree models in which the goal variable can take a discrete set of values; in these tree structures, leaves stand for class labels and branches for feature conjunctions that lead to those class labels. Regression trees are decision trees in which the goal variable is capable of taking continuous values, usually real numbers. More broadly, any type of object having pairwise dissimilarities, including categorical sequences, can be fitted with the regression tree concept [61].

Notable examples include decision trees, random forests, and gradient boosting approaches. Recursive binary split is used depending on criteria such as information gain or Gini impurity. These algorithms are strong against overfitting caused by ensemble approaches, demonstrate variety in terms of classification and regression functions, and produce a greater number of unique trees. Its cost-effective exploratory feature importance analysis capability leads to a wide range of applications in domains such as natural language processing and healthcare.

In [28,29], two WASD neuronet models were compared with tree models in time-series forecasting problems. In [33,34,36,38], four WASD neuronet models were compared with tree models in binary classification problems. In [40,44], two WASD neuronet models were compared with tree models in multiclass classification problems. All of these sources’ experimental results showed that WASD performed faster and more accurately than tree models. Some performance metrics comparing WASD and tree models are shown in

Table 6. Performance statistics: WASD versus tree.

	Time-Series Forec. in [29]			Binary Classif. in [38]			Multiclass Classific. in [40]
Statistic	WASD	Tree	Statistic	WASD	Tree	Statistic	WASD	Tree
MAE	4.9547	4.7250	MAE	0.0156	0.0363	MAE	1.2580	31.7133
RMSE	5.9633	6.0510	Precision	0.9586	0.9724	Precision	0.9782	0.4782
${\mathit{R}}^{\mathbf{2}}$	0.7191	0.5446	Accuracy	0.9844	0.9636	Accuracy	0.9782	0.4782
TC	2.5 s	0.57 s	F-score	0.9789	0.9656	F-score	0.9756	0.4900

and originate from the previously stated references. Consequently, in the instances covered there, the WASD neuronets perform better than the tree models.

4.6. Performance of WASD Versus Other Deep Learning Methods

The WASD neuronet has been compared with several other deep learning methods, such as logistic regression (LR), narrow neural networks (NNNs), long short-term memory (LSTM), and transformer (TRA) models. Particularly, in [33], a WASD neuronet model was compared with an LR model in binary classification problems. In [40,44], two WASD neuronet models were compared with NNN models in multiclass classification problems. In [44], a WASD neuronet model was compared with a TRA in a multiclass classification problems. In [42], a WASD neuronet model was compared with an LSTM model in regression problems. Some performance metrics comparing WASD and other deep learning methods are shown in

Table 7. Performance statistics: WASD versus other deep learning methods.

	Binary Classif. in [33]			Multiclass Classif. in [44]				Reg. Problem in [42]
Statistic	WASD	LR	Statistic	WASD	NNN	TRA	Statistic	WASD	LSTM
MAE	0.0945	0.2345	MAE	0.1055	109.8	68.54	MAPE	0.2115	7.7211
Precision	0.9089	0.8039	Precision	0.9845	0.5317	0.5570	RMSE	0.1431	1.4768
Accuracy	0.9054	0.7654	Accuracy	0.9845	0.5317	0.5570	${\mathit{R}}^{\mathbf{2}}$	0.9954	−0.1182
F-score	0.9057	0.7741	F-score	0.9863	0.5565	0.5184	TC	0.1 s	32 s

and originate from the previously stated references. All of these sources’ experimental results showed that the WASD neuronets outperform all the above deep learning methods.

Additionally, we offer

Table 8. Comparison between WASD and other machine learning algorithms.

Algorithms	Accuracy	Time Consumption	Cross Domain Adaptation	Popularity Nowadays
WASD	Comparatively high	Low	Comparatively high	Popular
SVM	Comparatively high	Ordinary	Comparatively high	Popular
GPR	High	Ordinary	Ordinary	Relatively low
KNN	Ordinary	Ordinary	Ordinary	Ordinary
KNB	Comparatively high	Ordinary	Comparatively high	Comparatively popular
Tree	Ordinary	Ordinary	Ordinary	Ordinary
LR	Ordinary	Ordinary	Ordinary	Relatively low
NNN	Ordinary	Ordinary	High	Popular
TRA	Ordinary	Ordinary	High	Popular
LSTM	Ordinary	Ordinary	High	Popular

to show the effectiveness and popularity of each machine learning algorithm in order to give a brief comparison between WASD and these methods.

Finally, a limitation of WASD performance is the absence of comparisons with more advanced models like lightweight networks [62], which are intended to be computationally efficient and compact, making them appropriate for resource-constrained environments like mobile and embedded devices [63]. However, this will have to be ascertained by future research.

4.7. Performance of WASD per Application Domain

Owing to its exceptional training speed, accuracy, and generalization, WASD was used in a wide range of application domains, including business, social science, engineering, economics, and medicine. We will examine a few exemplary works in these application domains in this section.

4.7.1. Medical Application

Machine learning-assisted diagnostic techniques have been used to diagnose a number of diseases in recent years, with encouraging diagnostic outcomes reported in the literature [64,65]. In machine learning-assisted medical diagnosis, the model typically learns from the dataset and then determines if a certain disease is positive or negative [66,67]. Because of its effectiveness and simplicity, the WASD method—among many machine learning algorithms—is frequently used for the detection of flat feet, breast cancer, and glomerular filtration rate prediction.

A group of disorders known as cancers have erratic cell proliferation and have the potential to infiltrate or spread to other bodily parts. Breast cancer is the most frequent type of cancer in women and has the greatest death rate. Rapidly proliferating cells in breast cancer cause breast lumps known as tumors, which are classified into two classes: benign and malignant. The benign tumors do not spread to other bodily parts, while the malignant ones do; that is to say, breast cancer is indicated by a malignant tumor located in the breast. These tumors can be identified and diagnosed by physical examination or image processing [68]. Consequently, treatment that may increase the chance of survival is made possible by early cancer stage discovery. A number of artificial intelligence approaches were proposed in [69,70,71] to improve the precision of the classification of breast cancer as benign and malignant; another artificial intelligence approach was proposed in [72] for the classification of breast tissue as breast tumor tissue or healthy breast tissue. This is because the conventional approach to cancer diagnosis mainly relies on the expertise of doctors and their visual examinations, which is restricted due to human errors. 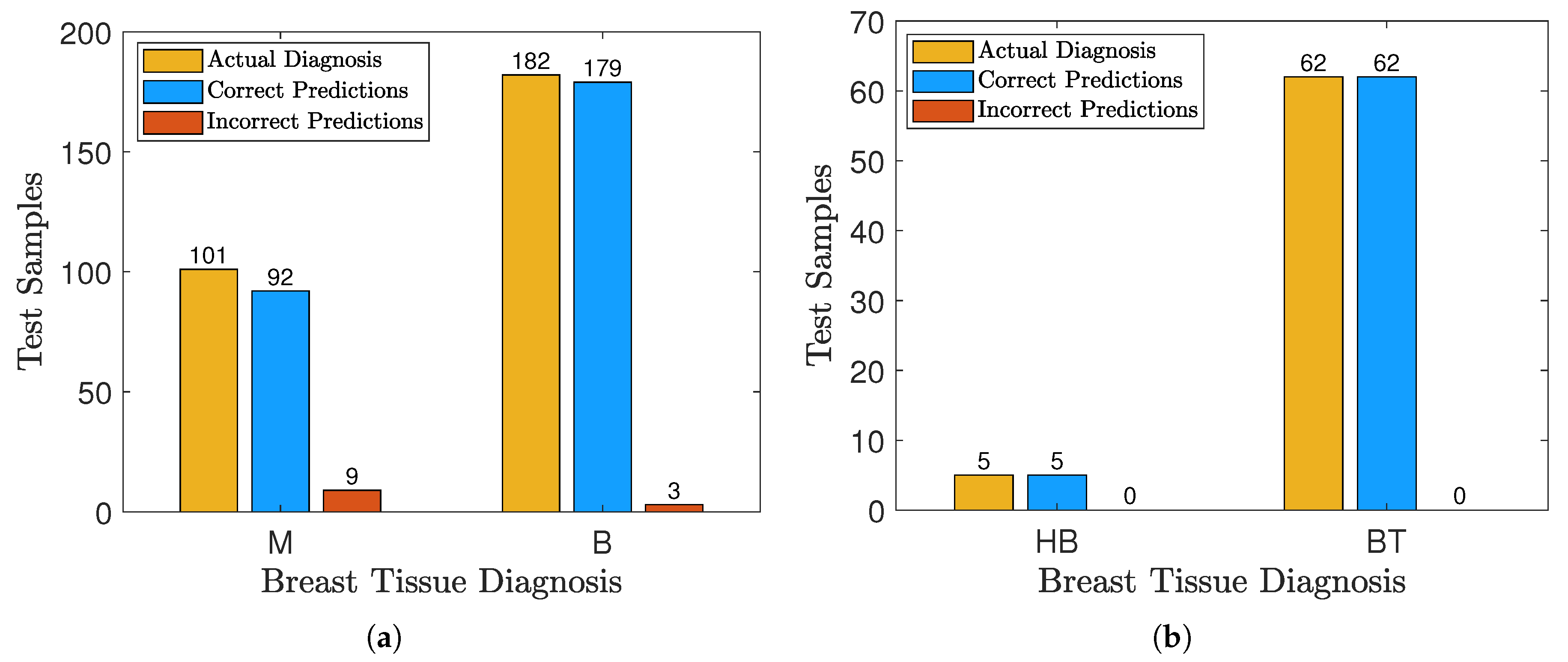In [13,43], two WASD models were applied on several diagnostic breast cancer datasets and demonstrated the models’ excellent efficiency and precision for predicting if the breast tissue is breast tumor tissue or healthy breast tissue. Figure 3 displays the performance of the WASD model on breast cancer prediction, as obtained from [43].

The great majority of outpatient foot disease cases include flat feet [73]. The foot condition known as “flat feet” causes the foot’s arch to collapse [74]. The research lacks a unified standard for diagnosing flat feet; however, a crucial indicator is the height of the medial longitudinal arch [75]. Between the knees and the femur, the arch creates an elastic connection that significantly lessens the stress applied to the bone [76]. Insufficient cushioning frequently leads to increased stresses on the knees, ankles, hips, and feet, which hurts these body parts [77]. Timely diagnosis of flat foot is crucial due to its high occurrence and associated pain. In [14,15,16], three WASD models were applied on several diagnostic flat foot datasets and demonstrated the models’ excellent efficiency and precision for classifying if the the foot of the object is flat or not.

Chronic kidney disease (CKD) has emerged as a major public health concern that poses a serious threat to people’s lives and health along with societal development and environmental changes [78]. Given that the glomerular filtration rate (GFR) is a frequently utilized marker for the early identification of chronic kidney disease (CKD), a reliable, efficient, and accurate approach for estimating GFR is important for clinical applications [79]. A WASD model was used on a dataset of CKD patients in [8], where it was shown to have exceptional accuracy and efficiency in predicting the patients’ GFR.

4.7.2. Engineering Application

With the exponential rise of artificial intelligence, current electronic technology, and information technology, several significant theoretical research discoveries have been proposed and evolved, including software and hardware implementations of an artificial neuronet [80]. In general, the ability of an artificial neuronet to generalize noise and fault tolerance and the capacity to predict unseen test data with cost and time savings are all significant advantages over traditional data analysis [81]. Because of its effectiveness and simplicity, the WASD method is one of the numerous machine learning algorithms used in engineering for chaos and system stabilization control.

In particular, in recent years, managing chaos has gained popularity as a research issue in the nonlinear sciences. One common strategy for managing chaos is the Ott, Grebogi, and Yorke (OGY) method [82]. By using the existence of an unstable fixed point nested within the chaotic attractor, small disturbances to the system stabilize the chaotic orbit. One prominent method for controlling chaos is the delayed feedback control (DFC) method, which is based on the OGY method [83,84]. Its advantage is that it does not require knowledge of the position of an unstable fixed point or unstable periodic orbit. Neuronet controllers, in general, offer an alternative approach to managing chaos. These include fuzzy neuronet models for fractional-order chaotic system synchronization [85], convolutional neuronets for time-series prediction [86], recurrent neuronets for breaking chaos-based cryptography [87], SVM models for wind power forecasting [88], Markov chain neuronets for energy management in hybrid electric vehicles [89], and hybrid neuronets for bus trip time prediction [90]. 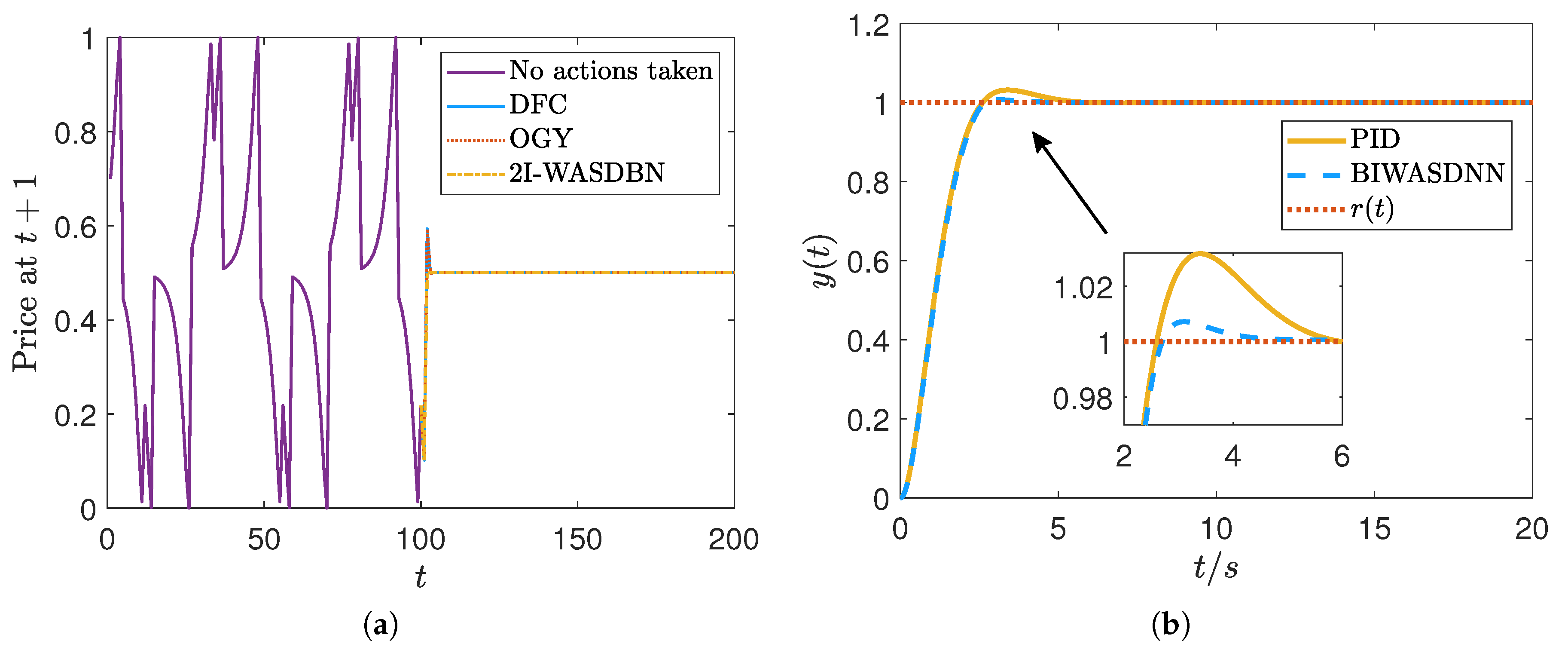A WASD model was used in [30] to control chaos, and it was shown to be quite competitive with, if not superior to, some of the most advanced deep learning techniques, as well as the conventional DFC and OGY approaches.

Conversely, since its invention several decades ago, proportional–integral–derivative (PID) controllers have been effectively applied in process-controlled industries such light industry, metallurgy, machinery, and power [91]. The feedback-based control loop technology known as the PID controller is widely used due to its ease of design and analysis, as well as its ease of implementation. Despite their straightforward design, ease of understanding, and versatility in controlling various control systems, PID controllers come with drawbacks [92]. The PID control system’s performance is set by tuning its parameters. A regulated system with improper tuning will function poorly, or even unstably [93]. In [42], a WASD-based method was introduced for replacing the PID controller in control systems with a neuronet feedback controller, leading to an equivalent or even higher performance of the feedback controlled system. Because integration and derivatives are not needed during the feedback process, the primary benefit of the WASD neuronet feedback controller over a PID controller is that it takes less computational power. Figure 4 displays the performance of the WASD models on chaos and system stabilization control, as obtained from [30,42].

4.7.3. Economics, Finance and Business Application

The finest practices in planning, financial management, and public administration have been implemented through the adoption of new, sophisticated computer techniques brought about by the advancement of information technology. Numerous scholarly investigations have indicated that the use of novel information and communication technology-driven methodologies is imperative for the reformation and improvement of public and financial management strategies [94]. The application of novel machine learning techniques has led to the adoption of enhanced intelligence methodologies for time-series forecasting problems in several scientific domains [95,96,97]. Because of its simplicity and efficiency, the WASD technique is one of the numerous machine learning algorithms that is frequently used in the business, finance, and economics domains.

Particularly, in the field of economics, the WASD method is widely applied in forecasting economic indicators such as the gross domestic product [39], balance of payments, listed shares, trade in goods, and liquidity conditions [41]. It has been also applied for predicting the Central Bank Intervention for interest rate stabilization [30] and predicting the United States public debt [8] and the Spanish public debt [98]. In the field of finance, the WASD method is widely applied in predicting investor’s views on stocks’ prices [27,29] and forecasting financial time-series [28]. In the field of business, the WASD method is widely applied in predicting employee attrition [33,35], credit card attrition [37] and customer churn [34], as well as classifying loan approval [38,45] and credit approval [36]. As obtained from [27,38], Figure 5 illustrates the effectiveness of the WASD models in predicting investor views on stock prices and classifying loan approval.

4.7.4. Social Science and Demography Application

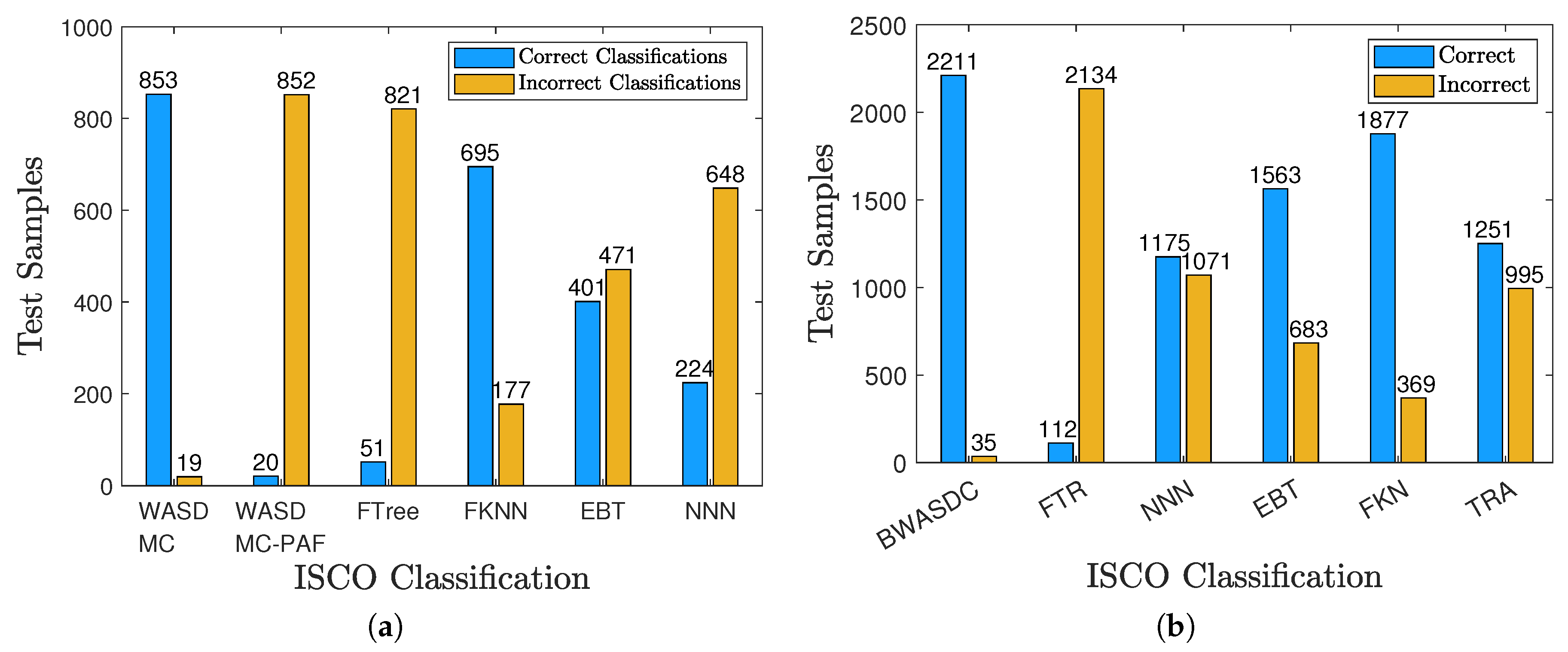
Multiclass classification tasks are common in social science research; examples include characterizing occupational mobility [99], performing case–control studies in the healthcare industry [100], investigating the correlation between changes in occupational characteristics and cancer [101], and assessing the feasibility of teleworking in certain jobs [102]. In particular, a number of classification schemes serve as the basis for the methodical monitoring of any population, ranging from the global populous to the constituents of small and medium-sized enterprises or communities [103]. For a range of work-related subjects, including administrative usage, employment statistics, social sciences, international trade, and commerce, which includes surveillance and analytical methodologies, an individual’s occupation (job title) or industry can be used to reflect occupational exposure [104]. For these ideas, there exist several national and international classification schemes that are updated on a regular basis [105]. As a result, in [40,44], two WASD models were applied for multiclass classification tasks and demonstrated the models’ excellent efficiency and precision for classifying job titles into the International Standard Classification of Occupations (ISCO) and the Occupational Information Network Standard Occupational Classification (O*NET-SOC). As obtained from [40,44], Figure 6 illustrates the effectiveness of the WASD models in classifying job titles and achieving crosswalk between job classification systems.

In contrast, the statistical analysis of human populations is known as demography [106]. In a number of domains, including education and policy-making, population has grown in importance. Reliability in population forecasting could aid policymakers in arriving at justifiable choices. Thus, there is always interest in such a topic [107]. Population forecasting is difficult and very unreliable [108]. Numerous elements (such as the natural environment, policy, culture, and disease) have an impact on the population. Evidently, it is challenging to predict the population with accuracy and precision [109]. Consequently, in [8,11], eight WASD models were applied for regression tasks and demonstrated the models’ excellent efficiency and precision for predicting the Russian, Chinese, European, Oceanian, Northern America, Indian, Asian, and world populations.

5. Conclusions and Future Directions

We discussed the evolution and uses of WASD over the past eighteen years in this review. The theory and principle of WASD were presented, along with a comprehensive set of techniques, including metaheuristics, to enhance WASD performance for certain learning tasks. For artificial intelligence-related problems in a range of domains, WASD is frequently chosen over other cutting-edge methodologies because of its quick speed, strong generalization, and simplicity of implementation. We discovered a number of intriguing research topics and avenues for further investigation through the survey.

In the context of big data, WASD may become increasingly significant. Big data machine learning challenges can now be resolved thanks to the development of deep learning architectures and efficient training algorithms. Although deep learning has produced amazing results, it has a high computational complexity and frequently takes a long time to train. In classification tasks, WASD performs admirably because it may achieve high accuracy in a relatively short amount of time. To learn from massive data, it will be intriguing to mix WASD and deep learning. With minimal training time, the hybrid network might be able to produce outcomes comparable to those of deep learning. Consequently, one limitation of the WASD performance is the absence of comparisons with more advanced neuronet models, especially when it comes to comparisons in scenarios involving vast amounts of data. However, this will have to be ascertained by future research.

Evolution is never stopped by WASD’s theoretical rationale. The most important concept for WASD is power-activated functions in the hidden layer, which allows for universal approximation and speeds up training dramatically. However, there is still an issue with explaining the unpredictability. Comparing WASD to other random processes, such as random forests, could be useful. Biological learning may be linked to WASD development in another exciting direction. It has been discovered by researchers that our brain’s neurons likewise learn by random mechanisms [110]. Given that the human brain served as the primary inspiration for artificial neuronets, it will be intriguing to look into the relationship between biological learning and WASD.