Analytical and Numerical Investigation of Adhesive-Bonded T-Shaped Steel–Concrete Composite Beams for Enhanced Interfacial Performance in Civil Engineering Structures
Abstract
1. Introduction
- -
- -
- Both continuous and discontinuous adhesive bonding models with different interface conditions (with or without gaps), addressing complexity not covered in existing stud/plate studies.
- -
- The T-section beam, commonly employed in multisectoral buildings and bridge construction, is selected for the analysis due to its structural relevance and practical implementation, different from I-section beams commonly used in the literature.
2. Materials and Methods: Theoretical Formulation and Solution Procedure
2.1. Solution Method
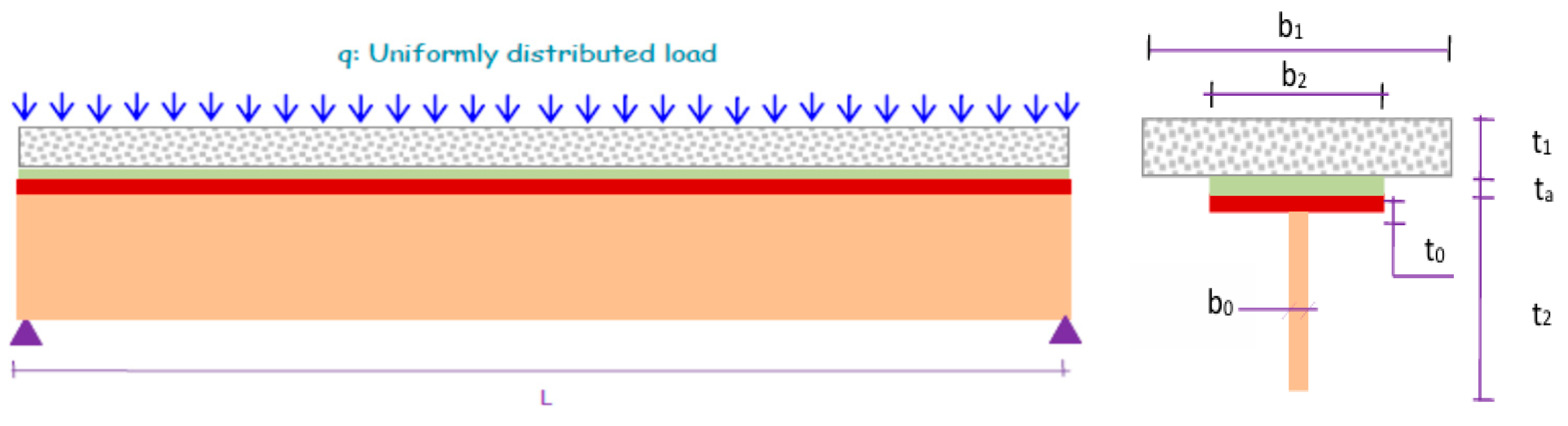
- Present the assumptions and the static calculation scheme.
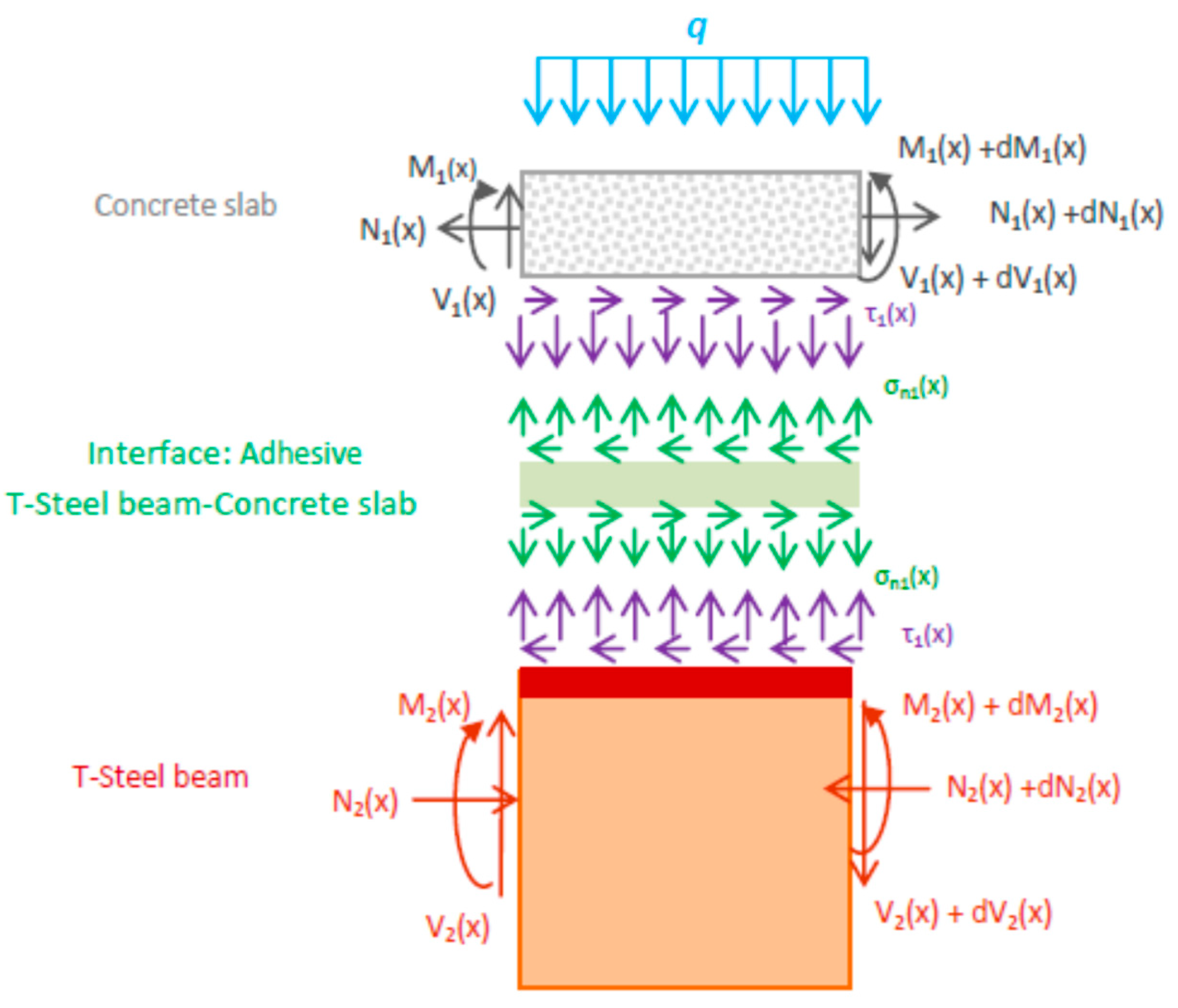
- Present the internal forces in the infinitesimal element of an adhesively bonded T-shaped steel–concrete composite beam to establish the load transfer between the bonds.
- Present the governing differential equation describing the interfacial shear stress distribution.
- Formulate the general solutions for loading conditions consisting of either concentrated forces or uniformly distributed loads.
- Derive the governing differential equation for the interfacial slip strain.
- Solve for the interfacial slip.
2.2. Assumptions of the New Solution
- -
- Linear Elasticity: All constituent materials, the concrete slab, the T-section steel beam, and the adhesive layer, are assumed to behave according to linear elastic constitutive laws.
- -
- Beam Geometry and Support Conditions: The composite beam is considered to be shallow and simply supported. Consequently, the classical assumption of plane sections remaining plane before and after bending is applied.
- -
- Interfacial Imperfection: The bond between the concrete slab and the T-steel beam is assumed to be imperfect. As such, relative slip is permitted at the interface, allowing for a realistic simulation of partial interaction behavior.
- -
- Adhesive Stress Transfer: The adhesive layer is considered to transfer only shear stresses induced by differential deformation between the bonded layers.
- -
- Adhesive Stress Distribution: Stresses within the adhesive layer are assumed to be uniform across the layer thickness. This assumption is justified when the adhesive thickness is small relative to the beam depth.
- -
- Global Bending Behavior: The overall deformation of the composite beam is governed by bending behavior, and other deformation modes such as torsion or axial effects are supposed negligible.
2.3. Stress Analysis at the Interface Between Concrete Slab and Steel Beam
2.4. Slip Distribution Along the Steel–Concrete Interface
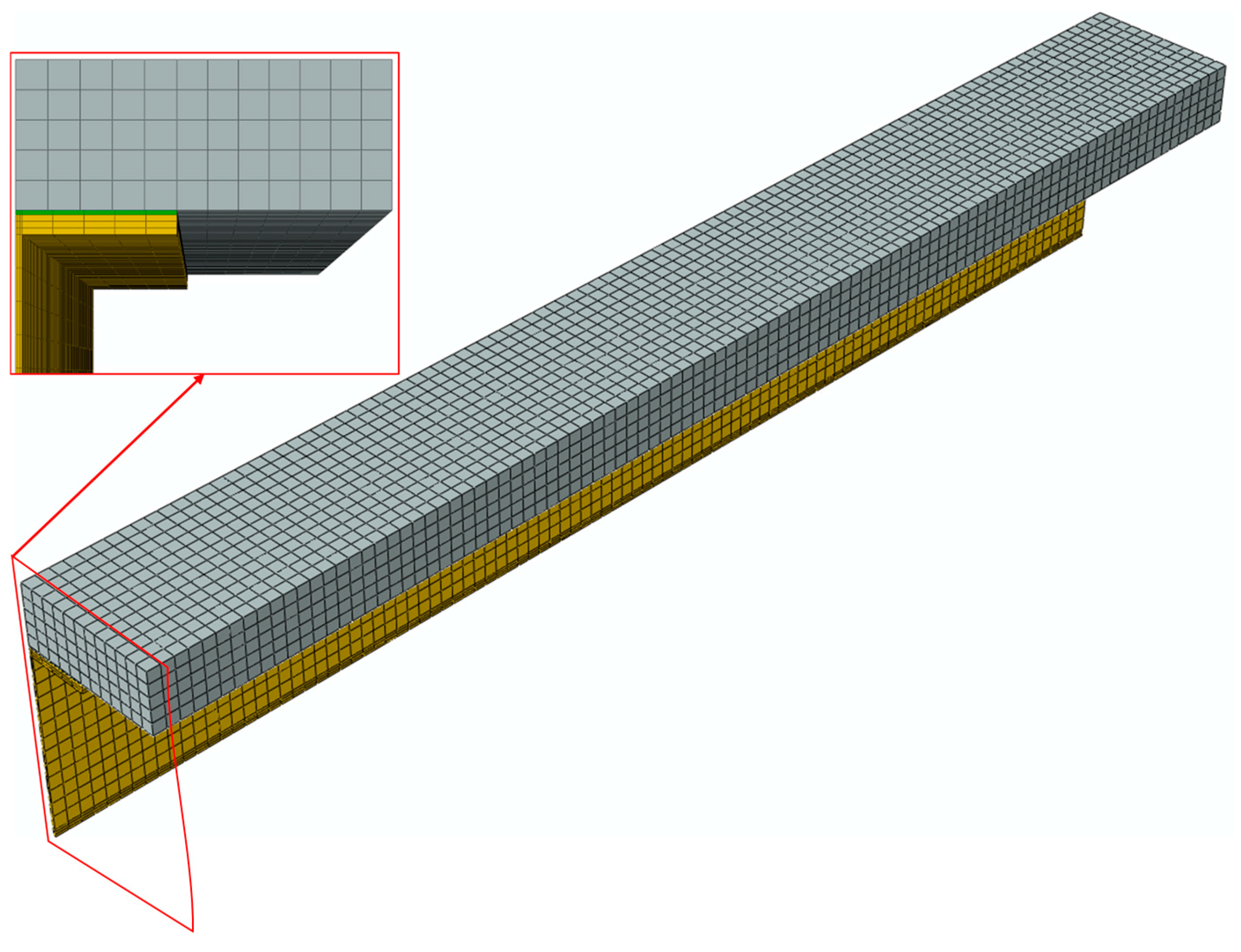
2.5. Finite Element Analysis Method
3. Results and Discussion
3.1. Materials and Geometry Data
3.2. Validation of the Analytical and the Finite Element Model
3.3. Parametric Analysis of Factors Influencing Slip in Steel–Concrete Bonds
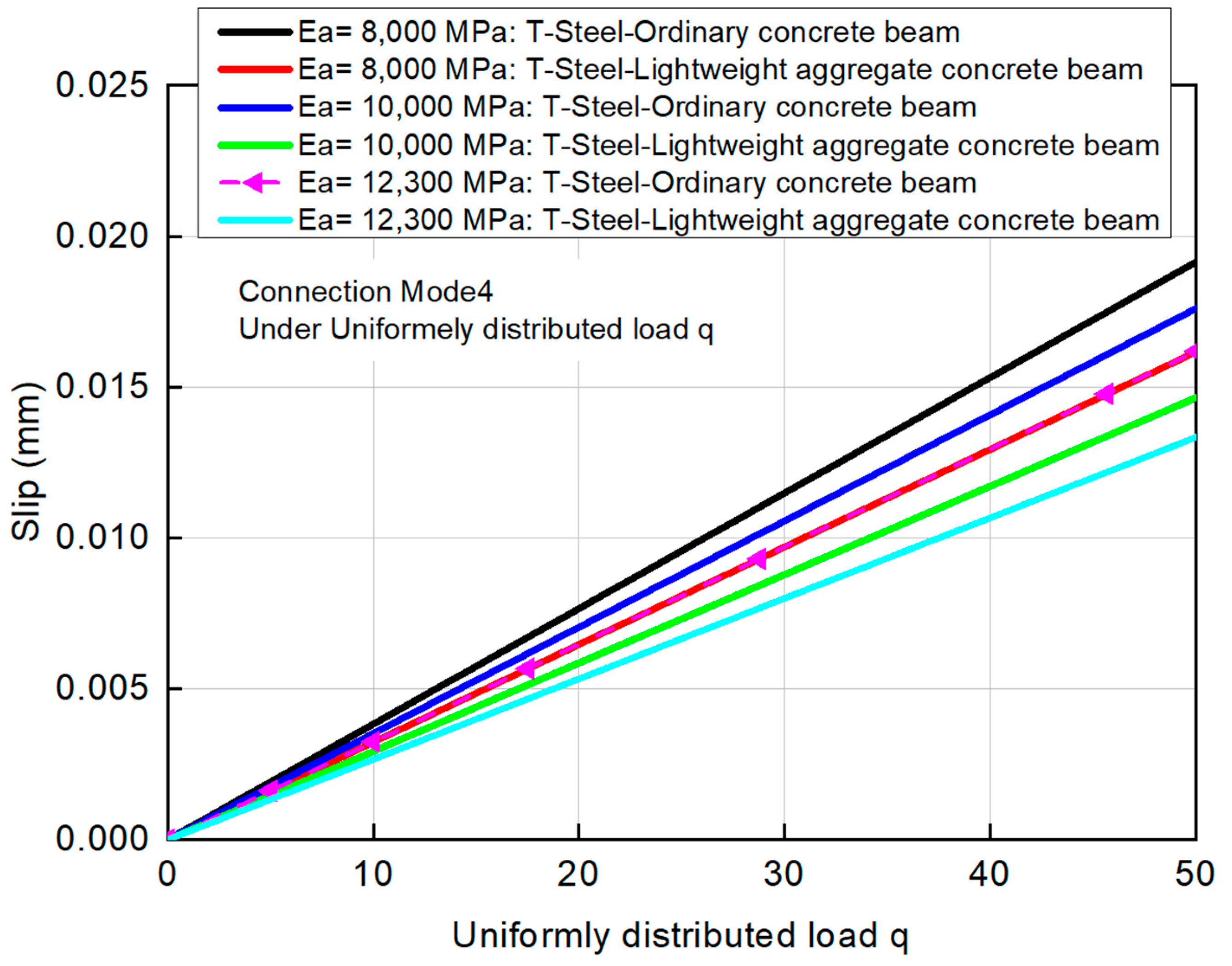
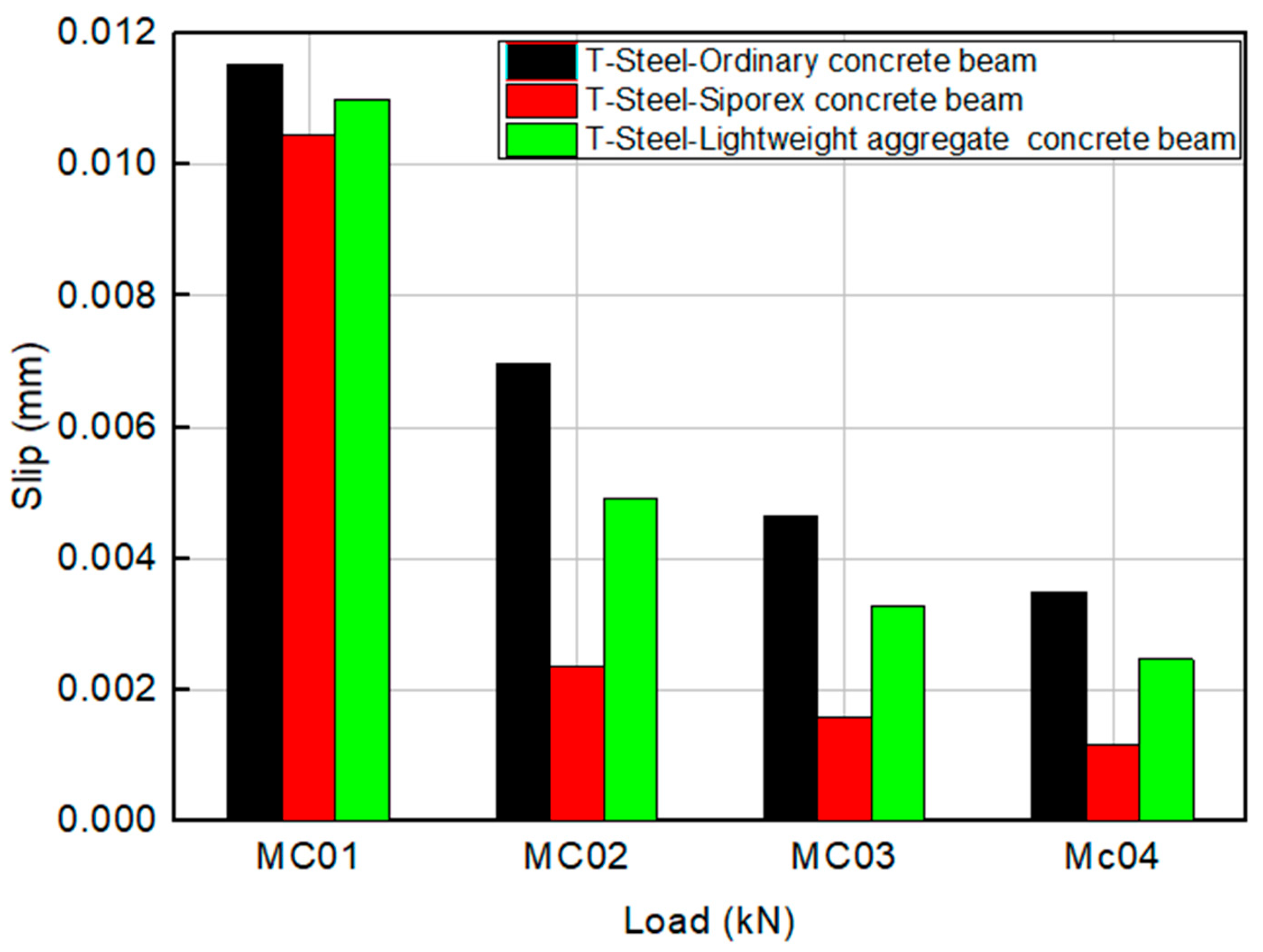
3.3.1. Effect of the Concrete Slab Material on Slip at the Steel–Concrete Interface
3.3.2. Effect of Young’s Modulus of Adhesive on Slip at the Steel–Concrete Interface
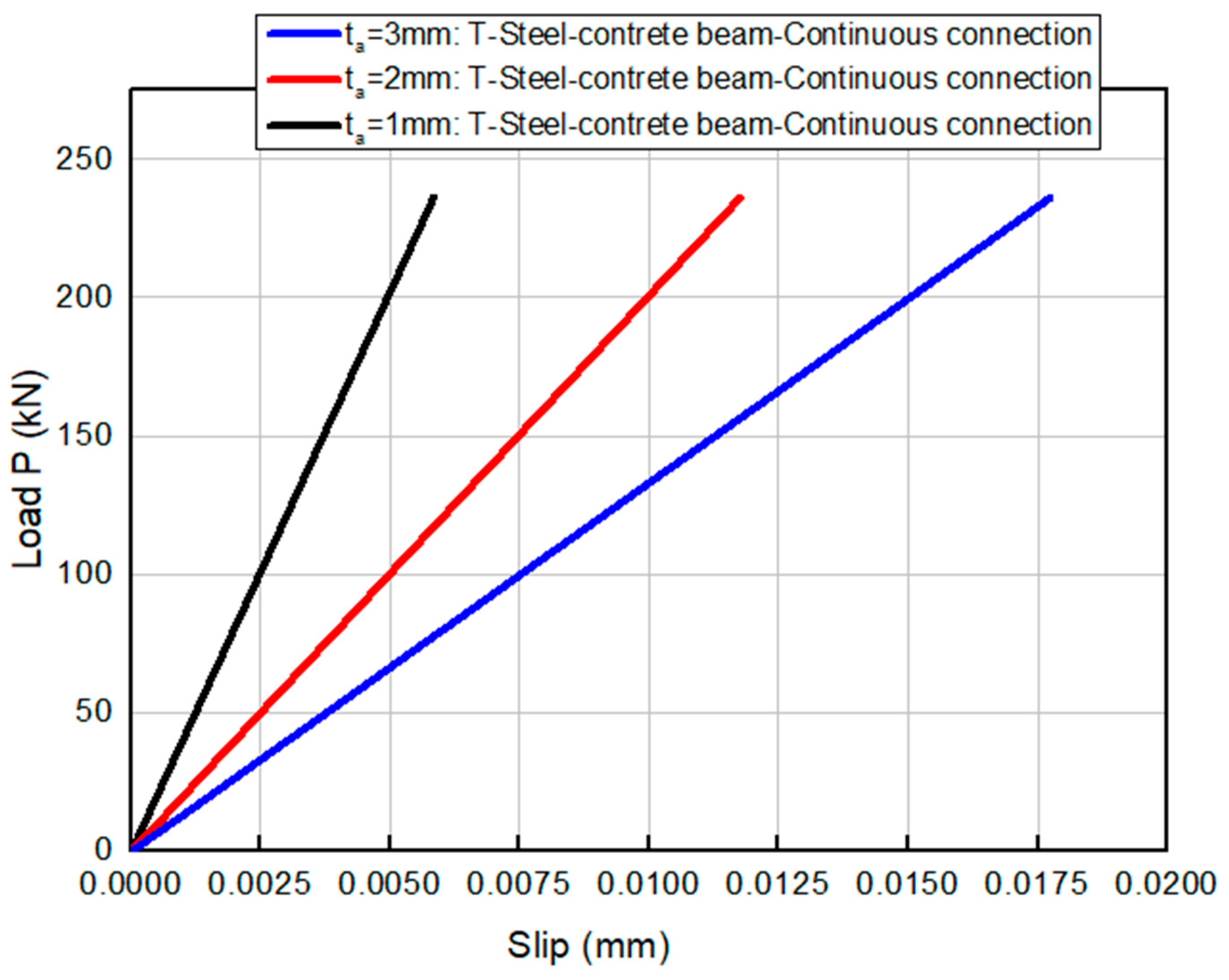
3.3.3. Effect of Adhesive Thickness on Slip at the Steel–Concrete Interface
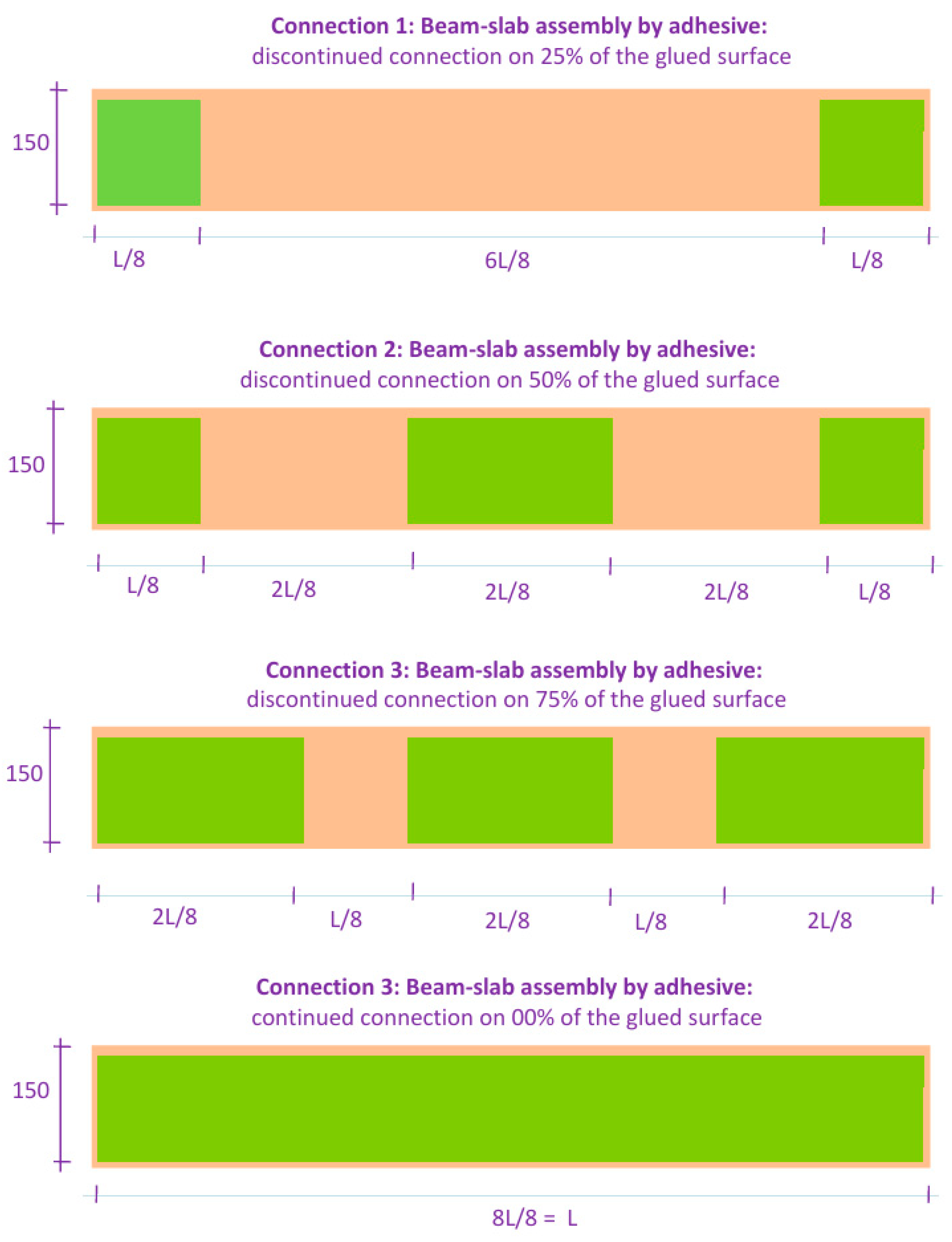
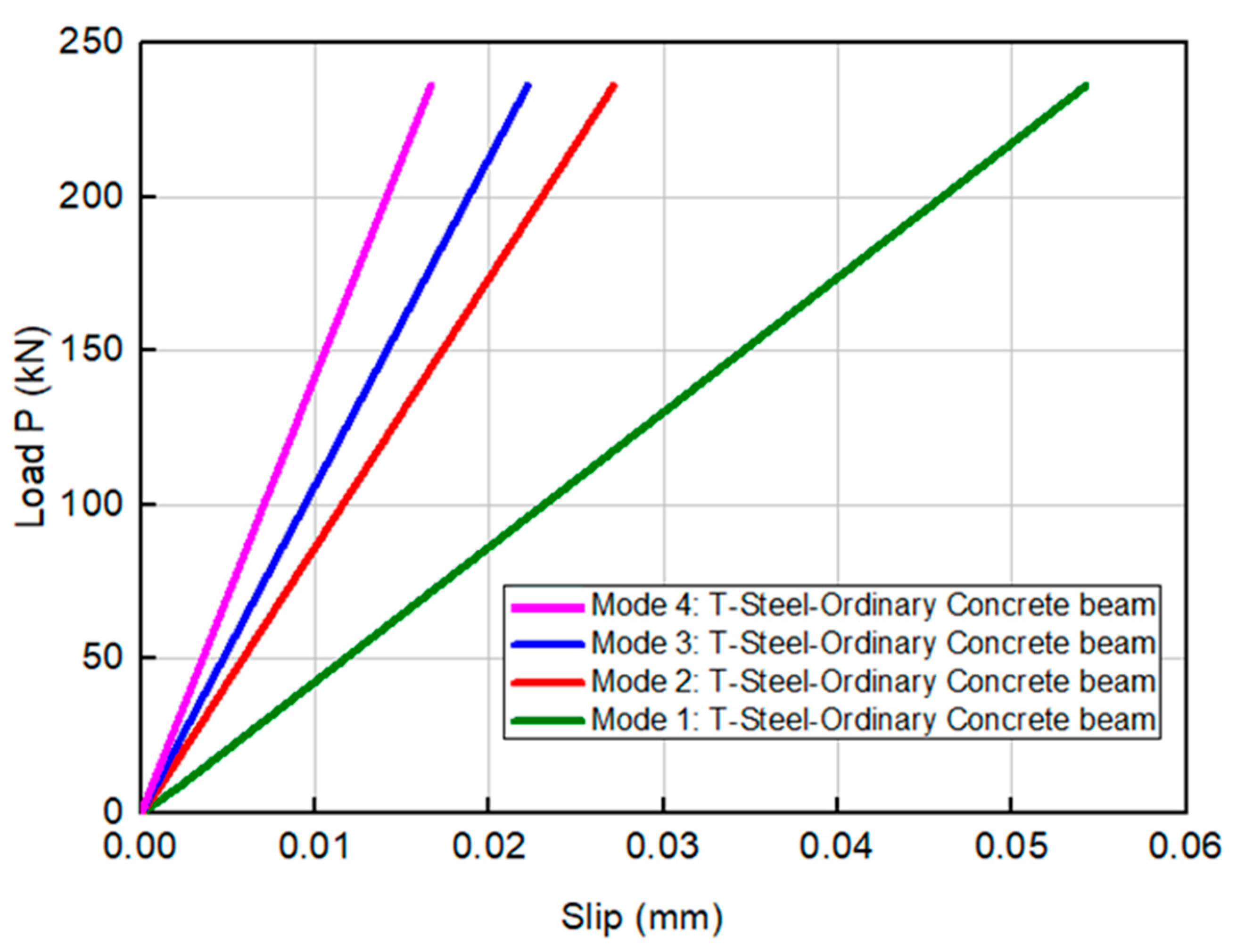
3.3.4. Effect of Connection Mode on Slip at the Steel–Concrete Interface
3.3.5. Effect of the Beam Length on Slip at the Steel–Concrete Interface
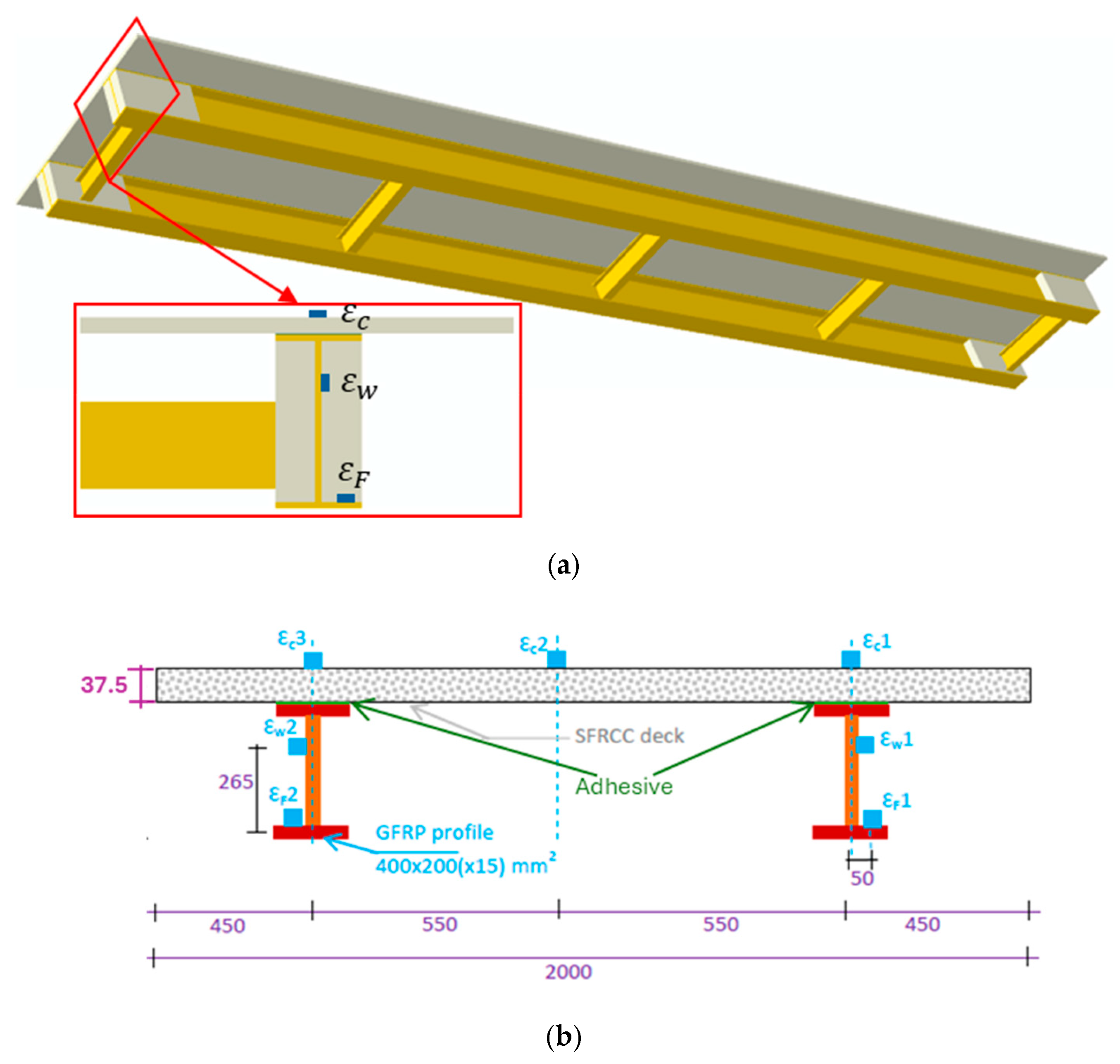
3.4. Case Study: Footbridge
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, S.; Xu, Y.; Zhong, H.; Mosallam, A.S.; Chen, Z. Investigation on interfacial anti-sliding behavior of high strength steel-UHPC composite beams. Compos. Struct. 2023, 316, 117036. [Google Scholar] [CrossRef]
- Cai, M.; Li, W.; Wan, Z.; Sheng, J.; Tan, J.; Ma, C. Cracking control technique for continuous steel–concrete composite girders under negative bending moment. Arch. Civ. Eng. 2023, 69, 239–251. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Yu, M.; Hu, X.; He, W.; Qin, K.; Zhu, Y.; Wei, X. Structural Design and Mechanical Behavior Investigation of Steel–Concrete Composite Decks of Narrow-Width Steel Box Composite Bridge. Buildings 2024, 14, 912. [Google Scholar] [CrossRef]
- Xin, Q.; Dou, Y.; Li, S. Fatigue Behavior of Prestressed Concrete Beams under Overload. J. Eng. Sci. Technol. Rev. 2017, 10, 124–131. [Google Scholar] [CrossRef]
- Berthet, J.F.; Yurtdas, I.; Delmas, Y.; Li, A. Evaluation of the adhesion resistance between steel and concrete by push out test. Int. J. Adhes. Adhes. 2011, 31, 75–83. [Google Scholar] [CrossRef]
- Wang, Y.H.; Yu, J.; Liu, J.P.; Zhou, B.X.; Chen, Y.F. Experimental study on assembled monolithic steel-prestressed concrete composite beam in negative moment. J. Constr. Steel Res. 2020, 167, 105667. [Google Scholar] [CrossRef]
- Henriques, D.; Gonçalves, R.; Sousa, C.; Camotim, D. GBT-based time-dependent analysis of steel–concrete composite beams including shear lag and concrete cracking effects. Thin-Walled Struct. 2020, 150, 106706. [Google Scholar] [CrossRef]
- Bensatallah, T.; Daouadji, T.H.; Abderezak, R.; Tounsi, A. Structural bonding for civil engineering structures: New model of composite I-steel–concrete beam strengthened with CFRP plate. Steel Compos. Struct. 2021, 41, 417–435. [Google Scholar] [CrossRef]
- Tounsi, A.; Daouadji, T.H.; Benyoucef, S. Interfacial stresses in FRP-plated RC beams: Effect of adherend shear deformations. Int. J. Adhes. Adhes. 2009, 29, 343–351. [Google Scholar] [CrossRef]
- Tahar, H.D.; Boussad, A.; Abderezak, R.; Rabia, B.; Fazilay, A.; Belkacem, A. Flexural behaviour of steel beams reinforced by carbon fibre reinforced polymer: Experimental and numerical study. Struct. Eng. Mech. 2019, 72, 409–420. [Google Scholar] [CrossRef]
- Xue, W.; Ding, M.; Wang, H.; Luo, Z. Static behavior and theoretical model of stud shear connectors. J. Bridge Eng. 2008, 13, 623–634. [Google Scholar] [CrossRef]
- Tang, L. Experimental study on HSS-concrete composite beams. J. Build. Struct. 2009, 30, 64–69. Available online: https://en.cnki.com.cn/Article_en/CJFDTOTAL-JZJB200902007.htm (accessed on 11 April 2025).
- Hegger, J.; Döinghaus, P. High performance steel and high-performance concrete in composite structures. In Composite Construction in Steel and Concrete IV; American Society of Civil Engineers: Reston, VA, USA, 2000; pp. 891–902. [Google Scholar]
- Du, H.; Hu, X.; Shi, D.; Xue, W. Flexural performance of composite beams using high-strength steel and high-strength concrete. Int. J. Steel Struct. 2021, 22, 27–41. [Google Scholar] [CrossRef]
- Karabulut, M. Nonlinear Load-Deflection Analysis of Steel Rebar-Reinforced Concrete Beams: Experimental, Theoretical and Machine Learning Analysis. Buildings 2025, 15, 432. [Google Scholar] [CrossRef]
- Karabulut, M. Machine learning-driven flexural performance prediction and experimental investigation of glass fiber-reinforced polymer bar-reinforced concrete beams. Polymers 2025, 17, 713. [Google Scholar] [CrossRef]
- Daouadji, T.H.; Abbès, B.; Bensatallah, T.; Abbès, F. Analysis of Interface Sliding in a Composite I-Steel–Concrete Beam Reinforced by a Composite Material Plate: The Effect of Concrete–Steel Connection Modes. J. Compos. Sci. 2025, 9, 273. [Google Scholar] [CrossRef]
- Daouadji, T.H.; Abderezak, R.; Rabia, B. Analysis of mechanical performance of continuous steel beams with variable section bonded by a prestressed composite plate. Steel Compos. Struct. 2024, 50, 183–199. [Google Scholar] [CrossRef]
- Xie, F.; Tian, W.; Li, S.; Diez, P.; Zlotnik, S.; Gonzalez, A.G. Experimental study on the structural performance of glass-fiber-reinforced concrete slabs reinforced with glass-fiber-reinforced polymer (GFRP) bars: A sustainable alternative to steel in challenging environments. Polymers 2025, 17, 1068. [Google Scholar] [CrossRef]
- Li, J.P.; Zhang, L.Y.; Zhu, Y.J.; Zhao, G.; Liu, F.Z.; Zhang, T. Finite Element Analysis of the Flexural Behavior of Steel Plate–High-Performance Concrete (HPC) Slab and Beam Composite Structures. Buildings 2024, 15, 27. [Google Scholar] [CrossRef]
- Mohammadi Dehnavi, M.M.; De Angelis, A.; Pecce, M.R. The effect of connection ductility on Composite steel–concrete bridges. Appl. Sci. 2024, 14, 963. [Google Scholar] [CrossRef]
- Zeng, W.; Fan, L.; Chen, F.; Zhu, S. Theoretical, experimental, and numerical simulation studies on interface slip in steel–concrete composite continuous beams with high-strength bolted connectors. Structures 2025, 71, 108126. [Google Scholar] [CrossRef]
- Jian, X.; Zhang, N.; Liu, H.; Zhao, Z.; Lei, M.; Chen, Z. Interface slip of steel–concrete composite beams reinforced with CFRP sheet under creep effect. Sci. Rep. 2022, 12, 22375. [Google Scholar] [CrossRef]
- Fan, L.; Xu, Y.M.; Tan, Y. Interface slip calculation of prefabricated steel–concrete composite beams with clustering studs. J. Jilin Univ. Eng. Technol. Ed. 2023, 53, 2533–2541. [Google Scholar] [CrossRef]
- Peng, F.; Xue, W.; Bai, L.; Du, M. Design Approach for Short-Term Deflection of Simple and Continuous Steel–Concrete Composite Beams Considering Interface Slip. J. Struct. Eng. 2025, 151, 04025072. [Google Scholar] [CrossRef]
- Tayeb, B.; Daouadji, T.H. Improved analytical solution for slip and interfacial stress in composite steel–concrete beam bonded with an adhesive. Adv. Mater. Res. 2020, 9, 133–153. [Google Scholar] [CrossRef]
- Bouazaoui, L.; Perrenot, G.; Delmas, Y.; Li, A. Experimental study of bonded steel concrete composite structures. J. Constr. Steel Res. 2007, 63, 1268–1278. [Google Scholar] [CrossRef]
- Gonilha, J.A.; Barros, J.; Correia, J.R.; Sena-Cruz, J.; Branco, F.A.; Ramos, L.F.; Gonçalves, D.; Alvim, M.R.; Santos, T. Static, dynamic and creep behaviour of a full-scale GFRP-SFRSCC hybrid footbridge. Compos. Struct. 2014, 118, 496–509. [Google Scholar] [CrossRef]



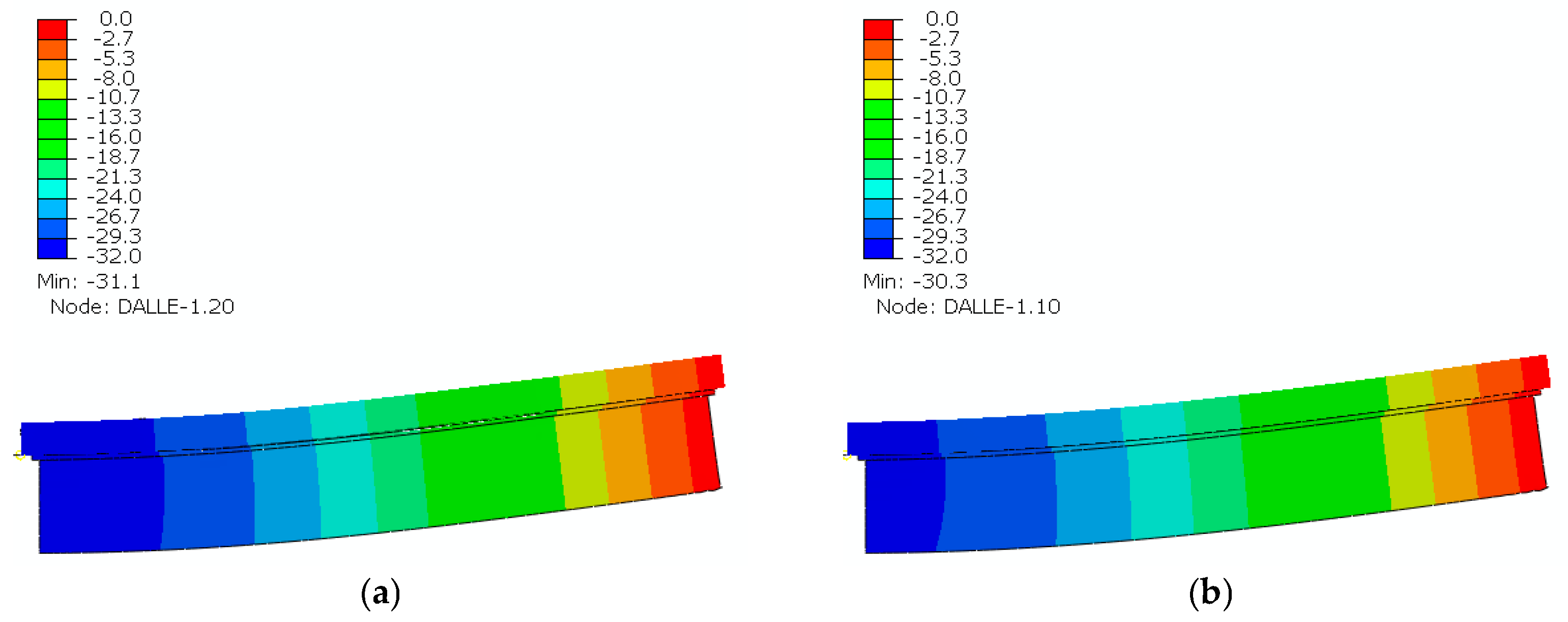
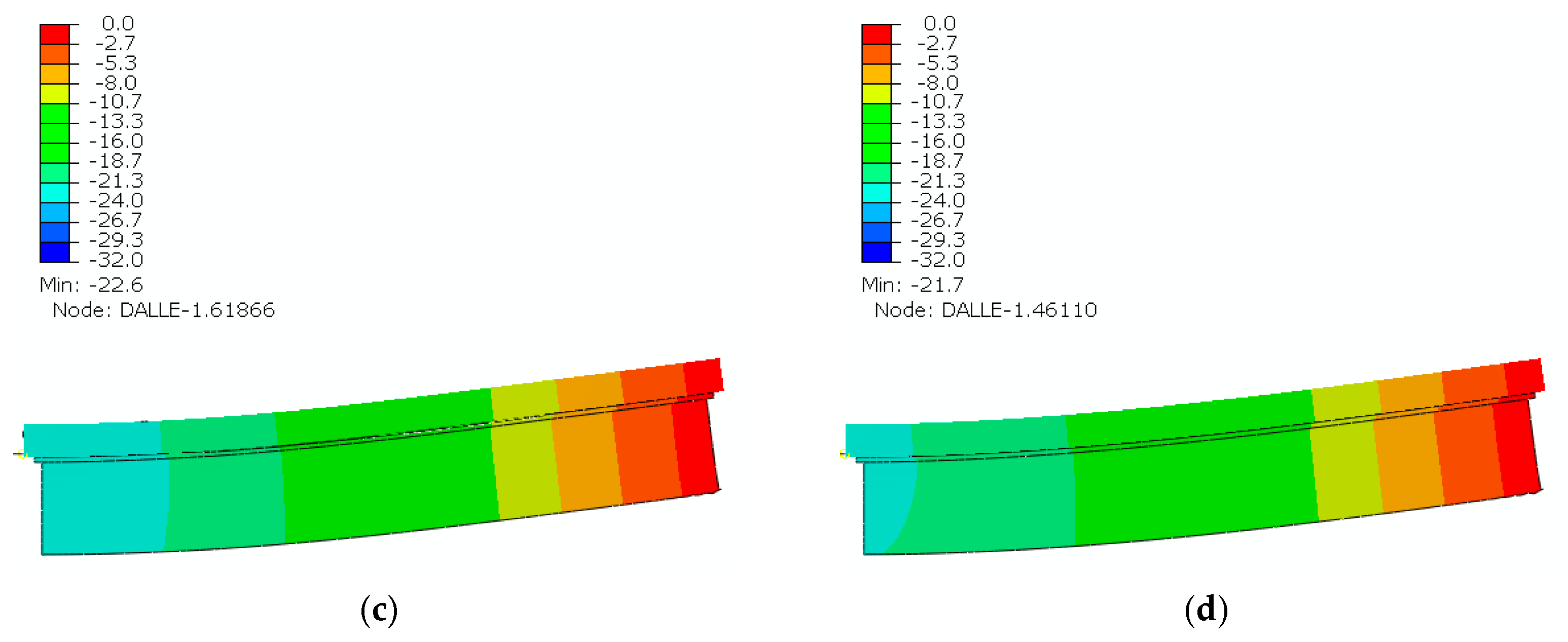


| References | Scope |
|---|---|
| [1,5,6,12,14,22,23] | Focus on experimental tests to characterize steel–concrete interface adhesion, sliding/slip behavior, and bond strength under various loading and reinforcement conditions. |
| [7,9,11,14,20,22,24,25] | Development of analytical, numerical, or finite-element models to predict interface slip, load transfer, flexural behavior, and connector performance in composite beams. |
| [8,9,10,17,23] | Studies involving the use of fiber-reinforced polymer (FRP) materials or composite plates to strengthen steel–concrete beams and analyze interfacial stress improvements. |
| [3,4,6,10,14,15,16,18,21] | Experimental and/or theoretical analysis of flexural capacity, crack control, fatigue, and ductility of steel–concrete composite beams, including machine learning approaches for behavior prediction. |
| [1,13,14,19] | Research on the use of high-performance steel, UHPC, or glass-fiber-reinforced polymer composites to improve structural performance and sustainability. |
| [2,6] | Techniques and experimental studies focused on controlling cracking under negative bending moments in composite girders and beams. |
| [18,22,25] | Studies on interface slip and structural response in continuous composite beams or those with variable cross-sections, often incorporating prestressing or bolted connectors. |
| Materials | Young’s Modulus (MPa) | Poisson Ratio | |
|---|---|---|---|
| Concrete slab | Ordinary concrete | ||
| Siporex concrete | |||
| Lightweight aggregate concrete | |||
| Adhesive | Adhesive between concrete slab and steel beam | ||
| T-shaped steel beam | Steel | ||
| Load | Connection Mode | Solution | Ordinary Concrete | Siporex Concrete | Lightweight Aggregate Concrete |
|---|---|---|---|---|---|
| Concentrated load P = 200 kN | Discontinuous | FEM | 0.0183 | 0.0355 | 0.0264 |
| Analytical | 0.01798 | 0.03472 | 0.02588 | ||
| Continuous | FEM | 0.0178 | 0.0340 | 0.0240 | |
| Analytical | 0.01851 | 0.03536 | 0.02496 | ||
| Uniformly distributed load q = 50 kN/mL | Discontinuous | FEM | 0.0375 | 0.0716 | 0.0535 |
| Analytical | 0.03843 | 0.0734 | 0.0548 | ||
| Continuous | FEM | 0.0336 | 0.0702 | 0.0504 | |
| Analytical | 0.03444 | 0.07195 | 0.05166 |
| Length (mm) | q = 100 kN/mL |
|---|---|
| 4000 | 0.04156 |
| 6000 | 0.06234 |
| 8000 | 0.08313 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daouadji, T.H.; Abbès, F.; Bensatallah, T.; Abbès, B. Analytical and Numerical Investigation of Adhesive-Bonded T-Shaped Steel–Concrete Composite Beams for Enhanced Interfacial Performance in Civil Engineering Structures. Inventions 2025, 10, 61. https://doi.org/10.3390/inventions10040061
Daouadji TH, Abbès F, Bensatallah T, Abbès B. Analytical and Numerical Investigation of Adhesive-Bonded T-Shaped Steel–Concrete Composite Beams for Enhanced Interfacial Performance in Civil Engineering Structures. Inventions. 2025; 10(4):61. https://doi.org/10.3390/inventions10040061
Chicago/Turabian StyleDaouadji, Tahar Hassaine, Fazilay Abbès, Tayeb Bensatallah, and Boussad Abbès. 2025. "Analytical and Numerical Investigation of Adhesive-Bonded T-Shaped Steel–Concrete Composite Beams for Enhanced Interfacial Performance in Civil Engineering Structures" Inventions 10, no. 4: 61. https://doi.org/10.3390/inventions10040061
APA StyleDaouadji, T. H., Abbès, F., Bensatallah, T., & Abbès, B. (2025). Analytical and Numerical Investigation of Adhesive-Bonded T-Shaped Steel–Concrete Composite Beams for Enhanced Interfacial Performance in Civil Engineering Structures. Inventions, 10(4), 61. https://doi.org/10.3390/inventions10040061






