Short-Term Forecasting of Total Aggregate Demand in Uncontrolled Residential Charging with Electric Vehicles Using Artificial Neural Networks

Abstract

Electric vehicles are gaining attention and being adopted by new users every day. Their widespread use creates a new scenario and challenge for the energy system due to the high energy storage demands they generate. Forecasting these loads using artificial neural networks has proven to be an efficient way of solving time series problems. This study employs a multilayer perceptron network with backpropagation training and Bayesian regularisation to enhance generalisation and minimise overfitting errors. The research aggregates real consumption data from 200 households and 348 electric vehicles. The developed method was validated using MAPE, which resulted in errors below 6%. Short-term forecasts were made across the four seasons, predicting the total aggregate demand of households and vehicles for the next 24 h. The methodology produced significant and relevant results for this problem using hybrid training, a few-neuron architecture, deep learning, fast convergence, and low computational cost, with potential for real-world application. The results support the electrical power system by optimising these loads, reducing costs and energy generation, and preparing a new scenario for EV penetration rates.

1. Introduction

One approach to fostering a cleaner and more sustainable world is to reduce the emission of polluting gases, such as $C{O}_2$, into the atmosphere. This gas significantly contributes to pollution, which drives climate change, environmental crises, and global instability, raising serious global concerns [1].

The transportation sector is closely linked to a country’s economic foundation and is a significant contributor to $C{O}_2$ emissions [2]. Additionally, the continued prevalence of combustion-based transportation has intensified its impact on climate change and energy crises [3].

The search for alternative and clean energy sources has become an essential option in this context, as pollution from the burning of fossil fuels in the transportation sector is having a significant impact and raising concerns for both the present and near future. As a result, hybrid electric vehicles (HEVs), battery electric vehicles (BEVs), and plug-in hybrid electric vehicles (PHEVs) are becoming increasingly popular and showing promise for a more sustainable future. The focus is on advancing global incentives and policies that accelerate the adoption of electric vehicles (EVs) and promote the decarbonization of transportation [4].

Charging the batteries of plug-in electric vehicles (PEVs) will lead to an increase in electricity demand in distribution networks. This increase is expected to cause voltage drops, thermal overloads, and higher losses [5]. PEVs create high load demand during charging, which could cause the electricity grid to fail in meeting its power delivery capacity, resulting in faults and complications. The main challenge for the electrical system regarding PEVs is how the charging demand can impact the power system, especially during peak consumption times, when vehicle loads are charged in public, private, or residential parking lots [6].

The increasing adoption of EVs will drive a substantial rise in power demand on distribution networks, due to the high and constant need for battery charging. This increase could potentially lead to significant challenges for the electrical system [7], as EV batteries require high power loads during charging, which the existing electrical grid may not always be able to support [5].

These new EV connections present a substantial challenge for the electrical power system, as EVs can be charged in private homes, commercial buildings, companies, and both private and public charging stations [6].

One approach to ensuring that energy demand aligns with consumption is to forecast electrical loads in the energy system, accounting for variations from hours to days, months, and years. This helps guarantee economic, strategic, and other advantages. Forecasting plays a crucial role in directly influencing important operational decisions, such as dispatch, unit commitment, and maintenance scheduling [8].

In this context, ensuring projections and forecasts of electrical loads in the short term has become a timely and relevant topic for concessionaires, the electrical energy market, and academic research. Load forecasting is not easy, as loads correlate not only between hours, days, weeks, or months but also with human behavior and exogenous variables, such as humidity, temperature, and seasons [8].

There are a wide variety of modeling techniques for forecasting electrical loads. These methods vary according to the operator’s experience [9] and even formal mathematical approaches, such as structural techniques [10], Bayesian methods [11], Box–Jenkins methods [12], fuzzy logic [13], and intelligent systems such as artificial neural networks (ANNs) [14].

The recent literature presents several works dealing with different methods to forecast the EV charging demand. Some of them can be cited as follows.

Mudgal et al. (2025) propose a work that classifies residential, workspace, and instantaneous station via Density-Based Spatial Clustering of Applications with noise (HDBSCAN) and the Elbow Method and the forecast method is performed with regression models including Random Forest, Support Vector Machines, and Logistic Regression [15].

Nazir et al. (2025) propose a model that improves energy forecasting for electric vehicles by employing an outlier correction using as forecasting technique a time series dense encoder [16].

Fahim et al. (2025) uses a Residual Dual BiLSTM–CNN path network for including missing EV charging data capturing the temporal and long term dependencies in various scenarios [17].

Mohsenimanesh and Entchev (2024) propose three charging strategies to reduce overall charging in peak periods based on predicted load using a hybrid machine learning approach combining similar day selection, complete ensemble mode decomposition, and deep neural networks [18].

Tang et al. (2024) propose a variational modal decomposition (VMD) frost and ice optimization algorithm (RIME)—bi-directional long and short memory neural network (Bi-LSTM)—to avoid the low accuracy problems [19].

Shi et al. (2024) propose a probabilistic load forecasting strategy with Gaussian process regression structured in a day-ahead manner, including features related to EV habits and weather information [20].

Lu et al. (2024) propose a method that contains a real time interaction with multi source information, as well as charging prices consumption along the way. A second order cone optimization is used to optimize the space-time distribution of regional charge load [21].

Gowda et al. (2024) employ transfer learning and model-agnostic meta learning with a pre-training base model, providing better results than classical methods with traditional LSTM [22].

Rasheed et al. (2023) propose an improved supervised learning based deep neural network incorporating Gated Recurrent Unit (GRU), long short-term memory (LSTM), Recurrent Neural Network (RNN), Fully Connected (FC), and Convolutional Neural Network (CNN) that improves the prediction-refining training process with additional features and information [23].

Yang et al. (2022) use an enhanced learning approach for solving the intractable forecasting problem, accommodating factors that affect the charging loads [24].

To improve the accuracy of short-term electric vehicle load forecasting, the authors (Sun et al., 2024) combined forecasting model based on the Sparrow Search Algorithm (SSA) and Support Vector Machine (SVM) [25].

The authors (Tang et al., 2023) propose the use of the frequency of charging piles with historical charging load values as input data for a LSTM (long short-term memory) neural network that executes the load forecasting [26].

Although these recent works available in the literature deal with different new techniques, the present work uses a traditional backpropagation with Bayesian regularization to perform EV load forecasting, providing similar results.

The introduction of artificial neural networks (ANNs) allows electrical charge forecasting problems to be solved with greater efficiency and accuracy, as this technique learns from historical data and stores certain information for future use [27]. This capability motivated the use of an ANN model in this research. ANN-based learning models are now widely applied in this field, particularly for forecasting charging demand and addressing simultaneous EV charging challenges, among other applications.

The use of artificial intelligence techniques means that problems such as predicting future loads can be implemented and solved efficiently, since ANNs learn from previous patterns and store this information for later use. The artificial neuron resembles the biological neuron that processes this information, storing the knowledge learned over time [27].

This work aims to apply an ANN based on the multilayer feedforward perceptron (MLP) [28] architecture, utilizing hybrid supervised backpropagation training with Bayesian regularization [29], to forecast the total demand generated by EV charging in residential settings. Forecasts were conducted for the next 24 h of total aggregate demand across each season of the year for comparative analysis.

This work aims to develop a methodology based on a feedforward network architecture with Bayesian regularization training to predict the charging demand of electric vehicles in a residential charging environment. The proposal is to apply this technique to solve the problem of short-term load forecasting for electric vehicles, predicting the total demand for uncoordinated charging in the next 24 h, in the four seasons of the year. The main contributions of this study are the use of a deep learning architecture and backpropagation training with a Bayesian model, this is a well-regarded approach in the literature to promote an application to a recent research topic that can be fully applied to short-term electric vehicle charging forecasting.

This research is different because it applies the forecast of the total demand for charging aggregated to households in the four seasons of the year, while most studies only seek forecasts for electric vehicles, thus exploring a gap in this area of study. In addition, the training proposed in this research includes a hybrid training, combining a BP training consolidated in the literature with a RB method, since most studies address only a single type of training.

2. Uncoordinated Residential EV Charging and Impacts

In uncoordinated residential charging, EVs start charging immediately upon being plugged into an outlet, allowing charging to occur at any time, 24 h a day. These loads exhibit highly random patterns and behavior. Currently, the electricity sector does not recommend this approach and provides little incentive for it, as it does not supply the necessary usage information for scheduled or delayed managed charging, which would optimize EV charging. By delaying the start of charging, EVs can be charged during off-peak times [30].

This charging method does not provide information on energy prices and operates without any control or strategy. EV users can plug in and unplug at any time, or even fully charge the battery whenever they choose [31].

The large-scale integration of EVs into the electrical power system will pose challenges due to the uncoordinated rise in EV connections in households, especially impacting the distribution system. These residential charging loads, combined with EV demand, can significantly increase peak loads, potentially resulting in power shortages, grid congestion, voltage and frequency instability, and failures in electrical components [32].

In this scenario, EV loads require a high level of connectivity for extended periods, often coinciding with peak residential demand. Since the current system is not designed to accommodate high rates of EV adoption, the widespread uncoordinated charging of EVs may adversely affect the distribution, generation, and transmission infrastructure of the electrical power system [33,34].

Generally, energy utilities represent demand through customer profiles based on different usage behaviors, using load curves over time [30]. Each curve corresponds to a distinct profile, such as public, residential, commercial, or industrial [35].

The impacts generated by EVs are substantial due to the high power requirements of aggregate charging and the large-scale adoption of EVs currently underway in the electric mobility sector [36]. The charging of plug-in electric vehicles (PEVs) and plug-in hybrid electric vehicles (PHEVs) will place additional load on the electrical energy system, increasing residential demand and creating a new total aggregate demand. These vehicles are primarily charged using residential outlets with Level 1 and Level 2 power, often when PEVs are parked in garages in the morning and evening [37].

The high connection rates of PEVs in the electrical distribution network create operational challenges [33]. Distribution systems were originally designed to handle conventional load capacities, like residential or commercial loads, based on typical consumer profiles. However, when PEVs are connected, these profiles and the energy demand change significantly due to the high power required over shorter periods for residential charging, as well as for buildings, commercial sites, and public charging stations [38].

3. EV Charging Demand Forecast

EV loads have specific characteristics that differ from residential loads, with unique spatial and temporal distribution profiles. This type of charging requires high power due to its highly periodic and fluctuating nature. EV charging curves exhibit multiple power peaks, particularly within short time intervals throughout the day [39].

In the conventional approach to time series forecasting, historical data and modeling simulations are utilized as the primary sources of information. In this manner, they serve a pivotal function in the domain of forecasting. However, the forecasting of EV-related data is inherently uncertain due to the novel nature of these vehicles and their associated load characteristics. Such load profiles exhibit growth rules and non-stationary and stochastic characteristics. It was observed that, in the case of time series data for which the output exhibits a certain degree of correlation over time, artificial neural networks (ANNs) are a more appropriate choice of modelling approach. This is because ANNs consider previous information in order to make new future projections [40].

The primary challenges associated with forecasting the aggregate charging demand for VEPs can be attributed to several factors, including the inherent volatility of electrical loads, the availability of publicly accessible data, the spatial and temporal distribution characteristics of charging, the diversity of charging modes, the varying rates of penetration of EVs in the network, the uncontrolled growth of charging, and the occurrence of demand spikes. These observations are supported by the findings of reference [40]. As the adoption of electric vehicles (EVs) continues to grow, it is anticipated that the demand for electricity for their charging will have a notable impact on the power grid.

Moreover, the necessity for a consistent and substantial power supply underscores the critical importance of EV charging infrastructure. The high power demand for charging electric vehicles (EVs) imposes significant constraints on the electric grid. In order to address this issue, there is a need to accurately predict the charging load of EVs in conjunction with residential charging. This will assist grid operators in effectively managing power distribution and making informed decisions, as cited in [41].

Short-term load forecasting has emerged as a crucial instrument for the intelligent regulation of electric vehicle (EV) charging systems. Nevertheless, such forecasting is not a straightforward undertaking. It necessitates the consideration of various factors, including a comprehensive understanding of the user profile and their consumption patterns. Electric vehicle (EV) charging loads exhibit distinctive characteristics compared to conventional loads. Such loads exhibit spatial and temporal distribution characteristics. The load exerts a considerable demand due to its highly periodic and fluctuating characteristics. The load curves of electric vehicles (EVs) exhibit a number of pronounced energy peaks, particularly over relatively short time periods [40].

The conventional approach to forecasting is based on historical electrical load data, which plays a pivotal role in load forecasting. However, forecasting with EVs presents a number of challenges due to the inherent uncertainties associated with a novel type of load, exhibiting the characteristics previously outlined. The load profiles of EVs exhibit growth rules and characteristics that have yet to be fully elucidated, necessitating extensive investigation [41].

The primary challenges in forecasting the charging demand for electric vehicles (EVs) encompass the characterization of the spatial and temporal distribution of EV loads. This entails the representation of such loads on multi-temporal and spatial scales, as well as the ability to transition between these scales. Additionally, the complexity of EV charging modes and management systems further complicates the prediction of charging demand. The charging of electric vehicles (EVs) occurs in a variety of environments, resulting in the generation of disparate charging profiles [40].

The varying penetration rates of EVs in different regions introduce another layer of complexity, as the rate of EVs plugged in determines the system’s capacity to support and meet load delivery needs. Additionally, the uncontrolled growth of EV charging and the emergence of consumption peaks pose further challenges [40].

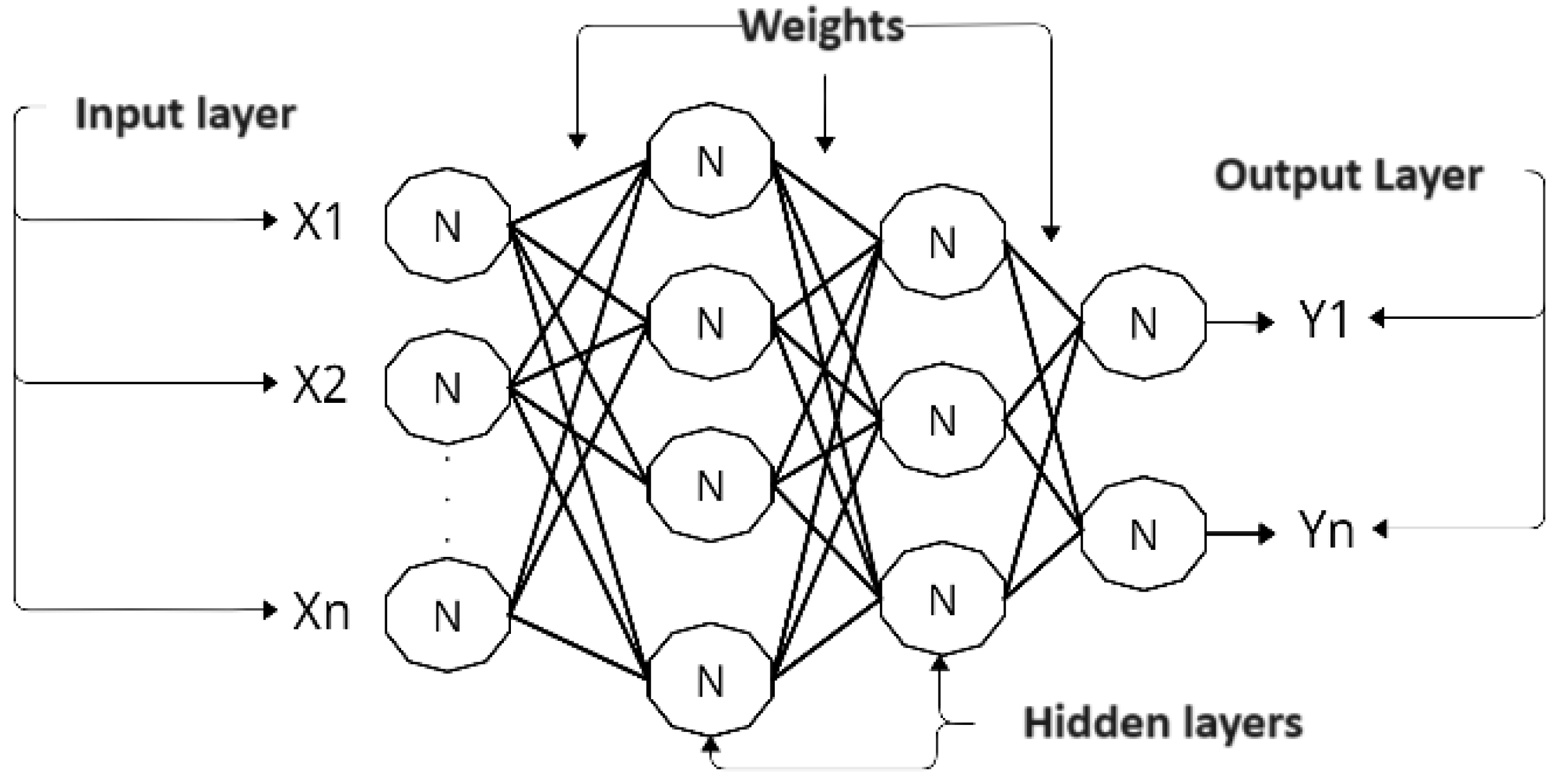
4. Multilayer Perceptron Artificial Neural Network

A multilayer feedforward network is characterized by a fully connected structure across all layers. A fundamental property of a multilayer feedforward network is that each neuron in any layer is connected to all other neurons in the previous layer. Consequently, the direction of the signal flow through the network follows a feedforward progression from left to right, propagating in layers [28]. A limitation of multi-layer feedforward networks is that they lack the capacity for feedback. In general, the multilayer feedforward network adds successive values to the inputs and to all neurons in the subsequent hidden and output layers, thereby ensuring that the neurons receive only the input connections [28].

Multilayer perceptron (MLP) [28] ANNs are fully connected layered architecture networks. Neurons in any network layer are always connected to all other neurons in the previous layer, which are interconnected directly in an input layer through weights. This type of network has layers in levels, i.e., an input layer containing one or more neurons, one or several hidden layers, and an output layer containing one or more neurons. Each layer has nodes, and each node is directly connected by weights with nodes in the next layer (Figure 1), with $[X_1,X_2,\dots ,X_n]$ being the network input signals; N being neurons; $weights$ representing the synaptic weights of the neuron N; and $[Y_1,Y_2,\dots ,Y_n]$ being the output signals from N neurons.

MLP transforms its linear inputs through a non-linear activation function (1) [27]:

$$x_o=f\left(\sum _{h=1}^H\left(x_h{w}_{h,o}\right)\right)$$

(1)

where f is the activation function of the o-th neuron of the output layer, $x_h$ is the output of the h-th hidden layer neuron, $w_{h,o}$ is the interconnection between the h-th neuron of the hidden layer and the o-th neuron of the output layer, and H is the size of the hidden layer. $x_o$ is the non-linear output of neuron o-th.

The transfer function, also called activation, defines the type of output of a neuron. The most common activation functions are the relay-type functions, the semi-linear function, the sigmoid function, and the hyperbolic tangent [42]. We can exemplify the hyperbolic tangent type sigmoid function (2):

$$f\left(x\right)={\displaystyle \frac{(1-e^{-\lambda x})}{(1+e^{-\lambda x})}}$$

(2)

where $\lambda$ is the slope of the curve.

5. Backpropagation Training with Bayesian Regularization

The most crucial attribute of a ANN is its capacity to learn from previously presented information, and it can even enhance the information through a learning process conducted by adjusting the weights. When training an ANN, the primary objective is to generate a performance that will produce a low learning error and, most importantly, for this learning to be able to represent an adequate response to new training data. If this occurs, we can conclude that the network has a robust capacity for generalizing data [28].

One of the methods considered effective in improving the generalization of a network training process is regularization. This method involves restricting the values of the weights in an ANN in order to minimize its performance function. The objective of this regularization is to maintain the weights at relatively low values, which allows the network to generate a more smoothly graded output [29].

The backpropagation (BP) training algorithm with Bayesian regularization (BR) minimizes a combination of quadratic errors and weights and then determines the correct combination to produce training output with high generalization ability [29].

This BR training aims to avoid training overfittings and improve generalization capacity. This training adds a new coefficient to the optimization process, which penalizes the objective function F by increasing the number of [29] coefficients.

In [29] regularization, the objective function F is modified using the sum of the mean squared errors coming from backpropagation, called $E_D$, and, subsequently, the objective function is increased by the term additional $E_w$, which is the sum of the squared errors of the network weights bias (3):

$$F=\beta E_D+\alpha E_w$$

(3)

with $\alpha$ and $\beta$ being the regularization parameters of the objective function. These variables control the training emphasis.While $\alpha \ll \beta$, training will focus on minimizing errors in the trained data, and while $\alpha \gg \beta$, training will prioritize minimizing the values of the weights generated by network errors.

The main training challenge is how the terms $\alpha$ and $\beta$ are defined to control the objective function. In the Bayesian process, weights are treated as random variables. After obtaining the training data, the weight density function is updated by the Bayes theorem (4).

$$P\left(W\right|D,\alpha ,\beta ,M)={\displaystyle \frac{P\left(D\right|W,\beta ,M\left)P\right(W|\alpha ,M)}{P\left(D\right|\alpha ,\beta ,M)}}$$

(4)

Depending on what M is the network architecture used, D is the training matrix; W is the weight matrix; $P\left(W\right|\alpha ,M)$ is the prior density, representing knowledge of the weights before any data was collected; $P\left(D\right|,W|,\beta ,M)$ is the likelihood function, which is the probability of a certain event occurring, considering the weights W; and $P\left(D\right|,\alpha ,\beta ,M)$ is the normalization factor, which guarantees that the total probability is 1.

If it is assumed that the data in the training set is of type Gaussian and its prior distribution for the weights is Gaussian, then probability densities can be written (5) in the following way:

$$\begin{array}{c}\hfill P\left(W\right|D,\alpha ,\beta ,M)={\displaystyle \frac{1}{Z_D^{\beta }}}{e}^{(-\beta E_D)}\\ \hfill \\ \hfill P\left(W\right|\alpha ,M)={\displaystyle \frac{1}{Z_W^{\alpha }}}{e}^{(-\alpha E_W)}\end{array}$$

(5)

being $Z_D^{\beta }={\left({\displaystyle \frac{\pi }{\beta )}}\right)}^{n/2}$ e $Z_W^{\alpha }={\left({\displaystyle \frac{\pi }{\alpha }}\right)}^{N/2}$.

Replacing these probabilities in (4), we can rewrite the calculation as follows (6):

$$\begin{array}{ccc}\hfill P\left(W\right|D,\alpha ,\beta ,M)& =& {\displaystyle \frac{\frac{1}{Z_W^{\alpha }}\frac{1}{Z_D^{\beta }}{e}^{(-(\beta E_D+\alpha E_W))}}{FN}}\hfill \\ \hfill \\ & =& \left({\displaystyle \frac{1}{Z_F(\alpha ,\beta )}}{e}^{-F\left(W\right)}\right)\hfill \end{array}$$

(6)

where $FN$ is the normalization factor.

In this Bayesian step, the optimal weights maximize the posterior probability $P\left(W\right|D,$$\alpha ,\beta ,M)$. Then, maximizing the posterior probability is equivalent to minimizing the regularized objective function $F=\beta E_D+\alpha E_W$.

In this step, the application of Bayes theorem is demonstrated to calculate the optimization of the parameters $\alpha$ and $\beta$ of the objective function F (7):

$$P(\alpha ,\beta |D,M)={\displaystyle \frac{P\left(D\right|\alpha ,\beta ,M\left)P\right(\alpha ,\beta \left|M\right)}{P\left(D\right|M)}}$$

(7)

According to the uniform prior density, $P(\alpha ,\beta |M)$ for the regularization parameters $\alpha$ and $\beta$; then, maximizing the posterior density is possible by calculating its likelihood function $P\left(D\right|\alpha ,\beta ,M)$. It is observed that this function is the normalization factor for (4). Assuming that all probabilities have a Gaussian form, the form for the given posterior density (4) is known. It was demonstrated in (6) and it can be solved (4) for the normalization factor (8):

$$\begin{array}{ccc}\hfill P\left(D\right|\alpha ,\beta ,M)& =& {\displaystyle \frac{P\left(D\right|W,\beta ,M\left)P\right(W|\alpha ,M)}{P\left(W\right|D,\alpha ,\beta ,M)}}\hfill \\ & =& {\displaystyle \frac{\left(\left[\frac{1}{Z_D^{\left(\beta \right)}}{e}^{(-\left(\beta E_D\right))}\right]\left[\frac{1}{Z_W^{\left(\alpha \right)}}{e}^{(-\left(\alpha E_W\right))}\right]\right)}{\frac{1}{Z_F^{(\alpha ,\beta )}}{e}^{(-\left(\alpha E_W\right))}}}\hfill \\ & =& {\displaystyle \frac{Z_F^{(\alpha ,\beta )}}{Z_D^{\left(\beta \right)}{Z}_W^{\left(\alpha \right)}}}{\displaystyle \frac{e^{(-\beta E_D-\alpha E_W)}}{e^{(-FW)}}}\hfill \\ & =& {\displaystyle \frac{Z_F^{(\alpha ,\beta )}}{Z_D^{\left(\beta \right)}{Z}_W^{\left(\alpha \right)}}}\hfill \end{array}$$

(8)

We can observe that the constants $Z_D^{\left(\beta \right)}$ and $Z_W^{\left(\alpha \right)}$, calculated in (5), are known. The only unknown constant is $Z_F^{(\alpha ,\beta )}$. Using the Taylor expansion, it is possible to expand $F\left(W\right)$ around the minimum point of the posterior density $W^{MP}$, where the gradient calculation is zero. Calculating the normalization constants,

$$Z_F\approx {\left(2\pi \right)}^{{\displaystyle \frac{N}{2}}}{(det\left({\left(H^{MP}\right)}^{-1}\right))}^{{\displaystyle \frac{1}{2}}}{e}^{(-F\left(W^{MP}\right))}$$

(9)

where $H=\beta {\nabla }^2{E}_D+\alpha {\nabla }^2{E}_D$ is a Hessian matrix of the objective function F.

With the result of the calculation in (8), it is possible to calculate the optimal values for $\alpha$ and $\beta$ at the minimum point. Calculating the derivative with respect to each of the log of (8) and setting them equal to zero will result in (10)

$$\begin{array}{c}\hfill {\alpha }^{MP}={\displaystyle \frac{\gamma }{2E_W\left(W^{MP}\right)}}\\ \hfill \\ \hfill {\beta }^{MP}={\displaystyle \frac{n-\gamma }{2E_D\left(W^{MP}\right)}}\end{array}$$

(10)

where $\gamma =N-2{\alpha }^{MP}{\left(H^{MP}\right)}^{-1}$ called the effective number of parameters and N is the total number of parameters in the network. The $\gamma$ parameter is a measure of how many neural network parameters are effectively used to minimize the error objective function. It can range from zero to N.

Calculation of the Gauss–Newton Approximation for the Hessian Matrix

BR training requires calculating the Hessian matrix (H) of the objective function $F\left(W\right)$ for the minimum point $W^{MP}$. This approximation can be calculated using the Levenberg–Marquardt optimization algorithm to find the minimum point [43].

Training was carried out according to the standard parameters of the Bayesian regularization training algorithm in the Matlab 2015b software (toolboxes) with the nntool function [29].

The default value for the maximum number of validation failures is set to infinity. This ensures that the training process continues until the optimal balance between errors and weights is achieved. The optimization function relies on the Jacobian matrix for calculations, where the performance metric is the sum of squared errors. Consequently, this training process uses the mean squared error (MSE) as its performance evaluation function.

Bayesian regularization takes place within the Levenberg–Marquardt algorithm. The backpropagation error known as backpropagation is used to calculate the Jacobian of performance in relation to the weight variables and the bias X [44]. Each variable is adjusted according to the Levenberg–Marquardt algorithm, described in Equation (11):

$$\begin{array}{c}\hfill jj=jXjX\\ \hfill \\ \hfill je=jXE\\ \hfill \\ \hfill dx={\displaystyle \frac{-(jj+Im\mu )}{je}}\end{array}$$

(11)

where

• E—all errors;
• I—identity matrix;
• $m\mu$—parameter of Marquardt.

The five steps required for Bayesian optimization of the regularization parameters, with the Gauss–Newton approximation for the H matrix, can be simplified as follows:

1.

Initialization of $\alpha$, $\beta$, and the weights. We choose $\alpha =0$, $\beta =1$, and use the Nguyem–Widrow method to initialize the weights [45]. After the first training step, the parameters of the objective function are recovered from the initial configuration.

2.

Execution of one stage of the Levenberg–Marquardt algorithm to minimize the objective function $F\left(W\right)=\beta E_D+\alpha E_W$.

3.

Calculation of the effective number of parameters $\gamma =N-2\alpha {\left(H\right)}^{-1}$ using the Gauss–Newton approximation for the matrix H available in the Levenberg–Marquardt training algorithm $H={\nabla }^{2}F\left(W\right)\approx 2\beta J^{T}J+2\alpha I_N$, where J is the Jacobian matrix of the errors of the training set [43].

4.

Calculation of new estimates for the parameters of the objective function $\alpha ={\displaystyle \frac{\gamma }{2E_W\left(W\right)}}$ and $\beta ={\displaystyle \frac{n-\gamma }{2E_D\left(W\right)}}$.

5.

Execution of steps 2 and 4 until convergence.

Table 1. Training parameters and MLP.

Parameters	Values
Activation function	Hyperbolic tangent
Number of neurons per layer	(5-6-2-1-1)
Number of hidden layers	3
Number of neurons per hidden layer	(6-2-1)
Performance function	Mean square error $\left(mse\right)$
BP learning rate	0.005
Bayesian regulation $\alpha$	0
Bayesian regulation $\beta$	1
Maximum number of iterations	1000
Performance goal	0
Marquardt Decrease Factor ($\mu$)	0.1
Marquardt increase factor ($\mu$)	10
Maximum Marquardt value ($\mu$)	1 $\times {10}^{10}$
Maximum fault value ahead	500
Minimum gradient value	1 $\times {10}^{-9}$
Training time	∞

Own authorship.

presents all the parameters and hyperparameters of the methodology proposed in this research. Where the best parameters for convergence of the prediction results were obtained the most reliable and robust architecture for the data studied in this research was obtained.

The fitness value of $\left(\mu \right)$ is increased by the Marquardt growth factor $\left(\mu \right)$ until Equation (11) results in a reduced performance value. This change is made by decreasing the decrement factor of the Marquardt parameter $\left(\mu \right)$. Bayesian regularization training will be interrupted as soon as any of these conditions occur:

• The maximum number of training epochs has been reached;
• The maximum time has been exceeded;
• Objective performance is minimized;
• The value of the performance gradient exceeds the chosen minimum value;
• $\left(\mu \right)$ exceeds the maximum validation failure value.

6. Materials and Methods

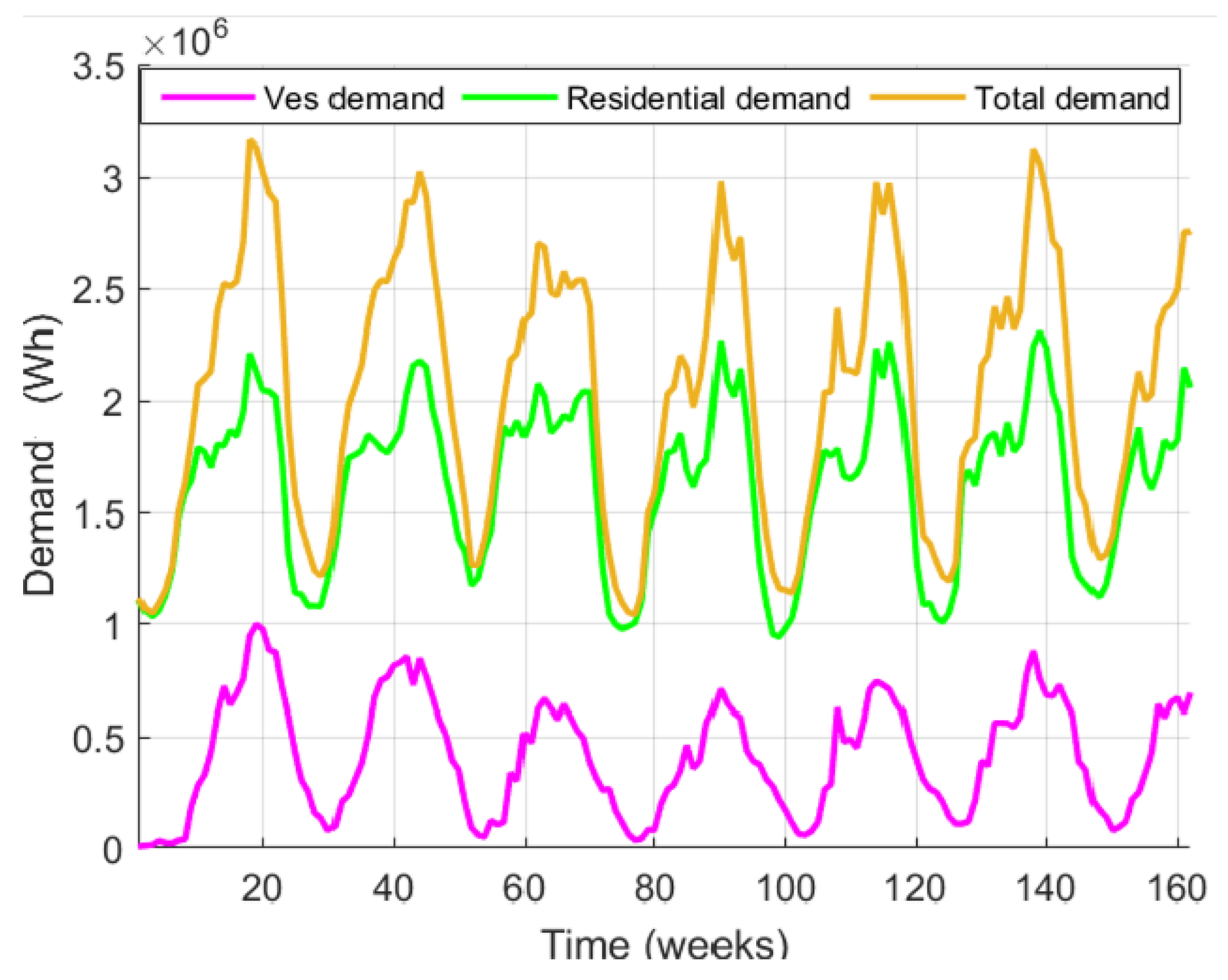
To apply the proposed method, the data set proposed is in reference [37]. The data are from 200 private residences in the Midwest region of the United States (USA). The household composition included 502 individuals and 348 EVs (Figure 2). The load profiles were measured regarding electrical power in Watts (W), with a resolution of 10 min over one year. VEPs with 60% load and Pluggable Hybrid Electric Vehicles (PHEV) with 40% load were considered, all charged with a level 1, plugged with a power of 1920 W.

As the original data has a resolution of 10 min in the very-short term, it was decided to group the measurements for a resolution of 1 h in the short term. All home measurements and all EV charging were added together each hour, forming measurements from 00:00 to 23:00. The transformation was done by reducing 144 measurements (10-min resolution) to 24 measurements (1 h resolution) each day.

The data was separated into two demands: the first represented by residential demand and the second by EV demand. A single column containing all measurements was generated for each demand by adding the 200 homes and 348 vehicles, forming vectors of 8760 × 1, data from the two consumptions over one year. The total demand (12) was obtained by the sum of all respective loads every hour, day, and month between the two demands, residential and EVs (Figure 2):

$$D_{total}=D_{residential}+D_{vehicles}$$

(12)

where $D_{total}$ is the total aggregate demand for forecasting, $D_{residential}$ is the total residential demand, and $D_{vehicles}$ is the total EV demand.

When separating the training and testing data sets, total aggregate demand was used. The total set made up of 8760 measurements was divided into the 4 seasons of the year, for the purpose of comparisons and analysis of seasonality. In this way, 4 forecasts were proposed for the next 24 h, one for each season of the year. The input and test matrices are composed of the following variables:

• Days: $[1\dots 31]$ = day variables;
• Weeks: $[1\dots 7]$ = variables for the weeks from Monday to Sunday;
• Months: $[1\dots 12]$ = variables from the months of January to December;
• Times: $[00\dots 23]$ = variables in hours $\left(h\right)$ in the 24 h period;
• Loads $\left(h\right)$: [total aggregate demand] = load variables referring to the hour $\left(h\right)$ in Watts.

The ANN output set is composed of the total aggregate demand variable, with $(h+1)$ representing the load measurements for the following hour $(h+1)$ in Watts.

The dataset was split into 83% for training and 17% for testing. The following will show how the training input and output matrices and the test input and output matrices were split and dimensioned.

For the fall season, the training input was [5 × 1847] and output [1 × 1847], and the test input was [5 × 359] and output [1 × 359]. For the summer season, the training input was [5 × 1823] and output [1 × 1823], and the test input was [5 × 383] and output [1 × 383]. For the spring season, the training input was [5 × 1799] and output [1 × 1799], and the test input was [5 × 383] and output [1 × 383]. For the winter season, the training input was [5 × 1847] and output [1 × 1847], and the test input was [5 × 359] and output [1 × 359].

Initially, it was decided to divide the 1 year database into the year’s four seasons, as climate change has direct links to consumption patterns and profiles of EVs and homes. With this, predictions become more realistic and perform better. To obtain a better configuration for the ANN architecture, exhaustive tests were carried out by varying the number of hidden layers and the number of neurons in the hidden layers. The best configuration found was the one with six neurons in the first hidden layer, two in the second hidden layer, and one in the third hidden layer. The hyperbolic tangent activation function was used.

The methodology used to evaluate forecast successes and errors was the mean absolute percentage error (MAPE) (13) [14].

$$\mathrm{MAPE}={\displaystyle \frac{1}{Num}}\sum _{h=1}^{Num}\left(\left|{\displaystyle \frac{C_{\left(h\right)}-C_{forecast\left(h\right)}}{C_{\left(h\right)}}}\right|\right)\times 100$$

(13)

where $Num$ is the total number of hours, $C_{\left(h\right)}$ is the actual value at time h, and $C_{forecast\left(h\right)}$ is the value predicted by the network at time h.

7. Results

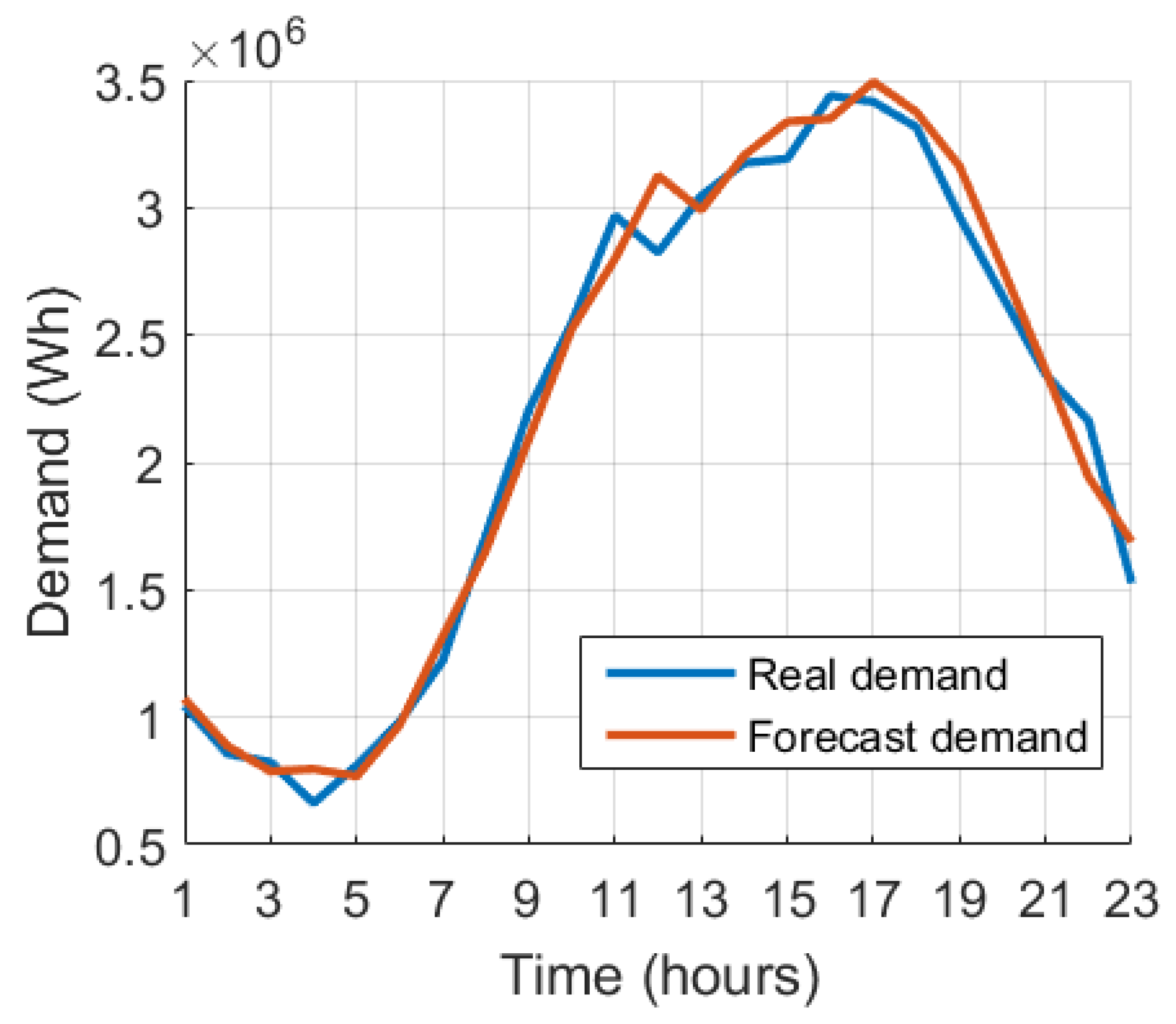
The MAPE results obtained for each season of the year are presented below.

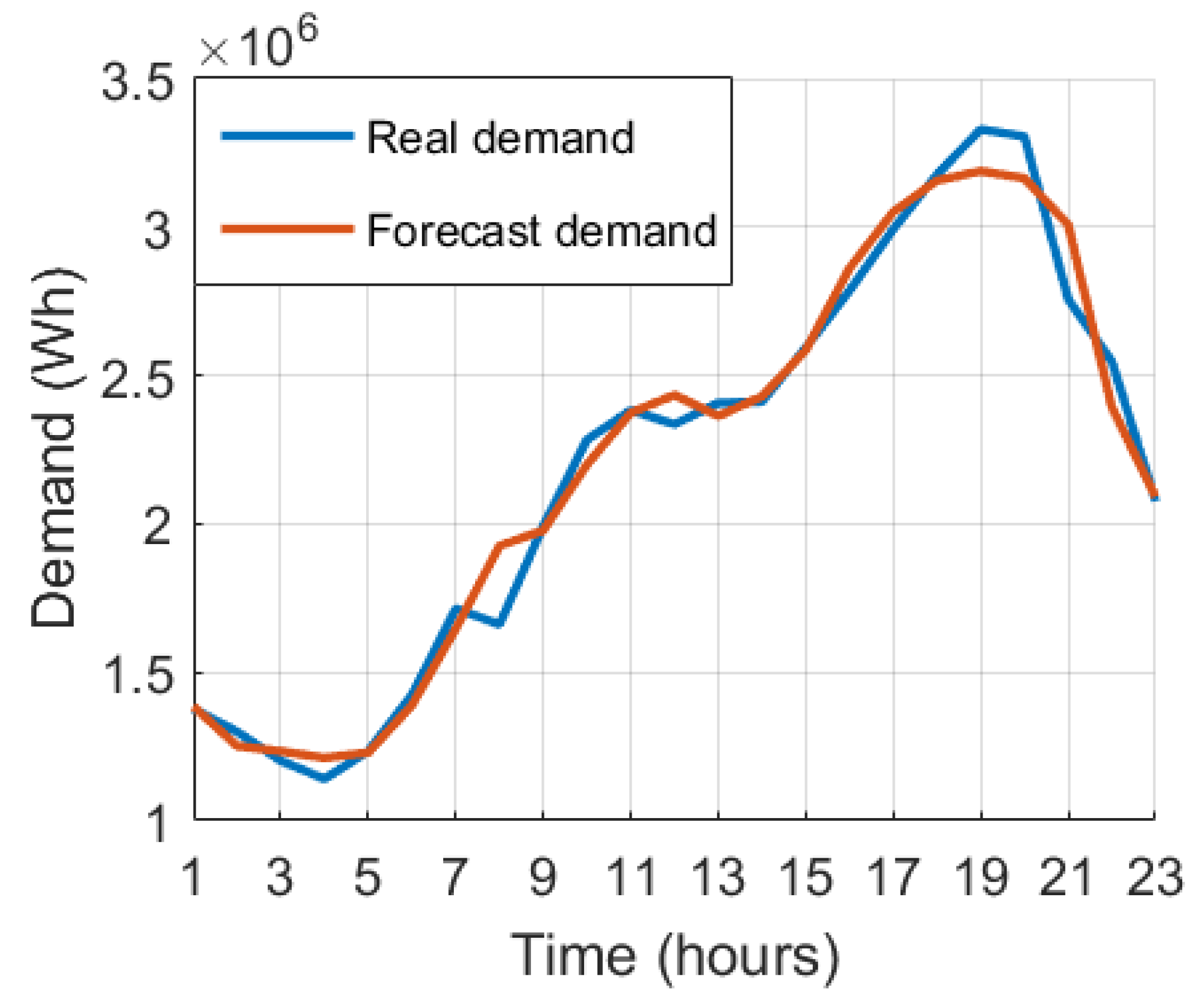
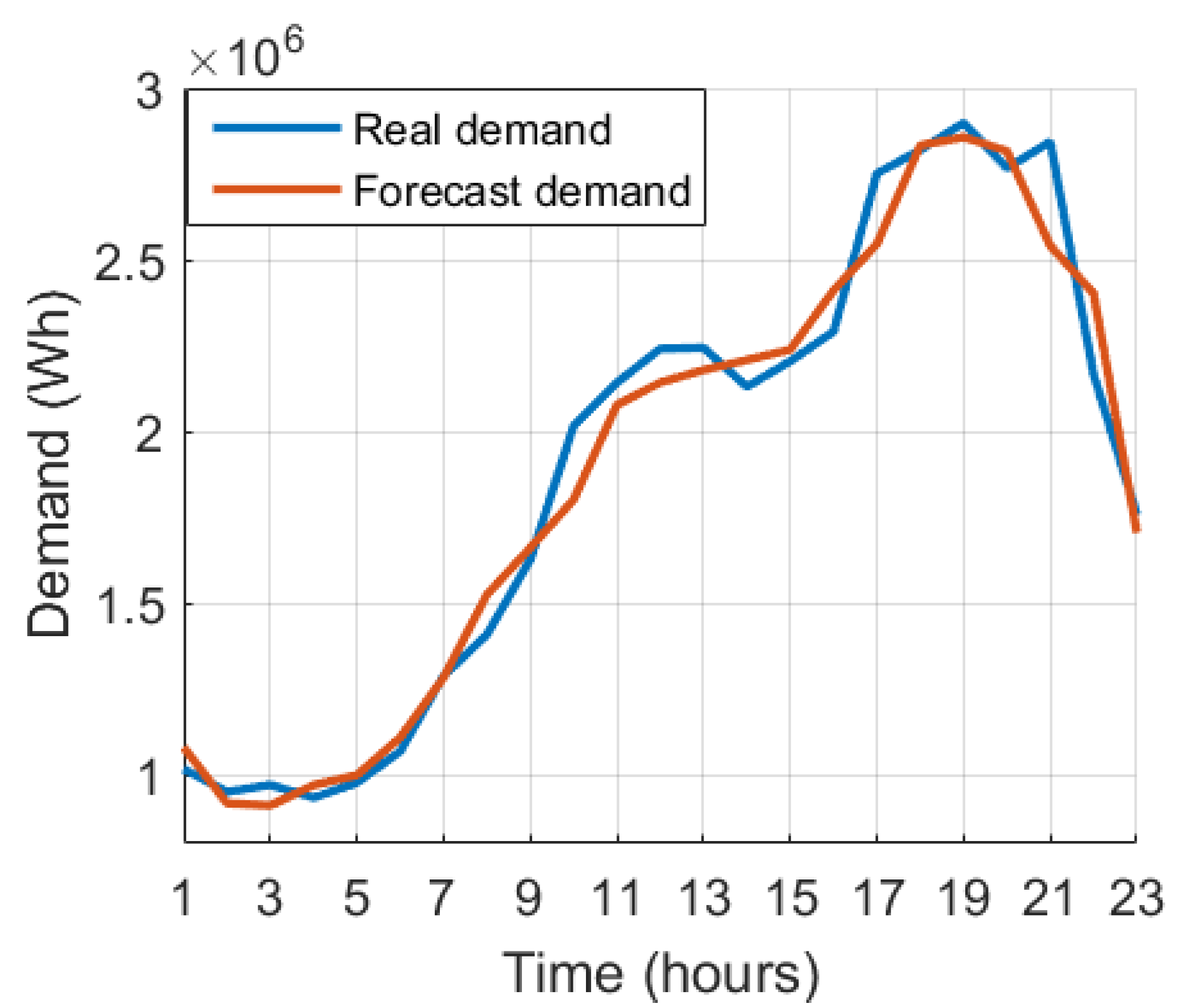
For spring, a MAPE of 4.5042% was obtained; for summer, a MAPE of 5.1180% was obtained; for fall, a MAPE of 3.6487% was obtained; and for winter, the MAPE was 3.3624%.

Figure 3, Figure 4, Figure 5 and Figure 6 present the results obtained for the forecasts in each season of the year.

The software used for modeling, training, and prediction was Matlab 2023b. In training, the data set is divided randomly by default; even when splitting the set into 83%, the algorithm divides this value in random order to make the training process more robust without being associated with a single answer.

Tests were carried out on the configurations of the hidden layers and their number of neurons, and it was observed that the best configuration of the network is with three hidden layers. This configuration was the best performing due to the accuracy and stability of the training response. It was noted that, with fewer than three hidden layers, the network loses precision, demonstrating a limitation of the network in training, and with more than three layers, the network loses training stability. The architecture of the proposed model achieved a significant improvement in the learning process, finding the best configuration of the numbers of neurons and hidden layers.

8. Discussion

It was evident that using only BP training did not produce a satisfactory response, necessitating the normalisation of electrical loads. Therefore, we opted for hybrid training. Even after normalising the electrical loads before applying BP training, the prediction was still inadequate since the RB algorithm automatically normalises between 0 and 1. Consequently, it was unnecessary to normalise the BP training with RB again in the proposed methodology. Combining the two types of training and joining BP to RB resulted in a significant improvement in the network’s performance.

These improvements increased the effectiveness of the proposed MLP architecture and hybrid training. When using a single hidden layer, the responses were satisfactory. However, adding more hidden layers improved the network’s performance, reaching its peak with the third hidden layer, where the training, testing, and prediction results were optimized.

Using deep learning in the methodology gave the network greater processing power and the ability to search for new information about electrical charges, enabling the extraction of more relevant data. Several studies in the literature employ a significant number of neurons in the hidden layers, ranging from 10 to 168 or more. However, this study achieved satisfactory results with just six, two, and one neurons in the respective hidden layers.

Several tests were performed, with variations in the number of hidden layers and neurons per layer, as well as the training parameters, in order to determine the optimal training parameters and network structure for prediction. Several applications were carried out throughout the year by varying the number of hidden layers in the MLP network. It was thus observed that the performance of each configuration varied according to the number of layers and neurons.

It was possible to observe that using only backpropagation training, the response is not satisfactory; highlighting why a hybrid training with Bayesian regularization is used. With the union of the two training sessions, the network obtained a significant improvement in results, as Bayesian regularization determines the probability of an event happening given the saved learning. With these improvements, the proposed architecture and technique increase its effectiveness.

In the spring forecast, the biggest errors were found during the night, between 7 p.m. and 9 p.m., with average errors of $\pm 10\%$. This is due to the peak generated by EVs during this period. It was also seen that in the morning, at precisely 9 am, the network showed an error of $10.644\%$.

It was observed that the highest load peaks due to the penetration of EVs are found in the morning (between 7 a.m. and 12 p.m.) and also at night (between 6 p.m. and 9 p.m.). With these peaks in residential demand, the maximum errors are found at these times. It was observed that between 1 p.m. and 6 p.m. the forecasts had low errors, caused by the low charge of the EVs.

The forecast for summer presented the biggest errors when compared to the other three seasons, with three very pronounced error times: in the morning, with a $20\%$ error (largest error); in the lunch period, with $10\%$ error; and at night, with $10\%$ error (between 9 and 10 p.m.).

For the winter period, the network obtained the lowest errors compared to the other seasons. However, it obtained a maximum error of $15.9345\%$ in the morning peak hour and at this point the network was optimistic; that is, it overestimated the demand at the predicted time.

The fall forecast resulted in the MAPE being just above the winter forecast. At peak loading times, the maximum error was $9.540\%$.

It is also observed that due to the amount of trained data from the winter and summer seasons being greater than the others, this division generated greater maximum errors than the others, around $15.934\%$ in the winter and $20.228\%$ in the summer.

The growth in the adoption of EVs in residential charging had a major impact on the electrical power system. The forecast of total loading demand presents itself as an important strategic tool in a scenario with a broad growth trend and with great openness for exploration and investigation.

The MLP network and the proposed training showed good generalization capacity, with satisfactory results and fast convergence, with training time between 5 and 15 s and 200 to 500 iterations. The use of three hidden layers was of great importance for the training generalization process, increasing the quality of the results. The proposed model showed an improvement in learning due to hybrid training, which resulted in more realistic responses, satisfying the need for reliable predictions with more precision and robustness.

9. Conclusions

As demand for PEV charging increases, problems and congestion will arise in the current and future power grids. This paper explores these issues. Accurate and realistic forecasting of this new demand is essential for projecting and managing these loads over time. While many studies focus solely on PEV load forecasting, this paper presents a promising and necessary approach that seeks to address environmental issues related to where PEVs are charged. The proposed methodology, which integrates residential and PEV demand, could be an effective way of addressing these challenges.

The increased use of EVs alongside residential electricity consumption has had a significant impact on the electrical power system. The forecast for EV charging demand indicates a broad growth trend with significant potential for further exploration.

Total demand forecasting presented itself as a promising option for future projections, having the ability to estimate new demands based on EV loads added to residential load, instead of just making forecasts in EVs. In this way, the ANN learned the behavior of residential loads, EVs, and both being used simultaneously.

It was observed that using three hidden layers improved the network’s training performance and produced the best results. This is because the Bayesian learning process avoids overfitting and underfitting. Using three hidden layers was important for the training generalisation process, improving the quality of the results. For tasks involving supporting generation, distribution and planning systems, load forecasts with an error margin of less than 5% can significantly reduce operating costs.

This work contributed to the study of EV charging demand aggregation in residential areas and involved applying Bayesian regularisation training to an MLP network to forecast total demand. It also involved developing the best parameters and configurations for hidden layers and the number of neurons. Another general contribution was the production of seasonal forecasts.

The proposed methodology presented promising answers to a topic in high and rapid expansion, relatively recent and with great potential for practical application in future research. The proposal, due to its efficiency and reliability in results, has the possibility of being implemented in order to assist in the development of a robust strategy, preparing the power system for new EV penetration rates. This work also has the potential to assist in the development of strategies for smart charging, optimizing the EV charging process.

The forecasting methodology proposed in this research could inform subsequent studies aimed at developing an electric vehicle (EV) charging strategy. This strategy would prepare the electrical energy system for new EV penetration, verify the expected impact of uncoordinated EV charging, and contribute to load forecasting by season.

In addition to these findings, the importance of hybrid training in this research should be emphasized, as the study aimed to improve upon and overcome the limitations of classical methods described in the literature. We found that the BP algorithm did not produce satisfactory or realistic results when used only with gradient descent. However, introducing Bayesian regularisation significantly advanced the training, testing, and prediction processes, resulting in notable improvements in MLP performance.

Future work will explore variations in training division and charging levels further, adding a level 2 to analyse the impact of various charging levels on the electrical grid. The research will also examine how artificial neural networks can be used to predict the optimal charging time, with the aim of reducing the impact on the electrical system.

Another suggestion is to create new forecast classifications beyond the short term, such as the very short and medium terms. This would allow us to make strategic projections for this new EV charging scenario and create forecasts in uncontrolled environments. This scenario is more similar to real-life usage and presents a greater challenge.