A Target-Temperature Monitoring System for Cyclotron Targets: Safety Device and Tool to Experimentally Validate Targetry Studies
Abstract
:1. Introduction
2. Materials and Methods
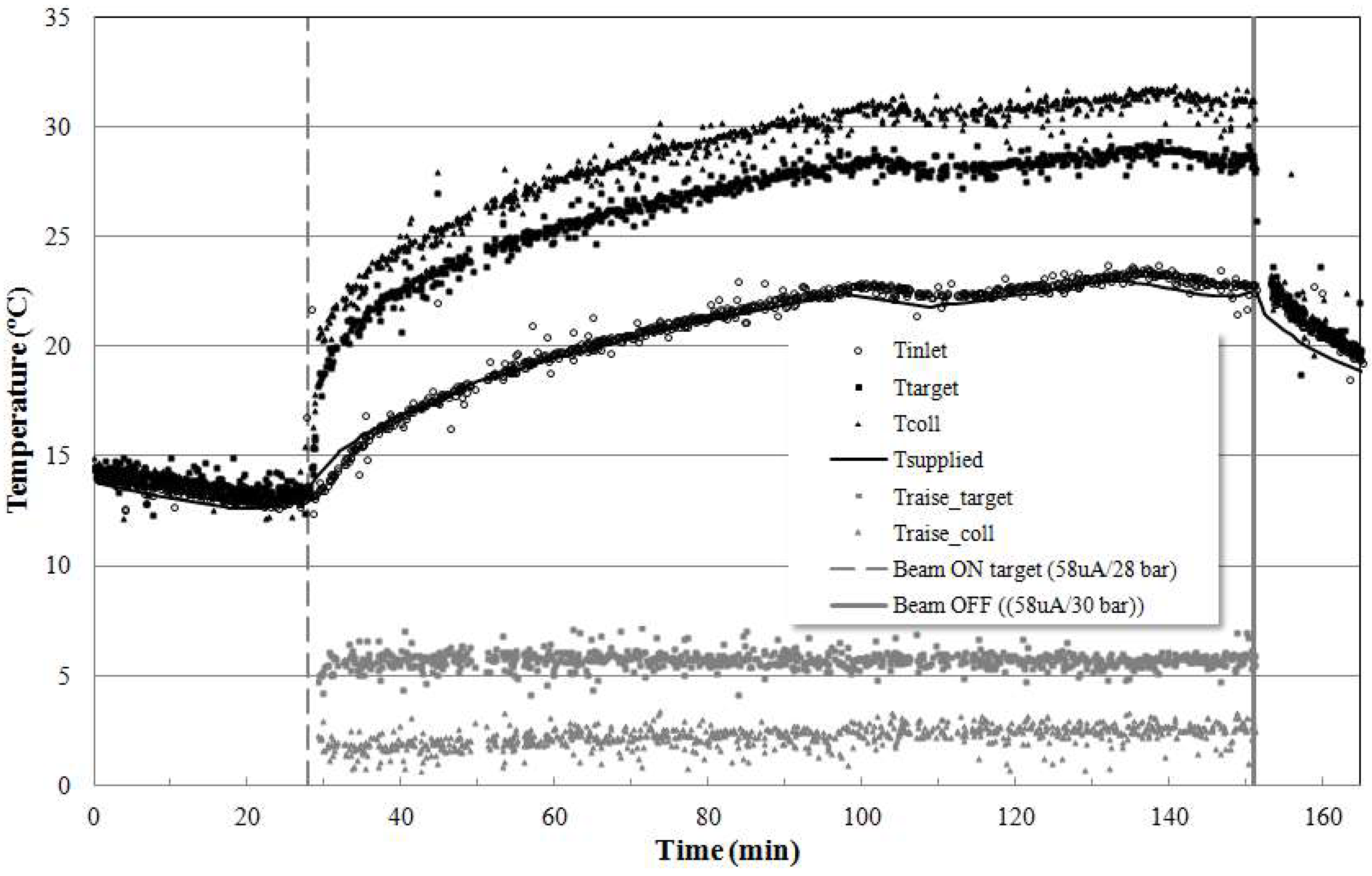
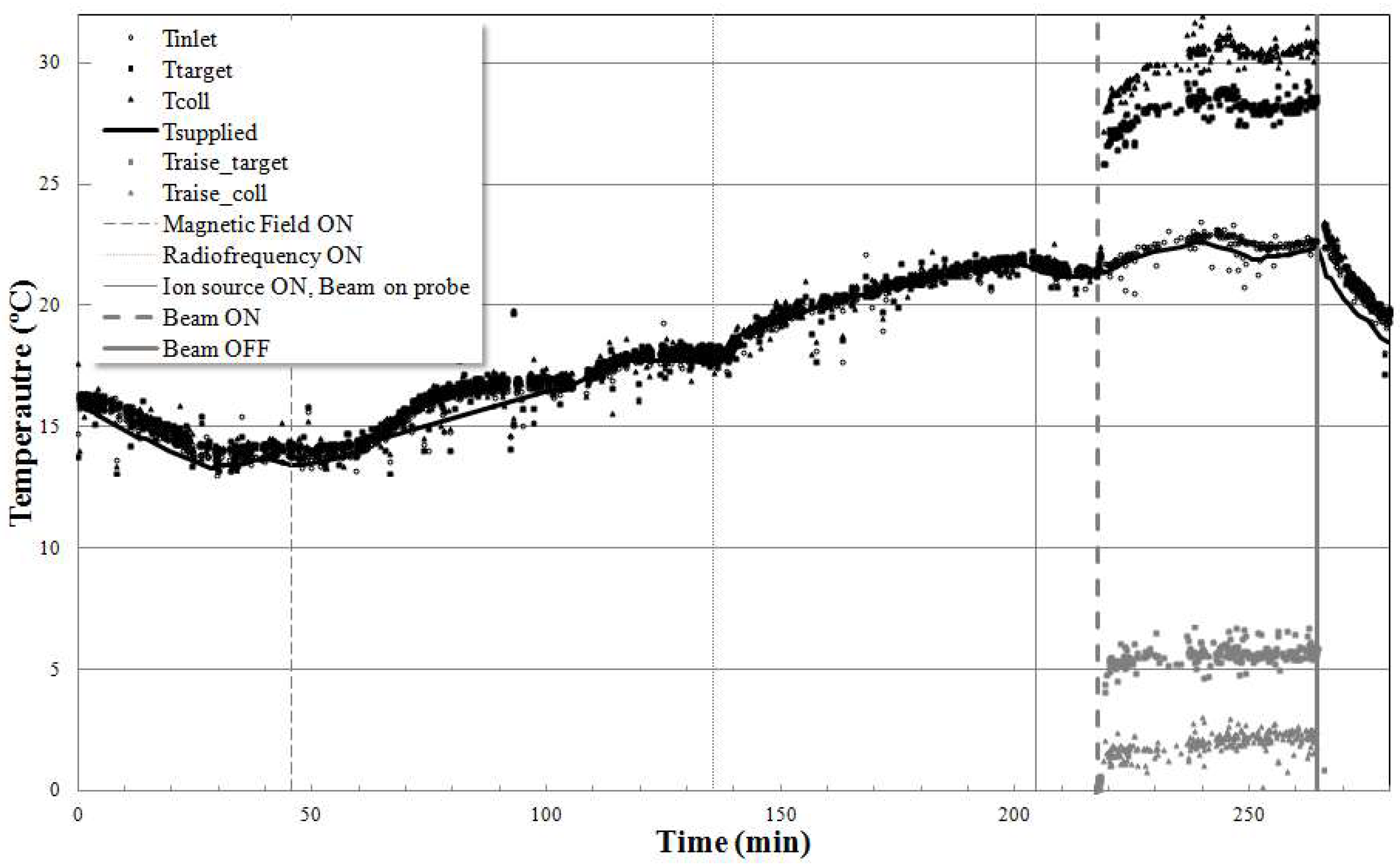
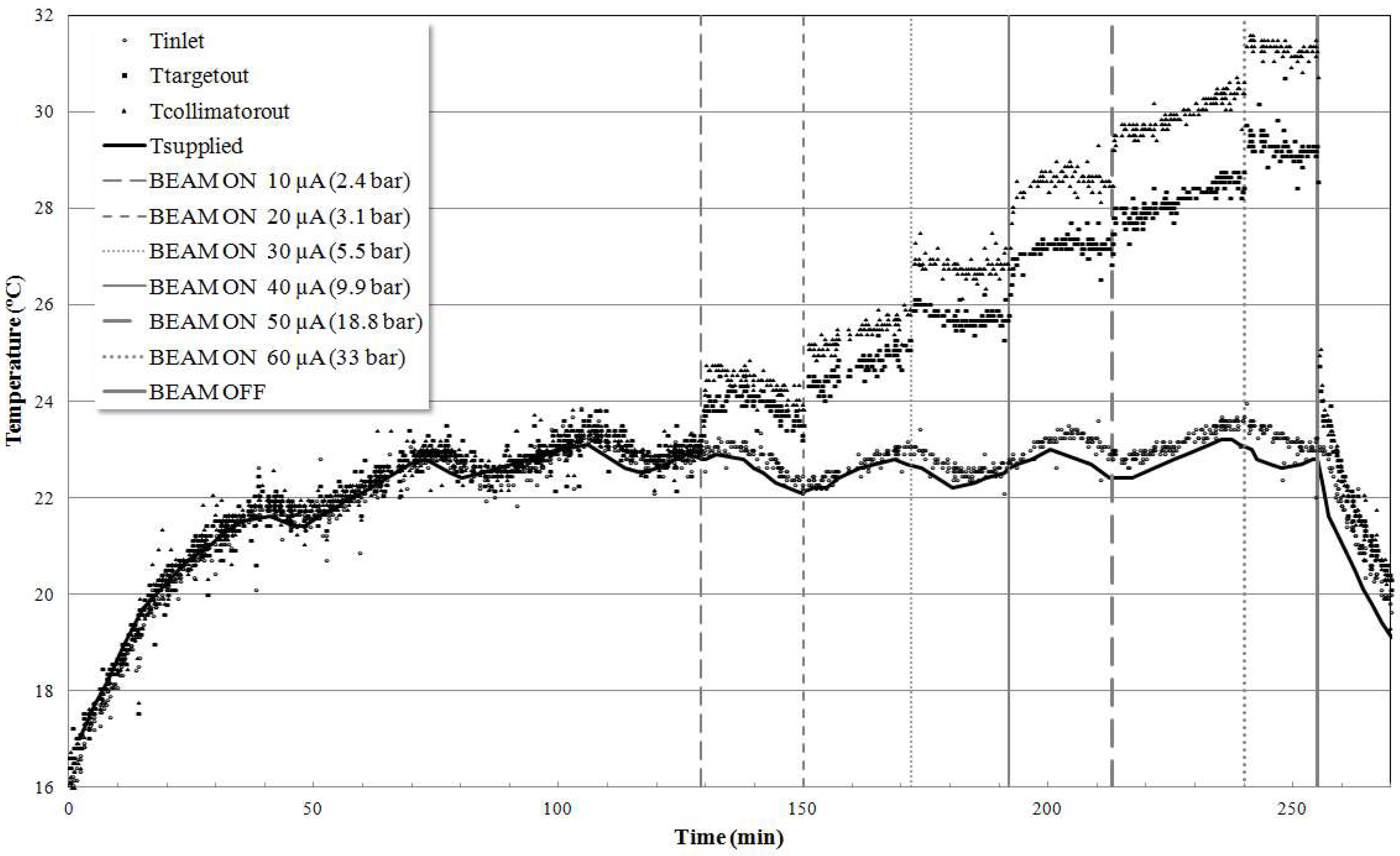
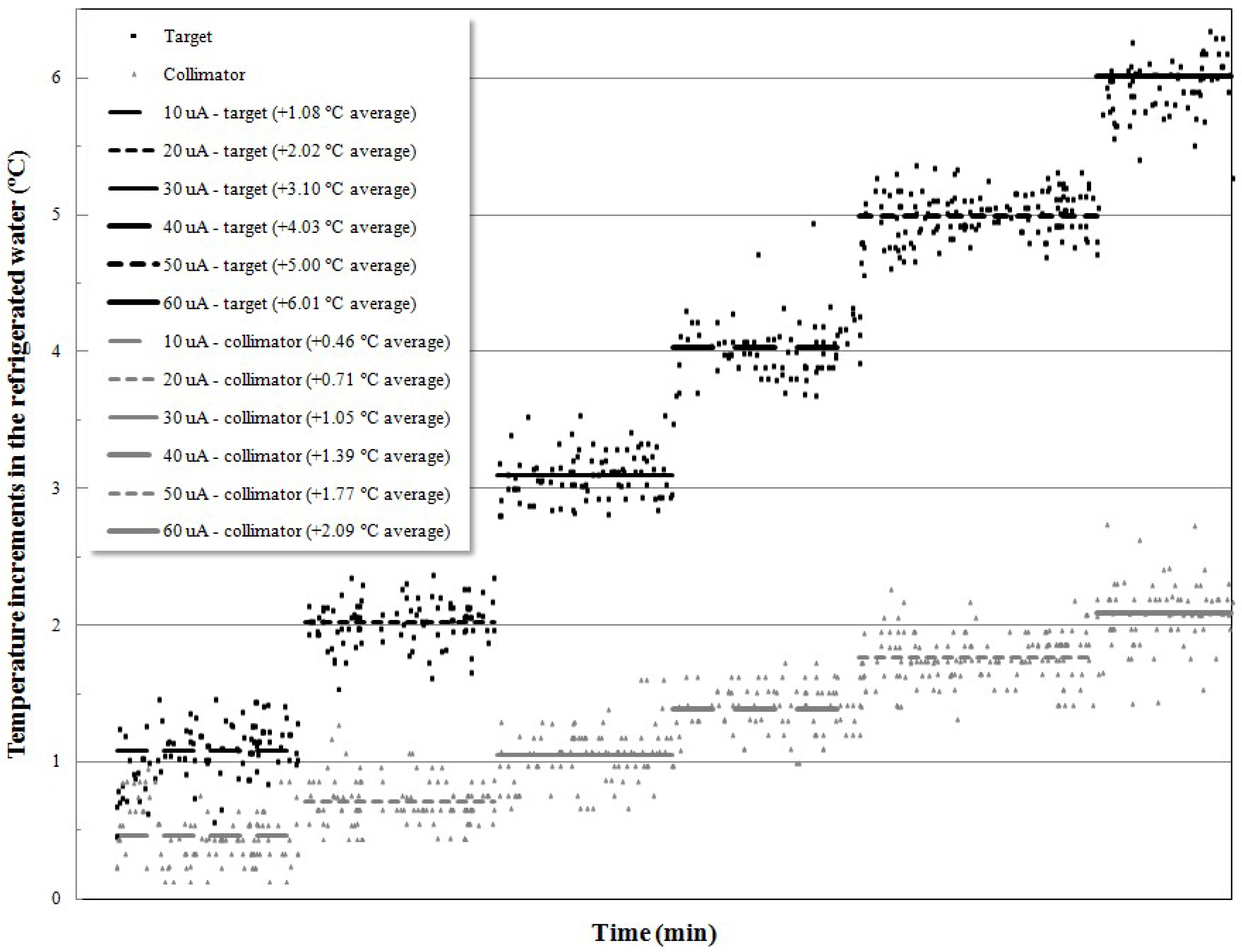
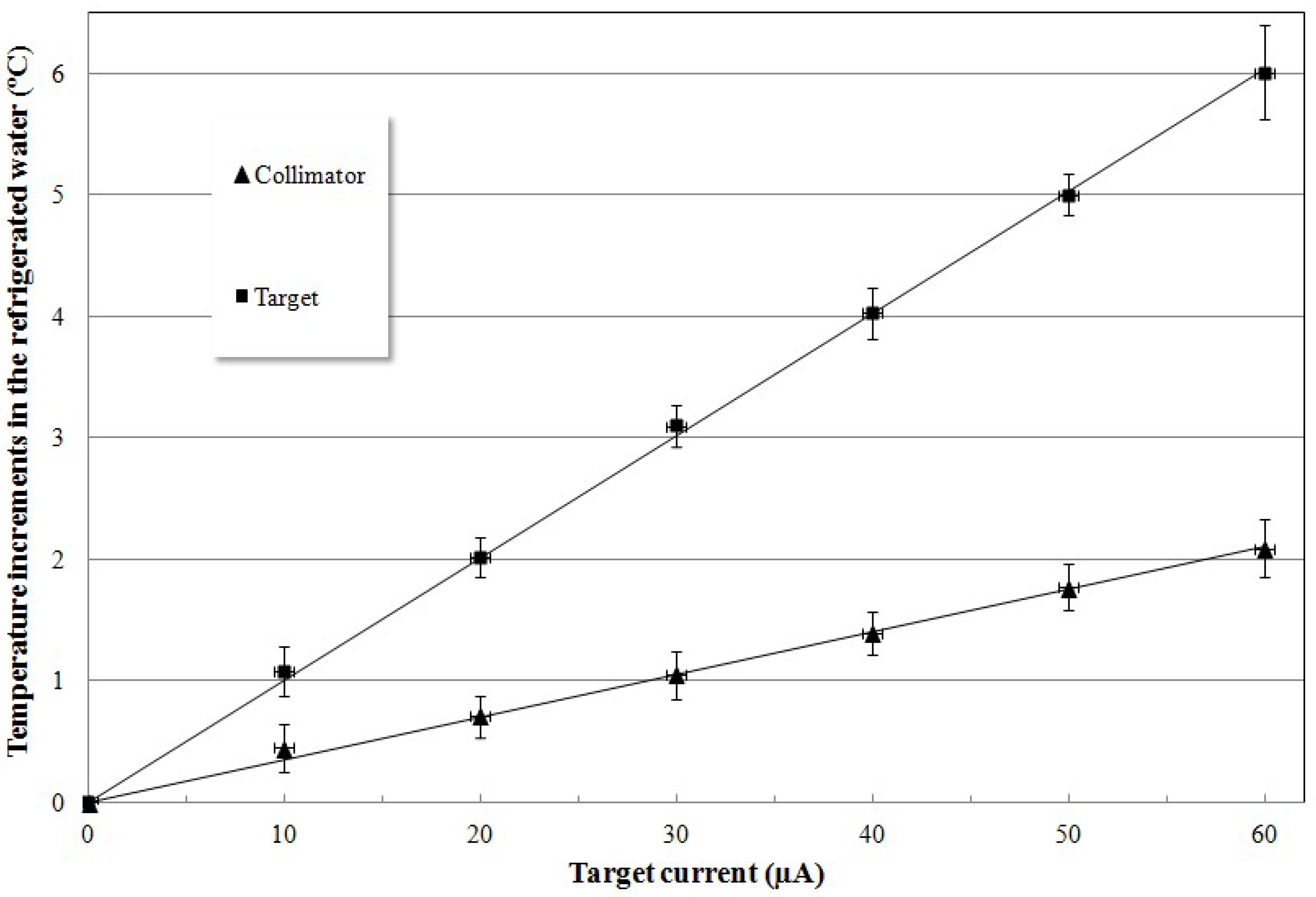
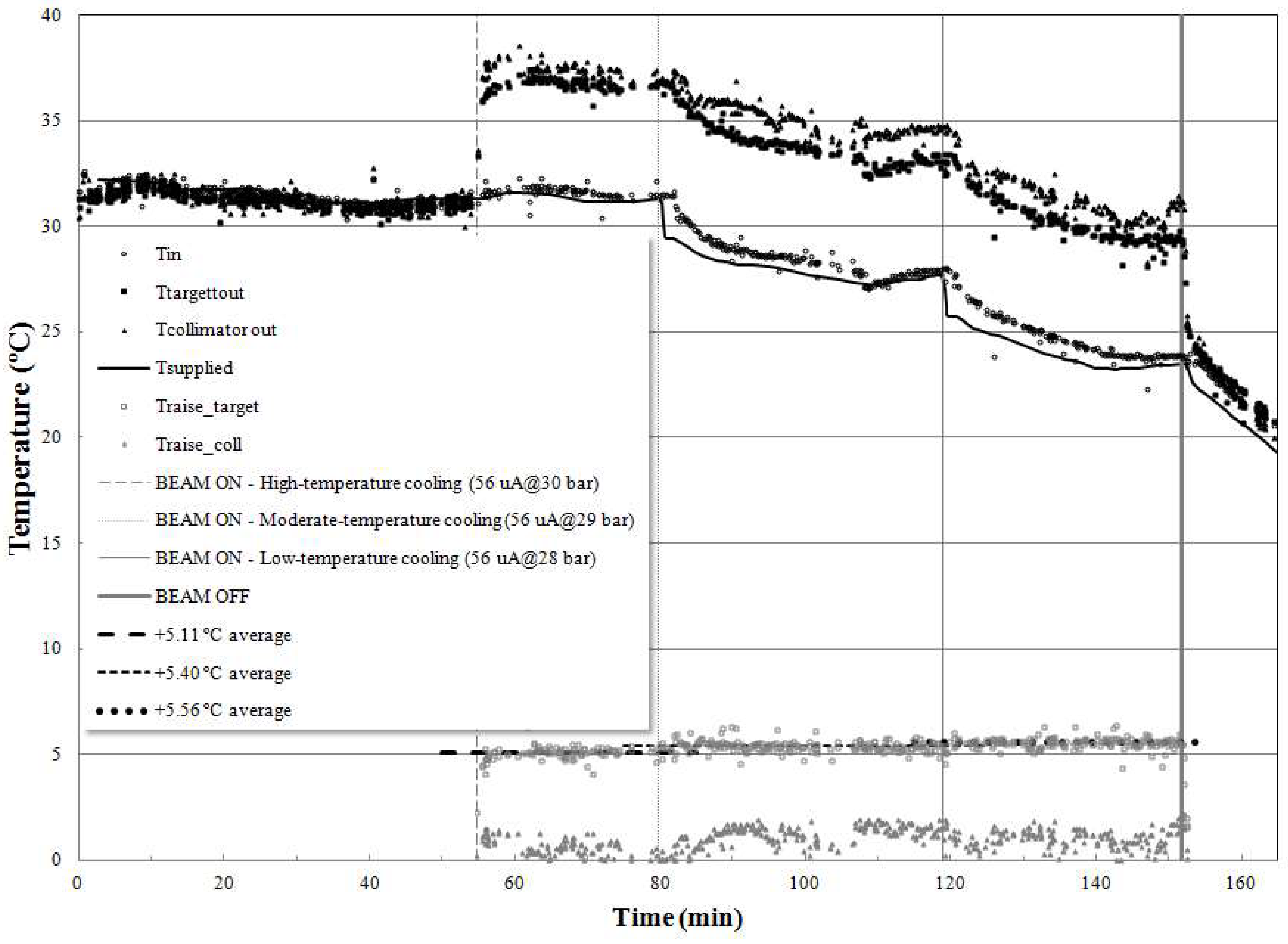
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nortier, F.M.; Stevenson, N.R.; Gelbart, W.Z. Investigation of the thermal performance of solid targets for radioisotope production. Nucl. Instrum. Methods 1995, A355, 236–241. [Google Scholar] [CrossRef]
- Heselius, S.-J.; Lindblom, P.; Solin, O. Optical studies of the influence of an intense ion beam on high-pressure gas targets. Int. J. Appl. Radiat. Isot. 1982, 33, 653–659. [Google Scholar] [CrossRef]
- Helus, F.; Uhlir, V.; Gasper, H. Contribution to cyclotron targetry: V. Measurement of the temperature in a gas target during irradiation. J. Radioanal. Nucl. Chem. 1996, 210, 233–235. [Google Scholar] [CrossRef]
- McCarthy, D.W.; Shefer, R.E.; Klinkowstein, R.E.; Bass, L.A.; Margeneau, W.H.; Cutler, C.S.; Anderson, C.J.; Welch, M.J. Efficient production of high specific activity 64Cu using a biomedical cyclotron. Nucl. Med. Biol. 1997, 24, 35–43. [Google Scholar] [CrossRef]
- Steyn, G.F.; Vermeulen, C. A Saturation Boiling Model for an Elongated Water Target Operating at a High Pressure during 18F Production Bombardments. Journal of Physics: Conference Series 2014. Available online: http://events.saip.org.za/getFile.py/access?contribId=329&sessionId=30&resId=1&materialId=paper&confId=14 (accessed on 9 May 2018).
- Steyn, G.F.; Vermeulen, C. Saturation conditions in elongated single-cavity boiling water targets. In Proceedings of the 15th international Worshop on Targetry and Target Chemistry—WTTC, Prague, Czech Republic, 18–21 August 2014; pp. 149–150. [Google Scholar]
- Gagnon, K.; Wilson, J.S.; Quarrie, S.A. Thermal modelling of a solid cyclotron target using finite element analysis: An experimental validation. In Proceedings of the 13th international Worshop on Targetry and Target Chemistry—WTTC, Roskilde, Denmark, 26–28 July 2010; p. 11. [Google Scholar]
- IBA, Louvain-la-Neuve, Belgium. Available online: https://www.iba-radiopharmasolutions.com/ (accessed on 20 June 2018).
- Devillet, F.; Geets, J.-M.; Ghyoot, M.; Kral, E.; Natergal, B.; Mooij, R.; Vosjan, M. Performance of IBA new conical shaped niobium [18O] water targets. In Proceedings of the 15th international Worshop on Targetry and Target Chemistry—WTTC, Prague, Czech Republic, 18–21 August 2014; pp. 145–148. [Google Scholar]
- SEMITEC Corporation, Japan. Available online: http://www.semitec.co.jp/ (accessed on 20 June 2018).
- USSENSOR CORP., USA. Available online: http://www.ussensor.com/ (accessed on 20 June 2018).
- Arduino. Available online: http://www.arduino.cc/ (accessed on 20 June 2018).
- CoolTermWin Software Package. Available online: http://freeware.the-meiers.org/ (accessed on 20 June 2018).
- Steinbach, J.; Guenther, K.; Loesel, E.; Grunwald, G.; Mikecz, P.; Ando, L.; Szelecsenyi, F.; Beyer, G.J. Temperature Course in small volume [18O] water targets for [18F] F-production. Appl. Radiat. Isot. 1990, 41, 753–756. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Do Carmo, S.J.C.; De Oliveira, P.M.; Alves, F. A Target-Temperature Monitoring System for Cyclotron Targets: Safety Device and Tool to Experimentally Validate Targetry Studies. Instruments 2018, 2, 9. https://doi.org/10.3390/instruments2030009
Do Carmo SJC, De Oliveira PM, Alves F. A Target-Temperature Monitoring System for Cyclotron Targets: Safety Device and Tool to Experimentally Validate Targetry Studies. Instruments. 2018; 2(3):9. https://doi.org/10.3390/instruments2030009
Chicago/Turabian StyleDo Carmo, Sergio J. C., Pedro M. De Oliveira, and Francisco Alves. 2018. "A Target-Temperature Monitoring System for Cyclotron Targets: Safety Device and Tool to Experimentally Validate Targetry Studies" Instruments 2, no. 3: 9. https://doi.org/10.3390/instruments2030009
APA StyleDo Carmo, S. J. C., De Oliveira, P. M., & Alves, F. (2018). A Target-Temperature Monitoring System for Cyclotron Targets: Safety Device and Tool to Experimentally Validate Targetry Studies. Instruments, 2(3), 9. https://doi.org/10.3390/instruments2030009