Magnetic Monopoles, Dyons and Confinement in Quantum Matter

Abstract

We show that magnetic monopoles appear naturally in granular quantum matter. Their condensation leads to a new state of matter, superinsulation, in which Cooper pairs are bound into purely electric pions by strings of electric flux. These electric flux tubes, the dual of Abrikosov vortices, prevent the separation of charge–hole pairs, thereby causing an infinite resistance, even at finite temperatures, the dual behaviour of superconductors. We will discuss the electric Meissner effect, asymptotic freedom and their measurements and describe the recent direct detection of a linear, confining potential by dynamic relaxation experiments. Finally, we consider dyons, excitations carrying both a magnetic and an electric charge, and show that a condensate of such dyons leads to a possible solution of the mysteries of the pseudogap state of high-$T_c$ cuprates.

1. Magnetic Monopoles

There is nothing preventing magnetic monopoles (for a review, see, e.g., [1]) in classical physics, where only the equations of motion matter. The Maxwell equations can be easily modified to include a four-current $m^{\mu }$ of magnetic charges g,

$$\begin{array}{c}{\partial }_{\mu }{F}^{\mu \nu }=qe{j}^{\nu },\\ {\partial }_{\mu }{\tilde{F}}^{\mu \nu }=g{m}^{\nu },\end{array}$$

(1)

where ${\tilde{F}}^{\mu \nu }=(1/2){ϵ}^{\mu \nu \alpha \beta }{F}_{\alpha \beta }$ is the dual electromagnetic field tensor (we use natural units $c=1$, $\hslash =1$, ${\epsilon }_0=1$, Greek letters for space-time indices and Einstein summation over equal Greek indices). The only reason they were not originally included is because they were not observed.

Things change in quantum mechanics, where off-shell paths weighted by an action become important. Most important, this action must have a local formulation in terms of the fields. To formulate a local action for electromagnetic fields, one must introduce the gauge potential $A_{\mu }$, and here the problems begin, because magnetic monopoles would seem to entail a singularity in the configuration of this gauge potential, the so-called Dirac string [1], see Figure 1. This is an infinitely thin and long solenoid bringing in the magnetic flux from infinity. Dirac realised, however, that this singularity is a coordinate singularity if the product of electric and magnetic charges is quantised,

$$qeg=2\pi n,n\in \mathbb{Z}.$$

(2)

Wherever the singularity lies, it can be displaced away by a gauge transformation so that local physics does not depend on its presence. Because of the Dirac quantisation condition, the string cannot be observed, even by non-local Aharonov–Bohm experiments.

Even if it can be placed along any desired line, the unavoidable presence of the Dirac string requires that, to admit magnetic monopoles, the gauge group has to be the compact group $U\left(1\right)$ rather than the non-compact group $\mathbb{R}$. The two are locally identical but not globally, because $U\left(1\right)$ is isomorphic to the circle $S^1$. The remaining singularity at the monopole location, the open end of the Dirac string, is the consequence of the compactness of the gauge group. There are two ways to get rid of this point singularity: either one considers $U\left(1\right)$ as the lowest-energy surviving symmetry after the spontaneous symmetry breaking of a larger compact group, such as the grand-unified groups (GUTs) $SU\left(5\right)$ or $SO\left(10\right)$, or one hides the $U\left(1\right)$ monopole singularities amidst the vertices of a lattice. The former monopoles were proposed by ‘t Hooft and Polyakov as possible solitons in GUTs [1]; they have energies of O(${10}^{16}$) Gev, so large that they could have been produced only in the big bang. Despite 40 years of dedicated searching, however, they have never been detected. The U(1) lattice monopoles were proposed by Polyakov [2,3] as examples of how compact $U\left(1\right)$ gauge theories change their character due to a proliferation of magnetic monopoles. This, however, has led to a proposal that such purely $U\left(1\right)$, much lighter monopoles are concretely realised in granular, inhomogeneous quantum materials which, after all, are microscopically akin to lattices [4].

2. Effective Electromagnetic Action for Quantum Materials

We shall consider charged quantum matter coupled to electromagnetic fields. By ”quantum” we mean here “very low temperatures”, where quantum effects become dominant. Such a quantum material is described by a generic Euclidean action (for a review, see, e.g., [5])

$$S=S_{\mathrm{matter}}+i\int d^{4}x{A}_{\mu }{j}_{\mu }+\frac{1}{4{\left(qe\right)}^2}\int d^{4}x{F}_{\mu \nu }{F}_{\mu \nu }.$$

(3)

To incorporate a finite temperature T, one has to restrict the Euclidean time integration to a finite domain of length $1/k_{B}T$ with periodic (for bosons) or antiperiodic (for fermions) boundary conditions. For simplicity of presentation, here we shall only consider zero temperature.

One can now integrate out the matter degrees of freedom to obtain the electromagnetic effective action for the material,

$$S_{\mathrm{eff}}\left(A_{\mu }\right)=\frac{1}{4{\left(qe\right)}^2}\int d^{4}x{F}_{\mu \nu }{F}_{\mu \nu }+S_{\mathrm{quantum}}\left(A_{\mu }\right).$$

(4)

This can be performed exactly if the matter action is quadratic or loop-by-loop in perturbation theory in the more generic case of higher-order interactions. This expression is the quantum equivalent of the familiar free energy of statistical mechanics, with the Maxwell term playing the role of internal energy and the quantum corrections $S_{\mathrm{quantum}}$ playing the role of the entropy. When this is performed at finite temperatures, the so-obtained expression takes into account both the corrections due to quantum and thermal fluctuations. The electromagnetic response of the material is then encoded in the induced current

$$j_{\mathrm{ind}}^{\mu }\left(x\right)=-i\frac{\delta }{\delta A_{\mu }\left(x\right)}{S}_{\mathrm{eff}}.$$

(5)

As a concrete example, let us mention the effective action for superconductors, whose derivative expansion is dominated by a photon mass term,

$$S_{\mathrm{eff}}=\frac{1}{2{\lambda }_{\mathrm{London}}^2}\int d^{3}x{A}_{\mu }{A}_{\mu }+\cdots$$

(6)

so that the electromagnetic response is given, after rotation back to Minkowski space-time, by the induced current

$${\mathbf{j}}_{\mathrm{ind}}=\frac{-1}{{\lambda }_{\mathrm{London}}^2}\mathbf{A}$$

(7)

which is the compact form of the familiar London equations

$$\begin{array}{c}\mathrm{rot}\mathbf{j}=\frac{-1}{{\lambda }_{\mathrm{London}}^2}\mathbf{B}\\ \frac{\partial }{\partial t}\mathbf{j}=\frac{1}{{\lambda }_{\mathrm{London}}^2}\mathbf{E}\end{array}$$

(8)

3. Compact Effective Action of Granular Insulators

The long-distance effective action for generic insulators is the usual Maxwell term

$$S_{\mathrm{eff}}=\frac{1}{4e_{\mathrm{eff}}^2}\int d^{4}x{F}_{\mu \nu }{F}_{\mu \nu },$$

(9)

with an effective, renormalised coupling constant $e_{\mathrm{eff}}$ and a velocity of light $v=1/\sqrt{\epsilon \mu }<1$. In this formulation, the action is formulated on an isotropic Euclidean space with “time" coordinate $x_0=vt$ and also, correspondingly, rescaled gauge potentials $A_0\to A_0/v$, which is easier for computations. To recover the physical (Euclidean) space-time, one has to make all velocities v explicit. Things change, however, when we are dealing with granular materials, with matter restricted to localised droplets of typical spacing ℓ (which we henceforth set to $\ell =1$ for simplicity of presentation), the prototype being fabricated Josephson junction arrays (for a review, see [6]). In this case, the effective action becomes a discrete “lattice model” with a lattice spacing $v{\ell }_0=\ell =1$ in the Euclidean time direction. There are two possible cases, the naïve non-compact discretisation of (9),

$$S_{\mathrm{eff}}=\frac{1}{4e_{\mathrm{eff}}^2}\sum _x{F}_{\mu \nu }{F}_{\mu \nu },$$

(10)

or the compact model [2,3]

$$S_{\mathrm{eff}}=\frac{1}{2e_{\mathrm{eff}}^2}\sum _{x,\mu \nu }\left(1-\cos \left(F_{\mu \nu }\right)\right),$$

(11)

which, of course, coincide up to the second order in the fields but which have very different global properties.

The compact model can also be formulated in the Villain representation by introducing integer plaquette variables $M_{\mu \nu }\in \mathbb{Z}$ constituting new degrees of freedom over which one has to sum in the partition function,

$$S_{\mathrm{eff}}=\frac{1}{4e_{\mathrm{eff}}^2}\sum _x\left(F_{\mu \nu }-2\pi M_{\mu \nu }\right)\left(F_{\mu \nu }-2\pi M_{\mu \nu }\right).$$

(12)

Even if the naïve variables $F_{\mu \nu }$ satisfy the Bianchi identity $d_i{\tilde{F}}_{i0}=\mathrm{div}{e}_{\mathrm{eff}}\mathbf{B}=0$ (with $d_i$ lattice derivatives), there is nothing to guarantee that the same equation is obeyed by the integer fields $M_{\mu \nu }$. Indeed, it can be easily shown that the overall compact magnetic field admits magnetic monopoles [2,3],

$$\frac{1}{e_{\mathrm{eff}}}{d}_i\left({\tilde{F}}_{i0}-2\pi {\tilde{M}}_{i0}\right)=\frac{2\pi }{e_{\mathrm{eff}}}{\delta }_{\mathbf{x},{\mathbf{x}}_0}.$$

(13)

Correspondingly, the entire compact effective action for granular insulators can be formulated as

$$S_{\mathrm{eff}}=\frac{1}{4e_{\mathrm{eff}}^2}\sum _x{F}_{\mu \nu }{F}_{\mu \nu }+\frac{{\pi }^2}{e_{\mathrm{eff}}^2}\sum _x{m}_{\mu }\frac{1}{-{\nabla }_4^2}{m}_{\mu },$$

(14)

where

$$m_{\mu }=d_{\nu }{\tilde{M}}_{\mu \nu }=\frac{1}{2}{ϵ}^{\mu \nu \alpha \beta }{d}_{\nu }{M}_{\alpha \beta },$$

(15)

is the topologically conserved four-current of magnetic monopoles and ${\nabla }_4^2$ is the (finite difference) Laplacian in four Euclidean dimensions. The first is the naïve non-compact action, and the second term describes the magnetic monopoles due to the compact nature of the effective action in granular quantum insulators. It remains to be determined what is the effect of such monopoles on the macroscopic properties of these materials. Before doing so, however, let us focus on some specific examples where they appear.

4. Quantum Wires and Josephson Junction Chains

Although there can be no magnetic monopoles in 1D, let us focus, for a moment, on the simplest example of granular quantum material, quantum wires, which can be modelled as Josephson junction chains (for a review, see [7]), see Figure 2. Essentially, these are materials made of superconducting islands arranged along a line (the vertices of a 1D lattice), each characterised by a phase of their angles, with Josephson coupling $E_J$, while, in the limit $C_0>>C$, the dual charge dynamics are well approximated by point interactions of the strength $E_C=2e/C$ on the islands and possible quantum tunnelling between the islands (the links of the 1D lattice) when the phases are aligned. For these materials, the matter action for the phases $\varphi$ (after integrating out the charges) is the compact global $O\left(2\right)$ model [3] in two Euclidean dimensions,

$$S_{\mathrm{matter}}=\frac{\kappa }{\pi }\sum _x\left(d_{\mu }\varphi +2\pi n_{\mu }\right)\left(d_{\mu }\varphi +2\pi n_{\mu }\right),$$

(16)

where $\kappa =\sqrt{{\pi }^2{E}_J/2E_C}$ and $n_{\mu }\in \mathbb{Z}$ are integers defined on the links of the lattice.

Upon minimally coupling the current $d_{\mu }\varphi$ to the gauge field $A_{\mu }$, the non-compact model ($n_{\mu }=0$) leads to the effective electromagnetic action

$$S_{\mathrm{eff}}=\frac{\pi }{4\kappa }\sum _x{A}_{\mu }{A}_{\mu },$$

(17)

showing that the quantum wire is superconducting. The effective action for the full compact model (16), however, is

$$\begin{array}{ccc}{S}_{\mathrm{eff}}& & =\frac{\pi }{4\kappa }\sum _x{A}_{\mu }{A}_{\mu }+4\pi \kappa \sum _{x}s\frac{1}{-{\nabla }_2^2}s,\hfill \\ s& & =-{ϵ}^{\mu \nu }{d}_{\mu }{n}_{\nu },\hfill \end{array}$$

(18)

where the integers $s_x$ on the 2D lattice represent instantons [3], i.e., solitons of the Euclidean action, which correspond to quantum tunnelling events in Minkowski space-time (for a review, see, e.g., [8]). These are events in which one of the phases makes a flip by a $2\pi$ angle and are, correspondingly, called quantum phase slips [9], see Figure 2. Because the potential for the quantum phase-slips instantons is logarithmic, they form a 2D Coulomb gas (for a review, see [10]) and thus undergo the famed Berezinskii–Kosterlitz–Thouless (BKT) transition [10]. Only for $\kappa <1$, they can proliferate. In this case, when a current is applied to the quantum wire, the balance between instantons of different chiralities is broken, and this imbalance turns the originally superconducting wire into a metal by creating a resistance [7].

5. The Superconductor-to-Superinsulator Transition in Quantum Films

Instantons due to the compactness of the effective action induce a superconductor-to-metal transition in 1D. While this is very interesting, it is not yet a dramatic effect. Things change in 2D, where the same type of instantons can induce an entire new state of matter.

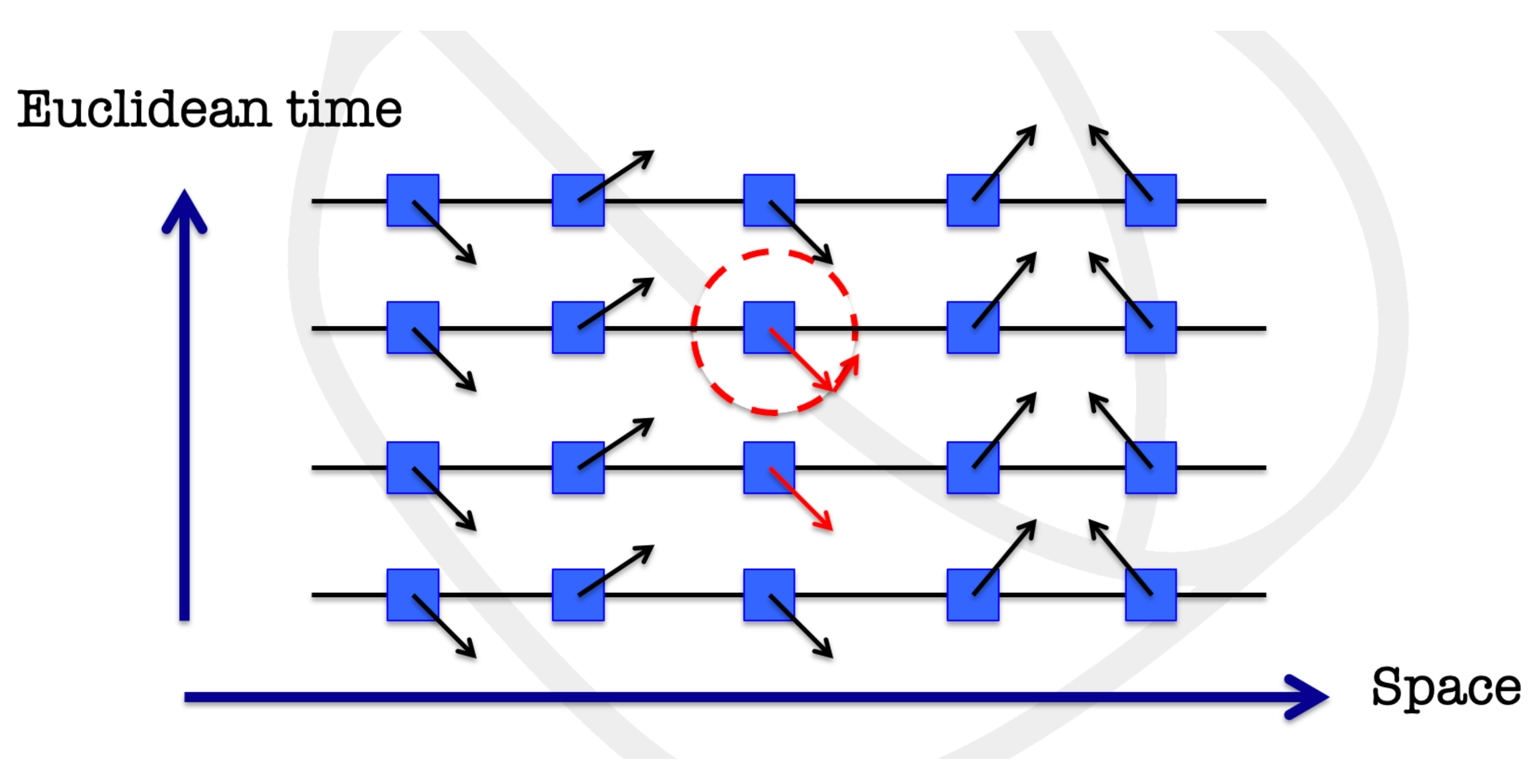
Let us thus consider the 2D generalisation of quantum wires, granular films which, correspondingly, can be modelled as Josephson junction arrays and we shall call “quantum films”. The main difference with respect to the 1D case is the presence of a new type of excitation: when the phases make a non-trivial circulation of an integer multiple of $2\pi$ on neighbouring droplets, we have a vortex in between, as shown in Figure 3. These, however, are not Abrikosov vortices; they have no normal state core and are thus Josephson-type vortices, like the ones in the XY model [10]. As a consequence, their dissipation is negligible, and they behave as dual excitations to charges. Moreover, they experience Aharonov–Casher phases when they go around charges or Aharonov–Bohm phases in the opposite case. These mutual statistics interactions, moreover, are the dominant ones at long distances and, as shown by Wilczek [11], they can be represented in a local form by introducing two fictitious gauge fields $a_{\mu }$ and $b_{\mu }$ with a mixed topological Chern–Simons action [12].

When the dynamical terms admitted by symmetry are also included, the matter action for the charge currents $Q_{\mu }$ and the vortex currents $M_{\mu }$ is given by [13,14,15]

$$S_{\mathrm{matter}}=\sum _{x}i\frac{1}{2\pi }{a}_{\mu }{ϵ}^{\mu \alpha \nu }{\partial }_{\alpha }{b}_{\nu }+\frac{1}{4e_v^2}{f}_{\mu \nu }{f}_{\mu \nu }+\frac{1}{4e_q^2}{g}_{\mu \nu }{g}_{\mu \nu }+i{a}_{\mu }{Q}_{\mu }+i{b}_{\mu }{M}_{\mu },$$

(19)

where $f_{\mu \nu }$ and $g_{\mu \nu }$ are the field strengths of the two gauge fields $a_{\mu }$ and $b_{\mu }$, respectively, and

$$\begin{array}{ccc}\hfill e_q^2& & =O\left(\frac{e^2}{2\pi d}\right)=8E_C,\hfill \\ \hfill e_v^2& & =O\left(\frac{\pi d}{e^2{\lambda }_L^2}\right)=4{\pi }^2{E}_J,\hfill \end{array}$$

(20)

are the typical electric and magnetic energy scales, respectively, with d the film thickness and ${\lambda }_L$ the bulk London penetration depth. The second equalities refer to the exact results for the modelling as Josephson junction arrays, as in the case of 1D chains [13,15].

Three phases can arise in the above model as a consequence of the competition between the charge and vortex orders. The first is the usual global superconducting order. The other two phases are a Bose metal phase [13], when both the charges and vortices are frozen by statistical interactions in the bulk and only 1D edge channels conduct, in which quantum phase slips induce a resistance as explained above, and a superinsulating phase, when vortices proliferate [13,16,17]. The effective electromagnetic action for the superinsulating phase is obtained by coupling to the electromagnetic gauge field $A_{\mu }$, setting $Q_{\mu }=0$ and integrating out the two fictitious gauge fields and is exactly the 2D version of (12) with

$$e_{\mathrm{eff}}^2\approx \frac{1}{\kappa },$$

(21)

with $\kappa =e_v/e_q$.

Actually, there is one important point to stress. The physics of thin films remains 2D only up to a screening length $O\left(d\epsilon \right)$, where $\epsilon$ is the relative dielectric permittivity of the insulating normal state (for a derivation, see [18]); at larger scales, the electric field lines “exit" the plane. The quantum transition to a superinsulating state thus corresponds to the limit $d\to 0$, $\epsilon \to \infty$ with a fixed screening length. In this limit, the effective Coulomb interaction coupling $e_{\mathrm{eff}}^2=e^2{\lambda }_L/d$ becomes very large. Because $v\to 0$ in the limit $\epsilon \to \infty$, it is only the electric components of the effective action that matter

$$S_{\mathrm{eff}}=\frac{1}{2e_{\mathrm{eff}}^2}\sum _{x,i}{\left(F_i+2\pi M_i\right)}^2=\frac{1}{2e_{\mathrm{eff}}^2}\sum _{x,i}{E}_i^2+\frac{2{\pi }^2}{e_{\mathrm{eff}}^2}\sum _{x,i}{m}_x\frac{1}{-{\nabla }_2^2}{m}_x,$$

(22)

where $F_{\mu }=(1/2){ϵ}_{\mu \alpha \beta }{F}_{\alpha \beta }$ is the dual electromagnetic tensor in 2D, $E_i$ denote the components of the electric field and $m=d_i{M}_i$ represent again the instantons due to the compactness of the model. When modelling quantum films as Josephson junction arrays, it is directly this purely electric action that is obtained [15].

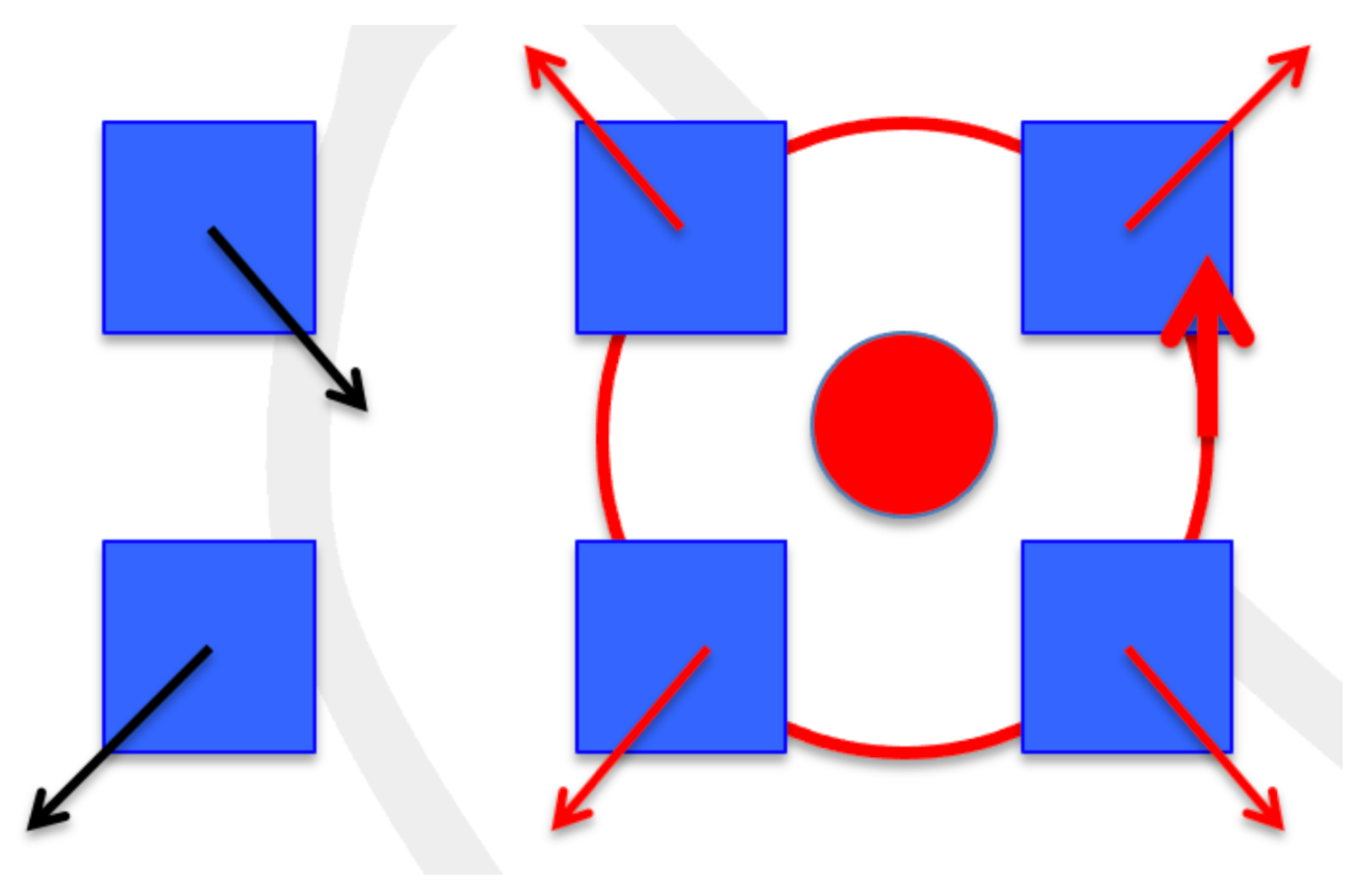
From the point of view of a 3D Euclidean space, the vector $F_{\mu }$ is simply the magnetic field, the component $F_0$ being its component in the “z-direction”, identified with the Euclidean time. The integers $M_0$ represent, correspondingly, the vortices. Because of the gauge invariance of the $b_{\mu }$ fictitious gauge field in (19), we have $d_{\mu }{M}_{\mu }=0$ and, thus, in Minkowski space-time coordinates,

$$m=d_i{M}_i=-d_t{M}_0.$$

(23)

i.e., the instantons are non-relativistic magnetic monopoles that interpolate between the one-vortex and zero-vortex sector (or the other way around when $M_0$ is negative), as shown in Figure 4. These magnetic monopole instantons are the 2D generalisation of quantum phase slips. Because their interaction, due to their non-relativistic nature, is again logarithmic, they proliferate only for a large effective coupling, i.e., for $\kappa <1$, when Coulomb interactions dominate magnetic ones.

6. Confinement and Superinsulation

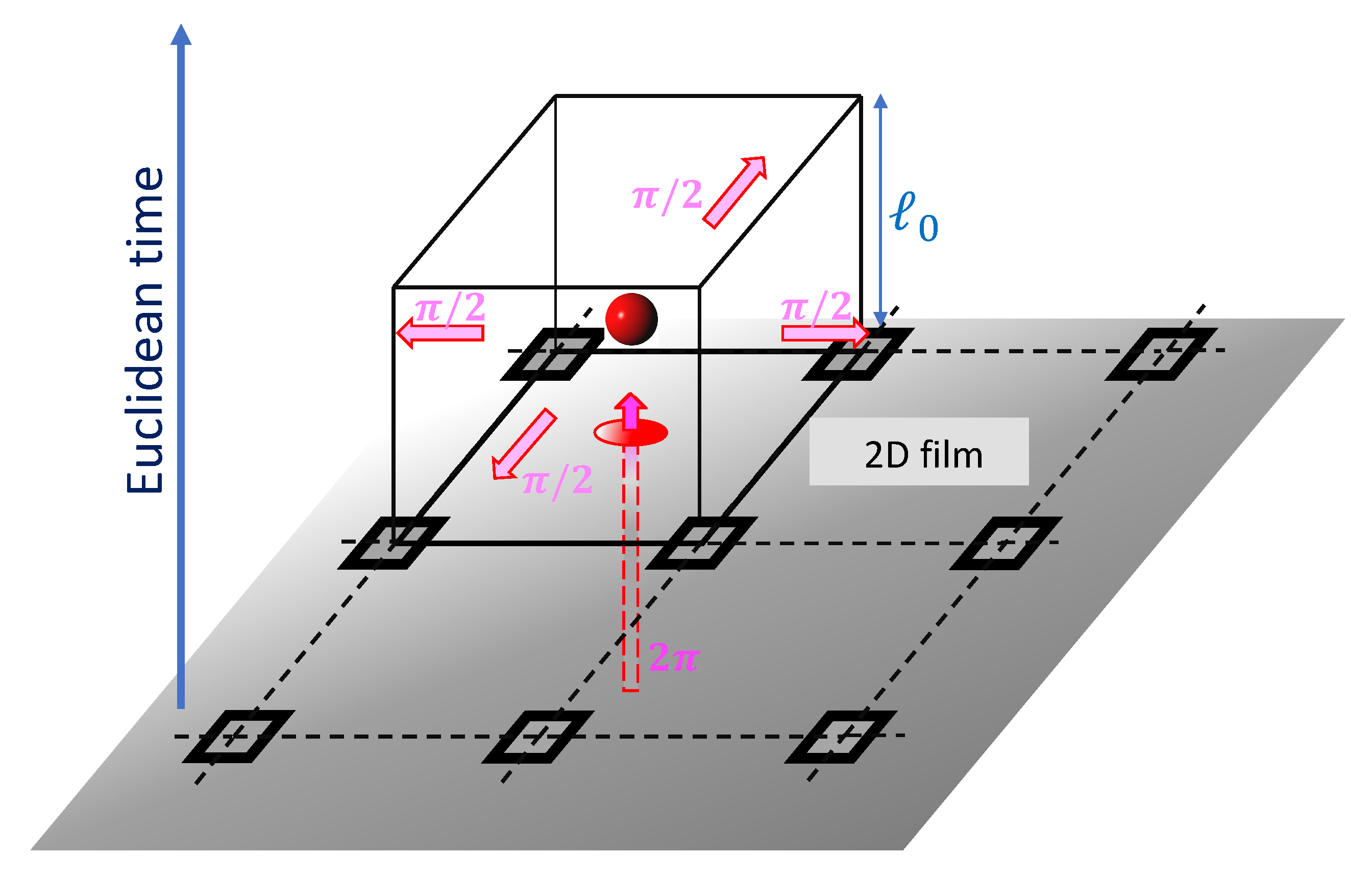
Granularity, intrinsic or emergent, is not confined to lower dimensions. The same type of granular structure has been recently detected in bulk superconductors [19]. In 3D, the core-less vortices sketched in Figure 3 become 1D extended objects, and there is nothing preventing these core-less vortices ending in magnetic monopole–antimonopole pairs. Two situations are possible: either the vortices have tension, as sketched in Figure 5, panel (a), and then we have only short magnetic dipoles, or they are tensionless, as sketched in Figure 5, panel (b), in which case there is no energy price in extending them from one monopole to infinity and then back to its antimonopole, i.e., they become Dirac strings and the system contains free magnetic monopoles.

Under certain conditions, these magnetic monopoles can Bose condense [20]. When this happens, applied electric fields are shielded by dissipationless magnetic monopole currents and can penetrate only in thin electric flux tubes, the dual of Abrikosov vortices. The crucial difference with respect to vortices, however, lies in the fact that electric flux tubes can end on charge–hole pairs inside the sample. These excitations are the purely electric equivalent of strong interaction pions, with Cooper pairs playing the role of quarks; the electric flux tubes joining the charge–hole pairs go under the name of confining strings [21,22]. They induce an attractive linear potential $V\left(r\right)=\sigma r$ between charges and holes at a separation r, where $\sigma$ is the string tension. Strings have a typical width $w={\lambda }_{\mathrm{el}}$ given by the range of the screened Coulomb interaction and a typical length scale $d_s=1/\sqrt{\sigma }$ determined by the string tension. Electric ± charges cannot be separated on distances larger than this scale for temperatures and applied voltages below critical values $T_c$ and $V_{\mathrm{c}1}$, respectively, which is the phenomenon of confinement known from the strong interaction. As a consequence, the resistance is strictly infinite for $T<T_c$ and $V<V_{\mathrm{c}1}$. This new state of matter, induced by the condensation of magnetic monopoles, is called superinsulation, the dual mirror of superconductivity. It was originally predicted in [13] and rediscovered independently 12 years later in [16]. Superinsulation has by now been experimentally detected in TiN, NbTiN, InO and NbSi films. 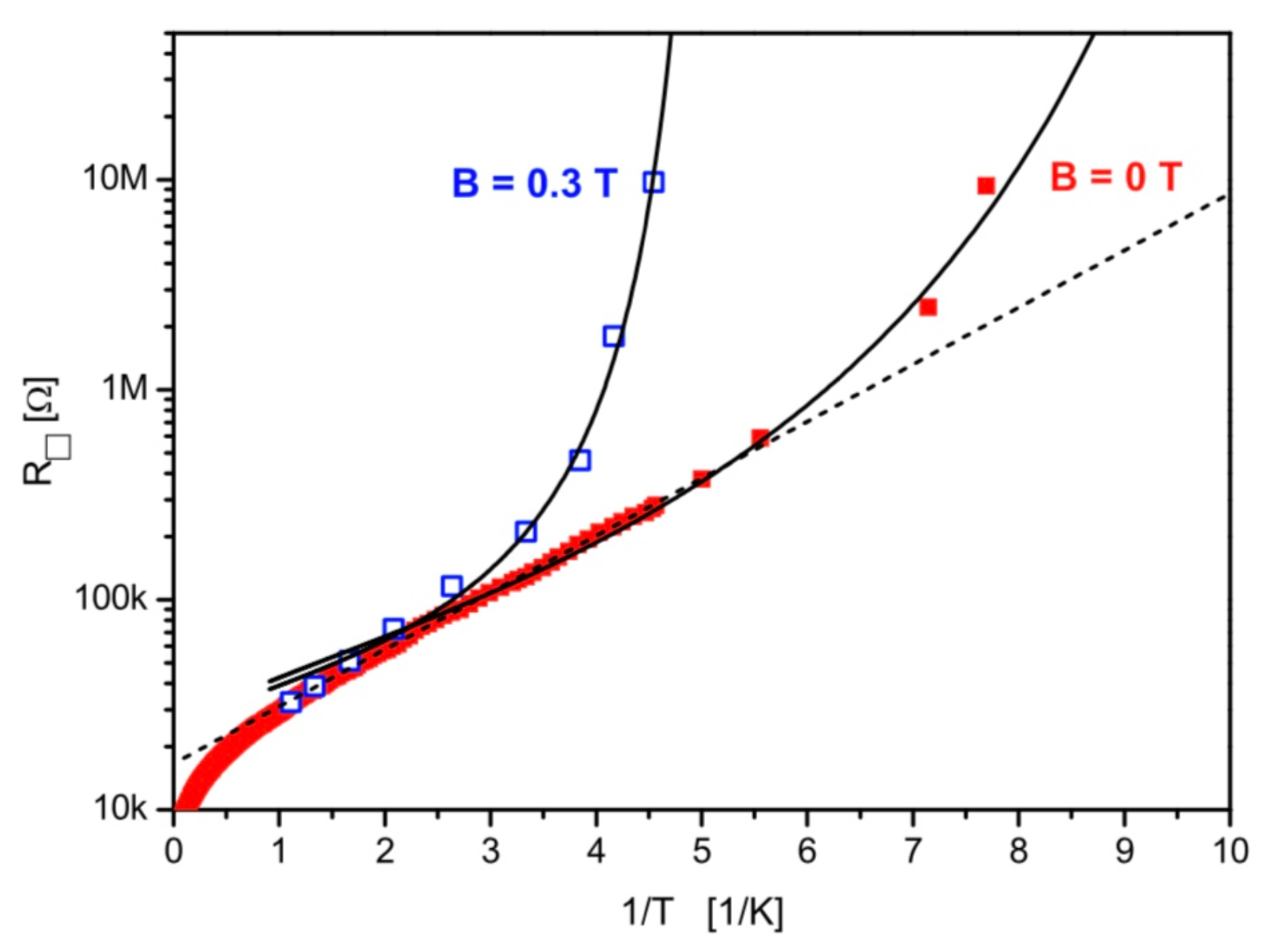Figure 6 shows the logarithmic plot of the sheet resistance of a NbTiN film as a function of $1/T$. The dashed straight line corresponds to the usual activated behaviour of an insulator. The data show an hyperactivated behaviour fitting the divergent BKT behaviour [10], with $T_c=0.062{}^{\circ }K$ without an applied magnetic field and with $T_c=0.175{}^{\circ }K$ at $B=0.3$ T.

The superinsulating state is characterised by the electric London equations [18] (in Minkowski space-time)

$$\begin{array}{ccc}\hfill {\partial }_t\mathbf{m}& & =\frac{v^2{\mathrm{\Lambda }}^2}{2\pi e_{\mathrm{eff}}}\mathbf{B},\hfill \\ \hfill \nabla \wedge \mathbf{m}& & =\frac{{\mathrm{\Lambda }}^2}{2\pi e_{\mathrm{eff}}}\mathbf{E},\hfill \end{array}$$

(24)

where $\mathrm{\Lambda }$ is the inverse length scale determined by the magnetic condensate density. Combined with the (static) dual Ampère law

$$\nabla \wedge \mathbf{E}=-\frac{2\pi }{e_{\mathrm{eff}}}\mathbf{m},$$

(25)

one obtains the Meissner screening of electric fields,

$$\begin{array}{ccc}& & \left({\nabla }^2-\frac{1}{{\lambda }_{\mathrm{el}}^2}\right)\mathbf{E}=0,\hfill \\ & & {\lambda }_{\mathrm{el}}=\frac{e_{\mathrm{eff}}}{\mathrm{\Lambda }}.\hfill \end{array}$$

(26)

The low-energy excitations of superinsulators are neutral pions, open strings with a charge–hole pair at the ends. If the applied voltage is smaller than the critical voltage $V_{\mathrm{c}1}=(\sigma L/2e)$, with L the sample length, the effective string tension

$${\sigma }_{\mathrm{eff}}=(\sigma -2eV/L),$$

(27)

remains positive and the pion size is smaller than the sample size, i.e., no electric field penetrates the sample and no current passes: this is the Meissner state of superinsulators. When the applied voltage exceeds the lower critical value $V_{\mathrm{c}1}$ but is still smaller than the upper critical value $V_{\mathrm{c}2}$, the pion size exceeds the sample size, and electric fields and currents penetrate in the form of flux tubes reaching from one end to the other of the sample: this is the mixed state of superinsulators. Finally, if the applied voltage is above the upper critical value $V_{\mathrm{c}2}$, the superinsulation is dynamically destroyed in favour of normal insulating behaviour. 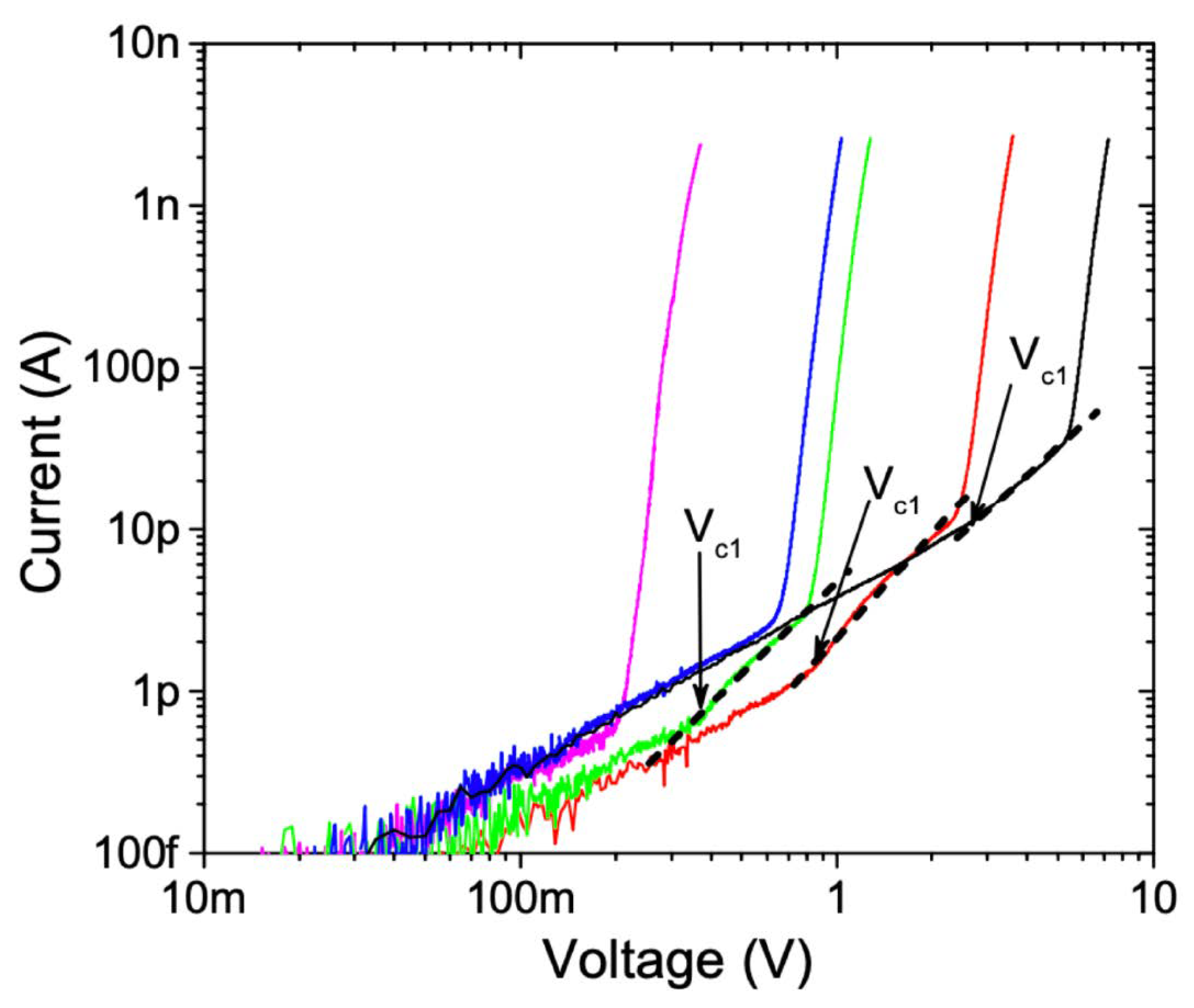The two critical electric fields ${\mathbf{E}}_{\mathrm{c}1}$ and ${\mathbf{E}}_{\mathrm{c}2}$ corresponding to the voltages $V_{\mathrm{c}1}$ and $V_{\mathrm{c}2}$ are independent of the system size and are dual to the two critical magnetic fields of type II superconductors (for a review, see [23]). A consequence of the two critical voltages is that two kinks appear in the I(V) curves of superinsulators, separating the three possible regimes. These are clearly seen in experiments [24], as shown in Figure 7. When the sample size $L\to \infty$, these curves vanish identically in the whole region $V<V_{\mathrm{c}1}$.

Strong interaction pions are very small and tightly bound, and their interior has never been observed directly, only via high-energy collision experiments. The electromagnetic interaction, however, is much weaker and thus we expect much larger electric pions. As we have seen above, the pion size can be increased by “stretching” the string with an external voltage. However, alternatively, we could try to measure the interior of the electric pions simply by performing experiments on samples so small that an entire pion does not fit on them. In this case, we expect an asymptotic freedom regime in which the string is “loose” but the Coulomb interaction is still screened on much smaller scales. In this regime, the Cooper pairs and holes in the pion interior are essentially free and, thus, we expect a metallic saturation of the resistance on such small samples. This is exactly what is seen in experiments [24], as shown in Figure 8. When the sample size is sufficiently decreased, the hyperactivated resistance behaviour goes over directly to a metallic saturation, showing that charges become free on such small samples. Note that this asymptotic freedom behaviour has nothing to do with the corresponding one of non-Abelian gauge theories, which describes their ultraviolet behaviour. This asymptotic freedom behaviour arises technically in a sine-Gordon model and describes the infrared fixed point of the theory.

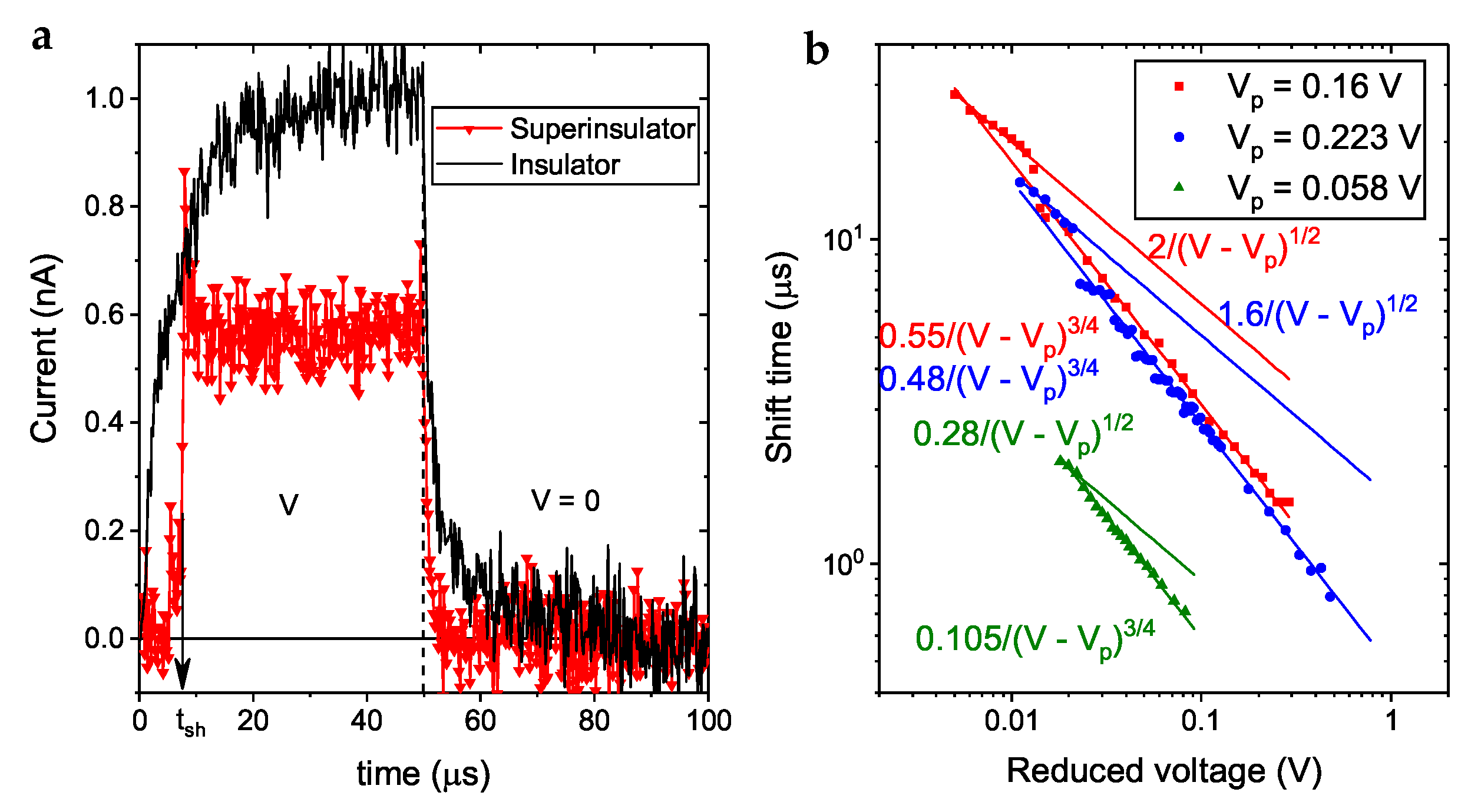
The potential binding ± charges in the superinsulating state can be measured directly by dynamic relaxation experiments [25], in which a voltage pulse is suddenly applied to the material. Figure 9 shows the result of such experiments for a NbTiN quantum film. In Panel (a), one can see the different responses of the normal insulator at 300 mK and the superinsulator at 20 mK. In the normal insulator, the current immediately starts to smoothly increase to its steady-state value. In the superinsulator, instead, there is a delay $t_{\mathrm{sh}}$ before the current jumps to its steady state. In panel (b), the scaling of this delay is shown as a function of the reduced voltage $(V-V_{\mathrm{c}1})$ (with $V_{\mathrm{c}1}$ denoted $V_p$ here).

The two kinks in the I(V) curves are clearly reflected in two different critical exponents $\mu$ in the scaling

$$t_{\mathrm{sh}}\propto {\left(V-V_{\mathrm{c}1}\right)}^{-\mu }.$$

(28)

The value $\mu =1/2$ corresponds to a jump from the Meissner state to the mixed state, and the value $\mu =3/4$ to a jump from the Meissner state to the normal insulating state. Let us consider the former. For such jumps, the effective tension (27) becomes negative and corresponds to a constant total repulsive force $F=(2eV/L-2e{V}_{\mathrm{c}1}/L)$, where we have used the value $V_{\mathrm{c}1}=(\sigma L/2e)$ of the lower critical voltage. This corresponds to a constant centre of mass acceleration $a=(4e/mL)(V-V_{\mathrm{c}1})$ for a charge–hole pair that is pulled apart by the applied voltage, where m is the mass of a Cooper pair. The equation of motion for the relative coordinate has the solution

$$r\left(t\right)=\frac{2e}{mL}\left(V-V_{\mathrm{c}1}\right)t^2.$$

(29)

The current starts to pass when this relative coordinate reaches the value L, i.e., after a shift time

$$t_{\mathrm{sh}}=\sqrt{\frac{m{L}^2}{2e}}{\left(V-V_{\mathrm{c}1}\right)}^{-1/2}.$$

(30)

This shows that the observed value $\mu =1/2$ of the dynamic critical exponent (28) is a direct confirmation of the confining linear potential in the superinsulating state.

7. Dyons, Oblique Confinement and the Pseudogap State

In 3D, the effective electromagnetic action may also contain a topological contribution, the so-called $\theta$ term of axion electrodynamics [26],

$$S_{\theta }=\frac{i\theta }{16{\pi }^2}\int d^{4}x{\tilde{F}}_{\mu \nu }{F}_{\mu \nu }=\frac{i\theta }{32{\pi }^2}\int d^{4}x{F}_{\mu }{ϵ}^{\mu \nu \alpha \beta }{F}_{\alpha \beta }=\frac{i\theta }{4{\pi }^2}\int d^{4}x\mathbf{E}·\mathbf{B},$$

(31)

where $\theta$ is an angle with periodicity $2\pi$ for fermionic systems and $4\pi$ for bosonic ones [27]. In the presence of the $\theta$-term, magnetic monopoles also acquire an electric charge $\theta /2\pi$ [28], and the effective electromagnetic action (12) is modified to

$$S_{\mathrm{eff}}=\frac{1}{4e_{\mathrm{eff}}^2}\sum _x\left(F_{\mu \nu }-2\pi M_{\mu \nu }\right)\left(F_{\mu \nu }-2\pi M_{\mu \nu }\right)+i\frac{\theta }{2\pi }{A}_{\mu }{m}_{\mu }.$$

(32)

Such charged magnetic monopoles are called “dyons”. A dyon condensate realises oblique confinement, [29] a state of matter in which the condensate carries both electric and magnetic quantum numbers and all excitations with quantum numbers not in the condensate are confined by strings [30]. This state is characterised by the oblique London equations [18] (in Minkowski space-time)

$$\begin{array}{ccc}\hfill {\partial }_t\mathbf{m}& & =\frac{v^2{\mathrm{\Lambda }}^2}{2\pi e_{\mathrm{eff}}}\left(\mathbf{B}+\frac{e_{\mathrm{eff}}^2}{2\pi v}\frac{\theta }{2\pi }\mathbf{E}\right),\hfill \\ \hfill \nabla \wedge \mathbf{m}& & =\frac{{\mathrm{\Lambda }}^2}{2\pi e_{\mathrm{eff}}}\left(\mathbf{E}-\frac{v{e}_{\mathrm{eff}}^2}{2\pi }\frac{\theta }{2\pi }\mathbf{B}\right).\hfill \end{array}$$

(33)

Combining these with the (static) Ampère laws

$$\begin{array}{ccc}\hfill \nabla \wedge \mathbf{B}& & =\frac{e_{\mathrm{eff}}\theta }{2\pi v}\mathbf{m},\hfill \\ \hfill \nabla \wedge \mathbf{E}& & =-\frac{2\pi }{e_{\mathrm{eff}}}\mathbf{m},\hfill \end{array}$$

(34)

one obtains the oblique screening length [30]

$${\lambda }_{\mathrm{theta}}=\frac{4\pi }{e_{\mathrm{eff}}\mathrm{\Lambda }}\frac{1}{\sqrt{{\left(\frac{4\pi }{e_{\mathrm{eff}}^2}\right)}^2+{\left(\frac{\theta }{\pi }\right)}^2}}.$$

(35)

In the strong coupling limit $e_{\mathrm{eff}}^2\gg 1$, the screening length becomes

$${\lambda }_{\theta }\to \frac{4{\pi }^2}{\theta e_{\mathrm{eff}}}\frac{1}{\mathrm{\Lambda }}.$$

(36)

Correspondingly, the gap $\mathrm{\Delta }=v/{\lambda }_{\theta }$ becomes dominated by the topological term and diverges. Indeed, in the strong coupling limit, the dyon condensate becomes a topological ground state [31] in which the only surviving gapless excitations are the boundary modes of a magnetic charge $2\pi /qe$, an electric charge $(\theta /2\pi )qe$ and fractional statistics [32] $\theta /2\pi$. This has subsequently led the authors of [33] to confuse a dyon condensate with a topological insulator. It is not an insulator though. Below a critical temperature, the bulk excitations are not gapped charges, as in an insulator, but neutral strings [30]. As a consequence, the dyon condensate has not the activated bulk resistance typical of topological insulators, but its resistance is infinite in an entire finite-temperature regime, i.e., it is a superinsulator, an oblique superinsulator.

We have seen how magnetic monopoles emerge naturally in granular, inhomogeneous quantum materials. One prominent example of a class of such materials is high-$T_c$ cuprates (particularly in the underdoped regime), in which inhomogeneities play a crucial role [34,35] and in which superconductivity has been established to arise in exactly such a percolation network as we have described above [36]. Various models were proposed for the origin of such local condensates [37,38]. This has led us to propose that the mysterious pseudogap state [39] of these high-$T_c$ materials is a dyon condensate with $\theta =2\pi$ [31]. This solves easily and simultaneously the puzzles of this mysterious ground state.

The presence of the $\theta$-term, of course, explains the observed magnetoelectric Kerr effect [40]. For $\theta =2\pi$, the boundary dyons have an electric charge $2e$ (for $q=2$) and fermionic statistics. This explains two more phenomena: first of all, the observed charge $2e$ of the carriers in the pseudogap state [41], and secondly, the $T^2$-resistance of these carriers [42]. Indeed, the charge carriers are boundary fermions living on a Chalker–Coddington network [43] where they are protected from scattering and localisation by symmetry and thus form a perfect Fermi liquid. Nematicity [44] is also an immediate consequence of a magnetic charge. The parent insulator phase of cuprates at extremely low doping is a 2D square spin Heisenberg antiferromagnet. If the mobile excitations carry only an electric charge, the corresponding symmetry is thus $C_4$. If, however, they carry a magnetic charge too, then the symmetry is broken down to diagonal $C_2$. Finally, the T-linear resistance of the field-exposed normal state in the overdoped regime [45] is easily obtained if the superconducting dome is posited as a coexistence phase of a normal charge condensate with the dyon condensate. When a sufficiently strong magnetic field destroys the charge condensate, the resulting bulk Cooper pairs are turned into fermions by statistical transmutation induced by the magnetic monopoles in the dyon condensate (for a review, see [18]). These fermions scatter with the collective fluctuations of the dyon condensate (playing a role analogous to phonons), inducing a T-linear resistance down to a Bloch–Grüneisen temperature which is much lower than typical Debye temperatures. Recently, an experiment was devised to confirm or disprove this topological model of the pseudogap state [46].

8. The Role of Disorder

The superconductor-to-superinsulator transition (with a possible Bose metal phase in between) is due to the competition of two quantum orders, a magnetic one and an electric one, and is driven by the effective strength of Coulomb interactions with respect to magnetic ones. This can be tuned by the film thickness, magnetic field, gate voltages or, indeed, disorder [47]. Contrary to what is sometimes suggested in the literature [48,49], however, disorder is irrelevant in the renormalisation sense; it has no influence on the nature of the quantum phases around the superconductor-to-superinsulator transition. From a theoretical point of view, the ground states of these phases can be obtained exactly in the absence of disorder [50]. The recent experiment [25] finally proves that the loss of carrier mobility is due to the linear potential induced by magnetic monopole instantons and not by localisation by disorder. Note that many phenomena typically associated with disorder, such as the breaking of thermalisation and ergodicity, are known to arise as a consequence of linear confining potentials in the complete absence of disorder [51,52].