Destructive Interference of the Superconducting Subband Condensates in the Quasi-1D Multigap Material Nanostructures
Abstract
1. Introduction
2. Materials and Methods
3. Results
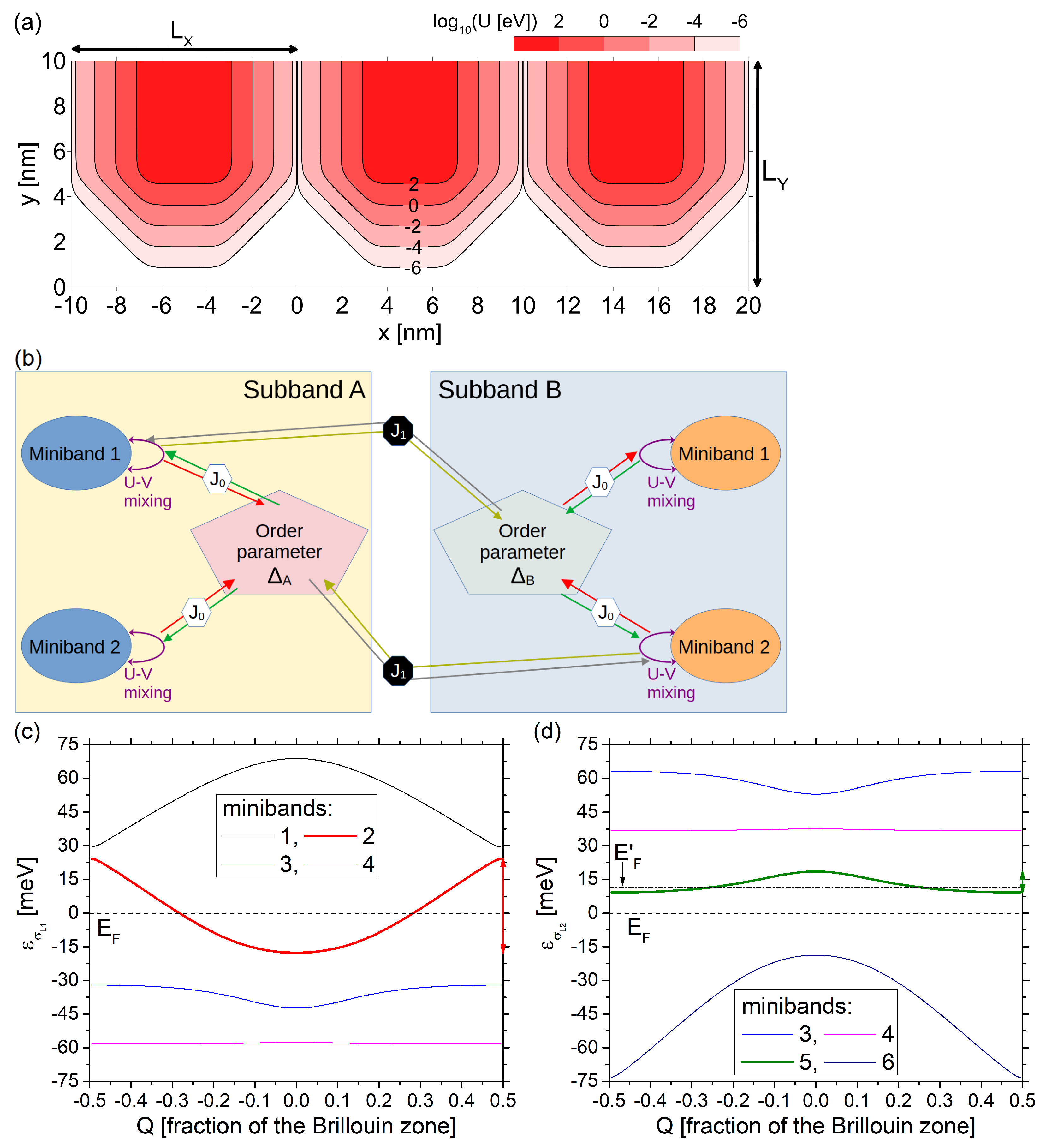
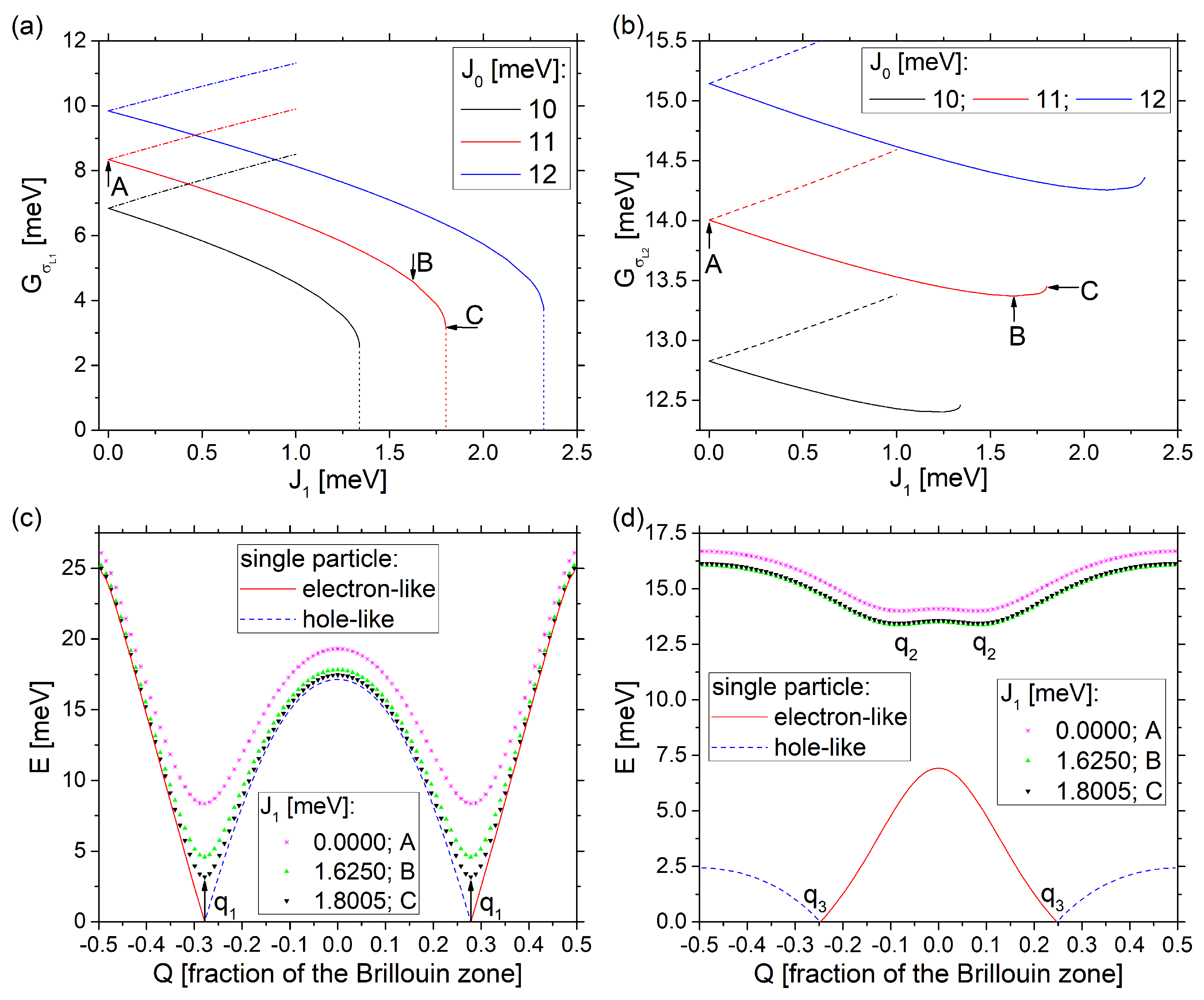
3.1. The Double-Metallic System
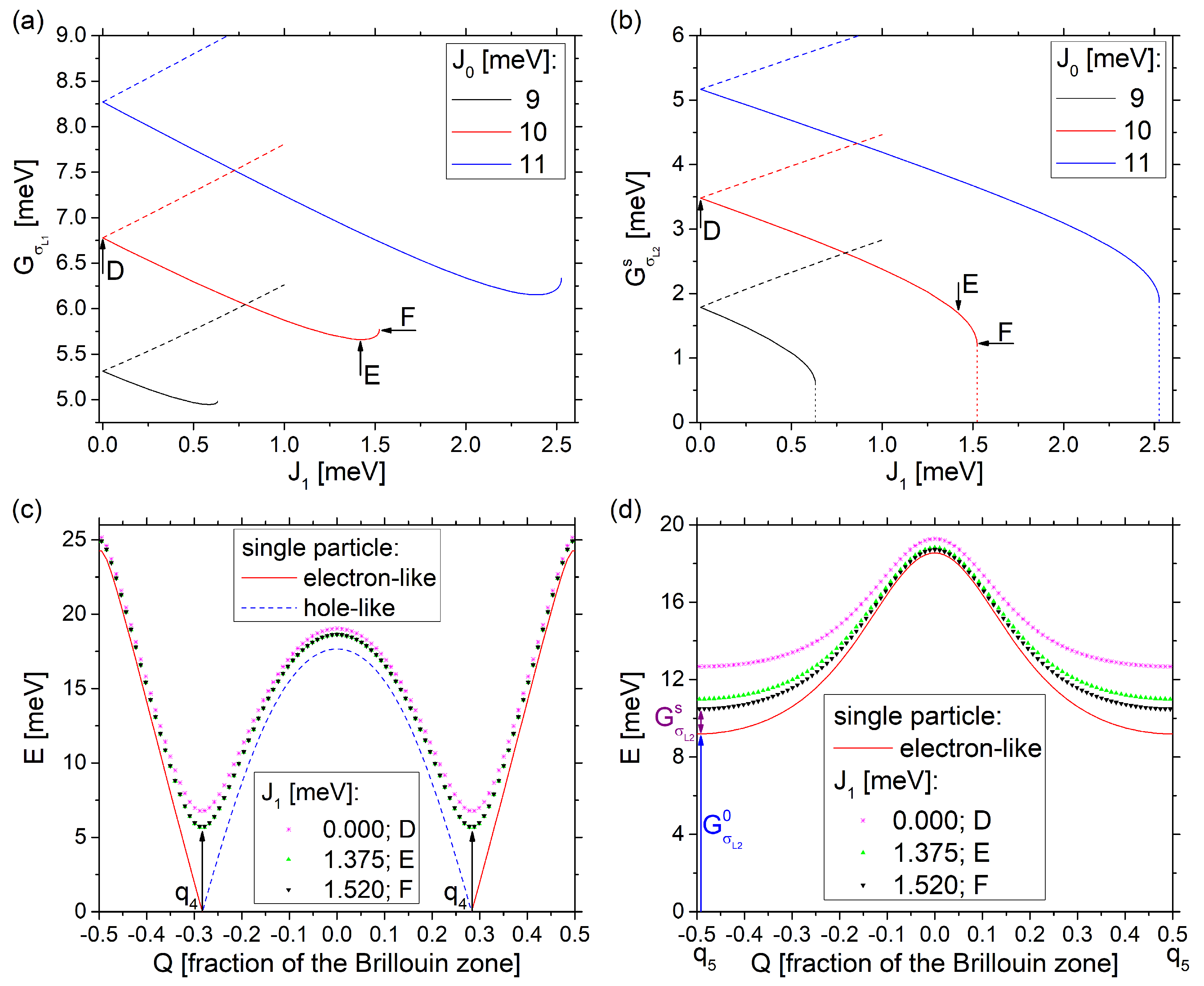
3.2. The Metallic-Insulating System
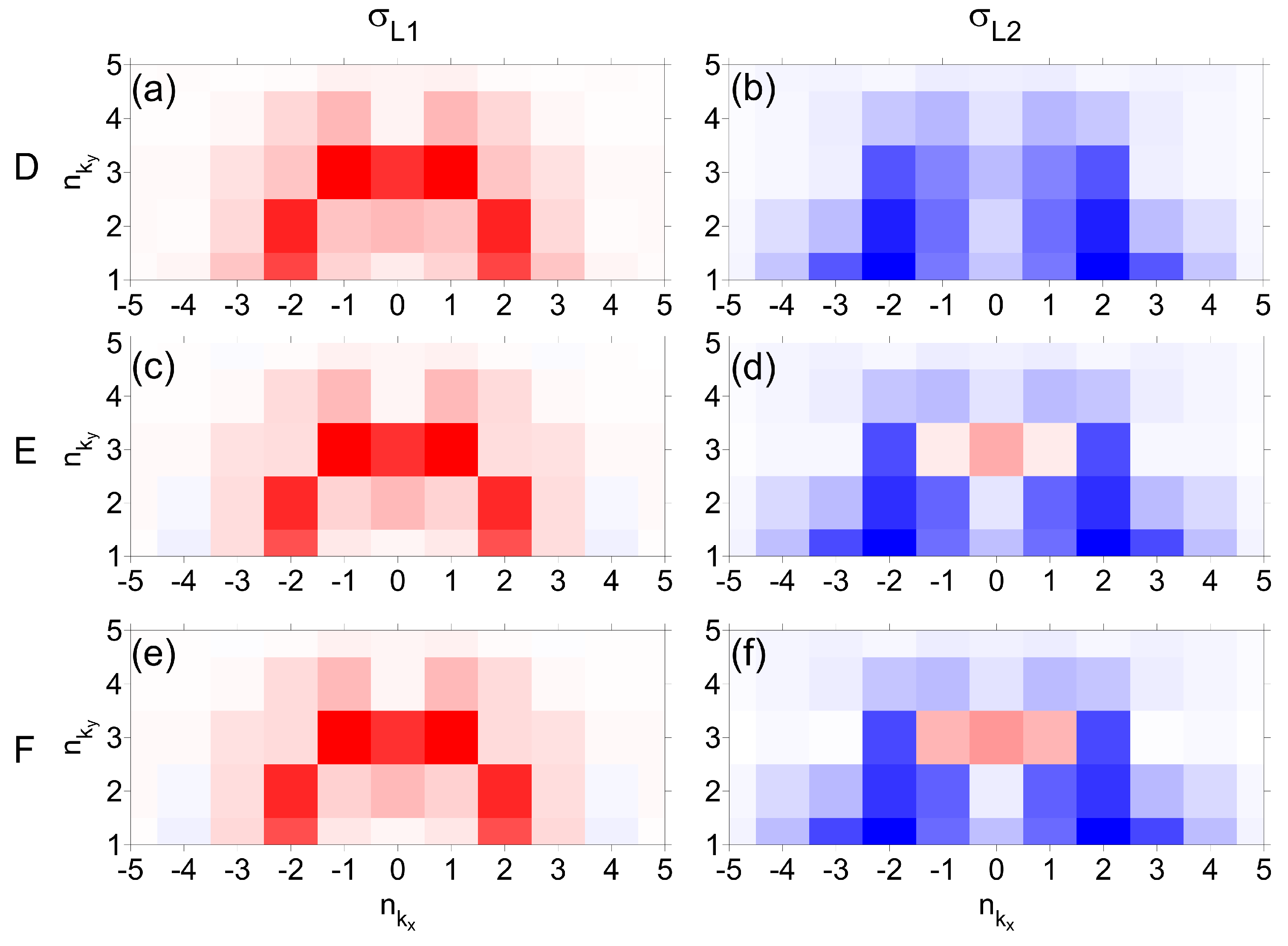
3.3. The Destructive Interference Parameter Subspace
4. Discussion
It (the relative sign of the gaps on different bands) generally encodes important information about the microscopic pairing interaction, since same-sign gaps (called pairing) generally arise from an attractive inter-band interaction, whereas opposite-sign gaps (called pairing) are usually the result of repulsion.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| Q1D | quasi-one-dimensional |
| SL | superlattice |
| BdG | Bogoliubov–de Gennes equations |
| SLBZ | SL Brillouin zone |
| M-M | double-metallic system |
| M-I | metallic-insulating system |
| LHS | left-hand side |
| RHS | right-hand side |
| DOS | density of states |
| BEC | Bose–Einstein condensate |
| BCS | Bardeen–Cooper–Schrieffer [theory/regime] |
| 2D | two dimensional |
| 3D | three dimensional |
Appendix A. Detailed Description of the BdG Model
Appendix A.1. The SL Geometry and Material Parametrisation
| Quantity | Band | Direction: Crystal (SL) | Value |
|---|---|---|---|
| m | lower | M (y) | |
| m | lower | K (x) | |
| meV | |||
| meV |
Appendix A.2. Single-Particle Model
Appendix A.3. Anderson Model
Appendix A.4. The Self-Consistent Under-Relaxation with Phase Control
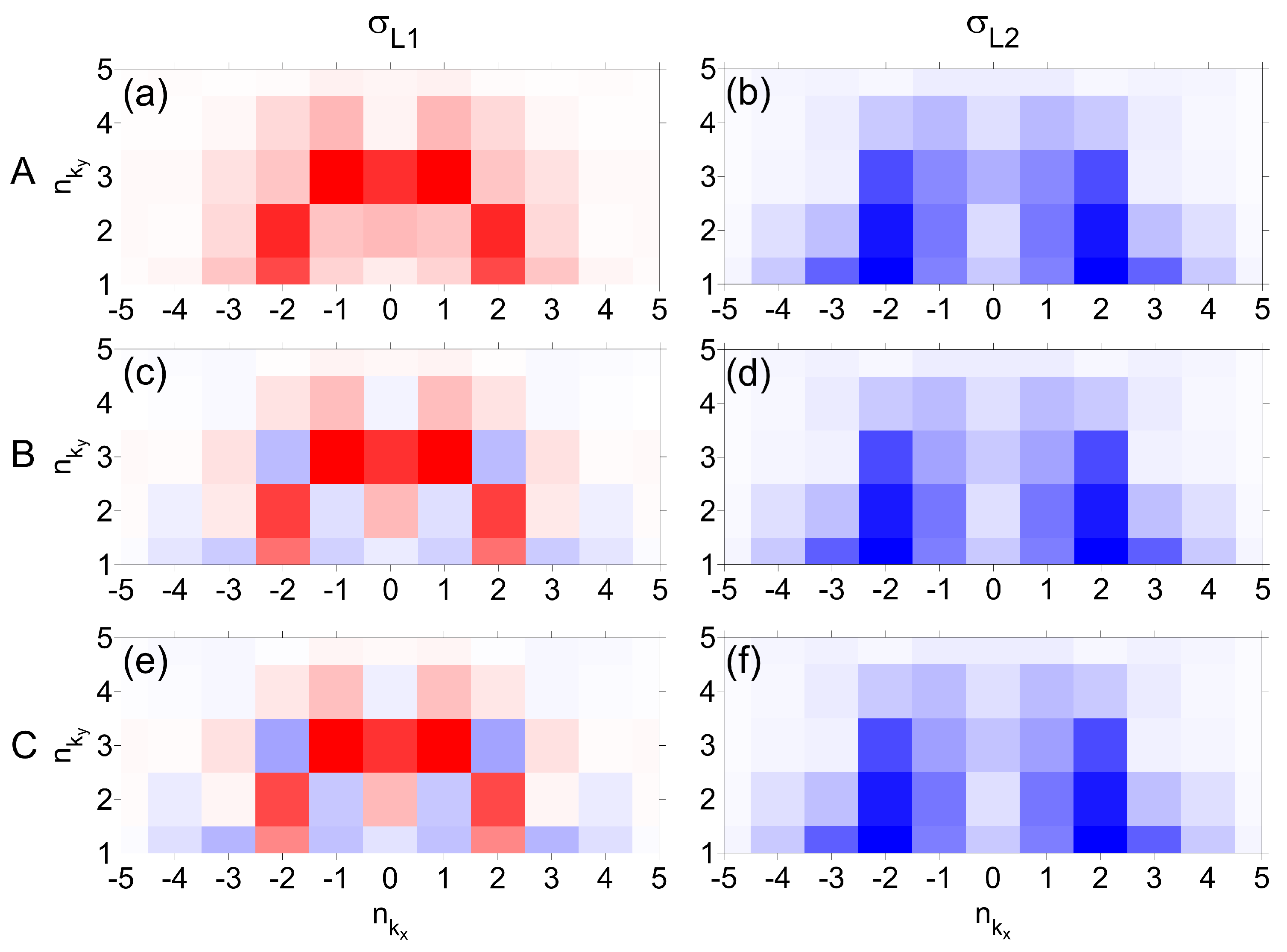
Appendix B. Definition of the Momentum Maps of Δ
Appendix C. Detailed Discussion about the Character of the Exchange-like Inter-Band Interactions and the Phases of the Partial Condensates
Our results are independent of the character of the interband interaction: for an attractive (repulsive) interaction, the gaps on two bands have the same (opposite) signs, but the thermodynamic properties discussed here remain the same.
It is however sufficient to note that there is no intra-band pairing in Equation (1a) ibid., in accordance with the assumption. In order for any interference to take place, two quantities of variable relative phases are required. In the very well known example of the wave interference, the energy as a measure of interference is proportional to instead of + . The roles of A and B are played by the and terms in our system. A similar effect, to the one found in [29], can also be found in Sections III and IV of [30].Both attractive and repulsive inter-band interactions increase for two bands (…), as illustrated by the fact that Equation (9) involve only : inter-band interactions do not induce inter-band pairing in the present model, but reinforce the intra-band pairing by second-order processes involving the other band.
References
- Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. Superconductivity of a striped phase at the atomic limit. Phys. C Supercond. 1998, 296, 269–280. [Google Scholar] [CrossRef]
- Bianconi, A. Feshbach shape resonance in multiband superconductivity in heterostructures. J. Supercond. 2005, 18, 625–636. [Google Scholar] [CrossRef]
- Shanenko, A.; Croitoru, M. Shape resonances in the superconducting order parameter of ultrathin nanowires. Phys. Rev. B 2006, 73, 012510. [Google Scholar] [CrossRef]
- Croitoru, M.D.; Shanenko, A.A.; Kaun, C.C.; Peeters, F.M. Superconducting nanowires: Interplay of discrete transverse modes with supercurrent. Phys. Rev. B 2009, 80, 024513. [Google Scholar] [CrossRef]
- Shanenko, A.A.; Croitoru, M.D.; Vagov, A.; Peeters, F.M. Giant drop in the Bardeen-Cooper-Schrieffer coherence length induced by quantum size effects in superconducting nanowires. Phys. Rev. B 2010, 82, 104524. [Google Scholar] [CrossRef]
- Chen, Y.; Shanenko, A.A.; Peeters, F.M. Hollow nanocylinder: Multisubband superconductivity induced by quantum confinement. Phys. Rev. B 2010, 81, 134523. [Google Scholar] [CrossRef]
- Thompson, C.J.; Blatt, J.M. Shape resonances in superconductors—II simplified theory. Phys. Lett. 1963, 5, 6–9. [Google Scholar] [CrossRef]
- Shanenko, A.A.; Croitoru, M.D.; Peeters, F.M. Oscillations of the superconducting temperature induced by quantum well states in thin metallic films: Numerical solution of the Bogoliubov–de Gennes equations. Phys. Rev. B 2007, 75, 014519. [Google Scholar] [CrossRef]
- Chen, Y.; Shanenko, A.A.; Peeters, F.M. Superconducting transition temperature of Pb nanofilms: Impact of thickness-dependent oscillations of the phonon-mediated electron-electron coupling. Phys. Rev. B 2012, 85, 224517. [Google Scholar] [CrossRef]
- Valentinis, D.; van der Marel, D.; Berthod, C. Rise and fall of shape resonances in thin films of BCS superconductors. Phys. Rev. B 2016, 94, 054516. [Google Scholar] [CrossRef]
- Cariglia, M.; Vargas-Paredes, A.; Doria, M.M.; Bianconi, A.; Milošević, M.V.; Perali, A. Shape-Resonant Superconductivity in Nanofilms: From Weak to Strong Coupling. J. Supercond. Nov. Magn. 2016, 29, 3081–3086. [Google Scholar] [CrossRef]
- Doria, M.M.; Cariglia, M.; Perali, A. Multigap superconductivity and barrier-driven resonances in superconducting nanofilms with an inner potential barrier. Phys. Rev. B 2016, 94, 224513. [Google Scholar] [CrossRef]
- Zhang, L.F.; Flammia, L.; Covaci, L.; Perali, A.; Milosevic, M.V. Multifaceted impact of a surface step on superconductivity in atomically thin films. Phys. Rev. B 2017, 96, 104509. [Google Scholar] [CrossRef]
- Flammia, L.; Zhang, L.F.; Covaci, L.; Perali, A.; Milošević, M.V. Superconducting nanoribbon with a constriction: A quantum-confined Josephson junction. Phys. Rev. B 2018, 97, 134514. [Google Scholar] [CrossRef]
- Mazziotti, M.V.; Valletta, A.; Raimondi, R.; Bianconi, A. Multigap superconductivity at an unconventional Lifshitz transition in a three-dimensional Rashba heterostructure at the atomic limit. Phys. Rev. B 2021, 103, 024523. [Google Scholar] [CrossRef]
- Mazziotti, M.V.; Bianconi, A.; Raimondi, R.; Campi, G.; Valletta, A. Spin–orbit coupling controlling the superconducting dome of artificial superlattices of quantum wells. J. Appl. Phys. 2022, 132, 193908. [Google Scholar] [CrossRef]
- Mazziotti, M.V.; Jarlborg, T.; Bianconi, A.; Valletta, A. Room temperature superconductivity dome at a Fano resonance in superlattices of wires. Europhys. Lett. 2021, 134, 17001. [Google Scholar] [CrossRef]
- Mazziotti, M.V.; Raimondi, R.; Valletta, A.; Campi, G.; Bianconi, A. Resonant multi-gap superconductivity at room temperature near a Lifshitz topological transition in sulfur hydrides. J. Appl. Phys. 2021, 130, 173904. [Google Scholar] [CrossRef]
- Bianconi, A. Multiband superconductivity in high Tc cuprates and diborides. J. Phys. Chem. Solids 2006, 67, 567–570. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Breakdown of the Migdal approximation at Lifshitz transitions with giant zero-point motion in the H3S superconductor. Sci. Rep. 2016, 6, 24816. [Google Scholar] [CrossRef]
- Salasnich, L.; Shanenko, A.A.; Vagov, A.; Aguiar, J.A.; Perali, A. Screening of pair fluctuations in superconductors with coupled shallow and deep bands: A route to higher-temperature superconductivity. Phys. Rev. B 2019, 100, 064510. [Google Scholar] [CrossRef]
- Saraiva, T.T.; Cavalcanti, P.J.F.; Vagov, A.; Vasenko, A.S.; Perali, A.; Dell’Anna, L.; Shanenko, A.A. Multiband Material with a Quasi-1D Band as a Robust High-Temperature Superconductor. Phys. Rev. Lett. 2020, 125, 217003. [Google Scholar] [CrossRef] [PubMed]
- Shanenko, A.A.; Saraiva, T.T.; Vagov, A.; Vasenko, A.S.; Perali, A. Suppression of fluctuations in a two-band superconductor with a quasi-one-dimensional band. Phys. Rev. B 2022, 105, 214527. [Google Scholar] [CrossRef]
- Pasek, W.J.; Degani, M.H.; de Andrade, M.C.; Maialle, M.Z. Band superconductivity in a periodic constricted nanoribbon structure. Superlattices Microstruct. 2021, 158, 107030. [Google Scholar] [CrossRef]
- Pasek, W.J.; Degani, M.H.; de Andrade, M.C.; Maialle, M.Z. Towards an effective mass model for the quasi-1D magnesium diboride superconducting nanostructures. Phys. E Low-Dimens. Syst. Nanostruct. 2022, 144, 115356. [Google Scholar] [CrossRef]
- Innocenti, D.; Poccia, N.; Ricci, A.; Valletta, A.; Caprara, S.; Perali, A.; Bianconi, A. Resonant and crossover phenomena in a multiband superconductor: Tuning the chemical potential near a band edge. Phys. Rev. B 2010, 82, 184528. [Google Scholar] [CrossRef]
- Vargas-Paredes, A.A.; Shanenko, A.A.; Vagov, A.; Milošević, M.V.; Perali, A. Crossband versus intraband pairing in superconductors: Signatures and consequences of the interplay. Phys. Rev. B 2020, 101, 094516. [Google Scholar] [CrossRef]
- Fernandes, R.M.; Haraldsen, J.T.; Wölfle, P.; Balatsky, A.V. Two-band superconductivity in doped SrTiO3 films and interfaces. Phys. Rev. B 2013, 87, 014510. [Google Scholar] [CrossRef]
- Valentinis, D.; van der Marel, D.; Berthod, C. BCS superconductivity near the band edge: Exact results for one and several bands. Phys. Rev. B 2016, 94, 024511. [Google Scholar] [CrossRef]
- Chubukov, A.V.; Eremin, I.; Efremov, D.V. Superconductivity versus bound-state formation in a two-band superconductor with small Fermi energy: Applications to Fe pnictides/chalcogenides and doped SrTiO3. Phys. Rev. B 2016, 93, 174516. [Google Scholar] [CrossRef]
- Trevisan, T.V.; Schütt, M.; Fernandes, R.M. Unconventional Multiband Superconductivity in Bulk SrTiO3 and LaAlO3/SrTiO3 Interfaces. Phys. Rev. Lett. 2018, 121, 127002. [Google Scholar] [CrossRef] [PubMed]
- Abel, M. Energy gap in hydride superconductors due to spin-amplified phonons. Results Phys. 2022, 43, 106042. [Google Scholar] [CrossRef]
- Bekaert, J.; Bignardi, L.; Aperis, A.; van Abswoude, P.; Mattevi, C.; Gorovikov, S.; Petaccia, L.; Goldoni, A.; Partoens, B.; Oppeneer, P.M.; et al. Free surfaces recast superconductivity in few-monolayer MgB2: Combined first-principles and ARPES demonstration. Sci. Rep. 2017, 7, 14458. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pasek, W.J.; Degani, M.H.; Maialle, M.Z. Destructive Interference of the Superconducting Subband Condensates in the Quasi-1D Multigap Material Nanostructures. Condens. Matter 2023, 8, 4. https://doi.org/10.3390/condmat8010004
Pasek WJ, Degani MH, Maialle MZ. Destructive Interference of the Superconducting Subband Condensates in the Quasi-1D Multigap Material Nanostructures. Condensed Matter. 2023; 8(1):4. https://doi.org/10.3390/condmat8010004
Chicago/Turabian StylePasek, Wojciech Julian, Marcos Henrique Degani, and Marcelo Zoéga Maialle. 2023. "Destructive Interference of the Superconducting Subband Condensates in the Quasi-1D Multigap Material Nanostructures" Condensed Matter 8, no. 1: 4. https://doi.org/10.3390/condmat8010004
APA StylePasek, W. J., Degani, M. H., & Maialle, M. Z. (2023). Destructive Interference of the Superconducting Subband Condensates in the Quasi-1D Multigap Material Nanostructures. Condensed Matter, 8(1), 4. https://doi.org/10.3390/condmat8010004






