Theoretical Study of Vibrational Properties of Peptides: Force Fields in Comparison and Ab Initio Investigation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Classical Calculations
- (1)
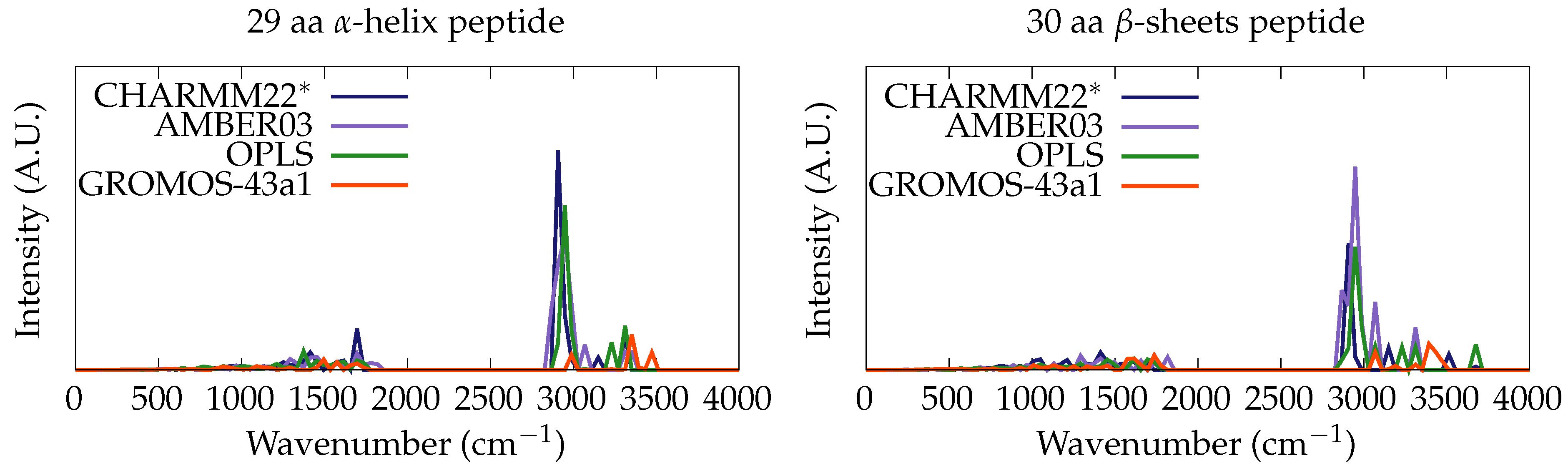
- -helix peptide from BSA protein (residues: 367–396, 29 aa long);
- (2)
- -sheet peptide from ConA protein (residues: 108–138, 30 aa long).
2.2. Ab Initio Calculations
3. Results and Discussion
3.1. Classical Normal Modes Analysis
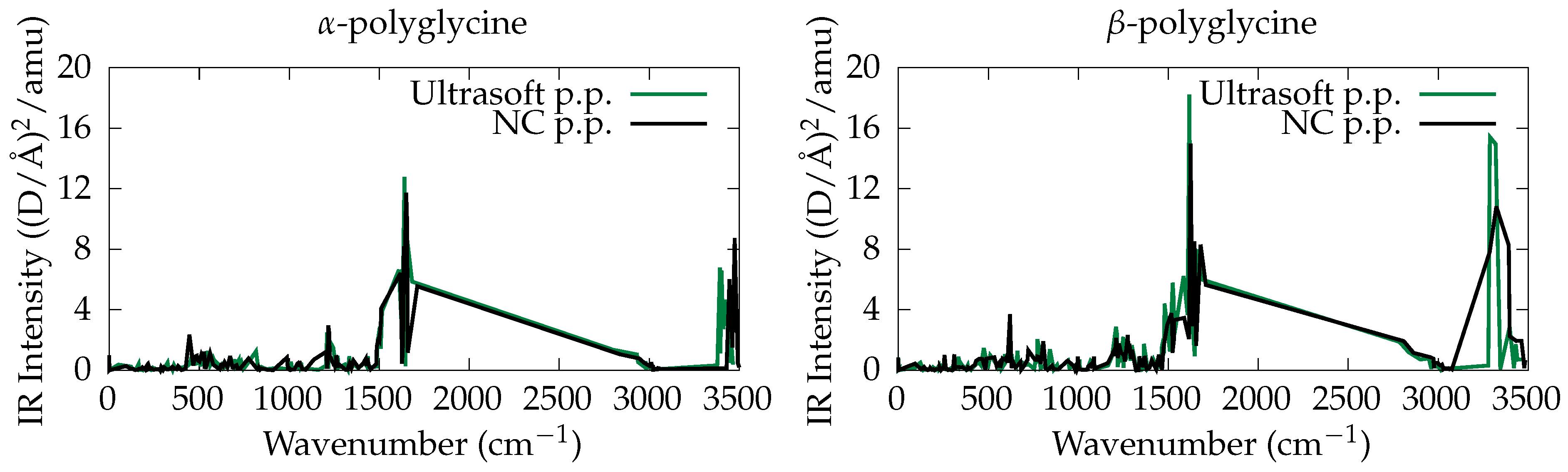
3.2. Ab Initio Phonon Calculation
- –
- peptide with NC PP (w/ QM relaxation): 11.7 (D/Å)/amu at 1650 cm;
- –
- peptide with US PP (w/ QM relaxation): 12.8 (D/Å)/amu at 1640 cm;
- –
- peptide with NC PP (w/o QM relaxation): 12.6 (D/Å)/amu at 1779 cm;
- –
- peptide with NC PP (w/ QM relaxation): 14.9 (D/Å)/amu at 1623 cm;
- –
- peptide with US PP (w/ QM relaxation): 18.2 (D/Å)/amu at 1617 cm;
- –
- peptide with NC PP (w/o QM relaxation): 18.8 (D/Å)/amu at 1734 cm.
- –
- 1.30 (NC pp w/ QM relaxation);
- –
- 1.45 (US pp w/ QM relaxation);
- –
- 1.50 (NC pp w/o QM relaxation).
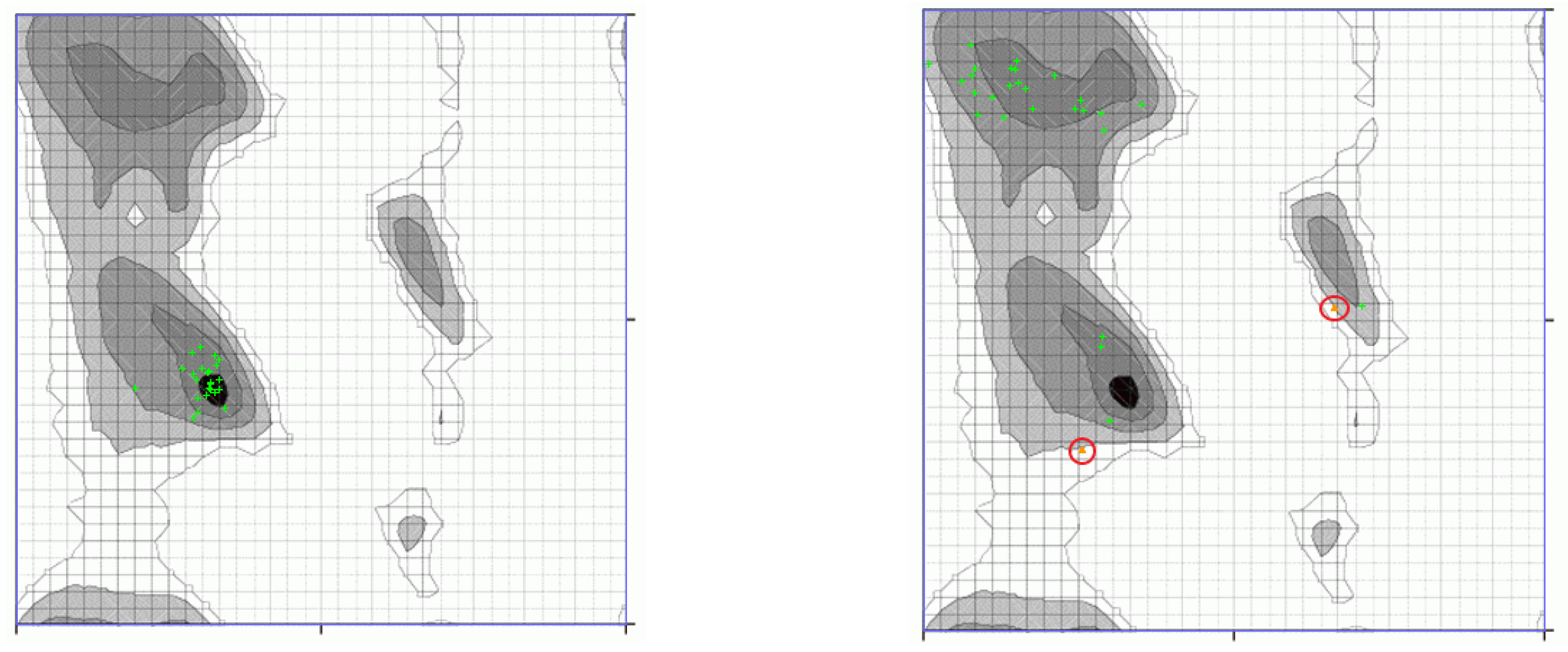
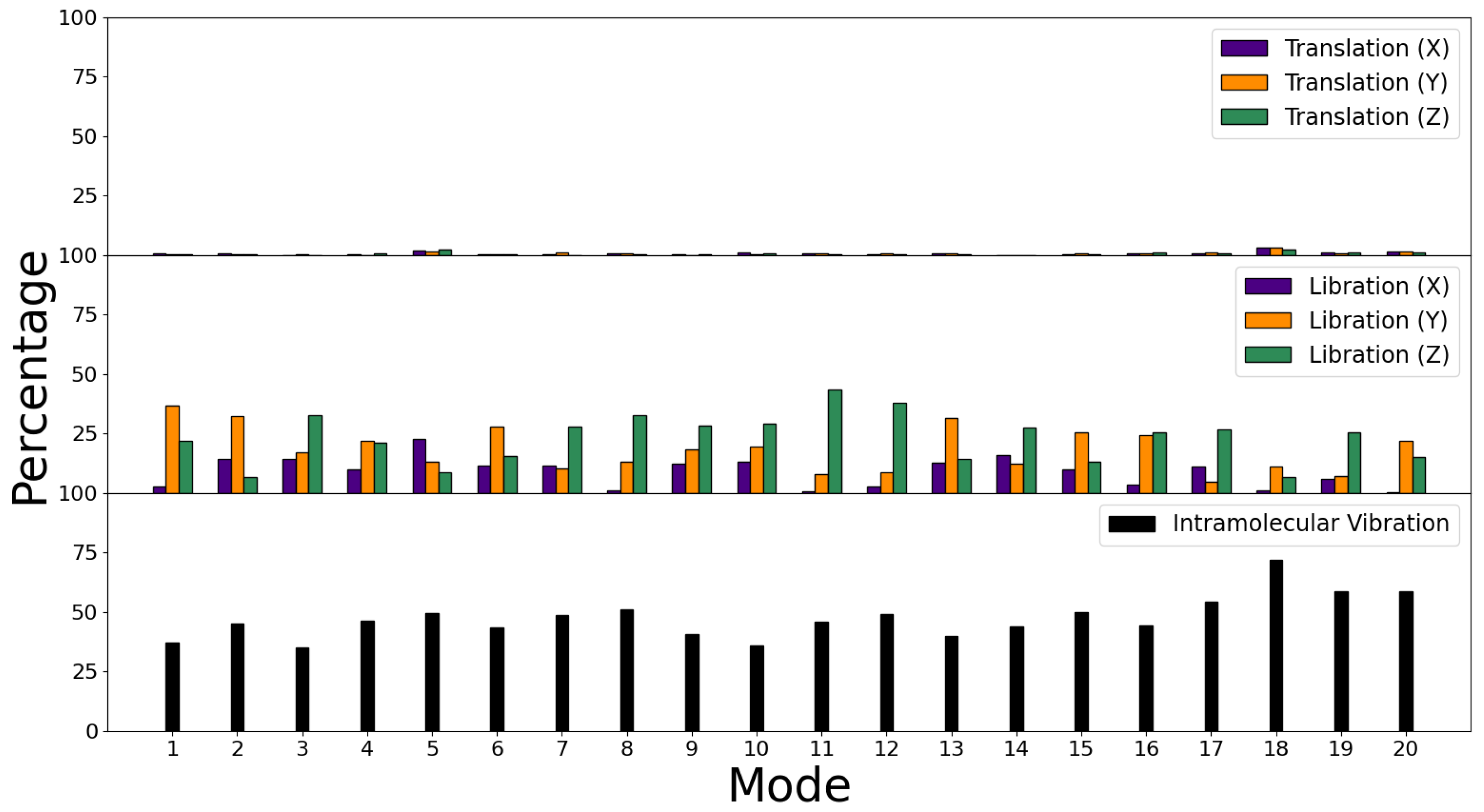
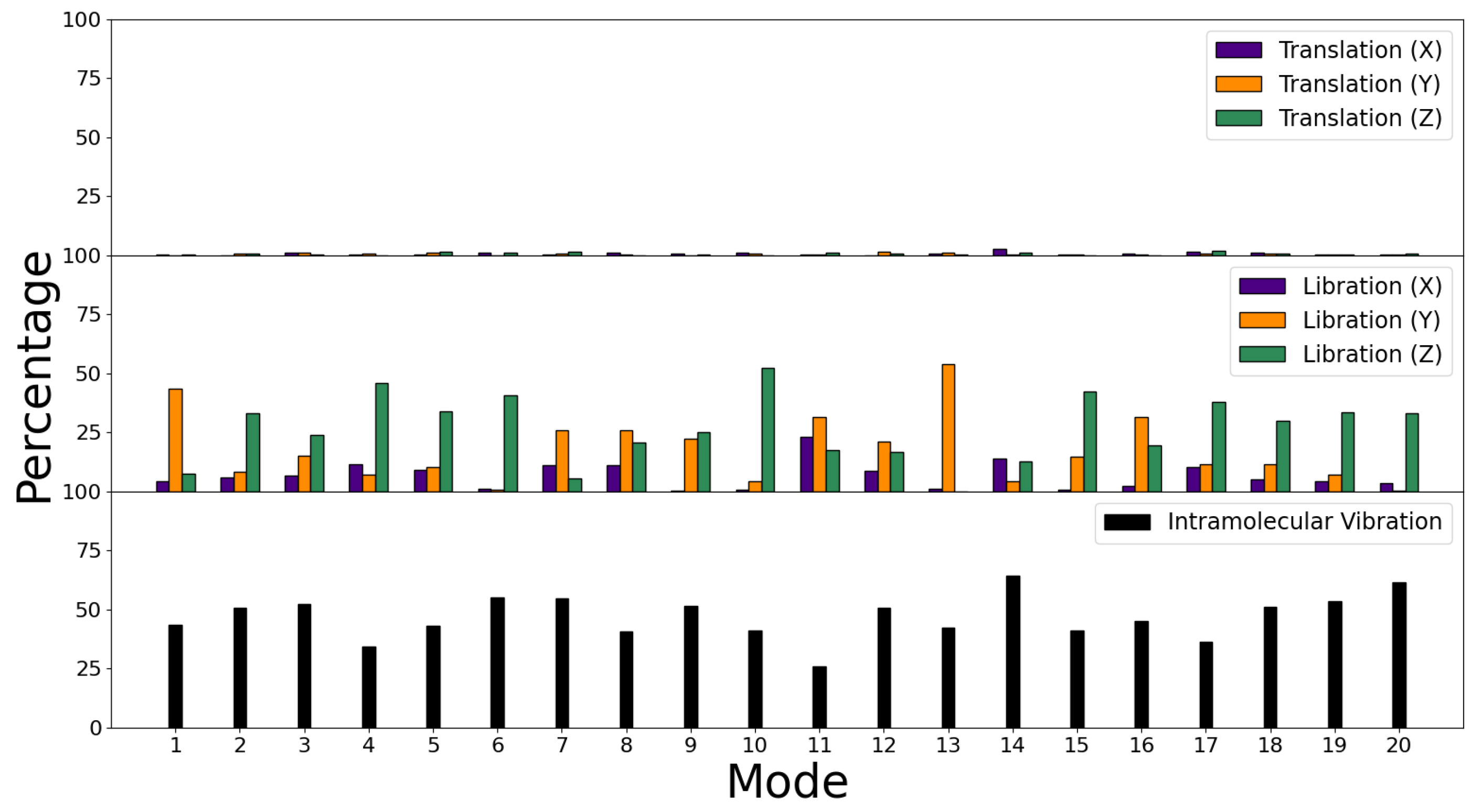
3.3. Decomposition of Molecular Modes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| FIR | far-infrared |
| MIR | mid-infrared |
| QM | quantum-mechanical |
| TDC | transition dipole coupling |
| TDM | transition dipole moment |
| DS | dipole strength |
| FF | force field |
| aa | amino acid/s |
| NM | normal mode/s |
| DFT | density functional theory |
| pp | pseudopotential |
| MD | Molecular Dynamics |
| VMD | Visual Molecular Dynamics |
| NC | norm-conserving |
| US | ultrasoft |
Appendix A
Appendix A.1
Appendix A.2
Appendix A.3

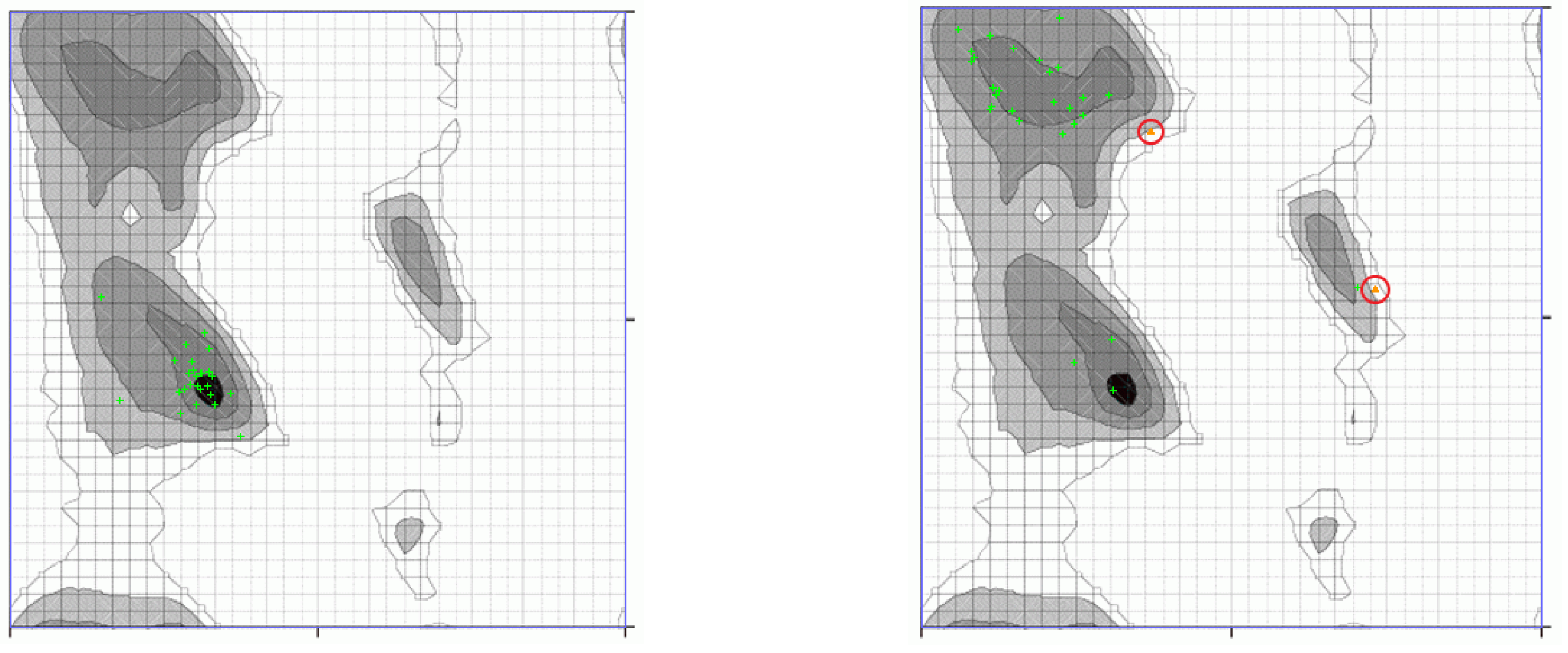

References
- Ripanti, F.; Luchetti, N.; Nucara, A.; Minicozzi, V.; Di Venere, A.; Filabozzi, A.; Carbonaro, M. Normal mode calculation and infrared spectroscopy of proteins in water solution: Relationship between amide I transition dipole strength and secondary structure. Int. J. Biol. Macromol. 2021, 185, 369–376. [Google Scholar] [CrossRef] [PubMed]
- Zandomeneghi, G.; Krebs, M.R.H.; McCammon, M.G.; Fändrich, M. FTIR reveals structural differences between native β-sheet proteins and amyloid fibrils. Protein Sci. 2004, 13, 3314–3321. [Google Scholar] [CrossRef] [PubMed]
- Carbonaro, M.; Ripanti, F.; Filabozzi, A.; Minicozzi, V.; Stellato, F.; Placidi, E.; Morante, S.; Di Venere, A.; Nicolai, E.; Postorino, P.; et al. Human insulin fibrillogenesis in the presence of epigallocatechin gallate and melatonin: Structural insights from a biophysical approach. Int. J. Biol. Macromol. 2018, 115, 1157–1164. [Google Scholar] [CrossRef] [PubMed]
- Jackson, M.; Mantsch, H.H. The Use and Misuse of FTIR Spectroscopy in the Determination of Protein Structure. Crit. Rev. Biochem. Mol. Biol. 1995, 30, 95–120. [Google Scholar] [CrossRef] [PubMed]
- Shivu, B.; Seshadri, S.; Li, J.; Oberg, K.A.; Uversky, V.N.; Fink, A.L. Distinct β-Sheet Structure in Protein Aggregates Determined by ATR–FTIR Spectroscopy. Biochemistry 2013, 52, 5176–5183. [Google Scholar] [CrossRef]
- Miller, L.M.; Bourassa, M.W.; Smith, R.J. FTIR spectroscopic imaging of protein aggregation in living cells. Biochim. Et Biophys. Acta (BBA)-Biomembr. 2013, 1828, 2339–2346. [Google Scholar] [CrossRef]
- Kandori, H. Structure/Function Study of Photoreceptive Proteins by FTIR Spectroscopy. Bull. Chem. Soc. Jpn. 2020, 93, 904–926. [Google Scholar] [CrossRef]
- Arrondo, J.L.R.; Muga, A.; Castresana, J.; Goñi, F.M. Quantitative studies of the structure of proteins in solution by fourier-transform infrared spectroscopy. Prog. Biophys. Mol. Biol. 1993, 59, 23–56. [Google Scholar] [CrossRef]
- Haris, P.I.; Severcan, F. FTIR spectroscopic characterization of protein structure in aqueous and non-aqueous media. J. Mol. Catal. B Enzym. 1999, 7, 207–221. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Hall, C.K. Molecular dynamics simulations of spontaneous fibril formation by random-coil peptides. Biophys. J. 2004, 87, 16180–16185. [Google Scholar] [CrossRef] [Green Version]
- Cabriolu, R.; Auer, S. Amyloid fibrillation kinetics: Insight from atomistic nucleation theory. J. Mol. Biol. 2011, 411, 275–285. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Zhu, Y.; Zhou, S.; An, X.; Zhang, Y.; Bai, Q.; He, Y.X.; Liu, H.; Yao, X. Experimental and theoretical insights into the inhibition mechanism of prion fibrillation by resveratrol and its derivatives. ACS Chem. Neurosci. 2017, 8, 2698–2707. [Google Scholar] [CrossRef]
- Baronio, C.M.; Barth, A. The Amide I spectrum of proteins—Optimization of transition dipole coupling parameters using density functional theory calculations. J. Phys. Chem. B 2020, 124, 1703–1714. [Google Scholar] [CrossRef] [PubMed]
- Amadei, A.; Daidone, I.; Di Nola, A.; Aschi, M. Theoretical-computational modelling of infrared spectra in peptides and proteins: A new frontier for combined theoretical-experimental investigations. Curr. Opin. Struct. Biol. 2010, 20, 155–161. [Google Scholar] [CrossRef] [PubMed]
- Alam, M.J.; Shabbir, A. Anharmonic vibrational studies of L-aspartic acid using HF and DFT calculations. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2012, 96, 992–1004. [Google Scholar] [CrossRef]
- Wang, J. Assessment of the Amide-I Local Modes in γ-and β-Turns of Peptides. Phys. Chem. Chem. Phys. 2009, 11, 5310–5322. [Google Scholar] [CrossRef]
- Kubelka, J.; Kim, J.; Bour, P.; Keiderling, T.A. Contribution of transition dipole coupling to amide coupling in IR spectra of peptide secondary structures. Vib. Spectrosc. 2006, 42, 63–73. [Google Scholar] [CrossRef]
- Jeon, J.; Yang, S.; Choi, J.H.; Cho, M. Computational vibrational spectroscopy of peptides and proteins in one and two dimensions. Acc. Chem. Res. 2009, 42, 1280–1289. [Google Scholar] [CrossRef]
- Barth, A.; Zscherp, C. What vibrations tell about proteins. Q. Rev. Biophys. 2002, 35, 369–430. [Google Scholar] [CrossRef]
- Jansen, T.L.C. Computational spectroscopy of complex systems. J. Chem. Phys. 2021, 155. [Google Scholar] [CrossRef]
- Cote, Y.; Nominé, Y.; Ramirez, J.; Hellwig, P.; Stote, R.H. Peptide-Protein Binding Investigated by Far-IR Spectroscopy and Molecular Dynamics Simulations. Biophys. J. 2017, 112, 2575–2588. [Google Scholar] [CrossRef] [PubMed]
- Gabas, F.; Conte, R.; Ceotto, M. Semiclassical Vibrational Spectroscopy of Biological Molecules Using Force Fields. J. Chem. Theory Comput. 2020, 16, 3476–3485. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer-Stenner, R.; Soffer, J.B.; Verbaro, D. Intrinsically Disordered Protein Analysis: Volume 1, Methods and Experimental Tools; Humana Press: Totowa, NJ, USA, 2012. [Google Scholar]
- Cimas, A.; Vaden, T.D.; De Boer, T.S.J.A.; Snoek, L.C.; Gaigeot, M.P. Vibrational spectra of small protonated peptides from finite temperature MD simulations and IRMPD spectroscopy. J. Chem. Theory Comput. 2009, 5, 1068–1078. [Google Scholar] [CrossRef]
- Yang, S.; Cho, M. Thermal Denaturation of Polyalanine Peptide in Water by Molecular Dynamics Simulations and Theoretical Prediction of Infrared Spectra: Helix- Coil Transition Kinetics. J. Phys. Chem. B 2007, 111, 605–617. [Google Scholar] [CrossRef]
- Hahn, S.; Ham, S.; Cho, M. Simulation studies of amide I IR absorption and two-dimensional IR spectra of β hairpins in liquid water. J. Phys. Chem. B. 2005, 109, 11789–11801. [Google Scholar] [CrossRef] [PubMed]
- Nevskaya, N.A.; Chirgadze, Y.N. Infrared spectra and resonance interactions of amide-I and II vibrations of α-helix. Biopolym. Orig. Res. Biomol. 1976, 15, 637–648. [Google Scholar] [CrossRef]
- Torii, H.; Tasumi, M. Theoretical analyses of the amide I infrared bands of globular proteins. Infrared Spectrosc. Biomol. 1996. [Google Scholar]
- Abe, Y.; Krimm, S. Normal vibrations of crystalline polyglycine I. Biopolym. Orig. Res. Biomol. 1972, 11, 1817–1839. [Google Scholar] [CrossRef]
- Kennehan, E.R.; Grieco, C.; Brigeman, A.N.; Doucette, G.S.; Rimshaw, A.; Bisgaier, K.; Giebink, N.C.; Asbury, J.B. Using molecular vibrations to probe exciton delocalization in films of perylene diimides with ultrafast mid-IR spectroscopy. Phys. Chem. Chem. Phys. 2017, 19, 24829–24839. [Google Scholar] [CrossRef]
- Lee, C.; Cho, M. Local amide I mode frequencies and coupling constants in multiple-stranded antiparallel β-sheet polypeptides. J. Phys. Chem. B 2004, 108, 20397–20407. [Google Scholar] [CrossRef]
- Demirdöven, N.; Cheatum, C.; Chung, H.; Khalil, M.; Knoester, J.; Tokmakoff, A. Two-dimensional infrared spectroscopy of antiparallel β-sheet secondary structure. J. Am. Chem. Soc. 2004, 126, 7981–7990. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jansen, T.L.C.; Dijkstra, A.G.; Watson, T.M.; Hirst, J.D.; Knoester, J. Modeling the amide I bands of small peptides. J. Chem. Phys. 2006, 125, 044312, Erratum in J. Chem. Phys. 2006, 136, 209901. [Google Scholar] [CrossRef] [PubMed]
- Cha, S.; Ham, S.; Cho, M. Amide I vibrational modes in glycine dipeptide analog: Ab initio calculation studies. J. Chem. Phys. 2002, 117, 740–750. [Google Scholar] [CrossRef]
- Gorbunov, R.D.; Kosov, D.S.; Stock, G. Ab initio-based exciton model of amide I vibrations in peptides: Definition, conformational dependence, and transferability. J. Chem. Phys. 2005, 122, 224904. [Google Scholar] [CrossRef]
- Henschel, H.; Andersson, A.T.; Jespers, W.; Ghahremanpour, M.; van der Spoel, D. Theoretical infrared spectra: Quantitative similarity measures and force fields. J. Chem. Theory Comput. 2020, 16, 3307–3315. [Google Scholar] [CrossRef]
- MacKerell, A.D., Jr.; Bashford, D.; Bellott, M.L.D.R.; Dunbrack, R.L., Jr.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Robertson, M.J.; Tirado-Rives, J.; Jorgensen, W.L. Improved peptide and protein torsional energetics with the OPLS-AA force field. J. Chem. Theory Comput. 2015, 11, 3499–3509. [Google Scholar] [CrossRef]
- Rappoport, D.; Crawford, N.R.M.; Furche, F.; Burke, K.; Wiley, C. Which functional should I choose. Comput. Inorg. Bioinorg. Chem. 2008, 594. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Zhang, F.; Hayashi, M.; Wang, H.W.; Tominaga, K.; Kambara, O.; Nishizawa, J.I.; Sasaki, T. Terahertz spectroscopy and solid-state density functional theory calculation of anthracene: Effect of dispersion force on the vibrational modes. J. Chem. Phys. 2014, 140, 174509. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Wang, H.W.; Tominaga, K.; Hayashi, M. Mixing of intermolecular and intramolecular vibrations in optical phonon modes: Terahertz spectroscopy and solid-state density functional theory. WIREs Comput. Mol. Sci. 2016, 6, 386–409. [Google Scholar] [CrossRef]
- Edwards, G.; Logan, R.; Copeland, M.; Reinisch, L.; Davidson, J.; Johnson, B.; Maciunas, R.; Mendenhall, M.; Ossoff, R.; Tribble, J.; et al. Tissue ablation by a free-electron laser tuned to the amide II band. Nature 1994, 371, 416–419. [Google Scholar] [CrossRef] [PubMed]
- Edwards, G.S.; Allen, S.J.; Haglund, R.F.; Nemanich, R.J.; Redlich, B.; Simon, J.D.; Yang, W.C. Applications of Free-Electron Lasers in the Biological and Material Sciences. Photochem. Photobiol. 2005, 81, 711–735. [Google Scholar] [CrossRef] [PubMed]
- Jašíková, L.; Roithová, J. Infrared Multiphoton Dissociation Spectroscopy with Free-Electron Lasers: On the Road from Small Molecules to Biomolecules. Chem. A Eur. J. 2018, 24, 3374–3390. [Google Scholar] [CrossRef] [PubMed]
- Putter, M.; von Helen, G.; Meijer, G. Mass selective infrared spectroscopy using a free electron laser. Chem. Phys. Lett. 1996, 258, 118–122. [Google Scholar] [CrossRef]
- Kawasaki, T.; Zen, H.; Ozaki, K.; Yamada, H.; Wakamatsu, K.; Ito, S. Application of mid-infrared free-electron laser for structural analysis of biological materials. J. Synchrotron Radiat. 2021, 28, 28–35. [Google Scholar] [CrossRef]
- Polfer, N.C.; Oomens, J. Vibrational spectroscopy of bare and solvated ionic complexes of biological relevance. Mass Spectrom. Rev. 2009, 28, 468–494. [Google Scholar] [CrossRef]
- Hill, J.R.; Dlott, D.D.; Rella, C.W.; Smith, T.I.; Schwettman, H.A.; Peterson, K.A.; Kwok, A.; Rector, K.D.; Fayer, M.D. Ultrafast infrared spectroscopy in biomolecules: Active site dynamics of heme proteins. Biospectroscopy 1996, 2, 277–299. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Fliege, J.; Svaiter, B.F. Steepest descent methods for multicriteria optimization. Math. Meth. Oper. Res. 2000, 51, 479–494. [Google Scholar] [CrossRef]
- Polyak, B.T. The conjugate gradient method in extremal problems. USSR Comput. Math. Math. Phys. 1969, 9, 94–112. [Google Scholar] [CrossRef]
- Liu, D.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Kaschner, R.; Hohl, D. Density functional theory and biomolecules: A study of glycine, alanine, and their oligopeptides. J. Phys. Chem. A 1998, 102, 5111–5116. [Google Scholar] [CrossRef]
- Kokalj, A. XCrySDen—A new program for displaying crystalline structures and electron densities. J. Mol. Graph. Model. 1999, 17, 176–179. [Google Scholar] [CrossRef]
- Schaftenaar, G.; Noordik, G.H. Molden: A pre- and post-processing program for molecular and electronic structures. J. Comput.-Aided Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef]
- Paraipan, A.A.; Luchetti, N.; Mosca Conte, A.; Pulci, O.; Missori, M. Low frequency vibrations of saccharides using terahertz time-domain spectroscopy and ab-initio simulations. 2022; in preparation. [Google Scholar]
- Anderson, R.J.; Weng, Z.; Campbell, R.K.; Jiang, X. Main-chain conformational tendencies of amino acids. Proteins Struct. Funct. Bioinform. 2005, 60, 679–689. [Google Scholar] [CrossRef] [PubMed]
- Grechko, M.; Zanni, M.T. Quantification of transition dipole strengths using 1D and 2D spectroscopy for the identification of molecular structures via exciton delocalization: Application to α-helices. J. Chem. Phys. 2012, 137, 184202. [Google Scholar] [CrossRef] [PubMed]
- Dunkelberger, E.B.; Grechko, M.; Zanni, M.T. Transition dipoles from 1D and 2D infrared spectroscopy help reveal the secondary structures of proteins: Application to amyloids. J. Phys. Chem. B 2015, 119, 14065–14075. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haris, P.I.; Chapman, D. The conformational analysis of peptides using fourier transform IR spectroscopy. Biopolymers 1995, 37, 251–263. [Google Scholar] [CrossRef] [PubMed]
- Bakshi, K.; Liyanage, M.R.; Volkin, D.B.; Middaugh, C.R. Fourier Transform Infrared Spectroscopy of Peptides. In Therapeutic Peptides: Methods and Protocols; Nixon, A.E., Ed.; Humana Press: Totowa, NJ, USA, 2014; pp. 255–269. [Google Scholar]

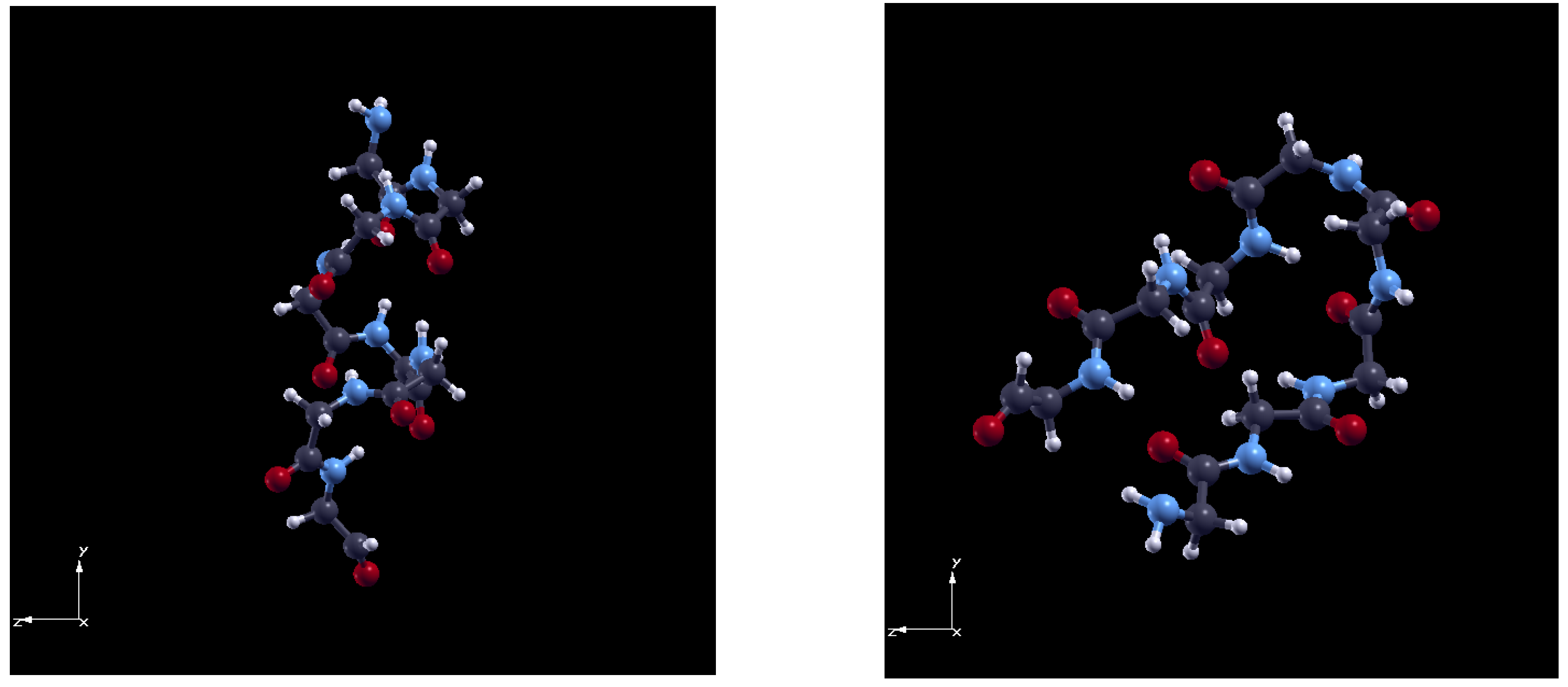

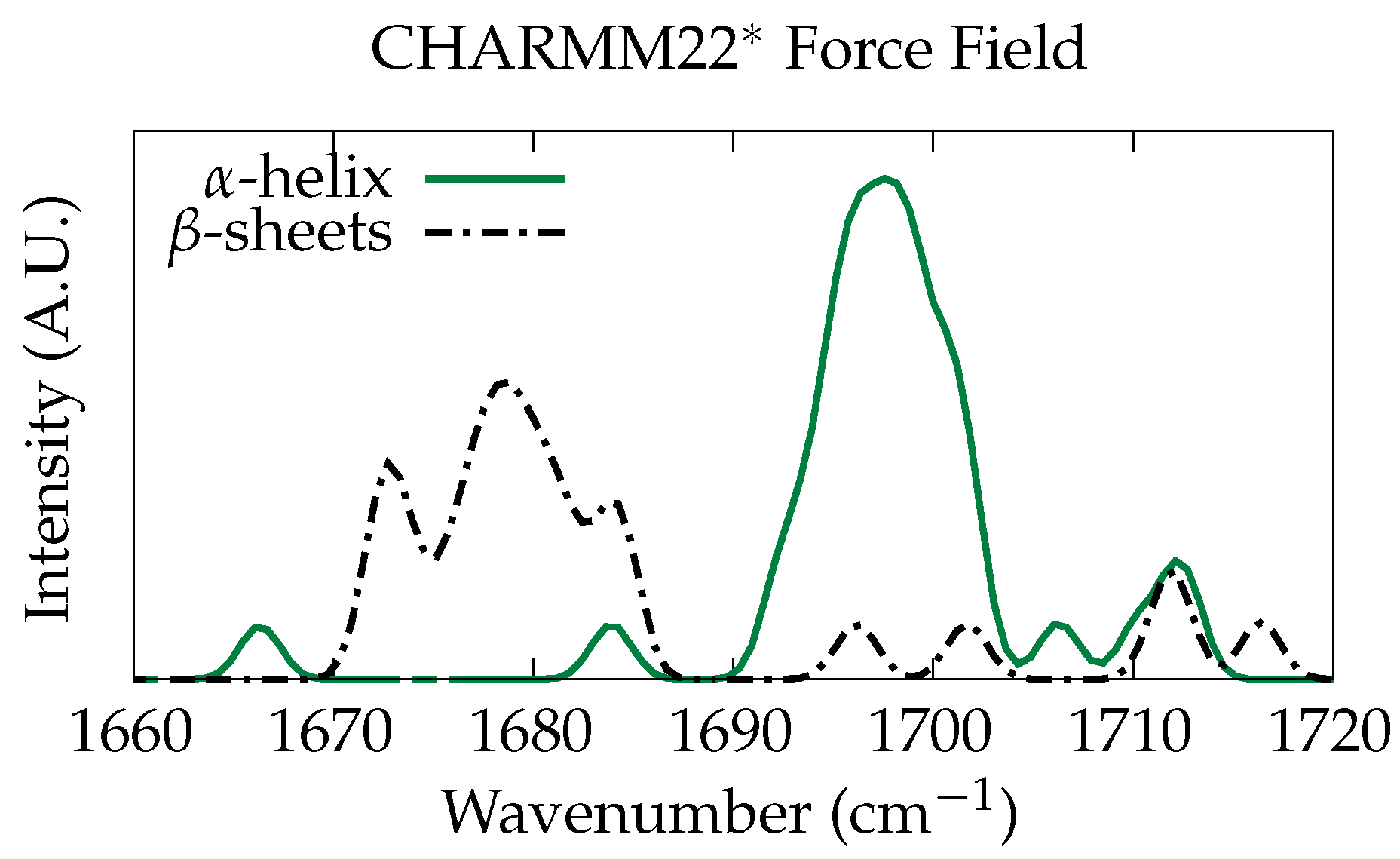

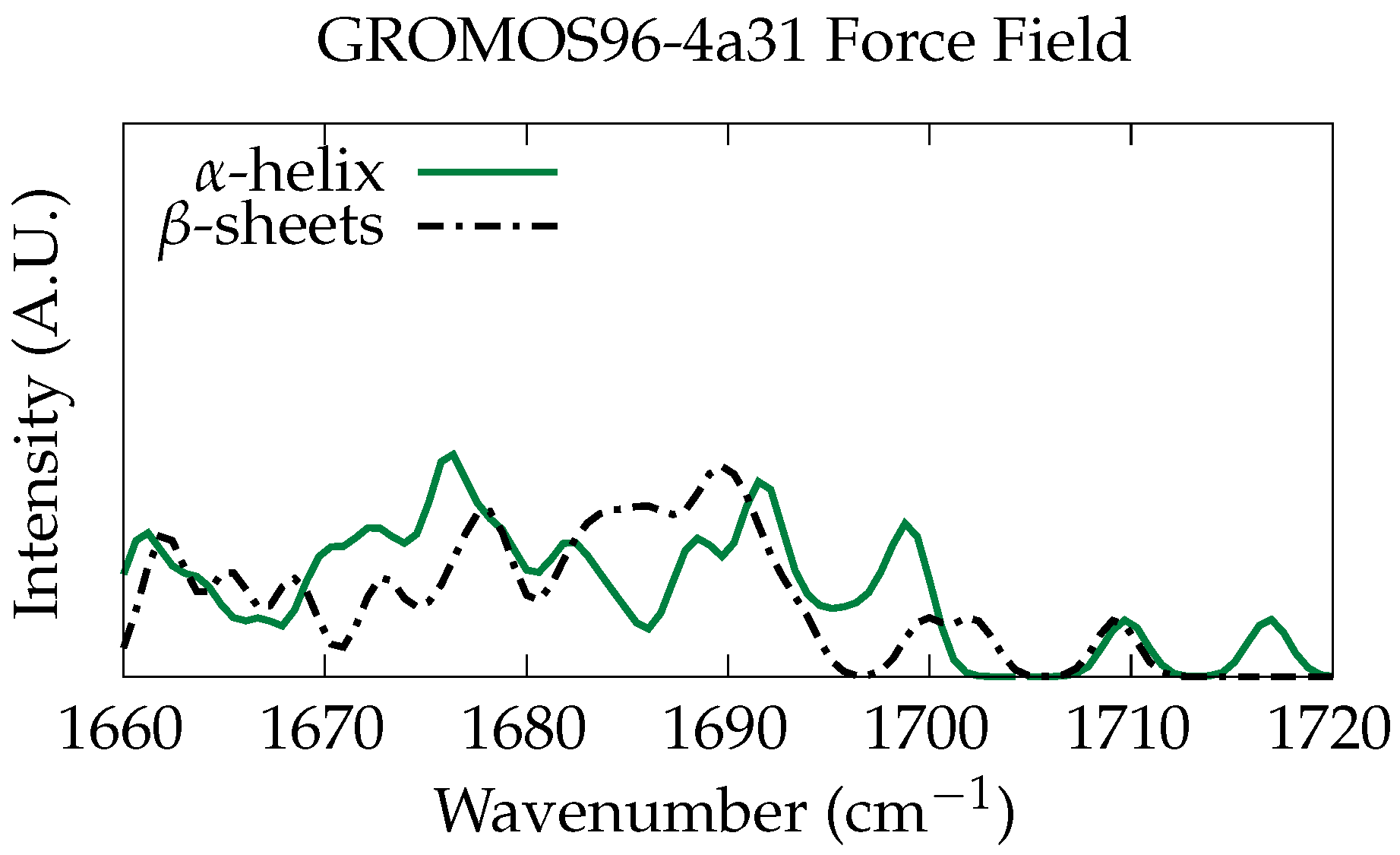


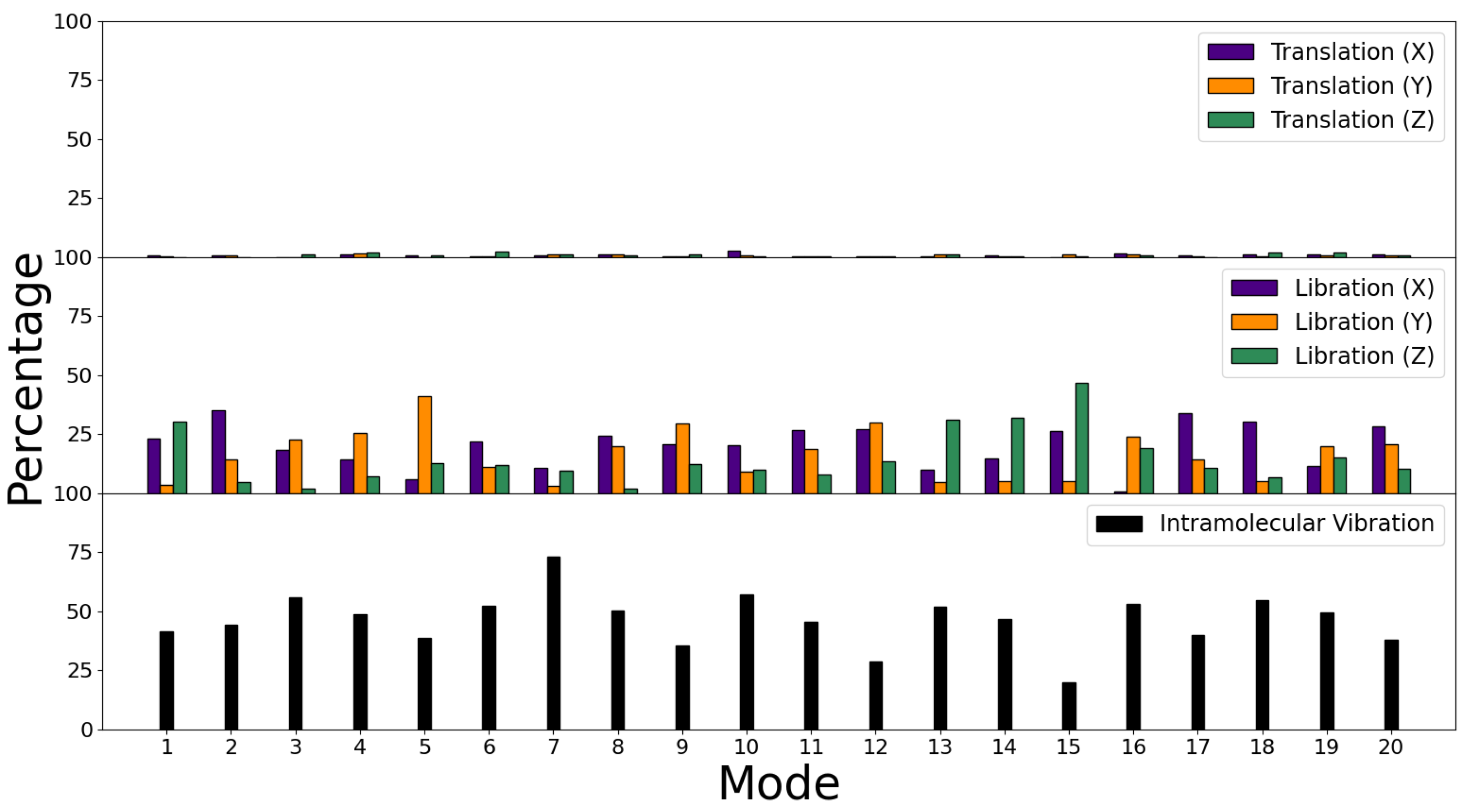

| Binding | Bending | Improper | Proper | |
|---|---|---|---|---|
| AMBER | Harm. | Harm. | Per. | Mult.-per. |
| CHARMM | Harm. | U-B | Harm. | Mult.-per. |
| OPLS | Harm. | Harm. | Harm. | R-B |
| GROMOS | 4th grade | Cos.-based | Harm. | Per. |
| Frequency (cm) | TDM (D) | DS (D) | |
|---|---|---|---|
| -helix | 1650/1640 | 0.346/0.362 | 0.120/0.131 |
| -sheets | 1623/1617 | 0.394/0.436 | 0.155/0.190 |
| Frequency (cm) | TDM (D) | DS (D) | |
|---|---|---|---|
| -helix | 1779 | 0.346 | 0.120 |
| -sheets | 1734 | 0.428 | 0.183 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luchetti, N.; Minicozzi, V. Theoretical Study of Vibrational Properties of Peptides: Force Fields in Comparison and Ab Initio Investigation. Condens. Matter 2022, 7, 53. https://doi.org/10.3390/condmat7030053
Luchetti N, Minicozzi V. Theoretical Study of Vibrational Properties of Peptides: Force Fields in Comparison and Ab Initio Investigation. Condensed Matter. 2022; 7(3):53. https://doi.org/10.3390/condmat7030053
Chicago/Turabian StyleLuchetti, Nicole, and Velia Minicozzi. 2022. "Theoretical Study of Vibrational Properties of Peptides: Force Fields in Comparison and Ab Initio Investigation" Condensed Matter 7, no. 3: 53. https://doi.org/10.3390/condmat7030053
APA StyleLuchetti, N., & Minicozzi, V. (2022). Theoretical Study of Vibrational Properties of Peptides: Force Fields in Comparison and Ab Initio Investigation. Condensed Matter, 7(3), 53. https://doi.org/10.3390/condmat7030053











