Abstract
Various solitary wave excitations are found for a Bose-Einstein condensate in presence of two hybrid potentials in the form of triple mixtures of optical lattices. One of these potentials comprises of a combination of two important lattice profiles, such as frustrated optical lattice and double-well super-lattice, within one. Another represents a composite lattice combination, resulting in a wider and deeper frustrated optical lattice. The dynamical equation for such a system is solved by the exact analytical method to obtain a bright solitary wave, periodic wave and cnoidal wave excitations. We also report Anderson localization, bifurcation of condensate at the center and a competition between two different types of localizations upon trap engineering. Dynamical and structural stability analyses are also carried out, which reveal the obtained solutions as extremely stable for structural noise incorporation and sufficiently stable for dynamical stability. These triple mixtures of optical lattices impart better tunability on the condensate profile, which has made this system a true quantum simulator.
1. Introduction
Solitary waves are spatially localized, non-decaying waves that retain their shape during propagation. They commonly arise due to the balance between nonlinearity and dispersion in a medium. In 1834, these waves were first observed by John Scott Russell in the Union Canal of Scotland, and these waves are widely studied for various systems such as optical fiber and Bose–Einstein condensate (BEC). The nonlinear Schrödinger equation (NLSE) is well-known to manifest bright and dark solitary waves. To study the solitary waves in a BEC of a dilute quantum gas, the Gross–Pitaevskii equation (GPE) with cubic nonlinearity is commonly used [1,2,3]. The solution of GPE supports a variety of solitary wave solutions. The bright and the dark solitons arise due to attractive and repulsive interatomic interactions, respectively. The bright soliton represents the propagation of a localized density elevation, whereas the dark soliton represents the propagation of the density depression of the condensate.
BEC, without external confinement, is ideally seen as a highly localized object in momentum space and a delocalized object in position space. However, spatial control can be incorporated, in practice, by engineering external potentials [4], which can reduce the system to lower dimensions and also bring in the possibility of a number of recent technological advancements. To study various applications in BEC, such as quantum simulation, an engineered optical lattice (OL) is of paramount importance. Two or more counter-propagating interfering laser beams (depending upon the dimension of the OL) form a standing wave with an array of crest-trough mixtures. For two constituent lasers, the standing wave is known as an OL for its similarity with the repetitive structure of the crystal lattice [5]. The laser arrangements determine the direction and dimension of the OL. Ultracold atoms are trapped in the troughs of the OL to form the BEC under specific conditions. With the observation of phenomena, such as Anderson-like localization [6,7], negative absolute temperature [8,9], quantum magnetism [10], quantum droplets [11], and fermionic BEC related to BCS-BEC crossover [12,13,14], studies related to BEC in OL have become an emerging direction. Recently, this subject has also established its prospects toward applications in precision measurements [15], matter-wave interferometry [16], large-scale magnetic simulators [17], as well as in spin liquids [18,19], quantum simulation [20,21,22], molecular dynamics [23,24,25], quantum machine learning [26,27], quantum metrology [28,29], quantum sensing [30,31], quantum communication, and quantum technologies [32,33,34,35]. Theoretical studies in this domain are mostly confined to the studies of bichromatic optical lattices (BOLs), with some works in higher-order OLs. On the other hand, the multi-fold OLs provide additional control of atom trapping and allow for more precise measurements, and it also helps in the study of complex solitons [36]. Finding exact solutions for BECs under various confinements is of paramount importance. The exact analytical solutions for BEC are available for potentials, such as harmonic, double-well, periodic, BOL, four-color optical lattice (FOL), triple well, etc. [37,38,39,40,41,42,43,44,45,46,47,48].
In this work, we aim to find the exact analytical solution for a BEC under triple optical lattice (TOL) of commensurate wavelengths. We introduce two examples of TOL, which can be used to trap a cigar-shaped BEC with cubic nonlinearity. The GPE for such a system is used to find the interrelation between the nonlinear and potential parameters. The exact analytical solution is then obtained for a variety of solitary wave excitations. A triple mixture of OLs imparts better tunability on the condensate profile. The stability of the obtained wavefunctions is also studied and demonstrated by adding random white noise to the wavefunction and also to the external trap.
2. Solitary Wave Solution Under the Novel TOL Traps
In this section, we intend to investigate the effects of two different combinations of TOL. An exact analytical model is constructed to discuss the dynamical behavior of 1D BEC and the allowed periods of the TOL combination. The TOL with commensurate wave numbers, , and should have been the obvious choice. However, it is found that this combination does not support a solitary wave excitation. Therefore, we have considered studying two TOLs with commensurate wavenumbers, (1) , and , and (2) and , and they are labeled as TOL-1 and TOL-2, respectively. Notice that the first lattice is a combination of prime numbered OLs, whereas the second TOL is of the composite type.
TOL-1:
TOL-2:
In Equations (1) and (2), the terms, ( for ), represent the potential depths. The lattice wave vector l is related to the recoil energy, , where M is the mass of the BEC atom, and is the wavelength of the primary laser. The lattice wave vector, in terms of the oscillator length in the radial direction, , is given by, , where is the radial frequency. The dimensionless GPE with cubic nonlinearity is given by,
Here, and are the space- and time-modulated terms for nonlinearity and loss/gain of the condensate atoms. is the external trapping potential, which will be taken, either TOL-1 or TOL-2. To demonstrate the results, we have considered the experimental parameters for quasi BEC with Li atoms with an s-wave scattering wavelength of nm, the transverse frequency of the laser Hz and m [5]. A direct solution to the above GPE with distributed coefficients is quite nontrivial, and thus, we use the following similarity transformation, which is known to map it to a known nonlinear equation with constant coefficients [3,49,50]:
where , , , and are the space-time varying amplitude, phase, traveling coordinate, and condensate form factor, respectively. Substituting this ansatz solution into Equation (3) will generate several consistency conditions, which will help us to get the exact solution along with a mapping to the nonlinear differential equation,
where G is the nonlinearity constant, which can be controlled by tuning the s-wave scattering length and can be negative or positive for attractive and repulsive interactions, respectively. Equation (5) is a well-known nonlinear partial differential equation, whose solutions are familiar as 12 Jacobi elliptic functions (three basic functions, , , and , and their combinations for , being the modulus parameter) [51]. Therefore, it is evident that one can have a wide range of available solutions depending upon the value of m. The other consistency conditions, obtained by substituting the similarity transformation of Equation (4) into the GPE, can be written as
Here, the subscripts represent the partial differentiation with respect to the corresponding variable. On further simplification, Equation (6) reveals that the coefficient of nonlinearity and the phase are dependent upon the amplitude, whereas the amplitude itself is dependent upon the traveling coordinate.
where is a time-dependent function that arises due to the integration concerning the space coordinate to capture any explicit time dependence of the condensate profile. To find the explicit form of the traveling coordinate, we need to consider the form of the external trapping potential. After substituting the expressions of the potentials from Equations (1) and (2), respectively, we find the expressions for amplitude, phase, loss/gain, and nonlinearity for both the TOLs as,
TOL-1:
TOL-2:
and are constants related to the power of the laser beams for TOL-1 and TOL-2, respectively. represents a dimensionless constant, which is physically related to the width of the condensate profile. The depth of the TOL potentials is determined by l, and :
TOL-1:
TOL-2:
From the expression of the above-mentioned laser parameters and the evaluated solution parameters, we can now write down the complete solutions with elliptic function, , for the attractive case () and with an elliptic function, , for the repulsive case ():
TOL-1:
TOL-2:
With the exact solutions in hand, we can now perform a detailed study on the condensate densities for different values of and , which depends upon the power of the laser beam. This comparative study suggests the relationship between the tuning of the potential and the condensate densities. Here, it is worth mentioning that one gets the localized excitation , periodic excitation , and cnoidal wave excitations .
3. Various Trap Configurations and Matter-Wave Density
The tunable potential profiles are depicted in Figure 1 and Figure 2 for TOL-1 and TOL-2, respectively. Figure 1a and Figure 2a are for , whereas negative is considered in Figure 1b and Figure 2b. The potential profile for TOL-1 becomes nearly sinusoidal, such as an OL, for small with a small amplitude. It is interesting to note that TOL-1 offers a frustrated optical lattice with a periodically laid out double-well super-lattice for larger (Figure 1). Hence, this triple mixture of OL enables us to generate a hybrid mixture of two important lattice profiles within one. This particular merit belongs to the primality nature of TOL-1. On the other hand, the sinusoidal pattern of TOL-2 for smaller is quite significant, unlike TOL-1 (Figure 2). In addition, it does not provide a double-well super-lattice but a wider frustrated optical lattice in comparison to TOL-1 for larger . By changing the sign of the laser power parameters ( and ), one can interchange the positions of the frustrated optical lattice by the double-well super-lattice for TOL-1 and frustrated depth by the main lattice depth for TOL-2. These interchanges are apparent in Figure 1 and Figure 2. The above variations of the external trap are novel, and we would like to study the effects of trap-engineering on the condensate density. Here, for simplicity, we will study the solution with no loss/gain of the condensate atoms for which and constant in Equation (3). Initially, we discuss the TOLs in the attractive domain () with , and later we focus on the variations of the modulus parameter m in the TOLs for the attractive () domain. In the accompanying figures, for better illustration purposes, all the potentials are placed (scaled with a peak value of ) alongside the normalized condensate density.
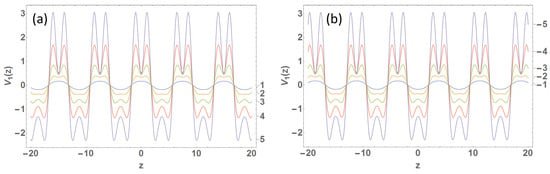
Figure 1.
A tunable TOL-1 trap by changing : (a) For and and (b) for and . The corresponding values of are labeled on the right side of every figure.
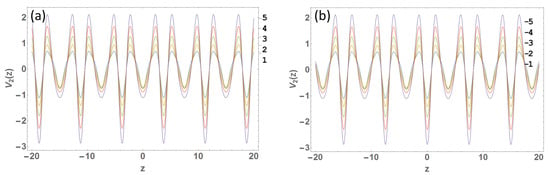
Figure 2.
A tunable TOL-2 trap by changing : (a) For and and (b) for and . The corresponding values of are labeled on the right side of every figure.
3.1. Localized Condensate Density for TOL-1
The density profiles for are illustrated in Figure 3 with the parameters , , , , and . Figure 3a approximately signifies an OL for , where the maximum of the OL is positioned at the origin (). When is increased, the maxima of the optical lattice produce smaller dips (compared to the OL-minima), which are called frustrated lattice sites, whereas the minima of the OL is associated with small elevations, producing a double well in each OL-minima. Initially (), the condensate density is a bright solitary wave with density maxima at the minima of the lattice. Soon after the appearance of the frustrated lattice sites, the condensate gets separated and becomes more localized and starts relocating the atoms in the central frustrated site for . A further increase in laser power will focus all the condensate atoms in the central frustrated site, manifesting an Anderson-like localization.
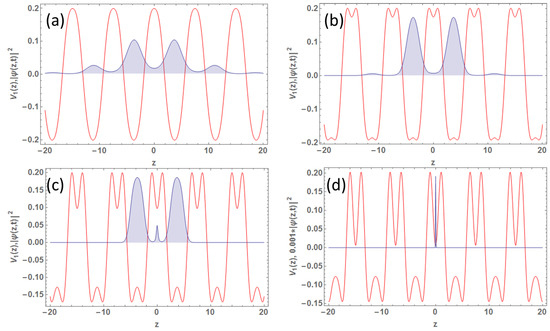
Figure 3.
Condensate density patterns (TOL-1) for : (a) for , (b) for , (c) for , and (d) for , alongside scaled potential with peak value . Other parameters are in dimensionless units: , , , , and .
The effect of the double-well super-lattice is more pronounced in Figure 4, where we take . In this domain, the center () contains a double-well, unlike the positive domain. For a larger magnitude of , the barriers of the double-wells become quite significant, which effectively bifurcates the cloud at the center. We observe a complete bifurcation of the localized cloud at the center due to the broadening of the intra-well barrier for .
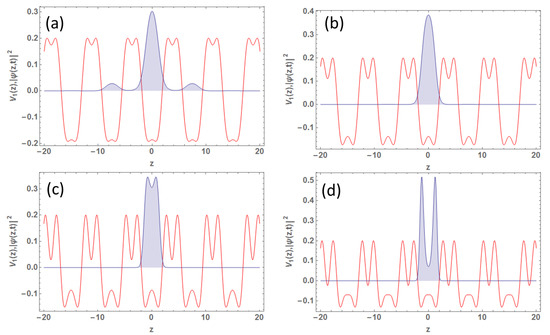
Figure 4.
Condensate density patterns (TOL-1) for : (a) for , (b) for , (c) for , and (d) for , alongside scaled potential with peak value . Other parameters are in dimensionless units: , , , , and .
3.2. Localized Condensate Density for TOL-2
The density profiles for in this case (TOL-2) is depicted in Figure 5 for , , , , and . The initial density pattern is quite different from the usual bi-periodic lattice, or the density explained for TOL-1. Even for smaller laser power, , we obtain a prominent frustrated lattice position, and accordingly, the density starts accumulating at those sites, even before reaching an overall localization of the cloud. In fact, there is competition between the two kinds of localization. Localization at frustrated sites is suppressed at the intermediate value (), whereas it dominates in Figure 5c,d and gets Anderson-localized. Figure 6 delineates the condensate density for . In this case, the central site is a deeper lattice site, but not of the frustrated kind. Hence, the finally localized cloud is not as sharp as the previous case. It is worth emphasizing that Figure 6c creates three very well-separated localized condensates. Such well-separated quantum objects can be useful for quantum information science.
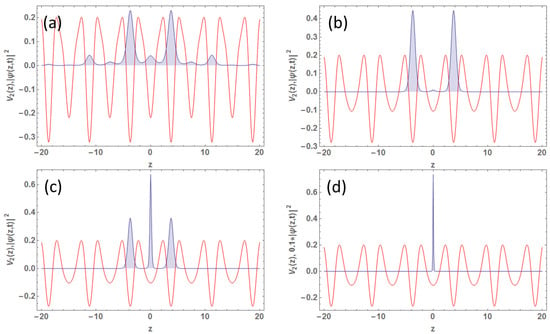
Figure 5.
Condensate density patterns (TOL-2) for : (a) for , (b) for , (c) for , and (d) for , alongside scaled potential with peak value . Other parameters are in dimensionless units: , , , , and .
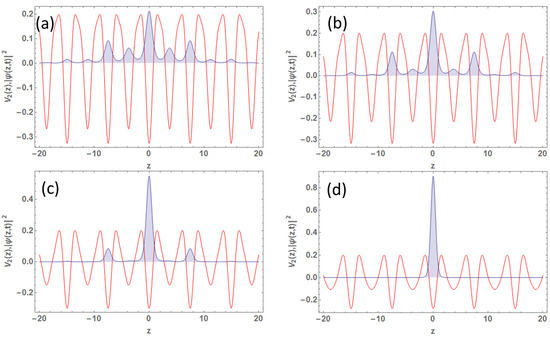
Figure 6.
Condensate density patterns (TOL-2) for : (a) for , (b) for , (c) for , and (d) for , alongside scaled potential with peak value . Other parameters are in dimensionless units: , , , , and .
3.3. Periodic and Cnoidal Matter-Wave Excitations
It is also intriguing to study the existence of periodic and cnoidal wave excitations, which are generally observed in nonlinear systems. A periodic density pattern in BEC is routinely studied in the context of OLs. Here, the modulus parameter controls the analytical form of a given type of excitation: provides periodic excitations, whereas manifests cnoidal matter-waves. In Figure 7, we have chosen a particular potential parameter for illustration ( for TOL-1 and for TOl-2). Figure 7a–d are for TOL-1, and Figure 7e–h are for TOL-2. The potential profile and the localized condensate density are also given along with periodic and cnoidal excitations for comparison. The modulations in the fine oscillation are visible in cnoidal waves, as shown in Figure 7c,g. The periodic wave also sees the effect of the potential, which is quite patterned in Figure 7d. The studies of cnoidal waves may be useful for studying supersolidity [52].
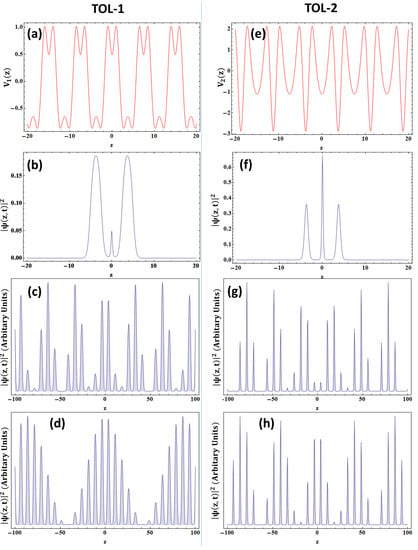
Figure 7.
Variation of condensate density with different modulus parameters : and for TOL-1 and TOL-2, respectively. The represented physical quantities for TOL-1 are (a) potential profile, (b) localized condensate density for , (c) density of cnoidal matter-wave for , and (d) density of periodic excitation for . The same physical quantities are represented for TOL- 2 in (e–h).
4. Dynamical Stability and Structural Stability
To show the fruitfulness of the exact solutions as obtained from the analytical method, stability analysis needs to be performed. The stability analyses are performed by considering two situations, namely, due to the noise in the wavefunction and hence in the density (i.e., the dynamical stability); and the in-built disturbance due to the noise in the potential (i.e., the structural stability). We have analyzed both situations from the GPE using the split-step Fourier Method (SSFM) [45,53,54] for both TOL-1 and TOL-2. We add random white noise to the wavefunctions and the potentials, then allow them to evolve with time. The noisy wavefunction and the noisy potentials are given by,
We have performed the stability analyses for a wide range of and values for TOL-1 and TOL-2. However, to demonstrate the stability of the analytically derived wavefunctions, we have chosen and . The amplitude of noise, is varied from to of the maximum value of the amplitude of the initial unperturbed wavefunction. While studying the dynamical stability, we first evolved the wavefunction without noise and the wavefunction with noise. The corresponding condensate density is compared by finding the deviation, i.e., , where stands for noisy wavefunction. We follow the same procedure for finding the deviation for structural stability where the noise is added to the potential: , where stands for the wavefunction with noise added to the potential. We have simulated the evolutions for 10000 time iterations with temporal and spatial step sizes, s and m. In Figure 8a,b, we depict the potentials (TOL-1 and TOL-2) without noise, condensate densities without noise and the deviations due to dynamical stability and structural stability for both cases. To enable us to illustrate all of them in one plot, the potentials are scaled by , and the deviations ( (in *) and (in ⨁)) are placed at () and (), respectively, where the magnitude of the deviation is represented by their amplitude variations.
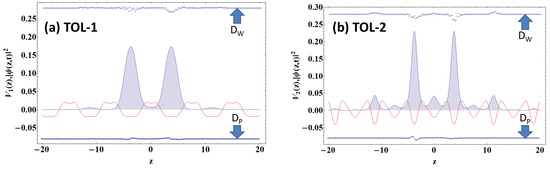
Figure 8.
Numerical stability analysis for : (a) TOL-1 with and (b) TOL-2 with . In both plots, the condensate densities are presented as filled plots, and the potential profiles are placed together by scaling with . The deviation values for dynamical stability, and for structural stability, , are shown at the coordinates () (upper plots) and () (lower plots), respectively, for both (a) and (b).
For Figure 8a,b the deviation values (in *) and (in ⨁) are shown in the figures with shifted coordinates at () (upper plots) and () (lower plots), respectively, with the potential being scaled with . We obtain attractive results where the solutions are extremely stable for structural noise incorporation, and the maximum deviation becomes only for both the potential profiles (TOL-1 and TOL-2). The dynamical stability also suggests considerably stable solutions, having a maximum deviation below . Hence, both the proposed triple optical lattices offer experimentally feasible platforms to study various solitary waves in BEC.
5. Conclusions
Even and odd combinations of OLs physically provide distinct environments for the condensate. We have introduced two varieties of odd numbered optical lattice-combination for BEC, which are not given due emphasize in the theory-literature, are addressed with triple optical lattices which manifest hybrid trap with a highly stable condensate compared to other traps. In addition to the localized excitation, periodic and cnoidal waves are also studied. Anderson localization, bifurcation of condensate at the center and a competition of different localizations upon trap engineering in these TOLs are reported. These triple mixtures of optical lattices impart better tunability on the condensate profile, which has made this system a true quantum simulator. For checking the utility of the results for experiments, we have performed dynamical and structural stability analyses. The solutions have come out as extremely stable for structural noise incorporation, having deviation below for both the potential profiles. The dynamical stability also suggests considerably stable solutions, having deviation below . Hence, both the proposed triple optical lattices offer favorable platforms to study various solitary waves in BEC and possible technological implications.
Author Contributions
Conceptualization, U.R.; formal analysis, P.B., B.H. and S.R.; investigation, P.B., B.H., S.R. and U.R.; methodology, P.B. and U.R.; software, B.H.; validation, S.R. and U.R.; visualization, P.B. and S.R.; writing—original draft preparation, P.B. and B.H.; writing—review and editing, S.R. and U.R.; supervision, U.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
P.B. is thankful to the Prime Minister Research Fellowship (PMRF), Government of India, for the financial support throughout the research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pethick, C.J.; Smith, H. Bose–Einstein Condensation in Dilute Gases; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Nath, A.; Roy, U. A unified model for an external trap in a cigar-shaped Bose–Einstein condensate. J. Phys. A Math. Theor. 2014, 47, 415301. [Google Scholar] [CrossRef]
- Salasnich, L.; Adhikari, S.K. Dimensional reduction and localization of a Bose-Einstein condensate in a quasi-1D bichromatic optical lattice. Acta Phys. Pol. A 2015, 128, 979. [Google Scholar] [CrossRef]
- Khaykovich, L.; Schreck, F.; Ferrari, G.; Bourdel, T.; Cubizolles, J.; Carr, L.D.; Castin, Y.; Salomon, C. Formation of a matter-wave bright soliton. Science 2002, 296, 1290–1293. [Google Scholar] [CrossRef] [PubMed]
- Schulte, T.; Drenkelforth, S.; Kruse, J.; Ertmer, W.; Arlt, J.; Sacha, K.; Zakrzewski, J.; Lewenstein, M. Routes towards Anderson-like localization of Bose-Einstein condensates in disordered optical lattices. Phys. Rev. Lett. 2005, 95, 170411. [Google Scholar] [CrossRef] [PubMed]
- Billy, J.; Josse, V.; Zuo, Z.; Bernard, A.; Hambrecht, B.; Lugan, P.; Clément, D.; Sanchez-Palencia, L.; Bouyer, P.; Aspect, A. Direct observation of Anderson localization of matter waves in a controlled disorder. Nature 2008, 453, 891–894. [Google Scholar] [CrossRef]
- Nath, A.; Bera, J.; Ghosh, S.; Roy, U. exact Analytical Model for Bose-einstein condensate at negative temperature. Sci. Rep. 2020, 10, 9016. [Google Scholar] [CrossRef]
- Kundu, N.; Nath, A.; Bera, J.; Ghosh, S.; Roy, U. Synergy between the Negative Absolute Temperature and the External Trap for a Bose-Einstein Condensate under Optical Lattices. Phys. Lett. A 2022, 427, 127922. [Google Scholar] [CrossRef]
- Yamamoto, D.; Fukuhara, T.; Danshita, I. Frustrated quantum magnetism with Bose gases in triangular optical lattices at negative absolute temperatures. Commun. Phys. 2020, 3, 56. [Google Scholar] [CrossRef]
- D’Errico, C.; Burchianti, A.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Minardi, F.; Fort, C. Observation of quantum droplets in a heteronuclear bosonic mixture. Phys. Rev. Res. 2019, 1, 033155. [Google Scholar] [CrossRef]
- Perali, A.; Pieri, P.; Pisani, L.; Strinati, G.C. BCS-BEC crossover at finite temperature for superfluid trapped Fermi atoms. Phys. Rev. Lett. 2004, 92, 220404. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Stajic, J.; Tan, S.; Levin, K. BCS–BEC crossover: From high temperature superconductors to ultracold superfluids. Phys. Rep. 2005, 412, 1–88. [Google Scholar] [CrossRef]
- Zwerger, W. The BCS-BEC Crossover and the Unitary Fermi Gas; Springer: Berlin/Heidelberg, Germany, 2011; Volume 836. [Google Scholar]
- Cronin, A.D.; Schmiedmayer, J.; Pritchard, D.E. Optics and interferometry with atoms and molecules. Rev. Mod. Phys. 2009, 81, 1051. [Google Scholar] [CrossRef]
- Billam, T.; Cornish, S.; Gardiner, S. Realizing bright-matter-wave-soliton collisions with controlled relative phase. Phys. Rev. A 2011, 83, 041602. [Google Scholar] [CrossRef]
- Struck, J.; Ölschläger, C.; Le Targat, R.; Soltan-Panahi, P.; Eckardt, A.; Lewenstein, M.; Windpassinger, P.; Sengstock, K. Quantum simulation of frustrated classical magnetism in triangular optical lattices. Science 2011, 333, 996–999. [Google Scholar] [CrossRef]
- Balents, L. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. [Google Scholar] [CrossRef]
- Yan, S.; Huse, D.A.; White, S.R. Spin-liquid ground state of the S= 1/2 kagome Heisenberg antiferromagnet. Science 2011, 332, 1173–1176. [Google Scholar] [CrossRef]
- Qiu, X.; Zou, J.; Qi, X.; Li, X. Precise programmable quantum simulations with optical lattices. Npj Quantum Inf. 2020, 6, 87. [Google Scholar] [CrossRef]
- Windpassinger, P.; Sengstock, K. Engineering novel optical lattices. Rep. Prog. Phys. 2013, 76, 086401. [Google Scholar] [CrossRef]
- Kundu, N.; Ghosh, S.; Roy, U. Quantum Simulation of Rogue Waves in Bose-Einstein Condensate: An Exact Analytical Method. Phys. Lett. A 2022, 128335. [Google Scholar] [CrossRef]
- Argüello-Luengo, J.; González-Tudela, A.; Shi, T.; Zoller, P.; Cirac, J.I. Quantum simulation of two-dimensional quantum chemistry in optical lattices. Phys. Rev. Res. 2020, 2, 042013. [Google Scholar] [CrossRef]
- Arlinghaus, S.; Holthaus, M. Controlled wave-packet manipulation with driven optical lattices. Phys. Rev. A 2011, 84, 063617. [Google Scholar] [CrossRef]
- Covey, J.P.; Moses, S.A.; Gärttner, M.; Safavi-Naini, A.; Miecnikowski, M.T.; Fu, Z.; Schachenmayer, J.; Julienne, P.S.; Rey, A.M.; Jin, D.S.; et al. Doublon dynamics and polar molecule production in an optical lattice. Nat. Commun. 2016, 7, 11279. [Google Scholar] [CrossRef] [PubMed]
- Casert, C.; Mills, K.; Vieijra, T.; Ryckebusch, J.; Tamblyn, I. Optical lattice experiments at unobserved conditions with generative adversarial deep learning. Phys. Rev. Res. 2021, 3, 033267. [Google Scholar] [CrossRef]
- Homid, A.; Abdel-Aty, M.; Qasymeh, M.; Eleuch, H. Efficient quantum gates and algorithms in an engineered optical lattice. Sci. Rep. 2021, 11, 15402. [Google Scholar] [CrossRef]
- Katori, H. Optical lattice clocks and quantum metrology. Nat. Photon. 2011, 5, 203–210. [Google Scholar] [CrossRef]
- Ghosh, S.; Bera, J.; Panigrahi, P.K.; Roy, U. Sub-fourier quantum metrology through bright solitary trains in Bose–Einstein condensate. Int. J. Quantum Inf. 2019, 17, 1950019. [Google Scholar] [CrossRef]
- Cameron, A.R.; Cheng, S.W.; Schwarz, S.; Kapahi, C.; Sarenac, D.; Grabowecky, M.; Cory, D.G.; Jennewein, T.; Pushin, D.A.; Resch, K.J. Remote state preparation of single-photon orbital-angular-momentum lattices. Phys. Rev. A 2021, 104, L051701. [Google Scholar] [CrossRef]
- Simon, D.S. Quantum sensors: Improved optical measurement via specialized quantum states. J. Sens. 2016, 2016, 6051286. [Google Scholar] [CrossRef]
- Yang, B.; Sun, H.; Huang, C.J.; Wang, H.Y.; Deng, Y.; Dai, H.N.; Yuan, Z.S.; Pan, J.W. Cooling and entangling ultracold atoms in optical lattices. Science 2020, 369, 550–553. [Google Scholar] [CrossRef]
- Howard, L.; Weinhold, T.; Shahandeh, F.; Combes, J.; Vanner, M.; White, A.; Ringbauer, M. Quantum hypercube states. Phys. Rev. Lett. 2019, 123, 020402. [Google Scholar] [CrossRef] [Green Version]
- Shukla, N.; Akhtar, N.; Sanders, B.C. Quantum tetrachotomous states: Superposition of four coherent states on a line in phase space. Phys. Rev. A 2019, 99, 063813. [Google Scholar] [CrossRef]
- Shukla, N.; Nimmrichter, S.; Sanders, B.C. Squeezed comb states. Phys. Rev. A 2021, 103, 012408. [Google Scholar] [CrossRef]
- Roy, U.; Atre, R.; Sudheesh, C.; Kumar, C.N.; Panigrahi, P.K. Complex solitons in Bose–Einstein condensates with two-and three-body interactions. J. Phys. B At. Mol. Opt. 2010, 43, 025003. [Google Scholar] [CrossRef]
- Serkin, V.N.; Hasegawa, A. Novel soliton solutions of the nonlinear Schrödinger equation model. Phys. Rev. Lett. 2000, 85, 4502. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Zhang, Z.; Liu, W. Dynamics of a bright soliton in Bose-Einstein condensates with time-dependent atomic scattering length in an expulsive parabolic potential. Phys. Rev. Lett. 2005, 94, 050402. [Google Scholar] [CrossRef]
- Belmonte-Beitia, J.; Pérez-García, V.M.; Vekslerchik, V.; Torres, P.J. Lie symmetries and solitons in nonlinear systems with spatially inhomogeneous nonlinearities. Phys. Rev. Lett. 2007, 98, 064102. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, D. Matter-wave solutions in Bose-Einstein condensates with harmonic and Gaussian potentials. Phys. Rev. E 2012, 85, 056608. [Google Scholar] [CrossRef]
- Bludov, Y.V.; Yan, Z.; Konotop, V. Dynamics of inhomogeneous condensates in contact with a surface. Phys. Rev. A 2010, 81, 063610. [Google Scholar] [CrossRef]
- Bronski, J.C.; Carr, L.D.; Deconinck, B.; Kutz, J.N. Bose-Einstein condensates in standing waves: The cubic nonlinear Schrödinger equation with a periodic potential. Phys. Rev. Lett. 2001, 86, 1402. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.; Salasnich, L. Localization of a Bose-Einstein condensate in a bichromatic optical lattice. Phys. Rev. A 2009, 80, 023606. [Google Scholar] [CrossRef] [Green Version]
- Nath, A.; Roy, U. Bose–Einstein condensate in a bichromatic optical lattice: An exact analytical model. Laser Phys. Lett. 2014, 11, 115501. [Google Scholar] [CrossRef]
- Halder, B.; Ghosh, S.; Basu, P.; Bera, J.; Malomed, B.; Roy, U. Exact Solutions for Solitary Waves in a Bose-Einstein Condensate under the Action of a Four-Color Optical Lattice. Symmetry 2021, 14, 49. [Google Scholar] [CrossRef]
- Dell’Anna, L.; Mazzarella, G.; Penna, V.; Salasnich, L. Entanglement entropy and macroscopic quantum states with dipolar bosons in a triple-well potential. Phys. Rev. A 2013, 87, 053620. [Google Scholar] [CrossRef]
- Witthaut, D.; Trimborn, F.; Hennig, H.; Kordas, G.; Geisel, T.; Wimberger, S. Beyond mean-field dynamics in open Bose-Hubbard chains. Phys. Rev. A 2011, 83, 063608. [Google Scholar] [CrossRef]
- Dutta, S.; Tsatsos, M.C.; Basu, S.; Lode, A.U. Management of the correlations of UltracoldBosons in triple wells. New J. Phys. 2019, 21, 053044. [Google Scholar] [CrossRef]
- Kengne, E.; Liu, W.M.; Malomed, B.A. Spatiotemporal engineering of matter-wave solitons in Bose–Einstein condensates. Phys. Rep. 2021, 899, 1–62. [Google Scholar] [CrossRef]
- Salasnich, L.; Parola, A.; Reatto, L. Effective wave equations for the dynamics of cigar-shaped and disk-shaped Bose condensates. Phys. Rev. A 2002, 65, 043614. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1964; Volume 55.
- Martone, G.I.; Recati, A.; Pavloff, N. Supersolidity of cnoidal waves in an ultracold Bose gas. Phys. Rev. Res. 2021, 3, 013143. [Google Scholar] [CrossRef]
- Nath, A.; Bera, J.; Ghosh, S.; Panigrahi, P.K.; Roy, U. Soliton dynamics for an ingenious trap combination in a Bose-Einstein condensate. Eur. Phys. J. D 2020, 74, 27. [Google Scholar] [CrossRef]
- Bera, J.; Ghosh, S.; Salasnich, L.; Roy, U. Matter-wave fractional revivals in a ring waveguide. Phys. Rev. A 2020, 102, 063323. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).