Detection of Two Phenomena Opposite to the Expected Ones
Abstract
1. Introduction
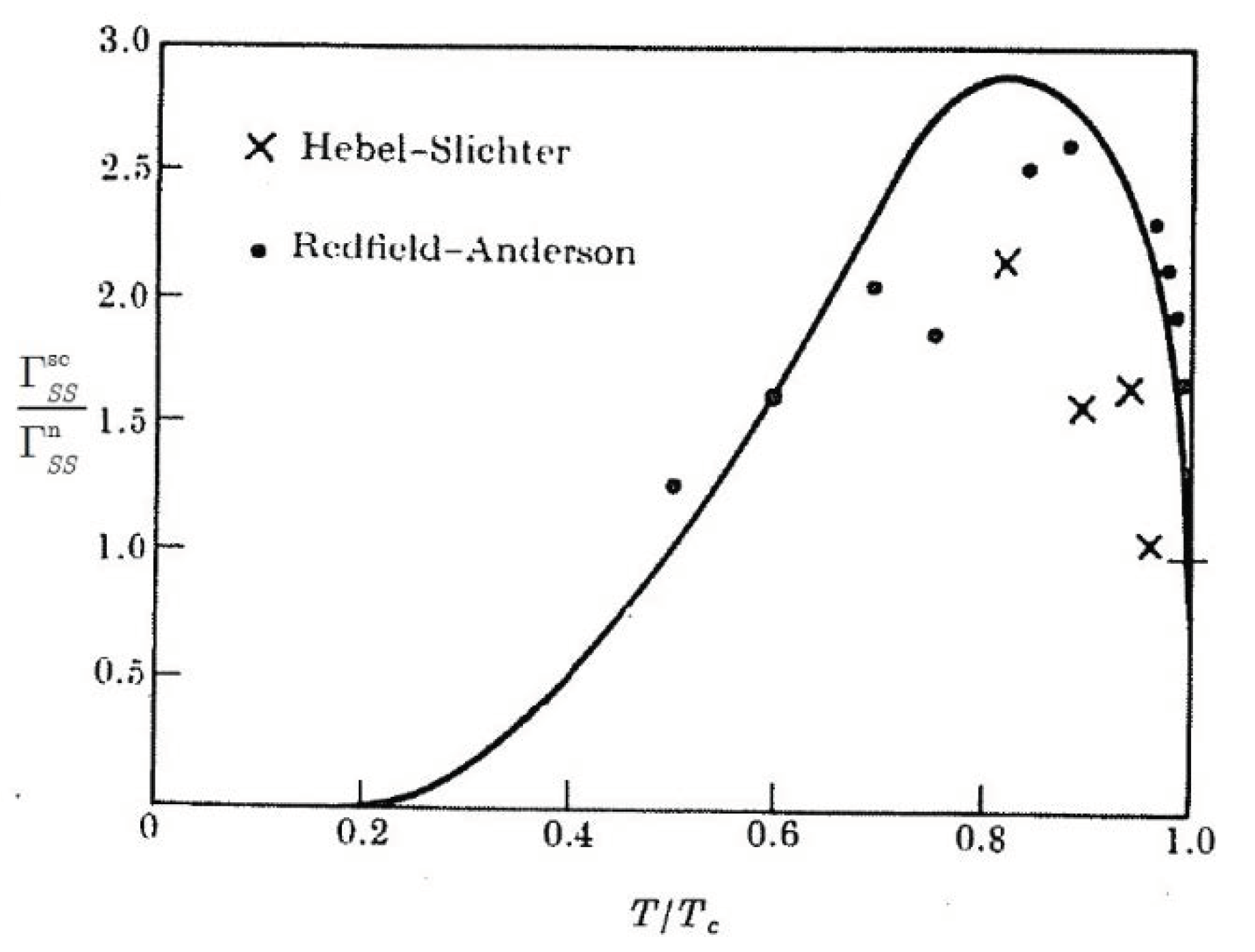
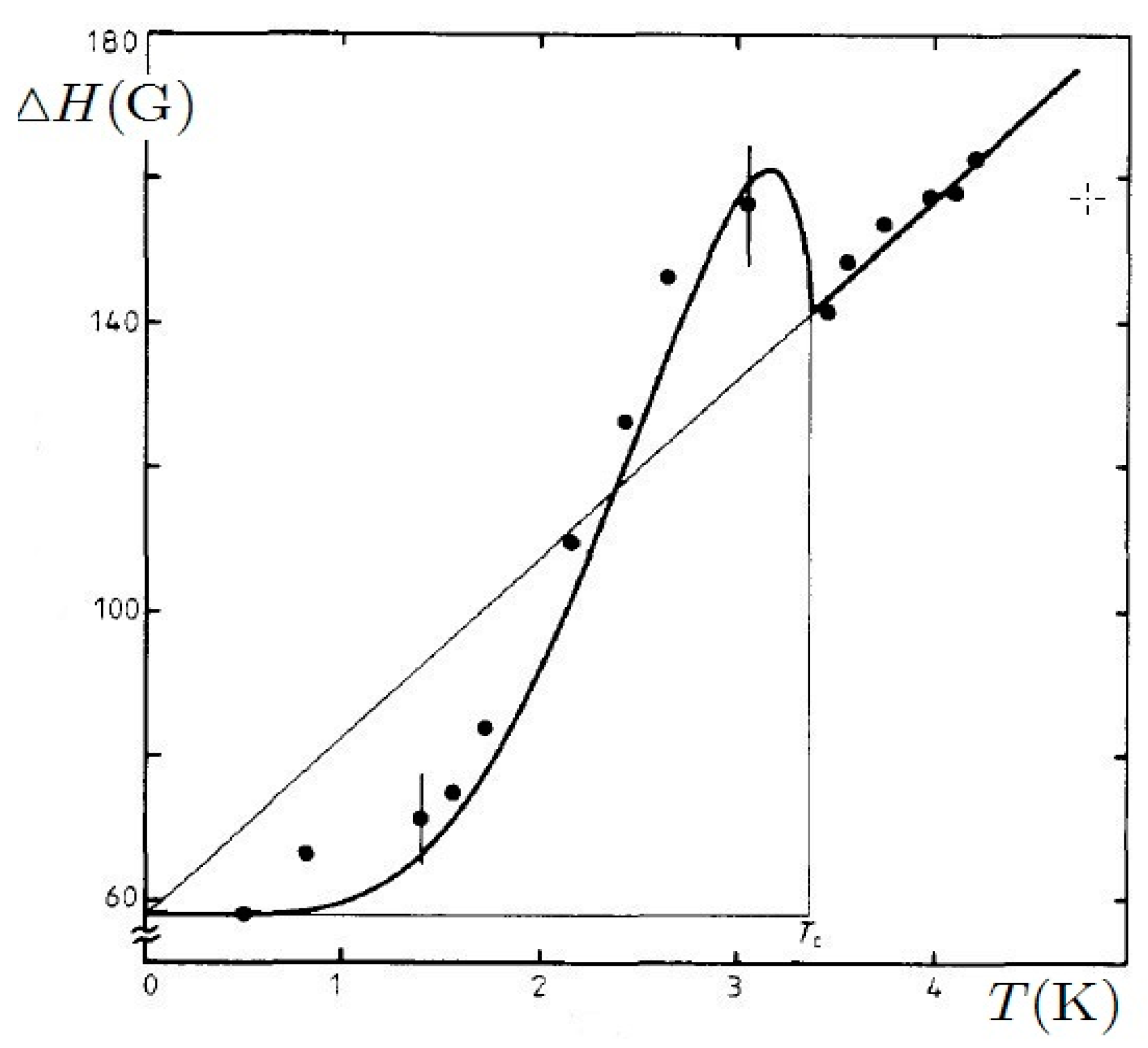
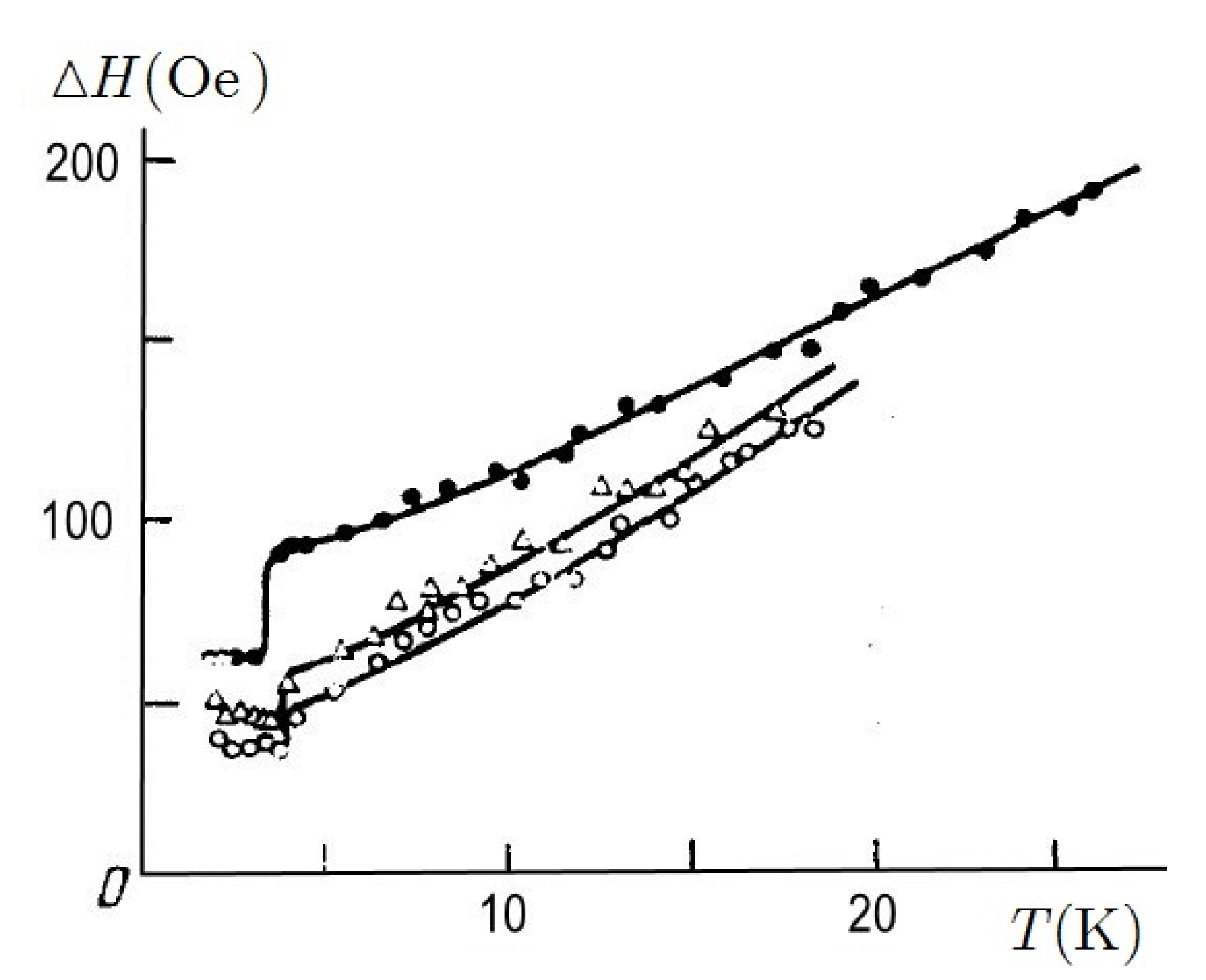
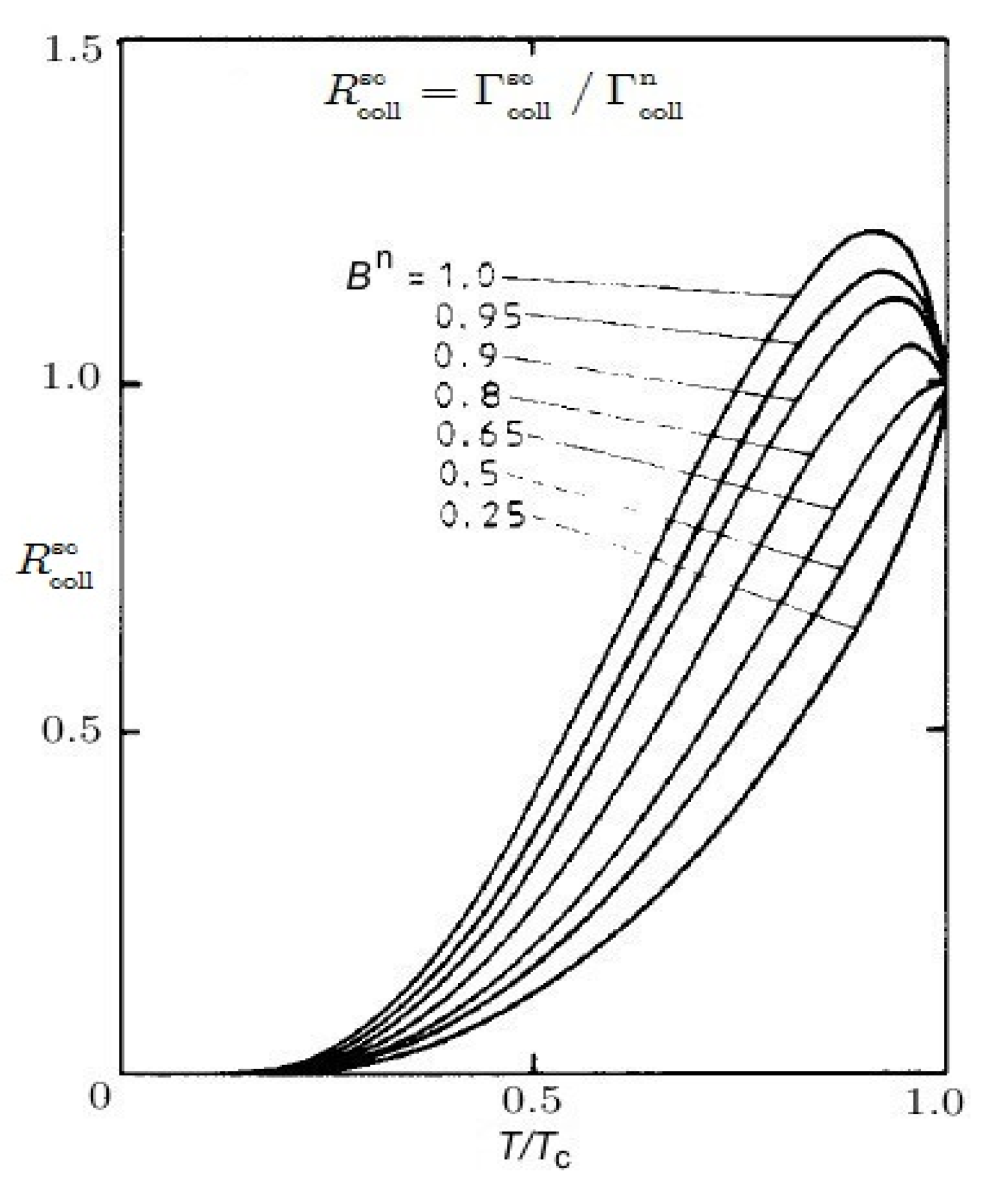
2. Peculiarities of the EPR Signal from Impurities in Superconductors
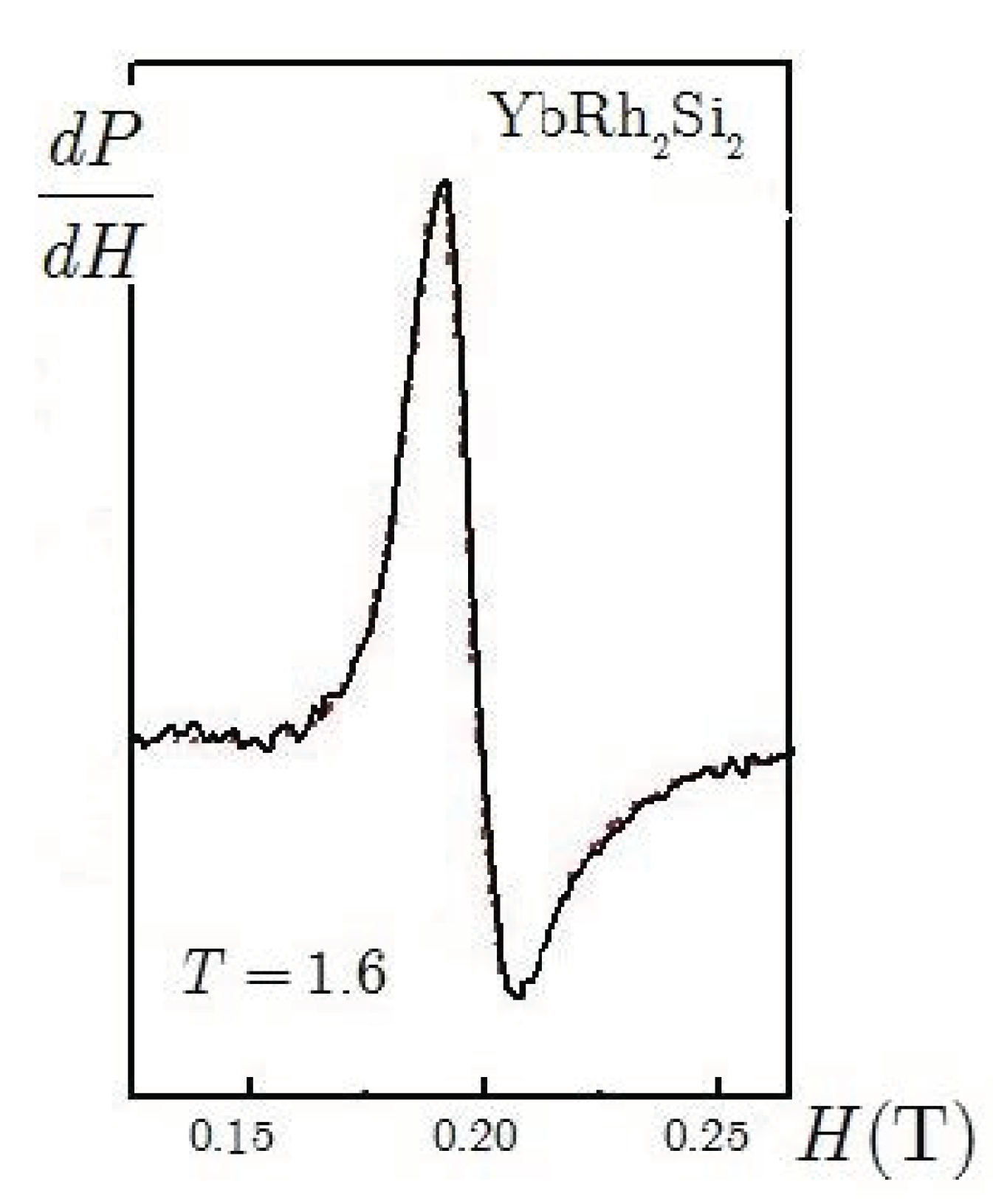
3. The EPR Signal below the Kondo Temperature
4. Conclusions
“60 years after the discovery of EPR in Kazan the method is able to contribute at the forefront in condensed matter physics, such as high temperature superconductivity. This is especially so if properly employed, and the results theoretically interpreted in a scholar way, as well as relate them to other important experiments. Because the EPR spectrometers used are standard, and low cost as are the samples, the research budgets are low; this puts the scientist in a serene mood without stress.”
Funding
Acknowledgments
Conflicts of Interest
References
- Müller, K.A. Paramagnetic resonance of Fe3+ in single crystals of SrTiO3. Helv. Phys. Acta 1958, 31, 173–204. (In German) [Google Scholar]
- Müller, K.A.; Kool, T.W. (Eds.) Properties of Perovskites and Other Oxides; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2010. [Google Scholar]
- Barnes, S.E. Theory of electron spin resonance of magnetic ions in metals. Adv. Phys. 1981, 30, 801–938. [Google Scholar] [CrossRef]
- Kochelaev, B.I.; Safina, A.M. Electron-Bottleneck Mode for Magnetic Impurities in Metal in the Case of Anisotropic Exchange Interactions. Phys. Solid State 2004, 46, 226–230. [Google Scholar] [CrossRef]
- Schrieffer, J.R. Theory of Superconductivity; W.A. Benjamin: Menlo Park, CA, USA, 1964. [Google Scholar]
- Hebel, L.C.; Slichter, C.P. Nuclear Spin Relaxation Rate in Normal and Superconducting Aluminium. Phys. Rev. 1959, 113, 1504–1519. [Google Scholar] [CrossRef]
- Redfield, A.G. Nuclear Spin Relaxation Time in Superconducting Aluminum. Phys. Rev. Lett. 1959, 3, 85–86. [Google Scholar] [CrossRef]
- Hebel, L.C. Theory of Nuclear Spin Relaxation in Superconductors. Phys. Rev. 1959, 116, 79–81. [Google Scholar] [CrossRef]
- Rettori, R.; Davidov, D.; Chaikin, P.; Orbach, R. Magnetic Resonance of a Localized Magnetic Moment in the Superconducting State: LaRu2:Gd. Phys. Rev. Lett. 1973, 30, 437–440. [Google Scholar] [CrossRef]
- Davidov, D.; Rettori, R.; Kim, H.M. Electron-spin resonance of a localized moment in the superconducting state: BRu2:Gd (B=La,Ce,Th). Phys. Rev. B 1974, 9, 147–153. [Google Scholar] [CrossRef]
- Tagirov, L.R.; Trutnev, K.F. Spin kinetics and EPR in superconductors. J. Phys. F Met. Phys. 1987, 17, 695–713. [Google Scholar] [CrossRef]
- Alekseevsky, N.E.; Garifullin, I.A.; Kochelaev, B.I.; Kharakhashyan, E.G. Electron resonance with localized magnetic moments of Er in superconducting La. Sov. Phys. JETP Lett. 1973, 18, 189–191. [Google Scholar]
- Alekseevsky, N.E.; Garifullin, I.A.; Kochelaev, B.I.; Kharakhashyan, E.G. Electron paramagnetic resonance for localized magnetic states in the superconducting La–Er system. Sov. Phys. JETP 1977, 45, 799–804. [Google Scholar]
- Kochelaev, B.I.; Kharakhashyan, E.G.; Garifullin, I.A.; Alekseevsky, N.E. Electron paramagnetic resonance of localized moments in a type-II superconductor. In Proceedings of the 18th AMPERE Congress, Nottingham, UK, 9–14 September 1974; North-Holland Pub. Co.: Amsterdam, The Netherlands, 1975; pp. 23–24. [Google Scholar]
- Maki, K. Theory of Electron-Spin Resonance in Gapless Superconductors. Phys. Rev. B 1973, 8, 191–199. [Google Scholar] [CrossRef]
- Kosov, A.A.; Kochelaev, B.I. Electron paramagnetic resonance on the localized magnetic moments in superconductors. Sov. Phys. JETP 1978, 47, 75–83. [Google Scholar]
- Kochelaev, B.I.; Tagirov, L.R.; Khusainov, M.G. Spatial dispersion of the spin susceptibility of conduction electrons in superconductors. Sov. Phys. JETP 1979, 49, 291–301. [Google Scholar]
- Kochelaev, B.I.; Tagirov, L.R. “Exchange-Field-Narrowing” process for the inhomogeneously broadened EPR lines in superconductors. Solid State Commun. 1985, 53, 961–966. [Google Scholar] [CrossRef]
- Bogolyubov, N.N.; Tyablikov, S.V. On an application of perturbation theory to the polar model of a metal. Zhurnal Ehksperimental’noj i Teoreticheskoj Fiziki 1949, 19, 251–255. [Google Scholar]
- Kochelaev, B.I. Magnetic properties and spin kinetics of a heavy-fermion Kondo lattice. Low Temp. Phys. 2017, 43, 93–103. [Google Scholar] [CrossRef][Green Version]
- Kondo, J. Resistance Minimum in Dilute Magnetic Alloys. Progr. Theor. Phys. 1964, 32, 37–49. [Google Scholar] [CrossRef]
- Baberschke, K.; Tsang, E. ESR Study of the Kondo Effect in Au:Yb. Phys. Rev. Lett. 1980, 45, 1512. [Google Scholar] [CrossRef]
- Abrikosov, A.A. Electron scattering on magnetic impurities in metals and anomalous resistivity effects. Physics 1965, 2, 5–20. [Google Scholar] [CrossRef]
- Suhl, H. Dispersion Theory of the Kondo Effect. Phys. Rev. 1965, 138, 515–522. [Google Scholar] [CrossRef]
- Sichelschmidt, J.; Ivanshin, V.A.; Ferstl, J.; Geibel, C.; Steglich, F. Low Temperature Electron Spin Resonance of the Kondo Ion in a Heavy Fermion Metal: YbRh2Si2. Phys. Rev. Lett. 2003, 91, 156401. [Google Scholar] [CrossRef]
- Sichelschmidt, J.; Wykhoff, J.; Krug von Nidda, H.-A.; Ferstl, J.; Geibel, C.; Steglich, F. Spin dynamics of YbRh2Si2 observed by electron spin resonance. J. Phys. Condens. Matter 2007, 19, 116204. [Google Scholar] [CrossRef]
- Anderson, P.W. A poor man’s derivation of scaling laws for the Kondo problem. J. Phys. C Solid State Phys. 1970, 3, 2436–2441. [Google Scholar] [CrossRef]
- Kochelaev, B.I.; Belov, S.I.; Skvortsova, A.M.; Kutuzov, A.S.; Sichelschmidt, J.; Wykhoff, J.; Geibel, C.; Steglich, F. Why could electron spin resonance be observed in a heavy fermion Kondo lattice? Eur. Phys. J. B 2009, 72, 485–489. [Google Scholar] [CrossRef]
- Kochelaev, B.I. Electron Paramagnetic Resonance in Superconducting Cuprates. In Springer Series in Materials Science 255: High-Tc Copper Oxide Superconductors and Related Novel Materials Dedicated to Prof. K. A. Müller on the Occasion of His 90th Birthday; Bussmann-Holder, A., Keller, H., Bianconi, A., Eds.; Springer: New York, NY, USA, 2017; pp. 165–175. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kochelaev, B.I. Detection of Two Phenomena Opposite to the Expected Ones. Condens. Matter 2020, 5, 56. https://doi.org/10.3390/condmat5040056
Kochelaev BI. Detection of Two Phenomena Opposite to the Expected Ones. Condensed Matter. 2020; 5(4):56. https://doi.org/10.3390/condmat5040056
Chicago/Turabian StyleKochelaev, Boris I. 2020. "Detection of Two Phenomena Opposite to the Expected Ones" Condensed Matter 5, no. 4: 56. https://doi.org/10.3390/condmat5040056
APA StyleKochelaev, B. I. (2020). Detection of Two Phenomena Opposite to the Expected Ones. Condensed Matter, 5(4), 56. https://doi.org/10.3390/condmat5040056



