SrTiO3—Glimpses of an Inexhaustible Source of Novel Solid State Phenomena
Abstract
1. Introduction
2. Routes of SrTiO3 toward Ferroelectricity and Other Collective States
- (i)
- In 1976, Uwe and Sakudo [5] succeeded in stabilizing uniaxial ferroelectricity in STO at liquid He temperature by intraplanar symmetry breaking with uniaxial stress perpendicularly to the c axis, . This was the first experience to overcome quantum paraelectricity of STO by an external perturbation.
- (ii)
- About 20 years later, in 1999, Itoh et al. [6] discovered a very efficient internal perturbation via isotopic exchange of 16O by 18O in order to establish the FE state at T0 ≈ 25–50 K.
- (iii)
- Again, 20 years later, in 2019, Nova et al. [7] realized transient FE in STO being metastable up to T > 290 K under optical strain due to intense femtosecond laser pulses, while Li et al. [8] recorded similar events after photoexcitation of quantum paraelectric STO with THz laser pulses in resonance with the FE soft mode at T < 36 K.
- (iv)
- Metallic behavior of n-type STO has been achieved by substituting transition-metal dopants, e.g., La3+ for Sr2+ [9], Nb5+ for Ti4+, or by reducing pure STO into SrTiO3-δ, 0 < δ < 1, where each oxygen vacancy generates two “doped” electrons [10]. The insulator-to-metal transformation occurs at a relatively low critical electron density n ≈ 1018 cm−3 [11], i.e., two orders of magnitude less than in the analogous case of barium titanate [12]. Here the word “metal” is not used in its common material meaning but merely stands for featuring metallic electronic conduction. A combined method of substitution and reduction was utilized in the case of Cr-doped STO [11]. A significant spatial correlation between oxygen vacancies and Cr3+ ions in bulk was established in thermally reduced Cr-doped STO. In the presence of electron donors, the Cr atoms change their valence from 4+ to 3+. Consequently, this reduction drives a symmetry change of the crystal field experienced by the Cr ions from cubic to axial [11], which may be controlled by means of thermal annealing and/or doping with electron donors. This capability of controlling oxygen vacancies or transition-metal dopants has been essential for the development of semiconducting electronic devices [13].
- (v)
- Theoretical predictions of superconductivity in degenerate semiconductors motivated research on reduced n-type STO, which revealed the critical temperature ≈ 0.28 K as early as 1964 [14]. However, 32 years later, perovskite-like cuprates were to open the door to modern high- superconductivity with ≈ 30 K [15] and to the physics Nobel Prize [16]. On the other hand, gated n-type STO has reached at most only ≈ 0.6 K [17].
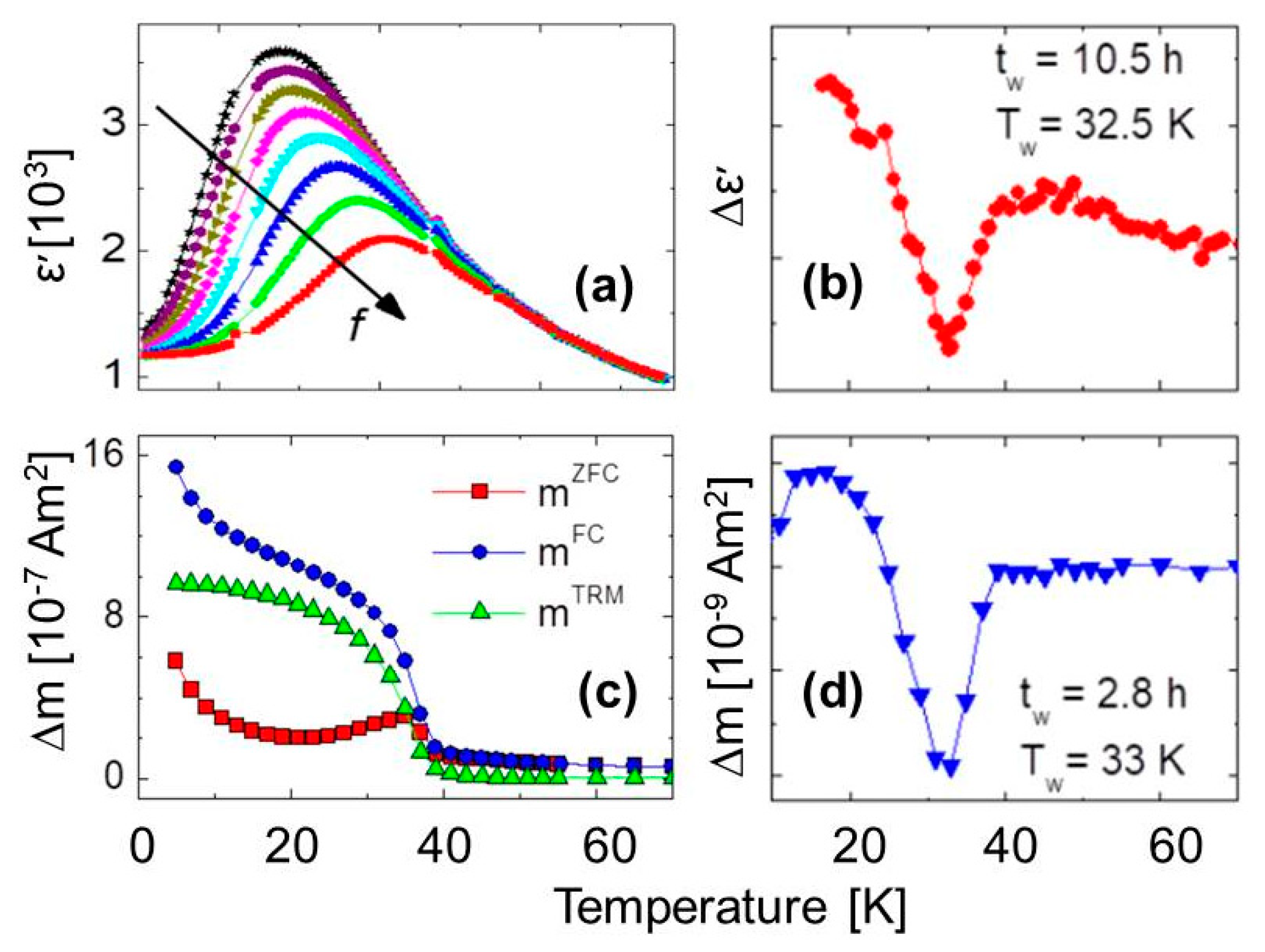
3. The Magnetoelectric Multiglass (Sr,Mn)TiO3
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Glossary
| FC | field cooling |
| FE | ferroelectric or ferroelectricity |
| FH | field heating |
| LB | linear birefringence |
| LSAT | (LaAlO3)0.29(SrAl0.5Ta0.5O3)0.71 |
| MT | metallic or metallicity |
| PLE | pulsed laser epitaxy |
| PNR | polar nanoregion |
| PT | phase transition |
| SC | superconductive or superconductivity |
| SCT | Sr1-xCaxTiO3 |
| STO | SrTiO3 |
| TRM | thermoremanence |
| ZFC | zero-field cooling |
| ZFH | zero-field heating |
References
- Müller, K.A.; Burkard, H. SrTiO3: An intrinsic quantum paraelectric below 4 K. Phys. Rev. B 1979, 19, 3593–3602. [Google Scholar] [CrossRef]
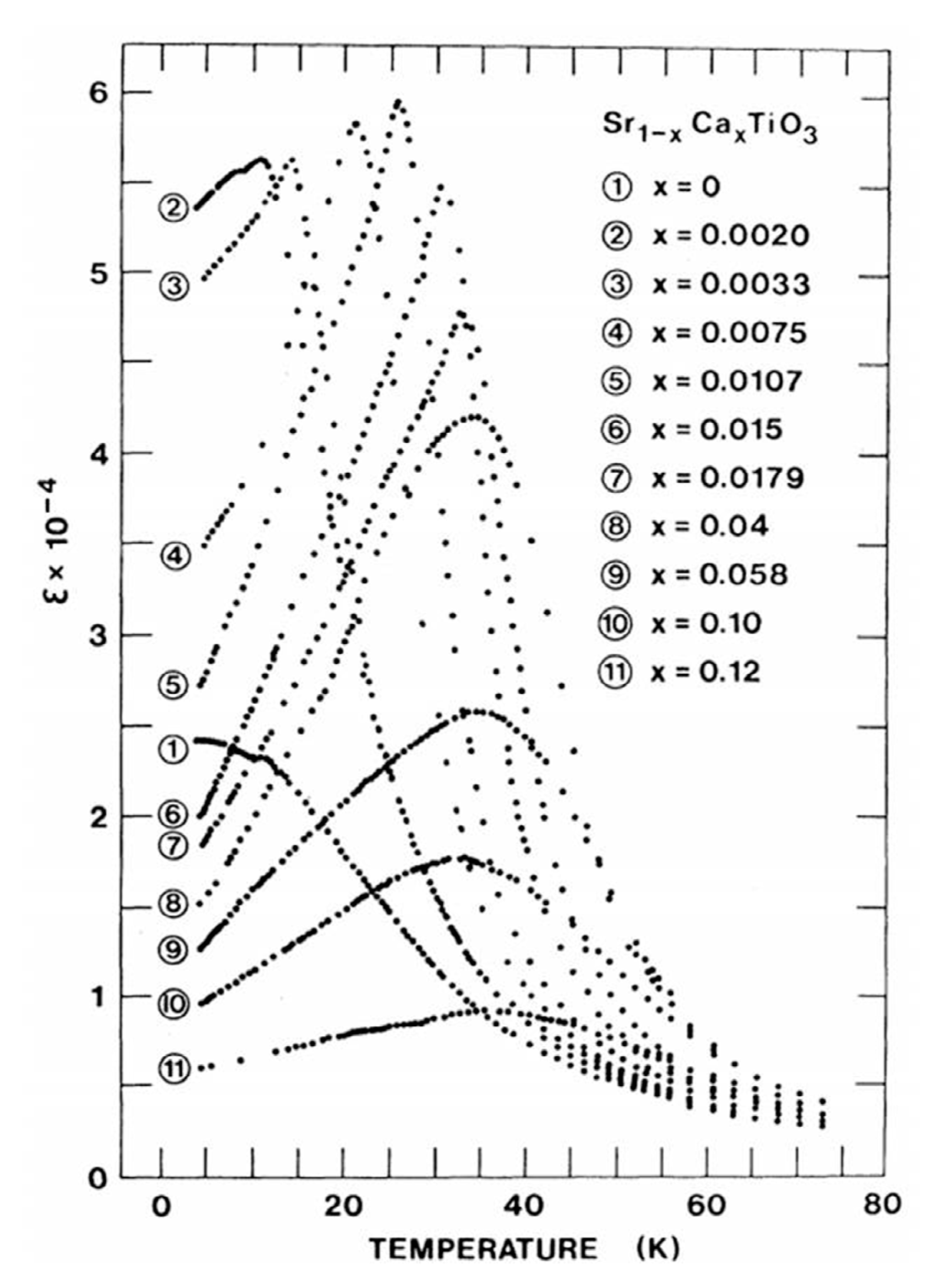
- Bednorz, J.G.; Müller, K.A. Sr1-xCaxTiO3: An XY quantum ferroelectric with transition to randomness. Phys. Rev. Lett. 1984, 52, 2289–2293. [Google Scholar] [CrossRef]
- Dec, J.; Kleemann, W. From Barrett to generalized quantum Curie-Weiss law. Solid State Commun. 1998, 106, 695–699. [Google Scholar] [CrossRef]
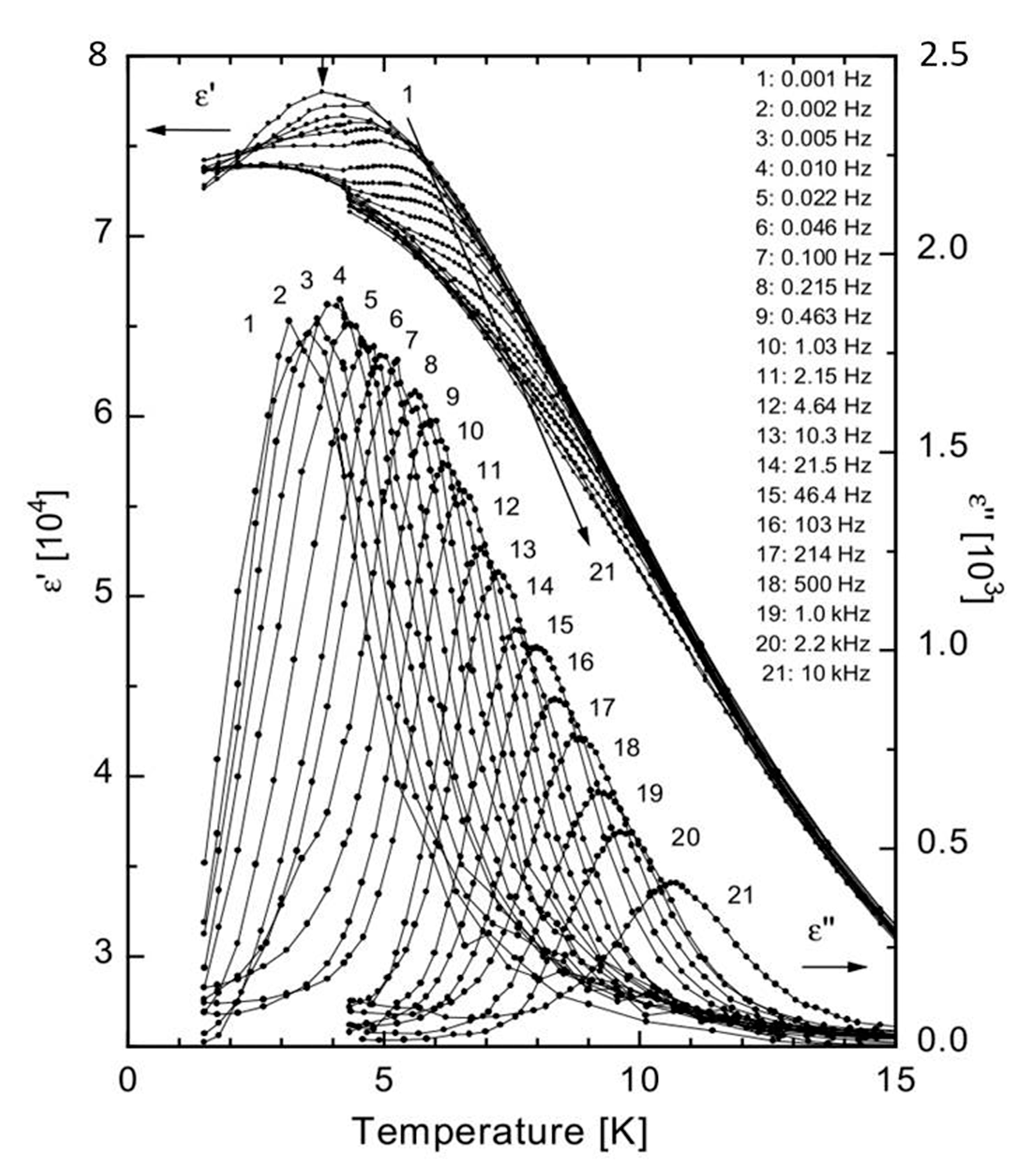
- Rowley, S.E.; Spalek, L.J.; Smith, R.P.; Dean, M.P.M.; Itoh, M.; Scott, J.F.; Lonzarich, G.G.; Saxena, S.S. Ferroelectric quantum criticality. Nat. Phys. 2014, 10, 367–372. [Google Scholar] [CrossRef]
- Uwe, H.; Sakudo, T. Stress-induced Ferroelectricity and soft phonon modes in SrTiO3. Phys. Rev. B 1976, 13, 271–286. [Google Scholar] [CrossRef]
- Itoh, M.; Wang, R.; Inaguma, Y.; Yamaguchi, T.; Shan, Y.-J.; Nakamura, T. Ferroelectricity induced by oxygen isotope exchange in strontium titanate perovskite. Phys. Rev. Lett. 1999, 82, 3540–3543. [Google Scholar] [CrossRef]
- Nova, T.F.; Disa, A.S.; Fechner, M.; Cavalleri, A. Metastable ferroelectricity in optically strained SrTiO3. Science 2019, 364, 1075–1079. [Google Scholar] [CrossRef]
- Li, X.; Qiu, T.; Zhang, J.; Baldini, E.; Lu, J.; Rappe, A.M.; Nelson, K.A. Terahertz field–induced ferroelec-tricity in quantum paraelectric SrTiO3. Science 2019, 364, 1079–1082. [Google Scholar] [CrossRef]
- Tokura, Y.; Taguchi, Y.; Okada, Y.; Fujishima, Y.; Arima, T.; Kumagai, K.; Iye, Y. Filling dependence of electronic properties on the verge of metal-Mott-insulator. Phys. Rev. Lett. 1993, 70, 2126–2129. [Google Scholar] [CrossRef]
- Spinelli, A.; Torija, M.A.; Liu, C.; Jan, C.; Leighton, C. Electronic transport in doped SrTiO3: Conduction and potential applications. Phys. Rev. B 2010, 81, 155110. [Google Scholar] [CrossRef]
- La Mattina, F.; Bednorz, J.G.; Alvarado, S.F.; Shengelaya, A.; Müller, K.A.; Keller, H. Controlled oxygen vacancies and space correlation with Cr3+ in SrTiO3. Phys. Rev. B 2009, 80, 075122. [Google Scholar] [CrossRef]
- Zhou, W.X.; Ariando, A. Review on Ferroelectric/polar metals. Jpn. J. Appl. Phys. 2020, 59, S10802. [Google Scholar] [CrossRef]
- Alvarado, S.P.; La Mattina, P.; Bednorz, J.G. Electroluminescence in SrTiO3: Cr single-crystal nonvolatile memory cells. Appl. Phys. A 2007, 89, 85–89. [Google Scholar] [CrossRef]
- Schooley, J.F.; Hosler, W.R.; Cohen, M.L. Superconductivity in semiconducting SrTiO3. Phys. Rev. Lett. 1964, 12, 474–475. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Possible high-Tc superconductivity in the Ba-La-Cu-0 system. Z. Phys. B Cond. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Perovskite-type oxides—The new approach to high-Tc superconductivity. Nobel Lect. Dec. 1987. Available online: https://www.nobelprize.org/uploads/2018/06/bednorz-muller-lecture.pdf (accessed on 1 April 2020). [CrossRef]
- Tomioka, Y.; Shirakawa, N.; Shibuya, K.; Inoue, I.H. Enhanced superconductivity close to a nonmagnetic quantum critical point in electron-doped strontium titanate. Nat. Commun. 2019, 10, 738. [Google Scholar] [CrossRef]
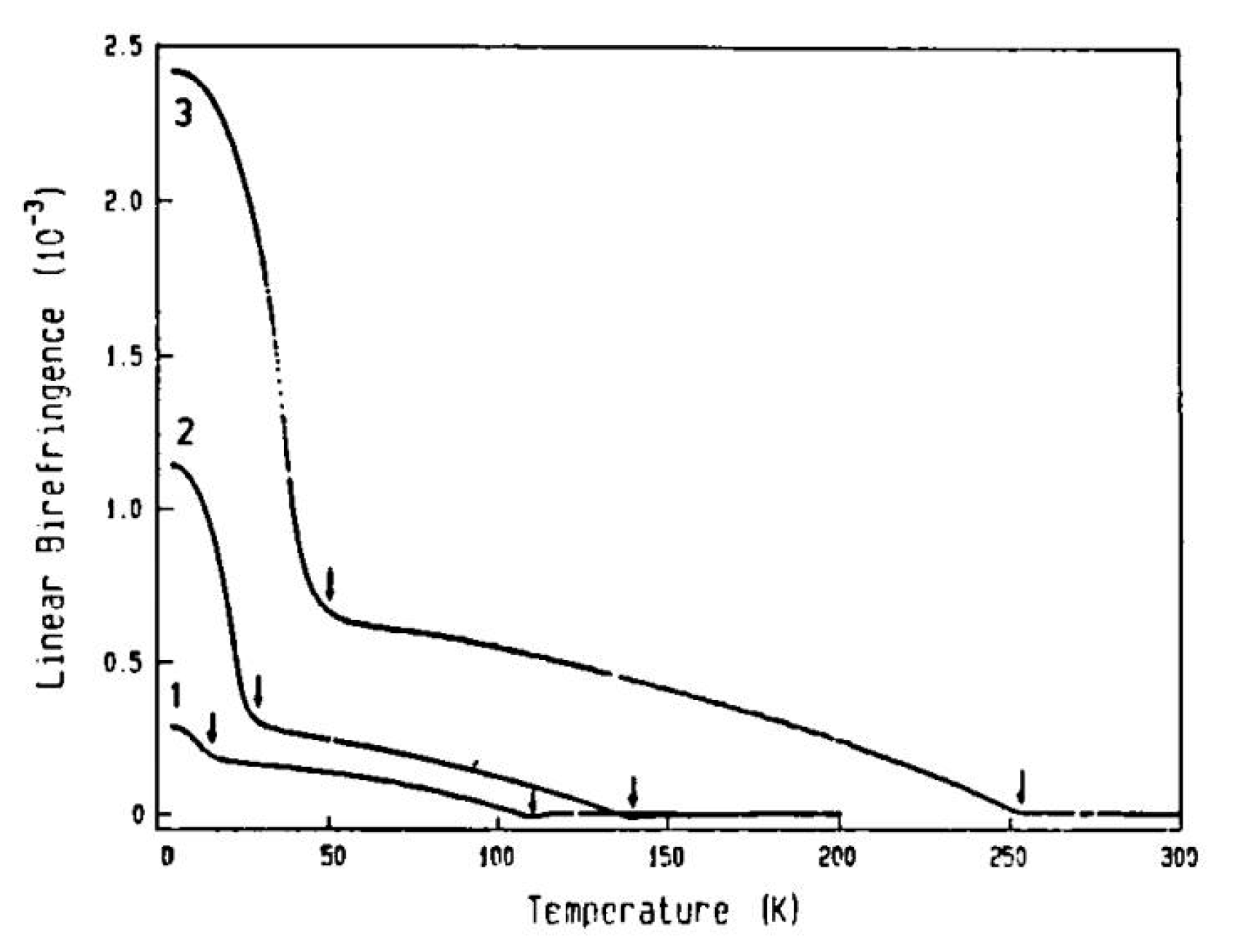
- Kleemann, W.; Schäfer, F.J.; Müller, K.A.; Bednorz, J.G. Domain state properties of the random-field xy-model system Sr1-xCaxTiO3. Ferroelectrics 1988, 80, 297–300. [Google Scholar] [CrossRef]
- Kleemann, W.; Kütz, S.; Rytz, D. Cluster glass and domain state properties of K1-xLixTaO3. Europhys. Lett. 1987, 4, 239–245. [Google Scholar] [CrossRef]
- Kleemann, W.; Albertini, A.; Chamberlin, R.V.; Bednorz, J.G. Relaxational dynamics of polar nano-domains in Sr1-xCaxTiO3, x = 0.002. Europhys. Lett. 1997, 37, 145–150. [Google Scholar] [CrossRef]
- Chamberlin, R.V.; Haines, D.N. Percolation model for relaxation in random systems. Phys. Rev. Lett. 1990, 65, 2197–2200. [Google Scholar] [CrossRef]
- Bedanta, S.; Kleemann, W. Supermagnetism. J. Phys. D Appl. Phys. 2009, 42, 013001. [Google Scholar] [CrossRef]
- Kleemann, W. Relaxor ferroelectrics: Cluster glass ground state via random fields and random bonds. Phys. Status Solidi B 2014, 251, 1993–2002. [Google Scholar] [CrossRef]
- Bianchi, U.; Kleemann, W.; Bednorz, J.G. Raman scattering of ferroelectric Sr1-xCaxTiO3, x = 0.007. J. Phys. Condens. Matter 1994, 6, 1229–1238. [Google Scholar] [CrossRef]
- Carpenter, M.A.; Howard, C.J.; Knight, K.S.; Zhang, Z. Structural relationships and a phase diagram for (Ca, Sr)TiO3 perovskites. J. Phys. Condens. Matter 2006, 18, 10725–10749. [Google Scholar] [CrossRef]
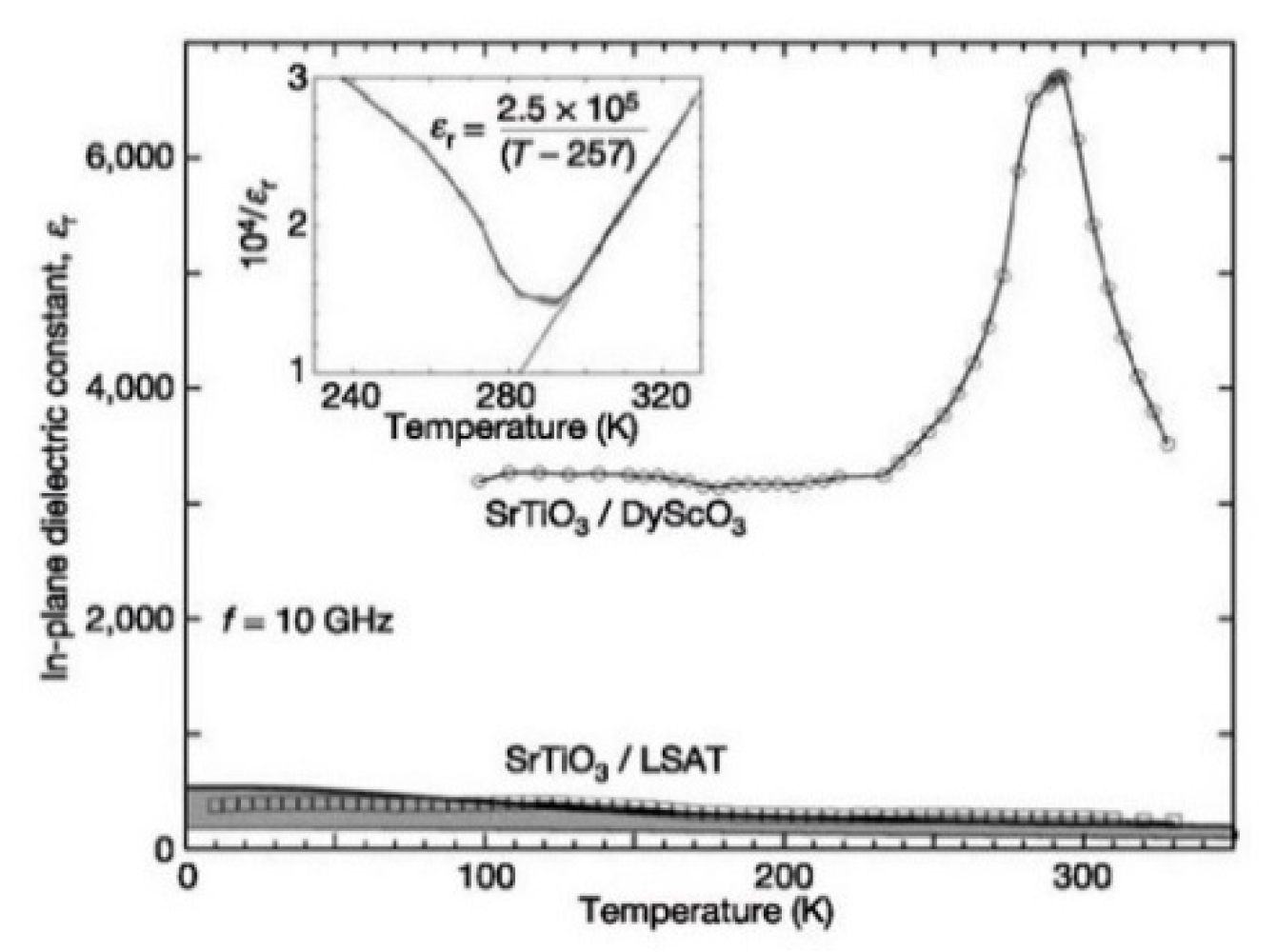
- Haeni, J.H.; Irvin, P.; Chang, W.; Uecker, R.; Reiche, P.; Li, Y.L.; Choudhury, S.; Tian, W.; Hawley, M.E.; Craigo, B.; et al. Room-temperature ferroelectricity in strained SrTiO3. Nature 2004, 430, 758–761. [Google Scholar] [CrossRef]
- Pertsev, N.A.; Tagantsev, A.K.; Setter, N. Phase transitions and strain-induced ferroelectricity in SrTiO3 epitaxial thin films. Phys. Rev. B 2000, 61, R825–R829. [Google Scholar] [CrossRef]
- Fuchs, D.; Schneider, C.W.; Schneider, R.; Rietschel, H. High dielectric constant and tunability of epitaxial thin film capacitors. J. Appl. Phys. 1999, 85, 7363–7369. [Google Scholar] [CrossRef]
- Stengel, M.; Spaldin, N.A. Origin of the dielectric dead layer in nanoscale capacitors. Nature 2006, 443, 679–682. [Google Scholar] [CrossRef]
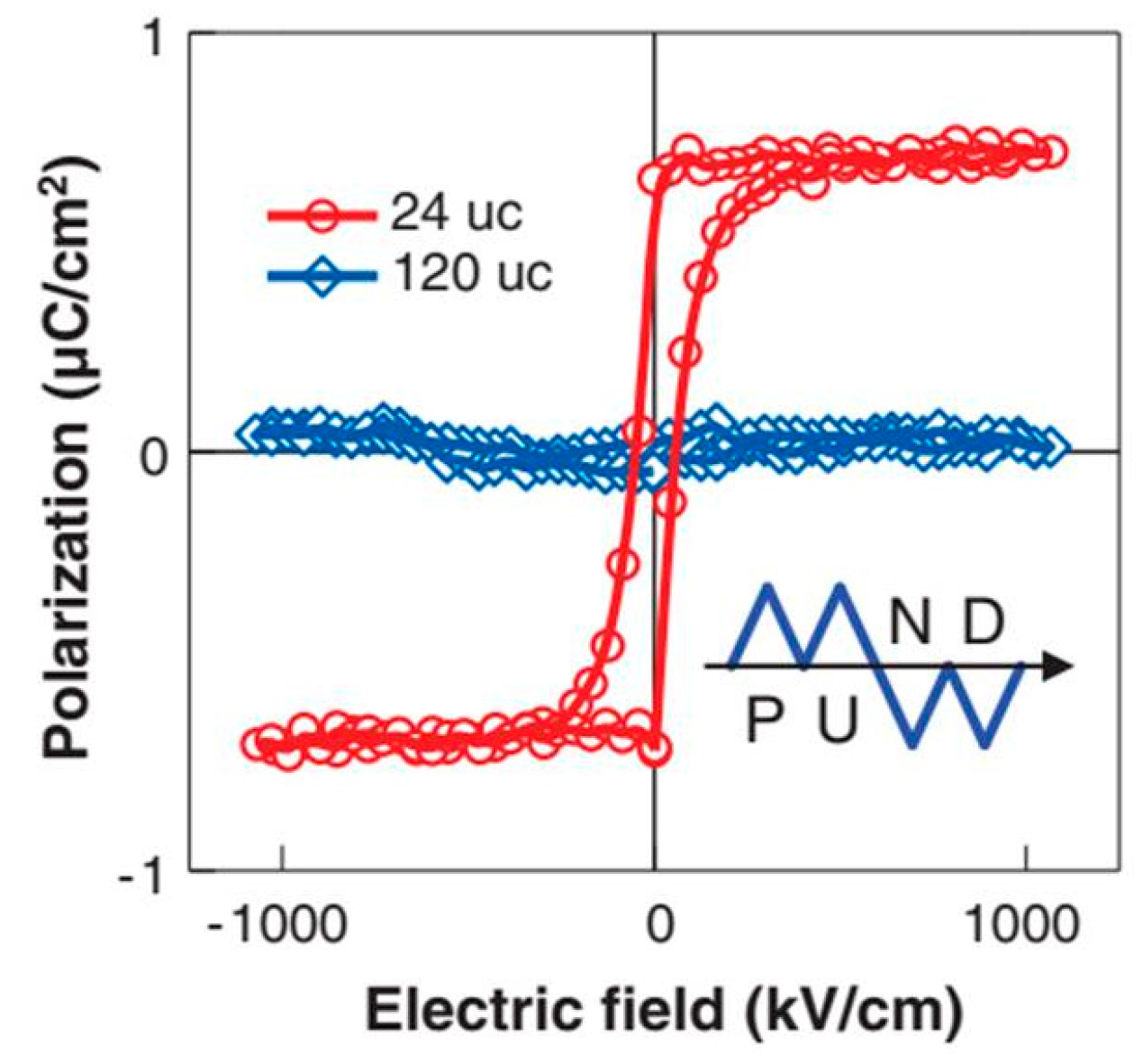
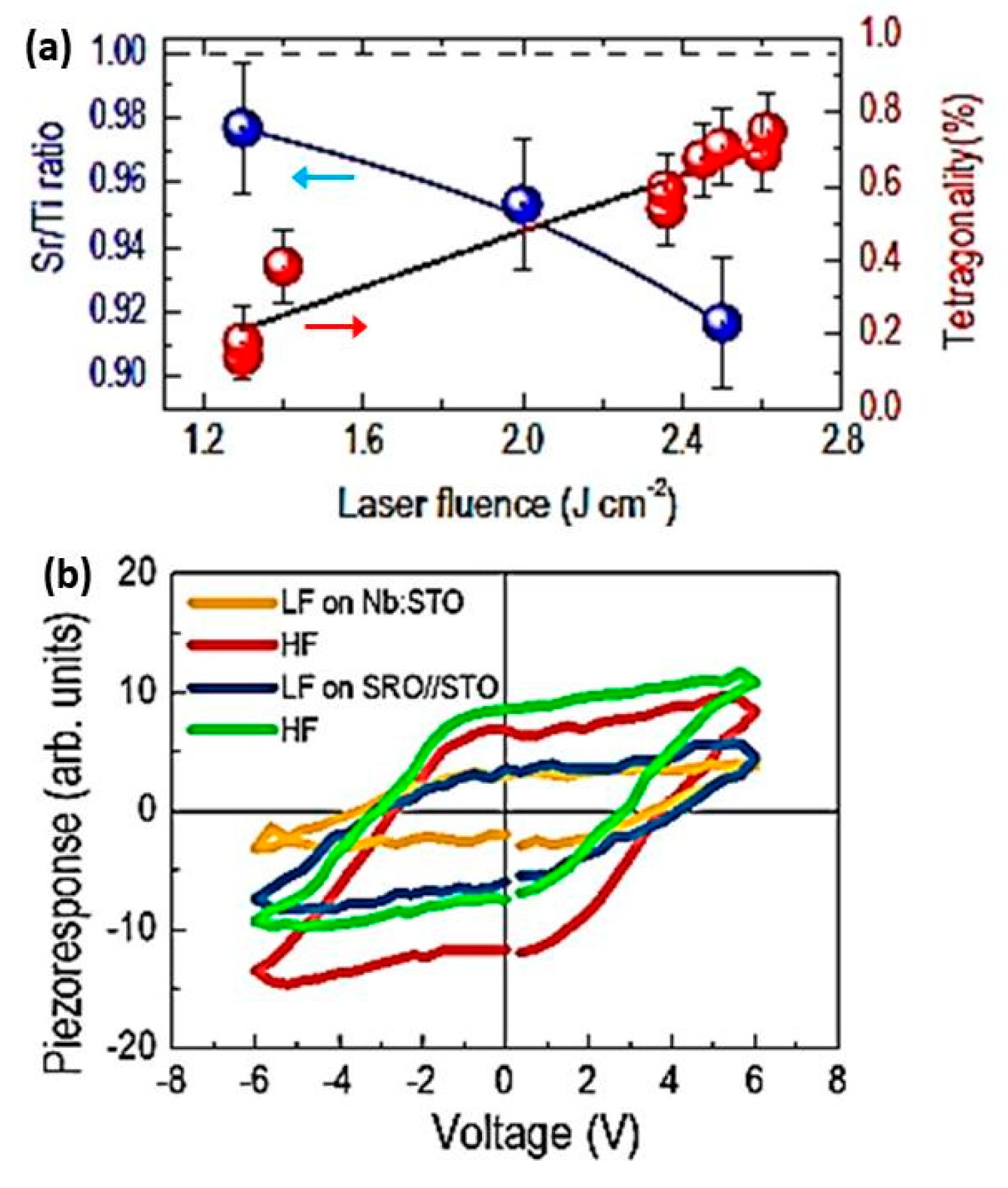
- Lee, D.; Lu, H.; Gu, Y.; Choi, S.-Y.; Li, S.-D.; Ryu, S.; Paudel, T.R.; Song, K.; Mikheev, E.; Lee, S.; et al. Emergence of room-temperature ferroelectricity at reduced dimensions. Science 2015, 349, 1314–1317. [Google Scholar] [CrossRef]
- Kang, K.T.; Seo, H.I.; Kwon, O.; Lee, K.; Bae, J.-S.; Chu, M.-W.; Chae, S.C.; Kim, Y.; Choi, W.S. Ferroelec-tricity in SrTiO3 epitaxial thin films via Sr-vacancy-induced tetragonality. Appl. Surf. Sci. 2020, 499, 143930. [Google Scholar] [CrossRef]
- Bréhin, J.; Trier, F.; Vicente-Arche, L.M.; Hemme, P.; Noël, P.; Cosset-Chéneau, M.; Attané, J.-P.; Vila, L.; Sander, A.; Gallais, Y.; et al. Switchable two-dimensional electron gas based on ferroelectric Ca: SrTiO3. Phys. Rev. Mater. 2020, 4, 041002. [Google Scholar] [CrossRef]
- Noël, P.; Trier, F.; Vicente-Arche, L.M.; Bréhin, J.; Vaz, D.C.; Garcia, V.; Fusil, S.; Barthélémy, A.; Vila, L.; Bibes, M.; et al. Non-volatile electric control of spin–charge conversion in a SrTiO3 Rashba system. Nature 2020, 580, 483–486. [Google Scholar] [CrossRef]
- Salmani-Rezaie, S.; Ahadi, K.; Strickland, W.M.; Stemmer, S. Order-disorder ferroelectric transition of strained SrTiO3. Phys. Rev. Lett. 2020, 125, 087601. [Google Scholar] [CrossRef]
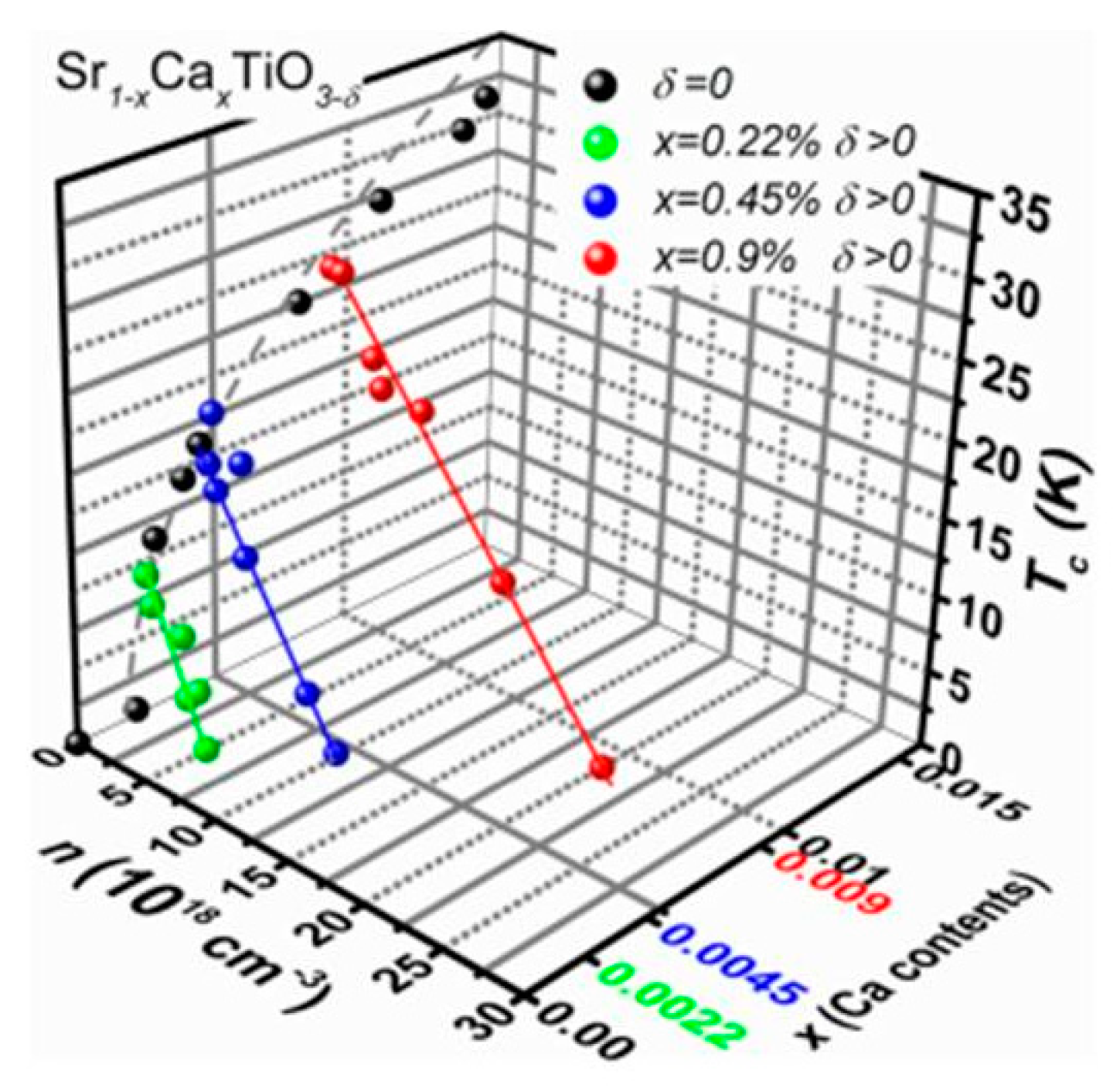
- Rischau, C.W.; Lin, X.; Grams, C.P.; Finck, D.; Harms, S.; Engelmayer, J.; Lorenz, T.; Gallais, Y.; Fauqué, B.; Hemberger, J.; et al. A ferroelectric quantum phase transition inside the superconducting dome of Sr1−xCaxTiO3−δ. Nat. Phys. 2017, 13, 643–648. [Google Scholar] [CrossRef]
- Wölfle, P.; Balatsky, A.V. Superconductivity at low density near a ferroelectric quantum critical point: Doped SrTiO3. Phys. Rev. B 2018, 98, 104505. [Google Scholar] [CrossRef]
- Takada, Y. Theory of superconductivity in polar semiconductors and its application to n-type semicon-ducting SrTiO3. J. Phys. Soc. Jpn. 1980, 49, 1267–1275. [Google Scholar] [CrossRef]
- Gabay, M.; Triscone, J.-M. Superconductivity: Ferroelectricity woos pairing. Nat. Phys. 2017, 13, 624–625. [Google Scholar] [CrossRef]
- Collignon, C.; Lin, X.; Rischau, C.W.; Fauqué, B.; Behnia, K. Metallicity and superconductivity in doped strontium titanate. Ann. Rev. Cond. Matt. Phys. 2019, 10, 25–44. [Google Scholar] [CrossRef]
- Wang, J.L.; Yang, L.W.; Rischau, C.W.; Xu, Z.K.; Ren, Z.; Lorenz, T.; Hemberger, J.; Lin, X.; Behnia, K. Charge transport in a polar metal. NPJ Quantum Mater. 2020, 4, 61–68. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/RKKY_interaction (accessed on 15 April 2020).
- Glinchuk, M.D.; Kondakova, I.V. Ruderman−Kittel−like interaction of electric dipoles in systems with carriers. Phys. Stat. Sol. 1992, 174, 193–197. [Google Scholar] [CrossRef]
- Schumann, T.; Galletti, L.; Jeong, H.; Ahadi, K.; Strickland, W.M.; Salmani-Rezaie, S.; Stemmer, S. Possible signatures of mixed-parity superconductivity in doped polar SrTiO3 films. Phys. Rev. B 2020, 101, 100503. [Google Scholar] [CrossRef]
- Itahashi, Y.M.; Ideue, T.; Saito, Y.; Shimizu, S.; Ouchi, T.; Nojima, T.; Iwasa, Y. Nonreciprocal transport in gate-induced polar superconductor SrTiO3. Sci. Adv. 2020, 6, eaay9120. [Google Scholar] [CrossRef] [PubMed]
- Binder, K.; Young, A.P. Spin glasses: Experimental facts, theoretical concepts, and open questions. Rev. Mod. Phys. 1986, 58, 801–976. [Google Scholar] [CrossRef]
- Binder, K.; Reger, J.D. Theory of orientational glasses: Models, concepts, simulations. Adv. Phys. 1992, 41, 547–627. [Google Scholar] [CrossRef]
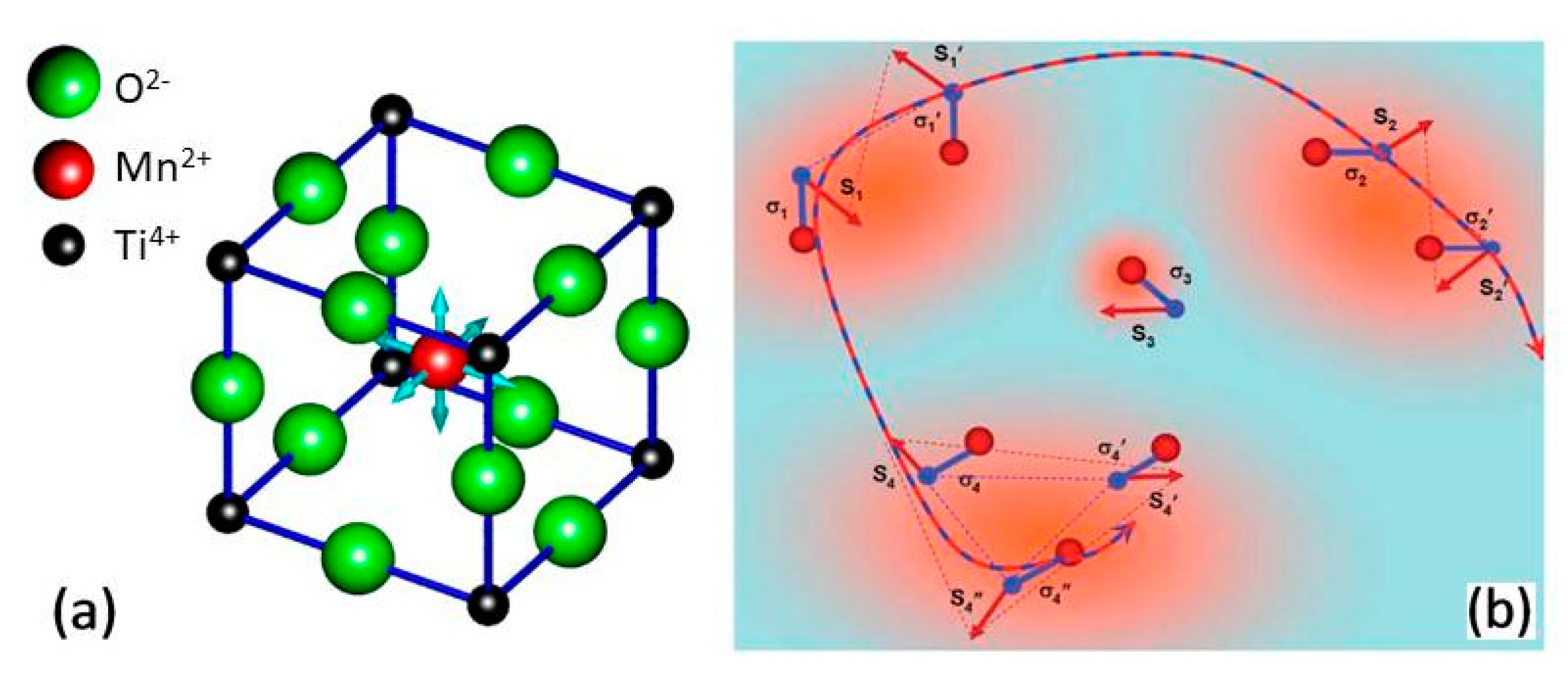
- Shvartsman, V.V.; Bedanta, S.; Borisov, P.; Kleemann, W.; Tkach, A.; Vilarinho, P.M. (Sr,Mn)TiO3: A magnetoelectric multiglass. Phys. Rev. Lett. 2008, 101, 165704. [Google Scholar] [CrossRef] [PubMed]
- Laguta, V.V.; Kondakova, I.V.; Bykov, I.P.; Glinchuk, M.D.; Tkach, A.; Vilarinho, P.M.; Jastrabik, L. Electron spin resonance investigation of Mn2+ ions and their dynamics in Mn-doped SrTiO3. Phys. Rev. B 2007, 76, 054104. [Google Scholar] [CrossRef]
- Lebedev, A.I.; Sluchinskaya, I.A.; Erko, A.; Kozlovskii, V.F. Direct evidence for off-centering of Mn impurity in SrTiO3. JETP Lett. 2009, 89, 457–460. [Google Scholar] [CrossRef]
- Levin, I.; Krayzman, V.; Woicik, J.C.; Tkach, A.; Vilarinho, P.M. X-ray absorption fine structure studies of Mn coordination in doped perovskite SrTiO3. Appl. Phys. Lett. 2010, 96, 052904. [Google Scholar] [CrossRef]
- Kleemann, W.; Bedanta, S.; Borisov, P.; Shvartsman, V.V.; Miga, S.; Dec, J.; Tkach, A.; Vilarinho, P.M. Multiglass order and magnetoelectricity in Mn2+ doped incipient ferroelectrics. Eur. Phys. J. B 2009, 71, 407–410. [Google Scholar] [CrossRef]
- Tkach, A.; Vilarinho, P.M.; Kholkin, A.L. Polar behavior in Mn-doped SrTiO3 ceramics. Appl. Phys. Lett. 2005, 86, 172902. [Google Scholar] [CrossRef]
- Tkach, A.; Vilarinho, P.M.; Kleemann, W.; Shvartsman, V.V.; Borisov, P.; Bedanta, S. Comment on “The origin of magnetism in Mn-doped SrTiO3”. Adv. Funct. Mater. 2013, 23, 2229–2230. [Google Scholar] [CrossRef]
- Tkach, A.; Okhay, O.; Wu, A.; Vilarinho, P.M.; Bedanta, S.; Shvartsman, V.V.; Borisov, P. Magnetic anomaly and dielectric tunability of (Sr,Mn)TiO3 thin films. Ferroelectrics 2012, 426, 274–281. [Google Scholar] [CrossRef]
- Ribeiro, R.A.P.; Andrés, J.; Longo, F.; Lazaro, S.R. Magnetism and multiferroic properties at MnTiO3 surfaces: A DFT study. Appl. Surf. Sci. 2018, 452, 463–472. [Google Scholar] [CrossRef]
- Shvartsman, V.V.; Bedanta, S.; Borisov, P.; Kleemann, W.; Tkach, A.; Vilarinho, P.M. Spin cluster glass and magnetoelectricity in Mn-doped KTaO3. J. Appl. Phys. 2010, 107, 103926. [Google Scholar] [CrossRef]
- Valant, M.; Kolodiazhnyi, T.; Axelsson, A.-K.; Babu, G.S.; Alford, N.M. Spin ordering in Mn-doped KTaO3? Chem. Mater. 2010, 22, 1952–1954. [Google Scholar] [CrossRef]
- Venturini, E.L.; Samara, G.A.; Laguta, V.V.; Glinchuk, M.D.; Kondakova, I.V. Dipolar centers in incipient ferroelectrics: Mn and Fe in KTaO3. Phys. Rev. B 2005, 71, 094111. [Google Scholar] [CrossRef]
- Golovina, I.S.; Shanina, B.D.; Geifman, I.N.; Andriiko, A.A.; Chernenko, L.V. Specific features of the EPR spectra of KTaO3:Mn nanopowders. Phys. Sol. State 2012, 54, 551–558. [Google Scholar] [CrossRef]
- Golovina, I.S.; Lemishko, S.V.; Morozovska, A.N. Percolation magnetism in ferroelectric nanoparticles. Nanoscale Res. Lett. 2017, 12, 382. [Google Scholar] [CrossRef]
- Singh, K.; Maignan, A.; Simon, C.; Hardy, V.; Pachoud, E.; Martin, C. The spin glass Delafossite CuFe0.5V0.5O2: A dipolar glass? J. Phys. Condens. Matter 2011, 23, 126005. [Google Scholar] [CrossRef]
- Choudhury, D.; Mandal, P.; Mathieu, R.; Hazarika, A.; Rajan, S.; Sundaresan, A.; Waghmare, U.V.; Knut, R.; Karis, O.; Nordblad, P.; et al. Near-room-temperature colossal magnetodielectricity and multiglass properties in partially disordered La2NiMnO6. Phys. Rev. Lett. 2012, 108, 127201. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.; Basu, T.; Shahee, A.; Singh, K.; Lalla, N.P.; Sampathkumaran, E.V. Multiglass properties and magnetoelectric coupling in the uniaxial anisotropic spin-cluster-glass Fe2TiO5. Phys. Rev. B 2014, 90, 144426. [Google Scholar] [CrossRef]
- Rathore, S.S.; Vitta, S. Effect of divalent Ba cation substitution with Sr on coupled “multiglass“ state in the magnetoelectric multiferroic compound Ba3NbFe3Si2O14. Sci. Rep. 2015, 5, 9751. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kleemann, W.; Dec, J.; Tkach, A.; Vilarinho, P.M. SrTiO3—Glimpses of an Inexhaustible Source of Novel Solid State Phenomena. Condens. Matter 2020, 5, 58. https://doi.org/10.3390/condmat5040058
Kleemann W, Dec J, Tkach A, Vilarinho PM. SrTiO3—Glimpses of an Inexhaustible Source of Novel Solid State Phenomena. Condensed Matter. 2020; 5(4):58. https://doi.org/10.3390/condmat5040058
Chicago/Turabian StyleKleemann, Wolfgang, Jan Dec, Alexander Tkach, and Paula M. Vilarinho. 2020. "SrTiO3—Glimpses of an Inexhaustible Source of Novel Solid State Phenomena" Condensed Matter 5, no. 4: 58. https://doi.org/10.3390/condmat5040058
APA StyleKleemann, W., Dec, J., Tkach, A., & Vilarinho, P. M. (2020). SrTiO3—Glimpses of an Inexhaustible Source of Novel Solid State Phenomena. Condensed Matter, 5(4), 58. https://doi.org/10.3390/condmat5040058





