Evaluation of Bunch Length by Measuring Coherent Synchrotron Radiation with a Narrow-Band Detector at LEBRA
Abstract
1. Introduction
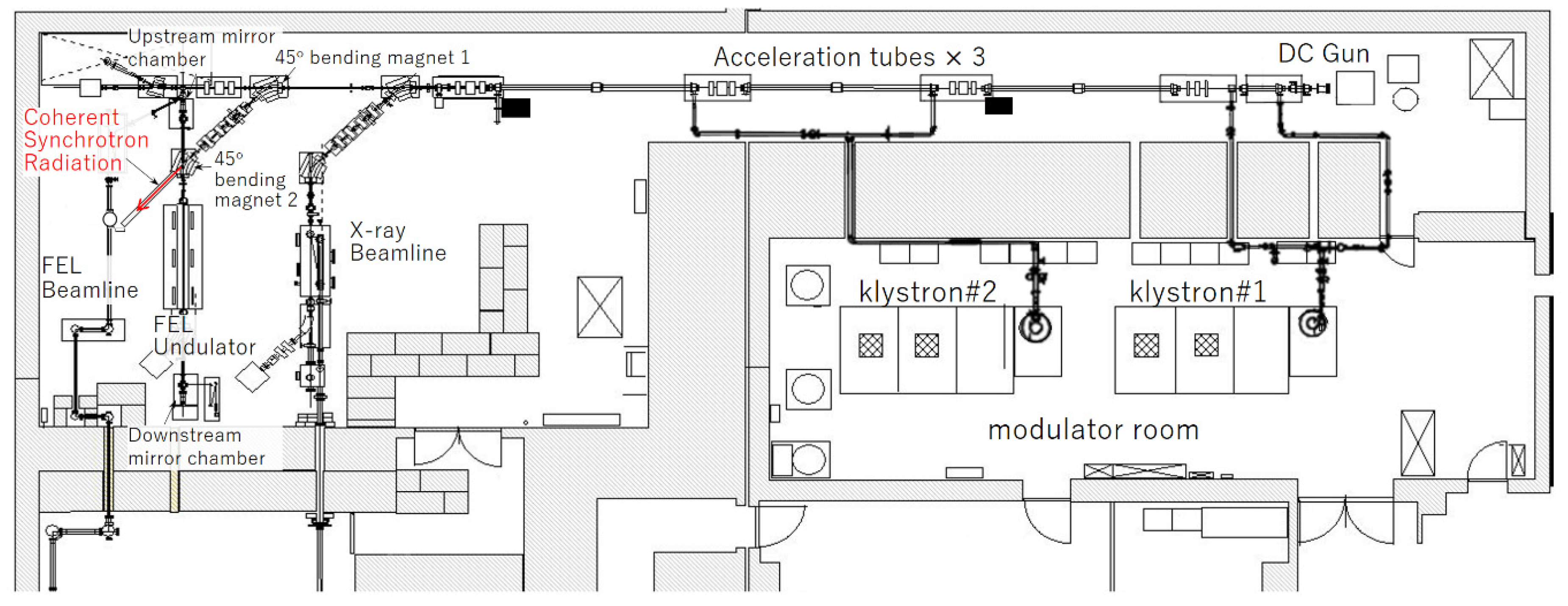
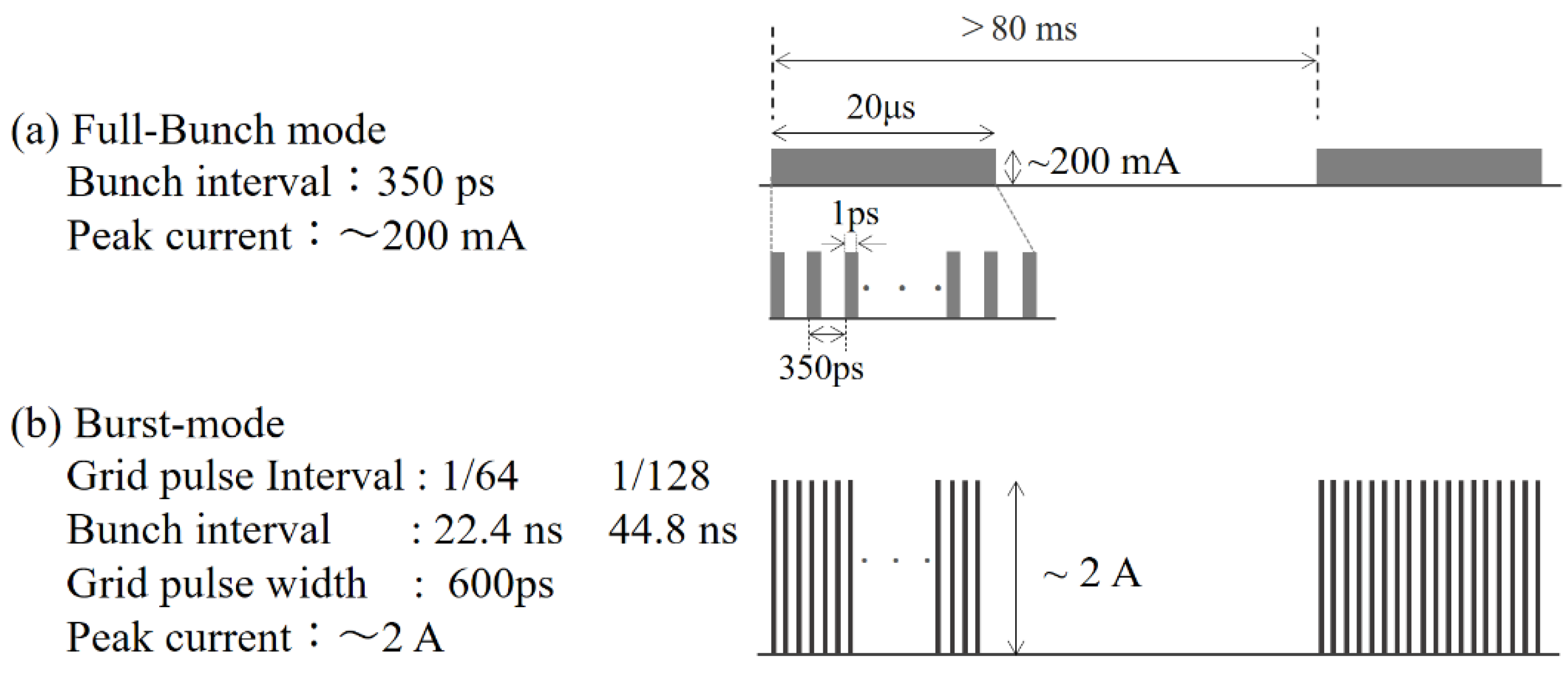
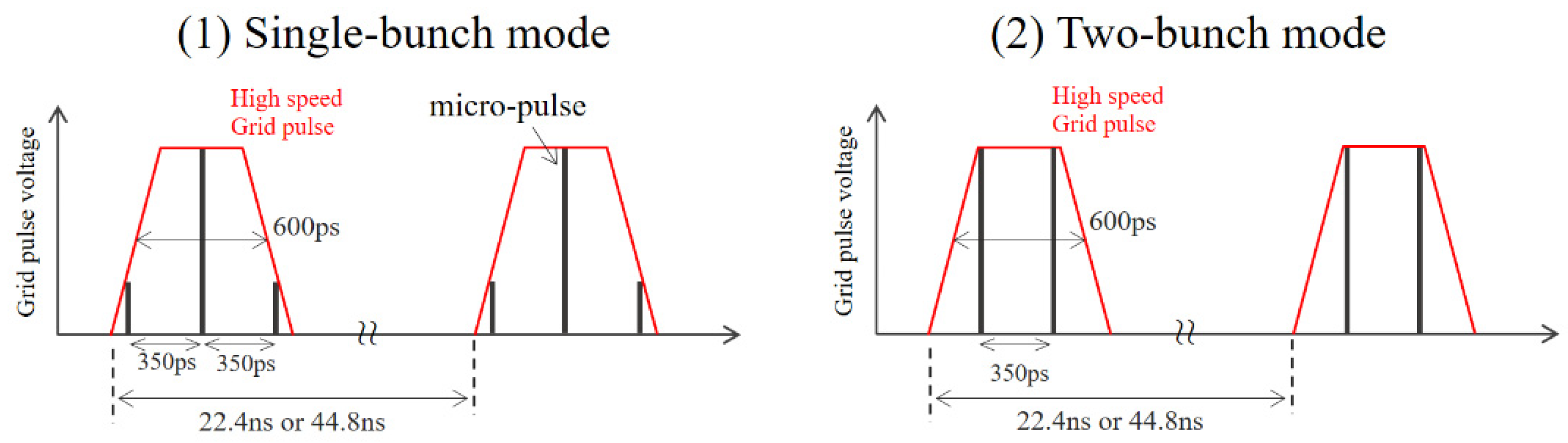
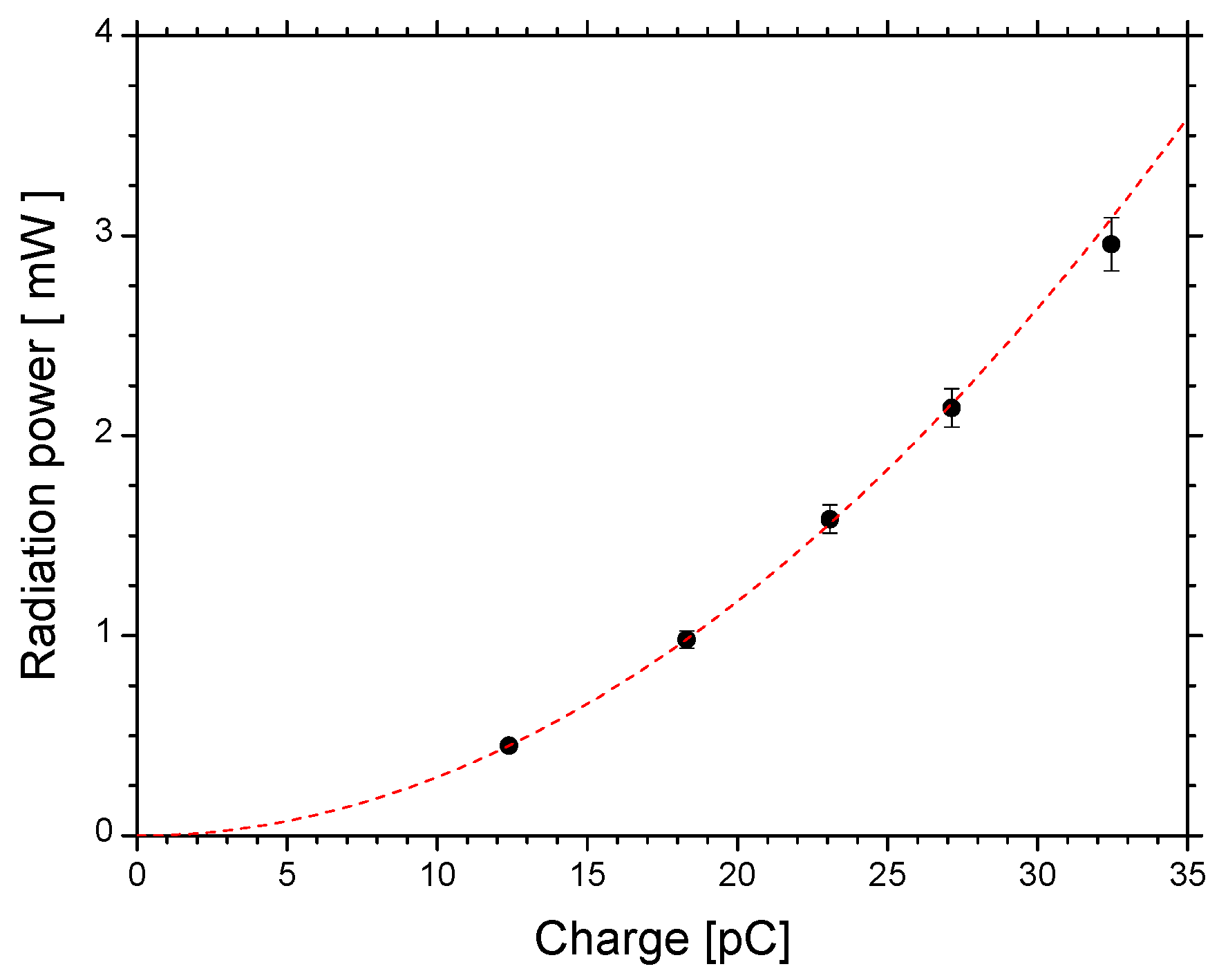
2. Coherent Synchrotron Radiation Source at LEBRA
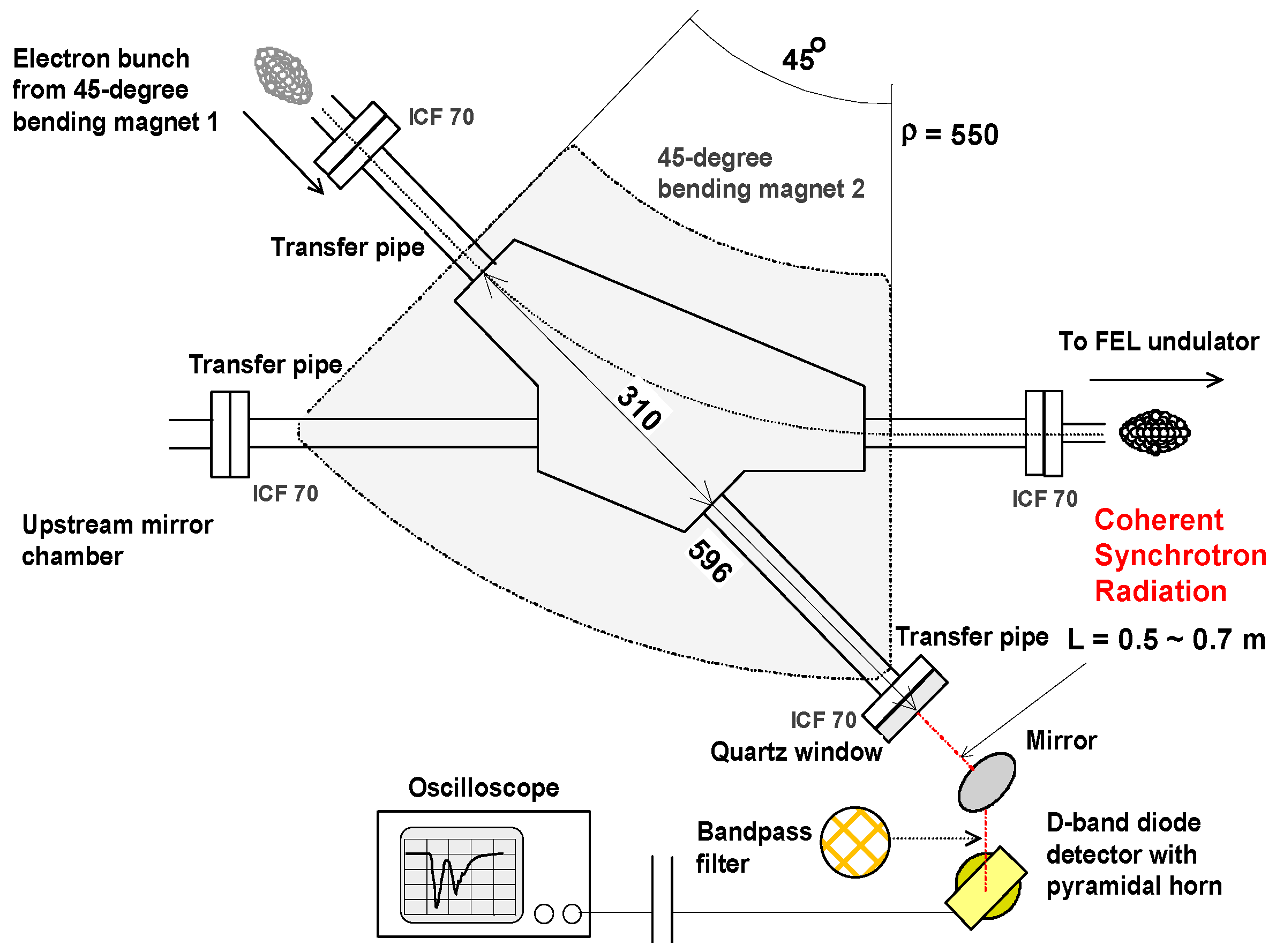
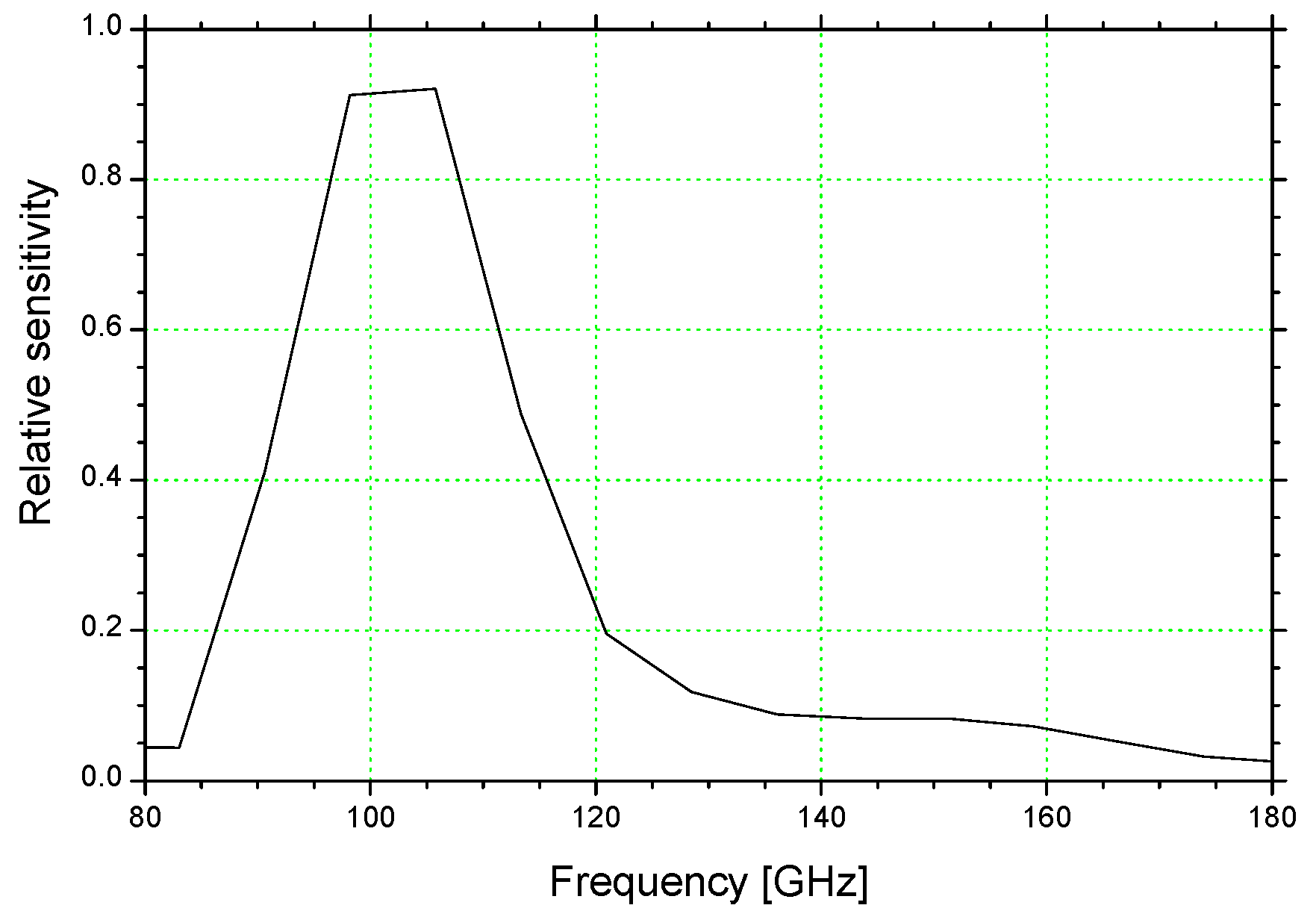
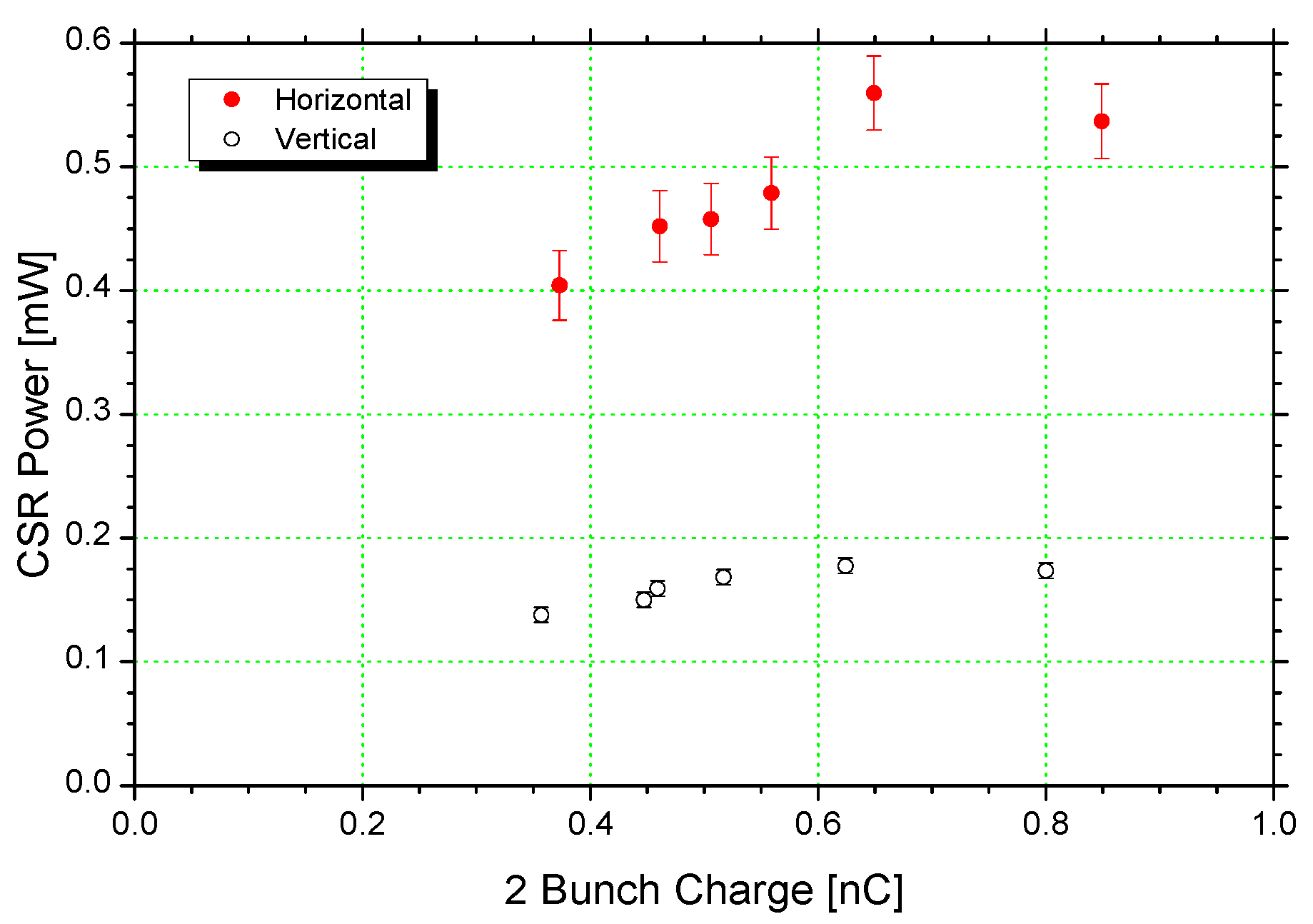
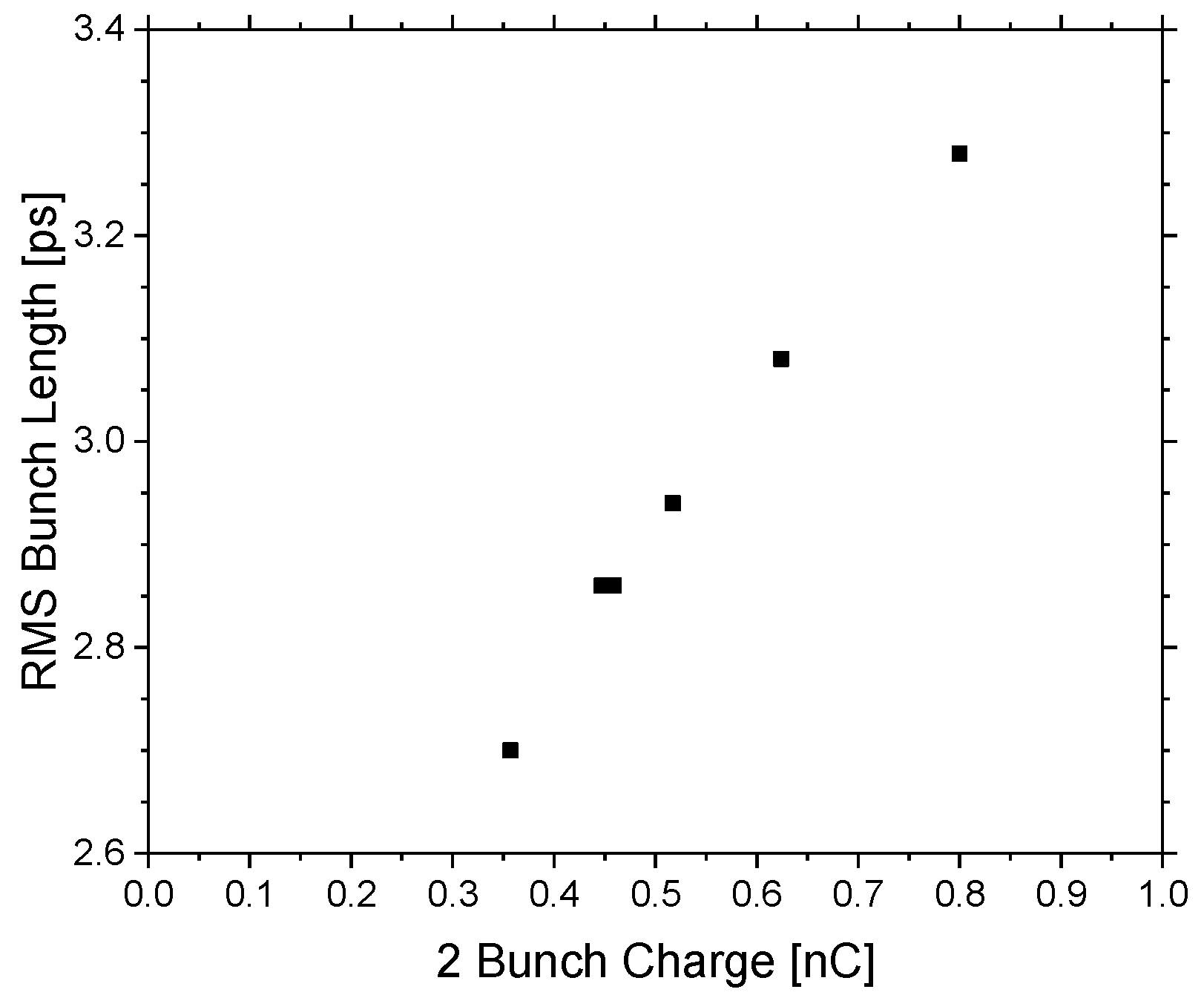
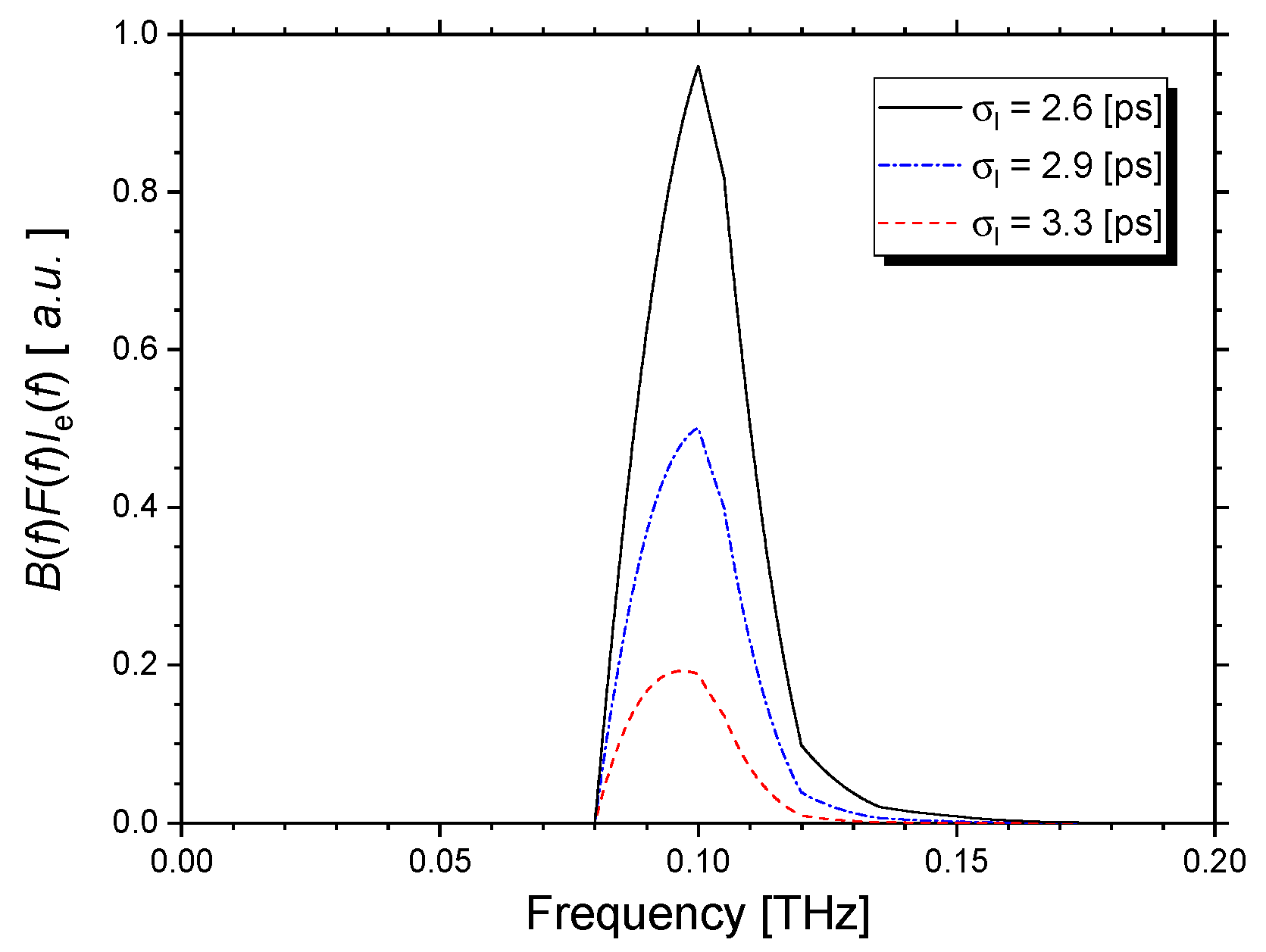
3. Bunch Length Measurement of CSR Power with Narrow-Band Detector
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Elias, L.R. Free-electron laser research at the University of California, Santa Barbara. IEEE J. Quantum Electron. 1987, 23, 1470–1475. [Google Scholar] [CrossRef]
- Nakazato, T.; Oyamada, M.; Niimura, N.; Urasawa, S.; Konno, O.; Kagaya, A.; Kato, R.; Kamiyama, T.; Torizuka, Y.; Nanba, T.; et al. Observation of coherent synchrotron radiation. Phys. Rev. Lett. 1989, 63, 1245. [Google Scholar] [CrossRef] [PubMed]
- Abo-Bakr, M.; Feikes, J.; Holldack, K.; Kuske, P.; Peatman, W.B.; Schade, U.; Wüstefeld, G.; Hübers, H.-W. Brilliant, Coherent Far-Infrared (THz) Synchrotron Radiation. Phys. Rev. Lett. 2003, 90, 094801. [Google Scholar] [CrossRef] [PubMed]
- Gensch, M.; Bittner, L.; Chesnov, A.; Delsim-Hashemi, H.; Drescher, M.; Faatz, B.; Feldhaus, J.; Fruehling, U.; Geloni, G.; Gerth, C.; et al. New infrared undulator beamline at FLASH. Infrared Phys. Technol. 2008, 51, 423. [Google Scholar] [CrossRef]
- Sei, N.; Kuroda, R.; Yasumoto, M.; Toyokawa, H.; Ogawa, H.; Koike, M.; Yamada, K. Measurement of intense coherent synchrotron radiation at frequencies around 0.1 THz using the compact S-band linac. J. Appl. Phys. 2008, 104, 114908. [Google Scholar] [CrossRef]
- Carr, G.L.; Martin, M.C.; McKinney, W.R.; Jordan, K.; Neil, G.R.; Williams, G.P. High-power terahertz radiation from relativistic electrons. Nature 2002, 420, 153. [Google Scholar] [CrossRef]
- Kim, K.J.; Shvyd’ko, Y.; Reiche, S. A Proposal for an X-Ray Free-Electron Laser Oscillator with an Energy-Recovery Linac. Phys. Rev. Lett. 2008, 100, 244802. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bożek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.-J.; et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641. [Google Scholar] [CrossRef]
- Pile, D. First light from SACLA. Nat. Photonics 2011, 5, 456. [Google Scholar] [CrossRef]
- Hajima, R. Energy Recovery Linacs for Light Sources. Rev. Accel. Sci. Technol. 2010, 3, 121. [Google Scholar] [CrossRef]
- Bilderback, D.H.; Sinclair, C.; Gruner, S.M. Technical Report: The Status of the Energy Recovery Linac Source of Coherent Hard X-rays at Cornell University. Synchrotron Radiat. News 2006, 19, 30–35. [Google Scholar] [CrossRef]
- Roux, R.; Couprie, M.-E.; Hara, T.; Bakker, R.; Visentin, B.; Billardon, M.; Roux, J. The Super-ACO FEL dynamics measured with a streak camera. J. Nucl. Instrum. Methods Phys. Res. Sect. A 1997, 393, 33–37. [Google Scholar] [CrossRef]
- Sei, N.; Yamada, K.; Ogawa, H.; Yasumoto, M.; Mikado, T. Electron Beam Qualities with and without Free Electron Laser Oscillations in the Compact Storage Ring NIJI-IV. Jpn. J. Appl. Phys. 2003, 42, 5848. [Google Scholar] [CrossRef]
- Lihn, H.; Kung, P.; Settakom, C.; Wiedemann, H.; Bocek, D. Measurement of subpicosecond electron pulses. Phys. Rev. E 1996, 53, 6413. [Google Scholar] [CrossRef]
- Ieiri, T. A real time bunch-length monitor using the beam spectrum and measurements of bunch lengthening. Nucl. Instrum. Methods Phys. Res. Sect. A 1993, 329, 371. [Google Scholar] [CrossRef]
- Otake, Y.; Maesaka, H.; Matsubara, S.; Inoue, S.; Yanagida, K.; Ego, H.; Kondo, C.; Sakurai, T.; Matsumoto, T.; Tomizawaakurai, H.; et al. Beam monitor system for an x-ray free electron laser and compact laser. Phys. Rev. Spéc. Top. Accel. Beams 2013, 16, 042802. [Google Scholar] [CrossRef]
- Sei, N.; Ogawa, H.; Hayakawa, K.; Tanaka, T.; Hayakawa, Y.; Nakao, K.; Sakai, T.; Nogami, K.; Inagaki, M. Observation of intense terahertz-wave coherent synchrotron radiation at LEBRA. J. Phys. D Appl. Phys. 2013, 46, 045104. [Google Scholar] [CrossRef]
- Sei, N.; Ogawa, H.; Hayakawa, K.; Tanaka, T.; Hayakawa, Y.; Nakao, K.; Sakai, T. Measurement of a bunch length of a relativistic electron beam using a narrow-band diode detector in a terahertz region. J. Jpn. Soc. Infrared Sci. Technol. 2015, 25, 97. (In Japanese) [Google Scholar]
- Hayakawa, Y.; Sato, I.; Hayakawa, K.; Tanaka, T.; Nakazawa, H.; Yokoyama, K.; Kanno, K.; Sakai, T.; Ishiwata, K.; Enomoto, A.; et al. First lasing of LEBRA FEL at Nihon University at a wavelength of 1.5 μm. Nucl. Instrum. Methods Phys. Res. Sect. A 2002, 483, 29. [Google Scholar] [CrossRef]
- Nakao, K.; Hayakawa, K.; Tanaka, T.; Hayakawa, Y.; Sakai, T.; Sato, I.; Nogami, K.; Inagaki, M. Analysis on variation factors of optical powerat the LEBRA FEL. In Proceedings of the FEL, Liverpool, UK, 23–28 August 2009; Volume 675. Available online: http://accelconf.web.cern.ch/AccelConf/FEL2009/papers/wepc75.pdf (accessed on 6 April 2020).
- Hayakawa, Y.; Sato, I.; Hayakawa, K.; Tanaka, T.; Yokoyama, K.; Kanno, K.; Sakai, T.; Ishiwata, K.; Nakao, K.; Hashimoto, E. Characteristics of the fundamental FEL and the higher harmonic generation at LEBRA. Nucl. Instrum. Methods Phys. Res. Sect. A 2003, 507, 404. [Google Scholar] [CrossRef]
- Nakao, K.; Tanaka, T.; Hayakawa, K.; Hayakawa, Y.; Nogami, K.; Inagaki, M. Lasing of FEL with the burst mode beam at LEBRA Nihon University. In Proceedings of the 8th Annual Meeting of Particle Accelerator Society of Japan, Tsukuba, Japan, 1–3 August 2011; Volume 1051. Available online: https://www.pasj.jp/web_publish/pasj8/proceedings/poster/TUPS072.pdf (accessed on 6 April 2020). (In Japanese).
- Yokoyama, K.; Sato, I.; Hayakawa, K.; Tanaka, T.; Hayakawa, Y.; Nakao, K. Measurement of electron bunch length at LEBRA. In Proceedings of the 1st Annual Meeting of Particle Accelerator Society of Japan and 29th Linear Accelerator Meeting in Japan, Funabashi, Japan, 4–6 August 2004; Volume 602. Available online: https://www.pasj.jp/web_publish/pasj1_lam29/WebPublish/5P58.pdf (accessed on 6 April 2020). (In Japanese).
- Smiths Interconnect on the Web (The Current Model Number is DET-06). Available online: https://www.smithsinterconnect.com/products/multi-function-rf-systems/mixers-and-detectors/general-purpose-detector-(det)/ (accessed on 24 April 2020).
- Takahashi, T.; Takami, K. Observation of THz coherent transition radiation from single-bunch beam at KURRI-LINAC as an intense pulsed light source. Infrared Phys. Technol. 2008, 51, 363. [Google Scholar] [CrossRef]
- Grischkowsky, D.; Keiding, S.; Van Exter, M.P.; Fattinger, C. Far-infrared time-domain spectroscopy with terahertz beams of dielectrics and semiconductors. J. Opt. Soc. Am. B 1990, 7, 2006. [Google Scholar] [CrossRef]
- Mira, N.; Robert, E.M. Terahertz Time-Domain Spectroscopy for Material Characterization. Proc. IEEE 2007, 95, 1658. [Google Scholar] [CrossRef]
- HITRAN on the Web. Available online: http://hitran.iao.ru/ (accessed on 29 February 2020).
- Jackson, J.D. Longitudinal plasma oscillations. J. Nucl. Energy 1960, 1, 171. [Google Scholar] [CrossRef]
- Kan, K.; Yang, J.; Kondoh, T.; Norizawa, K.; Yoshida, Y. Effects of emittance and space-charge in femtosecond bunch compression. Nucl. Instrum. Methods Phys. Res. Sect. A 2008, 597, 126. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakai, T.; Hayakawa, K.; Tanaka, T.; Hayakawa, Y.; Nogami, K.; Sei, N. Evaluation of Bunch Length by Measuring Coherent Synchrotron Radiation with a Narrow-Band Detector at LEBRA. Condens. Matter 2020, 5, 34. https://doi.org/10.3390/condmat5020034
Sakai T, Hayakawa K, Tanaka T, Hayakawa Y, Nogami K, Sei N. Evaluation of Bunch Length by Measuring Coherent Synchrotron Radiation with a Narrow-Band Detector at LEBRA. Condensed Matter. 2020; 5(2):34. https://doi.org/10.3390/condmat5020034
Chicago/Turabian StyleSakai, Takeshi, Ken Hayakawa, Toshinari Tanaka, Yasushi Hayakawa, Kyoko Nogami, and Norihiro Sei. 2020. "Evaluation of Bunch Length by Measuring Coherent Synchrotron Radiation with a Narrow-Band Detector at LEBRA" Condensed Matter 5, no. 2: 34. https://doi.org/10.3390/condmat5020034
APA StyleSakai, T., Hayakawa, K., Tanaka, T., Hayakawa, Y., Nogami, K., & Sei, N. (2020). Evaluation of Bunch Length by Measuring Coherent Synchrotron Radiation with a Narrow-Band Detector at LEBRA. Condensed Matter, 5(2), 34. https://doi.org/10.3390/condmat5020034




