Static Kinks in Chains of Interacting Atoms
Abstract
1. Introduction
2. An Atomic Chain in a Periodic Substrate Potential
Equilibrium Configuration in the Discrete Chain
3. Equation of the Static Kink in the Long-Wavelength Limit
3.1. Nearest-Neighbour Interactions
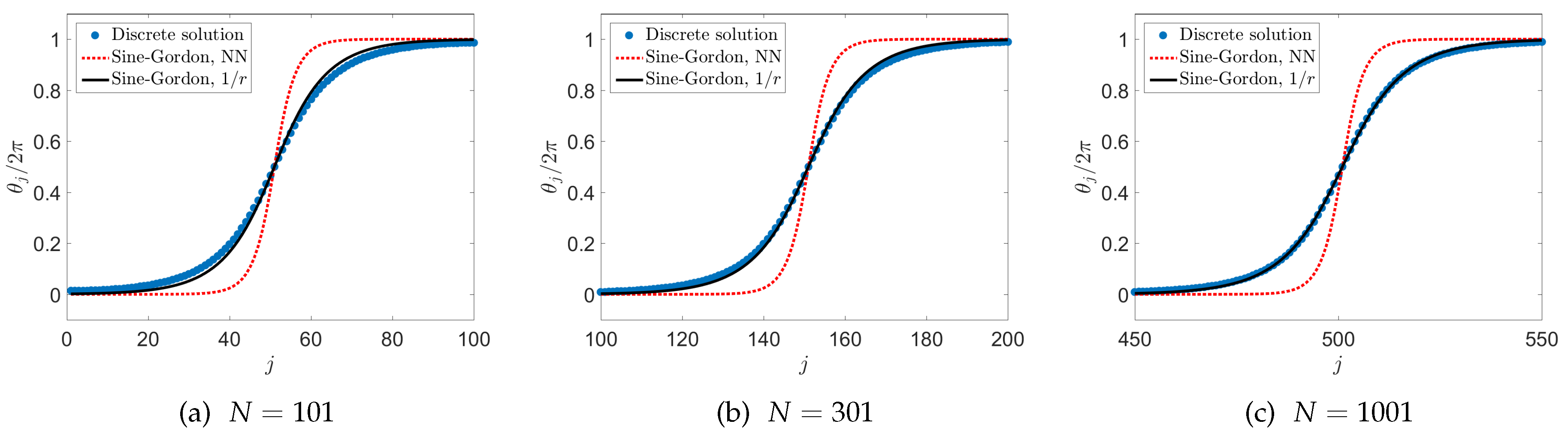
3.2. Power-Law Interactions
3.2.1. Power-Law Interactions With
3.2.2. Coulomb Interactions
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Frenkel, Y.I.; Kontorova, T.A. The model of dislocation in solid body. Zh. Eksp. Teor. Fiz. 1938, 8, 1340. [Google Scholar]
- Bak, P. Commensurate phases, incommensurate phases and the devil’s staircase. Rep. Prog. Phys. 1982, 45, 587–629. [Google Scholar] [CrossRef]
- Vanossi, A.; Manini, N.; Urbakh, M.; Zapperi, S.; Tosatti, E. Colloquium: Modeling friction: From nanoscale to mesoscale. Rev. Mod. Phys. 2013, 85, 529–552. [Google Scholar] [CrossRef]
- Braun, O.M.; Kivshar, Y.S. The Frenkel-Kontorova Model: Concepts, Methods, and Applications; Springer: Berlin/Heidelberger, Germany, 2004. [Google Scholar]
- Pokrovskij, V.L.; Talapov, A.L. Theory of Incommensurate Crystals; Harwood Academic Publishers: New York, NY, USA, 1984. [Google Scholar]
- Pokrovskij, V.L.; Talapov, A.L. Phase transitions and vibrational spectra of almost commensurate structures. Sov. J. Exp. Theor. Phys. 1978, 48, 579. [Google Scholar]
- Frank, F.C.; van der Merwe, J.H. One-dimensional dislocations. Proc. R. Soc. Lond. A Math. Phys. Sci. 1949, 198, 205–216. [Google Scholar]
- Rebbi, C.; Soliani, G. Solitons and Particles; World Scientific: Singapore, 1984. [Google Scholar]
- Dubin, D.H.E.; O’Neil, T.M. Trapped nonneutral plasmas, liquids, and crystals (the thermal equilibrium states). Rev. Mod. Phys. 1999, 71, 87–172. [Google Scholar] [CrossRef]
- Baier, S.; Mark, M.J.; Petter, D.; Aikawa, K.; Chomaz, L.; Cai, Z.; Baranov, M.; Zoller, P.; Ferlaino, F. Extended Bose-Hubbard Models with Ultracold Magnetic Atoms. Science 2016, 352, 201–205. [Google Scholar] [CrossRef]
- Schauss, P. Quantum simulation of transverse Ising models with Rydberg atoms. Quantum Sci. Technol. 2018, 3, 023001. [Google Scholar] [CrossRef]
- Garcia-Mata, I.; Zhirov, O.V.; Shepelyansky, D.L. Frenkel-Kontorova model with cold trapped ions. Eur. Phys. J. D 2007, 41, 325–330. [Google Scholar] [CrossRef][Green Version]
- Pruttivarasin, T.; Ramm, M.; Talukdar, I.; Kreuter, A.; Häffner, H. Trapped ions in optical lattices for probing oscillator chain models. New J. Phys. 2011, 13, 075012. [Google Scholar] [CrossRef][Green Version]
- Benassi, A.; Vanossi, A.; Tosatti, E. Nanofriction in cold ion traps. Nat. Commun. 2011, 2, 236. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Linnet, R.B.; Leroux, I.D.; Marciante, M.; Dantan, A.; Drewsen, M. Pinning an Ion with an Intracavity Optical Lattice. Phys. Rev. Lett. 2012, 109, 233005. [Google Scholar] [CrossRef] [PubMed]
- Enderlein, M.; Huber, T.; Schneider, C.; Schaetz, T. Single ions trapped in a one-dimensional optical lattice. Phys. Rev. Lett. 2012, 109, 233004. [Google Scholar] [CrossRef]
- Cetina, M.; Bylinskii, A.; Karpa, L.; Gangloff, D.; Beck, K.M.; Ge, Y.; Scholz, M.; Grier, A.T.; Chuang, I.; Vuletić, V. One-dimensional array of ion chains coupled to an optical cavity. New J. Phys. 2013, 15, 053001. [Google Scholar] [CrossRef]
- Hornekær, L.; Kjærgaard, N.; Thommesen, A.M.; Drewsen, M. Structural Properties of Two-Component Coulomb Crystals in Linear Paul Traps. Phys. Rev. Lett. 2001, 86, 1994–1997. [Google Scholar] [CrossRef] [PubMed]
- Kiethe, J.; Nigmatullin, R.; Kalincev, D.; Schmirander, T.; Mehlstäubler, T.E. Probing nanofriction and Aubry-type signatures in a finite self-organized system. Nat. Commun. 2017, 8, 15364. [Google Scholar] [CrossRef] [PubMed]
- Li, H.-K.; Urban, E.; Noel, C.; Chuang, A.; Xia, Y.; Ransford, A.; Hemmerling, B.; Wang, Y.; Li, T.; Häffner, H.; et al. Realization of translational symmetry in trapped cold ion rings. Phys. Rev. Lett. 2017, 118, 053001. [Google Scholar] [CrossRef]
- Pyka, K.; Keller, J.; Partner, H.P.; Nigmatullin, R.; Burgermeister, T.; Meier, D.M.; Kuhlmann, K.; Retzker, A.; Plenio, M.B.; Zurek, W.H.; et al. Topological defect formation and spontaneous symmetry breaking in ion Coulomb crystals. Nature Commun. 2013, 4, 2291. [Google Scholar] [CrossRef]
- Ulm, S.; Rossnagel, J.; Jacob, G.; Degunther, C.; Dawkins, S.T.; Poschinger, U.G.; Nigmatullin, R.; Retzker, A.; Plenio, M.B.; Schmidt-Kaler, F.; et al. Observation of the Kibble?Zurek scaling law for defect formation in ion crystals. Nat. Commun. 2013, 4, 2290. [Google Scholar] [CrossRef]
- Mielenz, M.; Brox, J.; Kahra, S.; Leschhorn, G.; Albert, M.; Schaetz, T.; Landa, H.; Reznik, B. Trapping of Topological-Structural Defects in Coulomb Crystals. Phys. Rev. Lett. 2013, 110, 133004. [Google Scholar] [CrossRef]
- Senko, C.; Smith, J.; Richerme, P.; Lee, A.; Campbell, W.C.; Monroe, C. Coherent Imaging Spectroscopy of a Quantum Many-Body Spin System. Science 2014, 345, 430–433. [Google Scholar] [CrossRef] [PubMed]
- Bakr, W.S.; Gillen, J.; Peng, A.; Fölling, S.; Greiner, M. A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice. Nature 2009, 462, 74–77. [Google Scholar] [CrossRef] [PubMed]
- Viteau, M.; Bason, M.G.; Radogostowicz, J.; Malossi, N.; Ciampini, D.; Morsch, O.; Arimondo, E. Rydberg Excitations in Bose-Einstein Condensates in Quasi-One-Dimensional Potentials and Optical Lattices. Phys. Rev. Lett. 2011, 107, 060402. [Google Scholar] [CrossRef]
- Brox, J.; Kiefer, P.; Bujak, M.; Landa, H.; Schaetz, T. Spectroscopy and Directed Transport of Topological Solitons in Crystals of Trapped Ions. Phys. Rev. Lett. 2017, 119, 153602. [Google Scholar] [CrossRef]
- Schneider, C.; Porras, D.; Schaetz, T. Experimental quantum simulations of many-body physics with trapped ions. Rep. Prog. Phys. 2012, 75, 024401. [Google Scholar] [CrossRef]
- Bylinskii, A.; Gangloff, D.; Vuletić, V. Tuning friction atom-by-atom in an ion-crystal simulator. Science 2015, 348, 1115–1118. [Google Scholar] [CrossRef]
- Gangloff, D.; Bylinskii, A.; Counts, I.; Jhe, W.; Vuletić, V. Velocity tuning of friction with two trapped atoms. Nat. Phys. 2015, 11, 915–919. [Google Scholar] [CrossRef]
- Counts, I.; Gangloff, D.; Bylinskii, A.; Hur, J.; Islam, R.; Vuletić, V. Multislip Friction with a Single Ion. Phys. Rev. Lett. 2017, 119, 043601. [Google Scholar] [CrossRef]
- Campa, A.; Dauxois, T.; Ruffo, S. Statistical mechanics and dynamics of solvable models with long-range interactions. Phys. Rep. 2009, 480, 57–159. [Google Scholar] [CrossRef]
- Laskin, N.; Zaslavsky, G. Nonlinear Fractional Dynamics on a Lattice with Long Range Interactions. Physica A 2006, 368, 38–54. [Google Scholar] [CrossRef]
- Kirkpatrick, K.; Lenzmann, E.; Staffilani, G. On the Continuum Limit for Discrete NLS with Long-Range Lattice Interactions. Commun. Math. Phys. 2013, 317, 563–591. [Google Scholar] [CrossRef]
- Bak, P.; Bruinsma, R. One-Dimensional Ising Model and the Complete Devil’s Staircase. Phys. Rev. Lett. 1982, 49, 249–251. [Google Scholar] [CrossRef]
- Pokrovsky, V.L.; Virosztek, A. Long-range interactions in commensurate-incommensurate phase transition. J. Phys. C Solid State Phys. 1983, 16, 4513–4525. [Google Scholar] [CrossRef]
- Mingaleev, S.F.; Gaididei, Y.B.; Majernikova, E.; Shpyrko, S. Kinks in the discrete sine-Gordon model with Kac-Baker long-range interactions. Phys. Rev. E 2000, 61, 4454–4460. [Google Scholar] [CrossRef]
- Braun, O.M.; Kivshar, Y.S.; Zelenskaya, I.I. Kinks in the Frenkel-Kontorova model with long-range interparticle interactions. Phys. Rev. B 1990, 41, 7118–7138. [Google Scholar] [CrossRef]
- Morigi, G.; Fishman, S. Dynamics of an ion chain in a harmonic potential. Phys. Rev. E 2004, 70, 066141. [Google Scholar] [CrossRef]
- Morigi, G.; Fishman, S. Eigenmodes and thermodynamics of a Coulomb chain in a harmonic potential. Phys. Rev. Lett. 2004, 93, 170602. [Google Scholar] [CrossRef]
- Dubin, D.H.E. Minimum energy state of the onedimensional Coulomb chain. Phys. Rev. E 1997, 55, 4017–4028. [Google Scholar] [CrossRef]
- Willis, C.; El-Batanouny, M.; Stancioff, P. Sine-Gordon kinks on a discrete lattice. I. Hamiltonian formalism. Phys. Rev. B 1986, 33, 1904–1911. [Google Scholar] [CrossRef]
- Gangloff, D.A.; Bylinskii, A.; Vuletić, V. Kinks and nanofriction: Structural phases in few-atom chains. Phys. Rev. D 2020, 2, 013380. [Google Scholar] [CrossRef]
- Kamsap, M.R.; Champenois, C.; Pedregosa-Gutierrez, J.; Mahler, S.; Houssin, M.; Knoop, M. Experimental demonstration of an efficient number diagnostic for long ion chains. Phys. Rev. A 2017, 95, 013413. [Google Scholar] [CrossRef]
- Lauprêtre, T.; Linnet, R.B.; Leroux, I.D.; Landa, H.; Dantan, A.; Drewsen, M. Controlling the potential landscape and normal modes of ion Coulomb crystals by a standing-wave optical potential. Phys. Rev. A 2019, 99, 031401. [Google Scholar] [CrossRef]
- Straube, A.V.; Louis, A.A.; Baumgartl, J.; Bechinger, C.; Dullens, R.P.A. Pattern formation in colloidal explosions. EPL 2011, 94, 48008. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landa, H.; Cormick, C.; Morigi, G. Static Kinks in Chains of Interacting Atoms. Condens. Matter 2020, 5, 35. https://doi.org/10.3390/condmat5020035
Landa H, Cormick C, Morigi G. Static Kinks in Chains of Interacting Atoms. Condensed Matter. 2020; 5(2):35. https://doi.org/10.3390/condmat5020035
Chicago/Turabian StyleLanda, Haggai, Cecilia Cormick, and Giovanna Morigi. 2020. "Static Kinks in Chains of Interacting Atoms" Condensed Matter 5, no. 2: 35. https://doi.org/10.3390/condmat5020035
APA StyleLanda, H., Cormick, C., & Morigi, G. (2020). Static Kinks in Chains of Interacting Atoms. Condensed Matter, 5(2), 35. https://doi.org/10.3390/condmat5020035




