Abstract
Bragg spectroscopy, one of the best established experimental techniques for high energy resolution X-ray measurements, has always been limited to the measurement of photons produced from well collimated (tens of microns) or point-like sources; recently, the VOXES collaboration at INFN National Laboratories of Frascati developed a prototype of a high resolution and high precision X-ray spectrometer working also with extended isotropic sources. The realized spectrometer makes use of Highly Annealed Pyrolitic Graphite (HAPG) crystals in a “semi”-Von Hamos configuration, in which the position detector is rotated with respect to the standard Von Hamos one, to increase the dynamic energy range, and shows energy resolutions at the level of 0.1% for photon energies up to 10 keV and effective source sizes in the range 400–1200 m in the dispersive plane. Such wide effective source dimensions are achieved using a double slit system to produce a virtual point-like source between the emitting target and the crystal. The spectrometer performances in terms of reflection efficiency and peak resolution depend on several parameters, among which a special role is played by the crystal mosaicity and thickness. In this work, we report the measurements of the Cu(K) and the Fe(K) lines performed with different mosaicity and thickness crystals in order to investigate the influence of the parameters on the peak resolution and on the reflection efficiency mentioned above.
Keywords:
X- and γ-ray instruments; X- and γ-ray sources, mirrors, gratings, and detectors; X-ray and γ-ray spectrometers; optical materials; X-ray diffraction; optical instruments and equipment PACS:
07.85.-m; 07.85.Fv; 07.85.Nc; 42.70.-a; 61.10.Nz; 07.60.-j
1. Introduction
High precision measurements of soft X-rays represent still today a very big challenge; nevertheless, such kind of measurements are strongly demanded in many fields of fundamental science, from particle and nuclear physics to quantum mechanics, as well as in astronomy and in several applications using synchrotron light sources or X-ray Free Electron Lasers (X-FEL) beams, in biology, medicine and industry. For several of these applications, in particular for nuclear physics experiments like those involving the measurement of exotic atoms’ radiative transitions, the detection of photons isotropically emitted from extended (non point-like) targets is required. Among the typically used solid state large area spectroscopic detectors, the Silicon Drift Detectors (SDDs), recently employed by the SIDDHARTA experiment [1] for exotic atoms’ transition lines measurements at the collider of the INFN National Laboratories of Frascati [2] represent the best options for wide and isotropic targets, in terms of energy resolution. The intrinsic resolution of such kind of detectors is nevertheless limited to ≃120 eV FWHM at 6–8 keV by the Fano Factor, making them unsuitable for those cases in which the photon energy has to be measured with a precision below 1 eV.
The superconducting microcalorimeters’ Transition Edge Sensors (TES), recently developed at NIST [3], represent a real possibility to obtain few eV FWHM at 6 keV; however, these kinds of detectors still have some limitations: a very small active area, prohibitively high costs of the complex cryogenic system needed to reach the operational temperature of ≃50 mK, and a response function which is still not properly under control.
A further alternative is represented by Bragg spectroscopy, one of the best established high resolution X-ray measurement techniques, where the X-ray energy spectrum can be otained exploiting photon reflection on crystals following the Bragg rule , where n is an integer number (order of reflection), is the photon wavelength, d is the crystal lattice constant and is the photon impinging angle on the crystal surface. If a monochromatic parallel X-ray beam has to be measured, the spectrum is obtained by several measurements with different values around the nominal Bragg angle ; on the contrary, if one needs to measure a polychromatic or isotropic beam of photons, the spectrum is obtained in one shot with a single using a position detector. In the first case, higher resolutions can be obtained with the drawback of a longer data taking; in the second case, in which the measurements presented in this work fall into, the faster exposure time is balanced by a higher background due to the beam divergence and the source size. As a consequence, when the photons emitted from extended isotropic sources (like a gaseous or liquid target) have to be measured, this method has been until now ruled out by the constraint to reduce the dimension of the target to a few tens of microns [4,5].
Experiments performed in the past at the Paul Scherrer Institute (PSI), measuring pionic atoms [6,7], pioneered the possibility to combine Charged Coupled Device detectors (CCDs) with silicon crystals, but the energy range achievable with that system was limited to few keV due to the crystal structure, and the silicon low intrinsic reflection efficiency required the construction of a very large spectrometer. The possibility to perform other fundamental measurements, like the precision determination of the mass measuring the radiative kaonic nitrogen transitions at the collider [8], has been also investigated, but the estimated efficiency of the proposed spectrometer was not sufficient to reach the required precision.
In the last several decades, the development of the Pyrolitic Graphite mosaic crystals [9,10,11] renewed the interest in Bragg spectrometers as possible candidates also for millimetric isotropic sources’ X-ray measurements. Mosaic crystals consist of a large number of nearly perfect small pyrolitic graphite crystallites, randomly misoriented around the lattice main direction; the FWHM of this random angular distribution is called mosaicity () and it makes it possible that even a photon not reaching the crystal with the exact Bragg energy-angle relation can find a properly oriented crystallite and be reflected [12]. This, together with a lattice spacing constant of 3514 Å, enables them to be highly efficient in diffraction in the 2–20 keV energy range, for the reflection order, while higher energies can be reached at higher reflection orders.
From the definition of mosaicity, it follows that those photons which find a properly oriented crystallite in the inner part of the crystal are reflected on the position detector slightly shifted with respect to the one coming from a surface crystallite; as a consequence of this unfocusing process, the peak resolution is worsened with respect to a standard non-mosaic crystal. For the same principle, for a given mosaicity, the thickness of the graphite crystal plays a fundamental role; for higher thickness, the reflection efficiency is enhanced at the expence of the peak resolution. This interplay between the above mentioned parameters has been investigated in the past with single or double crystal spectrometers providing parallel and monochromatic sources of few tens of microns. However, in spite of the results published and available in literature [12,13,14,15,16], it is still useful and intereresting to investigate how thickness and mosaicity influence the spectrometer response when almost millimetric sources are used.
Thanks to two different production mechanisms, Pyrolitic Graphite crystals can be obtained with different mosaicity and divided into two main families: Higly Annealed Pyrolitic Graphite crystals (HAPG) and Highly Oriented Pyrolitic Graphite (HOPG), showing lower and higher mosaicities, with consequently higher and lower resolutions, respectively. Both of these crystal types can be realised with different ad hoc geometries, making them suitable to be used in the Von Hamos configuration [17], combining the dispersion of a flat crystal with the focusing properties of cilindrically bent crystals.
Von Hamos spectrometers have been extensively used in the past providing very promising results in terms of spectral resolution [4,16,18] but all of the available works in literature report measurements for effective source dimensions of some tens of microns or parallel and monochromatic beams; these configurations are achieved either with microfocused X-ray tubes, or with a set of slits and collimators placed before the target to minimize the activated area. Possible spectrometer versions based on a full-cylinder geometry, to be used with a pixelated area detector instead of a monodimensional strip detector, are also possible; this may lead to an increase in both spectral resolution, thanks to a better integration of the bent lines produced by the crystal, and overall efficiency, thanks to a higher solid angle acceptance, but the effect of a hundred of microns source size are still to be tested [19].
In this work, we compare the response of three different thickness 206.7 mm curvature radius HAPG crystals and of two different mosaicity (HAPG and HOPG) 100 m thickness 103.4 mm curvature radius crystals to Cu(K) and Fe(K) lines, respectively. The resulting peak resolutions and reflection efficiencies will be discussed.
2. Spectrometer Setup and Geometry
2.1. Von Hamos Geometry
The spectrometer configuration used in the measurements presented in this work is the “semi” Von Hamos one, in which the X-ray source and the position detector are placed on the axis of a cylindrically bent crystal (see Figure 1); this geometrical scheme allows an improvement in the reflection efficiency due to the vertical focusing. As a consequence, for each X-ray energy, the source-crystal () and the source-detector () distances are determined by the Bragg angle () and the curvature radius of the crystal ():
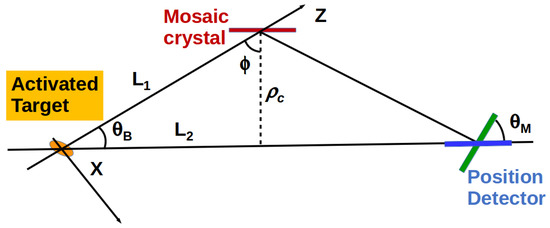
Figure 1.
Von Hamos schematic geometry schematic of the dispersive plane (not in scale): the X-ray source is pictured in orange, the HAPG/HOPG crystal in red and the position detector in blue and green for the standard and the “semi” Von Hamos configuration, respectively (for more details, see [20,21] and text). On the other hand, in the standard configuration, photons may impinge on the pixels almost parallel to their surface; the resulting short path through the silicon bulk of the pixel (450 m in the Mythen2-1D case) may result in non detected photons and hence to a lower efficiency. is the crystal curvature radius, is the Bragg angle, , is the position detector rotation angle with respect to standard VH configuration, is the source-crystal distance and is half the resulting source-detector distance.
In Figure 1, a schematic of the dispersive plane is shown where the X-ray source is sketched in orange, the HAPG/HOPG crystal in red and the position detector in blue and green for the standard and the “semi” Von Hamos configuration, respectively; this latter configuration is particularly suitable when used with strip detectors. On one hand, it allows for having a wider dynamic range, for a fixed spectrometer geometry, with respect to the standard one (for more details, see [20,21]). On the other hand, in the standard configuration, photons may impinge on the pixels almost parallel to their surface; the resulting short path through the silicon bulk of the pixel (450 m in the Mythen2-1D case) may result in non detected photons and hence to a lower efficiency. In the figure, is the crystal curvature radius, is the Bragg angle, , is the source-crystal distance, is half of the resulting source-detector distance and is the position detector rotation angle with respect to the standard Von Hamos configuration.
Spectrometer Components
A thin foil (target) is placed inside an aluminum box and activated by a XTF-5011 Tungsten anode X-ray tube, produced by Oxford Instruments (systems for research, Abingdon-on-Thames, UK), placed on top of the box; the center of the foil, placed on a rotated support prism, represents the origin of the reference frame in which Z is the direction of the characteristic photons emitted by the target and forming, with the x-axis, the Bragg reflection plane, while y is the vertical direction, along which primary photons generated by the tube are shot. Two adjustable motorized slits (Standa 10AOS10-1) with 1 m resolution are placed after the 5.9 mm diameter circular exit window of the aluminum box in order to shape the outcoming X-ray beam. The various used HAPG/HOPG crystals, produced by the Optigraph company in Berlin, Germany [10], are deposited on different curvature radii Thorlabs N-BK7 mm uncoated Plano-Concave Cylindrical lenses, held by a motorized mirror mount (STANDA 8MUP21-2) with a double axis ≪1 resolution and coupled to a 0.01 m motorized vertical translation stage (STANDA 8MVT40-13), a 4.5 resolution rotation stage (STANDA 8MR191-28) and two motorized 0.156 m linear translation stages (STANDA 8MT167-25LS). The position detector is a commercial MYTHEN2-1D 640 channels strip detector produced by DECTRIS (Zurich, Switzerland), having an active area of mm and whose strip width and thickness are, respectively, 50 m and 420 m; the MYTHEN2-1D detector is also coupled to a positioning motorized system identical to the one for the HAPG/HOPG holder. Finally, a standar Peltierd Cell is kept on top of the strip detector in order to stabilize its temperature in the working range of 18°–. The resulting 10-axis motorized positioning system is mounted on a set of Drylin rails and carriers to ensure better stability and alignment and, in addition, to easily adjust source-crystal-detector positions for each energy to be measured.
2.2. Source Size in Dispersion Plane
As pointed out in Section 1, the actual limitations on the possible usage of crystal spectrometers for extended targets are represented by the requirement of a point-like source; however, using a pair of slits as the one described in the previous section, it is possible to shape the beam of X-rays emitted by an extended and diffused target in such a way as to simulate a virtual point-like source.
Referring to Figure 2, this configuration is obtained setting the position ( and ) and the aperture ( and ) of each slit in order to create a virtual source between the two slits (, green solid lines on Figure 2), an angular acceptance , and an effective source (green) which can be, in principle, as wide as necessary. The angular acceptance could also be set to any value, provided it is large enough to ensure that all the corresponding to the lines to be measured are included.
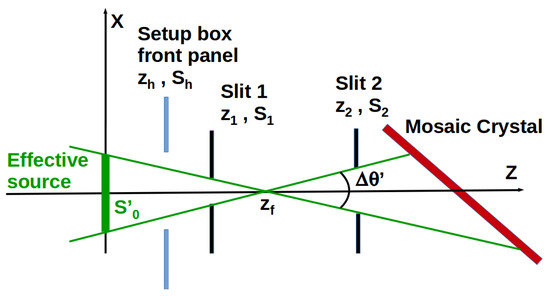
Figure 2.
Beam geometry on the dispersive plane (not in scale): the position ( and ) and the aperture ( and ) of two slits are used to create a virtual source between the two slits (, green solid lines), and effective source (green) and an angular acceptance ; the HAPG/HOPG crystal is pictured in red, the two slits are shown in black while and are the position and the diameter of the circular exit window of the aluminum box front panel (light blue), respectively.
For the following discussion, we call the photons leaving the target from the central position and meeting the Bragg rule “nominal”; since the photons are isotropically emitted from the whole target foil, some of them may have the correct energy and angle to be reflected but originate from a point of the target near the nominal one. As far as this mislocation is below the limit given by the mosaic spread of the crystal, such photons are also reflected under the signal peak worsening the spectral resolution; on the contrary, when this mislocation exceeds this limit, these photons are reflected outside the signal peak. In the same way, photons not emitted in parallel to the nominal ones may still impinge on the HAPG/HOPG crystals with an angle below its mosaic spread and be then reflected under the signal peak also affecting the spectral resolution. On the contrary, if the impinging angle is out of this limit, those photons are not reflected on the position detector. As a consequence, for each energy, there is the possibility to find the right slits configuration leading at the maximum source size keeping the resolution below the desired limit.
For each chosen pair, the corresponding values of the slits’ apertures and can be found; first, we define the position of the intersection point :
Then, the two slits’ apertures and the vertical illuminated region of the HAPG/HOPG are defined by:
2.3. Possible Effects of the Crystal Thickness
As introduced in Section 1, for a given crystal mosaicity, the graphite thickness has a double effect; on one side, increasing the thickness of the crystal leads to a higher reflectivity because of a higher probability to find a properly oriented crystallite; on the other side, photons reflected at different depths result slightly shifted on the position detector. In fact, two photons with exactly the same angle and energy would be both reflected from the same microcrystallite (if coming from the same point, so following the exact same path), but two photons with a slightly different energy (or angle) may penetrate more in the crystal before being reflected by a properly oriented microcrystallite. This introduces an additional and bigger misplacement on the position detector with respect to the one only due to the mosaicity. The situation is shown in the schematic of Figure 3: photons emitted from different part of the source (orange spot) with the same can be reflected at different depths in the crystal (red line) by two distinct crystallites (blue rectangulars), resulting in different positions (orange dotted line) and (black solid line) with respect to the nominal one with (, solid orange line).
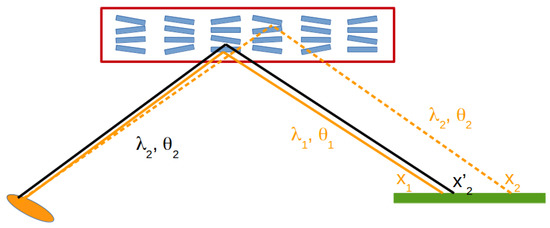
Figure 3.
Depth reflection schematic: photons emitted from different part of the source (orange spot) with the same can be reflected at different depths in the crystal (red line) by two distinct crystallites (blue rectangulars), resulting in different positions (orange dotted line) and (black solid line) with respect to the nominal one with (, solid orange line).
The above mentioned aberration effect is well known and studied (see for example [12]); however, it is interesting to check whether the worsening of the resolution due to the crystal thickness is still a dominant effect also when the effective source size is about 1 mm or if instead the broadening induced by the source size becomes more important.
3. Results
In this section, we present the spectra obtained for the Cu(K) and Fe(K) lines (see Table 1); for each measurement, the corresponding geometrical parameters are listed in Table 2, where is the central Bragg angle value used for the calculation. The crystal curvature radius is chosen in order to make a compromise between the energy resolution and the signal rate, since higher leads to longer paths meaning better resolution but higher X-ray absorption from the air. Slits’ positions and are chosen such as to have a vertical dispersion at the HAPG/HOPG position smaller than the crystal size (30 mm). The typical fitting function for peaks obtained with micrometric sources is a Lorentzian, which can be used to take into account the natural lineshape of the atomic transitions and, in case, the mosaic spread of a crystal; however, in our analysis, we carefully checked our spectra and fitted them either with a Lorentzian, a Gaussian, and a convolution of the 2 (Voigt function), and we concluded that, in our case, in which the dimension of the source is not a few microns anymore, the Gaussian shape better reproduces the broadening induced by the bigger source size. In the following subsections, the presented spectra are then fitted with Gaussian functions; for each acquired spectra, since the angular separation between Cu and Fe K lines is very small ((Cu) , (Fe) ), a linearity regime is assumed between the pixel position on the strip detector and the X-ray energy. The calibration is then obtained by a linear interpolation of the peak mean values obtained by the fits of the position spectra; this linear function is then used to convert position spectra into energy spectra. For each plot, the rate reported in the yellow box is calculated as the sum of the integrals of the K peaks divided by the data acquisition (DAQ) time (1 h DAQ for all the reported measurement).

Table 1.
List of the X-ray lines used in this work and the corresponding Bragg angles .

Table 2.
List of the measurements presented in this work and their main beam parameters.
3.1. Reflection Efficiency and Resolution for Different HAPG Thickness
We present the results obtained from several measurements of the Cu(K lines, using three different 206.7 mm curvature radius HAPG crystal of 20 m, 40 m, and 100 m thickness, all having a mosaicity, measured and declared by the producer, of . As an example, we show the comparison spectra obtained for each crystal for and with effective source sizes of 1000 m in Figure 4, while, for the other source sizes, the results are summarized in Table 3. In the figure, the three spectra for the 20 m, 40 m and 100 m cases are shown in the upper, middle and lower panels, respectively. For each measurement, the data taking time is one hour and the fitting function is a double Gaussian with common for the Cu lines and a polynomial for the background.
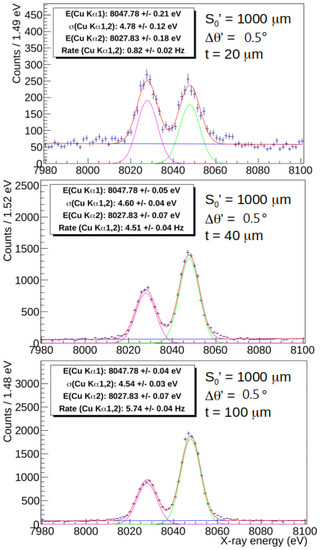
Figure 4.
Fitted spectra of Cu(K) lines for = 1000 m and : K, K, polynomial background and total fitting functions correspond to the green, violet, blue and red curves, respectively, while t in the text box refers to the thickness of the HAPG crystal.

Table 3.
Summary of the peak precisions, resolutions and total rates obtained in the different measurements.
3.2. Reflection Efficiency and Resolution for Different Crystal Mosaicities
An effect similar to the one due to the crystal thickness is played by the mosaicity: for a given thickness, an increase in the mosaicity leads to a higher reflectivity because of a higher probability to find a properly oriented crystallite but, as a drawback, a defocusing effect in the reflection plane is induced [4]. We present the results obtained from several measurements of the Fe(K) lines, using two different 103.4 mm curvature radius crystal of mosaicity (HAPG) and (HOPG); for each one, the data taking time is one hour and the fitting function is a double Gaussian with common for the Cu lines and a polynomial for the background. Unlike the measurements in Section 3.1, in this case, it was not possible to obtain spectra for the same for each value because of the geometrical limitations imposed by the Von Hamos configuration. For example, to have m and , slit aperture should be only 2 m, while to have m and , slit aperture should be only 7 m; for both values, not only is the rate not sufficient to acquire meaningful 1 h data taking spectra, but they are also below the error on the induced by the x and z position of the slits.
As an example, the comparison spectra obtained for the two type of crystal for and combination are presented in Figure 5, where the HAPG and HOPG spectra are shown in the upper and lower panels, respectively. The results obtained for difference combinations are reported in Table 3.
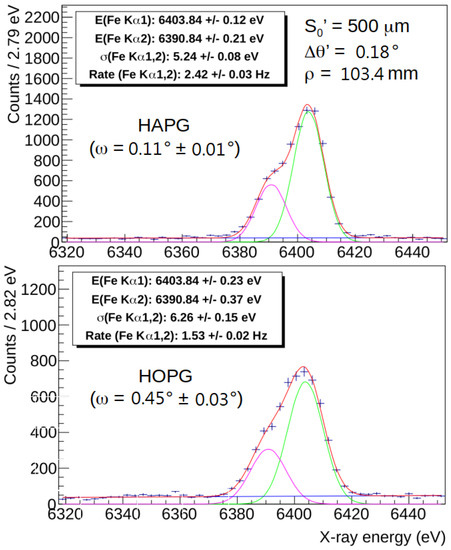
Figure 5.
Fitted spectra of Fe(K) lines for m and : K, K, polynomial background and total fitting functions correspond to the green, violet, blue and red curves, respectively.
The obtained peak precisions, resolutions and total rates obtained in the different measurements are summarized in Table 3.
4. Discussion
The different thickness measurements show that, for a given effective source size, the resolution worsening effect induced by the crystal thickness is not predominant anymore; on the contrary, the resolution broadening induced by the source size is more important. This is a very important result to be taken into account when X-rays emitted from extended isotropic sources have to be measured. It has to be noticed that the correct ratio between K and K, both in Copper and Iron, is 100:51; this ratio is somehow reversed in the spectra obtained with thin crystals (see Figure 4, top pad). This effect may be better explained using Figure 1 and Figure 2. The setup is prepared in order to have a nominal Bragg angle ( in Figure 1) tuned between the K and K peaks, around which the angular acceptance of Figure 2 is defined. If the crystal is a bit mispositioned (not centered) with respect to this nominal direction, it could result in a setup more aligned around one of the two peaks, in this case around K. Consequently, the probability to find properly oriented microcrystallites for K is lowered.
Concerning the mosaicity influence on the reflectivity and the resolution, a more detailed discussion can be carried out starting from the measurements. From the spectra, it is evident how, with the higher mosaicity of the HOPG crystal with respect to the HAPG, one causes a peak broadening, leading, in some cases, even to a non-separation of the two peaks, consistent with the expectation; on the contrary, the reason why there is not a corresponding increase in the measured rate is not intuitive and needs to be more carefully motivated.
We can start from the assumption that, for the same crystal thickness and dimensions, the amount of inner crystallites is always of the same order of magnitude regardless of the mosaicity value; then, according to what is available in literature [12,13,14,15,16] and what is declared by the crystal producers [10], the orientation distribution can be described with a Lorentzian, normalized to unity, of the form:
where is the crystal mosaicity . For each value (see Figure 2), for a single photon energy, the number of the properly oriented crystallites is given by:
For each measured spectrum, almost the 100% of the Fe(K photons will be in the interval being = Fe(K)−5 and = Fe(K)+5, where now is the Gaussian peak resolution obtained from the fits; this will correspond to a interval of being and where d is the graphite lattice parameter and is the Å conversion factor. The final number of properly oriented crystallites will then be:
The situation is shown in Figure 6, where the orientation distributions for the HAPG and HOPG are shown in each panel in red and black, respectively. The distributions are peaked around , which represents the nominal Bragg angle; the integrals of the two Gaussians are then reported for various intervals and show how the ratio between the HOPG and HAPG number of properly oriented crystallite is changing. As a consequence, in the case of the Fe(K lines, which are only 13 eV or 0.035 distant, the expected ratio is actually matching the expected values.
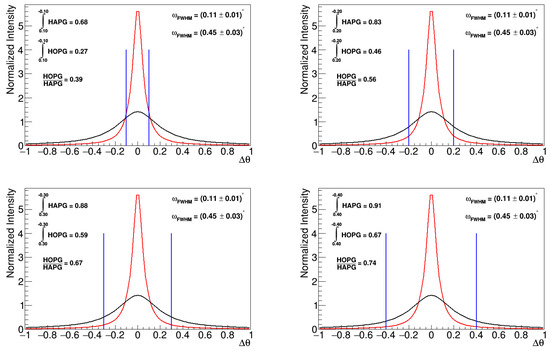
Figure 6.
Orientation distributions for the HAPG (red) and HOPG (black) crystals: the distributions are peaked around , which represents the nominal Bragg angle; the integrals of the two Gaussians are then reported for various intervals and show how the ratio between the HOPG and HAPG number of properly oriented crystallite is changing.
This description is reproducing the experimental data well, as shown in Figure 7, where, in the upper panel, the measured ratios for each pairs are shown, while, in the middle panel, the corresponding calculated integral ratios are reported. In the bottom pad, the difference between the previous two is reported to show how much the calculated values differ from the measured ones. The errors on the measured points are obtained propagating the errors on the peak fitting parameters, while the errors on the calculated ones take into account the errors on the crystal mosaicities declared by the producer. The errors are then propagated in the difference plot.
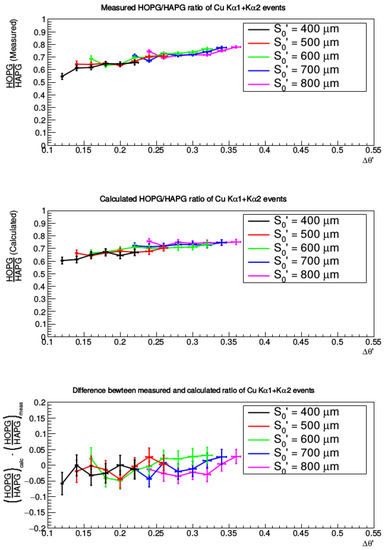
Figure 7.
Comparison of the measured (top) and calculated (middle) HOPG/HAPG rate ratios; subtraction of the two graphs is shown in the bottom pad. Each point of the upper and middle plots represents the sum of both K and K number of events for the HOPG crystal divided by the same quantity for the HAPG one.
5. Conclusions
In this work, we presented the measurements of the Cu(K) and the Fe(K) lines performed with different mosaicity, thickness and curvature radius crystals in order to investigate the influence of the above mentioned parameters on the peak resolution and on the reflection efficiency. The different thickness measurements show that, for a given effective source size, the resolution worsening effect induced by the crystal thickness is not predominant anymore with respect to the effect induced by the wider source size; therefore, higher thickness values ensure higher reflectivities leading to more precise determinations of the peak positions. This is a very important result to be taken into account when X-rays emitted from extended isotropic sources have to be measured.
Concerning the mosaicity influence on the reflectivity and the resolution, a more detailed discussion was carried out starting from the measurements. On one side, we confirmed that the higher mosaicity of the HOPG crystal with respect to the HAPG one causes a peak broadening, leading in some cases even to a non-separation of the two peaks; on the other side, we measured a higher number of reflected photons using the HAPG crystal with respect to using the HOPG one. We provided a semi-quantitative explanation of this behaviour, which is in good agreement with the measured ratios.
The proposed spectrometer shows promising results for future experiments in which, like for example in the case of exotic atoms’ transitions measurements, X-rays are emitted from a wide and diffused source. In these kinds of experiments, for a given spectrometer geometry, a proper choice of the crystal in terms of thickness and mosaicity becomes a crucial parameter to be set based on the main goals of the measurement and on the experimental conditions, like, for instance, the source emission rate and the solid angle acceptance. The correct combination of crystal parameters may in fact be chosen in order to obtain the desired combination of peak resolution and precision position determination. In the future, the possibility to use pixelated area detectors in a full-cylinder crystal configuration like the one mentioned in the Introduction, instead of linear strip detectors, will be also investigated; this may lead to an increase in both spectral resolution, thanks to a better integration of the bent lines produced by the crystal, and overall efficiency, thanks to a higher solid angle acceptance.
Author Contributions
Conceptualization, A.S.; methodology, A.S.; software, A.S.; formal analysis, A.S.; investigation, A.S.; data curation, A.S. and M.M.; resources, A.S., M.M. and F.S.; writing—original draft preparation, A.S.; writing—review and editing, A.S.; visualization, A.S.; supervision, A.S., C.C., and J.Z.; project administration, A.S.; funding acquisition, A.S. and J.Z.
Funding
This research was funded by the 5th National Scientific Committee of INFN in the framework of the Young Researcher Grant 2015, n. 17367/2015.
Acknowledgments
We thank the Laboratori Nazionali di Frascati INFN (LNF) and the Stefan-Meyer-Institut für subatomare Physik (SMI) staff, in particular the LNF Servizio Progettazione e Costruzione Meccanica (SPCM) service and Doris Pristauz-Telsnigg, for the support in the preparation of the setup.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bazzi, M.; Beer, G.; Bombelli, L.; Bragadireanu, A.M.; Cargnelli, M.; Corradi, G.; Curceanu, C.; d’Uffizi, A.; Fiorini, C.; Frizzi, T.; et al. A New Measurement of Kaonic Hydrogen X-rays. Phys. Lett. 2011, B704, 113–117. [Google Scholar] [CrossRef]
- Gallo, A.; Alesini, D.; Biagini, M.E.; Biscari, C.; Boni, R.; Boscolo, M.; Buonomo, B.; Clozza, A.; Delle Monache, G.; Di Pasquale, E.; et al. DAFNE status report. Conf. Proc. 2006, C060626, 604–606. [Google Scholar]
- Doriese, W.B.; Abbamonte, P.; Alpert, B.K.; Bennett, D.A.; Denison, E.V.; Fang, Y.; Fischer, D.A.; Fitzgerald, C.P.; Fowler, J.W.; Gard1, J.D.; et al. A practical superconducting-microcalorimeter X-ray spectrometer for beamline and laboratory science. Rev. Sci. Instrum. 2017, 88, 053108. [Google Scholar] [CrossRef] [PubMed]
- Legall, H.; Stiel, H.; Antonov, A.; Grigorieva, I.; Arkadiev, V.; Bjeoumikhov, A. A new generation of X-ray optics based on pyrolitic graphite. In Proceedings of the FEL 2006, Berlin, Germany, 27 August–1 September 2006; p. 798. [Google Scholar]
- Barnsley, R.; Peacock, N.; Dunn, J.; Melnick, I.; Coffey, I.; Rainnie, J.; Tarbutt, M.; Nelms, N. Versatile high resolution crystal spectrometer with X-ray charge coupled device detector. Rev. Sci. Instrum. 2003, 74, 2388. [Google Scholar] [CrossRef]
- Anagnostopoulos, D.; Biri, S.; Borchert, G.; Breunlich, W.; Cargnelli, M.; Egger, J.-P.; Fuhrmann, H.; Gotta, D.; Giersch, M.; Gruber, A.; et al. The Pionic Hydrogen Experiment at PSI. Hyperfine Interact. 2001, 138, 131–140. [Google Scholar] [CrossRef]
- Trassinelli, M.; Anagnostopoulos, D.; Borchert, G.; Dax, A.; Egger, J.-P.; Gotta, D.; Hennebach, M.; Indelicato, P.; Liu, Y.-W.; Manil, B.; et al. Measurement of the charged pion mass using X-ray spectroscopy of exotic atoms. Phys. Lett. 2016, B759, 583–588. [Google Scholar] [CrossRef]
- Beer, G.; Bragadireanu, A.; Breunlich, W.; Cargnelli, M.; Curceanu, C.; Egger, J.-P.; Fuhrmann, H.; Guaraldo, C.; Giersch, M.; Iliescu, M.; et al. A new method to obtain a precise value of the mass of the charged kaon. Phys. Lett. 2002, B535, 52–58. [Google Scholar] [CrossRef]
- Antonov, A.A.; Baryshev, V.; Grigoryeva, I.; Kulipanov, G.; Terekhov, Y.V.; Shipkov, N. First results on application of short-focus monochromators from formed pyrolytic graphite for X-ray fluorescent analysis using synchrotron radiation. Rev. Sci. Instrum. 1989, 60, 2462–2463. [Google Scholar] [CrossRef]
- Optigraph References. Available online: http://www.optigraph.eu/references.html#ref_07 (accessed on 3 April 2019).
- Del Rio, M.S.; Gambaccini, M.; Pareschi, G.; Taibi, A.; Tuffanelli, A.; Freund, A.K. Focusing properties of mosaic crystals. Proc. SPIE 1998, 3448, 246–255. [Google Scholar]
- Gerlach, M.; Anklamm, L.; Antonov, A.; Grigorieva, I.; Holfelder, I.; Kanngießer, B.; Legall, H.; Malzer, W.; Schlesiger, C.; Beckhoff, B. Characterization of HAPG mosaic crystals using synchrotron radiation. J. Appl. Cryst. 2015, 48, 1381–1390. [Google Scholar] [CrossRef]
- Ice, G.; Sparks, C. Mosaic crystal X-ray spectrometer to resolve inelastic background from anomalous scattering experiments. Nucl. Instrum. Methods Phys. Res. A 1990, 291, 110–116. [Google Scholar] [CrossRef]
- Legall, H.; Stiel, H.; Arkadiev, V.; Bjeoumikhov, A. High spectral resolution X-ray optics with highly oriented pyrolytic graphite. Opt. Express 2006, 14, 4570–4576. [Google Scholar] [CrossRef] [PubMed]
- Zastrau, U.; Brown, C.; Döppner, T.; Glenzer, S.; Gregori, G.; Lee, H.; Marschner, H.; Toleikis, S.; Wehrhan, O.; Förster, E. Focal aberrations of large-aperture HOPG von-Hamos X-ray spectrometers. JINST 2012, 7, P09015. [Google Scholar] [CrossRef]
- Zastrau, U.; Woldegeorgis, A.; Förster, E.; Loetzsch, R.; Marschner, H.; Uschmann, I. Characterization of strongly-bent HAPG crystals for von-Hámos X-ray spectrographs. JINST 2013, 8, P10006. [Google Scholar] [CrossRef]
- Von Hamos, L.V. Röentgenspektroskopie und Abbildung mittels gekrümmter Kristallreflektoren. I. Geometrisch-optische Betrachtungen. Ann. Physik 1933, 409, 716. [Google Scholar] [CrossRef]
- Shevelko, A.P.; Kasyanov, Y.S.; Yakushev, O.F.; Knight, L.V. Compact focusing von Hamos spectrometer for quantitative X-ray spectroscopy. Rev. Sci. Instrum. 2002, 73, 3458. [Google Scholar] [CrossRef]
- Anklamm, L.; Anklamm, L.; Schlesiger, C.; Malzer, W.; Grötzsch, D.; Neitzel, M.; Kanngießer, B. A novel von Hamos spectrometer for efficient X-ray emission spectroscopy in the laboratory. Rev. Sci. Instrum. 2014, 85, 053110. [Google Scholar] [CrossRef] [PubMed]
- Scordo, A.; Shi, H.; Curceanu, C.; Miliucci, M.; Sirghi, F.; Zmeskal, J. VOXES, a new high resolution X-ray spectrometer for low yield measurements with diffused sources. Acta Phys. Polon. 2017, B48, 1715. [Google Scholar] [CrossRef]
- Scordo, A.; Curceanu, C.; Miliucci, M.; Sirghi, F.; Zmeskal, J. Development of a compact HAPG crystal Von Hamos X-ray spectrometer for extended and diffused sources. arXiv, 2019; arXiv:1903.02826. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).