Quantized Alternate Current on Curved Graphene
Abstract
1. Introduction
2. The Dirac Equation in Curved Space and Graphene
Theory of Strained Graphene
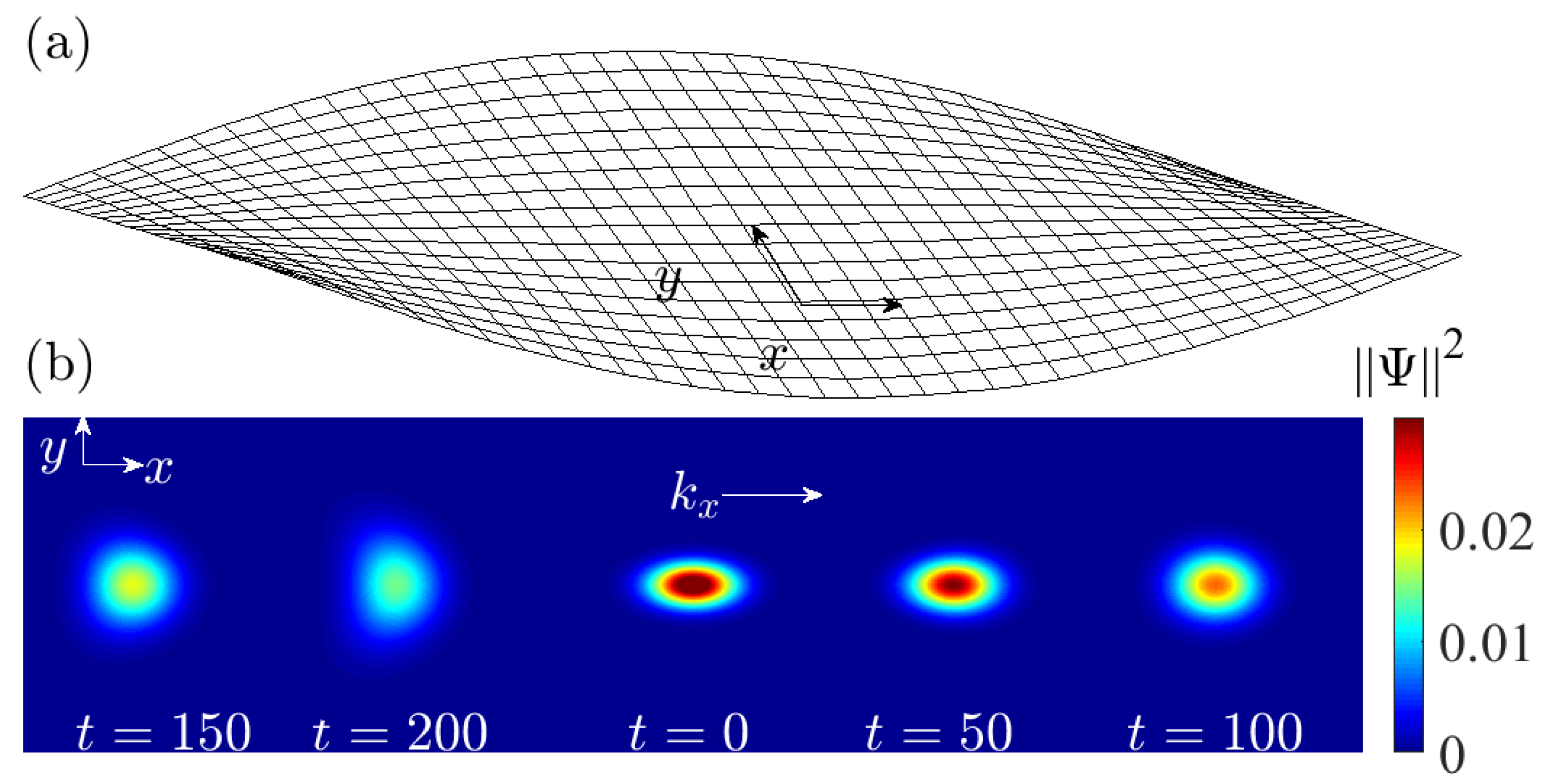
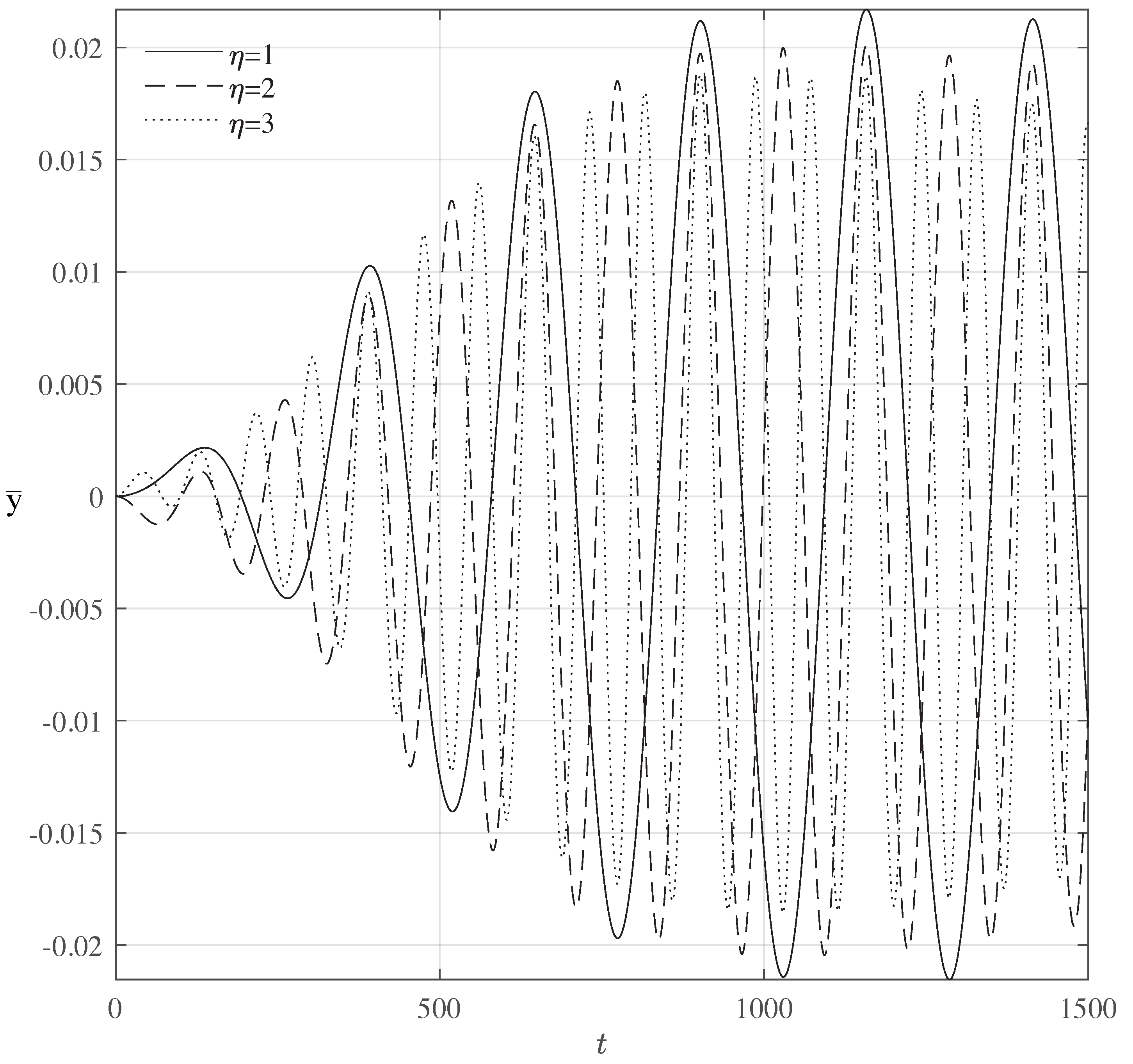
3. Quantized Alternating Current Graphene Strip
4. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Curved-Space Quantum Lattice Boltzmann
Appendix A.1. The Dirac Equation
Appendix A.2. Diagonal Streaming Operator
- Rotation: The spinor is rotated by ,
- Collisions and curvature: The collision and force operators are applied to the rotated spinor,where denotes an auxiliary field,where is the lattice direction and is the collision term, Equation (A3). The upper sign applies to the spin-up components and the lower sign to the spin-down components .
- Streaming: The spinor components are streamed to the closest grid points along the lattice direction ,
- Inverse Rotation: The spinor is rotated back via ,
- Repeat steps 2–4 for the next spatial direction.
Appendix B. Berry Phase Relation to the Spin Connection
References
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fizika 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 1982, 49, 1804–1807. [Google Scholar] [CrossRef]
- Haroche, S. Nobel Lecture: Controlling photons in a box and exploring the quantum to classical boundary. Rev. Mod. Phys. 2013, 85, 1083–1102. [Google Scholar] [CrossRef]
- Bennett, C.; Bernstein, E.; Brassard, G.; Vazirani, U. Strengths and weaknesses of quantum computing. SIAM J. Comput. 1997, 26, 1510–1523. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575. [Google Scholar]
- Cirac, J.I.; Zoller, P. Goals and opportunities in quantum simulation. Nat. Phys. 2012, 8, 264. [Google Scholar] [CrossRef]
- Schreiber, M.; Hodgman, S.S.; Bordia, P.; Lüschen, H.P.; Fischer, M.H.; Vosk, R.; Altman, E.; Schneider, U.; Bloch, I. Observation of many-body localization of interacting fermions in a quasirandom optical lattice. Science 2015, 349, 842–845. [Google Scholar] [CrossRef]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153–185. [Google Scholar] [CrossRef]
- Mehonic, A.; Vrajitoarea, A.; Cueff, S.; Hudziak, S.; Howe, H.; Labbé, C.; Rizk, R.; Pepper, M.; Kenyon, A.J. Quantum conductance in silicon oxide resistive memory devices. Sci. Rep. 2013, 3, 2708. [Google Scholar] [CrossRef] [PubMed]
- Jurcevic, P.; Lanyon, B.P.; Hauke, P.; Hempel, C.; Zoller, P.; Blatt, R.; Roos, C.F. Quasiparticle engineering and entanglement propagation in a quantum many-body system. Nature 2014, 511, 202. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, Y.; Davidovich, L.; Zagury, N. Quantum random walks. Phys. Rev. A 1993, 48, 1687–1690. [Google Scholar] [CrossRef] [PubMed]
- Succi, S.; Benzi, R. Lattice Boltzmann equation for quantum mechanics. Phys. D Nonlinear Phenom. 1993, 69, 327–332. [Google Scholar] [CrossRef]
- Succi, S.; Fillion-Gourdeau, F.; Palpacelli, S. Quantum lattice Boltzmann is a quantum walk. EPJ Quantum Technol. 2015, 2, 12. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Mosco, N.; Perinotti, P.; Tosini, A. Solutions of a two-particle interacting quantum walk. Entropy 2018, 20, 435. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Erba, M.; Perinotti, P. Isotropic quantum walks on lattices and the Weyl equation. Phys. Rev. A 2017, 96, 062101. [Google Scholar] [CrossRef]
- Brouwer, P.W. Enter the Majorana Fermion. Science 2012, 336, 989–990. [Google Scholar] [CrossRef]
- Karski, M.; Förster, L.; Choi, J.M.; Steffen, A.; Alt, W.; Meschede, D.; Widera, A. Quantum walk in position space with single optically trapped atoms. Science 2009, 325, 174–177. [Google Scholar] [CrossRef] [PubMed]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Informational derivation of quantum theory. Phys. Rev. A 2011, 84, 012311. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Perinotti, P. Quantum cellular automaton theory of light. Ann. Phys. 2016, 368, 177–190. [Google Scholar] [CrossRef]
- Konno, N. Quantum walks and quantum cellular automata. In Cellular Automata; Umeo, H., Morishita, S., Nishinari, K., Komatsuzaki, T., Bandini, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 12–21. [Google Scholar]
- Bisio, A.; D’Ariano, G.M.; Tosini, A. Quantum field as a quantum cellular automaton: The Dirac free evolution in one dimension. Ann. Phys. 2015, 354, 244–264. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A Math. Phys. Sci. 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, S. Topological states of condensed matter. Nat. Mater. 2017, 16, 1062. [Google Scholar] [CrossRef]
- Ryder, L.H. Quantum Field Theory, 2nd ed.; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Das Sarma, S.; Adam, S.; Hwang, E.H.; Rossi, E. Electronic transport in two-dimensional graphene. Rev. Mod. Phys. 2011, 83, 407–470. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43. [Google Scholar] [CrossRef]
- De Oliveira, J.B.; de Oliveira, I.S.S.; Padilha, J.E.; Miwa, R.H. Tunable magnetism and spin-polarized electronic transport in graphene mediated by molecular functionalization of extended defects. Phys. Rev. B 2018, 97, 045107. [Google Scholar] [CrossRef]
- Flouris, K.; Mendoza Jimenez, M.; Debus, J.D.; Herrmann, H.J. Confining massless Dirac particles in two-dimensional curved space. Phys. Rev. B 2018, 98, 155419. [Google Scholar] [CrossRef]
- Debus, J.D. Flows in Curved Spaces. Ph.D. Thesis, ETH-Zürich, Zurich, Switzerland, 2016. [Google Scholar]
- Kaku, M. Quantum Field Theory: A Modern Introduction; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Debus, J.-D.; Mendoza, M.; Herrmann, H.J. Shifted Landau levels in curved graphene sheets. arXiv, 2018; arXiv:1803.01345. [Google Scholar]
- Oliva-Leyva, M.; Naumis, G.G. Generalizing the Fermi velocity of strained graphene from uniform to nonuniform strain. Phys. Lett. A 2015, 379, 2645–2651. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959–2007. [Google Scholar] [CrossRef]
- Lapitski, D.; Dellar, P.J. Convergence of a three-dimensional quantum lattice Boltzmann scheme towards solutions of the Dirac equation. Philos. Trans. R. Soc. A 2011, 369, 2155–2163. [Google Scholar] [CrossRef]
- Dellar, P.J.; Lapitski, D.; Palpacelli, S.; Succi, S. Isotropy of three-dimensional quantum lattice Boltzmann schemes. Phys. Rev. E 2011, 83, 046706. [Google Scholar] [CrossRef]
- Palpacelli, S.; Succi, S. The Quantum Lattice Boltzmann Equation: Recent Developments. Commun. Comput. Phys. 2008, 4, 980–1007. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flouris, K.; Succi, S.; Herrmann, H.J. Quantized Alternate Current on Curved Graphene. Condens. Matter 2019, 4, 39. https://doi.org/10.3390/condmat4020039
Flouris K, Succi S, Herrmann HJ. Quantized Alternate Current on Curved Graphene. Condensed Matter. 2019; 4(2):39. https://doi.org/10.3390/condmat4020039
Chicago/Turabian StyleFlouris, Kyriakos, Sauro Succi, and Hans J. Herrmann. 2019. "Quantized Alternate Current on Curved Graphene" Condensed Matter 4, no. 2: 39. https://doi.org/10.3390/condmat4020039
APA StyleFlouris, K., Succi, S., & Herrmann, H. J. (2019). Quantized Alternate Current on Curved Graphene. Condensed Matter, 4(2), 39. https://doi.org/10.3390/condmat4020039





