Energy Response of Silicon Drift Detectors for Kaonic Atom Precision Measurements
Abstract
1. Introduction
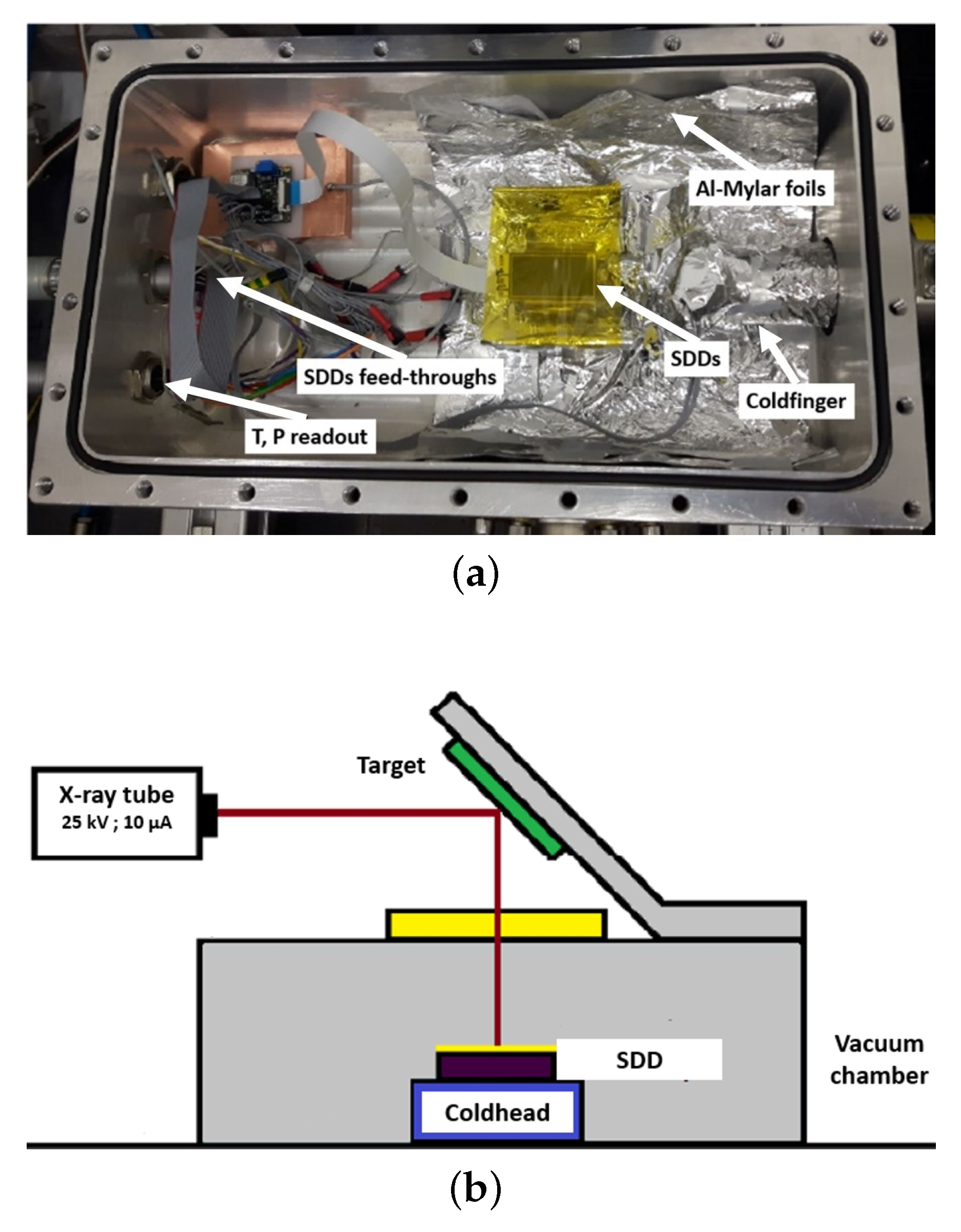
2. Materials and Methods
3. Results and Discussion
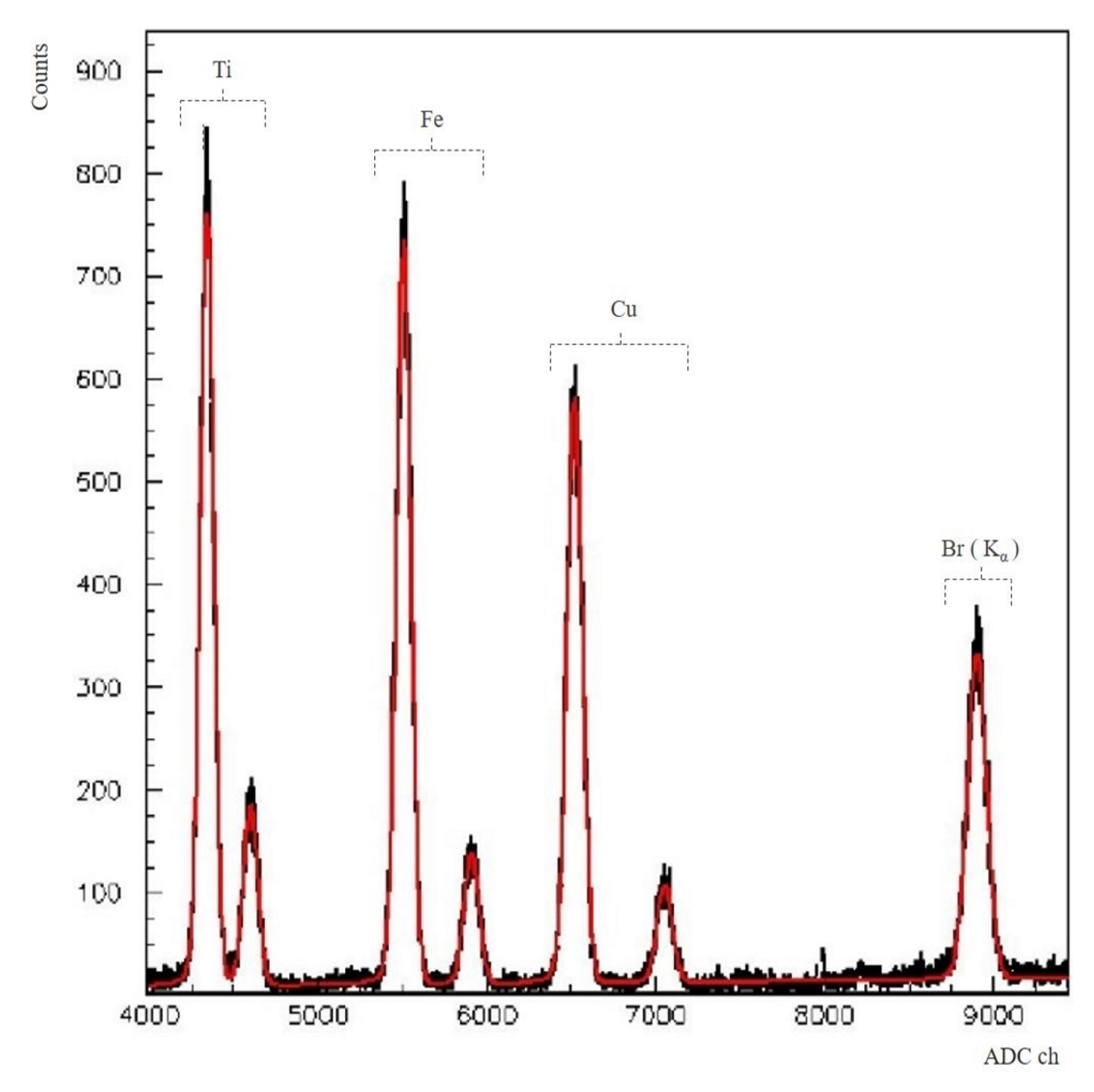
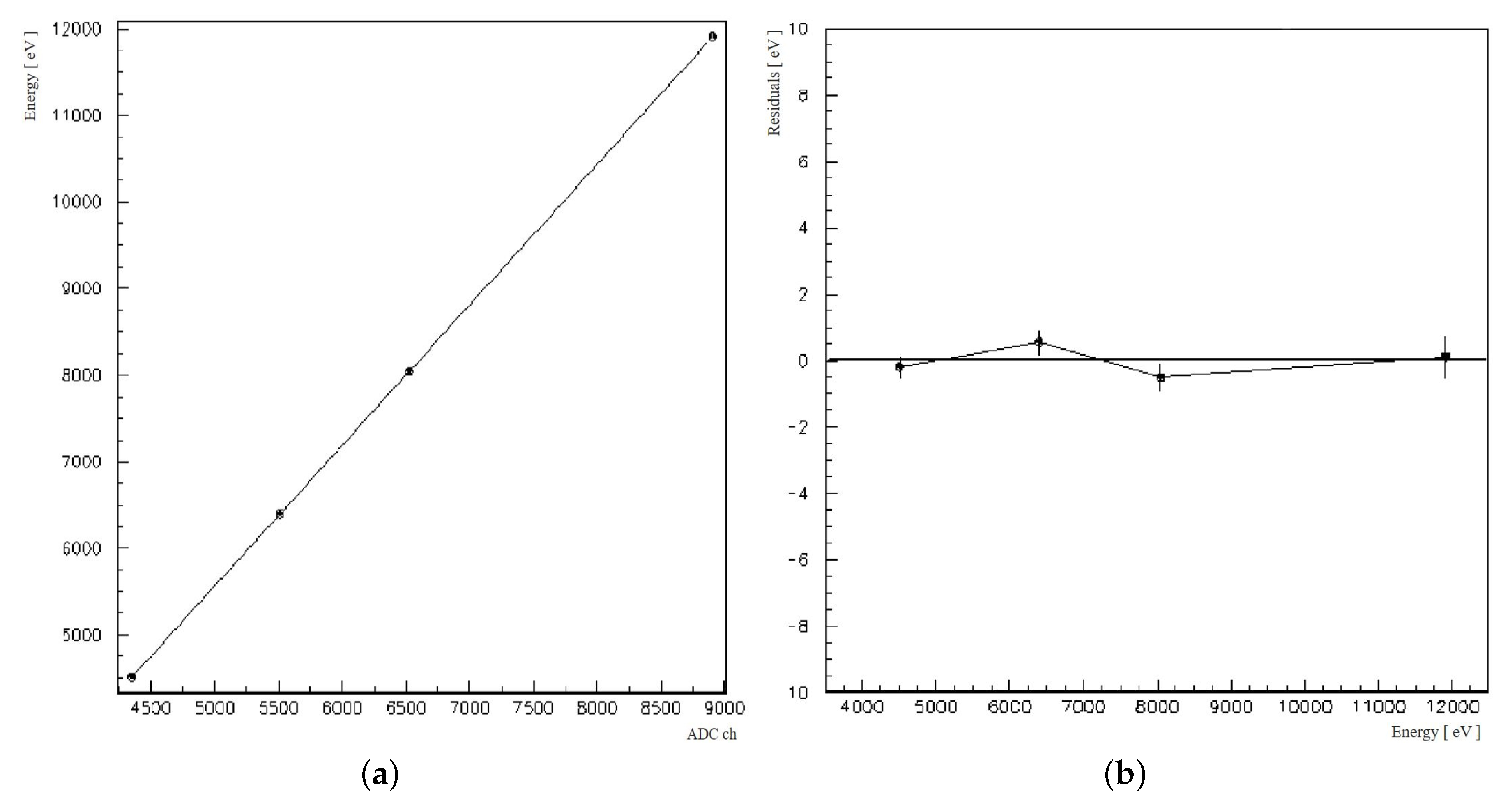
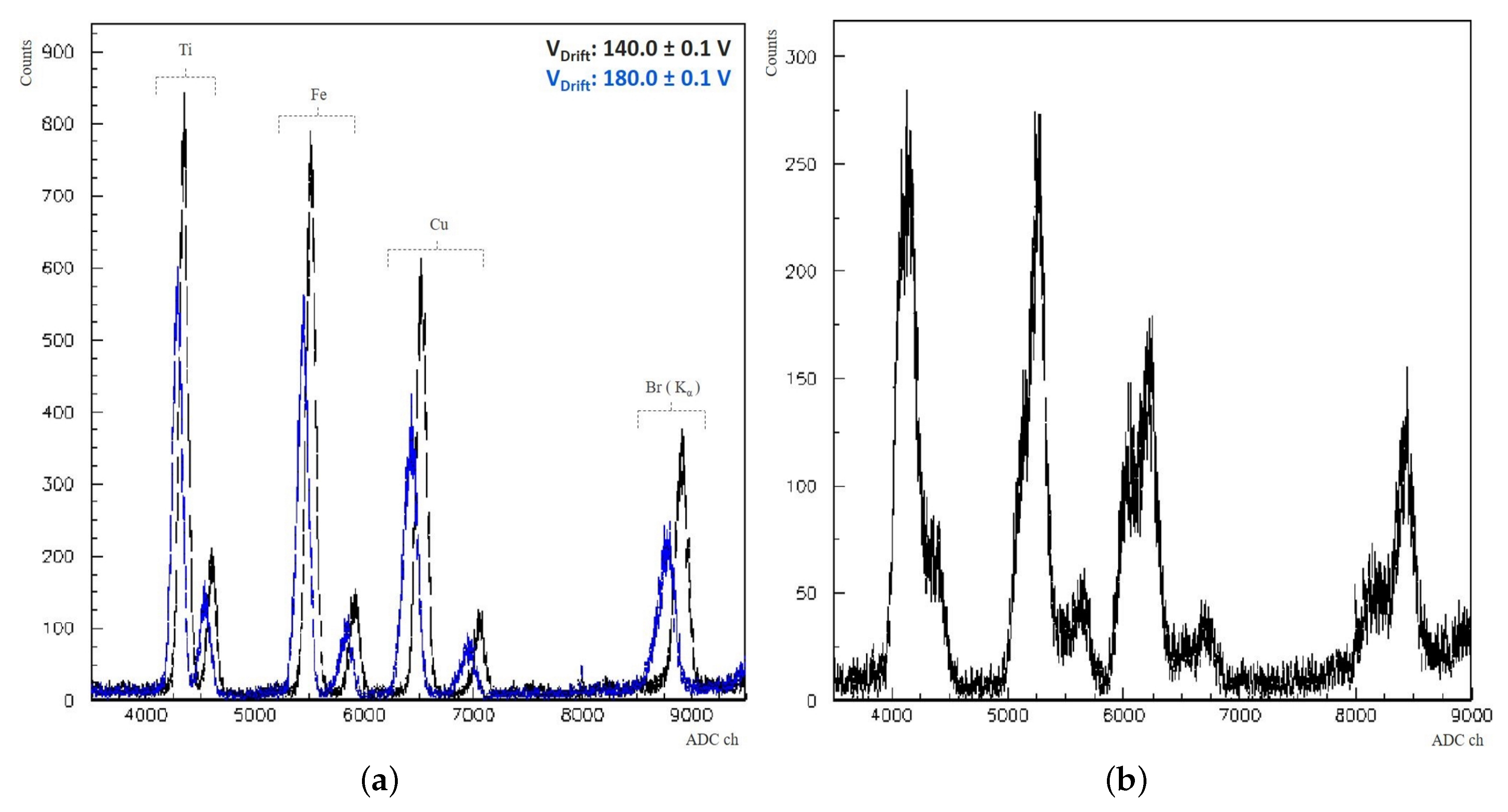
3.1. Energy Calibration
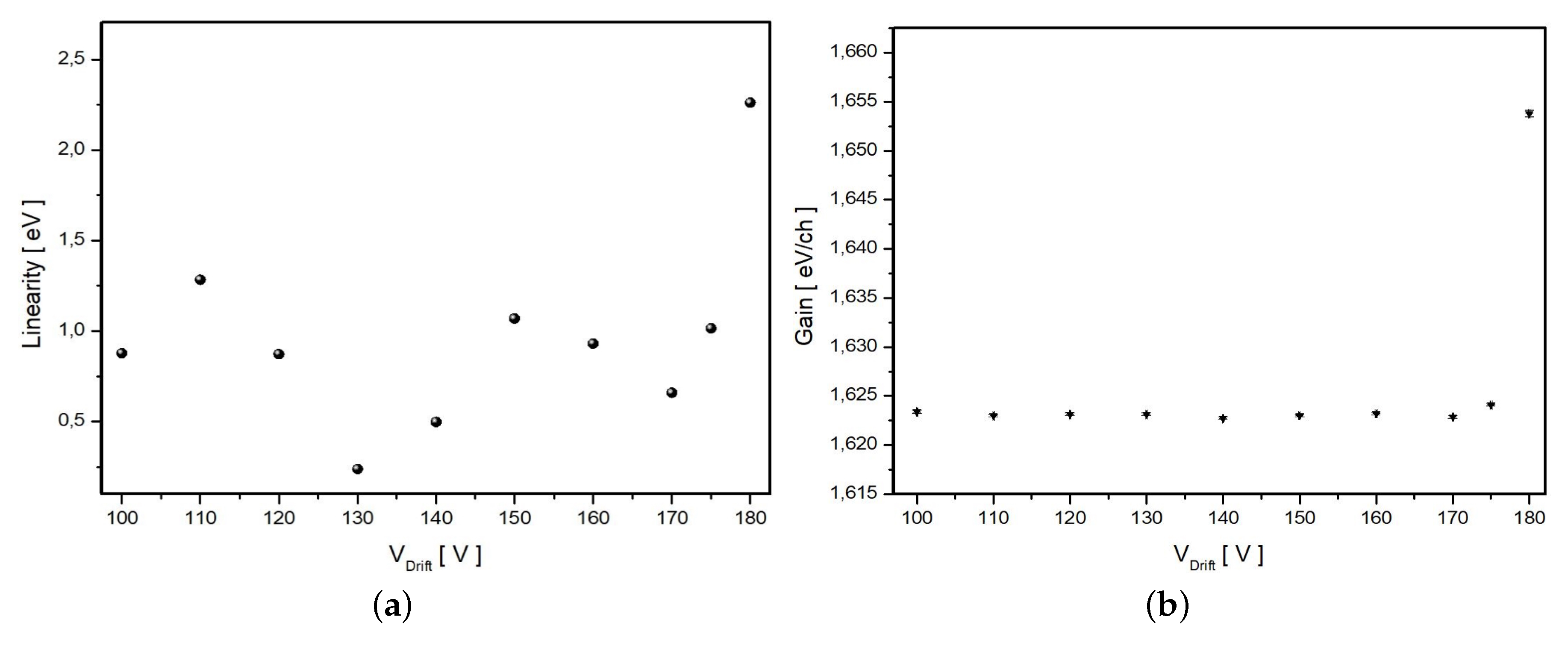
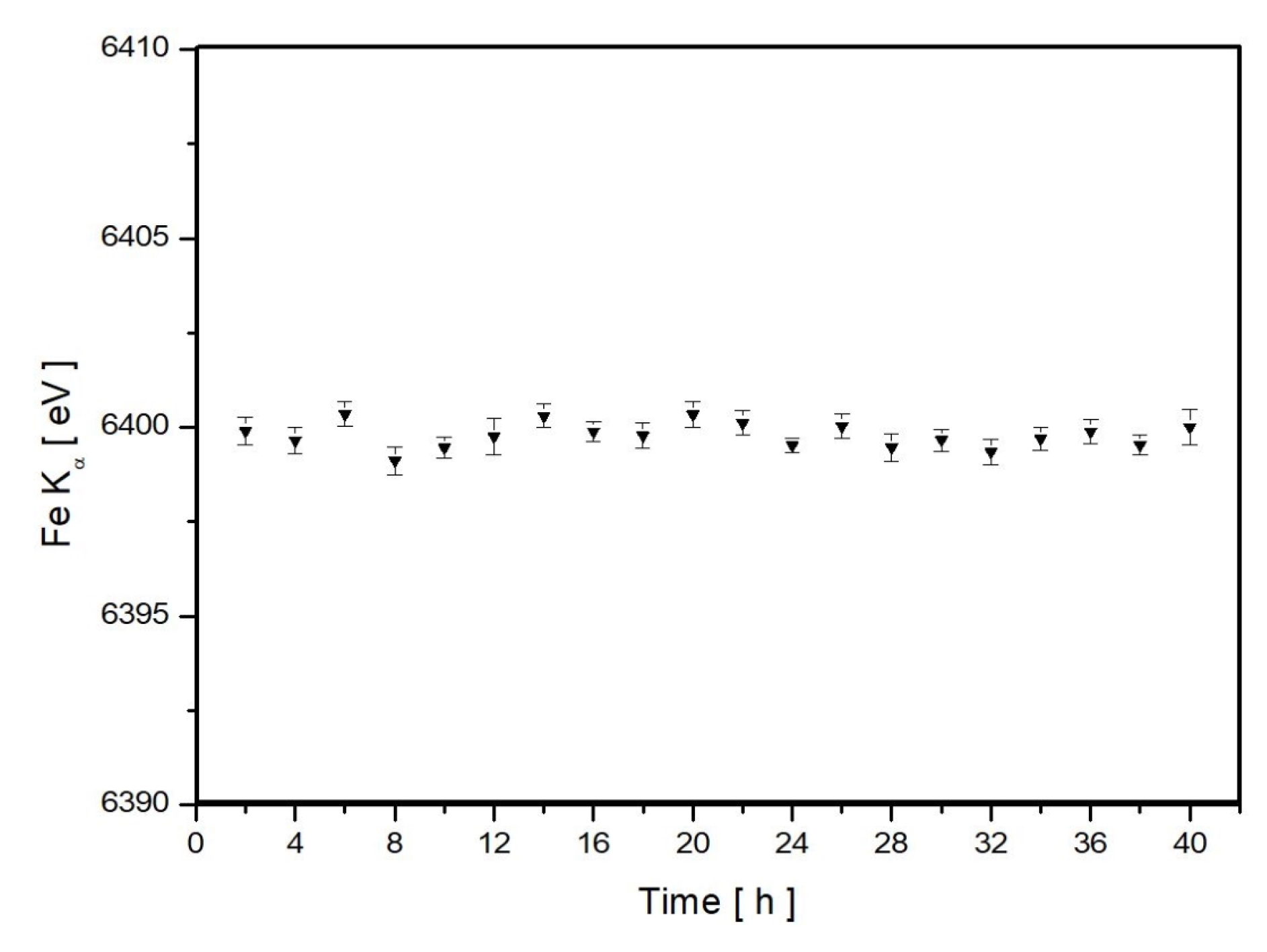
3.2. Stability
- X-ray tube voltage: 23.0 ± 0.1 kV;
- X-ray tube current: 10.0 ± 0.1 A;
- SDDs temperature: 121.6 ± 0.1 K;
- SDDs V: 140.0 ± 0.1 V;
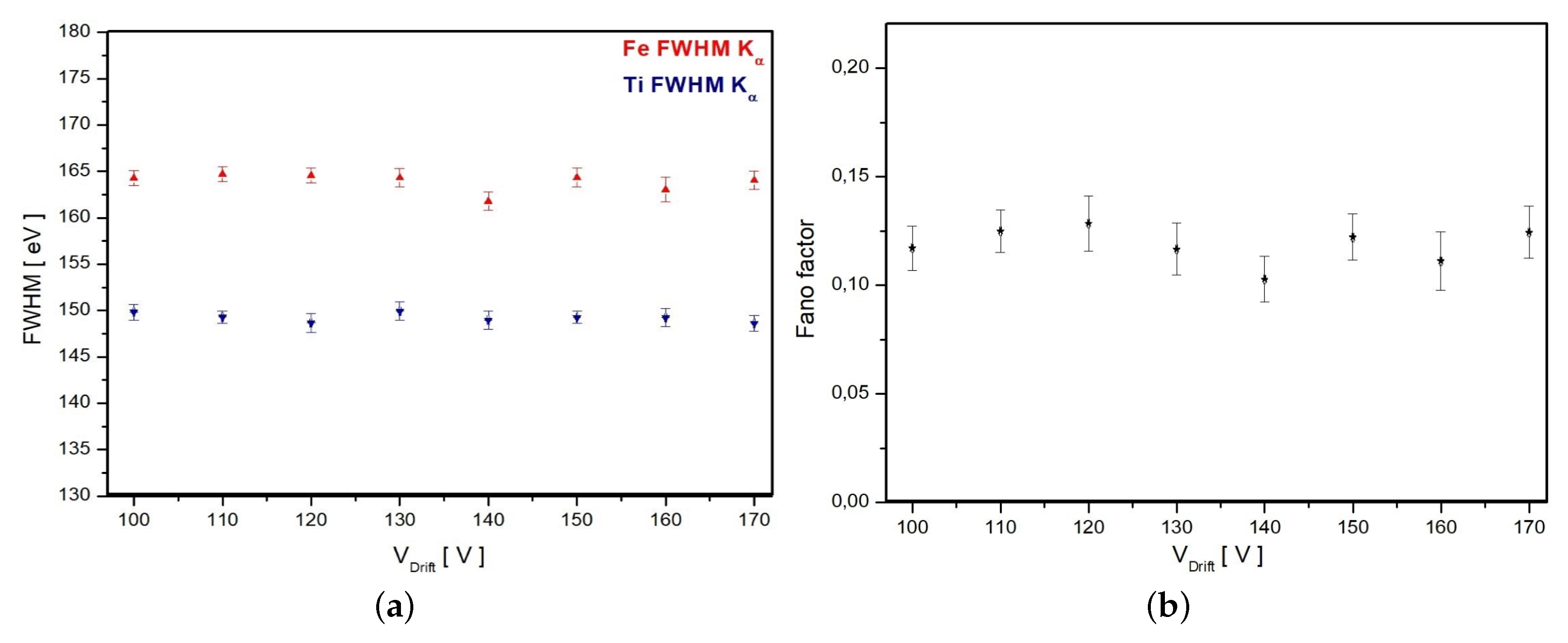
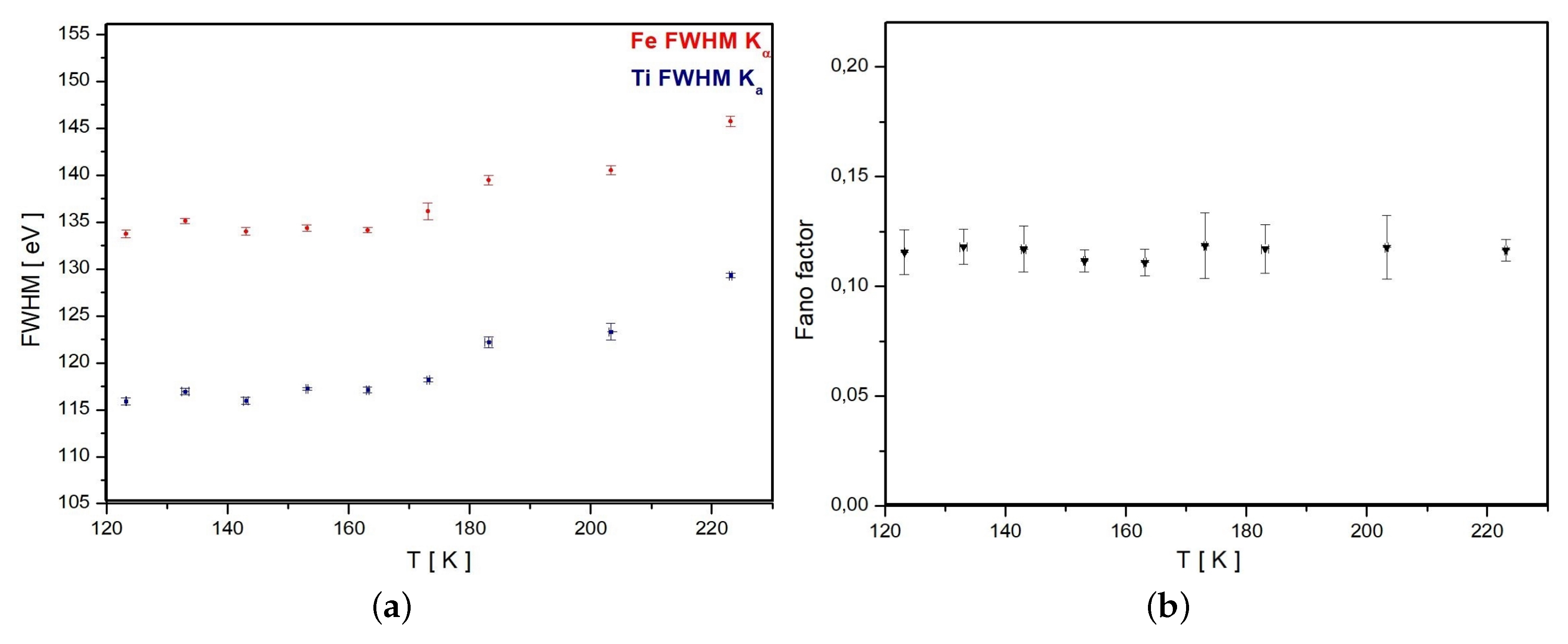
3.3. Energy Resolution
- is the intrinsic spread given by the statistical fluctuation in the number of the charge created by the incoming radiation. For a Gaussian distribution, it is due to the energy of the line (), the electron hole pair creation energy () and the correction of the Fano factor (F), accordingly to the relation ;
- is the thermal and electronic noise contribution;
- is due to the incomplete charge collection;
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gatti, E.; Rehak, P. Semiconductor drift chamber—An application of a novel charge transport scheme. Nucl. Instrum. Meth. Phys. Res. 1984, 225, 608–614. [Google Scholar] [CrossRef]
- Gatti, E.; Rehak, P. Silicon drift chambers—First results and optimum processing of signals. Nucl. Instrum. Meth. Phys. Res. A 1984, 226, 129–141. [Google Scholar] [CrossRef]
- Lechner, P.; Eckbauer, S.; Hartmann, R.; Krisch, S.; Hauff, D.; Richter, R.; Soltau, H.; Strüder, L.; Fiorini, C.; Gatti, E.; et al. Silicon drift detectors for high resolution room temperature X-ray spectroscopy. Nucl. Instrum. Meth. Phys. Res. A 1996, 377, 346–351. [Google Scholar] [CrossRef]
- Rehak, P.; Gatti, E.; Longoni, A.; Kemmer, J.; Holl, P.; Klanner, R.; Lutz, G.; Wylie, A. Semiconductor drift chambers for position and energy measurements. Nucl. Instrum. Meth. Phys. Res. A 1985, 235, 224–234. [Google Scholar] [CrossRef]
- Iwasaki, M.; Hayano, R.S.; Ito, T.M.; Nakamura, S.N.; Terada, T.P.; Gill, D.R.; Lee, L.; Olin, A.; Salomon, M.; Yen, S.; et al. Observation of Kaonic Hydrogen Kα X-Rays. Phys. Rev. Lett. 1997, 78, 3067–3069. [Google Scholar] [CrossRef]
- Bazzi, M.; Beer, G.; Bombelli, L.; Bragadireanu, A.M.; Cargnelli, M.; Corradi, G.; Curceanu, C.P.; d’Uffizi, A.; Fiorini, C.; Frizzi, T.; et al. A new measurement of kaonic hydrogen X-rays. Phys. Lett. B 2011, 704, 113–117. [Google Scholar] [CrossRef]
- Okada, S.; Beer, G.; Bhang, H.; Cargnelli, M.; Chiba, J.; Choi, S.; Curceanu, C.; Fukuda, Y.; Hanaki, T.; Hayano, R.S.; et al. Precision measurement of the 3d→2p X-ray energy in kaonic 4He. Phys. Lett. B 2007, 653, 387–391. [Google Scholar] [CrossRef]
- Bazzi, M.; Beer, G.; Bombelli, L.; Bragadireanu, A.M.; Cargnelli, M.; Corradi, G.; Curceanu, C.; d’Uffizi, A.; Fiorini, C.; Frizzi, T.; et al. Kaonic helium-4 X-ray measurement in SIDDHARTA. Phys. Lett. B 2009, 681, 310–314. [Google Scholar] [CrossRef]
- Bazzi, M.; Beer, G.; Bombelli, L.; Bragadireanu, A.M.; Cargnelli, M.; Corradi, G.; Curceanu, C.; d’Uffizi, A.; Fiorini, C.; Frizzi, T.; et al. First measurement of kaonic helium-3 X-rays. Phys. Lett. B 2011, 697, 199–202. [Google Scholar] [CrossRef] [PubMed]
- Bazzi, M.; Beer, G.; Bellotti, G.; Berucci, C.; Bragadireanu, A.M.; Bosnar, D.; Cargnelli, M.; Curceanu, C.; Butt, A.D.; d’Uffizi, A.; et al. K-series X-ray yield measurement of kaonic hydrogen atoms in a gaseous target. Nucl. Phys. A 2016, 954, 7–16. [Google Scholar] [CrossRef]
- Bazzi, M.; Beer, G.; Berucci, C.; Bragadireanu, A.M.; Cargnelli, M.; Curceanu, C.; d’Uffizi, A.; Fiorini, C.; Ghio, F.; Guaraldo, C.; et al. L-series X-ray yields of kaonic 3He and 4He atoms in gaseous targets. Eur. Phys. J. A 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Van Gysel, M.; Lemberge, P.; Van Espen, P. Implementation of a spectrum fitting procedure using a robust peak model. X-ray Spectrom. 2003, 32, 434–441. [Google Scholar] [CrossRef]
- Bertuccio, C.; Castoldi, A.; Longoni, A.; Sampietro, M.; Gauthier, C. New electrode geometry and potential distribution for soft X-ray drift detectors. Nucl. Instrum. Meth. Phys. Res. A 1992, 312, 613–616. [Google Scholar] [CrossRef]
- Mazziotta, M.N. Electron–hole pair creation energy and Fano factor temperature dependence in silicon. Nucl. Instrum. Meth. Phys. Res. A 2008, 584, 436–439. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miliucci, M.; Iliescu, M.; Amirkhani, A.; Bazzi, M.; Curceanu, C.; Fiorini, C.; Scordo, A.; Sirghi, F.; Zmeskal, J. Energy Response of Silicon Drift Detectors for Kaonic Atom Precision Measurements. Condens. Matter 2019, 4, 31. https://doi.org/10.3390/condmat4010031
Miliucci M, Iliescu M, Amirkhani A, Bazzi M, Curceanu C, Fiorini C, Scordo A, Sirghi F, Zmeskal J. Energy Response of Silicon Drift Detectors for Kaonic Atom Precision Measurements. Condensed Matter. 2019; 4(1):31. https://doi.org/10.3390/condmat4010031
Chicago/Turabian StyleMiliucci, Marco, Mihail Iliescu, Aidin Amirkhani, Massimiliano Bazzi, Catalina Curceanu, Carlo Fiorini, Alessandro Scordo, Florin Sirghi, and Johann Zmeskal. 2019. "Energy Response of Silicon Drift Detectors for Kaonic Atom Precision Measurements" Condensed Matter 4, no. 1: 31. https://doi.org/10.3390/condmat4010031
APA StyleMiliucci, M., Iliescu, M., Amirkhani, A., Bazzi, M., Curceanu, C., Fiorini, C., Scordo, A., Sirghi, F., & Zmeskal, J. (2019). Energy Response of Silicon Drift Detectors for Kaonic Atom Precision Measurements. Condensed Matter, 4(1), 31. https://doi.org/10.3390/condmat4010031






