Role of the Electron–Phonon Interaction in the Superconductivity of the 2-Dimensional Sn/Si(111) Interface
Abstract
1. Introduction
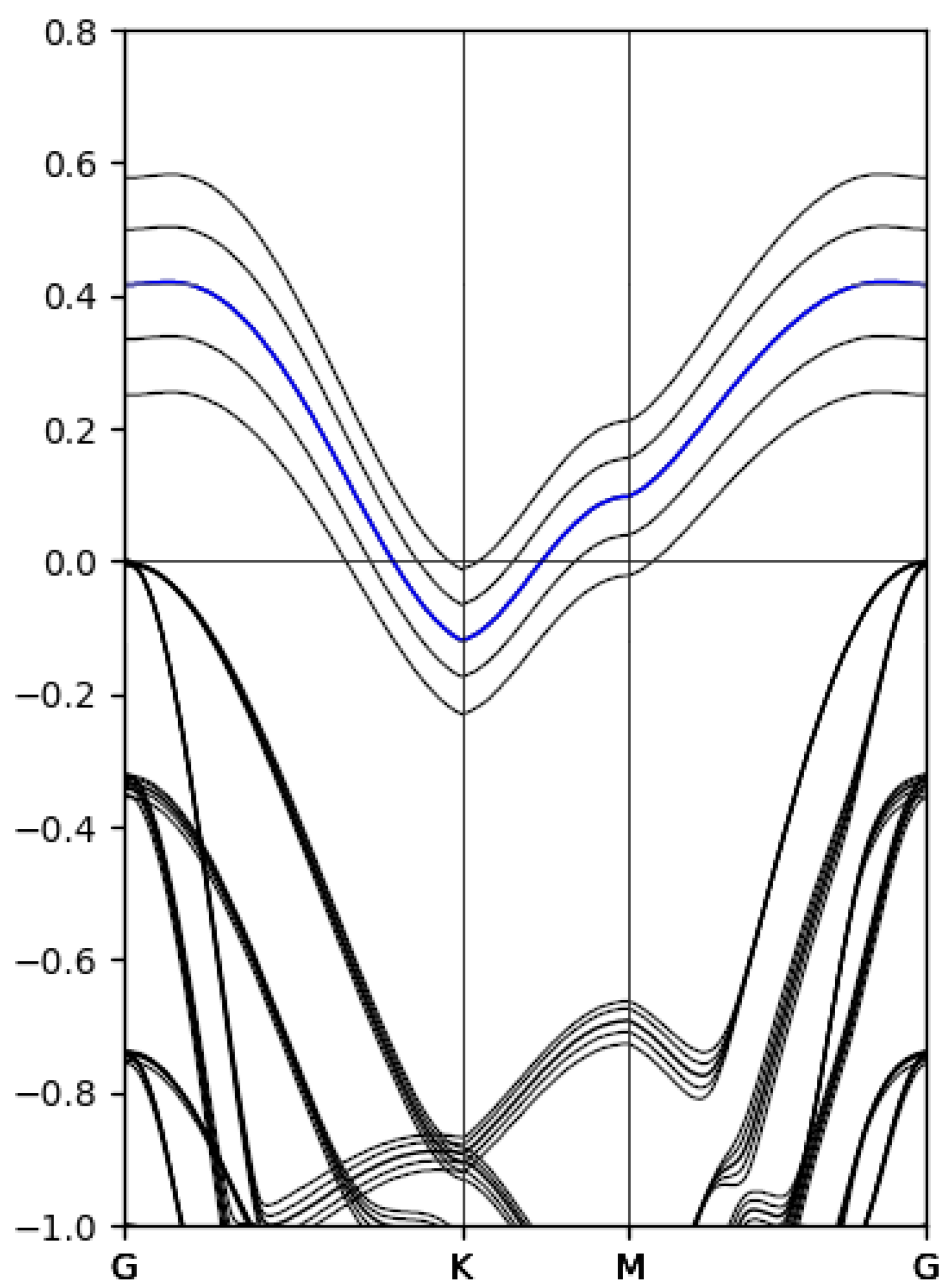
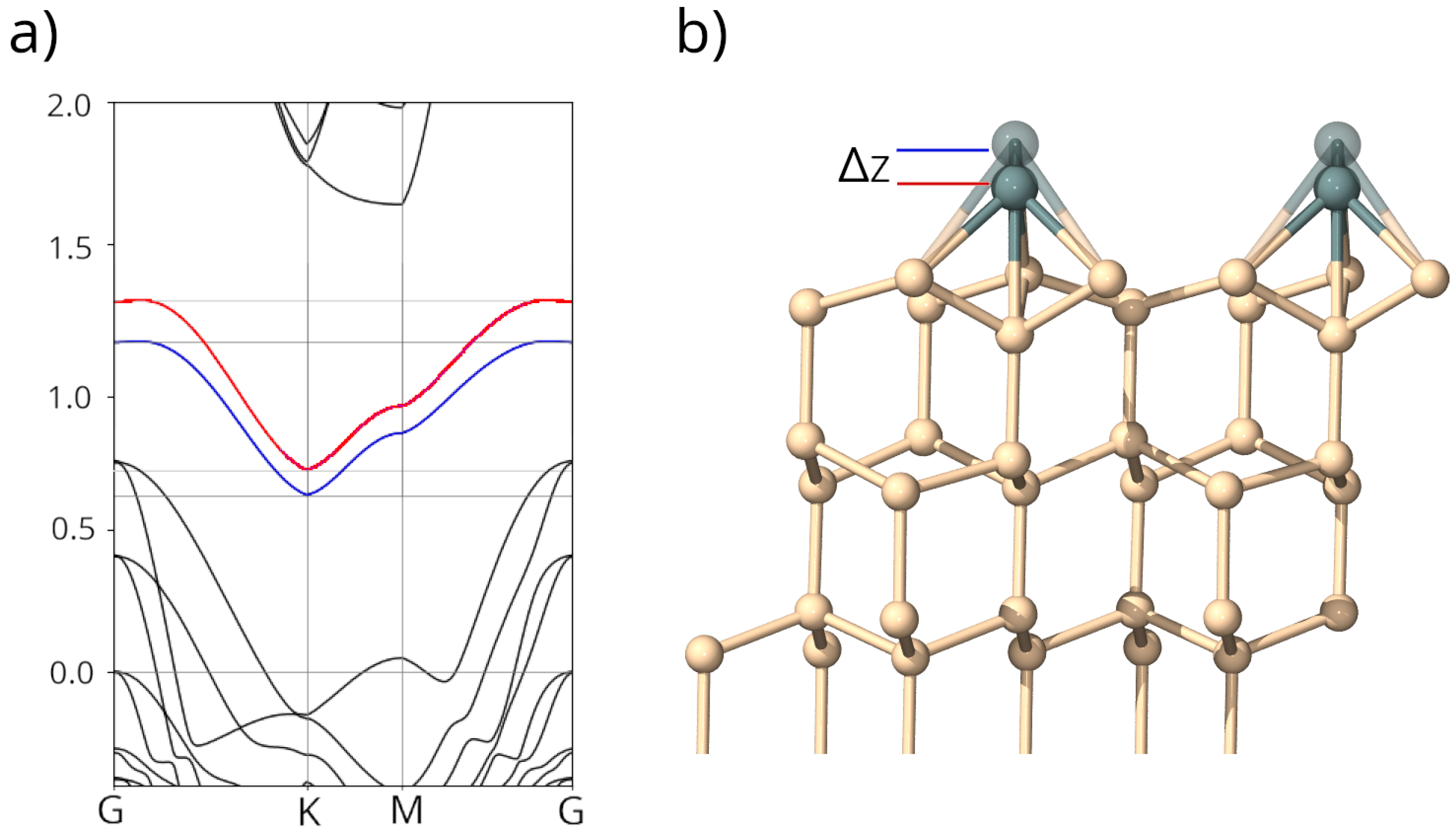
2. Sn/Si(111)–() Interface: Surface Geometry, Surface Bands, the Electron–Phonon Coupling and the Hubbard Interaction
3. Mott Phase for and Surface States for p-Doping
4. Magnetism or Superconductivity?
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Details of the DFT Calculations
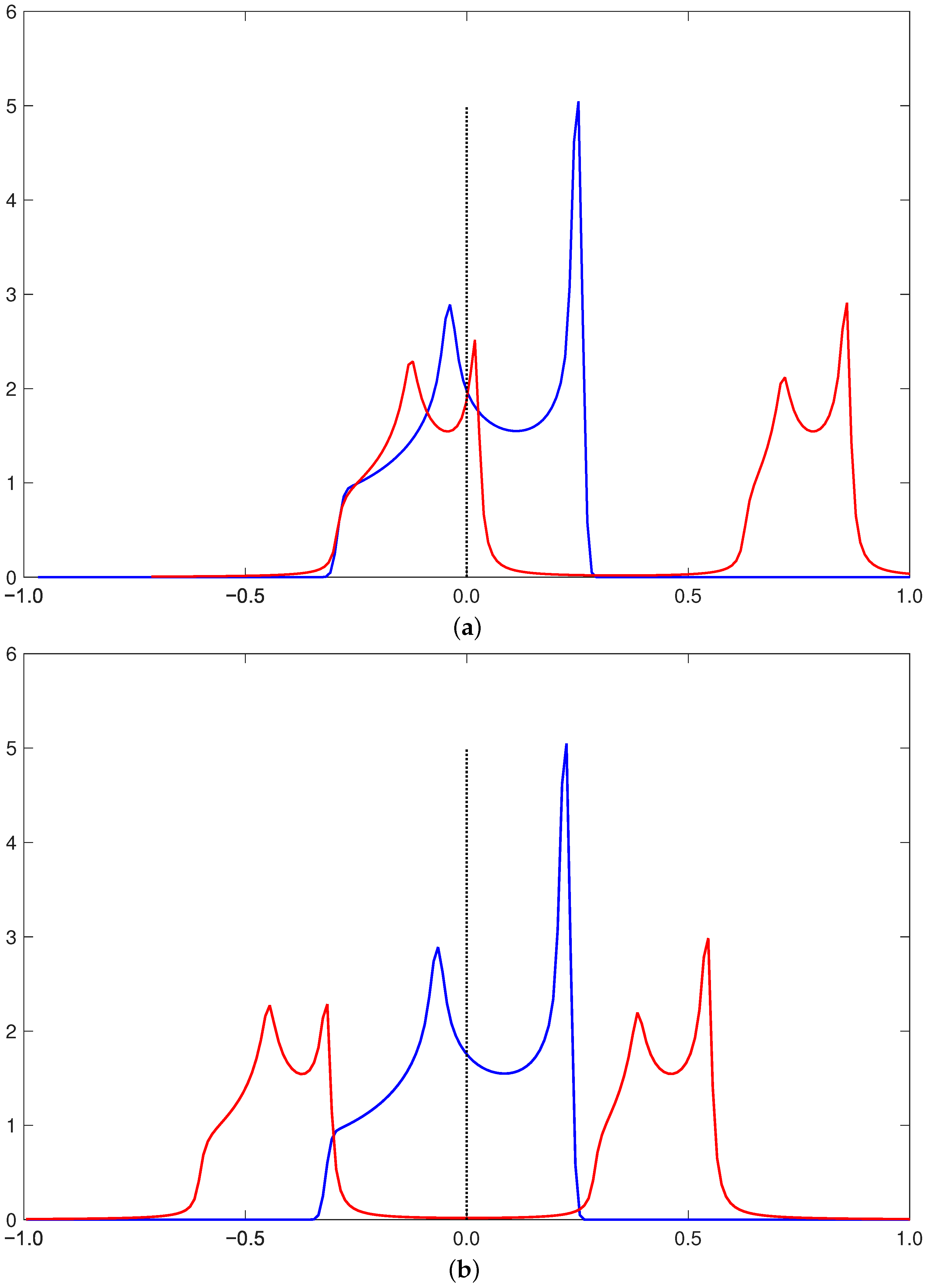
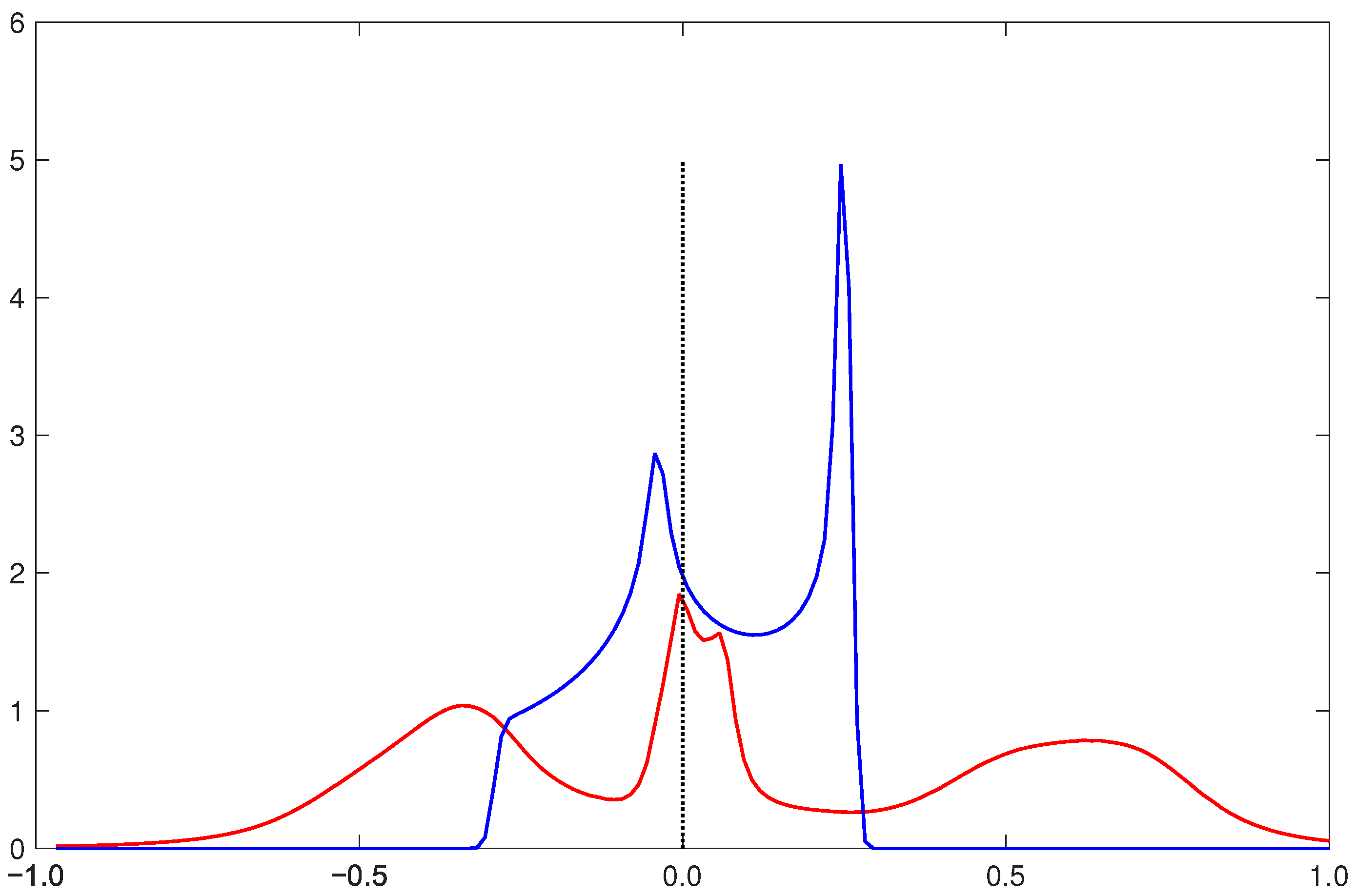
Appendix B. The Attractive Interaction
References
- Snijders, P.C.; Weitering, H.H. Colloquium: Electronic instabilities in self-assembled atom wires. Rev. Mod. Phys. 2010, 82, 307–329. [Google Scholar] [CrossRef]
- Zangwill, A. Physics at Surfaces; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Kong, P.; Zhang, X.; Wang, J.; Tian, W.; Ni, Y.; Sun, B.; Wang, H.; Wang, H.; Feng, Y.P.; Chen, Y. Electron-phonon coupling superconductivity and tunable topological state in carbon-rich selenide monolayers. Phys. Rev. B 2023, 107, 184115. [Google Scholar] [CrossRef]
- Liu, S.; Hou, J.; Duan, Q. Theoretical Prediction of Phonon-Mediated Superconductivity in 2D ZrBx (x = 4 and 6) Monolayers. J. Phys. Chem. C 2023, 127, 23069–23076. [Google Scholar] [CrossRef]
- Chen, J.; Cui, P.; Zhang, Z. Ferroelectricity-Tuned Band Topology and Superconductivity in 2D Materials and Related Heterostructures. Adv. Funct. Mater. 2024, 34, 2408625. [Google Scholar] [CrossRef]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 1973, 6, 1181. [Google Scholar] [CrossRef]
- Sharma, M.M.; Sharma, P.; Karn, N.K.; Awana, V.P.S. Comprehensive review on topological superconducting materials and interfaces. Supercond. Sci. Technol. 2022, 35, 083003. [Google Scholar] [CrossRef]
- Wu, X.; Ming, F.; Smith, T.S.; Liu, G.; Ye, F.; Wang, K.; Johnston, S.; Weitering, H.H. Superconductivity in a Hole-Doped Mott-Insulating Triangular Adatom Layer on a Silicon Surface. Phys. Rev. Lett. 2020, 125, 117001. [Google Scholar] [CrossRef]
- Ming, F.; Wu, X.; Chen, C.; Wang, K.; Mai, P.; Maier, T.; Strockoz, J.; Venderbos, J.; González, C.; Ortega, J.; et al. Evidence for chiral superconductivity on a silicon surface. Nat. Phys. 2023, 19, 500–506. [Google Scholar] [CrossRef]
- Uhrberg, R.I.G.; Zhang, H.M.; Balasubramanian, T.; Jemander, S.T.; Lin, N.; Hansson, G.V. Electronic structure of Sn/Si(111) : Indications of a low-temperature phase. Phys. Rev. B 2000, 62, 8082–8086. [Google Scholar] [CrossRef]
- Ortega, J.; Pérez, R.; Flores, F. Dynamical fluctuations and the ↔3×3 transition in α-Sn/Ge(111) and Sn/Si(111). J. Phys. Condens. Matter 2002, 14, 5979. [Google Scholar] [CrossRef]
- Modesti, S.; Petaccia, L.; Ceballos, G.; Vobornik, I.; Panaccione, G.; Rossi, G.; Ottaviano, L.; Larciprete, R.; Lizzit, S.; Goldoni, A. Insulating Ground State of Sn/Si(111)-()R30∘. Phys. Rev. Lett. 2007, 98, 126401. [Google Scholar] [CrossRef]
- Ming, F.; Johnston, S.; Mulugeta, D.; Smith, T.S.; Vilmercati, P.; Lee, G.; Maier, T.A.; Snijders, P.C.; Weitering, H.H. Realization of a Hole-Doped Mott Insulator on a Triangular Silicon Lattice. Phys. Rev. Lett. 2017, 119, 266802. [Google Scholar] [CrossRef] [PubMed]
- Nair, M.N.; Palacio, I.; Mascaraque, A.; Michel, E.G.; Taleb-Ibrahimi, A.; Tejeda, A.; González, C.; Martín-Rodero, A.; Ortega, J.; Flores, F. Giant electron-phonon interaction for a prototypical semiconductor interface: Sn/Ge(111)-(3×3). Phys. Rev. B 2023, 107, 045303. [Google Scholar] [CrossRef]
- Carpinelli, J.M.; Weitering, H.H.; Plummer, E.W.; Stumpf, R. Direct observation of a surface charge density wave. Nature 1996, 381, 398–400. [Google Scholar] [CrossRef]
- Carpinelli, J.M.; Weitering, H.H.; Bartkowiak, M.; Stumpf, R.; Plummer, E.W. Surface Charge Ordering Transition: α Phase of Sn/Ge(111). Phys. Rev. Lett. 1997, 79, 2859–2862. [Google Scholar] [CrossRef]
- Avila, J.; Mascaraque, A.; Michel, E.G.; Asensio, M.C.; LeLay, G.; Ortega, J.; Pérez, R.; Flores, F. Dynamical Fluctuations as the Origin of a Surface Phase Transition in Sn/Ge(111). Phys. Rev. Lett. 1999, 82, 442–445. [Google Scholar] [CrossRef]
- Pérez, R.; Ortega, J.; Flores, F. Surface Soft Phonon and the ↔ 3 × 3 Phase Transition in Sn/Ge(111) and Sn/Si(111). Phys. Rev. Lett. 2001, 86, 4891–4894. [Google Scholar] [CrossRef] [PubMed]
- Schuwalow, S.; Grieger, D.; Lechermann, F. Realistic modeling of the electronic structure and the effect of correlations for Sn/Si(111) and Sn/Ge(111) surfaces. Phys. Rev. B 2010, 82, 035116. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with QUANTUM ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Zahedifar, M.; Kratzer, P. Phonon-induced electronic relaxation in a strongly correlated system: The Sn/Si(111) () adlayer revisited. Phys. Rev. B 2019, 100, 125427. [Google Scholar] [CrossRef]
- Halbig, B.; Bass, U.; Geurts, J.; Sanna, S. Vibration signatures of the structural phase transition of Sn/Ge(111) compared to Sn/Si(111). Phys. Rev. B 2019, 100, 035437. [Google Scholar] [CrossRef]
- Mahan, G.D. Many-Particle Physics; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Koller, W.; Meyer, D.; Hewson, A.C. Dynamic response functions for the Holstein-Hubbard model. Phys. Rev. B 2004, 70, 155103. [Google Scholar] [CrossRef][Green Version]
- Pankratov, O.; Scheffler, M. Hubbard correlations and charge transfer at the GaAs(110) surface with alkali adsorbates. Phys. Rev. Lett. 1993, 70, 351–354. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Holt-Saunders International Editions; Saunders College: Philadelphia, PA, USA, 1976. [Google Scholar]
- Flores, F.; Ortega, J.; Pérez, R. Many-Body Effects and the Metal–Insulator Transition at Semiconductor Surfaces and Interfaces. Surf. Rev. Lett. 1999, 6, 411–433. [Google Scholar] [CrossRef]
- Monch, W. Vital volumes: Semiconductor surfaces and interfaces. In Springer Series in Surface Science; Springer: Berlin/Heidelberg, Germany, 1993; Volume 26, p. 366. [Google Scholar]
- Martin-Rodero, A.; Flores, F.; Baldo, M.; Pucci, R. A new solution to the Anderson-Newns Hamiltonian of chemisorption. Solid State Commun. 1982, 44, 911–914. [Google Scholar] [CrossRef]
- Martín-Rodero, A.; Louis, E.; Flores, F.; Tejedor, C. Interpolative solution for the periodic Anderson model of mixed-valence compounds. Phys. Rev. B 1986, 33, 1814–1822. [Google Scholar] [CrossRef] [PubMed]
- Kajueter, H.; Kotliar, G. New Iterative Perturbation Scheme for Lattice Models with Arbitrary Filling. Phys. Rev. Lett. 1996, 77, 131–134. [Google Scholar] [CrossRef] [PubMed]
- Flores, F.; Levy-Yeyati, A.; Martin-Rodero, A.; Merino, J. Many-body effects in low dimensional systems. Phys. Low Dimens. Struct. 1994, 1, 23. [Google Scholar]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13–125. [Google Scholar] [CrossRef]
- Hewson, A.C. The Kondo Problem to Heavy Fermions; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Karakuzu, S.; Tocchio, L.F.; Sorella, S.; Becca, F. Superconductivity, charge-density waves, antiferromagnetism, and phase separation in the Hubbard-Holstein model. Phys. Rev. B 2017, 96, 205145. [Google Scholar] [CrossRef]
- Jeckelmann, E.; Zhang, C.; White, S.R. Metal-insulator transition in the one-dimensional Holstein model at half filling. Phys. Rev. B 1999, 60, 7950–7955. [Google Scholar] [CrossRef]
- Grzybówski, P.; Micnas, R. Superconductivity and Charge-Density Wave Phase in the Holstein Model: A Weak Coupling Limit. Acta Phys. Pol. A 2007, 111, 453. [Google Scholar] [CrossRef]
- Hewson, A.C.; Meyer, D. Numerical renormalization group study of the Anderson-Holstein impurity model. J. Phys. Condens. Matter 2002, 14, 427. [Google Scholar] [CrossRef]
- Jeon, G.S.; Park, T.H.; Choi, H.Y. Numerical renormalization-group study of the symmetric Anderson-Holstein model: Phonon and electron spectral functions. Phys. Rev. B 2003, 68, 045106. [Google Scholar] [CrossRef]
- Martin-Rodero, A.; Levy Yeyati, A.; Flores, F.; Monreal, R.C. Interpolative approach for electron-electron and electron-phonon interactions: From the Kondo to the polaronic regime. Phys. Rev. B 2008, 78, 235112. [Google Scholar] [CrossRef]
- Martín-Rodero, A.; Flores, F. Solution for the U-negative Hubbard superconductor including second-order correlation effects. Phys. Rev. B 1992, 45, 13008–13016. [Google Scholar] [CrossRef]
- Cortés, R.; Tejeda, A.; Lobo, J.; Didiot, C.; Kierren, B.; Malterre, D.; Michel, E.G.; Mascaraque, A. Observation of a Mott Insulating Ground State for Sn/Ge(111) at Low Temperature. Phys. Rev. Lett. 2006, 96, 126103. [Google Scholar] [CrossRef]
- de Gennes, P.G. Superconductivity of Metals and Alloys; Benjamin: Amsterdam, The Netherlands, 1966. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flores, F.; Trabada, D.G.; Martín-Rodero, Á.; Ortega, J. Role of the Electron–Phonon Interaction in the Superconductivity of the 2-Dimensional Sn/Si(111) Interface. Condens. Matter 2025, 10, 51. https://doi.org/10.3390/condmat10030051
Flores F, Trabada DG, Martín-Rodero Á, Ortega J. Role of the Electron–Phonon Interaction in the Superconductivity of the 2-Dimensional Sn/Si(111) Interface. Condensed Matter. 2025; 10(3):51. https://doi.org/10.3390/condmat10030051
Chicago/Turabian StyleFlores, Fernando, Daniel G. Trabada, Álvaro Martín-Rodero, and José Ortega. 2025. "Role of the Electron–Phonon Interaction in the Superconductivity of the 2-Dimensional Sn/Si(111) Interface" Condensed Matter 10, no. 3: 51. https://doi.org/10.3390/condmat10030051
APA StyleFlores, F., Trabada, D. G., Martín-Rodero, Á., & Ortega, J. (2025). Role of the Electron–Phonon Interaction in the Superconductivity of the 2-Dimensional Sn/Si(111) Interface. Condensed Matter, 10(3), 51. https://doi.org/10.3390/condmat10030051






