Impact of Molecular π-Bridge Modifications on Triphenylamine-Based Donor Materials for Organic Photovoltaic Solar Cells
Abstract
1. Introduction
2. Chromophores and Computational Methods
3. Results and Discussion
3.1. Frontier Molecular Orbital (FMO) Analysis
3.2. Electronic Absorption Spectral
3.3. Ionization Potential and Electron Affinity
3.4. Reorganization Energy
3.5. Molecular Electrostatic Potential
4. Photovoltaic Properties
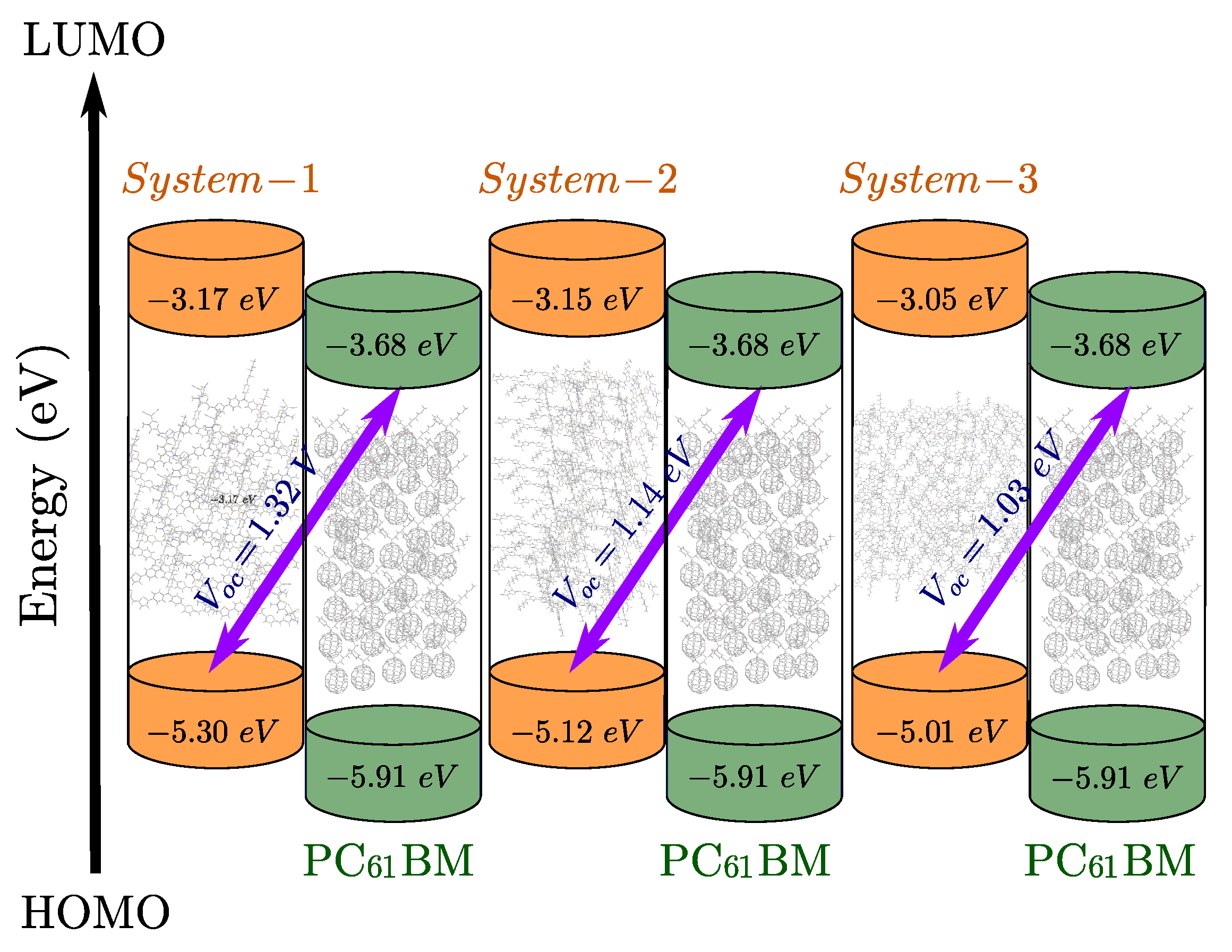
4.1. Open-Circuit Voltage () Investigation
4.2. Fill Factor (FF)
4.3. Short-Circuit Current Density ()
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, Q.; Jia, Z.; Meng, L.; Zhang, J.; Zhang, H.; Huang, W.; Yuan, J.; Gao, F.; Wan, Y.; Zhang, Z.; et al. Promoting charge separation resulting in ternary organic solar cells efficiency over 17.5%. Nano Energy 2020, 78, 105272. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, J.; Bi, P.; Ren, J.; Wang, Y.; Yang, Y.; Liu, X.; Zhang, S.; Hou, J. Tandem organic solar cell with 20.2% efficiency. Joule 2022, 6, 171–184. [Google Scholar] [CrossRef]
- Yuan, X.; Zhao, Y.; Xie, D.; Pan, L.; Liu, X.; Duan, C.; Huang, F.; Cao, Y. Polythiophenes for organic solar cells with efficiency surpassing 17%. Joule 2022, 6, 647–661. [Google Scholar] [CrossRef]
- Cai, Y.; Li, Y.; Wang, R.; Wu, H.; Chen, Z.; Zhang, J.; Ma, Z.; Hao, X.; Zhao, Y.; Zhang, C.; et al. A well-mixed phase formed by two compatible non-fullerene acceptors enables ternary organic solar cells with efficiency over 18.6%. Adv. Mater. 2021, 33, 2101733. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Jiang, Y.; Liu, F.; Ran, G.; Huang, F.; Wang, W.; Zhang, W.; Zhang, C.; Hou, J.; Zhu, X. Organic solar cells with over 19% efficiency enabled by a 2D-conjugated non-fullerene acceptor featuring favorable electronic and aggregation structures. Adv. Mater. 2023, 35, 2300363. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, M.; Xu, J.; Li, C.; Yan, J.; Zhou, G.; Zhong, W.; Hao, T.; Song, J.; Xue, X.; et al. Single-junction organic solar cells with over 19% efficiency enabled by a refined double-fibril network morphology. Nat. Mater. 2022, 21, 656–663. [Google Scholar] [CrossRef]
- Jia, Z.; Ma, Q.; Chen, Z.; Meng, L.; Jain, N.; Angunawela, I.; Qin, S.; Kong, X.; Li, X.; Yang, Y.; et al. Near-infrared absorbing acceptor with suppressed triplet exciton generation enabling high performance tandem organic solar cells. Nat. Commun. 2023, 14, 1236. [Google Scholar] [CrossRef]
- Schygulla, P.; Beutel, P.; Heckelmann, S.; Höhn, O.; Klitzke, M.; Schön, J.; Oliva, E.; Predan, F.; Schachtner, M.; Siefer, G.; et al. Quadruple Junction Solar Cell with 47.6% Conversion Efficiency under Concentration. In Proceedings of the 20th International Conference on Metal Organic Vapor Phase Epitaxy (ICMOVPE XX), Stuttgart, Germany, 4–9 July 2022. [Google Scholar]
- Scharber, M.C.; Sariciftci, N.S. Efficiency of bulk-heterojunction organic solar cells. Prog. Polym. Sci. 2013, 38, 1929–1940. [Google Scholar] [CrossRef] [PubMed]
- Hussain, R.; Mehboob, M.Y.; Khan, M.U.; Khalid, M.; Irshad, Z.; Fatima, R.; Anwar, A.; Nawab, S.; Adnan, M. Efficient designing of triphenylamine-based hole transport materials with outstanding photovoltaic characteristics for organic solar cells. J. Mater. Sci. 2021, 56, 5113–5131. [Google Scholar] [CrossRef]
- Nuhash, M.M.; Alam, I.; Islam, A. Manufacturing Processes of Solution-processed Organic Solar cells and Recent Advances. In Proceedings of the Third International Conference on Industrial & Mechanical Engineering and Operations Management (IMEOM), Dhaka, Bangladesh, 26–27 December 2020; pp. 26–27. [Google Scholar]
- Nhari, L.M.; El-Shishtawy, R.M.; Lu, Q.; Li, Y.; Asiri, A.M. Novel Triarylamine-Based Hole Transport Materials: Synthesis, Characterization and Computational Investigation. Materials 2021, 14, 3128. [Google Scholar] [CrossRef]
- Joseph, V.; Xia, J.; Sutanto, A.A.; Jankauskas, V.; Momblona, C.; Ding, B.; Rakstys, K.; Balasaravanan, R.; Pan, C.H.; Ni, J.S.; et al. Triarylamine-functionalized imidazolyl-capped bithiophene hole transporting material for cost-effective perovskite solar cells. ACS Appl. Mater. Interfaces 2022, 14, 22053–22060. [Google Scholar] [CrossRef]
- Echeverry, C.A.; Insuasty, A.; Herranz, M.Á.; Ortíz, A.; Cotta, R.; Dhas, V.; Echegoyen, L.; Insuasty, B.; Martín, N. Organic dyes containing 2-(1,1-dicyanomethylene)rhodanine as an efficient electron acceptor and anchoring unit for dye-sensitized solar cells. Dyes Pigm. 2014, 107, 9–14. [Google Scholar] [CrossRef]
- Civalleri, B.; Zicovich-Wilson, C.M.; Valenzano, L.; Ugliengo, P. B3LYP augmented with an empirical dispersion term (B3LYP-D*) as applied to molecular crystals. Cryst. Eng. Comm 2008, 10, 405–410. [Google Scholar] [CrossRef]
- Hung, Y.C.; Jiang, J.C.; Chao, C.Y.; Su, W.F.; Lin, S.T. Theoretical Study on the Correlation between Band Gap, Bandwidth, and Oscillator Strength in Fluorene-Based Donor- Acceptor Conjugated Copolymers. J. Phys. Chem. B 2009, 113, 8268–8277. [Google Scholar] [CrossRef]
- Crossley, D.L.; Vitorica-Yrezabal, I.; Humphries, M.J.; Turner, M.L.; Ingleson, M.J. Highly Emissive Far Red/Near-IR Fluorophores Based on Borylated Fluorene–Benzothiadiazole Donor–Acceptor Materials. Chem.- Eur. J. 2016, 22, 12439–12448. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Liu, M.; Zhang, Y.; Liu, Z.; Yang, Y.; Zhao, L. Recent development on narrow bandgap conjugated polymers for polymer solar cells. Polymers 2017, 9, 39. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H.; et al. Gaussian 16; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Takano, Y.; Houk, K. Benchmarking the conductor-like polarizable continuum model (CPCM) for aqueous solvation free energies of neutral and ionic organic molecules. J. Chem. Theory Comput. 2005, 1, 70–77. [Google Scholar] [CrossRef]
- Mennucci, B. Polarizable continuum model. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 386–404. [Google Scholar] [CrossRef]
- Ans, M.; Iqbal, J.; Ahmad, Z.; Muhammad, S.; Hussain, R.; Eliasson, B.; Ayub, K. Designing three-dimensional (3D) non-fullerene small molecule acceptors with efficient photovoltaic parameters. ChemistrySelect 2018, 3, 12797–12804. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Shan, T.; Wang, Y.; Zhu, L.; Li, T.; Liu, F.; Zhong, H. Tuning the molecular geometry and packing mode of non-fullerene acceptors by altering the bridge atoms towards efficient organic solar cells. Mater. Chem. Front. 2020, 4, 2462–2471. [Google Scholar] [CrossRef]
- Zahid, S.; Rasool, A.; Ans, M.; Yaseen, M.; Iqbal, J. Quantum chemical approach of donor–π–acceptor based arylborane–arylamine macrocycles with outstanding photovoltaic properties toward high-performance organic solar cells. Energy Fuels 2021, 35, 15018–15032. [Google Scholar] [CrossRef]
- Madrid-Úsuga, D.; Melo-Luna, C.A.; Insuasty, A.; Ortiz, A.; Reina, J.H. Optical and electronic properties of molecular systems derived from rhodanine. J. Phys. Chem. A 2018, 122, 8469–8476. [Google Scholar] [CrossRef]
- Louis, E.; San-Fabián, E.; Díaz-García, M.A.; Chiappe, G.; Vergés, J.A. Are electron affinity and ionization potential intrinsic parameters to predict the electron or hole acceptor character of amorphous molecular materials? J. Phys. Chem. Lett. 2017, 8, 2445–2449. [Google Scholar] [CrossRef]
- Ahmed, S.; Dutta, R.; Kalita, D.J. Strategical designing of diketopyrrolopyrrole-thiophene based donor-acceptor type organic oligomers and study their transport properties: A DFT/TD-DFT perspective. Chem. Phys. Lett. 2019, 730, 14–25. [Google Scholar] [CrossRef]
- Li, Y.; Qi, D.; Sun, C.; Zhao, M. Spectra and charge transport of polar molecular photoactive layers used for solar cells. J. Chem. 2015, 2015. [Google Scholar] [CrossRef]
- Akram, S.J.; Hadia, N.; Iqbal, J.; Mehmood, R.F.; Iqbal, S.; Shawky, A.M.; Asif, A.; Somaily, H.; Raheel, M.; Khera, R.A. Impact of various heterocyclic π-linkers and their substitution position on the opto-electronic attributes of the A–π–D–π–A type IECIO-4F molecule: A comparative analysis. RSC Adv. 2022, 12, 20792–20806. [Google Scholar] [CrossRef] [PubMed]
- Rafiq, M.; Salim, M.; Noreen, S.; Khera, R.A.; Noor, S.; Yaqoob, U.; Iqbal, J. End-capped modification of dithienosilole based small donor molecules for high performance organic solar cells using DFT approach. J. Mol. Liq. 2022, 345, 118138. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Q.S.; Li, Z.S. Molecular Engineering in Perovskite Solar Cells: A Computational Study on 2-Mercaptopyridine Derivatives as Surface Passivators against Water. Adv. Mater. Interfaces 2022, 9, 2101881. [Google Scholar] [CrossRef]
- Gurney, R.S.; Lidzey, D.G.; Wang, T. A review of non-fullerene polymer solar cells: From device physics to morphology control. Rep. Prog. Phys. 2019, 82, 036601. [Google Scholar] [CrossRef]
- Ma, L.; Yu, Z.; Ma, W.; Qing, S.; Wu, J. Assessment and study on the impact on environment by multi-crystalline silicon preparation by metallurgical route. Silicon 2019, 11, 1383–1391. [Google Scholar] [CrossRef]
- Yu, J.; Zheng, Y.; Huang, J. Towards high performance organic photovoltaic cells: A review of recent development in organic photovoltaics. Polymers 2014, 6, 2473–2509. [Google Scholar] [CrossRef]
- Liang, Z.; Zhang, Y.; Xu, H.; Chen, W.; Liu, B.; Zhang, J.; Zhang, H.; Wang, Z.; Kang, D.H.; Zeng, J.; et al. Out-of-plane cations homogenise perovskite composition for solar cells. Nature 2023, 624, 557–563. [Google Scholar] [CrossRef]
- Sweetnam, S.; Graham, K.R.; Ngongang Ndjawa, G.O.; Heumuller, T.; Bartelt, J.A.; Burke, T.M.; Li, W.; You, W.; Amassian, A.; McGehee, M.D. Characterization of the polymer energy landscape in polymer: Fullerene bulk heterojunctions with pure and mixed phases. J. Am. Chem. Soc. 2014, 136, 14078–14088. [Google Scholar] [CrossRef] [PubMed]
- Tang, A.; Xiao, Z.; Ding, L.; Zhou, E. ~1.2 V open-circuit voltage from organic solar cells. J. Semicond. 2021, 42, 070202. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, X.; Jiang, H.; Zhou, X.; Zhang, L.; Pan, F.; Qiao, X.; Ma, D.; Ma, W.; Ding, L.; et al. Organic Solar Cells Based on High Hole Mobility Conjugated Polymer and Nonfullerene Acceptor with Comparable Bandgaps and Suitable Energy Level Offsets Showing Significant Suppression of Jsc–Voc Trade-Off. Sol. RRL 2019, 3, 1900079. [Google Scholar] [CrossRef]
- Azzouzi, M.; Kirchartz, T.; Nelson, J. Factors controlling open-circuit voltage losses in organic solar cells. Trends Chem. 2019, 1, 49–62. [Google Scholar] [CrossRef]
- Afzal, Z.; Hussain, R.; Khan, M.U.; Khalid, M.; Iqbal, J.; Alvi, M.U.; Adnan, M.; Ahmed, M.; Mehboob, M.Y.; Hussain, M.; et al. Designing indenothiophene-based acceptor materials with efficient photovoltaic parameters for fullerene-free organic solar cells. J. Mol. Model. 2020, 26, 137. [Google Scholar] [CrossRef]
- Hussain, R.; Khan, M.U.; Mehboob, M.Y.; Khalid, M.; Iqbal, J.; Ayub, K.; Adnan, M.; Ahmed, M.; Atiq, K.; Mahmood, K. Enhancement in photovoltaic properties of N,N-diethylaniline based donor materials by bridging core modifications for efficient solar cells. ChemistrySelect 2020, 5, 5022–5034. [Google Scholar] [CrossRef]
- Jao, M.H.; Liao, H.C.; Su, W.F. Achieving a high fill factor for organic solar cells. J. Mater. Chem. A 2016, 4, 5784–5801. [Google Scholar] [CrossRef]
- Qi, B.; Wang, J. Fill factor in organic solar cells. Phys. Chem. Chem. Phys. 2013, 15, 8972–8982. [Google Scholar] [CrossRef]
- Alharbi, F.H.; Rashkeev, S.N.; El-Mellouhi, F.; Lüthi, H.P.; Tabet, N.; Kais, S. An efficient descriptor model for designing materials for solar cells. Npj Comput. Mater. 2015, 1, 15003. [Google Scholar] [CrossRef]
- American Society for Testing and Materials (ASTM). Standard G159, West Conshoken, PA, USA. Available online: http://rredc.nrel.gov/solar/spectra/am1.5/ (accessed on 26 May 2025).
- Green, M.A.; Dunlop, E.D.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Hao, X. Solar cell efficiency tables (version 56). Prog. Phot. Res. Appl. 2020, 28, 629–638. [Google Scholar] [CrossRef]
- El Assyry, A.; Jdaa, R.; Benali, B.; Addou, M.; Zarrouk, A. Optical and photovoltaic properties of new quinoxalin-2 (1H)-one-based DA organic dyes for efficient dye-sensitized solar cell using DFT. J. Mater. Environ. Sci 2015, 6, 2612–2623. [Google Scholar]
- Madrid-Úsuga, D.; Mora-Leon, A.G.; Cabrera-Espinoza, A.M.; Insuasty, B.; Ortiz, A. Theoretical characterization of photoactive molecular systems based on BODIPY-derivatives for the design of organic solar cells. Comput. Theor. Chem. 2021, 1197, 113165. [Google Scholar] [CrossRef]
- Jungbluth, A.; Kaienburg, P.; Riede, M. Charge transfer state characterization and voltage losses of organic solar cells. J. Phys. Mater. 2022, 5, 024002. [Google Scholar] [CrossRef]

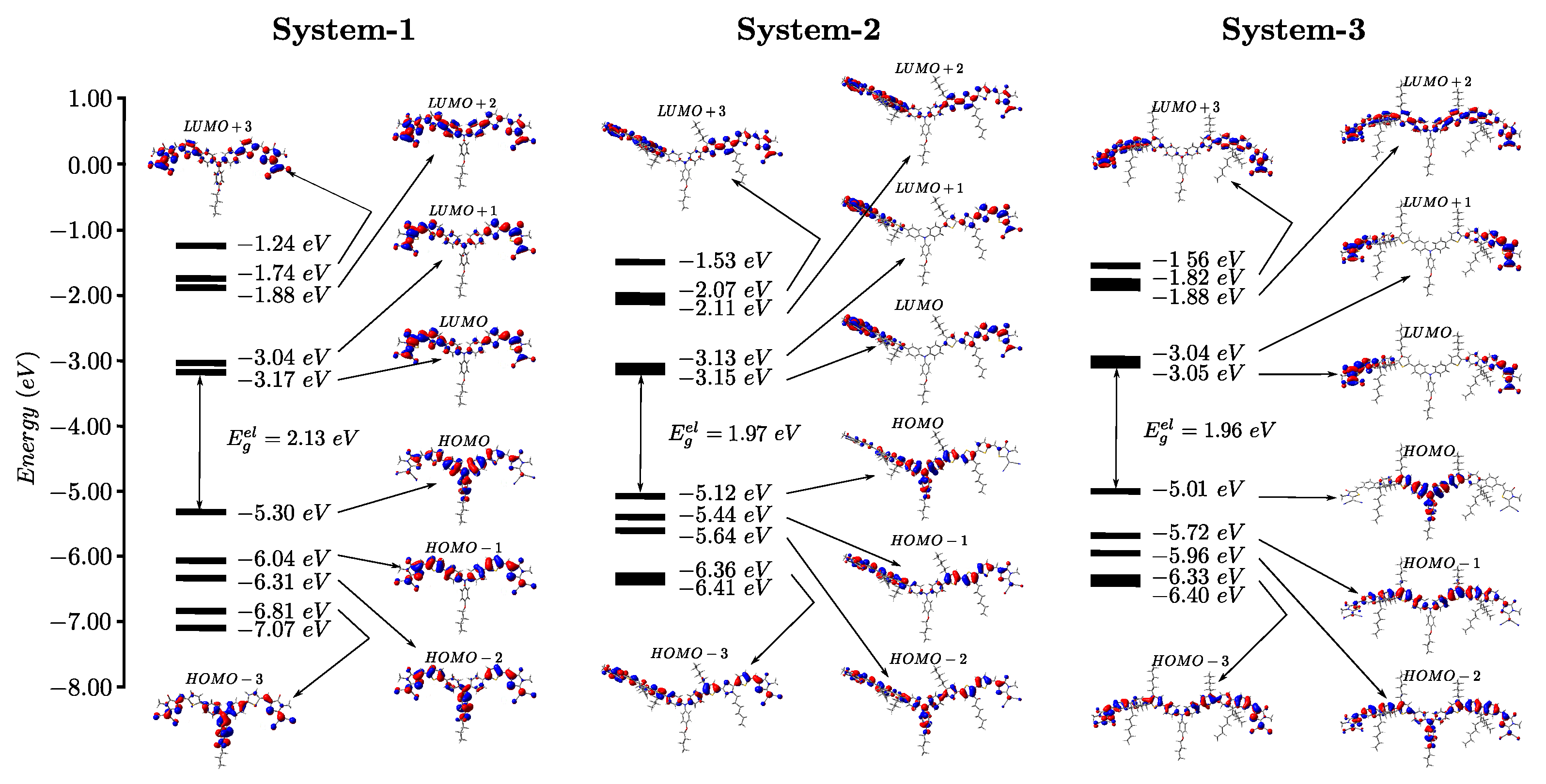

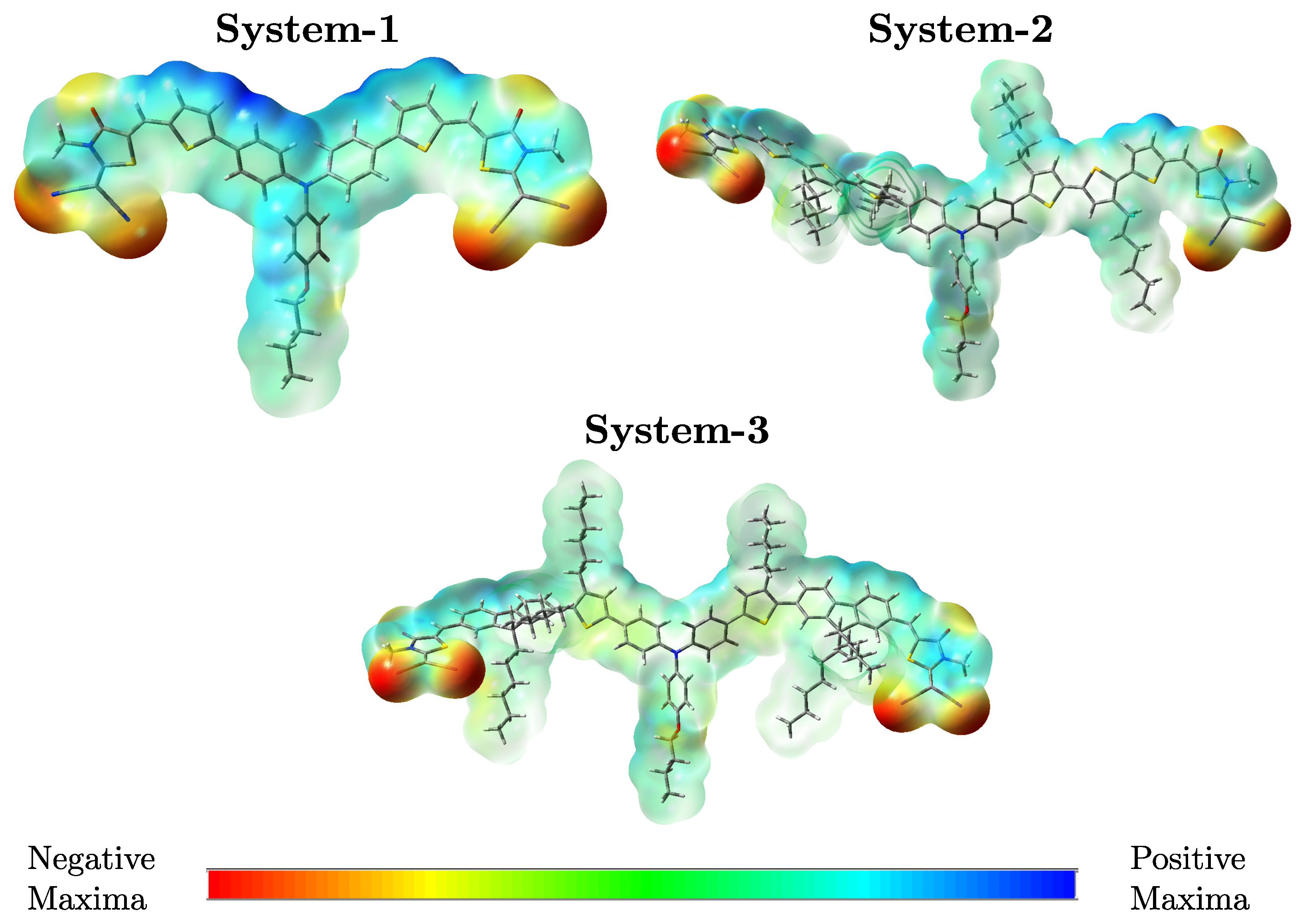
| System | (nm) | (eV) | (eV) | (eV) |
|---|---|---|---|---|
| Gas Phase | ||||
| System-1 | 462.40 | −5.58 | −3.28 | 2.30 |
| System-2 | 494.83 | −5.28 | −3.18 | 2.10 |
| System-3 | 407.60 | −5.07 | −3.10 | 1.97 |
| EtOH | ||||
| System-1 | 449.62 | −5.30 | −3.17 | 2.13 |
| System-2 | 525.55 | −5.12 | −3.15 | 1.97 |
| System-3 | 417.69 | −5.01 | −3.05 | 1.96 |
| System | States | (nm) | (eV) | LHE | |
|---|---|---|---|---|---|
| Gas Phase | |||||
| System-1 | 462.40 | 2.681 | 2.549 | 0.9972 | |
| 335.04 | 3.701 | 0.292 | |||
| System-2 | 494.83 | 2.506 | 3.368 | 0.9995 | |
| 355.31 | 3.489 | 0.159 | |||
| 318.93 | 3.888 | 0.243 | |||
| System-3 | 407.60 | 3.042 | 3.238 | 0.9994 | |
| 337.73 | 3.671 | 0.569 | |||
| EtOH | |||||
| System-1 | 499.62 | 2.482 | 2.725 | 0.9981 | |
| 347.78 | 3.565 | 0.320 | |||
| System-2 | 525.55 | 2.359 | 3.509 | 0.9996 | |
| 369.69 | 3.354 | 0.233 | |||
| 326.14 | 3.802 | 0.397 | |||
| System-3 | 417.69 | 2.968 | 3.447 | 0.9996 | |
| 347.79 | 3.565 | 0.404 | |||
| Systems | (eV) | (eV) | (eV) | (eV) | (D) |
|---|---|---|---|---|---|
| EtOH | |||||
| System-1 | 0.316 | 0.201 | 5.379 | 3.284 | 13.504 |
| System-2 | 0.142 | 0.233 | 5.302 | 3.325 | 16.762 |
| System-3 | 0.317 | 0.198 | 5.198 | 3.374 | 18.258 |
| Gas Phase | |||||
| System-1 | 0.261 | 0.220 | 6.768 | 2.084 | 9.063 |
| System-2 | 0.164 | 0.285 | 6.502 | 2.121 | 11.672 |
| System-3 | 0.219 | 0.209 | 6.309 | 1.937 | 13.042 |
| System | (eV) | (V) | (mA/cm2) | (%) | |
|---|---|---|---|---|---|
| System-1 | 0.51 | 1.32 | 9.52 | 0.810 | 10.18 |
| System-2 | 0.53 | 1.14 | 12.21 | 0.786 | 10.95 |
| System-3 | 0.63 | 1.03 | 11.85 | 0.774 | 9.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madrid-Úsuga, D.; Suárez, O.J.; Portacio, A. Impact of Molecular π-Bridge Modifications on Triphenylamine-Based Donor Materials for Organic Photovoltaic Solar Cells. Condens. Matter 2025, 10, 52. https://doi.org/10.3390/condmat10040052
Madrid-Úsuga D, Suárez OJ, Portacio A. Impact of Molecular π-Bridge Modifications on Triphenylamine-Based Donor Materials for Organic Photovoltaic Solar Cells. Condensed Matter. 2025; 10(4):52. https://doi.org/10.3390/condmat10040052
Chicago/Turabian StyleMadrid-Úsuga, Duvalier, Omar J. Suárez, and Alfonso Portacio. 2025. "Impact of Molecular π-Bridge Modifications on Triphenylamine-Based Donor Materials for Organic Photovoltaic Solar Cells" Condensed Matter 10, no. 4: 52. https://doi.org/10.3390/condmat10040052
APA StyleMadrid-Úsuga, D., Suárez, O. J., & Portacio, A. (2025). Impact of Molecular π-Bridge Modifications on Triphenylamine-Based Donor Materials for Organic Photovoltaic Solar Cells. Condensed Matter, 10(4), 52. https://doi.org/10.3390/condmat10040052





