Numerical Simulation of Aquaculture-Derived Organic Matter Sedimentation in a Temperate Intensive Aquaculture Bay Based on a Finite-Volume Coastal Ocean Model
Abstract
1. Introduction
2. Materials and Methods
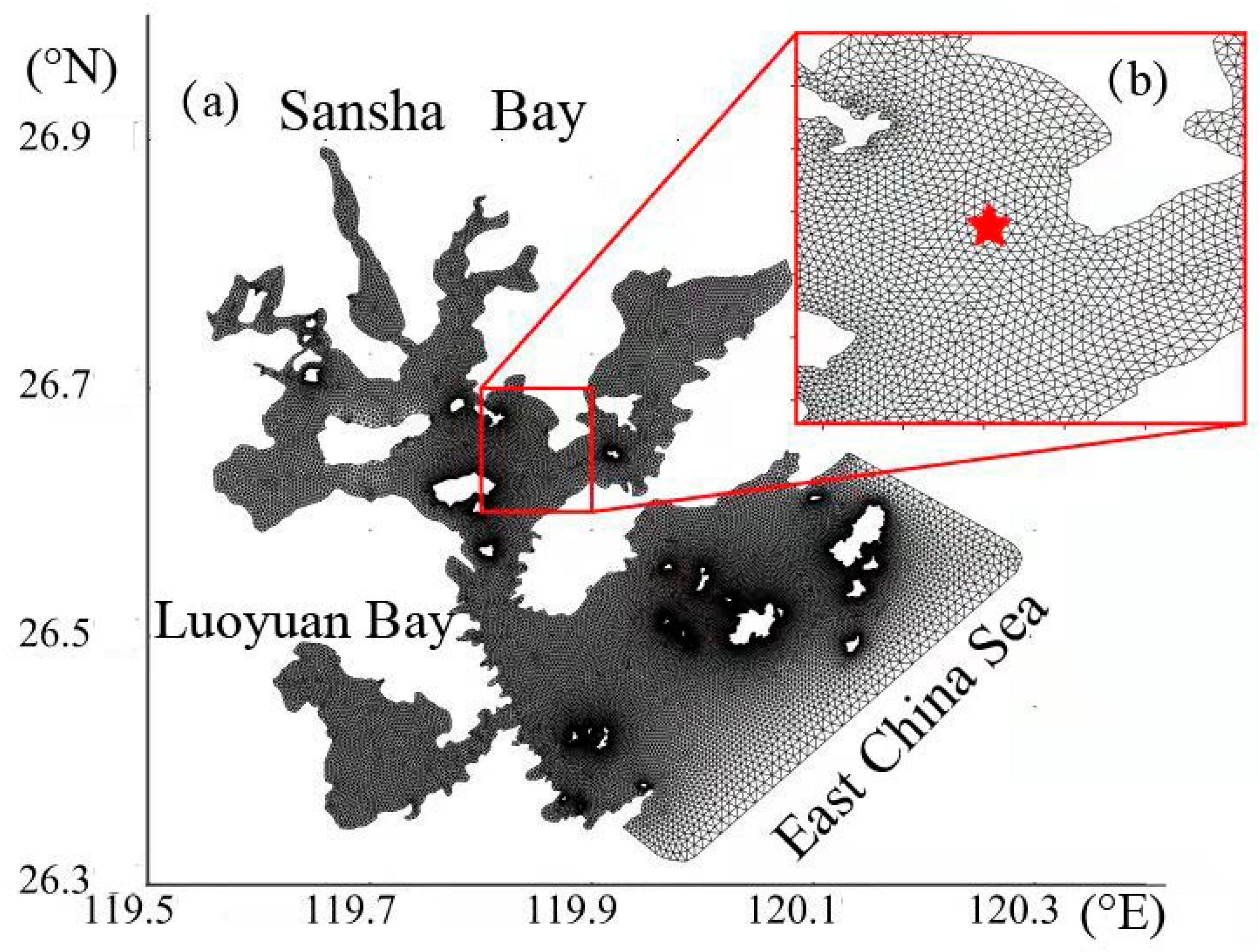
2.1. Study Region and Experimental Cage Unit
2.2. Model Configuration
2.3. Hydrodynamic Model
2.3.1. Description of the σ Coordinate System
2.3.2. Equations in the σ-Coordinate System
2.3.3. Grid Division
2.3.4. Setting Boundary Conditions
2.3.5. Model Operation
2.3.6. Determination of the Tidal Structure and Current Pattern
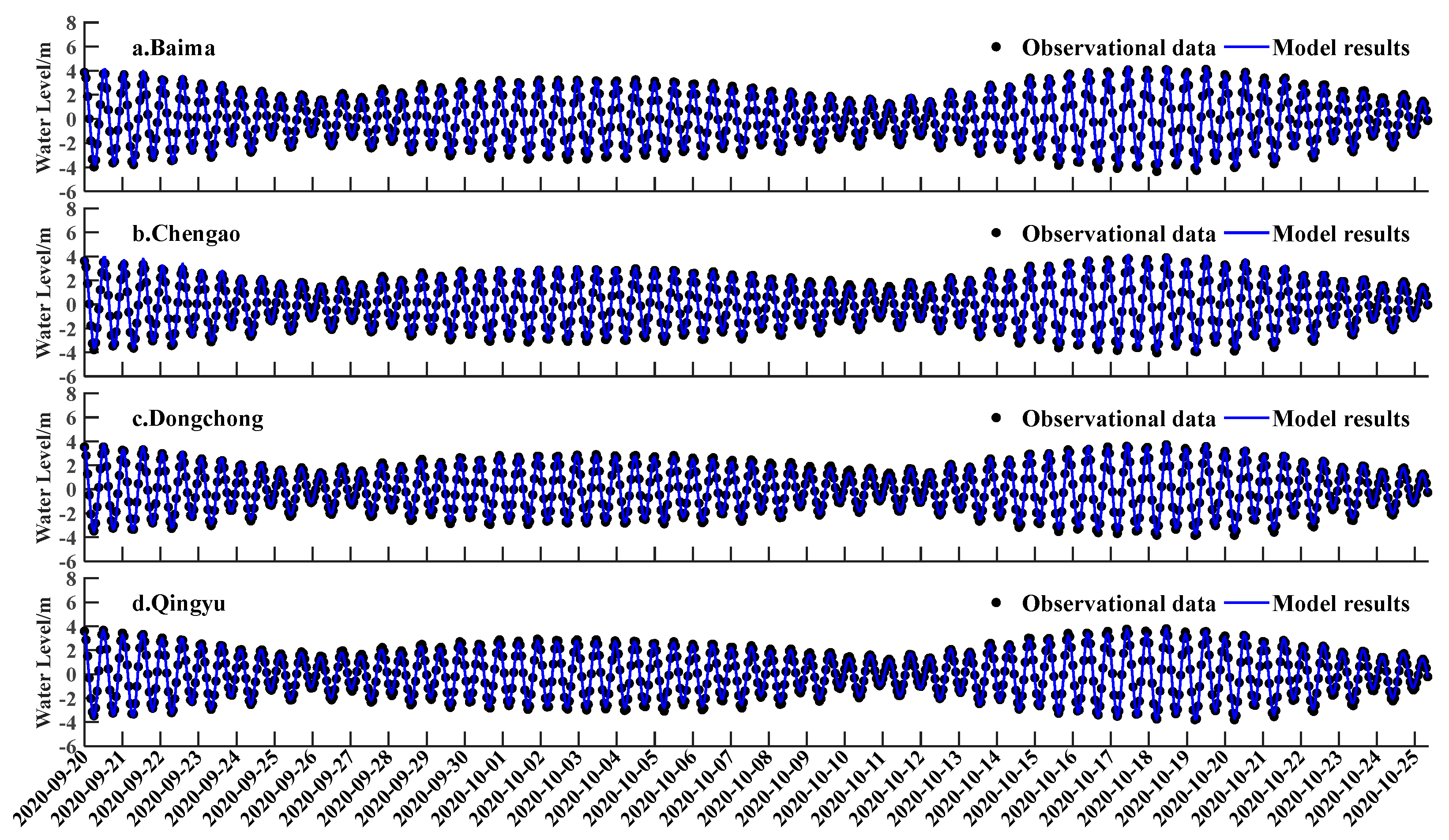
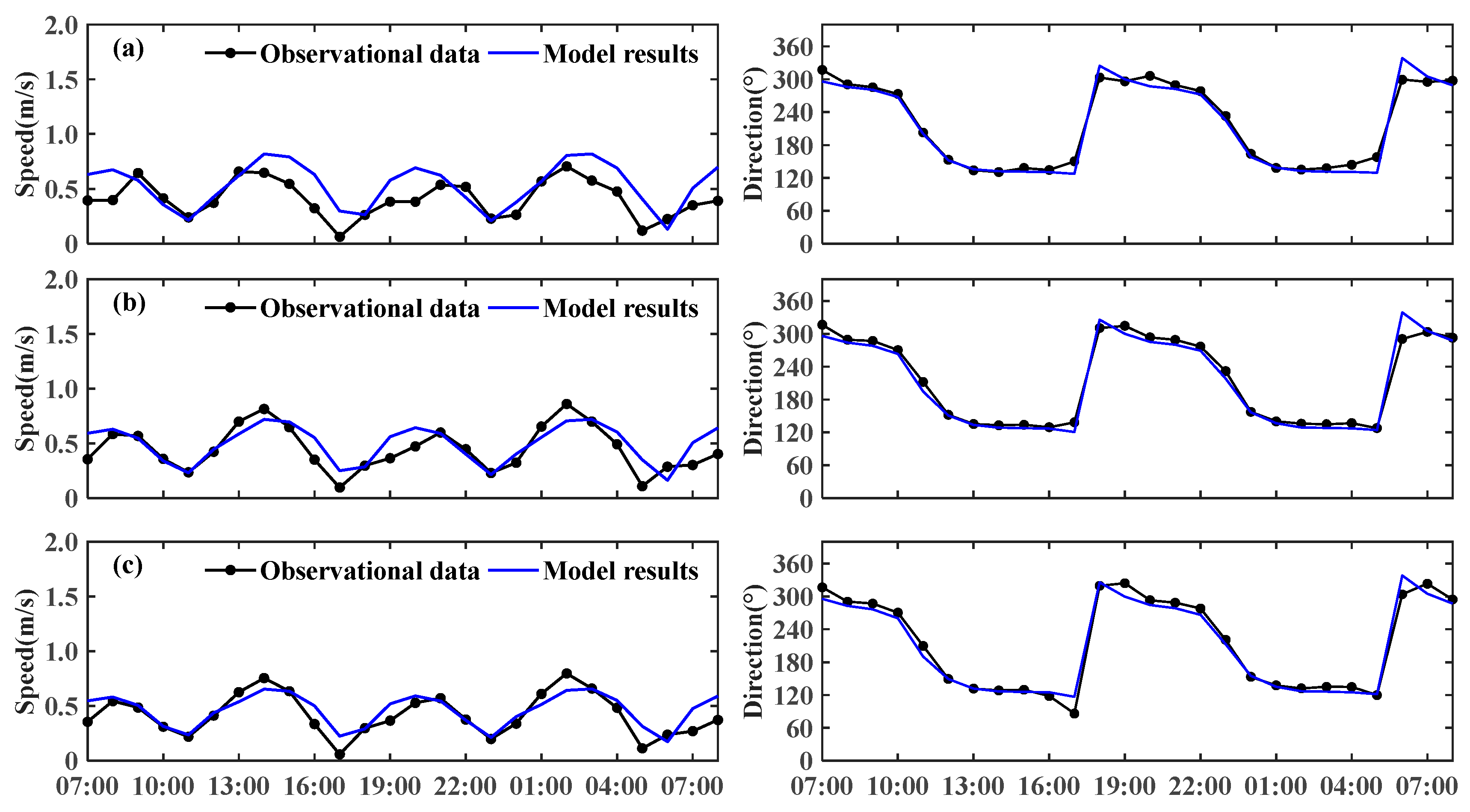
2.3.7. Verification of the Tidal Structure and Current Pattern
2.4. Lagrangian Particle Tracking Model
2.4.1. Equations in the σ-Coordinate System
2.4.2. Parameter Setting
2.5. Scenarios and Contents of Numerical Simulations
3. Results
3.1. Hydrodynamic Characteristics of Sansha Bay
3.1.1. Tidal Structure
3.1.2. Current Velocities and Directions
3.2. Sedimentation Characteristics of Feces and Residual Feed
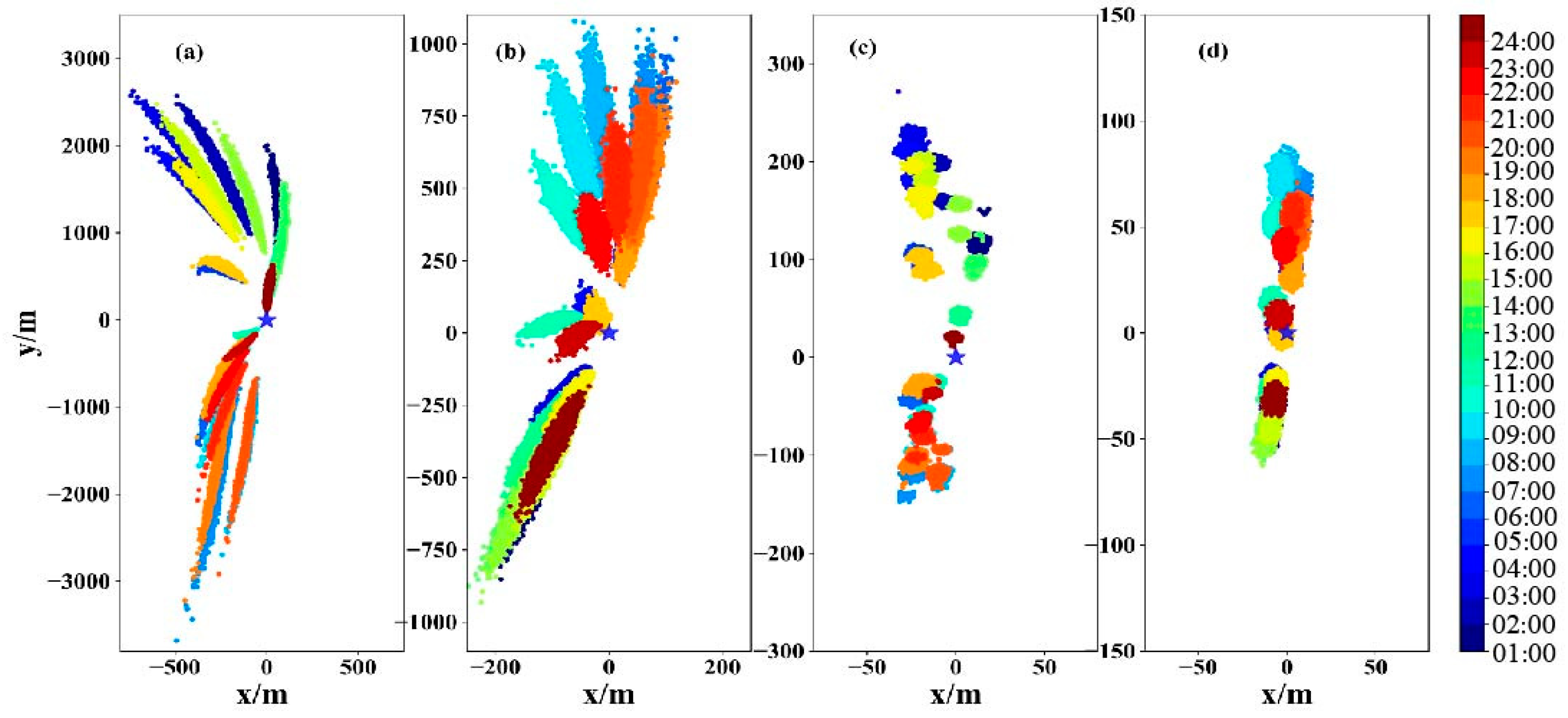
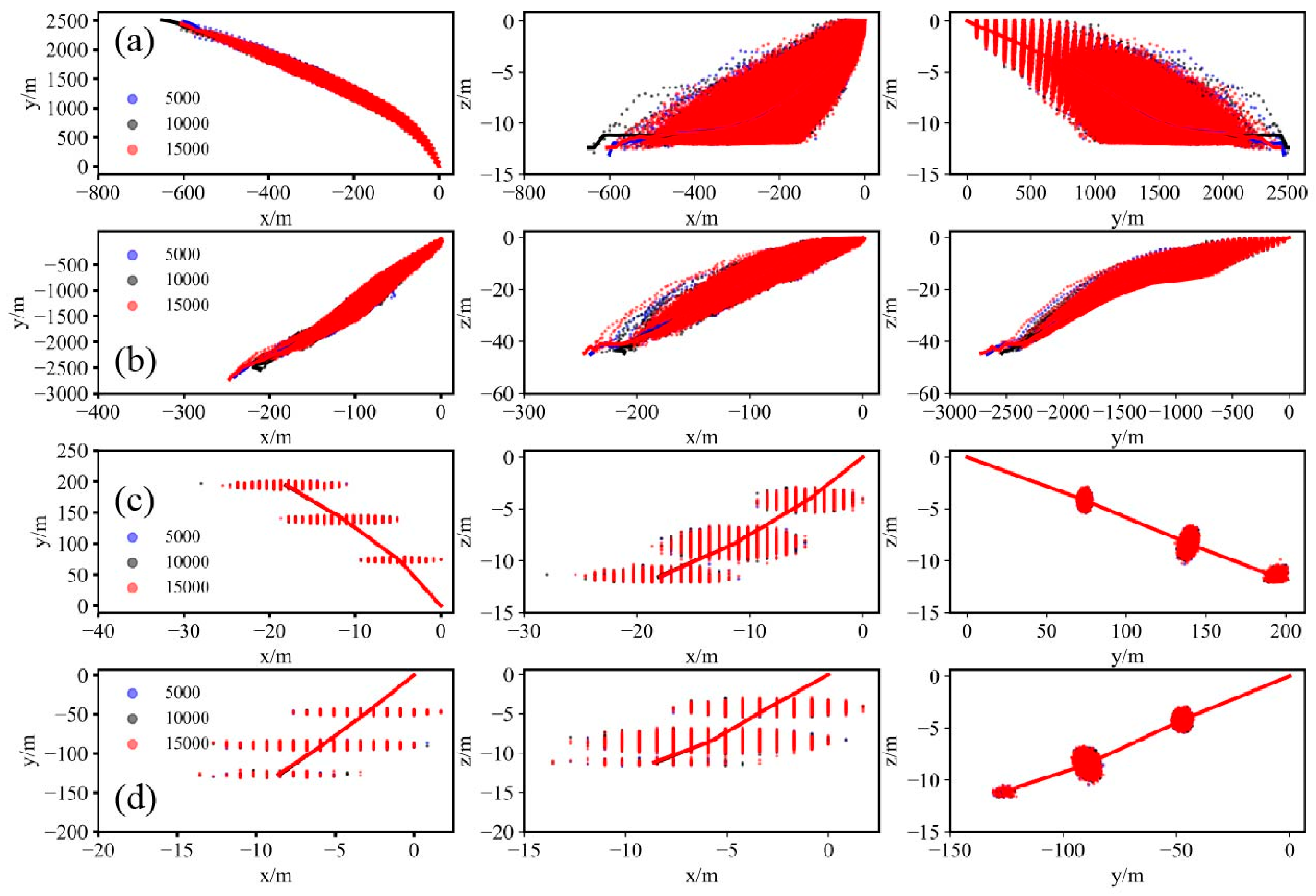
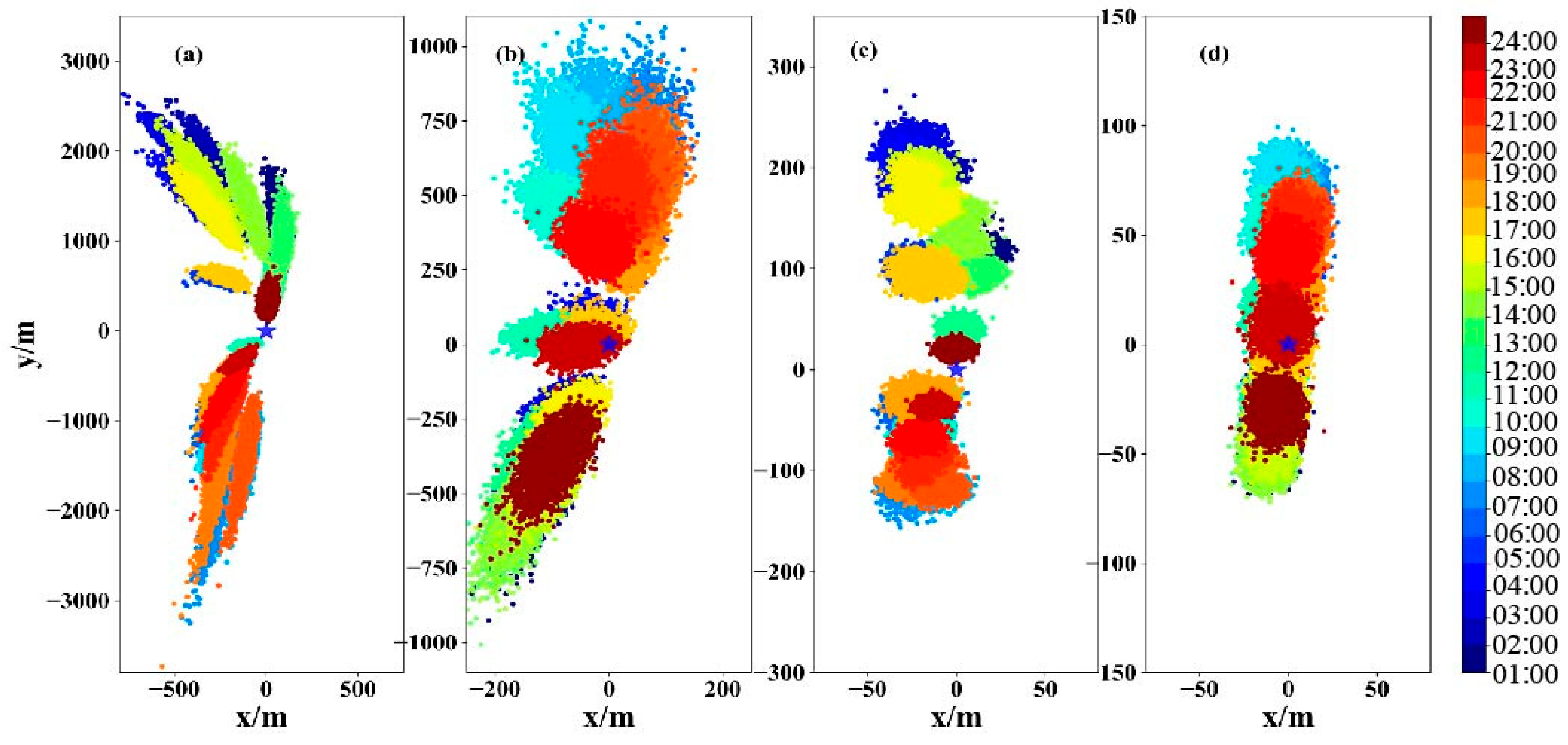
3.2.1. Dispersion Distance of Feces and Residual Feed
3.2.2. Effect of the Feeding Intensity on the Sedimentation Characteristics of Feces and Residual Feed
4. Discussion
4.1. Model Accuracy and Sensitivity Analysis
4.2. Hydrodynamic Characteristics of Sansha Bay
4.3. Horizontal Dispersion Distance and Settling Time of AOM in Sansha Bay
4.4. Main Factors Affecting the AOM Sedimentations in Sansha Bay
4.5. Environmental Effect of the AOM Deposition in Sansha Bay
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yokoyama, H.; Abo, K.; Ishihi, Y. Quantifying aquaculture-derived organic matter in the sediment in and around a coastal fish farm using stable carbon and nitrogen isotope ratios. Aquaculture 2006, 254, 411–425. [Google Scholar] [CrossRef]
- Qi, Z.H.; Shi, R.J.; Yu, Z.H.; Han, T.T.; Li, C.H.; Xu, S.M.; Xu, S.N.; Liang, Q.Y.; Yu, W.; Lin, H.Z.; et al. Nutrient release from fish cage aquaculture and mitigation strategies in Daya Bay, southern China. Mar. Poll. Bull. 2019, 146, 399–407. [Google Scholar] [CrossRef]
- Holmer, M.; Marba, N.; Diaz-Almela, E.; Duarte, C.M.; Tsapakis, M.; Danovaro, R. Sedimentation of organic matter from fish farms in oligotrophic Mediterranean assessed through bulk and stable isotope (δ13C and δ15N) analyses. Aquaculture 2007, 262, 268–280. [Google Scholar] [CrossRef]
- Zhulay, I.; Reiss, K.; Reiss, H. Effects of aquaculture fallowing on the recovery of macrofauna communities. Mar. Poll. Bull. 2015, 97, 381–390. [Google Scholar] [CrossRef]
- Go, Y.S.; Kim, C.S.; Lee, W.C.; Lee, D.H. A stable isotopic approach for quantifying aquaculture-derived organic matter deposition dynamics in the sediment of a coastal fish farm. Mar. Poll. Bull. 2023, 192, 115132. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.Q.; Ji, W.W.; Fu, J.; Ma, Z.L.; Zhou, J. Sedimentation characteristics of derived organic compounds in cage culture of large yellow croaker in Sansha Bay. J. Fish. Sci. China. 2020, 27, 709–719. [Google Scholar] [CrossRef]
- Doglioli, A.M.; Magaldi, M.G.; Vezzulli, L.; Tucci, S. Development of a numerical model to study the dispersion of wastes coming from a marine fish farm in the Ligurian Sea (western Mediterranean). Aquaculture 2003, 231, 215–235. [Google Scholar] [CrossRef]
- Riera, R.; Pérez, Ó.; Cromey, C.; Rodríguez, M.; Ramos, E.; Álvarez, O.; Domínguez, J.; Monterroso, Ó.; Tuya, F. MACAROMOD: A tool to model particulate waste dispersion and benthic impact from offshore sea-cage aquaculture in the Macaronesian region. Ecol. Modell. 2017, 361, 122–134. [Google Scholar] [CrossRef]
- Telfer, T.C.; Bostock, J.; Oliver, R.L.; Corner, R.A.; Falconer, L. CAPOT: A flexible rapid assessment model to estimate local deposition of fish cage farm wastes. Mar. Environ. Res. 2022, 182, 105788. [Google Scholar] [CrossRef] [PubMed]
- Bureau of Statistics of Ningde city. Statistical Yearbook of Ningde City; Bureau of Statistics of Ningde City: Ningde City, China, 2020. [Google Scholar]
- Bureau of Fishery, Ministry of Agriculture. China Fisheries Statistical Yearbook; Bureau of Fishery, Ministry of Agriculture: Beijing City, China, 2020. [Google Scholar]
- Ji, W.W.; Yokoyama, H.; Fu, J.; Zhou, J. Effects of intensive fish farming on sediments of a temperate bay characterised by polyculture and strong currents. Aquacult. Rep. 2021, 19, 100579. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Oceanic. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Telfer, T.; Falconer, L.; Kaas, H.; Jackson, D. TAPAS-tools for assessment and planning of aquaculture sustainability-Horizon2020. Impact 2018, 8, 9–11. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Zhang, J.H.; Liu, Y.; Sun, K.; Zhang, C.; Wu, W.G.; Teng, F. Numerical assessment of the environmental impacts of deep sea cage culture in the Yellow Sea, China. Sci. Total Environ. 2020, 706, 135752. [Google Scholar] [CrossRef] [PubMed]
- Cromey, C.J.; Nickell, T.D.; Black, K.D. DEPOMOD—Modelling the deposition and biological effects of waste solids from marine cage farms. Aquaculture 2002, 214, 211–239. [Google Scholar] [CrossRef]
- Lin, H.; Chen, Z.; Hu, J.; Cucco, A.; Zhu, J.; Sun, Z.; Huang, L. Numerical simulation of the hydrodynamics and water exchange in Sansha Bay. Ocean Eng. 2017, 139, 85–94. [Google Scholar] [CrossRef]
- Jiang, X.; Tu, J.; Fan, D. The influence of a suspended cage aquaculture farm on the hydrodynamic environment in a semienclosed Bay, SE China. Front. Mar. Sci. 2022, 8, 779866. [Google Scholar] [CrossRef]
- Lin, H.Y.; Chen, Z.Z.; Hu, J.Y.; Cucco, A.; Sun, Z.Y.; Chen, X.R.; Huang, L.F. Impact of cage aquaculture on water exchange in Sansha Bay. Cont. Shelf Res. 2019, 188, 103963. [Google Scholar] [CrossRef]
- Wang, X.Y.; Cuthbertson, A.; Gualtieri, C.; Shao, D.D. A Review on Mariculture Effluent: Characterization and Management Tools. Water 2020, 12, 2991. [Google Scholar] [CrossRef]
- Chen, Y.S.; Beveridge, M.; Telfer, T.C. Physical characteristics of commercial pelleted Atlantic salmon feeds and consideration of implications for modeling of waste dispersion through sedimentation. Aquacult. Int. 1999, 7, 89–100. [Google Scholar] [CrossRef]
- Csanady, G.T. Circulation in the Coastal Ocean; Springer: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Lin, H.Y.; Hu, J.Y.; Zhu, J.; Cheng, P.; Chen, Z.Z.; Sun, Z.Y.; Chen, D.W. Tide- and wind-driven variability of water level in Sansha Bay, Fujian, China. Front. Earth Sci. 2016, 11, 332–346. [Google Scholar] [CrossRef]
- Suara, K.; Khanarmuei, M.; Ghosh, A.; Yu, Y.Y.; Zhang, H.; Soomere, T.; Brown, R.J. Material and debris transport patterns in Moreton Bay, Australia: The influence of Lagrangian coherent structures. Sci. Total Environ. 2020, 721, 137715. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.K.; Tu, J.B.; Yu, J.J.; Fan, D.D. Hydrodynamic processes of the bottom boundary layer and suspended sediment transport in the Sansha Bay in summer. Mar. Sci. 2021, 45, 1–12. [Google Scholar] [CrossRef]


| Parameter Name | Parameter Setting |
|---|---|
| Number of grid nodes | 25,792 |
| Number of grid cells | 48,646 |
| Minimal grid mesh | 25 m |
| Time step | Outer membrane: 1 s, inner membrane: 5 s |
| Total simulation time | 35 days |
| Bottom friction coefficient | 0.001 |
| Vertical layers | 6 |
| Parameter | Parameter Setting |
|---|---|
| Horizontal dispersion coefficient | 0.01 m2 s–1 |
| Vertical dispersion coefficient | 0.001 m2 s–1 |
| Time step | Outer membrane: 300 s, inner membrane: 60 s |
| Settling velocity of feces | 0.007 m s–1 |
| Settling velocity of residual feed | 0.07 m s–1 |
| Number of released particles | 5000, 10,000, 15,000 |
| Site | Longitude (°E) | Latitude (°N) | M2 | S2 | K1 | O1 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Baima | 119.73 | 26.73 | 0.41 | –2.57 | –4.32 | –2.08 | –0.17 | 3.10 | 0.35 | –1.18 |
| Chengao | 119.73 | 26.62 | –1.25 | –0.88 | –3.07 | –0.36 | –0.17 | 3.57 | 0.34 | –0.41 |
| Dongchong | 119.83 | 26.55 | 3.30 | –0.13 | 1.92 | 0.22 | 0.25 | 4.09 | 0.19 | 0.69 |
| Qingyu | 119.72 | 26.36 | 1.74 | 2.57 | 2.22 | 3.78 | 0.33 | 3.26 | 0.06 | 0.76 |
| Mean absolute error | —— | —— | 1.68 | 1.54 | 2.88 | 1.61 | 0.92 | 3.51 | 0.24 | 0.76 |
| Layers | Current Velocities (m s–1) | Current Direction (°) |
|---|---|---|
| 0.2 H | 0.152 | 9.88 |
| 0.6 H | 0.103 | 9.52 |
| 0.8 H | 0.098 | 10.42 |
| Scenarios | Feces (m) | Residual Feed (m) | ||
|---|---|---|---|---|
| Neap Tide | Spring Tide | Neap Tide | Spring Tide | |
| 01:00 | 498.3 | 1126.5 | 47.1 | 118.8 |
| 02:00 | 391.7 | 1635.9 | 36.8 | 188.4 |
| 03:00 | 208.8 | 1805.7 | 23.0 | 217.1 |
| 04:00 | 70.5 | 1493.8 | 4.6 | 189.1 |
| 05:00 | 357.5 | 626.3 | 31.5 | 104.3 |
| 06:00 | 549.9 | 736.0 | 52.4 | 44.5 |
| 07:00 | 634.0 | 1635.4 | 66.7 | 120.3 |
| 08:00 | 675.6 | 1326.3 | 74.2 | 117.4 |
| 09:00 | 631.8 | 916.7 | 71.4 | 82.9 |
| 10:00 | 426.5 | 618.4 | 52.0 | 62.7 |
| 11:00 | 101.8 | 190.2 | 15.8 | 26.0 |
| 12:00 | 346.1 | 477.4 | 28.1 | 39.9 |
| 13:00 | 526.6 | 952.1 | 48.8 | 96.8 |
| 14:00 | 532.5 | 1314.3 | 52.9 | 142.9 |
| 15:00 | 424.1 | 1589.2 | 42.3 | 186.1 |
| 16:00 | 229.1 | 1355.6 | 24.5 | 167.6 |
| 17:00 | 45.7 | 635.5 | 3.8 | 95.8 |
| 18:00 | 323.2 | 579.0 | 26.9 | 32.8 |
| 19:00 | 501.3 | 1451.4 | 49.2 | 108.7 |
| 20:00 | 552.5 | 1325.6 | 59.7 | 116.3 |
| 21:00 | 500.8 | 945.7 | 55.2 | 84.7 |
| 22:00 | 335.8 | 694.6 | 40.2 | 67.0 |
| 23:00 | 52.7 | 328.5 | 9.5 | 38.5 |
| 24:00 | 382.2 | 280.0 | 30.9 | 20.9 |
| High water | 101.8 | 626.6 | 15.8 | 104.3 |
| Low water | 45.7 | 190.2 | 3.8 | 26.0 |
| Ebb moment | 532.5 | 1326.3 | 52.9 | 117.4 |
| Rush moment | 552.5 | 1589.2 | 59.7 | 186.1 |
| Particle Type | Tidal Stencils | Feeding Moments | Horizontal Dispersion Distance (m) | Settling Time (min) | ||||
|---|---|---|---|---|---|---|---|---|
| 5000 | 10,000 | 15,000 | 5000 | 10,000 | 15,000 | |||
| Feces | Spring tide | High water | 626.6 | 625.4 | 625.3 | 35.2 | 35.1 | 35.2 |
| Ebb moment | 1326.3 | 1321.5 | 1320.6 | 34.6 | 34.4 | 34.4 | ||
| Low water | 190.2 | 189.9 | 189.5 | 19.6 | 19.5 | 19.4 | ||
| Rush moment | 1589.2 | 1584.9 | 1583.1 | 29.6 | 29.5 | 29.5 | ||
| Neap tide | High water | 101.8 | 101.5 | 101.3 | 30.7 | 30.6 | 30.6 | |
| Ebb moment | 532.5 | 530.0 | 529.9 | 28.6 | 28.5 | 28.5 | ||
| Low water | 45.7 | 45.5 | 45.6 | 23.5 | 23.4 | 23.4 | ||
| Rush moment | 552.5 | 551.0 | 550.2 | 26.5 | 26.4 | 26.4 | ||
| Residual feed | Spring tide | High water | 104.3 | 104.3 | 104.2 | 4.0 | 4.0 | 4.0 |
| Ebb moment | 117.4 | 117.4 | 117.4 | 3.0 | 3.0 | 3.0 | ||
| Low water | 26.0 | 26.1 | 26.0 | 2.0 | 2.0 | 2.0 | ||
| Rush moment | 186.1 | 186.1 | 186.0 | 3.1 | 3.1 | 3.1 | ||
| Neap tide | High water | 15.8 | 15.8 | 15.8 | 3.6 | 3.6 | 3.6 | |
| Ebb moment | 52.9 | 52.9 | 52.9 | 3.0 | 3.0 | 3.0 | ||
| Low water | 3.8 | 3.8 | 3.7 | 3.0 | 3.0 | 3.0 | ||
| Rush moment | 59.7 | 59.6 | 59.6 | 3.0 | 3.0 | 3.0 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, J.; Yu, R.; Huang, Q.; Yuan, S.; Zhou, J. Numerical Simulation of Aquaculture-Derived Organic Matter Sedimentation in a Temperate Intensive Aquaculture Bay Based on a Finite-Volume Coastal Ocean Model. Fishes 2025, 10, 483. https://doi.org/10.3390/fishes10100483
Fu J, Yu R, Huang Q, Yuan S, Zhou J. Numerical Simulation of Aquaculture-Derived Organic Matter Sedimentation in a Temperate Intensive Aquaculture Bay Based on a Finite-Volume Coastal Ocean Model. Fishes. 2025; 10(10):483. https://doi.org/10.3390/fishes10100483
Chicago/Turabian StyleFu, Jing, Ran Yu, Qingze Huang, Sanling Yuan, and Jin Zhou. 2025. "Numerical Simulation of Aquaculture-Derived Organic Matter Sedimentation in a Temperate Intensive Aquaculture Bay Based on a Finite-Volume Coastal Ocean Model" Fishes 10, no. 10: 483. https://doi.org/10.3390/fishes10100483
APA StyleFu, J., Yu, R., Huang, Q., Yuan, S., & Zhou, J. (2025). Numerical Simulation of Aquaculture-Derived Organic Matter Sedimentation in a Temperate Intensive Aquaculture Bay Based on a Finite-Volume Coastal Ocean Model. Fishes, 10(10), 483. https://doi.org/10.3390/fishes10100483







