Logical Analogies: Interpretations, Oppositions, and Probabilism
Abstract
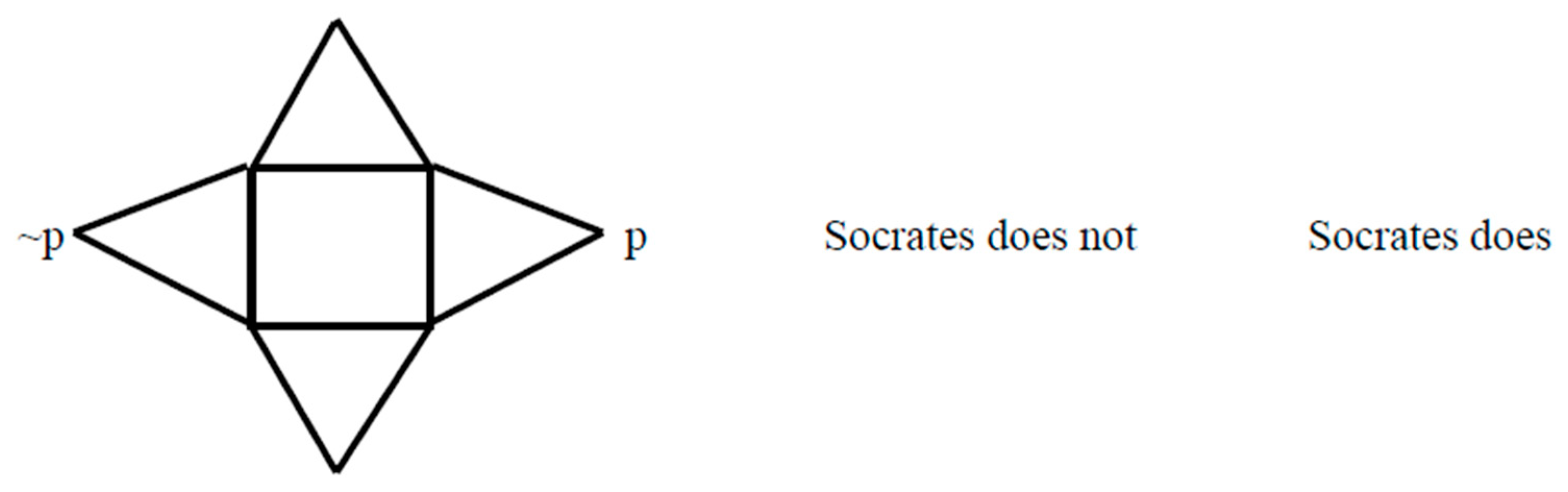
:1. The Logical Systems
| Sp = df ~W~p |
| Wp = df ~S~p |
| Sp S~p | ~W~p ~Wp | |
| ~S~p ~Sp | Wp W~p |
| Sp⊃p | ~Wp⊃~p | |
| p⊃Wp | ~p⊃~Sp |
2. Modality
| □p⊃p | □~p⊃~p | |
| p⊃◊p | ~p⊃◊~p, |
| □p | □~p | ~◊~p | ~◊p | |
| ~□~p | ~□p | ◊p | ◊~p.2 |
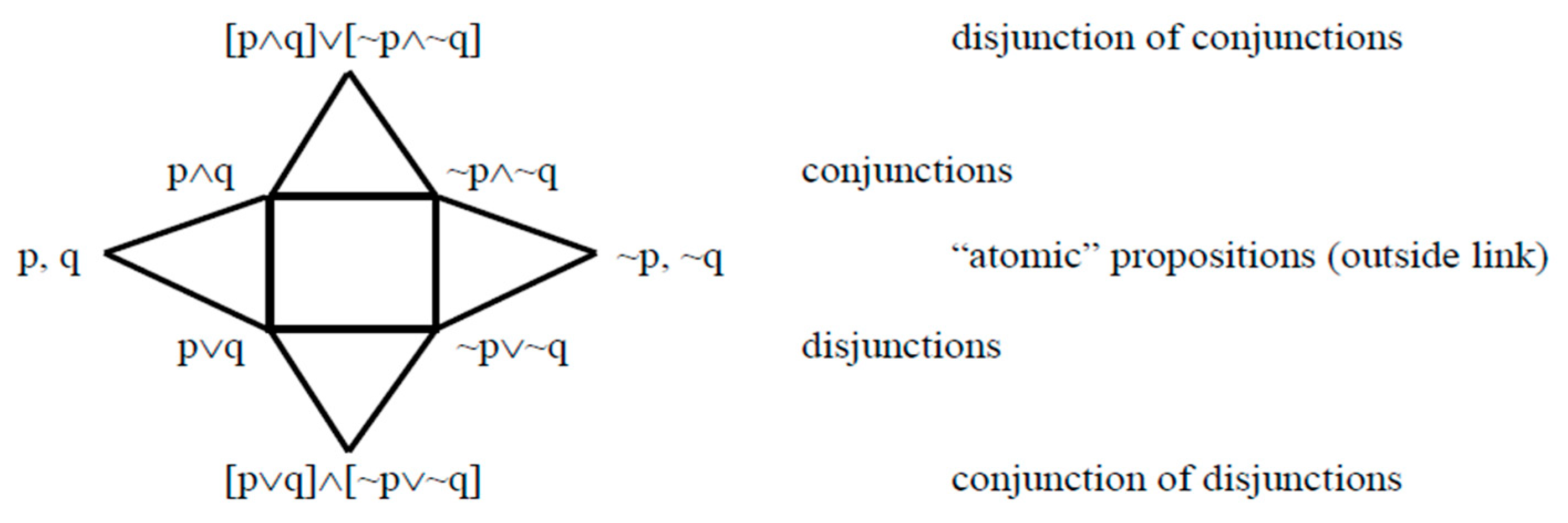
3. Propositional Relations
| [p∧q]⊃p and [p∧q]⊃q | [~p∧~q]⊃~p and [~p∧~q]⊃~q | |
| p⊃[p∨q] and q⊃[p∨q] | ~p⊃[~p∨~q] and ~q⊃[~p∨~q] |
4. Quantification
| ∀xϕx⊃ϕa | ∀x~ϕx⊃~ϕa | |
| ϕa⊃∃xϕx | ~ϕa⊃∃x~ϕx, |
5. Deontic Logic
| Op = df ~M~p | Socrates should do p just in case he may not leave p undone |
| Mp = df ~O~p | Socrates may do p just in case he is not obliged to leave p undone |
| Op = ~M~p |
| O~p = ~Mp = Fp |
| ~Op = M~p = Np |
| ~O~p = Mp, |
| Op | ~Op | ~M~p | ~Mp | |||
| ~O~p | ~Op | Mp | M~p. |
6. Behavior
| Op⊃p | Fp⊃~p | |
| p⊃Mp | ~p⊃Np. |
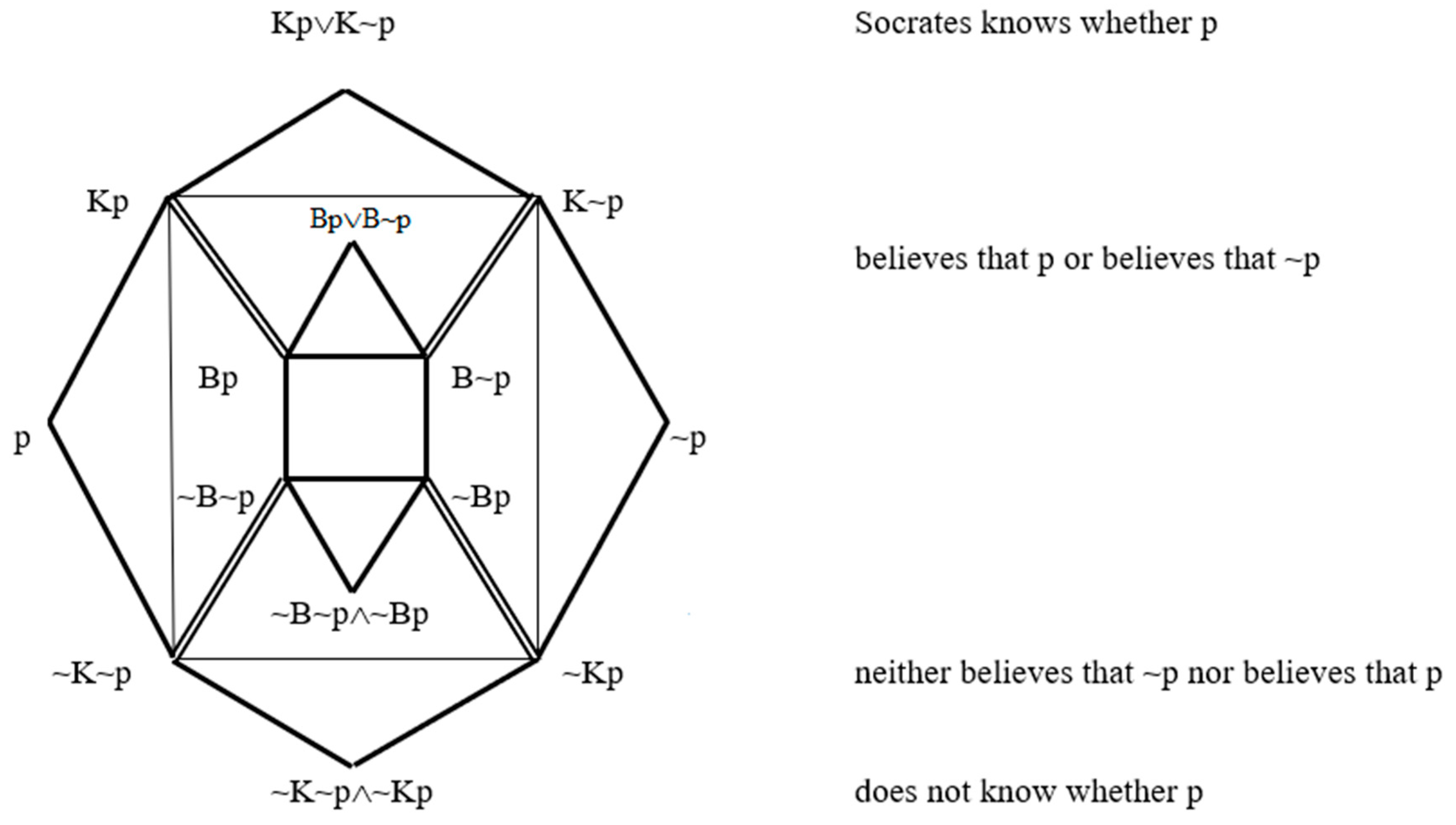
7. The Logic of Knowledge
| Dp∧◊[λ∧~Dp] |
| * Kp⊃p and K~p⊃~p | what Socrates knows is true | |
| * p⊃~K~p and ~p⊃~Kp | he does not know what is false. |
8. The Logic of Belief
9. The Logic of Knowledge and Belief Combined
| Kp⊃Bp | K~p⊃B~p | |
| ~B~p⊃~K~p | ~Bp⊃~Kp. |
10. Probabilism
- *
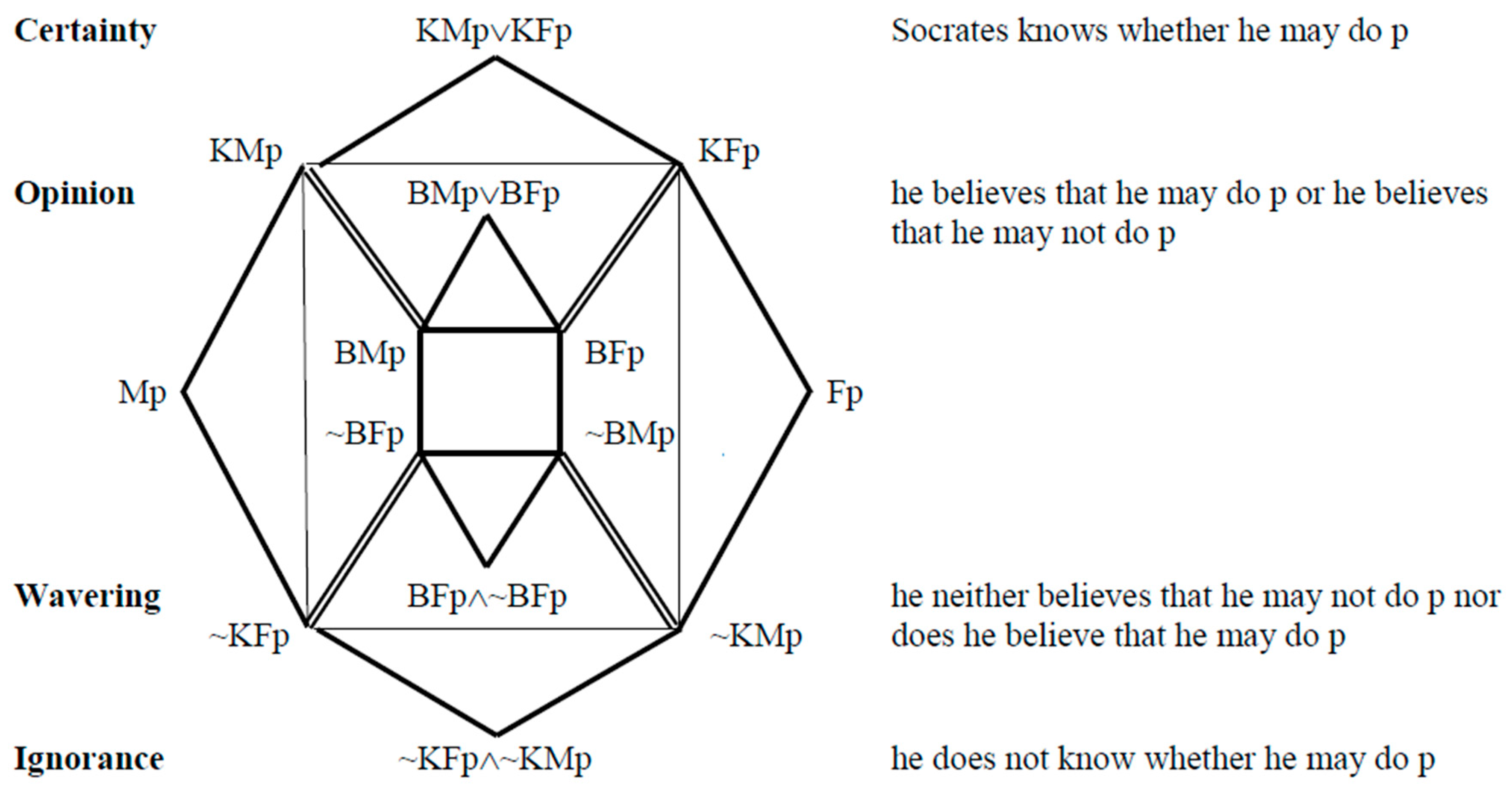
- Certainty: Socrates is sure that he must or may effect the state-of-affairs p if he has a “sound grounds” for his attitude (KOp, KMp or their negative forms) and no reason, or only “slight (levis)” ones, for the opposite. In this state truth would be “manifested” (KOp⊃Op, KMp⊃Mp). He then knows whether he may or may not act:
KMp∨KFp - *
- Opinion: Socrates believes that he should or may effect p when his reasons are “sound enough” or “sounder than the opposite”. “And so, although the truth is not “manifested, still there is a notable appearance of the truth”18. Hence, he opines that some act is licit or forbidden:
and he is then said to be “afraid of being wrong”.BMp∨BFp - *
- Wavering19: Socrates wavers “positively” when he suspends assent because the reasons for both positions (Fp and Mp) are “equally sound”. Hence in wavering, he does not believe that he may not, nor does he believe that he may:
~B~Mp∧~BMp. - *
- Ignorance or “negative wavering”: Socrates suspends his assent when his reasons for both sides (“parts”) are totally lacking. He therefore does not know whether he may or may not act:
~K~Mp∧~KMp.
- *
- that Socrates knows that he may do p implies that he believes that he may: KMp⊃BMp (also KFp⊃Bfp);
- *
- that he does not believe that he may not do implies that he does not know that he may not: ~BFp⊃~Kfp (also ~Mp⊃~KMp).
- *
- that Socrates knows that he may do p implies that he may: KMp⊃Mp (or KFp⊃Fp);
- *
- that he may do p implies that he does not know that he is forbidden: Mp⊃~KFp (or Fp⊃~KMp).
11. Analogy
Funding
Acknowledgments
Conflicts of Interest
References
- Hughes, G.H.; Cresswell, M.J. An Introduction to Modal Logic; Methuen and Co.: London, UK, 1968. [Google Scholar]
- Plato. Charmides.
- Von Wright, G.H. Deontic Logic. Mind 1951, 60, 1–15. [Google Scholar] [CrossRef]
- Von Wright, G.H. An Essay in Modal Logic; North Holland: Amsterdam, The Netherlands, 1951. [Google Scholar]
- Redmond, W. A Logic of Religious Faith and Development. In The Rationality of Theism; Rodopi: Amsterdam, The Netherlands, 2000; Number 73; pp. 35–59. [Google Scholar]
- Redmond, W. Lógica Simbólica para Todos; University of Vera Cruz: Xalapa, Vera Cruz, Mexico, 1999. [Google Scholar]
- Redmond, W. Lógica. deber, virtud. Areté Revista de filosofía 1999, 11, 755–772. [Google Scholar]
- Redmond, W. Conscience as Moral Judgment: The Probabilist Blending of the Logics of Knowledge and Responsibility. J. Relig. Ethics 1998, 26, 389–405. [Google Scholar]
- Redmond, W. A Logic of Faith. Philos. Relig. 1990, 27, 165–180. [Google Scholar] [CrossRef]
- Knuuttila, S. Modalities in Medieval Philosophy; Routledge: London, UK, 1993. [Google Scholar]
- Leibniz, G.W. Elementa juris naturalis (1671-2). In Sämtliche Schriften und Briefe; O. Reichl: Darmstadt, Germany, 1927; Volume 6, pp. 431–485. [Google Scholar]
- Burkhardt, H. Logik und Semiotik in der Philosophie von Leibniz; Philosophia Verlag: Munich, Germany, 1980. [Google Scholar]
- Merkelbach, B.H. De virtutibus moralibus. In Summa Theologiae Moralis; Desclée de Brouwer: Louvain, Belgium, 1954; Volume 2. [Google Scholar]
- Hintikka, J. Knowledge and Belief: An Introduction to the Logic of the Two Notions; Cornell University Press: Ithaca, NY, USA, 1962. [Google Scholar]
- Aquinas, T. Summa Theologiae.
- Moore, G.E. Ethics; Holt and Co.: New York, NY, USA, 1912. [Google Scholar]
- Aristoteles. Topics.
| 1 | I use the following propositional symbols: ~p (negation: “not p”), p⊃q (implication: “if p then q”); p∧q (conjunction: “p and q”); p∨q (disjunction: “p or q”); p≡q (equivalence: “p if and only if q”); p|q (non-conjunction: ~[p∧q]: “not: p and q”); p≈q (contradiction or non-equivalence: ~[p≡q]: “if p not q and if q not p”). Quantifiers: ∀xϕx: “for all x, phi-x” and ∃xϕx: “there is at least one x such that phi-x” (where ϕx is a sentence containing x). Modal symbols: □p: “it is necessary that p” and ◊p: “it is possible that p”. | ||||||
| 2 | Hughes and Cresswell [1], pp. 30ff. | ||||||
| 3 | Traditionally, the square has been applied to general propositions governed by words like omnis, aliquis, nullus, aliquis...non, a in the square:
| ||||||
| 4 | Plato spoke of “τὰ δέοντα πράττειν” [2] (Charmides 164 B) and “debere” in Latin was used of moral duty. The words “may”, “must”, and the like are obviously to be taken here only in the moral sense. | ||||||
| 5 | |||||||
| 6 | Note that the phrases “ought not”, “should not”, and “may not” (in my dialect of English) usually mean O~p rather than ~Op or M~p. | ||||||
| 7 | Here, we must take “p” as “Socrates does p”, so that Op should be read “it ought to be the case that Socrates does p”. | ||||||
| 8 | Merkelbach [13], p. 63. | ||||||
| 9 | Thus, the state-of-affairs p is not physically necessary; nor is it therefore logically necessary (◊[λ∧~p]⊃~□p). | ||||||
| 10 | Hintikka 1962, Section 1.1. “Epistemic” refers to knowing, although it is used in a general sense to include believing; “doxastic” refers only to believing. | ||||||
| 11 | We need not use Hintikka’s symbol “a” for the epistemic agent. He uses the letters “P” and “C” to indicate the weak counterparts of Kp and Bp (~K~p and ~B~p), which he glosses as “it is possible, for all (Socrates) knows, that p” and “it is compatible with everything that (Socrates) believes that p”. | ||||||
| 12 | Also, [Kp∨K~p]⊃[ Bp∨B~p] and [~B~p∧~Bp]⊃[~K~p∧~Kp]. | ||||||
| 13 | The word was first used by the Spanish Dominican Bartolomé de Medina (1527–1580). | ||||||
| 14 | On being certain and knowing, see Hintikka Sections 5.8 and 5.9. | ||||||
| 15 | Merkelbach, 62. The doctrine of St. Thomas Aquinas ([15], 2–2:1–16.) lies in the background. He distinguished among knowing, opining, suspecting, and wavering (scire, opinari, suspicari, dubitare) according to assent to a proposition (assensionem) and adherence (adhaesio) to its truth-value. His “epistemic calculus” can be approximately described with the help of the operators Kp and Bp (Figure 13): For Thomas faith is truth-entailing but knowledge-eschewing, for when someone assents to p on religious grounds, then p, but also ~Kp. Hintikka calls such a state not logically, but “epistemically”, inconsistent (~K[p∧~Kp] is a theorem of the epistemic system). It is also, like “Moore’s paradox” (p∧~Bp), doxastically inconsistent (~B[p∧~Bp]). Cf. Hintikka pp. 71ff and 79ff, Moore [16] p. 125; [5,9]. | ||||||
| 16 | Hintikka, Section 2.6. Any argument, not only moral, can be “probable”. The concept goes back to Aristotle’s “dialectical” arguments: ἐξ ἐνδόξων: those that seem true “to all or most or the wise; to all or most of them or to the best known or esteemed”, Topica I (100B22) [17]. | ||||||
| 17 | Merkelbach, 62–63. These “systems” (with their variations) are highly nuanced, and our symbolic rendering is only approximate. | ||||||
| 18 | Merkelbach, 63–4; vide Redmond 1998. There are degrees of the probable: “truly and solidly” (probable), “quite”, “more”, “much more (or less)”, “most probable”, “equally probable”, ... (ibid. 66–67); a “fuzzy logic” would represent these differences. | ||||||
| 19 | “Suspicion” is included in wavering, for “reason accepts what is little as if it were nothing” (quod parum est quasi nihil accipit ratio), [15] (1–2:14:4); Merkelbach, 63. | ||||||
| 20 | Both positions were condemned by the Catholic church (Merkelbach, 70 and 72). For a more detailed description see Redmond 1998. The probablist did not lack humor; the Cistercian John Caramuel was called the “Prince of the Laxists”, and another laxist, Antonio Diana, a Theatine priest, was said to be “the lamb who taketh away the sins of the world” (agnus qui abstulit peccata mundi)! |









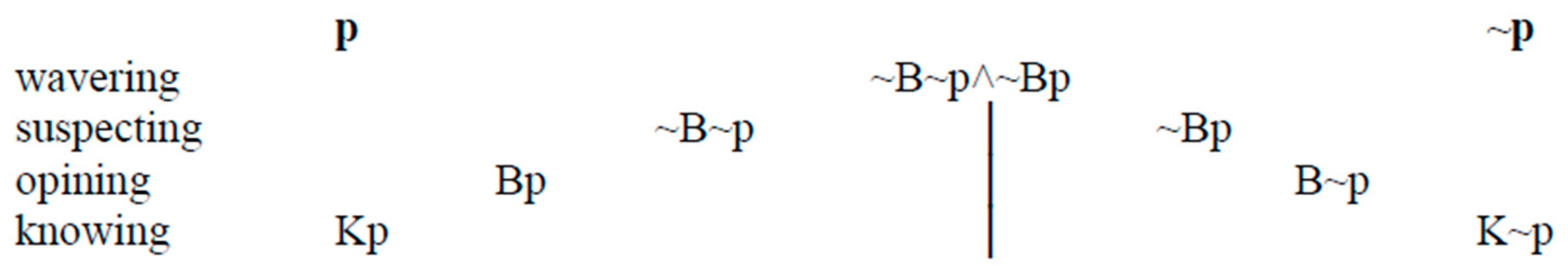

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Redmond, W. Logical Analogies: Interpretations, Oppositions, and Probabilism. Philosophies 2019, 4, 13. https://doi.org/10.3390/philosophies4020013
Redmond W. Logical Analogies: Interpretations, Oppositions, and Probabilism. Philosophies. 2019; 4(2):13. https://doi.org/10.3390/philosophies4020013
Chicago/Turabian StyleRedmond, Walter. 2019. "Logical Analogies: Interpretations, Oppositions, and Probabilism" Philosophies 4, no. 2: 13. https://doi.org/10.3390/philosophies4020013
APA StyleRedmond, W. (2019). Logical Analogies: Interpretations, Oppositions, and Probabilism. Philosophies, 4(2), 13. https://doi.org/10.3390/philosophies4020013



