Comparing Nanomechanical Properties and Membrane Roughness Along the Aging of Human Erythrocytes
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. AFM Setup
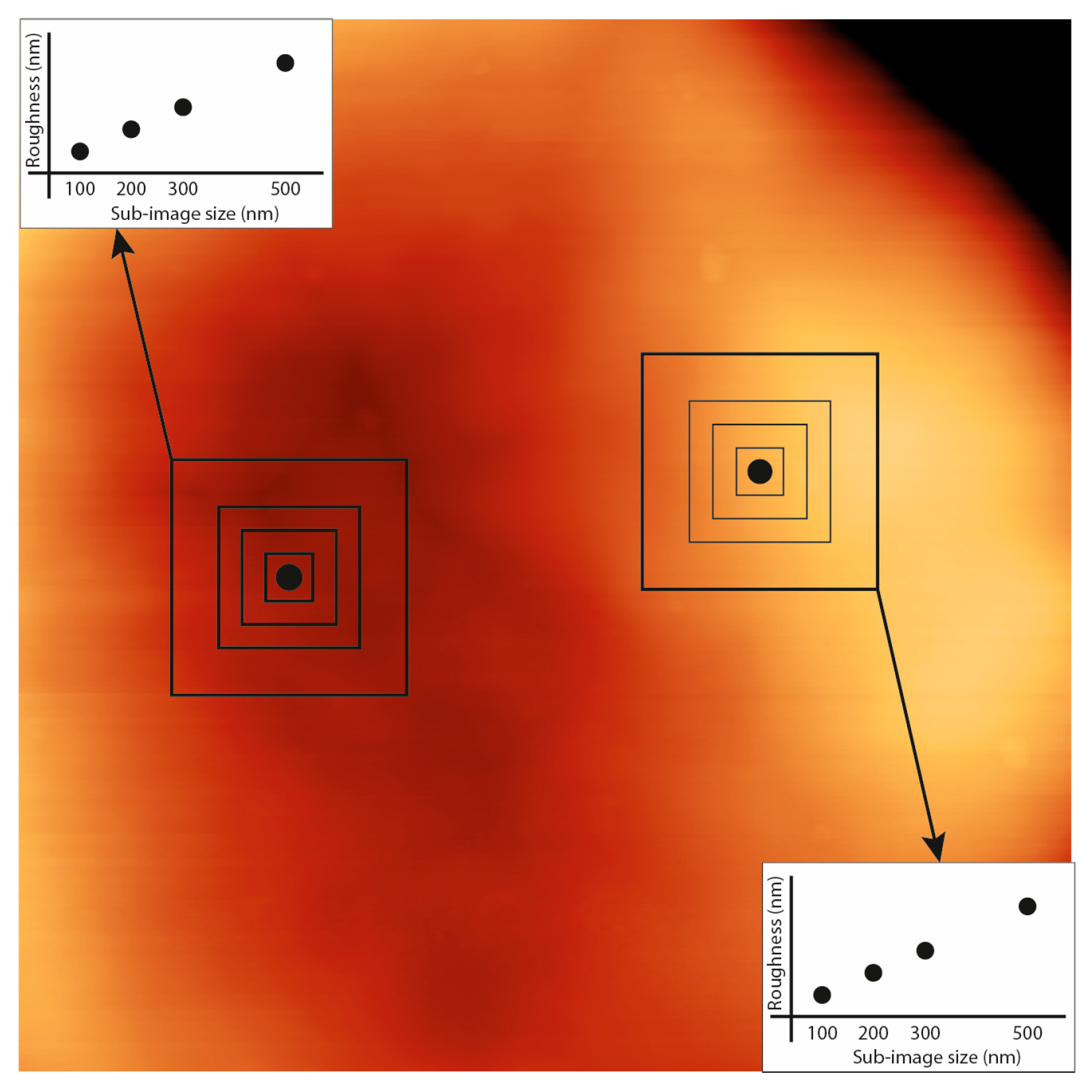
2.3. Image Analysis and Roughness Calculation
2.4. Nanomechanical Properties
2.5. Statistical Analysis
3. Results and Discussion
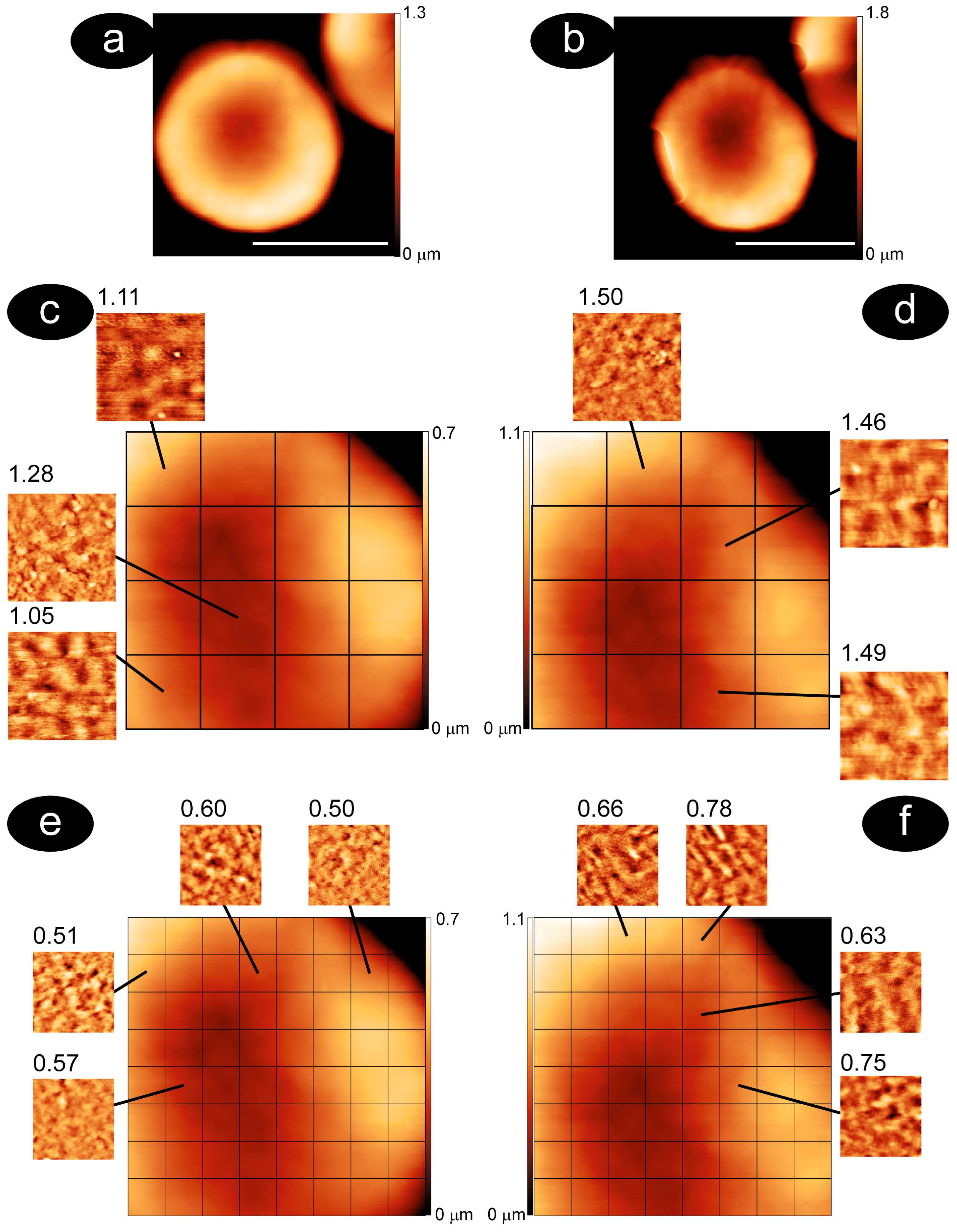
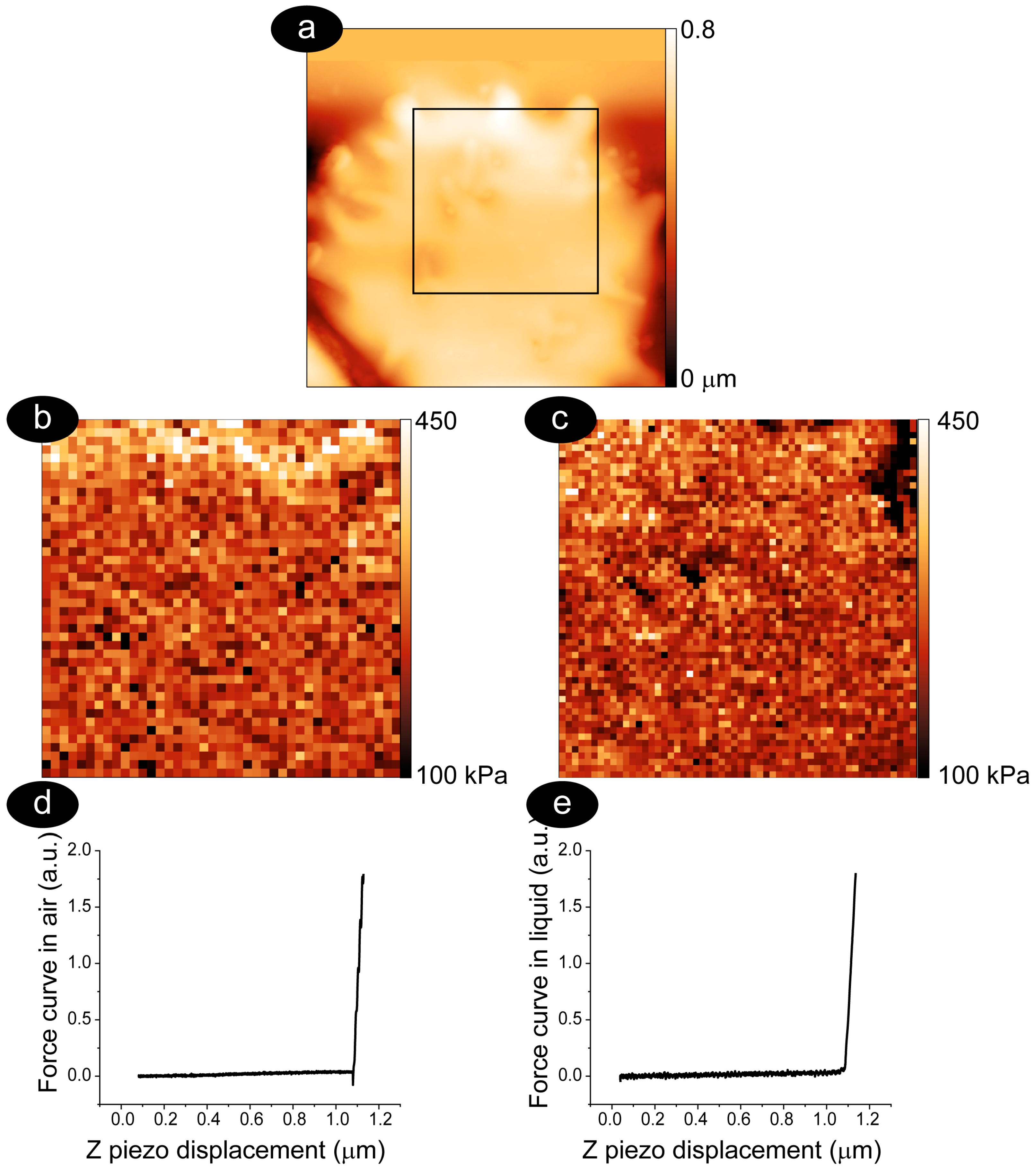
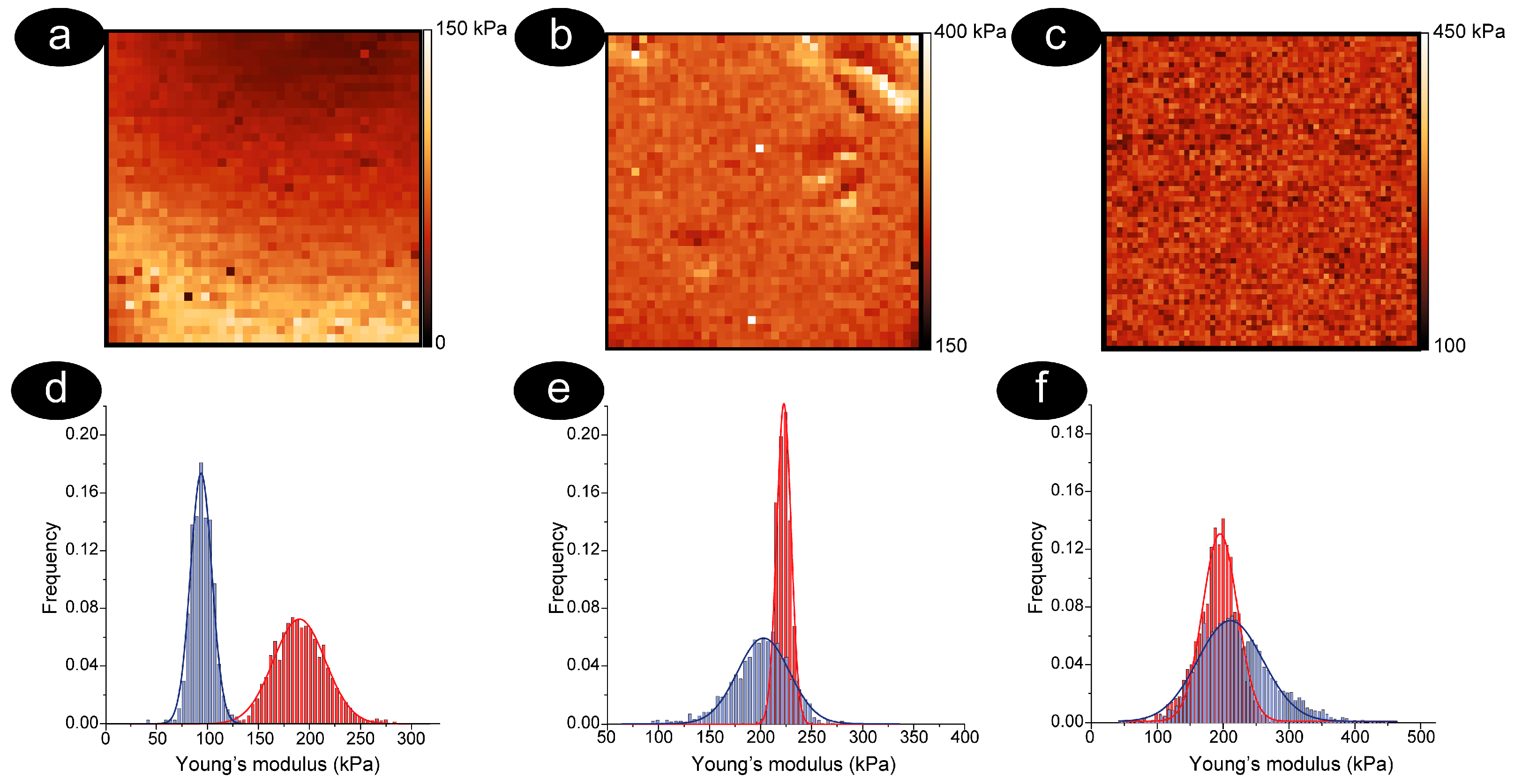
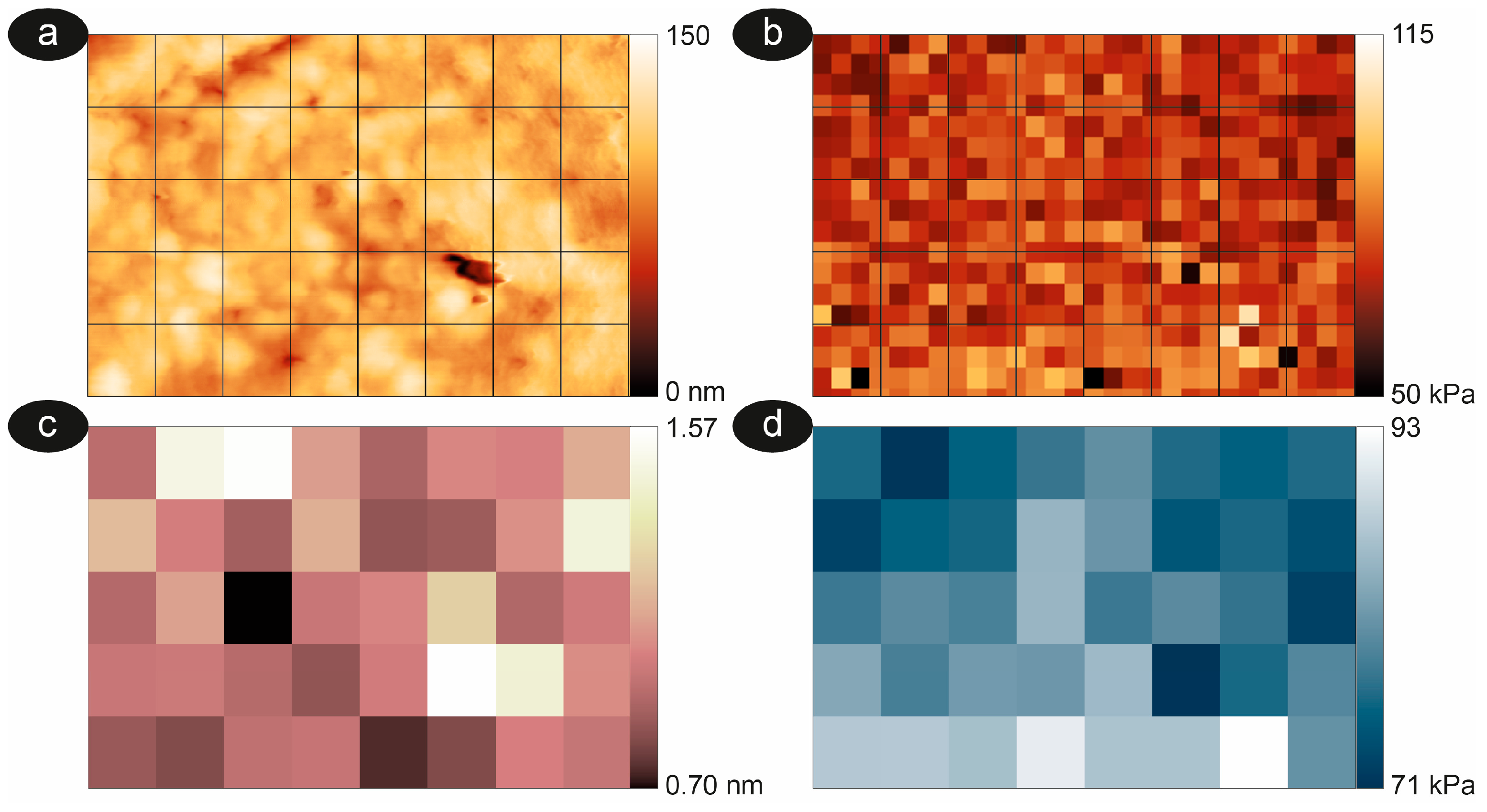
3.1. Methodology to Compare Membrane Roughness and Cell Nanomechanics in Air and Buffer
3.2. The RBCs Aging
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, C.-Y.J.; Kim, K.-C.; Park, H.-W.; Song, J.-H.; Lee, C.-H. Rheological properties of erythrocytes from male hypercholesterolemia. Microvasc. Res. 2004, 67, 133–138. [Google Scholar] [CrossRef]
- Chien, S.; King, R.G.; Skalak, R.; Usami, S.; Copley, A.L. Viscoelastic properties of human blood and red cell suspensions. Biorheology 1975, 12, 341–346. [Google Scholar] [CrossRef]
- Mehri, R.; Mavriplis, C.; Fenech, M. Red blood cell aggregates and their effect on non-Newtonian blood viscosity at low hematocrit in a two-fluid low shear rate microfluidic system. PLoS ONE 2018, 13, e0199911. [Google Scholar] [CrossRef]
- Wajihah, S.A.; Sankar, D.S. A review on non-Newtonian fluid models for multi-layered blood rheology in constricted arteries. Arch. Appl. Mech. 2023, 93, 1771–1796. [Google Scholar] [CrossRef]
- Girasole, M.; Dinarelli, S. 6.4 Blood Cells. In Volume 2 Biomedical Applications; Malgorzata, L., Daniel, N., Manfred, R., Alessandro, P., Eds.; De Gruyter: Berlin, Germany, 2023; pp. 231–258. [Google Scholar]
- Li, C.; Liu, K.K. Nanomechanical characterization of red blood cells using optical tweezers. J. Mater. Sci. Mater. Med. 2008, 19, 1529–1535. [Google Scholar] [CrossRef] [PubMed]
- Barns, S.; Balanant, M.A.; Sauret, E.; Flower, R.; Saha, S.; Gu, Y. Investigation of red blood cell mechanical properties using AFM indentation and coarse-grained particle method. Biomed. Eng. Online 2017, 16, 140. [Google Scholar] [CrossRef] [PubMed]
- Moras, M.; Lefevre, S.D.; Ostuni, M.A. From Erythroblasts to Mature Red Blood Cells: Organelle Clearance in Mammals. Front. Physiol. 2017, 8, 1076. [Google Scholar] [CrossRef] [PubMed]
- Safeukui, I.; Buffet, P.A.; Deplaine, G.; Perrot, S.; Brousse, V.; Ndour, A.; Nguyen, M.; Mercereau-Puijalon, O.; David, P.H.; Milon, G.; et al. Quantitative assessment of sensing and sequestration of spherocytic erythrocytes by the human spleen. Blood 2012, 120, 424–430. [Google Scholar] [CrossRef]
- Antonelou, M.H.; Kriebardis, A.G.; Papassideri, I.S. Aging and death signalling in mature red cells: From basic science to transfusion practice. Blood Transfus. 2010, 8 (Suppl. 3), s39–s47. [Google Scholar] [CrossRef]
- Adamson, J.W. New blood, old blood, or no blood? N. Engl. J. Med. 2008, 358, 1295–1296. [Google Scholar] [CrossRef]
- Huang, Y.X.; Wu, Z.J.; Mehrishi, J.; Huang, B.T.; Chen, X.Y.; Zheng, X.J.; Liu, W.J.; Luo, M. Human red blood cell aging: Correlative changes in surface charge and cell properties. J. Cell. Mol. Med. 2011, 15, 2634–2642. [Google Scholar] [CrossRef]
- Mohanty, J.; Nagababu, E.; Rifkind, J.M. Red blood cell oxidative stress impairs oxygen delivery and induces red blood cell aging. Front. Physiol. 2014, 5, 84. [Google Scholar] [CrossRef]
- Bosman, G.J.C.G.M.; Werre, J.M.; Willekens, F.L.A.; Novotný, V.M.J. Erythrocyte ageing in vivo and in vitro: Structural aspects and implications for transfusion. Transfus. Med. 2008, 18, 335–347. [Google Scholar] [CrossRef]
- Waugh, R.E.; Narla, M.; Jackson, C.W.; Mueller, T.J.; Suzuki, T.; Dale, G.L. Rheologic properties of senescent erythrocytes: Loss of surface area and volume with red blood cell age. Blood 1992, 79, 1351–1358. [Google Scholar] [CrossRef]
- Girasole, M.; Dinarelli, S.; Boumis, G. Structure and function in native and pathological erythrocytes: A quantitative view from the nanoscale. Micron 2012, 43, 1273–1286. [Google Scholar] [CrossRef] [PubMed]
- Pompeo, G.; Girasole, M.; Cricenti, A.; Boumis, G.; Bellelli, A.; Amiconi, S. Erythrocyte death in vitro induced by starvation in the absence of Ca(2+). Biochim. Et Biophys. Acta 2010, 1798, 1047–1055. [Google Scholar] [CrossRef] [PubMed]
- Spinelli, S.; Straface, E.; Gambardella, L.; Caruso, D.; Falliti, G.; Remigante, A.; Marino, A.; Morabito, R. Aging Injury Impairs Structural Properties and Cell Signaling in Human Red Blood Cells; Açaì Berry Is a Keystone. Antioxidants 2023, 12, 848. [Google Scholar] [CrossRef]
- Dinarelli, S.; Longo, G.; Germanova-Taneva, S.; Todinova, S.; Krumova, S.; Girasole, M. Surprising Structural and Functional Properties of Favism Erythrocytes Are Linked to Special Metabolic Regulation: A Cell Aging Study. Int. J. Mol. Sci. 2023, 24, 637. [Google Scholar] [CrossRef] [PubMed]
- Dinarelli, S.; Longo, G.; Francioso, A.; Mosca, L.; Girasole, M. Mechano-Transduction Boosts the Aging Effects in Human Erythrocytes Submitted to Mechanical Stimulation. Int. J. Mol. Sci. 2022, 23, 10180. [Google Scholar] [CrossRef]
- Girasole, M.; Pompeo, G.; Cricenti, A.; Longo, G.; Boumis, G.; Bellelli, A.; Amiconi, S. The how, when, and why of the aging signals appearing on the human erythrocyte membrane: An atomic force microscopy study of surface roughness. Nanomed.-Nanotechnol. Biol. Med. 2010, 6, 760–768. [Google Scholar] [CrossRef]
- Girasole, M.; Pompeo, G.; Cricenti, A.; Congiu-Castellano, A.; Andreola, F.; Serafino, A.; Frazer, B.H.; Boumis, G.; Amiconi, G. Roughness of the plasma membrane as an independent morphological parameter to study RBCs: A quantitative atomic force microscopy investigation. Biochim. Et Biophys. Acta 2007, 1768, 1268–1276. [Google Scholar] [CrossRef] [PubMed]
- Carelli-Alinovi, C.; Dinarelli, S.; Sampaolese, B.; Misiti, F.; Girasole, M. Morphological changes induced in erythrocyte by amyloid beta peptide and glucose depletion: A combined atomic force microscopy and biochemical study. Biochim. Et Biophys. Acta Biomembr. 2019, 1861, 236–244. [Google Scholar] [CrossRef]
- Dinarelli, S.; Girasole, M.; Longo, G. Methods for Atomic Force Microscopy of Biological and Living Specimens. Methods Mol. Biol. 2018, 1814, 529–539. [Google Scholar] [CrossRef]
- Miranda, A.; Gómez-Varela, A.I.; Stylianou, A.; Hirvonen, L.M.; Sánchez, H.; De Beule, P.A.A. How did correlative atomic force microscopy and super-resolution microscopy evolve in the quest for unravelling enigmas in biology? Nanoscale 2021, 13, 2082–2099. [Google Scholar] [CrossRef] [PubMed]
- Müller, D.J.; Dumitru, A.C.; Lo Giudice, C.; Gaub, H.E.; Hinterdorfer, P.; Hummer, G.; De Yoreo, J.J.; Dufrêne, Y.F.; Alsteens, D. Atomic Force Microscopy-Based Force Spectroscopy and Multiparametric Imaging of Biomolecular and Cellular Systems. Chem. Rev. 2021, 121, 11701–11725. [Google Scholar] [CrossRef]
- Dinarelli, S.; Longo, G.; Dietler, G.; Francioso, A.; Mosca, L.; Pannitteri, G.; Boumis, G.; Bellelli, A.; Girasole, M. Erythrocyte’s aging in microgravity highlights how environmental stimuli shape metabolism and morphology. Sci. Rep. 2018, 8, 5277. [Google Scholar] [CrossRef] [PubMed]
- Cross, S.E.; Jin, Y.S.; Rao, J.; Gimzewski, J.K. Nanomechanical analysis of cells from cancer patients. Nat. Nanotechnol. 2007, 2, 780. [Google Scholar] [CrossRef]
- Abidine, Y.; Constantinescu, A.; Laurent, V.M.; Sundar Rajan, V.; Michel, R.; Laplaud, V.; Duperray, A.; Verdier, C. Mechanosensitivity of Cancer Cells in Contact with Soft Substrates Using AFM. Biophys. J. 2018, 114, 1165–1175. [Google Scholar] [CrossRef]
- Suresh, S.; Spatz, J.; Mills, J.P.; Micoulet, A.; Dao, M.; Lim, C.T.; Beil, M.; Seufferlein, T. Connections between single-cell biomechanics and human disease states: Gastrointestinal cancer and malaria. Acta Biomater. 2005, 1, 15–30. [Google Scholar] [CrossRef]
- Raman, A.; Trigueros, S.; Cartagena, A.; Stevenson, A.P.Z.; Susilo, M.; Nauman, E.; Contera, S.A. Mapping nanomechanical properties of live cells using multi-harmonic atomic force microscopy. Nat. Nanotechnol. 2011, 6, 809–814. [Google Scholar] [CrossRef]
- Van Vliet, K.J.; Bao, G.; Suresh, S. The biomechanics toolbox: Experimental approaches for living cells and biomolecules. Acta Mater. 2003, 51, 5881–5905. [Google Scholar] [CrossRef]
- Haase, K.; Pelling, A.E. Investigating cell mechanics with atomic force microscopy. J. R. Soc. Interface 2015, 12, 20140970. [Google Scholar] [CrossRef]
- Dufrêne, Y.F.; Pelling, A.E. Force nanoscopy of cell mechanics and cell adhesion. Nanoscale 2013, 5, 4094–4104. [Google Scholar] [CrossRef] [PubMed]
- Lux, S.E., IV. Anatomy of the red cell membrane skeleton: Unanswered questions. Blood 2016, 127, 187–199. [Google Scholar] [CrossRef]
- Nigra, A.D.; Casale, C.H.; Santander, V.S. Human erythrocytes: Cytoskeleton and its origin. Cell. Mol. Life. Sci. 2020, 77, 1681–1694. [Google Scholar] [CrossRef]
- Mohandas, N.; Gallagher, P.G. Red cell membrane: Past, present, and future. Blood 2008, 112, 3939–3948. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.-Y.; Li, X.; Karniadakis, G.E. Modeling of biomechanics and biorheology of red blood cells in type 2 diabetes mellitus. Biophys. J. 2017, 113, 481–490. [Google Scholar] [CrossRef] [PubMed]
- Pivkin, I.V.; Peng, Z.; Karniadakis, G.E.; Buffet, P.A.; Dao, M.; Suresh, S. Biomechanics of red blood cells in human spleen and consequences for physiology and disease. Proc. Natl. Acad. Sci. USA 2016, 113, 7804–7809. [Google Scholar] [CrossRef] [PubMed]
- Maciaszek, J.L.; Lykotrafitis, G. Sickle cell trait human erythrocytes are significantly stiffer than normal. J. Biomech. 2011, 44, 657–661. [Google Scholar] [CrossRef]
- Rakshak, R.; Bhatt, S.; Sharma, S.; Agharkar, R.; Bodakhe, S.; Srivastava, R. Characterizing morphological alterations in blood related disorders through Atomic Force Microscopy. Nanotheranostics 2024, 8, 330–343. [Google Scholar] [CrossRef]
- Amorim, M.; Batista, J.A.; Junior, F.M.; Fontes, A.; Santos-Oliveira, R.; Rebelo Alencar, L.M. New Insights into Hemolytic Anemias: Ultrastructural and Nanomechanical Investigation of Red Blood Cells Showed Early Morphological Changes. J. Biomed. Nanotechnol. 2022, 18, 405–421. [Google Scholar] [CrossRef]
- Benech, J.C.; Benech, N.; Zambrana, A.I.; Rauschert, I.; Bervejillo, V.; Oddone, N.; Damián, J.P. Diabetes increases stiffness of live cardiomyocytes measured by atomic force microscopy nanoindentation. Am. J. Physiology. Cell Physiol. 2014, 307, C910–C919. [Google Scholar] [CrossRef]
- Eaton, P.; Zuzarte-Luis, V.; Mota, M.M.; Santos, N.C.; Prudêncio, M. Infection by Plasmodium changes shape and stiffness of hepatic cells. Nanomed. Nanotechnol. Biol. Med. 2012, 8, 17–19. [Google Scholar] [CrossRef]
- Nagao, E.; Kaneko, O.; Dvorak, J.A. Plasmodium falciparum-Infected Erythrocytes: Qualitative and Quantitative Analyses of Parasite-Induced Knobs by Atomic Force Microscopy. J. Struct. Biol. 2000, 130, 34–44. [Google Scholar] [CrossRef]
- Sot, J.; García-Arribas, A.B.; Abad, B.; Arranz, S.; Portune, K.; Andrade, F.; Martín-Nieto, A.; Velasco, O.; Arana, E.; Tueros, I.; et al. Erythrocyte Membrane Nanomechanical Rigidity Is Decreased in Obese Patients. Int. J. Mol. Sci. 2022, 23, 1920. [Google Scholar] [CrossRef] [PubMed]
- Nardini, M.; Ciasca, G.; Lauria, A.; Rossi, C.; Di Giacinto, F.; Romanò, S.; Di Santo, R.; Papi, M.; Palmieri, V.; Perini, G.; et al. Sensing red blood cell nano-mechanics: Toward a novel blood biomarker for Alzheimer’s disease. Front. Aging Neurosci. 2022, 14, 932354. [Google Scholar] [CrossRef]
- Taneva, S.G.; Todinova, S.; Andreeva, T. Morphometric and Nanomechanical Screening of Peripheral Blood Cells with Atomic Force Microscopy for Label-Free Assessment of Alzheimer’s Disease, Parkinson’s Disease, and Amyotrophic Lateral Sclerosis. Int. J. Mol. Sci. 2023, 24, 14296. [Google Scholar] [CrossRef] [PubMed]
- Strijkova-Kenderova, V.; Todinova, S.; Andreeva, T.; Bogdanova, D.; Langari, A.; Danailova, A.; Krumova, S.; Zlatareva, E.; Kalaydzhiev, N.; Milanov, I.; et al. Morphometry and Stiffness of Red Blood Cells-Signatures of Neurodegenerative Diseases and Aging. Int. J. Mol. Sci. 2021, 23, 227. [Google Scholar] [CrossRef] [PubMed]
- Suresh, S. Mechanical response of human red blood cells in health and disease: Some structure-property-function relationships. J. Mater. Res. 2006, 21, 1871–1877. [Google Scholar] [CrossRef]
- Hekele, O.; Goesselsberger, C.G.; Gebeshuber, I.C. Nanodiagnostics performed on human red blood cells with atomic force microscopy. Mater. Sci. Technol. 2008, 24, 1162–1165. [Google Scholar] [CrossRef]
- Dumitru, A.C.; Poncin, M.A.; Conrard, L.; Dufrêne, Y.F.; Tyteca, D.; Alsteens, D. Nanoscale membrane architecture of healthy and pathological red blood cells. Nanoscale Horiz. 2018, 3, 293–304. [Google Scholar] [CrossRef]
- Matias, Z.; Lopes, C.S.; Santos, N.C.; Carvalho, F.A. Nanotechnology meets medicine: Applications of atomic force microscopy in disease. Biophys. Rev. 2025, 17, 359–384. [Google Scholar] [CrossRef]
- Efremov, Y.M.; Okajima, T.; Raman, A. Measuring viscoelasticity of soft biological samples using atomic force microscopy. Soft Matter 2020, 16, 64–81. [Google Scholar] [CrossRef] [PubMed]
- Kozlova, E.; Chernysh, A.; Moroz, V.; Kozlov, A.; Sergunova, V.; Sherstyukova, E.; Gudkova, O. Two-step process of cytoskeletal structural damage during long-term storage of packed red blood cells. Blood Transfus. 2021, 19, 124–134. [Google Scholar] [CrossRef]
- Wang, K.; Li, Z.; Egini, O.; Wadgaonkar, R.; Jiang, X.-C.; Chen, Y. Atomic force microscopy reveals involvement of the cell envelope in biomechanical properties of sickle erythrocytes. BMC Biol. 2023, 21, 31. [Google Scholar] [CrossRef] [PubMed]
- Sergunova, V.; Leesment, S.; Kozlov, A.; Inozemtsev, V.; Platitsina, P.; Lyapunova, S.; Onufrievich, A.; Polyakov, V.; Sherstyukova, E. Investigation of Red Blood Cells by Atomic Force Microscopy. Sensor 2022, 22, 2055. [Google Scholar] [CrossRef]
- DeVenuto, F.; Brenneman, G.; Wilson, S.M. Rejuvenation of human red blood cells during liquid storage. Transfusion 1974, 14, 338–344. [Google Scholar] [CrossRef] [PubMed]
- Hutter, J.L.; Bechhoefer, J. Calibration of Atomic-Force Microscope Tips. Rev. Sci. Instrum. 1993, 64, 1868–1873. [Google Scholar] [CrossRef]
- Necas, D.; Klapetek, P. Gwyddion: An open-source software for SPM data analysis. Cent. Eur. J. Phys. 2012, 10, 181–188. [Google Scholar] [CrossRef]
- Dinarelli, S.; Girasole, M.; Longo, G. FC_analysis: A tool for investigating atomic force microscopy maps of force curves. BMC Bioinform. 2018, 19, 258. [Google Scholar] [CrossRef]
- Mendová, K.; Otáhal, M.; Drab, M.; Daniel, M. Size Matters: Rethinking Hertz Model Interpretation for Cell Mechanics Using AFM. Int. J. Mol. Sci. 2024, 25, 7186. [Google Scholar] [CrossRef] [PubMed]
- Sneddon, I.N. The Relation between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Bilodeau, G.G. Regular Pyramid Punch Problem. J. Appl. Mech. 1992, 59, 519–523. [Google Scholar] [CrossRef]
- Kim, K.M.; Lui, L.Y.; Browner, W.S.; Cauley, J.A.; Ensrud, K.E.; Kado, D.M.; Orwoll, E.S.; Schousboe, J.T.; Cummings, S.R. Association Between Variation in Red Cell Size and Multiple Aging-Related Outcomes. J. Gerontol. A Biol. Sci. Med. Sci. 2021, 76, 1288–1294. [Google Scholar] [CrossRef] [PubMed]
- Simpson, L.O. Blood from healthy animals and humans contain nondiscocytic erythrocytes. Br. J. Haematol. 1989, 73, 561–564. [Google Scholar] [CrossRef]
- Calò, A.; Romin, Y.; Srouji, R.; Zambirinis, C.P.; Fan, N.; Santella, A.; Feng, E.; Fujisawa, S.; Turkekul, M.; Huang, S.; et al. Spatial mapping of the collagen distribution in human and mouse tissues by force volume atomic force microscopy. Sci. Rep. 2020, 10, 15664. [Google Scholar] [CrossRef]
- Alsteens, D. Probing living cell dynamics and molecular interactions using atomic force microscopy. Biophys. Rev. 2024, 16, 663–677. [Google Scholar] [CrossRef]
- McKee, C.T.; Last, J.A.; Russell, P.; Murphy, C.J. Indentation versus tensile measurements of Young’s modulus for soft biological tissues. Tissue Eng. Part B Rev. 2011, 17, 155–164. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Stylianou, A.; Chliveros, G.; Malamou, A. Determining Spatial Variability of Elastic Properties for Biological Samples Using AFM. Micromachines 2023, 14, 182. [Google Scholar] [CrossRef]
- Kilpatrick, J.I.; Revenko, I.; Rodriguez, B.J. Nanomechanics of Cells and Biomaterials Studied by Atomic Force Microscopy. Adv. Healthc. Mater. 2015, 4, 2456–2474. [Google Scholar] [CrossRef]
- Lopes, C.S.; Pronto-Laborinho, A.C.; Conceição, V.A.; Freitas, T.; Matias, G.L.; Gromicho, M.; Santos, N.C.; de Carvalho, M.; Carvalho, F.A. Erythrocytes’ surface properties and stiffness predict survival and functional decline in ALS patients. Biofactors 2024, 50, 558–571. [Google Scholar] [CrossRef]
- Gov, N.S.; Safran, S.A. Red Blood Cell Membrane Fluctuations and Shape Controlled by ATP-Induced Cytoskeletal Defects. Biophys. J. 2005, 88, 1859–1874. [Google Scholar] [CrossRef]
- Xu, Z.; Zheng, Y.; Wang, X.; Shehata, N.; Wang, C.; Sun, Y. Stiffness increase of red blood cells during storage. Microsyst. Nanoeng. 2018, 4, 17103. [Google Scholar] [CrossRef]
- Kozlova, E.; Chernysh, A.; Moroz, V.; Sergunova, V.; Gudkova, O.; Manchenko, E. Morphology, membrane nanostructure and stiffness for quality assessment of packed red blood cells. Sci. Rep. 2017, 7, 7846. [Google Scholar] [CrossRef] [PubMed]
- Gov, N.S. Less is more: Removing membrane attachments stiffens the RBC cytoskeleton. New J. Phys. 2007, 9, 429. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, X.; Zhang, C.; Dao, M.; Gong, X. Evolution of surface area and membrane shear modulus of matured human red blood cells during mechanical fatigue. Sci. Rep. 2023, 13, 8563. [Google Scholar] [CrossRef] [PubMed]
- Roduit, C.; Longo, G.; Benmessaoud, I.; Volterra, A.; Saha, B.; Dietler, G.; Kasas, S. Stiffness tomography exploration of living and fixed macrophages. J. Mol. Recognit. 2012, 25, 241–246. [Google Scholar] [CrossRef] [PubMed]
- Prado, G.; Farutin, A.; Misbah, C.; Bureau, L. Viscoelastic transient of confined red blood cells. Biophys. J. 2015, 108, 2126–2136. [Google Scholar] [CrossRef]
- Klarl, B.A.; Lang, P.A.; Kempe, D.S.; Niemoeller, O.M.; Akel, A.; Sobiesiak, M.; Eisele, K.; Podolski, M.; Huber, S.M.; Wieder, T.; et al. Protein kinase C mediates erythrocyte “programmed cell death” following glucose depletion. Am. J. Physiol. Cell Physiol. 2006, 290, C244–C253. [Google Scholar] [CrossRef]
- Castagnola, M.; Messana, I.; Sanna, M.T.; Giardina, B. Oxygen-linked modulation of erythrocyte metabolism: State of the art. Blood Transfus. 2010, 8 (Suppl. 3), s53–s58. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Longo, G.; Dinarelli, S.; Collacchi, F.; Girasole, M. Comparing Nanomechanical Properties and Membrane Roughness Along the Aging of Human Erythrocytes. Methods Protoc. 2025, 8, 86. https://doi.org/10.3390/mps8040086
Longo G, Dinarelli S, Collacchi F, Girasole M. Comparing Nanomechanical Properties and Membrane Roughness Along the Aging of Human Erythrocytes. Methods and Protocols. 2025; 8(4):86. https://doi.org/10.3390/mps8040086
Chicago/Turabian StyleLongo, Giovanni, Simone Dinarelli, Federica Collacchi, and Marco Girasole. 2025. "Comparing Nanomechanical Properties and Membrane Roughness Along the Aging of Human Erythrocytes" Methods and Protocols 8, no. 4: 86. https://doi.org/10.3390/mps8040086
APA StyleLongo, G., Dinarelli, S., Collacchi, F., & Girasole, M. (2025). Comparing Nanomechanical Properties and Membrane Roughness Along the Aging of Human Erythrocytes. Methods and Protocols, 8(4), 86. https://doi.org/10.3390/mps8040086





