Comparing Models of Lateral Station-Keeping for Pitching Hydrofoils
Abstract
1. Introduction
2. Materials and Methods
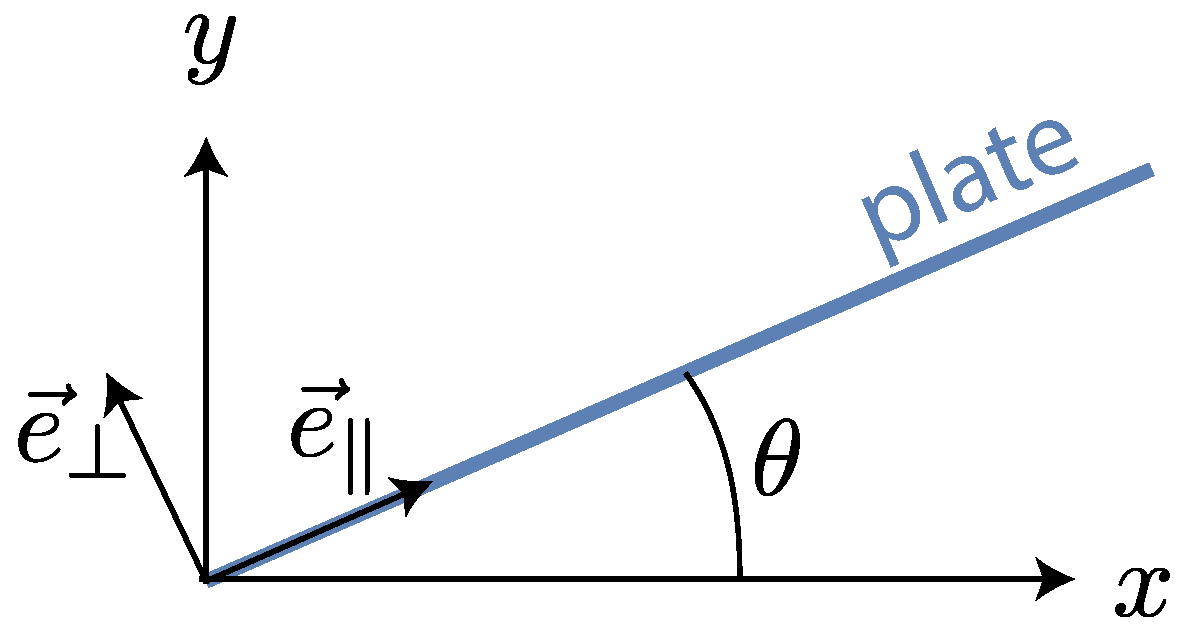
2.1. Water Channel Setup
2.1.1. Tethered Hydrofoil Tests
2.1.2. Maneuvering Experiments
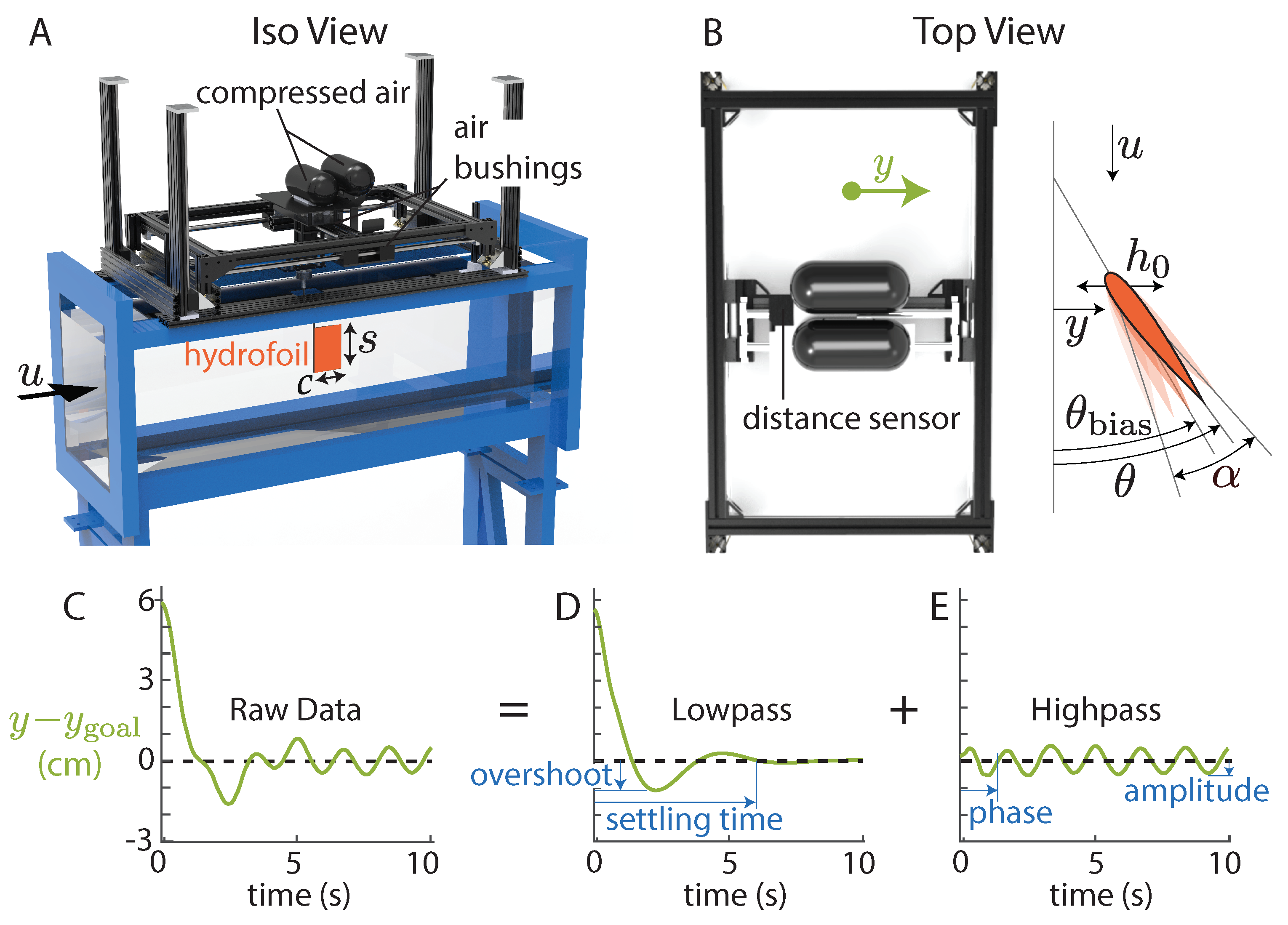
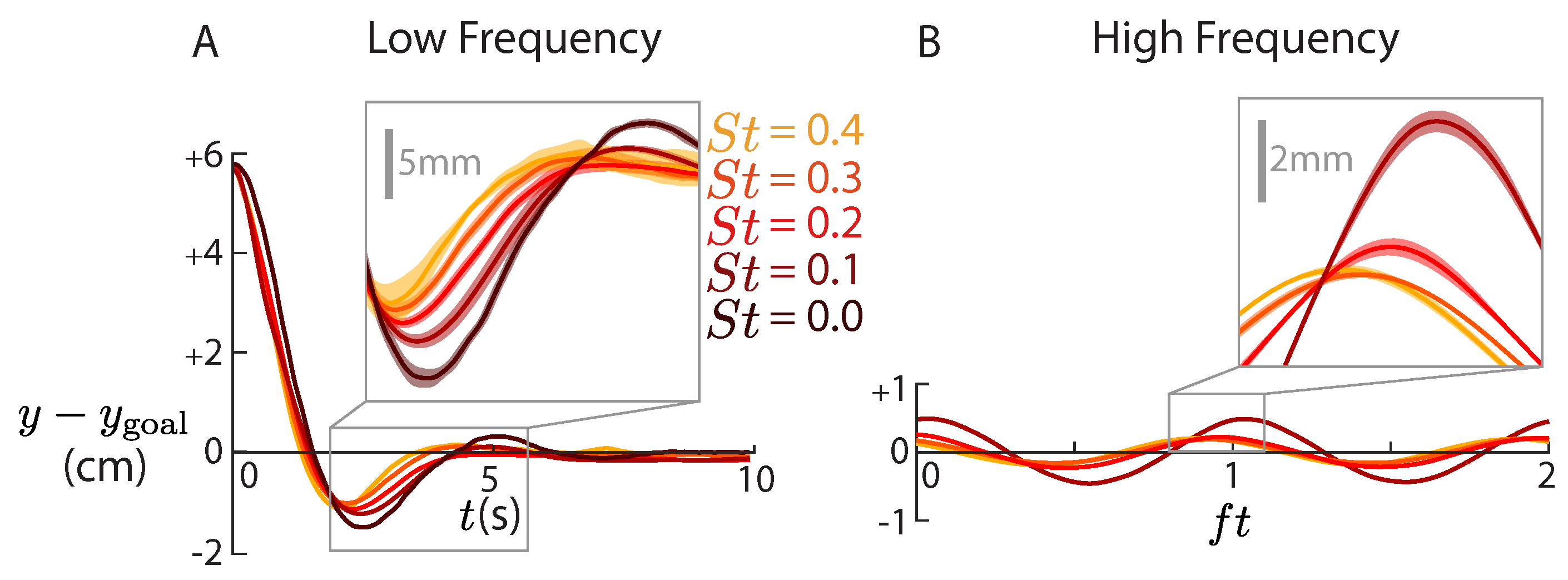
3. Water Channel Results
4. Theoretical Modelling
4.1. Theodorsen Model
4.2. Theodorsen with Finite Aspect Ratio Corrections
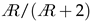 , where
, where 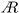 is the aspect ratio (). For the added mass forces, Ref. [26] found that the added mass of a finite rectangular plate scales approximately with
is the aspect ratio (). For the added mass forces, Ref. [26] found that the added mass of a finite rectangular plate scales approximately with 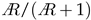 . Following [18], we used these two corrections to modify the constants in Equation (6):
. Following [18], we used these two corrections to modify the constants in Equation (6): 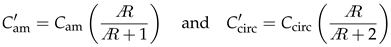
4.3. Theodorsen with Vectored Garrick
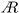 corrections and even if the small angle assumption of Theodorsen is relaxed by using non-linear added mass forces (see Appendix A). The resulting lift () is the same lift predicted by thin airfoil theory [27], meaning that Theodorsen predicts no contribution to the time-averaged lift force from the pitch oscillations. In contrast, our experiments show lift force increases with both pitch bias and pitching frequency (Figure 2A).
corrections and even if the small angle assumption of Theodorsen is relaxed by using non-linear added mass forces (see Appendix A). The resulting lift () is the same lift predicted by thin airfoil theory [27], meaning that Theodorsen predicts no contribution to the time-averaged lift force from the pitch oscillations. In contrast, our experiments show lift force increases with both pitch bias and pitching frequency (Figure 2A).4.4. Semiempirical Model
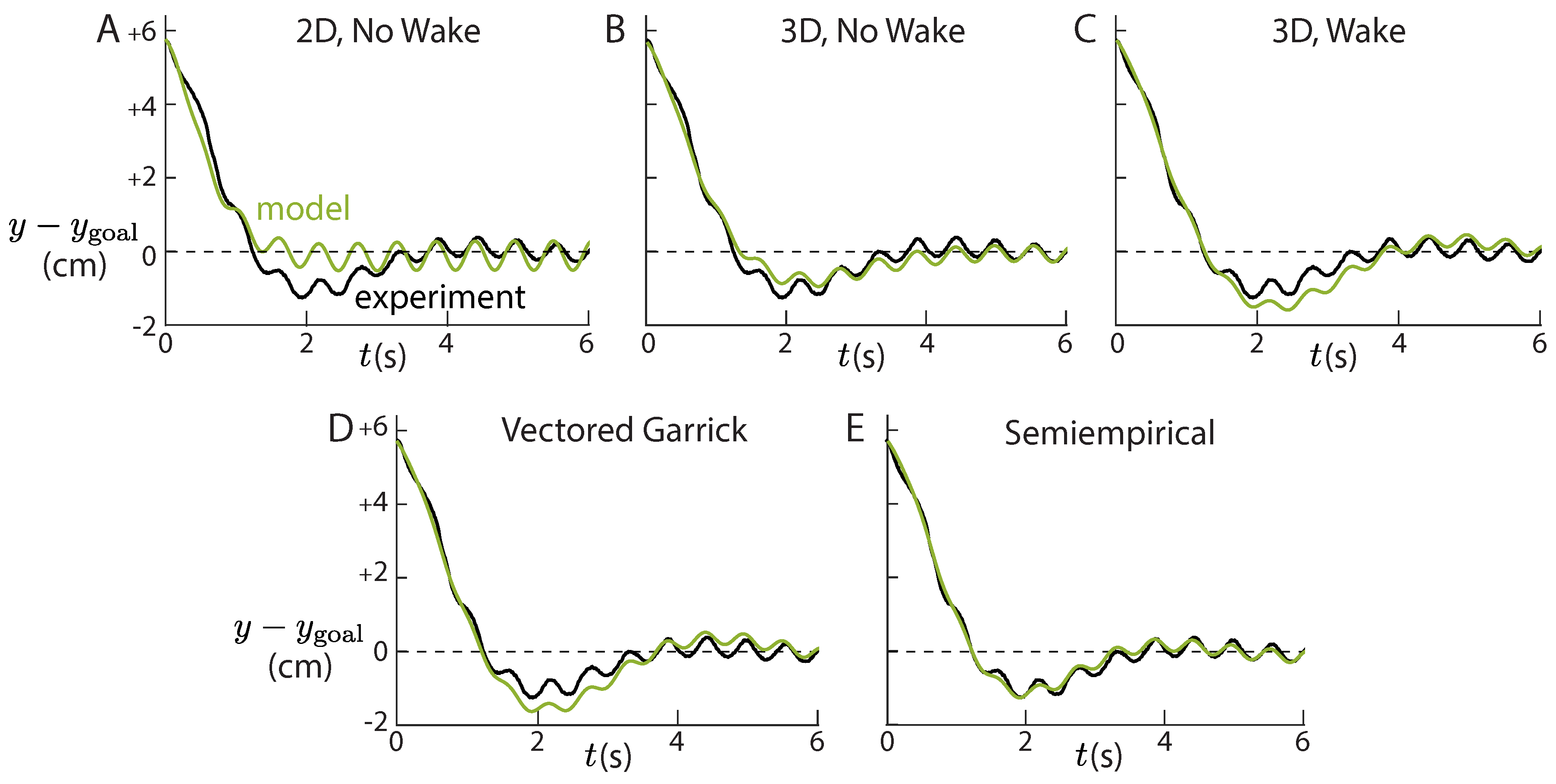
4.5. Testing the Theoretical Models
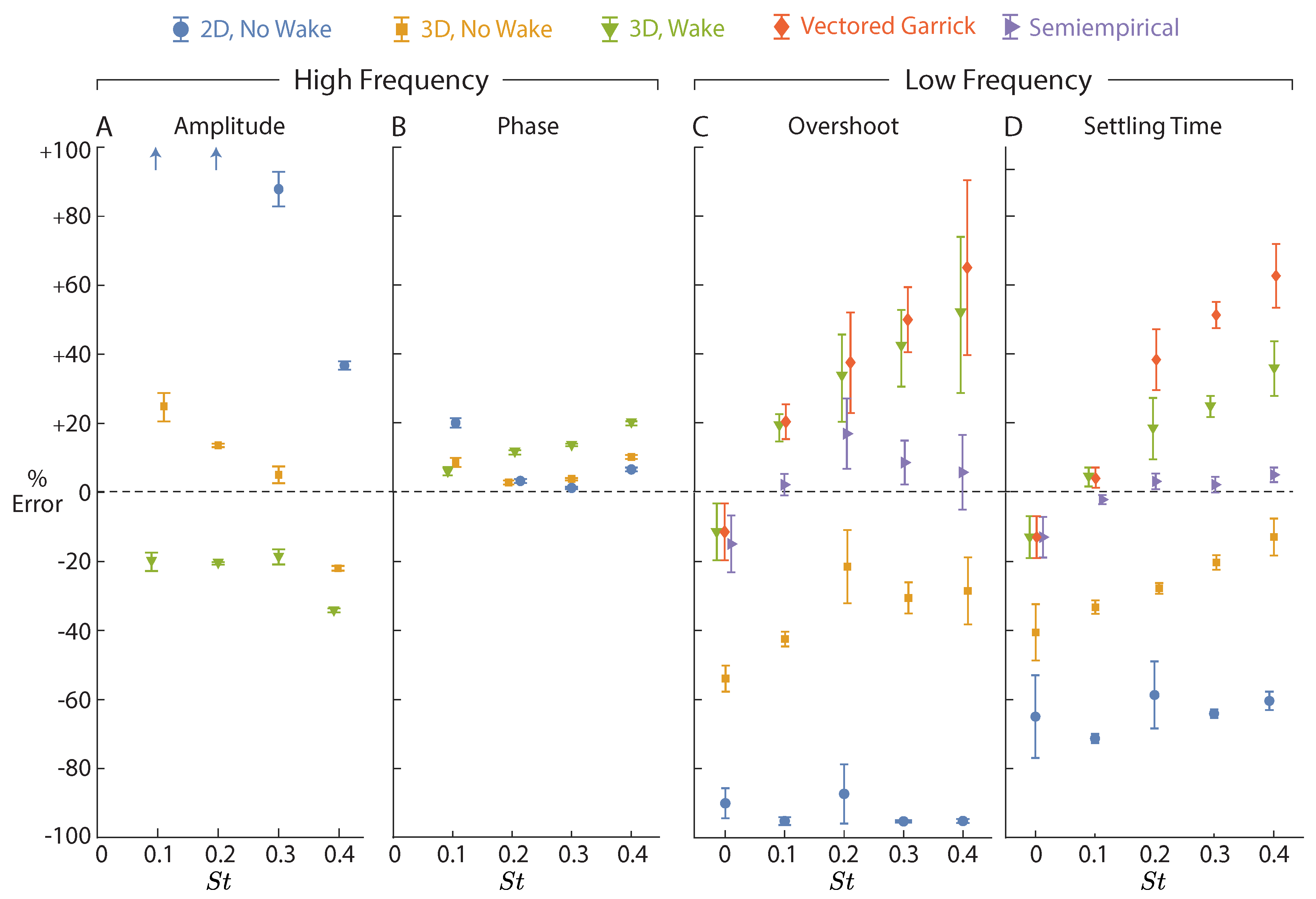
4.5.1. High Frequency Predictions
4.5.2. Low Frequency Predictions
4.5.3. Summary of Model Testing
- 2D Theodorsen No Wake
- High frequency solution is from Equation (24) with and , and 2D coefficients and are used.
- 3D Theodorsen No Wake
- High frequency solution is the same as 2D Theodorsen No Wake, except the 3D coefficients and are used.
- Low frequency solution is the same as 2D Theodorsen No Wake, except the 3D coefficients and are used.
- 3D Theodorsen Wake
- High frequency solution is from Equation (24), where the 3D coefficients and are used.
- Vectored Garrick
- High frequency solution is the same as 3D Theodorsen Wake.
- Low frequency solution is from Equation (21) using the same as the 3D Theodorsen Wake model.
- Semiempirical
- High frequency solution is the same as 3D Theodorsen Wake.
- Low frequency solution from Equation (23) using the same as the 3D Theodorsen Wake model.
5. Model Testing and Discussion
5.1. High Frequency Model Predictions
5.2. Low Frequency Model Predictions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Weihs, D. Hydromechanics of fish schooling. Nature 1973, 241, 290. [Google Scholar] [CrossRef]
- Pavlov, D.; Kasumyan, A. Patterns and mechanisms of schooling behavior in fish: A review. J. Ichthyol. 2000, 40, S163. [Google Scholar]
- Liao, J.C. A review of fish swimming mechanics and behaviour in altered flows. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 1973–1993. [Google Scholar] [CrossRef] [PubMed]
- Partridge, B.; Pitcher, T. Evidence against a hydrodynamic function for fish schools. Nature 1979, 279, 418. [Google Scholar] [CrossRef] [PubMed]
- Blake, R.W. The energetics of hovering in the mandarin fish (Synchropus picturatus). J. Exp. Biol. 1979, 82, 25–33. [Google Scholar]
- Webb, P.W. The effect of solid and porous channel walls on steady swimming of steelhead trout Oncorhynchus mykiss. J. Exp. Biol. 1993, 178, 97–108. [Google Scholar]
- Quinn, D.B.; Moored, K.W.; Dewey, P.A.; Smits, A.J. Unsteady propulsion near a solid boundary. J. Fluid Mech. 2014, 742, 152–170. [Google Scholar] [CrossRef]
- Weihs, D. Stability versus maneuverability in aquatic locomotion. Integr. Comp. Biol. 2002, 42, 127–134. [Google Scholar] [CrossRef]
- Moyle, P.B.; Cech, J.J. Fishes: An Introduction to Ichthyology; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Bandyopadhyay, P.R. Maneuvering hydrodynamics of fish and small underwater vehicles. Integr. Comp. Biol. 2002, 42, 102–117. [Google Scholar] [CrossRef]
- Webb, P.W. Control of posture, depth, and swimming trajectories of fishes. Integr. Comp. Biol. 2002, 42, 94–101. [Google Scholar] [CrossRef]
- Anderson, J.M.; Chhabra, N.K. Maneuvering and stability performance of a robotic tuna. Integr. Comp. Biol. 2002, 42, 118–126. [Google Scholar] [CrossRef] [PubMed]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter; Technical Report; National Advisory Committee for Aeronautics, Langley Aeronautical Lab: Langley Field, VA, USA, 1935. [Google Scholar]
- Garrick, I.E. Propulsion of a Flapping and Oscillating Airfoil; Technical Report; National Advisory Committee for Aeronautics, Langley Aeronautical Lab: Langley Field, VA, USA, 1936. [Google Scholar]
- Read, D.A.; Hover, F.S.; Triantafyllou, M.S. Forces on oscillating foils for propulsion and maneuvering. J. Fluids Struct. 2003, 17, 163–183. [Google Scholar] [CrossRef]
- Licht, S.; Polidoro, V.; Flores, M.; Hover, F.S.; Triantafyllou, M.S. Design and projected performance of a flapping foil AUV. IEEE J. Ocean. Eng. 2004, 29, 786–794. [Google Scholar] [CrossRef]
- Wu, Z.; Yu, J.; Tan, M.; Zhang, J. Kinematic Comparison of Forward and Backward Swimming and Maneuvering in a Self-Propelled Sub-Carangiform Robotic Fish. J. Bion. Eng. 2014, 11, 199–212. [Google Scholar] [CrossRef]
- Ayancik, F.; Zhong, Q.; Quinn, D.B.; Brandes, A.; Bart-Smith, H.; Moored, K.W. Scaling laws for the propulsive performance of three-dimensional pitching propulsors. J. Fluid Mech. 2019, 871, 1117–1138. [Google Scholar] [CrossRef]
- Moored, K.W.; Quinn, D.B. Inviscid Scaling Laws of a Self-Propelled Pitching Airfoil. AIAA J. 2018, 1–15. [Google Scholar] [CrossRef]
- Young, J.; Morris, S.; Schutt, R.; Williamson, C. Effect of hybrid-heave motions on the propulsive performance of an oscillating airfoil. J. Fluids Struct. 2019. [Google Scholar] [CrossRef]
- Collette, B.B.; Nauen, C.E. Scombrids of the World: An Annotated and Illustrated Catalogue of Tunas, Mackerels, Bonitos and Related Species Known to Date; FAO: Rome, Italy, 1983; ISBN -Nr. 92-5-101381-0. [Google Scholar]
- Estess, E.; Klinger, D.; Coffey, D.; Gleiss, A.; Rowbotham, I.; Seitz, A.C.; Rodriguez, L.; Norton, A.; Block, B.; Farwell, C. Bioenergetics of captive yellowfin tuna (Thunnus albacares). Aquaculture 2017, 468. [Google Scholar] [CrossRef]
- Niu, R.; Palberg, T. Modular approach to microswimming. Soft Matter 2018, 14, 7554–7568. [Google Scholar] [CrossRef]
- Wu, T.Y. Fish swimming and bird/insect flight. Ann. Rev. Fluid Mech. 2011, 43, 25–58. [Google Scholar] [CrossRef]
- Green, M.A.; Rowley, C.W.; Smits, A.J. The unsteady three-dimensional wake produced by a trapezoidal pitching panel. J. Fluid Mech. 2011, 685, 117–145. [Google Scholar] [CrossRef]
- Brennen, C.E. A Review of Added Mass and Fluid Inertial Forces; Naval Civil Engineering Laboratory: Port Hueneme, CA, USA, 1982. [Google Scholar]
- Prandtl, L. Essentials of Fluid Dynamics: With Applications to Hydraulics, Aeronautics, Meteorology and Other Subjets; Blackie and Son: London, UK, 1953. [Google Scholar]
- Smits, A.J. Undulatory and oscillatory swimming. J. Fluid Mech. 2019, 874 P1. [Google Scholar] [CrossRef]
- Brunton, S.L.; Rowley, C.W. Empirical state-space representations for Theodorsen’s lift model. J. Fluids Struct. 2013, 38, 174–186. [Google Scholar] [CrossRef]
- De Breuker, R.; Abdalla, M.; Milanese, A.; Marzocca, P. Optimal Control of Aeroelastic Systems Using Synthetic Jet Actuators; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008. [Google Scholar]
- Buchholz, J.H.; Smits, A.J. On the evolution of the wake structure produced by a low-aspect-ratio pitching panel. J. Fluid Mech. 2006, 546, 433–443. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.; Streitlien, K.; Barrett, D.; Triantafyllou, M. Oscillating foils of high propulsive efficiency. J. Fluid Mech. 1998, 360, 41–72. [Google Scholar] [CrossRef]
- Quinn, D.B.; Lauder, G.V.; Smits, A.J. Maximizing the efficiency of a flexible propulsor using experimental optimization. J. Fluid Mech. 2015, 767, 430–448. [Google Scholar] [CrossRef]
- Akhtar, I.; Mittal, R.; Lauder, G.V.; Drucker, E. Hydrodynamics of a biologically inspired tandem flapping foil configuration. Theor. Comput. Fluid Dyn. 2007, 21, 155–170. [Google Scholar] [CrossRef]
- Boschitsch, B.M.; Dewey, P.A.; Smits, A.J. Propulsive performance of unsteady tandem hydrofoils in an in-line configuration. Phys. Fluids 2014, 26, 051901. [Google Scholar] [CrossRef]
- Dewey, P.A.; Quinn, D.B.; Boschitsch, B.M.; Smits, A.J. Propulsive performance of unsteady tandem hydrofoils in a side-by-side configuration. Phys. Fluids 2014, 26, 041903. [Google Scholar] [CrossRef]
- Webb, P.W.; Weihs, D. Stability versus maneuvering: challenges for stability during swimming by fishes. Integr. Comp. Biol. 2015, 55, 753–764. [Google Scholar] [CrossRef]
- Sedov, L. Two-Dimensional Problems in Hydrodynamics and Aerodynamics; Interscience Publishers: New York, NY, USA, 1965. [Google Scholar]
| a | Tip-to-tip pitching amplitude | F | Real part of the Theodorsen function |
|---|---|---|---|
| Variables for the State-space Theodorsen | Force perpendicular to incoming flow | ||
| Notation for placeholders | Force parallel to incoming flow | ||
 | Aspect ratio of the hydrofoil | Lateral force | |
| c | Chord length of the hydrofoil | G | Imaginary part of the Theodorsen function |
| Theodorsen lift deficiency function | Heaving amplitude of the hydrofoil | ||
| Added mass coefficient | Bessel functions of the first and second kind | ||
Finite 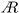 added mass coefficient added mass coefficient | k | Reduced frequency of the pitching motion | |
| Circulatory force coefficient | Proportional controller gain | ||
Finite 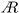 circulatory force coefficient circulatory force coefficient | m | Mass of the airfoil and attached rig | |
| Lift coefficient | s | Span of the airfoil | |
| Added mass component of Theodorsen lift | Strouhal number of the pitching motion | ||
| Circulatory component of Theodorsen lift | u | Incoming flow speed | |
| Empirical lift coefficient | State-space Theodorsen wake downwash | ||
| Theodorsen model lift coefficient | y | Lateral position of the airfoil | |
| Thrust coefficient | Complex heaving motion for Theodorsen | ||
| Empirical thrust coefficient | Angular amplitude of flapping motion | ||
| Garrick model thrust coefficient | Hydrofoil angle relative to water channel | ||
| Lateral force coefficient | Complex pitching motion for Theodorsen | ||
| Empirical lateral force coefficient | Pitch bias relative to incoming flow | ||
| Garrick model lateral force coefficient | Hydrofoil pitch bias | ||
| Semiempirical lateral force coefficient | Density of water | ||
| Theodorsen model lateral force coefficient | Phase of the heaving relative to pitching | ||
| f | Flapping frequency (Hz) | Dimensionless leading edge vorticity |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunnarson, P.; Zhong, Q.; Quinn, D.B. Comparing Models of Lateral Station-Keeping for Pitching Hydrofoils. Biomimetics 2019, 4, 51. https://doi.org/10.3390/biomimetics4030051
Gunnarson P, Zhong Q, Quinn DB. Comparing Models of Lateral Station-Keeping for Pitching Hydrofoils. Biomimetics. 2019; 4(3):51. https://doi.org/10.3390/biomimetics4030051
Chicago/Turabian StyleGunnarson, Peter, Qiang Zhong, and Daniel B. Quinn. 2019. "Comparing Models of Lateral Station-Keeping for Pitching Hydrofoils" Biomimetics 4, no. 3: 51. https://doi.org/10.3390/biomimetics4030051
APA StyleGunnarson, P., Zhong, Q., & Quinn, D. B. (2019). Comparing Models of Lateral Station-Keeping for Pitching Hydrofoils. Biomimetics, 4(3), 51. https://doi.org/10.3390/biomimetics4030051





