Design of a Humanoid Upper-Body Robot and Trajectory Tracking Control via ZNN with a Matrix Derivative Observer
Abstract
1. Introduction
- A 22-DOF humanoid upper-body robotic system is presented, consisting of a pair of 8-DOF arms, a 3-DOF torso, and a 3-DOF head. The design is inspired by human biomechanics. Workspace analysis demonstrates that the proposed system exhibits superior kinematic performance.
- A cost-effective, interference-resistant hollow joint module based on resolver feedback is developed. Compared with traditional encoder-based solutions, this design offers improved electromagnetic immunity and modular scalability, making it well-suited for highly redundant robotic systems.
- To overcome the reliance on unavailable Jacobian derivatives in the existing ZNN literature, an integration-enhanced matrix derivative observer (IEMDO) is proposed. The observer ensures asymptotic convergence and significantly enhances numerical stability and real-time feasibility of ZNN-based inverse kinematics solutions.
- The proposed IEMDO is embedded into the ZNN control framework and implemented on the developed humanoid platform. Both simulation and physical experiments validate the effectiveness, robustness, and practical feasibility of the proposed system and algorithm.
2. Mechanical and Electrical System Design
2.1. Overview of Upper-Body Mechanical Subsystems
2.1.1. Redundant Dual-Arm Mechanism
2.1.2. Three-DOF Torso Design
2.1.3. Vision-Driven Head Assembly
2.1.4. Resolver-Based Hollow Joint Modules
2.2. Electrical Design
2.3. System Integration and Kinematic Parameter Setup
3. Trajectory Tracking via ZNN with Jacobian Derivative Observer
3.1. Problem Formulation and ZNN Framework
3.2. Matrix Derivative Observer Design
3.3. Theoretical Analysis
4. Simulation
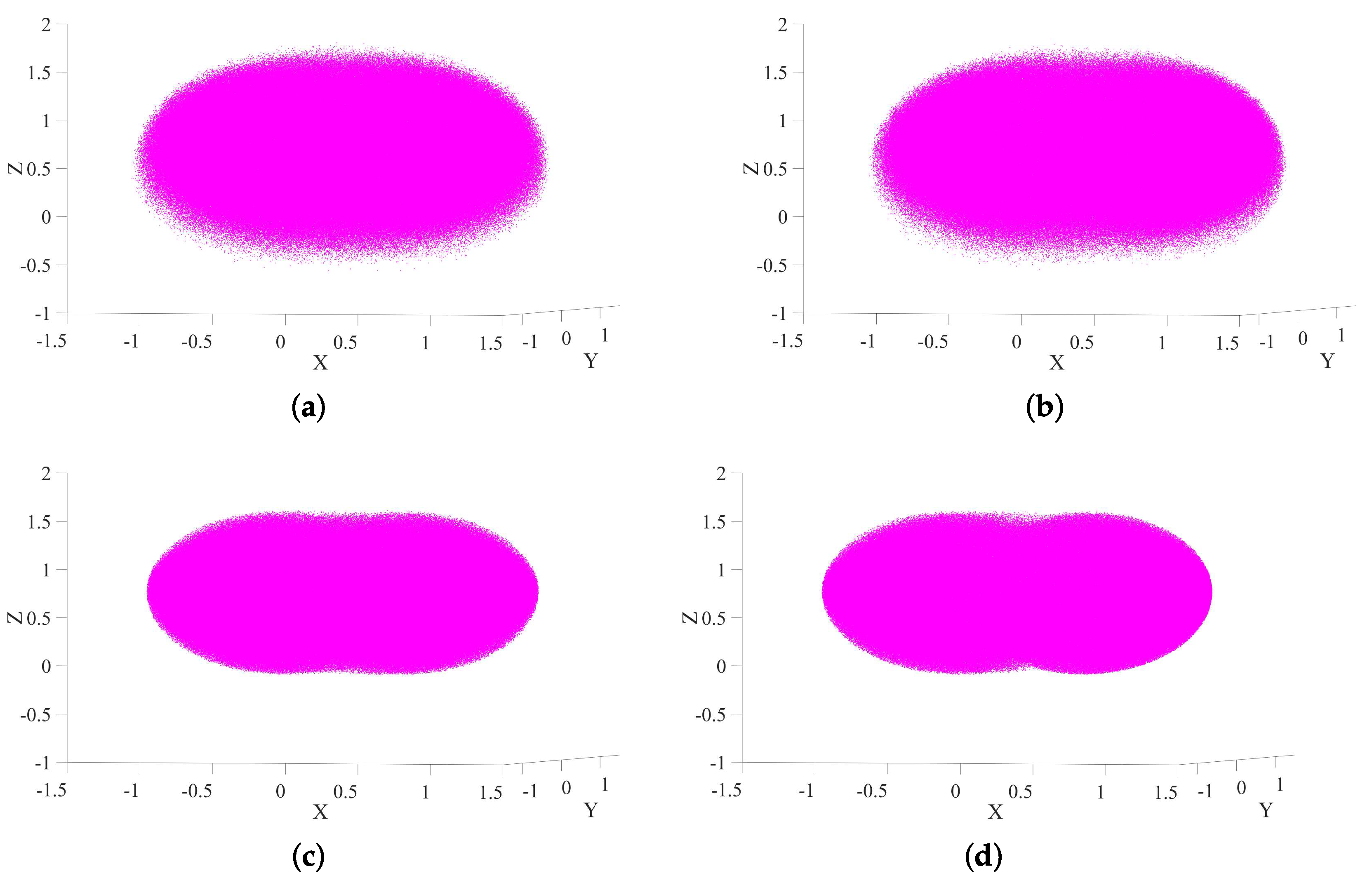
4.1. Kinematic Workspace Evaluation and Comparative Analysis
- Configuration 1 (Proposed Design): The complete 22-DOF model, featuring a 3-DOF torso and dual 8-DOF arms.
- Configuration 3 (8-DOF Arms, Fixed Torso): A 19-DOF model without torso joints, isolating the contribution of the 8-DOF arm design.
- Configuration 4 (Baseline: 7-DOF Arms, Fixed Torso): A 17-DOF model without both torso and additional shoulder joints, representing a baseline configuration common to many classic humanoids like ASIMO or early-generation platforms.
4.2. Validation and Comparative Analysis of the Matrix Derivative Observer
4.3. Trajectory Tracking Control of the Humanoid Upper-Body Robot
5. Experiment on Designed Humanoid Upper-Body Robot
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, F.; Demiris, Y. Learning garment manipulation policies toward robot-assisted dressing. Sci. Robot. 2022, 7, eabm6010. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.L.; Kemp, C.C. A direct physical interface for navigation and positioning of a robotic nursing assistant. Adv. Robot. 2011, 25, 605–627. [Google Scholar] [CrossRef]
- Smith, C.; Karayiannidis, Y.; Nalpantidis, L.; Gratal, X.; Qi, P.; Dimarogonas, D.V.; Kragic, D. Dual arm manipulation—A survey. Robot. Auton. Syst. 2012, 60, 1340–1353. [Google Scholar] [CrossRef]
- Kostavelis, I.; Gasteratos, A. Robots in crisis management: A survey. In Proceedings of the International Conference on Information Systems for Crisis Response and Management in Mediterranean Countries; Springer: Cham, Switzerland, 2017; pp. 43–56. [Google Scholar]
- Diftler, M.; Mehling, J.; Abdallah, M.; Radford, N.; Bridgwater, L.; Sanders, A.; Askew, R.; Linn, D.; Yamokoski, J.; Permenter, F.; et al. Robonaut 2—The first humanoid robot in space. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2178–2183. [Google Scholar] [CrossRef]
- Borst, C.; Wimbock, T.; Schmidt, F.; Fuchs, M.; Brunner, B.; Zacharias, F.; Giordano, P.R.; Konietschke, R.; Sepp, W.; Fuchs, S.; et al. Rollin’ Justin—Mobile platform with variable base. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 1597–1598. [Google Scholar] [CrossRef]
- Jung, T.; Lim, J.; Bae, H.; Lee, K.K.; Joe, H.M.; Oh, J.H. Development of the Humanoid Disaster Response Platform DRC-HUBO+. IEEE Trans. Robot. 2018, 34, 1–17. [Google Scholar] [CrossRef]
- Asfour, T.; Waechter, M.; Kaul, L.; Rader, S.; Weiner, P.; Ottenhaus, S.; Grimm, R.; Zhou, Y.; Grotz, M.; Paus, F. ARMAR-6: A High-Performance Humanoid for Human-Robot Collaboration in Real-World Scenarios. IEEE Robot. Autom. Mag. 2019, 26, 108–121. [Google Scholar] [CrossRef]
- Kaneko, K.; Kaminaga, H.; Sakaguchi, T.; Kajita, S.; Morisawa, M.; Kumagai, I.; Kanehiro, F. Humanoid Robot HRP-5P: An Electrically Actuated Humanoid Robot with High-Power and Wide-Range Joints. IEEE Robot. Autom. Lett. 2019, 4, 1431–1438. [Google Scholar] [CrossRef]
- Yousefi-Koma, A.; Maleki, B.; Maleki, H.; Amani, A.; Bazrafshani, M.A.; Keshavarz, H.; Iranmanesh, A.; Yazdanpanah, A.; Alai, H.; Salehi, S.; et al. SURENAIV: Towards A Cost-effective Full-size Humanoid Robot for Real-world Scenarios. In Proceedings of the 2020 IEEE-RAS 20th International Conference on Humanoid Robots (Humanoids), Munich, Germany, 19–21 July 2021; pp. 142–148. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; Yu, Z.; Dong, Y.; Zhang, R.; Huang, Q. Intuitive and Versatile Full-body Teleoperation of A Humanoid Robot. In Proceedings of the 2021 IEEE International Conference on Advanced Robotics and Its Social Impacts (ARSO), Tokoname, Japan, 8–10 July 2021; pp. 176–181. [Google Scholar] [CrossRef]
- Sim, J.; Kim, S.; Park, S.; Kim, S.; Kim, M.; Park, J. Design of JET Humanoid Robot with Compliant Modular Actuators for Industrial and Service Applications. Appl. Sci. 2021, 11, 6152. [Google Scholar] [CrossRef]
- Schwartz, M.; Sim, J.; Ahn, J.; Hwang, S.; Lee, Y.; Park, J. Design of the Humanoid Robot TOCABI. In Proceedings of the 2022 IEEE-RAS 21st International Conference on Humanoid Robots (Humanoids), Ginowan, Japan, 28–30 November 2022; pp. 322–329. [Google Scholar] [CrossRef]
- Sun, Z.; Yang, H.; Ma, Y.; Wang, X.; Mo, Y.; Li, H.; Jiang, Z. BIT-DMR: A Humanoid Dual-Arm Mobile Robot for Complex Rescue Operations. IEEE Robot. Autom. Lett. 2022, 7, 802–809. [Google Scholar] [CrossRef]
- Jiang, Z.; Ma, Y.; Cao, X.; Shen, M.; Yin, C.; Liu, H.; Cui, J.; Sun, Z.; Huang, X.; Li, H. FC-EODR: Immersive Humanoid Dual-Arm Dexterous Explosive Ordnance Disposal Robot. Biomimetics 2023, 8, 67. [Google Scholar] [CrossRef]
- Dafarra, S.; Pattacini, U.; Romualdi, G.; Rapetti, L.; Grieco, R.; Darvish, K.; Milani, G.; Valli, E.; Sorrentino, I.; Viceconte, P.M.; et al. iCub3 avatar system: Enabling remote fully immersive embodiment of humanoid robots. Sci. Robot. 2024, 9, eadh3834. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, S. Design and analysis of a general recurrent neural network model for time-varying matrix inversion. IEEE Trans. Neural Netw. 2005, 16, 1477–1490. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Y.; Tan, N.; Cai, B. Zhang neural network solving for time-varying full-rank matrix Moore–Penrose inverse. Computing 2011, 92, 97–121. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, T.; Wang, M.; Zheng, L. An Exponential-Type Anti-Noise Varying-Gain Network for Solving Disturbed Time-Varying Inversion Systems. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3414–3427. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Zhu, J.; Zhao, L.; Chen, L.; Chen, L.; Gong, J. A Robust Predefined-Time Convergence Zeroing Neural Network for Dynamic Matrix Inversion. IEEE Trans. Cybern. 2023, 53, 3887–3900. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Li, L.; Huang, W.; Li, X.; Jia, L. A New Predefined Time Zeroing Neural Network with Drop Conservatism for Matrix Flows Inversion and Its Application. IEEE Trans. Cybern. 2024, 54, 752–761. [Google Scholar] [CrossRef]
- Hu, Z.; Xiao, L.; Li, K.; Li, K.; Li, J. Performance analysis of nonlinear activated zeroing neural networks for time-varying matrix pseudoinversion with application. Appl. Soft Comput. 2021, 98, 106735. [Google Scholar] [CrossRef]
- Zhang, B.; Zheng, Y.; Li, S.; Chen, X.; Mao, Y. Fixed-time convergence ZNN model for solving rectangular dynamic full-rank matrices inversion. Expert Syst. Appl. 2024, 251, 123992. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, Y.; Li, S. Integration-Enhanced Zhang Neural Network for Real-Time-Varying Matrix Inversion in the Presence of Various Kinds of Noises. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 2615–2627. [Google Scholar] [CrossRef]
- Sun, Z.; Li, F.; Jin, L.; Shi, T.; Liu, K. Noise-tolerant neural algorithm for online solving time-varying full-rank matrix Moore–Penrose inverse problems: A control-theoretic approach. Neurocomputing 2020, 413, 158–172. [Google Scholar] [CrossRef]
- Tan, Z.; Xiao, L.; Chen, S.; Lv, X. Noise-Tolerant and Finite-Time Convergent ZNN Models for Dynamic Matrix Moore–Penrose Inversion. IEEE Trans. Ind. Inform. 2020, 16, 1591–1601. [Google Scholar] [CrossRef]
- Tan, Z.; Li, W.; Xiao, L.; Hu, Y. New Varying-Parameter ZNN Models with Finite-Time Convergence and Noise Suppression for Time-Varying Matrix Moore–Penrose Inversion. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2980–2992. [Google Scholar] [CrossRef]
- Xu, F.; Li, Z.; Nie, Z.; Shao, H.; Guo, D. New Recurrent Neural Network for Online Solution of Time-Dependent Underdetermined Linear System with Bound Constraint. IEEE Trans. Ind. Inform. 2019, 15, 2167–2176. [Google Scholar] [CrossRef]
- Xu, F.; Li, Z.; Nie, Z.; Shao, H.; Guo, D. Zeroing Neural Network for Solving Time-Varying Linear Equation and Inequality Systems. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2346–2357. [Google Scholar] [CrossRef] [PubMed]
- Li, W. Predefined-Time Convergent Neural Solution to Cyclical Motion Planning of Redundant Robots Under Physical Constraints. IEEE Trans. Ind. Electron. 2020, 67, 10732–10743. [Google Scholar] [CrossRef]
- Wu, W.; Zheng, B. Two New Zhang Neural Networks for Solving Time-Varying Linear Equations and Inequalities Systems. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 4957–4965. [Google Scholar] [CrossRef] [PubMed]
- Jin, L.; Du, W.; Ma, D.; Jiao, L.; Li, S. Pseudoinverse-Free Recurrent Neural Dynamics for Time-Dependent System of Linear Equations with Constraints on Variable and Its Derivatives. IEEE Trans. Syst. Man, Cybern. Syst. 2024, 54, 4966–4975. [Google Scholar] [CrossRef]
- Yin, H.; Jin, H.; Ju, F.; Ge, M.; Zhao, J. Motion Planning of Humanoid Upper-Body Robot Using an Integration-Enhanced Differentiator-Based Method: A Time-Varying Linear Equations Approach. IEEE Trans. Ind. Inform. 2024, 20, 7391–7403. [Google Scholar] [CrossRef]
- Bagheri, M.; Ajoudani, A.; Lee, J.; Caldwell, D.G.; Tsagarakis, N.G. Kinematic analysis and design considerations for optimal base frame arrangement of humanoid shoulders. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2710–2715. [Google Scholar] [CrossRef]
- Cao, B.; Sun, K.; Gu, Y.; Jin, M.; Liu, H. Humanoid Robot Torso Motion Planning Based on Manipulator Pose Dexterity Index. IOP Conf. Ser. Mater. Sci. Eng. 2020, 853, 012040. [Google Scholar] [CrossRef]
- Yin, H.; Jin, H.; Ju, F.; Liu, J.; Zhao, M.; Zhao, J. Kinematic Control of Humanoid Upper Body Robot Using Virtual Flexible Joint Dynamics Primitive and Quasi-Sliding Mode Observer. IEEE Trans. Ind. Electron. 2025, 1–14. [Google Scholar] [CrossRef]
- Ju, F.; Jin, H.; Zhao, J. A Kinematic Decoupling Whole-body Control Method for a Mobile Humanoid Upper Body Robot. In Proceedings of the 2023 International Conference on Frontiers of Robotics and Software Engineering (FRSE), Changsha, China, 16–18 June 2023; pp. 85–90. [Google Scholar] [CrossRef]





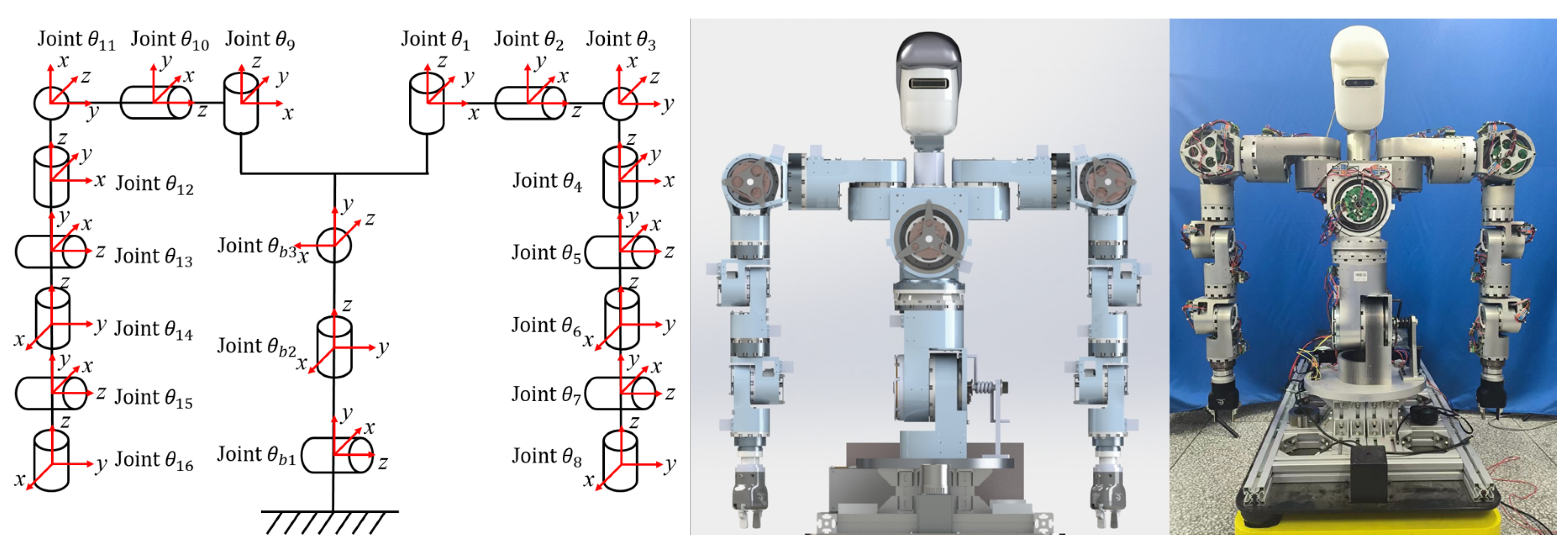







| Robot | Head DOFs | Torso DOFs | Arm DOFs |
|---|---|---|---|
| Robonaut2 [5] | 3 | 1 | 7 |
| Justin [6] | 2 | 3 | 7 |
| HUBO [7] | 1 | 1 | 8 |
| ARMAR 6 [8] | 2 | 1 | 8 |
| HRP-5P [9] | 2 | 3 | 9 |
| SURENA IV [10] | 3 | 2 | 7 |
| BHR-6 [11] | 2 | 3 | 4 |
| JET [12] | 2 | 2 | 7 |
| TOCABI [13] | 2 | 1 | 7 |
| BIT-DMR [14] | 2 | 0 | 7 |
| FC-EODR [15] | 2 | 1 | 7 |
| iCub 3 [16] | 3 | 3 | 7 |
| Joint | Offset of | Range (°) | |||
|---|---|---|---|---|---|
| 180 | 90 | −0.0155 | 0 | ||
| −90 | 90 | 0.377 | 0 | ||
| 180 | 90 | 0.0345 | |||
| 90 | 90 | 0.1445 | 0 | ||
| 90 | 90 | 0 | |||
| 90 | 90 | 0 | 0 | ||
| 90 | 90 | −0.2662 | 0 | ||
| 90 | 90 | 0 | 0 | ||
| 90 | 90 | −0.2482 | 0 | ||
| 180 | 90 | 0 | 0 | ||
| 0 | 0 | −0.345 | 0 |
| Configuration | DOFs | Total | Common | PTCWA |
|---|---|---|---|---|
| 1 | 22 DOF | 10.754 | 5.3398 | 57.4242 |
| 2 | 20 DOF | 10.6714 | 3.6937 | 39.4169 |
| 3 | 19 DOF | 6.2286 | 2.3854 | 14.8577 |
| 4 | 17 DOF | 5.7297 | 1.1403 | 6.5335 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, H.; Jin, H.; Peng, Y.; Wang, Z.; Liu, J.; Ju, F.; Zhao, J. Design of a Humanoid Upper-Body Robot and Trajectory Tracking Control via ZNN with a Matrix Derivative Observer. Biomimetics 2025, 10, 505. https://doi.org/10.3390/biomimetics10080505
Yin H, Jin H, Peng Y, Wang Z, Liu J, Ju F, Zhao J. Design of a Humanoid Upper-Body Robot and Trajectory Tracking Control via ZNN with a Matrix Derivative Observer. Biomimetics. 2025; 10(8):505. https://doi.org/10.3390/biomimetics10080505
Chicago/Turabian StyleYin, Hong, Hongzhe Jin, Yuchen Peng, Zijian Wang, Jiaxiu Liu, Fengjia Ju, and Jie Zhao. 2025. "Design of a Humanoid Upper-Body Robot and Trajectory Tracking Control via ZNN with a Matrix Derivative Observer" Biomimetics 10, no. 8: 505. https://doi.org/10.3390/biomimetics10080505
APA StyleYin, H., Jin, H., Peng, Y., Wang, Z., Liu, J., Ju, F., & Zhao, J. (2025). Design of a Humanoid Upper-Body Robot and Trajectory Tracking Control via ZNN with a Matrix Derivative Observer. Biomimetics, 10(8), 505. https://doi.org/10.3390/biomimetics10080505







