A Biomimetic Microchannel Heat Sink for Enhanced Thermal Performance in Chip Cooling
Abstract
1. Introduction
2. Establishment and Validation of Physical Model
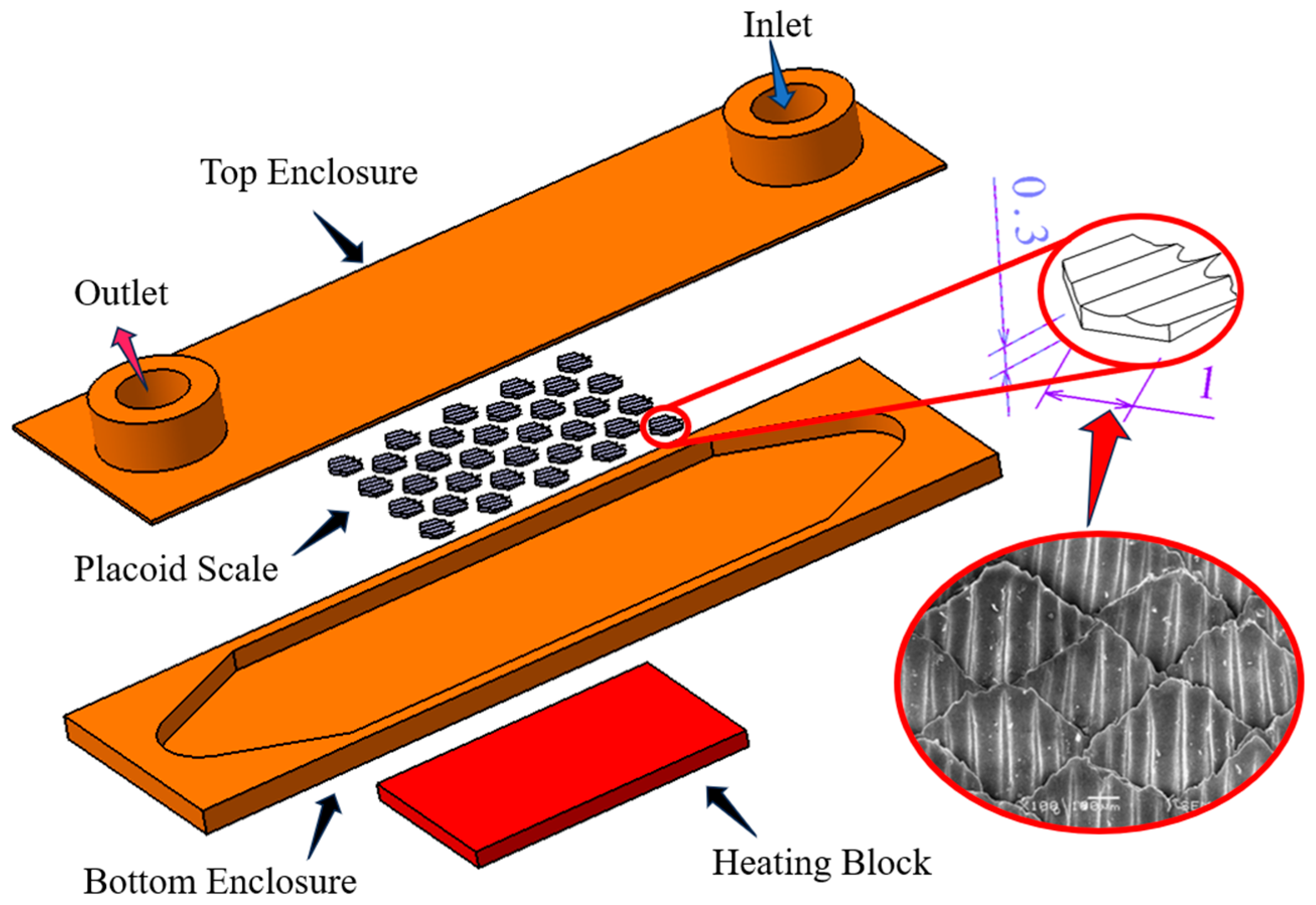
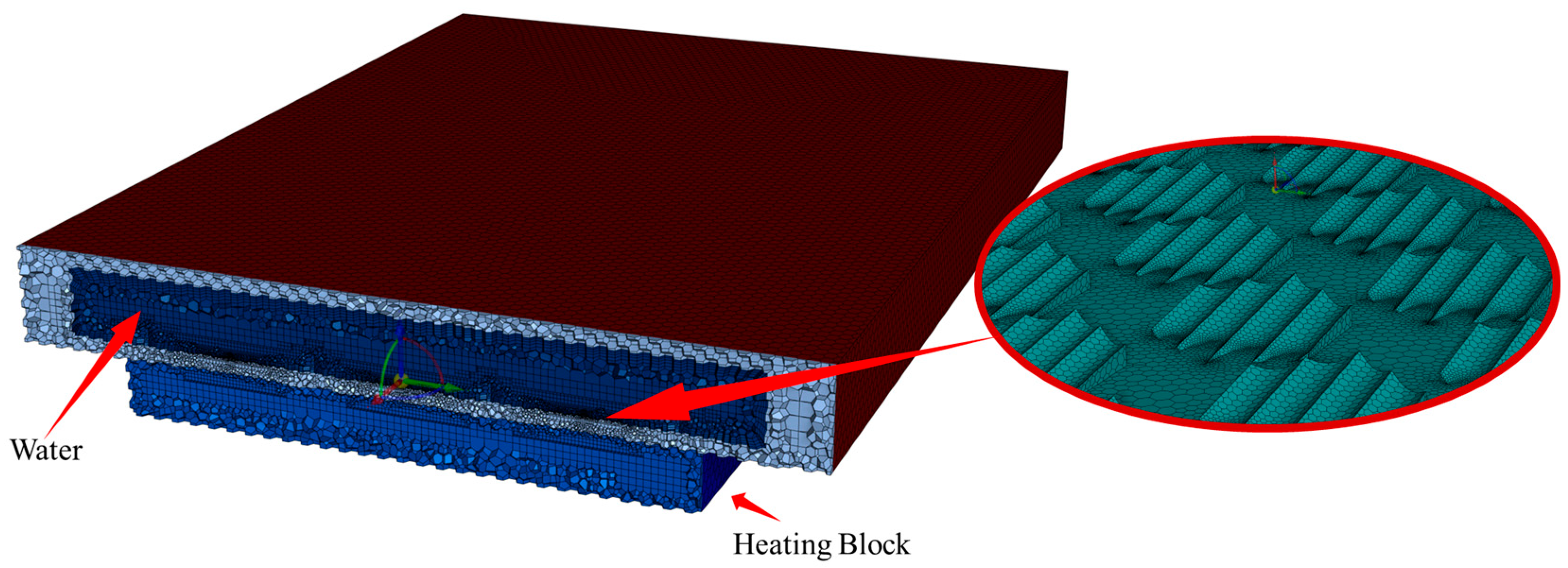
2.1. Model Description
2.2. Governing Equation Creation and Boundary Condition Setting
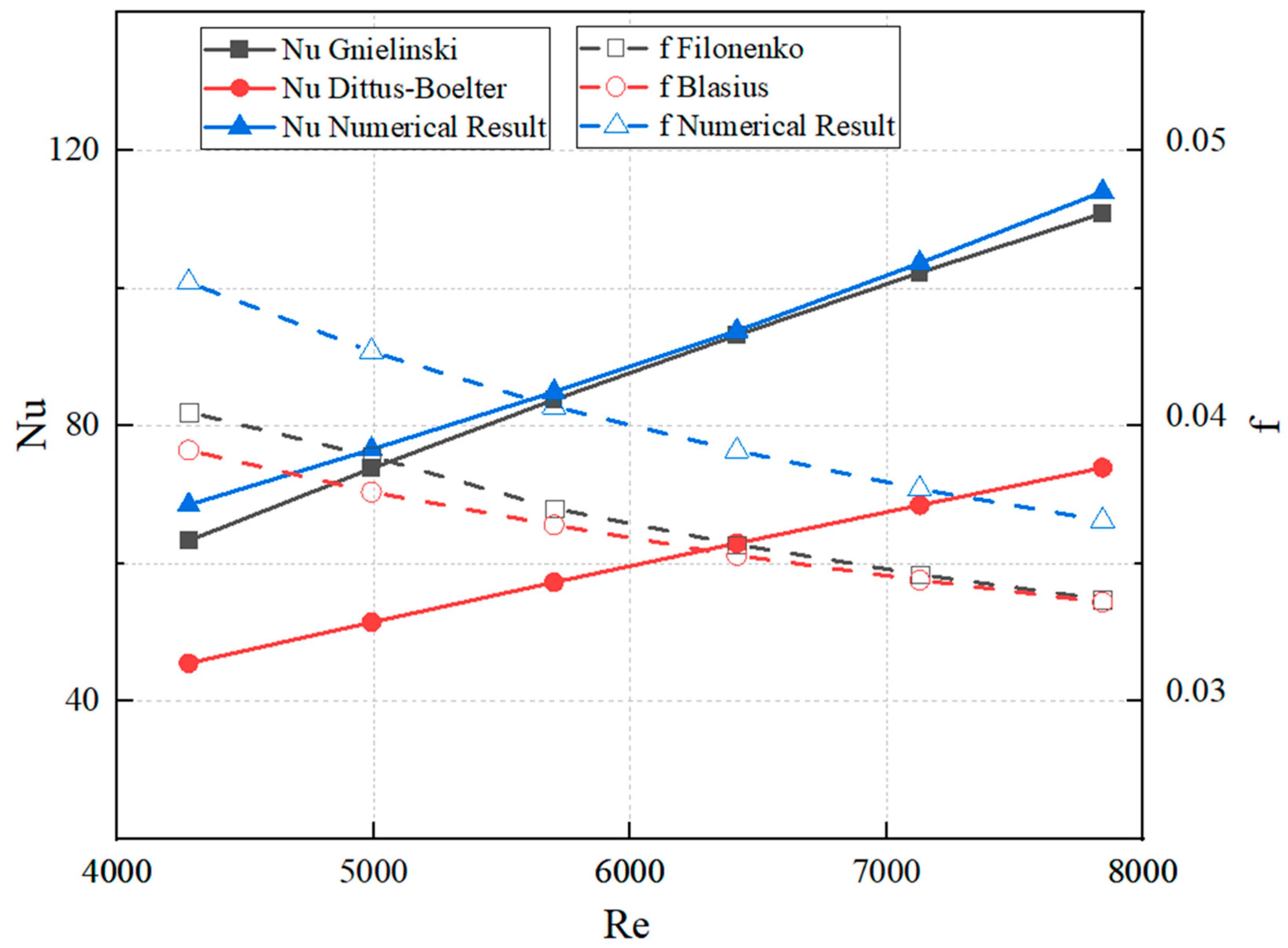
2.3. Validation of Coupling Model
3. Simulation and Validation of Bionic Microchannel Heat Sink
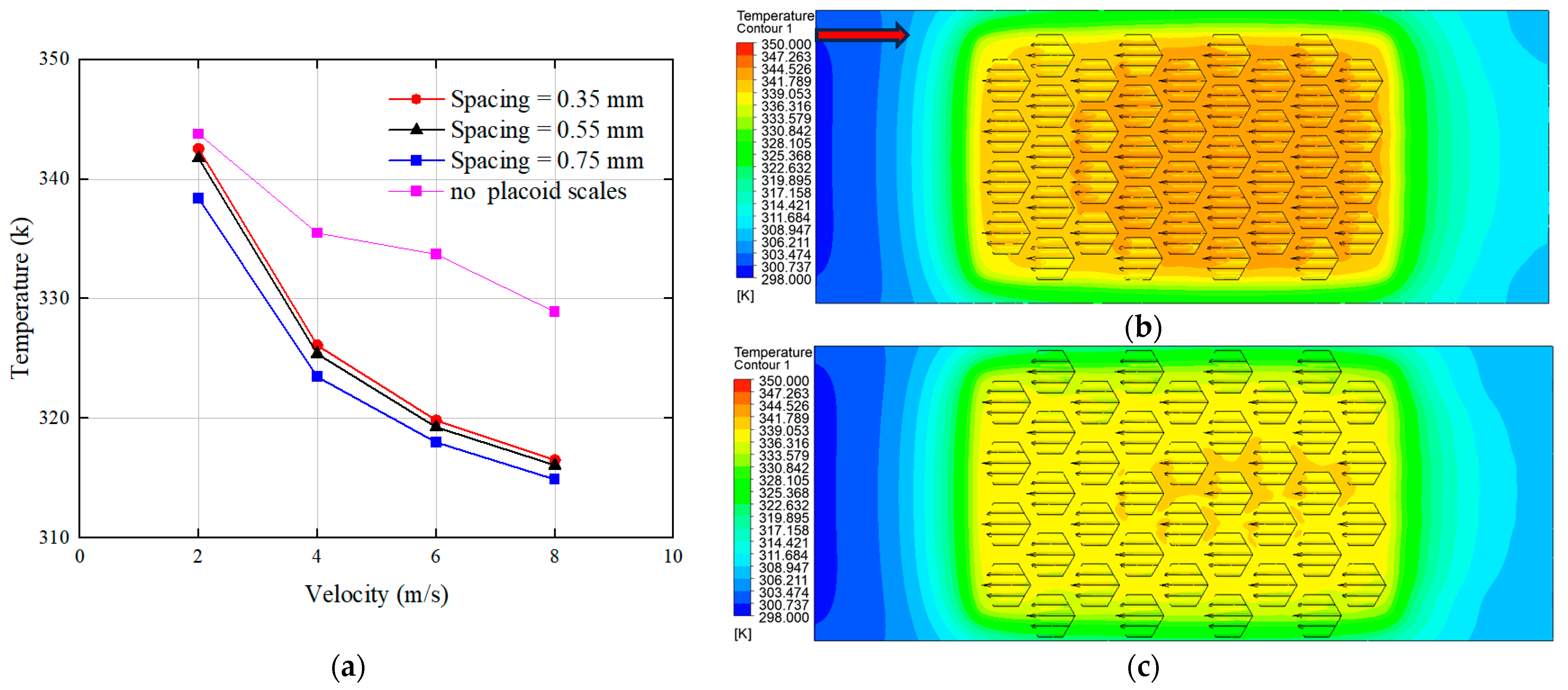
3.1. Effect of Arrangement Pattern on Performance of MCHS
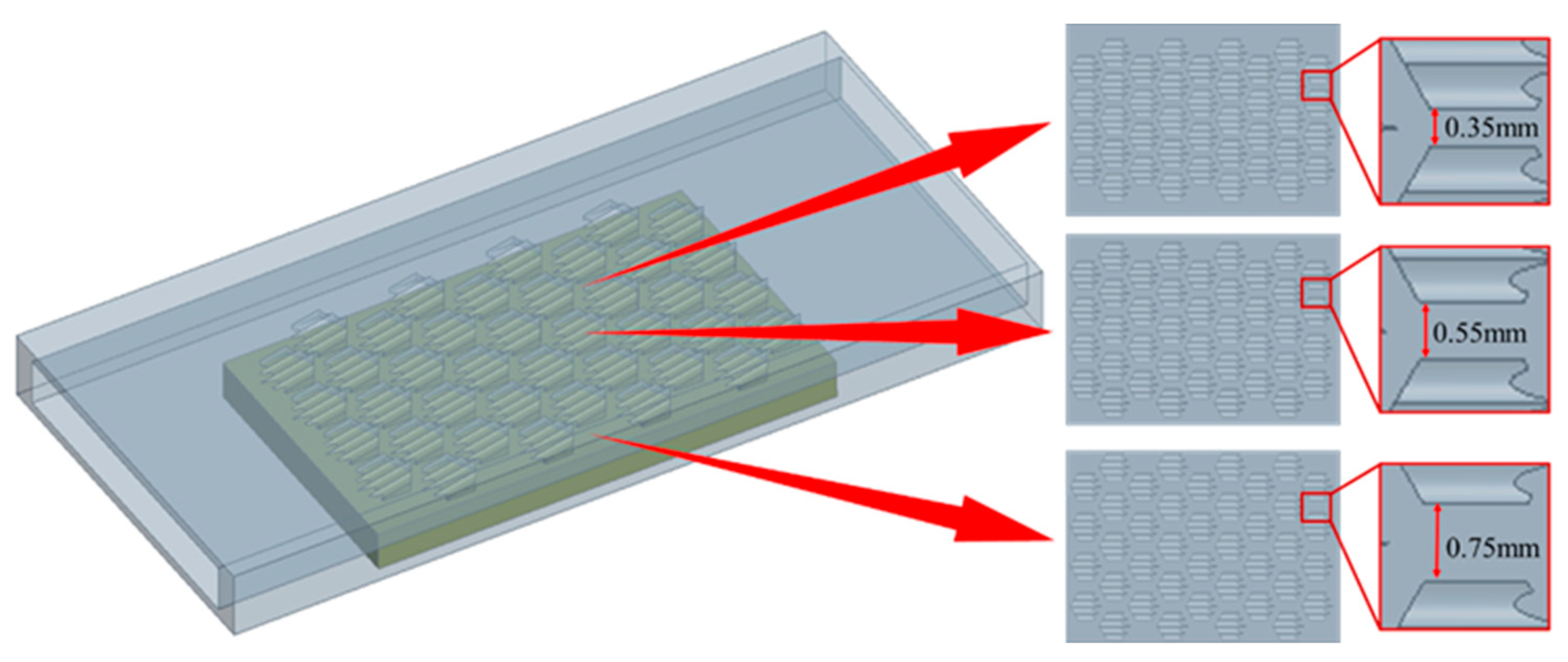
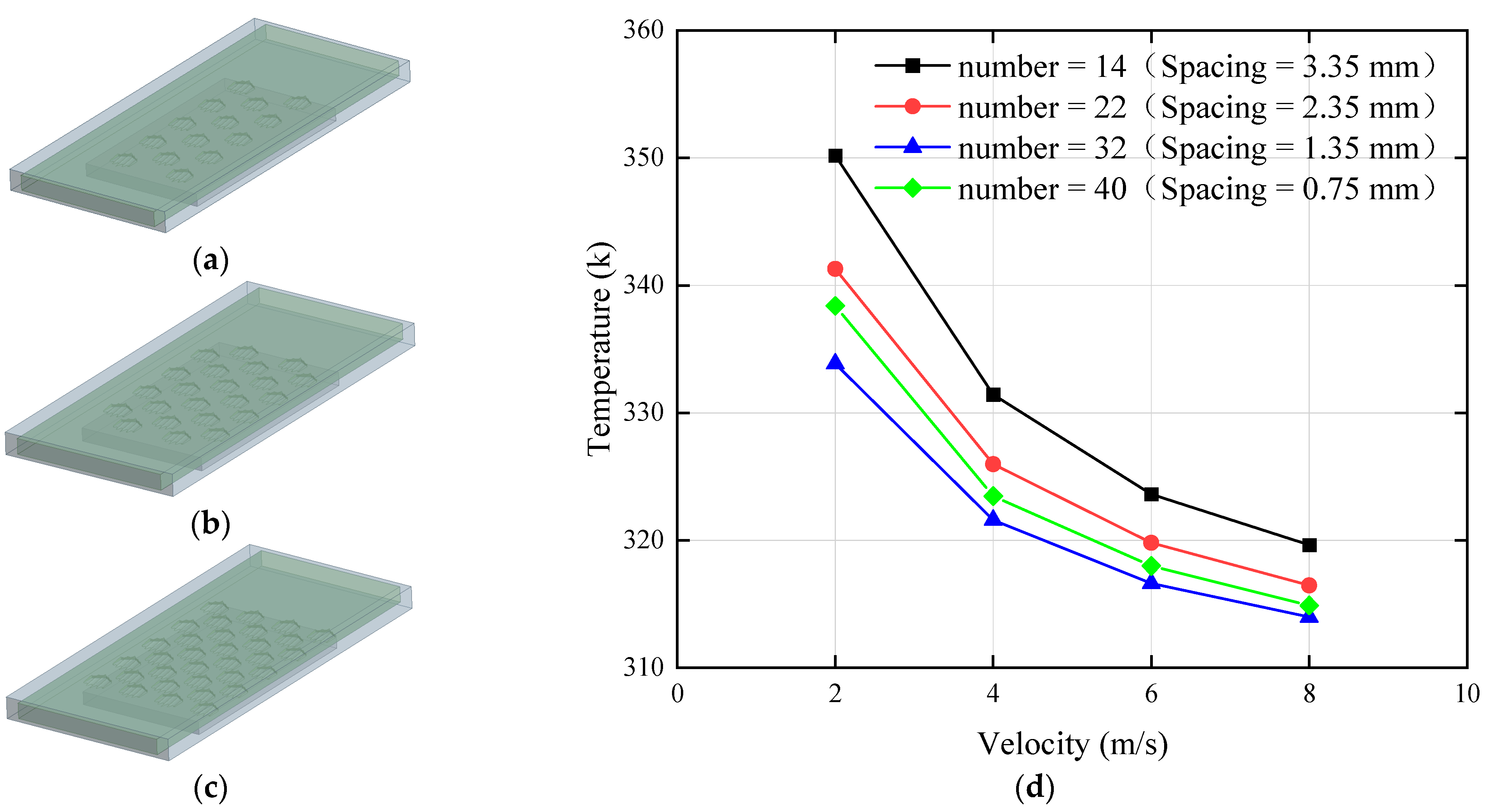
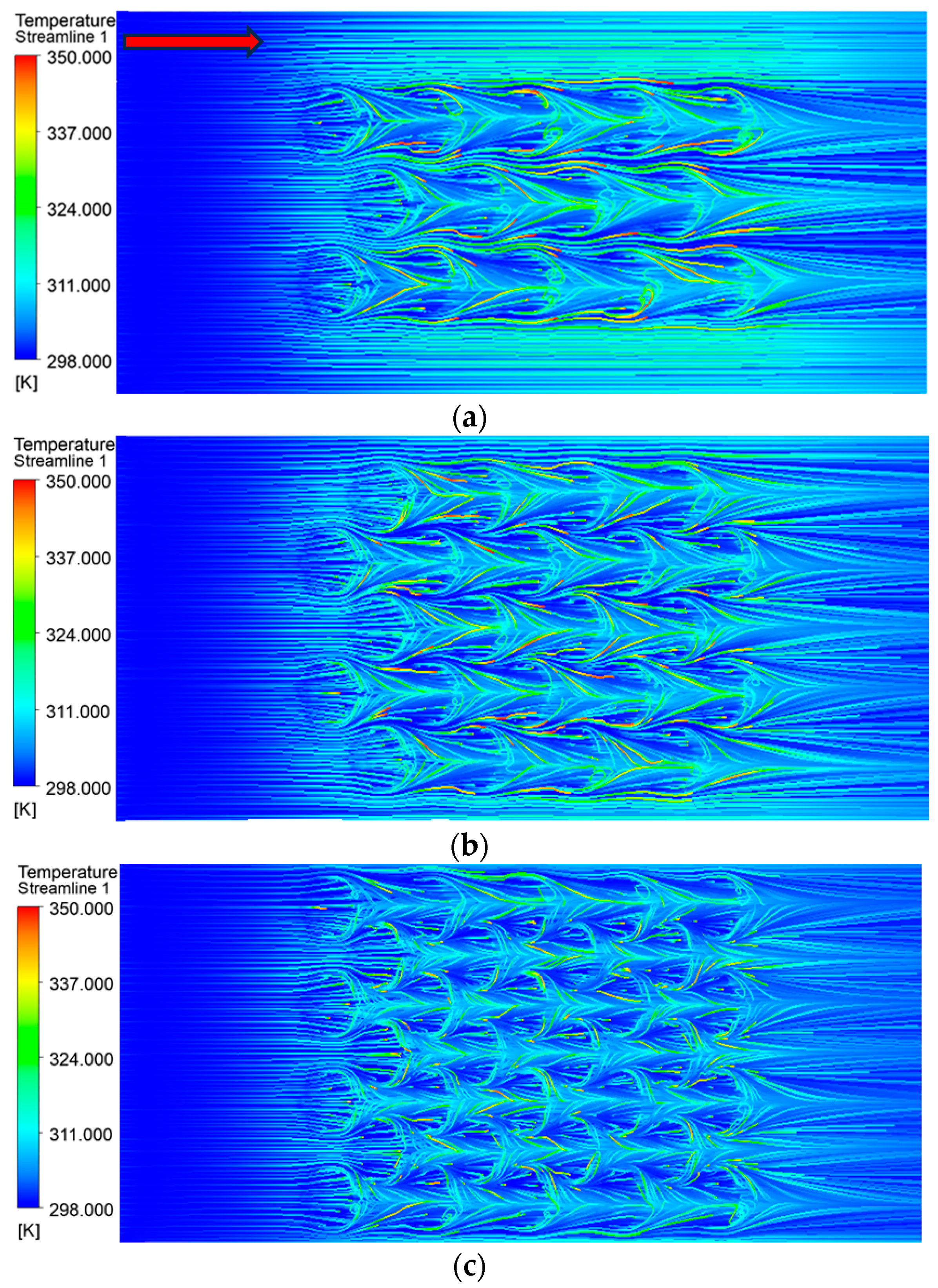
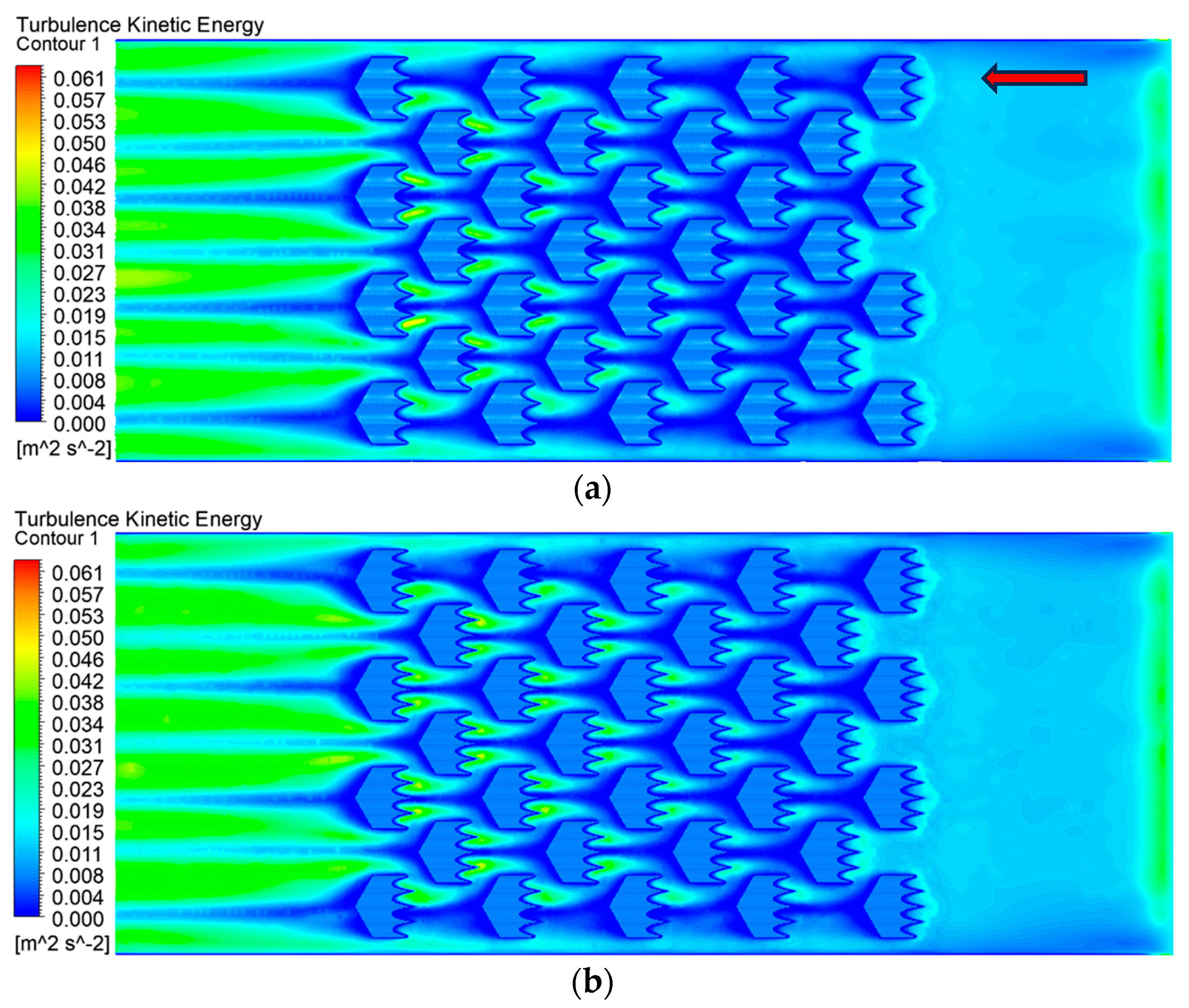
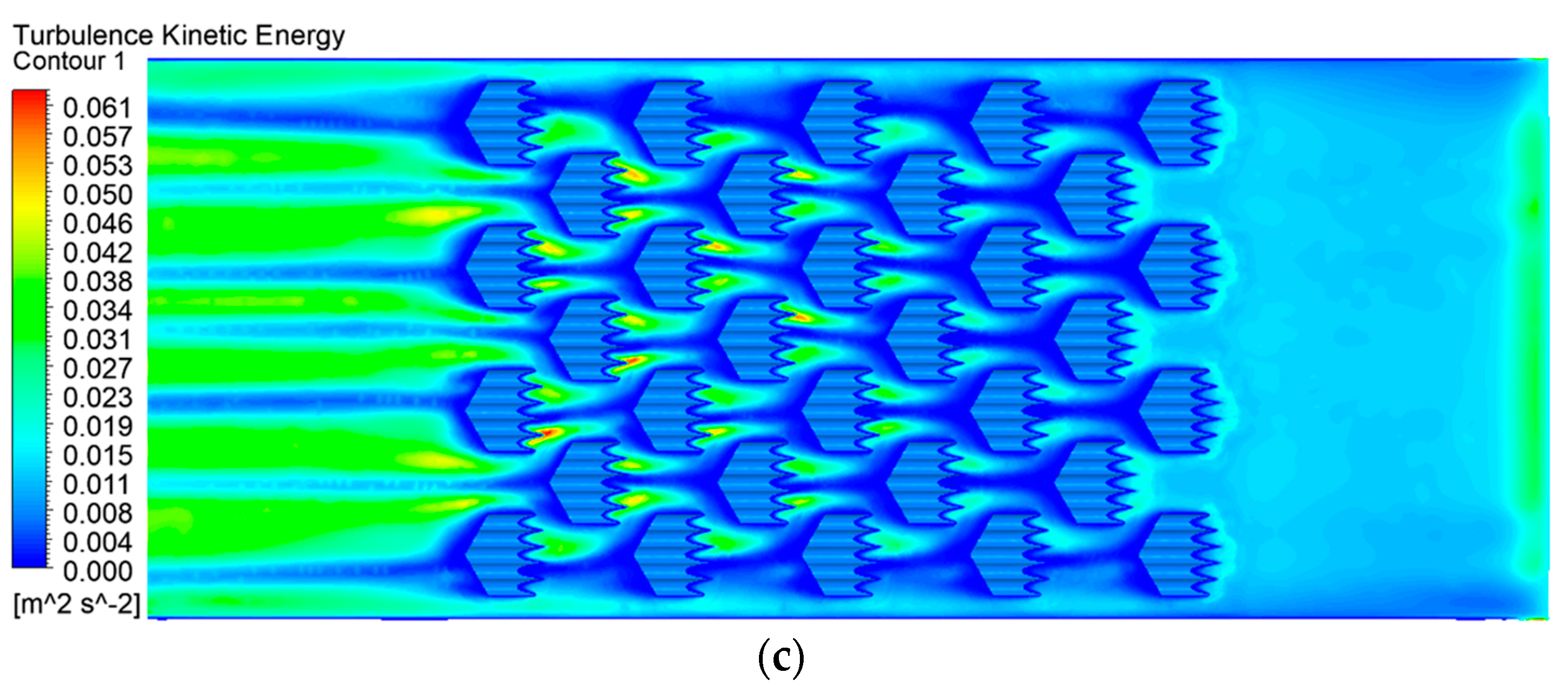
3.2. Effect of Different Number of Structures on Performance of MCHS
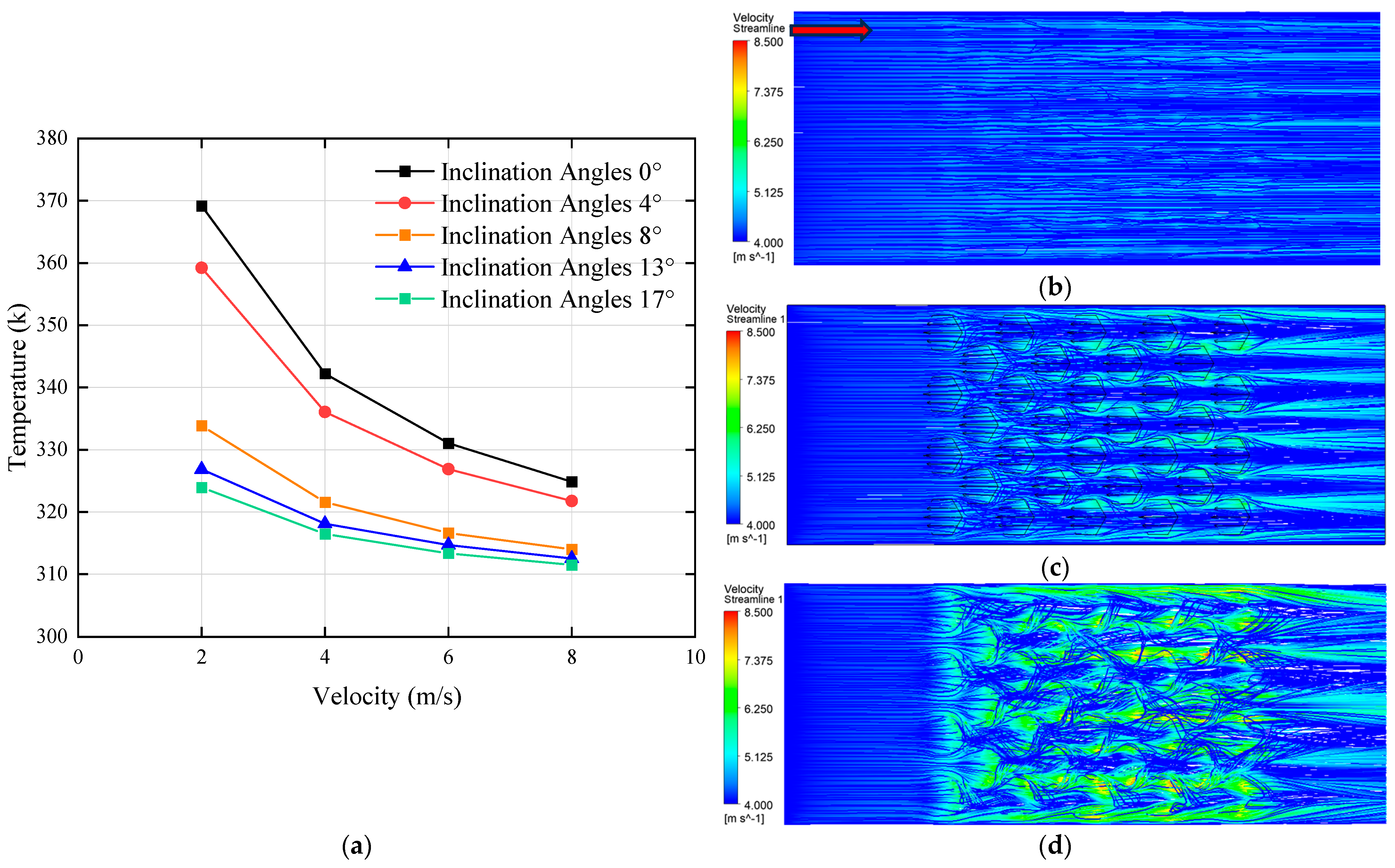
3.3. Effect of Inclination Angles on Performance of MCHS
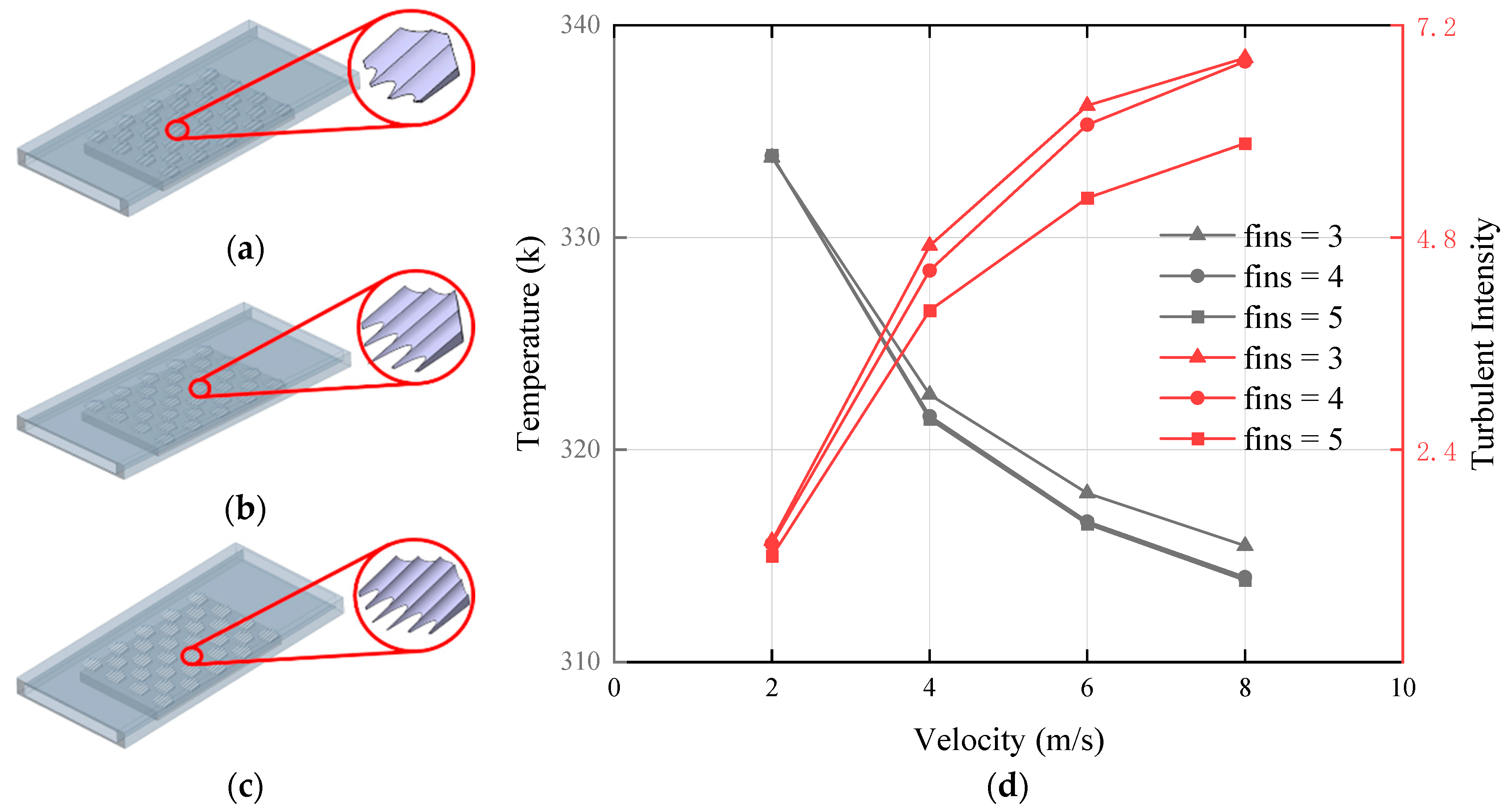
3.4. Effect of Different Number of Fins on Performance of MCHS
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bar-Cohen, A. Gen-3 Thermal Management Technology: Role of Microchannels and Nanostructures in an Embedded Cooling Paradigm. J. Nanotechnol. Eng. Med. 2013, 4, 020907. [Google Scholar] [CrossRef]
- Tullius, J.F.; Tullius, T.K.; Bayazitoglu, Y. Optimization of short micro pin fins in minichannels. Int. J. Heat Mass Transf. 2012, 55, 3921–3932. [Google Scholar] [CrossRef]
- Kim, K.-S.; Won, M.-H.; Kim, J.-W.; Back, B.-J. Heat pipe cooling technology for desktop PC CPU. Appl. Therm. Eng. 2003, 23, 1137–1144. [Google Scholar] [CrossRef]
- Tuckerman, D.B.; Pease, R.F.W. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Deng, D.; Zeng, L.; Sun, W. A review on flow boiling enhancement and fabrication of enhanced microchannels of microchannel heat sinks. Int. J. Heat Mass Transf. 2021, 175, 121332. [Google Scholar] [CrossRef]
- Criscuolo, G.; Markussen, W.B.; Meyer, K.E.; Kærn, M.R. High heat flux flow boiling of R1234yf, R1234ze(E) and R134a in high aspect ratio microchannels. Int. J. Heat Mass Transf. 2022, 186, 122215. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Yang, F.; Alam, T.; Jiang, M.; Qu, X.; Kong, F.; Khan, A.S.; Liu, M.; Alwazzan, M. Supercapillary architecture-activated two-phase boundary layer structures for highly stable and efficient flow boiling heat transfer. Adv. Mater. 2020, 32, 1905117. [Google Scholar] [CrossRef] [PubMed]
- Tu, J.; Shi, J.; Chen, L.; Liu, J.; Li, C.; Wei, J. Surface termination of the diamond microchannel and single-phase heat transfer performance. Int. J. Heat Mass Transf. 2022, 199, 123481. [Google Scholar] [CrossRef]
- Hsu, W.-T.; Lee, D.; Lee, N.; Yun, M.; Cho, H.H. Enhancement of flow boiling heat transfer using heterogeneous wettability patterned surfaces with varying inter-spacing. Int. J. Heat Mass Transf. 2021, 164, 120596. [Google Scholar] [CrossRef]
- Zhao, Q.; Qiu, J.; Zhou, J.; Lu, M.; Li, Q.; Chen, X. Visualization study of flow boiling characteristics in open microchannels with different wettability. Int. J. Heat Mass Transf. 2021, 180, 121808. [Google Scholar] [CrossRef]
- Drummond, K.P.; Weibel, J.A.; Garimella, S.V. Two-phase flow morphology and local wall temperatures in high-aspect-ratio manifold microchannels. Int. J. Heat Mass Transf. 2020, 153, 119551. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Q.; Chen, X. Micro pin fins with topologically optimized configurations enhance flow boiling heat transfer in manifold microchannel heat sinks. Int. J. Heat Mass Transf. 2023, 206, 123956. [Google Scholar] [CrossRef]
- Deng, D.; Zeng, L.; Sun, W.; Pi, G.; Yang, Y. Experimental study of flow boiling performance of open-ring pin fin microchannels. Int. J. Heat Mass Transf. 2021, 167, 120829. [Google Scholar] [CrossRef]
- Li, W.; Li, C.; Wang, Z.; Chen, Y. Enhanced flow boiling in microchannels integrated with supercapillary pinfin fences. Int. J. Heat Mass Transf. 2022, 183, 122185. [Google Scholar] [CrossRef]
- Liu, Z.; Yao, X.; Cheng, X.; Wu, H.; Wang, H.; Shen, H. Experimental study on two-phase boiling in wavy copper microchannels fabricated with ultrafast laser micromachining. J. Micromech. Microeng. 2020, 30, 065011. [Google Scholar] [CrossRef]
- Wang, G.; Sheng, K.; Wang, Y.; Ding, G.; Xie, D. Thermal hydraulic performance of tree-like microchannel heat sink with high branching level based on the improved Murray’s law. Int. J. Heat Mass Transf. 2024, 231, 125875. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, W.; Wang, L.; Xie, W. Heat and mass transfer characteristics of leaf-vein-inspired microchannels with wall thickening patterns. Int. J. Heat Mass Transf. 2016, 101, 1273–1282. [Google Scholar] [CrossRef]
- Wang, Z.; Li, B.; Luo, Q.-Q.; Zhao, W. Effect of wall roughness by the bionic structure of dragonfly wing on microfluid flow and heat transfer characteristics. Int. J. Heat Mass Transf. 2021, 173, 121201. [Google Scholar] [CrossRef]
- Dey, P.; Hedau, G.; Saha, S.K. Experimental and numerical investigations of fluid flow and heat transfer in a bioinspired surface enriched microchannel. Int. J. Therm. Sci. 2019, 135, 44–60. [Google Scholar] [CrossRef]
- Goh, A.L.; Ooi, K.T. Scale-inspired enhanced microscale heat transfer in macro geometry. Int. J. Heat Mass Transf. 2017, 113, 141–152. [Google Scholar] [CrossRef]
- Li, P.; Guo, D.; Huang, X. Heat transfer enhancement, entropy generation and temperature uniformity analyses of shark-skin bionic modified microchannel heat sink. Int. J. Heat Mass Transf. 2020, 146, 118846. [Google Scholar] [CrossRef]
- Fu, Y.F.; Yuan, C.Q.; Bai, X.Q. Marine drag reduction of shark skin inspired riblet surfaces. Biosurf. Biotribol. 2017, 3, 11–24. [Google Scholar] [CrossRef]
- Wang, J.; Yang, R.; Gao, S.; Weng, F.; Wang, Y.; Liao, W.-H.; Guo, P. Modulated vibration texturing of hierarchical microchannels with controllable profiles and orientations. CIRP J. Manuf. Sci. Technol. 2020, 30, 58–67. [Google Scholar] [CrossRef]
- Wang, X.; Wen, G.; Wei, Y. Aerodynamic Noise Simulation of a Super-High-Rise Building Facade with Shark-Like Grooved Skin. Biomimetics 2024, 9, 570. [Google Scholar] [CrossRef]
- Santos, L.M.; Lang, A.; Wahidi, R.; Bonacci, A.; Gautam, S. Understanding Low-Speed Streaks and Their Function and Control through Movable Shark Scales Acting as a Passive Separation Control Mechanism. Biomimetics 2024, 9, 378. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.-Y.; Huang, Z.-P.; Wang, M.-J.; Wang, T.; Jin, Y. Vacuum casting replication of micro-riblets on shark skin for drag-reducing applications. J. Mater. Process. Technol. 2012, 212, 198–202. [Google Scholar] [CrossRef]
- Wagner, W.; Pruß, A. The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef]
- Song, G.; Chen, H.; Zhang, Y.; Wei, J.; Ma, X. Reviews: Applications of optimization algorithm for microchannel and microchannel heat sink on heat transfer. Int. J. Heat Fluid Flow 2024, 108, 109451. [Google Scholar] [CrossRef]
- Gao, C.; Lan, X.; He, Z.; Xin, G.; Wang, X.; Xin, Q. Temperature uniformity analysis and multi-objective optimization of a small-scale variable density alternating obliquely truncated microchannel. Therm. Sci. Eng. Prog. 2023, 38, 101652. [Google Scholar] [CrossRef]
- Tabatabaei Malazi, M.; Kaya, K.; Dalkılıç, A.S. A computational case study on the thermal performance of a rectangular microchannel having circular pin-fins. Case Stud. Therm. Eng. 2023, 49, 103111. [Google Scholar] [CrossRef]
- Du, J.; Fang, Y. Bioinspired spider-web microchannel with five-input-four-output manifold: Enhanced thermal performance for 10,000 kW/m2 chip-scale embedded cooling. Int. J. Heat Fluid Flow 2025, 114, 109794. [Google Scholar] [CrossRef]
- Zhou, J.; Lu, M.; Zhao, Q.; Hu, D.; Qin, H.; Chen, X. Thermal design of microchannel heat sinks using a contour extraction based on topology optimization (CEBTO) method. Int. J. Heat Mass Transf. 2022, 189, 122703. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, Y.; Zhang, D.; Xie, G. Flow Characteristic and Heat Transfer for Non-Newtonian Nanofluid in Rectangular Microchannels with Teardrop Dimples/Protrusions. Open Phys. 2017, 15, 197–206. [Google Scholar] [CrossRef]
- Xu, Z.; Han, Z.; Wang, J.; Liu, Z. The characteristics of heat transfer and flow resistance in a rectangular channel with vortex generators. Int. J. Heat Mass Transf. 2018, 116, 61–72. [Google Scholar] [CrossRef]
- Esmaeilzadeh, A.; Amanifard, N.; Deylami, H.M. Comparison of simple and curved trapezoidal longitudinal vortex generators for optimum flow characteristics and heat transfer augmentation in a heat exchanger. Appl. Therm. Eng. 2017, 125, 1414–1425. [Google Scholar] [CrossRef]
- Wang, G.; Ruan, H.; Peng, H.; Xu, Q.; Lai, L.; Xie, D.; Neha, N.N. Numerical investigation on hydrothermal performance of microchannel heat sink with impingement jet inlet arrays. Int. Commun. Heat Mass Transf. 2025, 165, 109013. [Google Scholar] [CrossRef]
- Bian, J.; Cao, X.; Yang, W.; Edem, M.A.; Yin, P.; Jiang, W. Supersonic liquefaction properties of natural gas in the Laval nozzle. Energy 2018, 159, 706–715. [Google Scholar] [CrossRef]
- Allimant, A.; Planche, M.P.; Bailly, Y.; Dembinski, L.; Coddet, C. Progress in gas atomization of liquid metals by means of a De Laval nozzle. Powder Technol. 2009, 190, 79–83. [Google Scholar] [CrossRef]
- Dai, Y.; Shi, J.; Cheng, X.; Zhang, Z.; He, Y.; Tao, W. Numerical study on the cavitation flow characteristics of high-pressure fuel in injector orifices based on compressible non-isothermal model. AIP Adv. 2023, 13, 115205. [Google Scholar] [CrossRef]

| No. | Grid Number | (pa) | Deviation (%) | (K) | Deviation (%) |
|---|---|---|---|---|---|
| Mesh 1 | 590,067 | 27,797.30 | 2.79 | 17.961 | 3.29 |
| Mesh 2 | 1,032,617 | 28,311.54 | 0.92 | 18.331 | 1.21 |
| Mesh 3 | 1,475,168 | 28,568.66 | 0.09 | 18.516 | 0.19 |
| Mesh 4 | 2,212,752 | 28,594.37 | - | 18.553 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Shi, Y.; Chen, J.; Dai, Y. A Biomimetic Microchannel Heat Sink for Enhanced Thermal Performance in Chip Cooling. Biomimetics 2025, 10, 459. https://doi.org/10.3390/biomimetics10070459
Wang K, Shi Y, Chen J, Dai Y. A Biomimetic Microchannel Heat Sink for Enhanced Thermal Performance in Chip Cooling. Biomimetics. 2025; 10(7):459. https://doi.org/10.3390/biomimetics10070459
Chicago/Turabian StyleWang, Kaichen, Yan Shi, Junjie Chen, and Yuchi Dai. 2025. "A Biomimetic Microchannel Heat Sink for Enhanced Thermal Performance in Chip Cooling" Biomimetics 10, no. 7: 459. https://doi.org/10.3390/biomimetics10070459
APA StyleWang, K., Shi, Y., Chen, J., & Dai, Y. (2025). A Biomimetic Microchannel Heat Sink for Enhanced Thermal Performance in Chip Cooling. Biomimetics, 10(7), 459. https://doi.org/10.3390/biomimetics10070459






