Investigation of Droplet Spreading and Rebound Dynamics on Superhydrophobic Surfaces Using Machine Learning
Abstract
1. Introduction
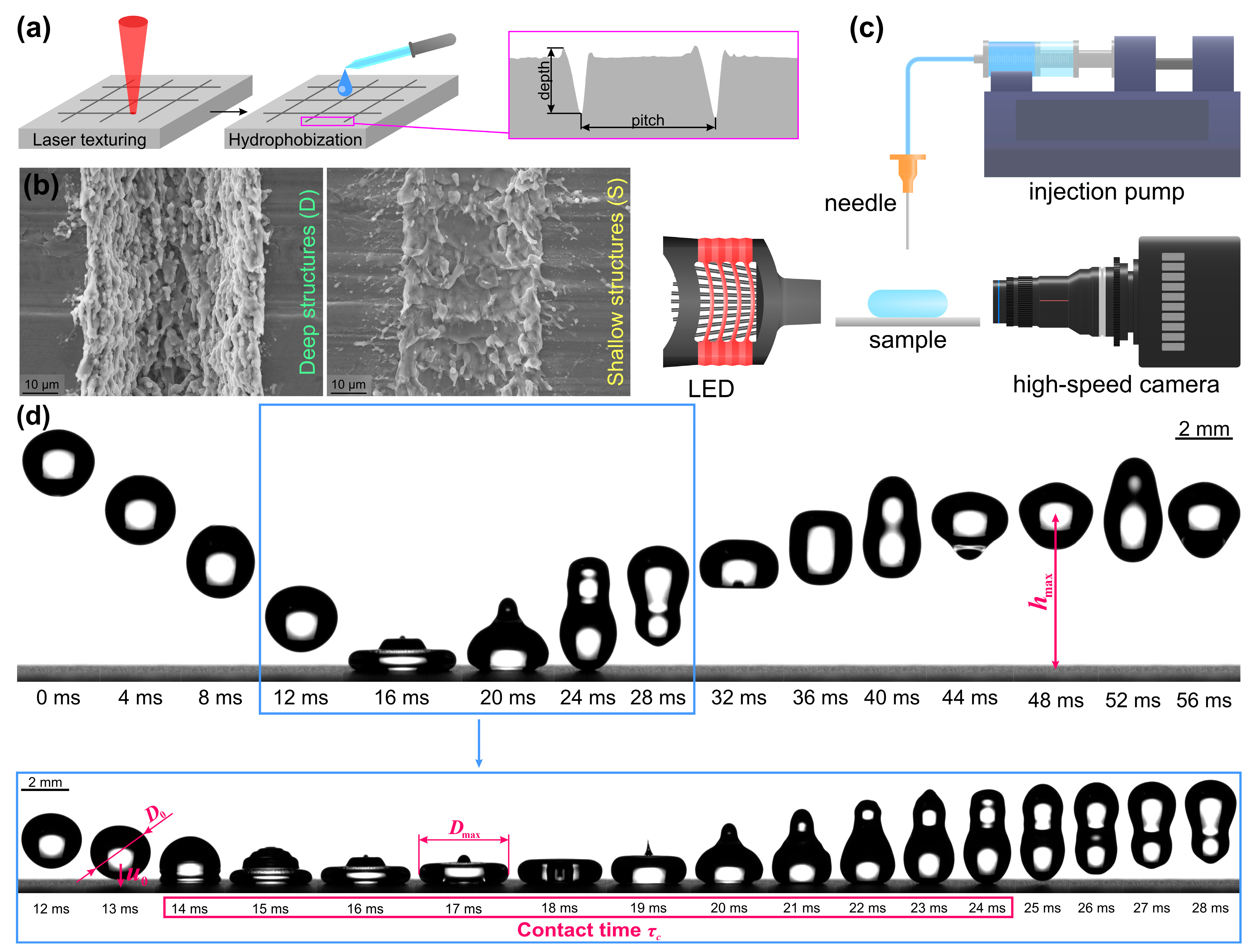
2. Materials and Methods
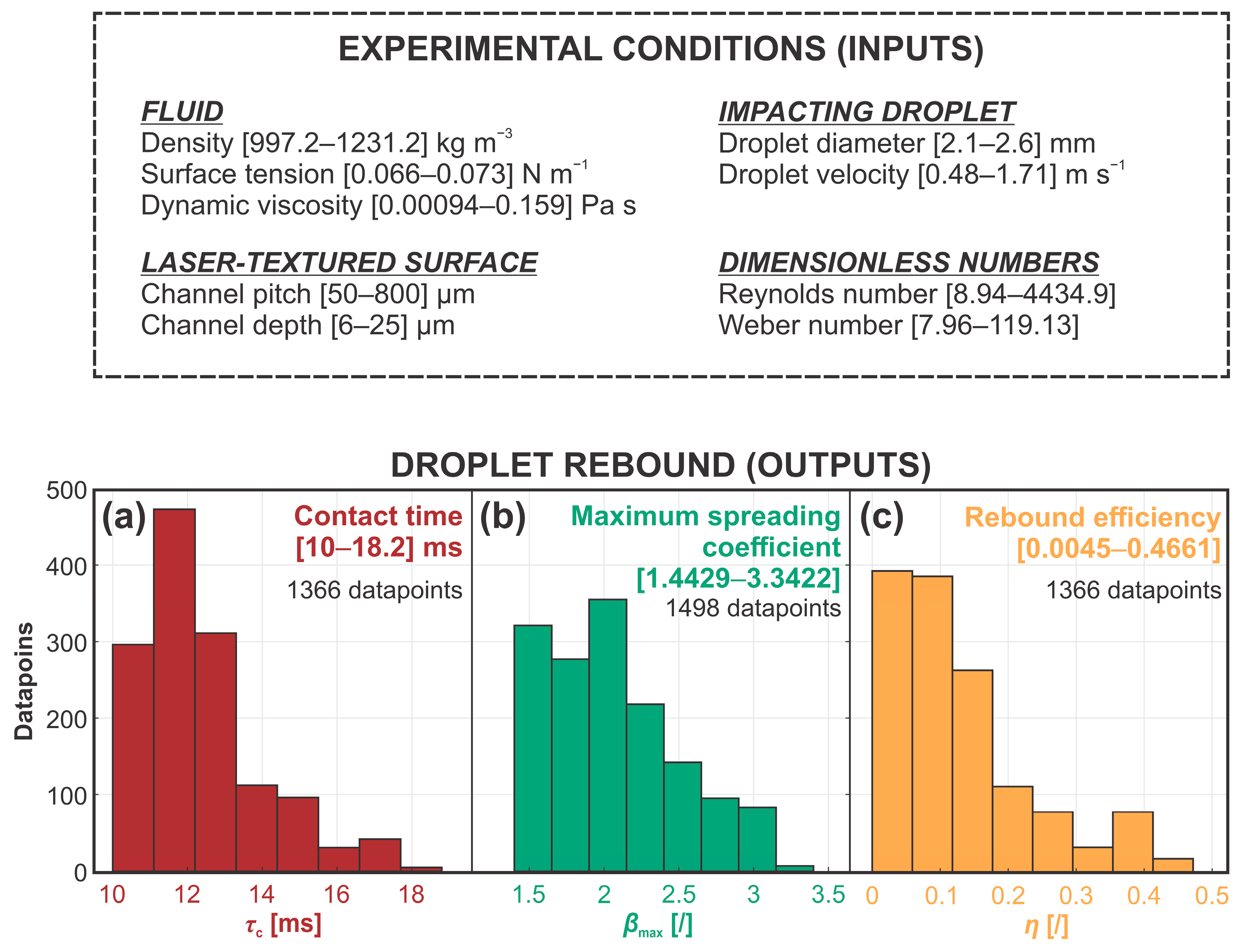
2.1. Data Preparation
3. Results and Discussion
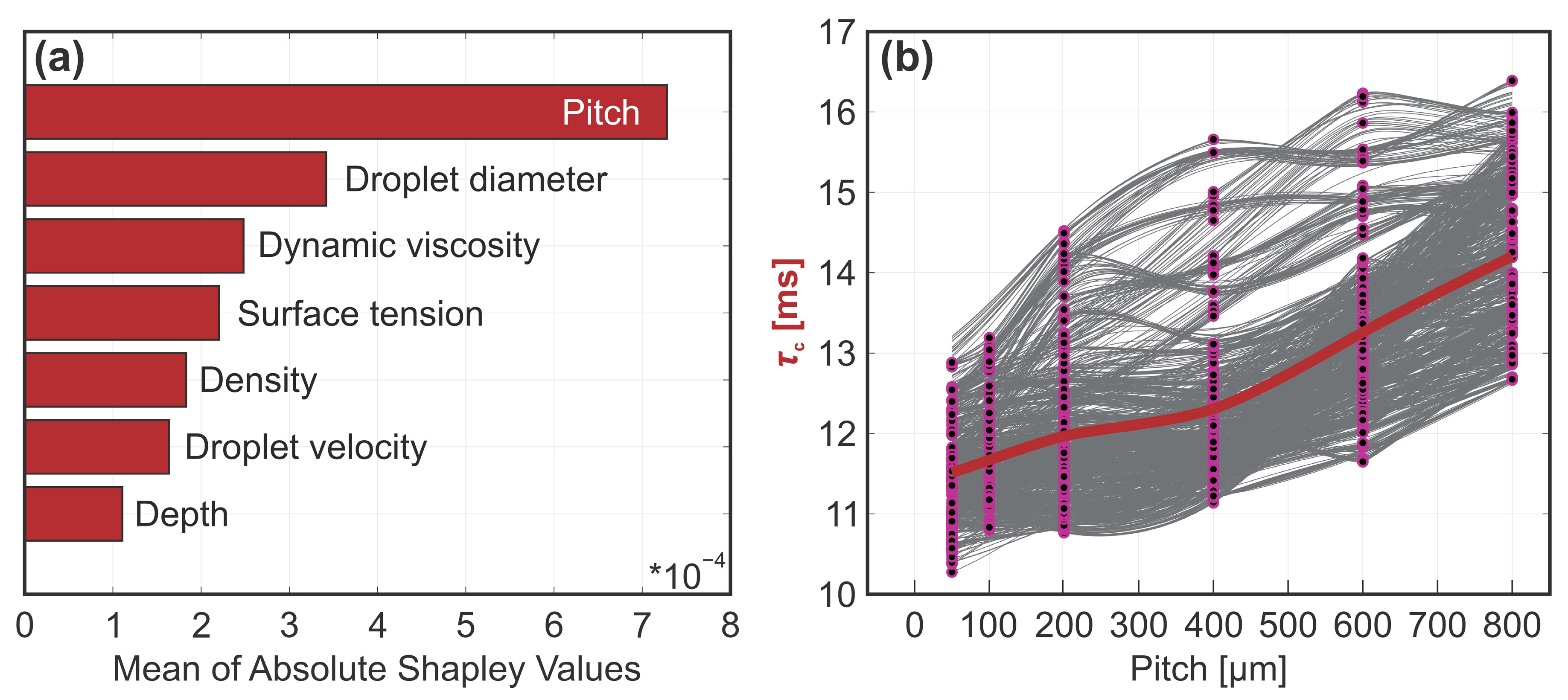
3.1. Contact Time
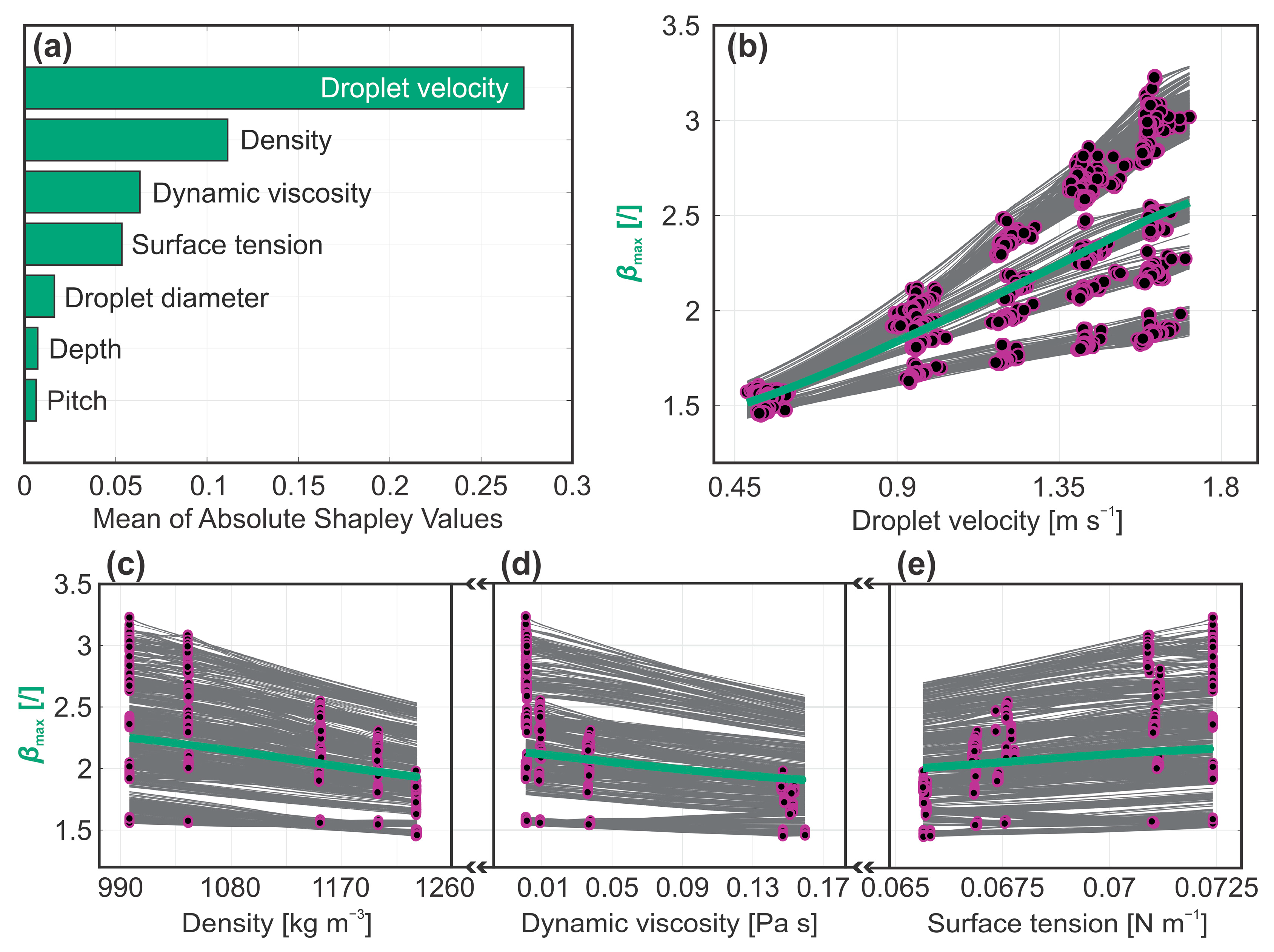
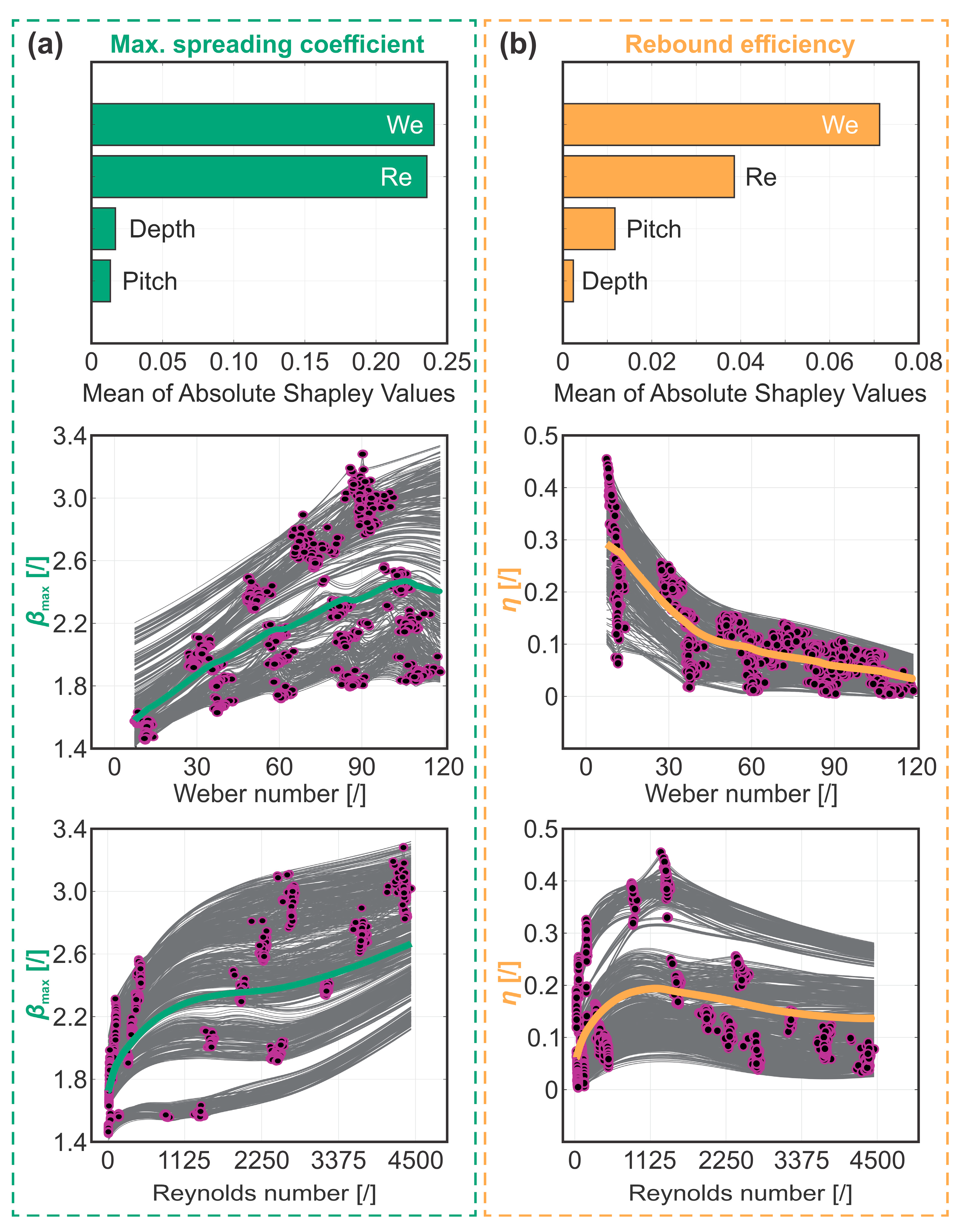
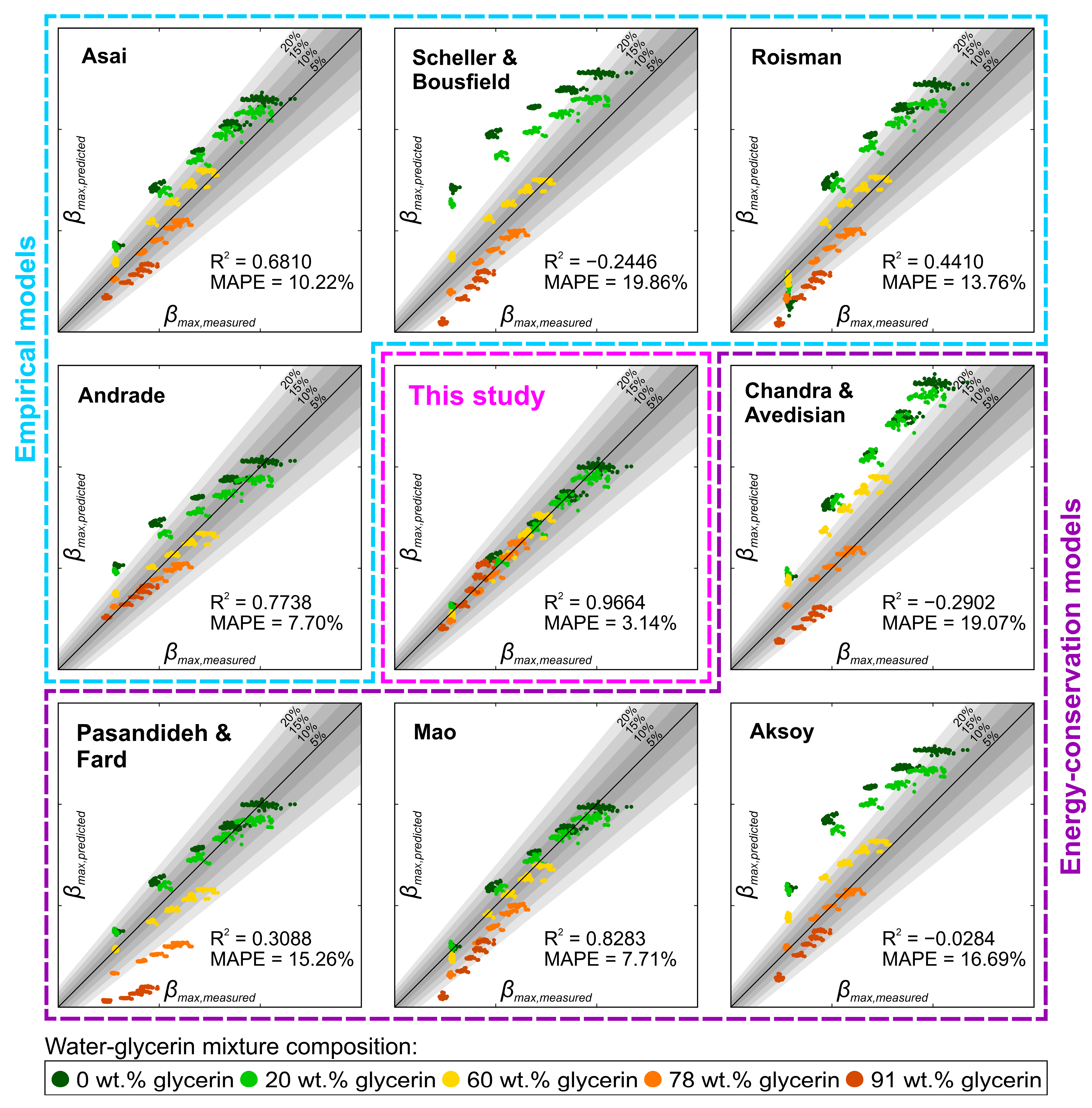
3.2. Maximum Spreading Coefficient
3.3. Rebound Efficiency
3.4. Prediction with Dimensionless Numbers—Re, We
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barthlott, W.; Neinhuis, C. Purity of the Sacred Lotus, or Escape from Contamination in Biological Surfaces. Planta 1997, 202, 1–8. [Google Scholar] [CrossRef]
- Neinhuis, C.; Barthlott, W. Characterization and Distribution of Water-Repellent, Self-Cleaning Plant Surfaces. Ann. Bot. 1997, 79, 667–677. [Google Scholar] [CrossRef]
- Thickett, S.C.; Neto, C.; Harris, A.T. Biomimetic Surface Coatings for Atmospheric Water Capture Prepared by Dewetting of Polymer Films. Adv. Mater. 2011, 23, 3718–3722. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wu, J.; Hedhili, M.N.; Yang, X.; Wang, P. Inkjet Printing for Direct Micropatterning of a Superhydrophobic Surface: Toward Biomimetic Fog Harvesting Surfaces. J. Mater. Chem. A 2015, 3, 2844–2852. [Google Scholar] [CrossRef]
- Yu, Z.; Yun, F.F.; Wang, Y.; Yao, L.; Dou, S.; Liu, K.; Jiang, L.; Wang, X. Desert Beetle-Inspired Superwettable Patterned Surfaces for Water Harvesting. Small 2017, 13, 1701403. [Google Scholar] [CrossRef]
- Fürstner, R.; Barthlott, W.; Neinhuis, C.; Walzel, P. Wetting and Self-Cleaning Properties of Artificial Superhydrophobic Surfaces. Langmuir 2005, 21, 956–961. [Google Scholar] [CrossRef]
- Rodič, P.; Može, M.; Golobič, I.; Milošev, I. Functionalisation of the Aluminium Surface by CuCl2 Chemical Etching and Perfluoro Silane Grafting: Enhanced Corrosion Protection and Improved Anti-Icing Behaviour. Metals 2024, 14, 1118. [Google Scholar] [CrossRef]
- Rodič, P.; Kovač, N.; Kralj, S.; Jereb, S.; Golobič, I.; Može, M.; Milošev, I. Anti-Corrosion and Anti-Icing Properties of Superhydrophobic Laser-Textured Aluminum Surfaces. Surf. Coatings Technol. 2024, 494, 131325. [Google Scholar] [CrossRef]
- Daniello, R.J.; Waterhouse, N.E.; Rothstein, J.P. Drag Reduction in Turbulent Flows over Superhydrophobic Surfaces Drag Reduction in Turbulent Flows over Superhydrophobic Surfaces. Phys. Fluids 2009, 21, 085103. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Zhang, Y.Q.; Wang, Z.H.; An, Q.D.; Xiao, Z.Y.; Xiao, L.P.; Zhai, S.R. Controllable Construction of Multifunctional Superhydrophobic Coating with Ultra-Stable Efficiency for Oily Water Treatment. J. Colloid Interface Sci. 2022, 628, 356–365. [Google Scholar] [CrossRef]
- Jereb, S.; Zupančič, M.; Može, M.; Golobič, I. Predicting the Drop Size Passing through a Superhydrophobic Orifice. Phys. Fluids 2022, 34, 117117. [Google Scholar] [CrossRef]
- Rioboo, R.; Tropea, C.; Marengo, M. Outcomes from a Drop Impact on Solid Surfaces. At. Sprays 2001, 11, 155–165. [Google Scholar] [CrossRef]
- Richard, D.; Quéré, D. Bouncing Water Drops. Europhys. Lett. 2000, 50, 769–775. [Google Scholar] [CrossRef]
- Rioboo, R.; Marengo, M.; Tropea, C. Time Evolution of Liquid Drop Impact onto Solid, Dry Surfaces. Exp. Fluids 2002, 33, 112–124. [Google Scholar] [CrossRef]
- Jiang, S.; Xiong, H.; Tian, B.; Yu, Z. A New Criterion for the Splashing of a Droplet on Dry Surface from High-Fidelity Simulations. Appl. Sci. 2024, 14, 8553. [Google Scholar] [CrossRef]
- Heidari, E.; Daeichian, A.; Sobati, M.A.; Movahedirad, S. Prediction of the Droplet Spreading Dynamics on a Solid Substrate at Irregular Sampling Intervals: Nonlinear Auto-Regressive EXogenous Artificial Neural Network Approach (NARX-ANN). Chem. Eng. Res. Des. 2020, 156, 263–272. [Google Scholar] [CrossRef]
- Tembely, M.; Vadillo, D.C.; Dolatabadi, A.; Soucemarianadin, A. A Machine Learning Approach for Predicting the Maximum Spreading Factor of Droplets upon Impact on Surfaces with Various Wettabilities. Processes 2022, 10, 1141. [Google Scholar] [CrossRef]
- Pierzyna, M.; Burzynski, D.A.; Bansmer, S.E.; Semaan, R. Data-Driven Splashing Threshold Model for Drop Impact on Dry Smooth Surfaces. Phys. Fluids 2021, 33, 123317. [Google Scholar] [CrossRef]
- Azimi Yancheshme, A.; Hassantabar, S.; Maghsoudi, K.; Keshavarzi, S.; Jafari, R.; Momen, G. Integration of Experimental Analysis and Machine Learning to Predict Drop Behavior on Superhydrophobic Surfaces. Chem. Eng. J. 2021, 417, 127898. [Google Scholar] [CrossRef]
- Azimi Yancheshme, A.; Enayati, S.; Kashcooli, Y.; Jafari, R.; Ezzaidi, H.; Momen, G. Dynamic Behavior of Impinging Drops on Water Repellent Surfaces: Machine Learning-Assisted Approach to Predict Maximum Spreading. Exp. Therm. Fluid Sci. 2022, 139, 110743. [Google Scholar] [CrossRef]
- Keshavarzi, S.; Sourati, J.; Momen, G.; Jafari, R. Temperature-Dependent Droplet Impact Dynamics of a Water Droplet on Hydrophobic and Superhydrophobic Surfaces: An Experimental and Predictive Machine Learning–Based Study. Int. J. Heat Mass Transf. 2022, 195, 123190. [Google Scholar] [CrossRef]
- Au-Yeung, L.; Tsai, P.A. Predicting Impact Outcomes and Maximum Spreading of Drop Impact on Heated Nanostructures Using Machine Learning. Langmuir 2023, 39, 18327–18341. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Hou, Y.; Shang, Y.; Zhong, X. BPNN and CNN-Based AI Modeling of Spreading and Icing Pattern of a Water Droplet Impact on a Supercooled Surface. AIP Adv. 2022, 12, 45209. [Google Scholar] [CrossRef]
- Yee, J.; Igarashi, D.; Miyatake, S.; Tagawa, Y. Prediction of the Morphological Evolution of a Splashing Drop Using an Encoder-Decoder. Mach. Learn. Sci. Technol. 2023, 4, 25002. [Google Scholar] [CrossRef]
- Dickerson, A.K.; Alam, M.E.; Buckelew, J.; Boyum, N.; Turgut, D. Predictive Modeling of Drop Impact Force on Concave Targets. Phys. Fluids 2022, 34, 102112. [Google Scholar] [CrossRef]
- Može, M.; Jereb, S.; Lovšin, R.; Berce, J.; Zupančič, M.; Golobič, I. Dataset on Droplet Spreading and Rebound Behavior of Water and Viscous Water-Glycerol Mixtures on Superhydrophobic Surfaces with Laser-Made Channels. Data Br. 2025, 111697. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 2017, 4766–4775. [Google Scholar]
- Richard, D.; Clanet, C.; Quéré, D. Contact Time of a Bouncing Drop. Nature 2002, 417, 811. [Google Scholar] [CrossRef]
- Goldstein, A.; Kapelner, A.; Bleich, J.; Pitkin, E. Peeking Inside the Black Box: Visualizing Statistical Learning with Plots of Individual Conditional Expectation. J. Comput. Graph. Stat. 2015, 24, 44–65. [Google Scholar] [CrossRef]
- Asai, A.; Shioya, M.; Hirasawa, S.; Okazaki, T. Impact of an Ink Drop on Paper. JIST 1993, 37, 205–207. [Google Scholar]
- Scheller, B.L.; Bousfield, D.W. Newtonian Drop Impact with a Solid Surface. AIChE J. 1995, 41, 1357–1367. [Google Scholar] [CrossRef]
- Roisman, I.V. Inertia Dominated Drop Collisions. II. An Analytical Solution of the Navier-Stokes Equations for a Spreading Viscous Film. Phys. Fluids 2009, 21, 52104. [Google Scholar] [CrossRef]
- Andrade, R.; Skurtys, O.; Osorio, F. Experimental Study of Drop Impacts and Spreading on Epicarps: Effect of Fluid Properties. J. Food Eng. 2012, 109, 430–437. [Google Scholar] [CrossRef]
- Chandra, S.; Avedisian, C.T. On the Collision of a Droplet with a Solid Surface. Proc. R. Soc. A Math. Phys. Eng. Sci. 1991, 432, 13–41. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Qiao, Y.M.; Chandra, S.; Mostaghimi, J. Capillary Effects during Droplet Impact on a Solid Surface. Phys. Fluids 1996, 8, 650–659. [Google Scholar] [CrossRef]
- Mao, T.; Kuhn, D.C.S.; Tran, H. Spread and Rebound of Liquid Droplets upon Impact on Flat Surfaces. AIChE J. 1997, 4, 2169–2179. [Google Scholar] [CrossRef]
- Aksoy, Y.T.; Eneren, P.; Koos, E.; Vetrano, M.R. Spreading of a Droplet Impacting on a Smooth Flat Surface: How Liquid Viscosity Influences the Maximum Spreading Time. Phys. Fluids 2022, 34, 042106. [Google Scholar] [CrossRef]
- Zhang, X.; Li, K.; Liu, X.; Wu, X.; Song, Q.; Min, J.; Ji, B.; Wang, S.; Zhao, J. Droplet Impact Dynamics on Different Wettable Surfaces at Moderate Weber Numbers. Colloids Surfaces A Physicochem. Eng. Asp. 2024, 695, 134250. [Google Scholar] [CrossRef]
- Gauthier, A.; Symon, S.; Clanet, C.; Quéré, D. Water Impacting on Superhydrophobic Macrotextures. Nat. Commun. 2015, 6, 8001. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.; Min, J. Maximum Spreading of Droplets Impacting Spherical Surfaces. Phys. Fluids 2019, 31, 92102. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.; Yang, Y.; Wang, X. Impact Dynamics of a Droplet on Superhydrophobic Cylinders Structured with a Macro Ridge. Langmuir 2023, 39, 6375–6386. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Liu, Q.; Lin, Z. Dynamical Behavior of Droplets Transiently Impacting on Superhydrophobic Microstructures. Phys. Fluids 2020, 32, 103304. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Yi, X.; He, F.; Niu, F.; Hao, P. Effect of Wettability on Droplet Impact: Spreading and Splashing. Exp. Therm. Fluid Sci. 2021, 124, 110369. [Google Scholar] [CrossRef]
- Jha, A.; Chantelot, P.; Clanet, C.; Quéré, D. Viscous Bouncing. Soft Matter 2020, 16, 7270–7273. [Google Scholar] [CrossRef]
- Zhao, S.; Ma, Z.; Song, M.; Tan, L.; Zhao, H.; Ren, L. Golden Section Criterion to Achieve Droplet Trampoline Effect on Metal-Based Superhydrophobic Surface. Nat. Commun. 2023, 14, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Sun, L.; Mehrizi, A.A.; Lin, S.; Guo, J.; Chen, L. Successive Rebounds of Impinging Water Droplets on Superhydrophobic Surfaces. Langmuir 2022, 38, 3860–3867. [Google Scholar] [CrossRef]
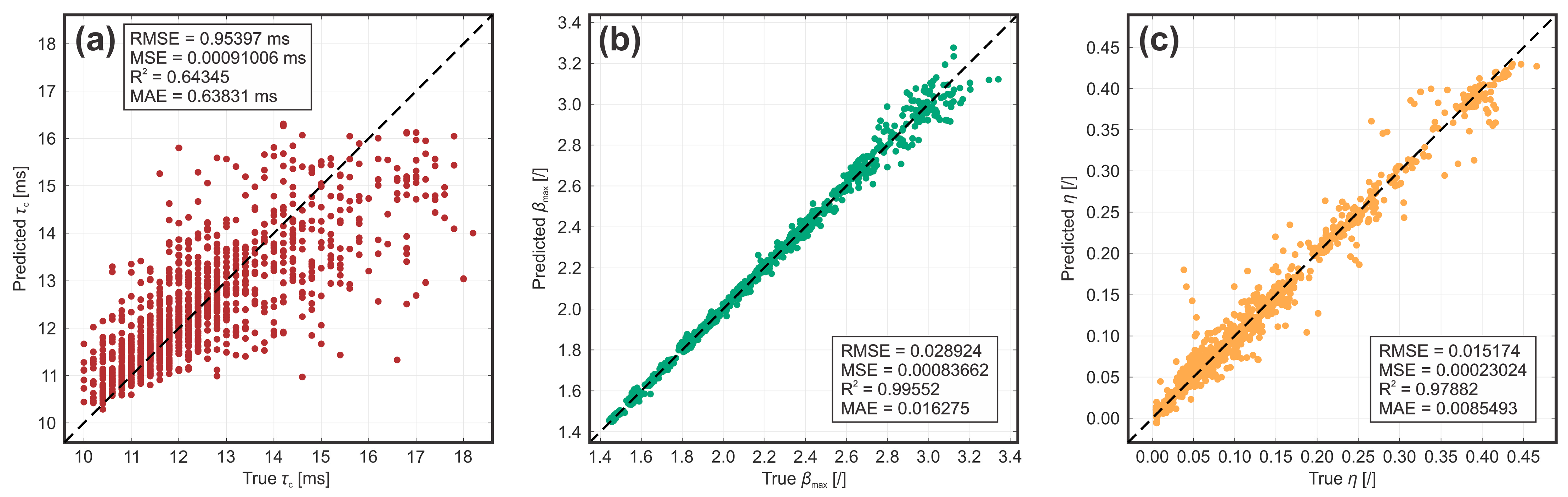
| Predicted Parameter | RMSE | MSE | R2 | MAE |
|---|---|---|---|---|
| Rebound efficiency | 0.017097 | 0.000292 | 0.9731 | 0.01051 |
| Maximum spreading coefficient | 0.037139 | 0.001379 | 0.9926 | 0.02082 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jereb, S.; Berce, J.; Lovšin, R.; Zupančič, M.; Može, M.; Golobič, I. Investigation of Droplet Spreading and Rebound Dynamics on Superhydrophobic Surfaces Using Machine Learning. Biomimetics 2025, 10, 357. https://doi.org/10.3390/biomimetics10060357
Jereb S, Berce J, Lovšin R, Zupančič M, Može M, Golobič I. Investigation of Droplet Spreading and Rebound Dynamics on Superhydrophobic Surfaces Using Machine Learning. Biomimetics. 2025; 10(6):357. https://doi.org/10.3390/biomimetics10060357
Chicago/Turabian StyleJereb, Samo, Jure Berce, Robert Lovšin, Matevž Zupančič, Matic Može, and Iztok Golobič. 2025. "Investigation of Droplet Spreading and Rebound Dynamics on Superhydrophobic Surfaces Using Machine Learning" Biomimetics 10, no. 6: 357. https://doi.org/10.3390/biomimetics10060357
APA StyleJereb, S., Berce, J., Lovšin, R., Zupančič, M., Može, M., & Golobič, I. (2025). Investigation of Droplet Spreading and Rebound Dynamics on Superhydrophobic Surfaces Using Machine Learning. Biomimetics, 10(6), 357. https://doi.org/10.3390/biomimetics10060357








